RF-SML: A SAR-Based Multi-Granular and Real-Time Localization Method for RFID Tags
Abstract
:1. Introduction
2. Background
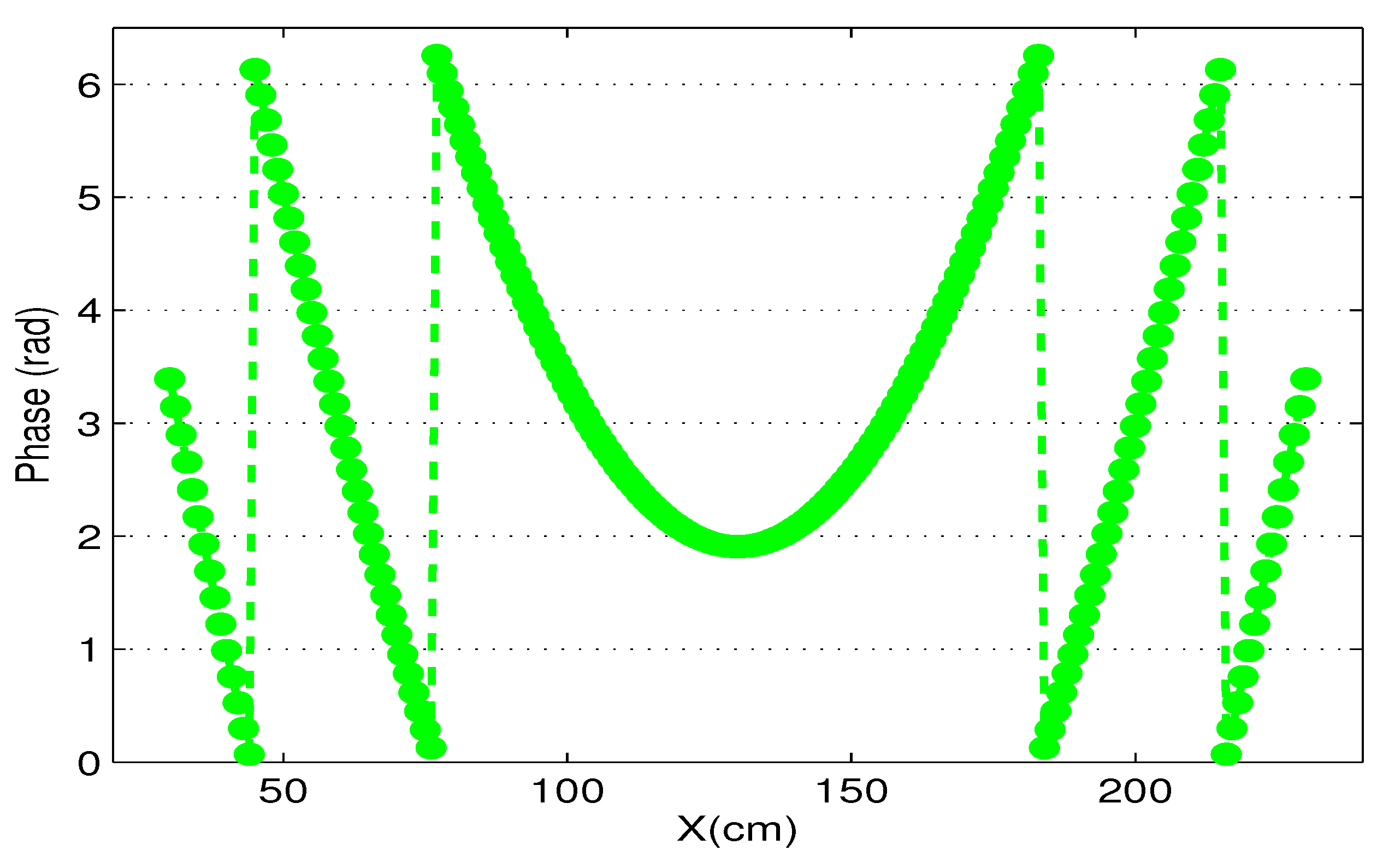
2.1. UHF-RFID Phase Model
2.2. UHF-RFID RSSI Model
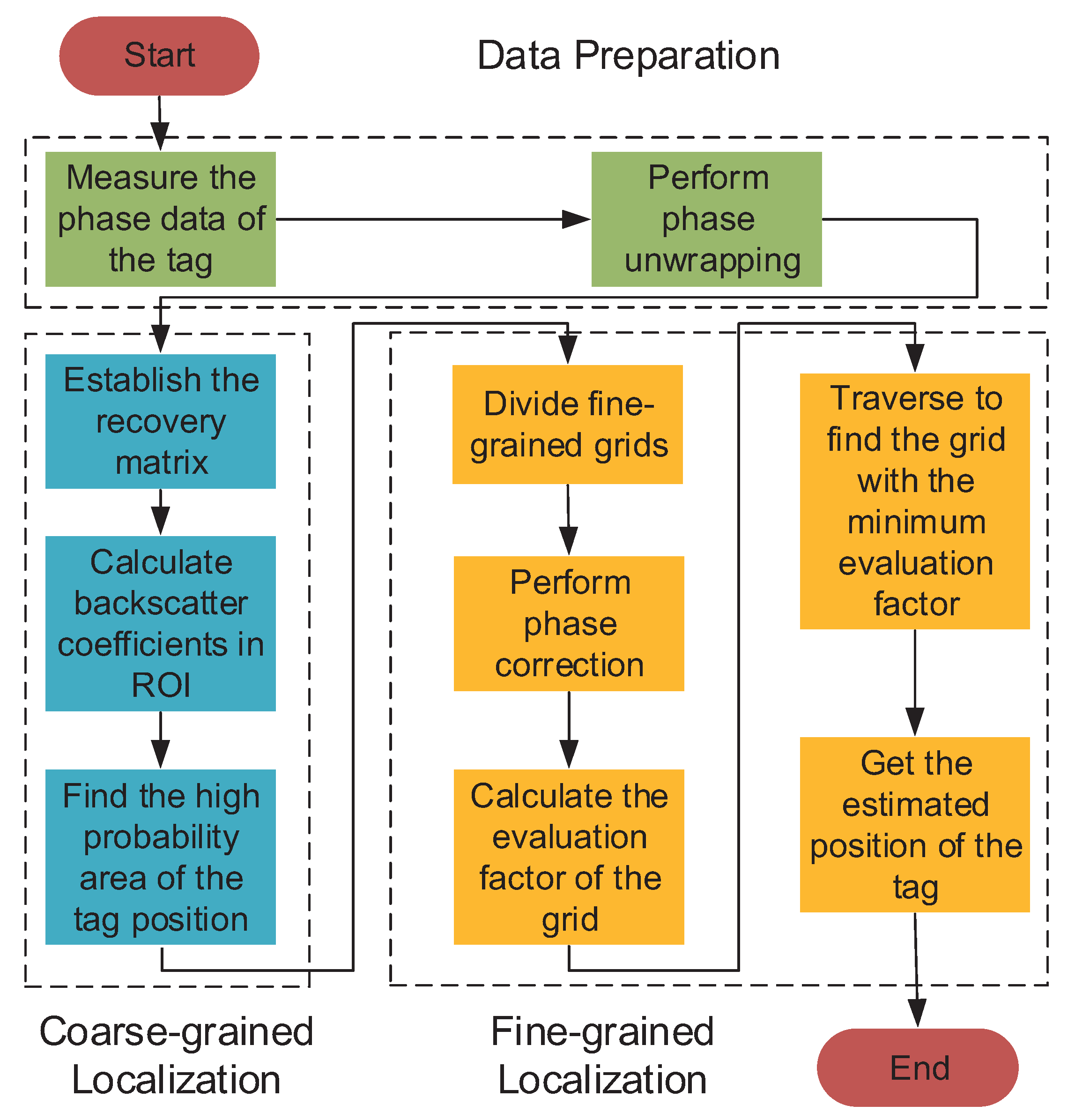
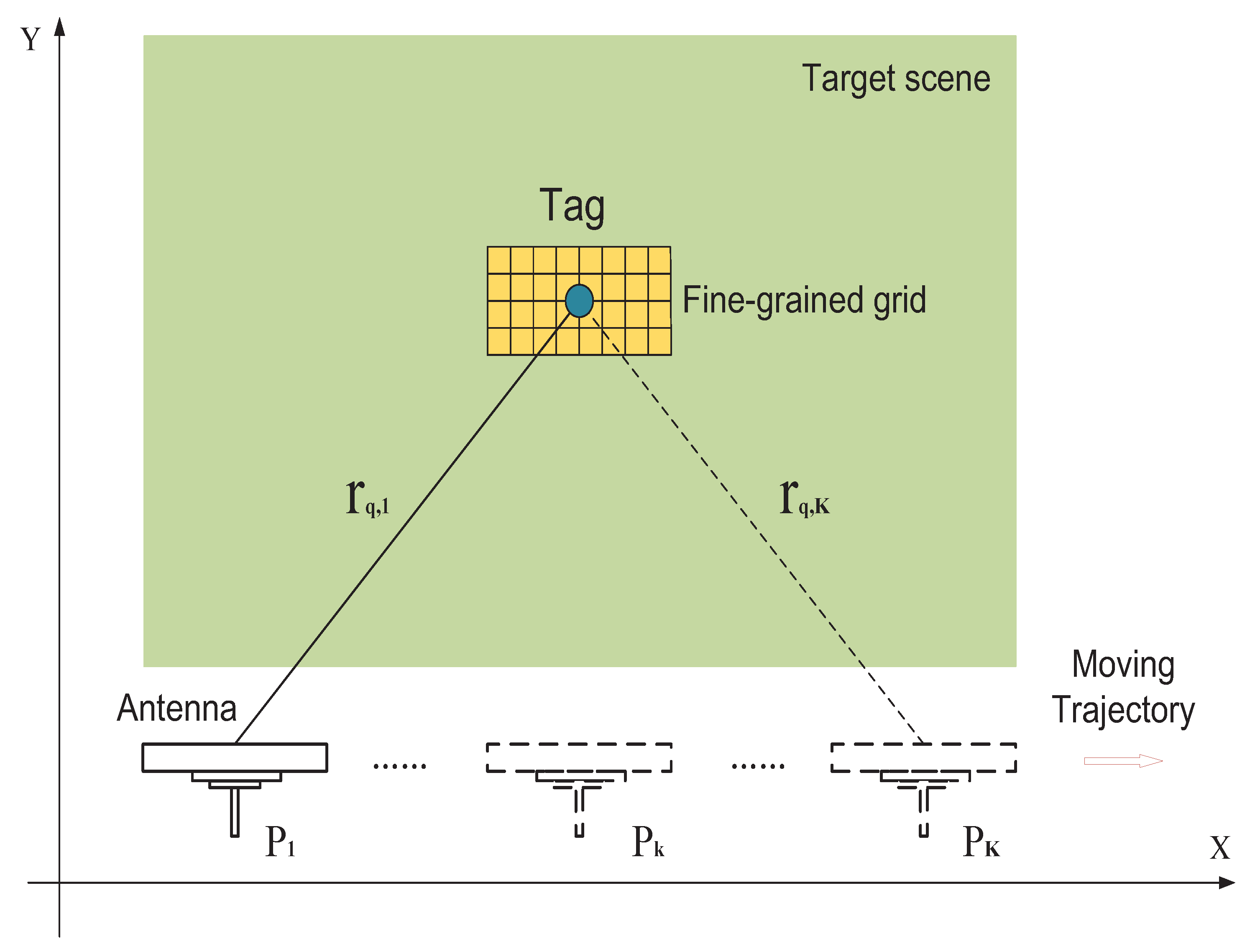
3. RF-SML Localization Methodology and Model
3.1. Basic Method of RF-SML
3.2. Localization with Phase Correction
3.2.1. Correction with Phase Unwrapping
3.2.2. Correction for the Phase Offset of Hardware Devices
3.2.3. Correction for the Phase Offset of the Phase Center
4. Measurement and Performance Analysis
4.1. Experimental Setup
4.2. Analysis of Affecting Factor Parameters
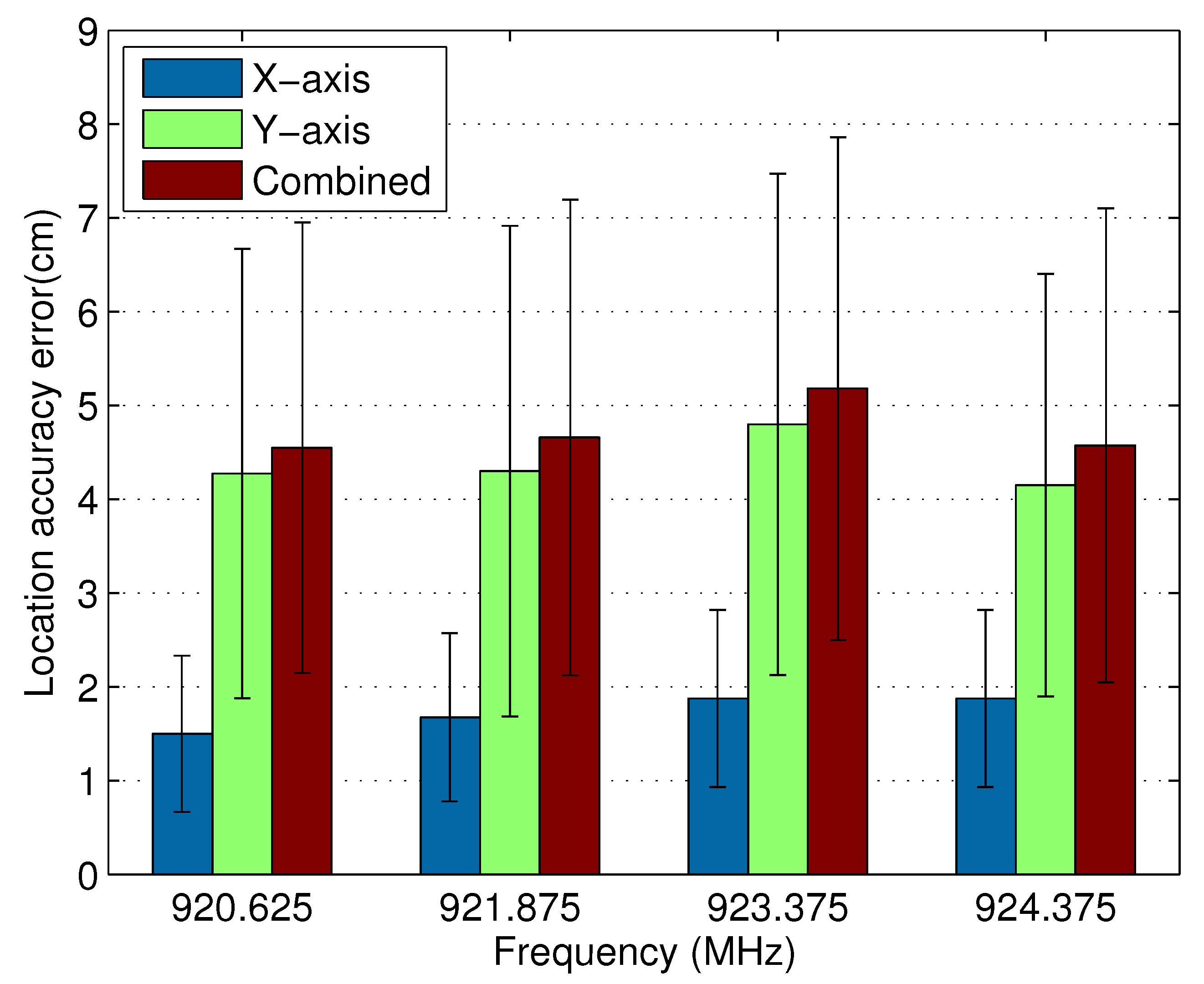
4.2.1. The Impact of Carrier Frequency
4.2.2. The Impact of Sampling Interval
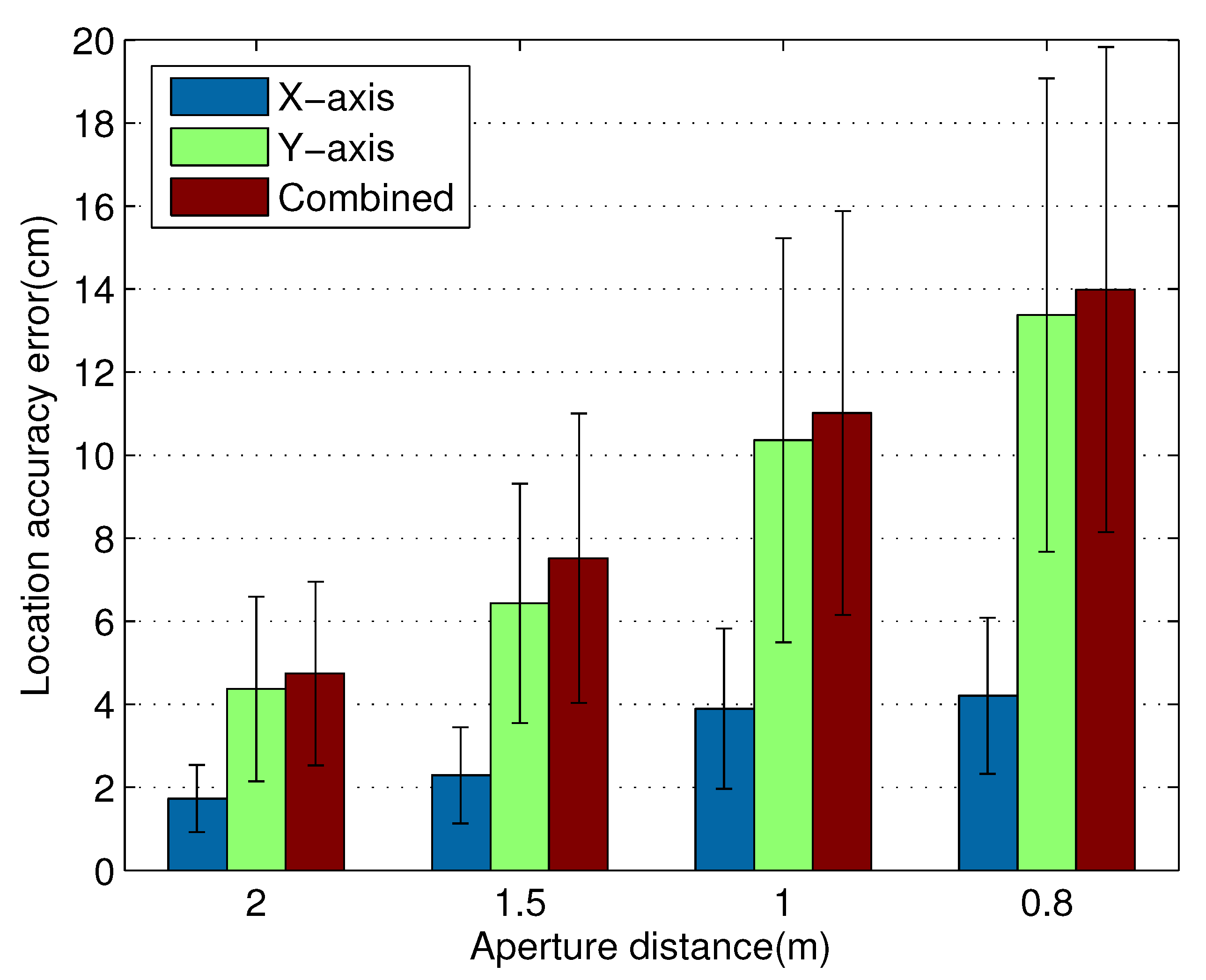
4.2.3. The Impact of Reader Antenna Movement Distance
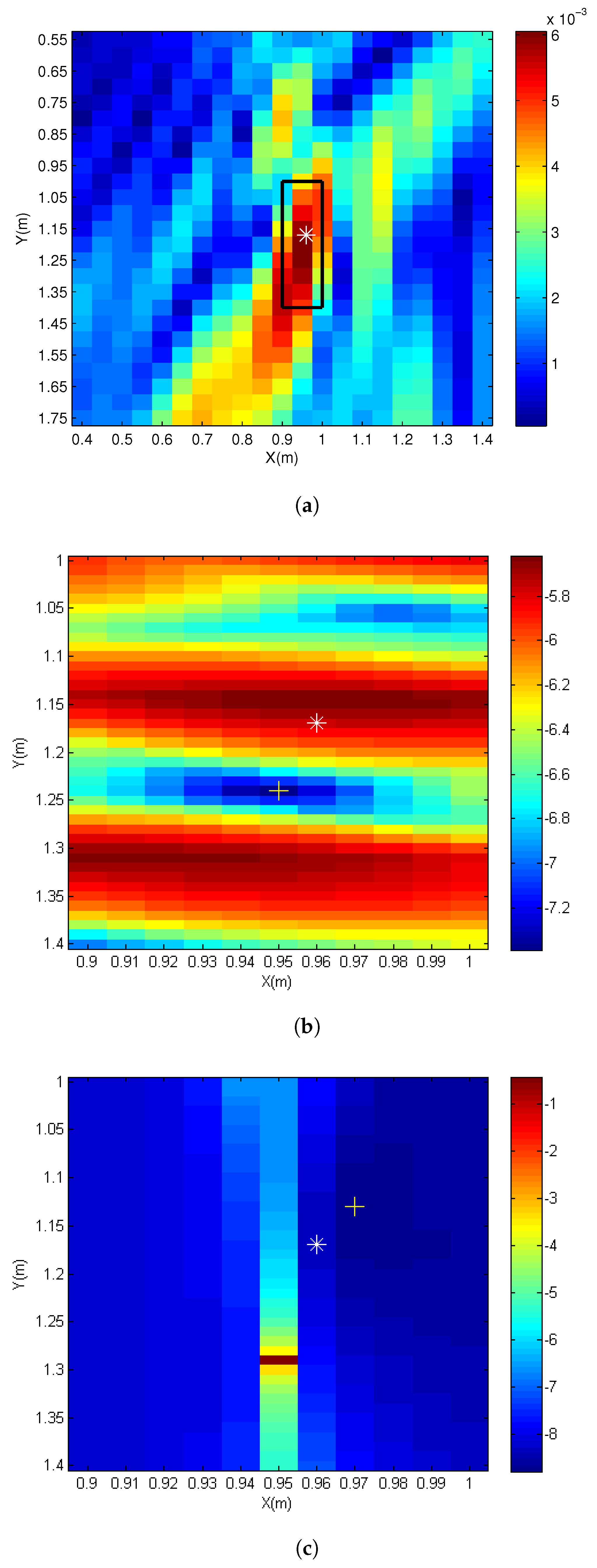
4.3. Performance of RF-SML
4.3.1. Localization Accuracy
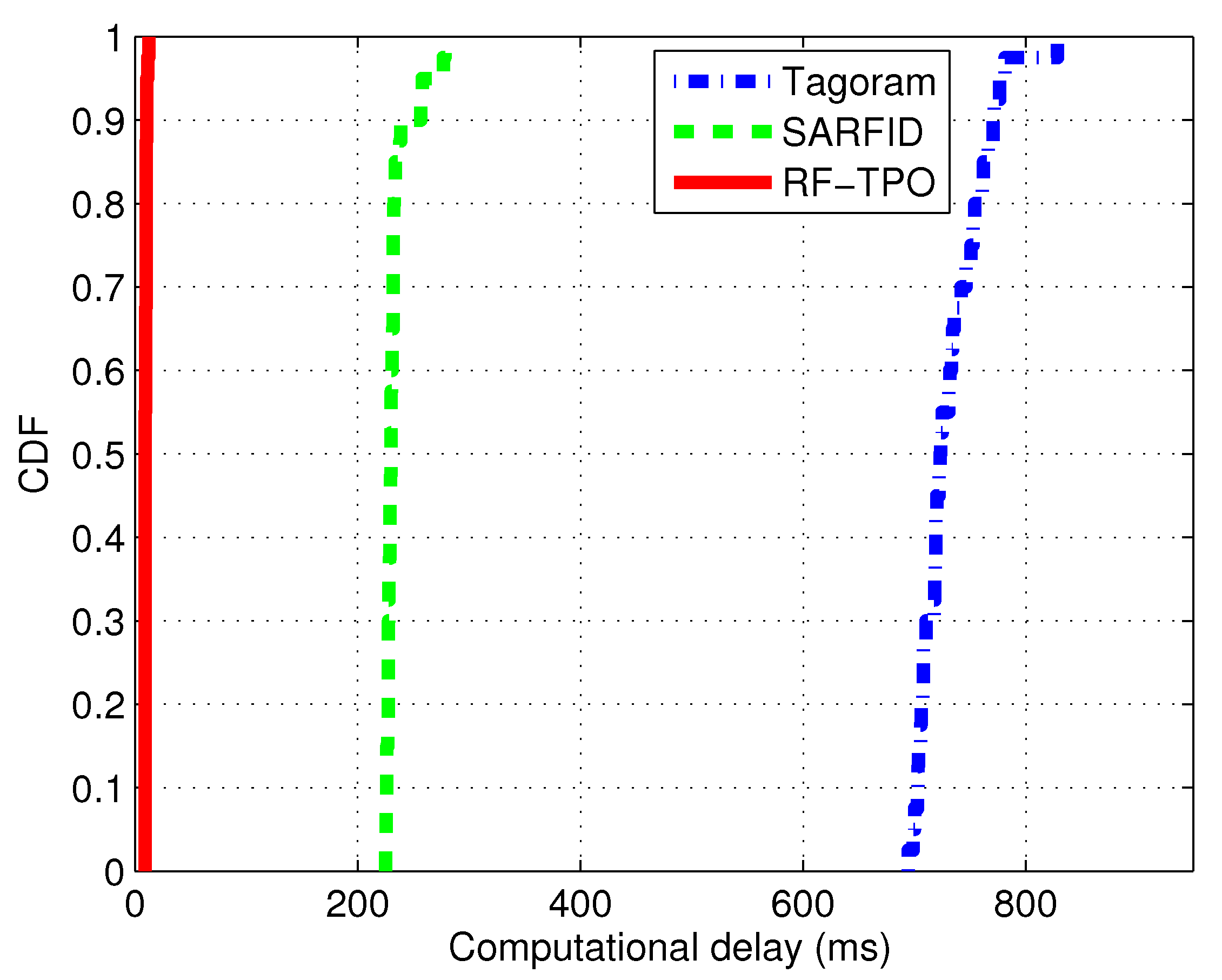
4.3.2. Computational Latency
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| IoT | Internet of Things |
| UHF | Ultra-High Frequency |
| RFID | Radio Frequency Identification |
| COTS | Commercial-Off-The-Shelf |
| RSSI | Received Signal Strength Indicator |
| ToA | Time of Arrival |
| TDoA | Time Difference of Arrival |
| PDoA | Phase difference of arrival |
| AoA | Angle of arrival |
| SAR | Synthetic Aperture Radar |
| ISAR | Inverse Synthetic Aperture Radar |
| NLOS | Non-Line-of-Sight |
| LOS | Line-of-Sight |
| CDF | Cumulative Distribution Function |
References
- Kuutti, S.; Fallah, S.; Katsaros, K.; Dianati, M.; Mccullough, F.; Mouzakitis, A. A Survey of the State-of-the-Art Localization Techniques and Their Potentials for Autonomous Vehicle Applications. IEEE Internet Things J. 2018, 5, 829–846. [Google Scholar] [CrossRef]
- Park, J.; Kim, Y.J.; Lee, B.K. Passive Radio-Frequency Identification Tag-Based Indoor Localization in Multi-Stacking Racks for Warehousing. Appl. Sci. 2020, 10, 3623. [Google Scholar] [CrossRef]
- Ma, L.; Liu, M.; Wang, H.; Yang, Y.; Wang, N.; Zhang, Y. WallSense: Device-Free Indoor Localization Using Wall-Mounted UHF RFID Tags. Sensors 2018, 19, 68. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ma, Y.; Wang, B.; Gao, X.; Ning, W. The Gray Analysis and Machine Learning for Device-Free Multitarget Localization in Passive UHF RFID Environments. IEEE Trans. Ind. Inform. 2020, 16, 802–813. [Google Scholar] [CrossRef]
- Ma, Y.; Song, L.; Zhao, Y.; Liu, K. A tight outer bound of the degrees of freedom for the MIMO interference channel with the delayed CSIT and partial local feedback. J. Frankl. Inst. 2015, 352, 291–310. [Google Scholar] [CrossRef]
- Ma, Y.; Tian, C.; Jiang, Y. A Multitag Cooperative Localization Algorithm Based on Weighted Multidimensional Scaling for Passive UHF RFID. IEEE Internet Things J. 2019, 6, 6548–6555. [Google Scholar] [CrossRef]
- El-Absi, M.; Zheng, F.; Abuelhaija, A.; Abbas, A.H.; Kaiser, T. Indoor Large-Scale MIMO-Based RSSI Localization with Low-Complexity RFID Infrastructure. Sensors 2020, 20, 3933. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Xiong, H.; Ding, H.; Zheng, L. TDOA-Based Joint Synchronization and Localization Algorithm for Asynchronous Wireless Sensor Networks. IEEE Trans. Commun. 2020, 68, 3107–3124. [Google Scholar] [CrossRef]
- Geng, C.; Yuan, X.; Huang, H. Exploiting Channel Correlations for NLOS ToA Localization with Multivariate Gaussian Mixture Models. IEEE Wirel. Commun. Lett. 2020, 9, 70–73. [Google Scholar] [CrossRef]
- Scherhäufl, M.; Pichler, M.; Stelzer, A. Robust localization of passive UHF RFID tag arrays based on phase-difference-of-arrival evaluation. In Proceedings of the IEEE Topical Conference on Wireless Sensors and Sensor Networks (WiSNet), San Diego, CA, USA, 25–28 January 2015; pp. 47–49. [Google Scholar]
- Zheng, Y.; Sheng, M.; Liu, J.; Li, J. Exploiting AoA Estimation Accuracy for Indoor Localization: A Weighted AoA-Based Approach. IEEE Wirel. Commun. Lett. 2019, 8, 65–68. [Google Scholar] [CrossRef]
- Wang, Y.; Ho, K.C. Unified Near-Field and Far-Field Localization for AOA and Hybrid AOA-TDOA Positionings. IEEE Trans. Wireless Commun. 2018, 17, 1242–1254. [Google Scholar] [CrossRef]
- Wu, X.; Deng, F.; Chen, Z. RFID 3D-LANDMARC Localization Algorithm Based on Quantum Particle Swarm Optimization. Electronics 2018, 7, 19. [Google Scholar]
- Shi, W.; Du, J.; Cao, X.; Yu, Y.; Cao, Y.; Yan, S.; Ni, C. IKULDAS: An Improved kNN-Based UHF RFID Indoor Localization Algorithm for Directional Radiation Scenario. Sensors 2019, 19, 968. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, M.; Ma, L.; Wang, N.; Zhang, Y.; Yang, Y.; Wang, H. Passive Multiple Target Indoor Localization Based on Joint Interference Cancellation in an RFID System. Sensors 2019, 8, 426. [Google Scholar] [CrossRef] [Green Version]
- Zafari, F.; Gkelias, A.; Leung, K.K. A Survey of Indoor Localization Systems and Technologies. IEEE Commun. Surv. Tutor. 2019, 21, 2568–2599. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Zhang, Z.; Gao, N.; Xiao, Y.; Meng, Z.; Li, Z. Cost-Effective Wearable Indoor Localization and Motion Analysis via the Integration of UWB and IMU. Sensors 2020, 20, 344. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.; Gao, Z.; Zhao, Y. RFID Indoor Localization Techniques. In Positioning and Navigation in Complex Environments; Yu, K., Ed.; IGI Global: Hershey, PA, USA, 2018; pp. 142–192. [Google Scholar]
- Mulloni, V.; Donelli, M. Chipless RFID Sensors for the Internet of Things: Challenges and Opportunities. Sensors 2020, 20, 2135. [Google Scholar] [CrossRef] [Green Version]
- Fu, X.; Pedross-Engel, A.; Arnitz, D.; Watts, C.M.; Sharma, A.; Reynolds, M.S. Simultaneous Imaging, Sensor Tag Localization, and Backscatter Uplink via Synthetic Aperture Radar. IEEE Trans. Microw. Theory Tech. 2018, 66, 1570–1578. [Google Scholar] [CrossRef]
- Miesen, R.; Kirsch, F.; Vossiek, M. UHF RFID Localization Based on Synthetic Apertures. IEEE Trans. Autom. Sci. Eng. 2013, 10, 807–815. [Google Scholar] [CrossRef]
- Buffi, A.; Motroni, A.; Nepa, P.; Tellini, B.; Cioni, R. A SAR-Based Measurement Method for Passive-Tag Positioning with a Flying UHF-RFID Reader. IEEE Trans. Instrum. Meas. 2019, 68, 845–853. [Google Scholar] [CrossRef]
- Shangguan, L.; Jamieson, K. The Design and Implementation of a Mobile RFID Tag Sorting Robot. In Proceedings of the 14th Annual International Conference on Mobile Systems, Applications, and Services (MOBISYS), Singapore, 26–30 June 2016; pp. 31–42. [Google Scholar]
- Parr, A.; Miesen, R.; Vossiek, M. Inverse SAR approach for localization of moving RFID tags. In Proceedings of the IEEE International Conference on RFID (RFID), Orlando, FL, USA, 30 April–2 May 2013; pp. 104–109. [Google Scholar]
- Scherhäufl, M.; Pichler, M.; Stelzer, A. Localization of passive UHF RFID tags based on inverse synthetic apertures. In Proceedings of the IEEE International Conference on RFID (RFID), Orlando, FL, USA, 8–10 April 2014; pp. 82–88. [Google Scholar]
- Yang, L.; Chen, Y.; Li, X.; Xiao, C.; Li, M.; Liu, Y. Tagoram: Real-Time Tracking of Mobile RFID Tags to High Precision Using COTS Devices. In Proceedings of the 20th Annual International Conference on Mobile Computing and Networking (MOBICOM), Maui, HI, USA, 7–11 September 2014; pp. 237–248. [Google Scholar]
- Buffi, A.; Nepa, P.; Lombardini, F. A Phase-Based Technique for Localization of UHF-RFID Tags Moving on a Conveyor Belt: Performance Analysis and Test-Case Measurements. IEEE Sens. J. 2015, 15, 387–396. [Google Scholar] [CrossRef]
- Duan, C.; Yang, L.; Lin, Q.; Liu, Y. Tagspin: High Accuracy Spatial Calibration of RFID Antennas via Spinning Tags. IEEE Trans. Mob. Comput. 2018, 17, 2438–2451. [Google Scholar] [CrossRef]
- Shen, L.; Zhang, Q.; Pang, J.; Xu, H.; Xue, D. ANTspin: Efficient Absolute Localization Method of RFID Tags via Spinning Antenna. Sensors 2019, 19, 2194. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, J.; Katabi, D. Dude, Where’s My Card? RFID Positioning That Works with Multipath and Non-Line of Sight. ACM SIGCOMM Comput. Commun. Rev. 2013, 43, 51–62. [Google Scholar] [CrossRef]
- Bu, Y.; Xie, L.; Gong, Y.; Liu, J.; He, B.; Cao, J.; Ye, B.; Lu, S. RF-3DScan: RFID-based 3D Reconstruction on Tagged Packages. IEEE Trans. Mob. Comput. 2019. [Google Scholar] [CrossRef]
- Fu, Y.; Wang, C.; Liu, R.; Liang, G.; Zhang, H.; Ur Rehman, S. Moving Object Localization Based on UHF RFID Phase and Laser Clustering. Sensors 2018, 18, 825. [Google Scholar] [CrossRef] [Green Version]
- Rehman, S.U.; Liu, R.; Zhang, H.; Liang, G.; Qayoom, A. Localization of Moving Objects Based on RFID Tag Array and Laser Ranging Information. Electronics 2019, 8, 887. [Google Scholar] [CrossRef] [Green Version]
- Zhao, R.; Zhang, Q.; Li, D.; Chen, H.; Wang, D. A novel accurate synthetic aperture RFID localization method with high radial accuracy. In Proceedings of the IEEE 18th International Symposium on a World of Wireless, Mobile and Multimedia Networks (WoWMoM), Macau, China, 12–15 June 2017; pp. 1–9. [Google Scholar]
- Parr, A.; Miesen, R.; Vossiek, M. Comparison of Phase-Based 3D Near-Field Source Localization Techniques for UHF RFID. Sensors 2016, 16, 978. [Google Scholar] [CrossRef] [Green Version]
- Buffi, A.; Pino, M.R.; Nepa, P. Experimental validation of a SAR-Based RFID localization technique exploiting an automated handling system. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 2795–2798. [Google Scholar] [CrossRef]
- Ma, Y.; Liu, H.; Zhang, Y.; Jiang, Y. The Influence of the Non-ideal Phase Offset on SAR-Based Localization in Passive UHF RFID. IEEE Trans. Antennas Propag. 2020. [Google Scholar] [CrossRef]
- Qiu, L.; Huang, Z.; Wirström, N.; Voigt, T. 3DinSAR: Object 3D localization for indoor RFID applications. In Proceedings of the IEEE International Conference on RFID (RFID), Orlando, FL, USA, 3–5 May 2016; pp. 1–8. [Google Scholar]
- Nikitin, P.V.; Martinez, R.; Ramamurthy, S.; Leland, H.; Spiess, G.; Rao, K.V.S. Phase based spatial identification of UHF RFID tags. In Proceedings of the IEEE International Conference on RFID (RFID), Orlando, FL, USA, 14–16 April 2010; pp. 102–109. [Google Scholar]







© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Y.; Ma, Y.; Liu, H.; Zhang, Y. RF-SML: A SAR-Based Multi-Granular and Real-Time Localization Method for RFID Tags. Electronics 2020, 9, 1447. https://doi.org/10.3390/electronics9091447
Jiang Y, Ma Y, Liu H, Zhang Y. RF-SML: A SAR-Based Multi-Granular and Real-Time Localization Method for RFID Tags. Electronics. 2020; 9(9):1447. https://doi.org/10.3390/electronics9091447
Chicago/Turabian StyleJiang, Yue, Yongtao Ma, Hankai Liu, and Yunlei Zhang. 2020. "RF-SML: A SAR-Based Multi-Granular and Real-Time Localization Method for RFID Tags" Electronics 9, no. 9: 1447. https://doi.org/10.3390/electronics9091447
APA StyleJiang, Y., Ma, Y., Liu, H., & Zhang, Y. (2020). RF-SML: A SAR-Based Multi-Granular and Real-Time Localization Method for RFID Tags. Electronics, 9(9), 1447. https://doi.org/10.3390/electronics9091447




