Approaching the Optimal Solution of the Maximal α-quasi-clique Local Community Problem
Abstract
1. Introduction
2. Main Definitions and Notations
The Maximal quasi-clique Local Community Problem
- the first one, introduced in [10] and later improved by [11], is called RANK-NUM-NEIGHS (RNN). It is a greedy and iterative algorithm. At first iteration, the local community is only composed of the starting node. Then, iteratively some nodes are chosen from the neighborhood to enlarge the community. The choice of nodes is based on the number of common neighbors the nodes have with the community provided that the satisfy the rule.
- The last one was given in [20], where the authors studied what they called the query-driven maximum quasi-clique (QMQ) search. A method that aims to find the largest -quasi-clique containing a given set of nodes. Their proposal is based on the notion of core tree to organize dense subgraphs recursively.
- In a telecommunication network, where each node represents a person and there is an edge between two nodes if and only if they exchanged a phone call. An application in anomaly detection is finding communities that are almost cliques. According to [21]: “Detecting nodes whose neighbors are very well connected (near-cliques) or not connected (stars) turn out to be strange: in most social networks, friends of friends are often friends, but either extreme (clique or star) is suspicious”.
- In biology is the clustering of protein-protein interaction (PPI) networks to detect functional groups. As discussed in [24] recently, experimental techniques have generated a large amount of protein–protein interaction (PPI) data.
- In social network analysis, as pointed out by [25], on real data the communities are far away from being highly dense. Therefore, the detection of quasi-clique can be much more appropriated than detection complete cliques.
- Furthermore, very recently, in [26], the approach based on cliques was used to analyze FIFA World Cup referees’ networks.
3. The Upper Bound
3.1. The Importance of Calculating an Upper Bound
3.2. Calculation of the Upper Bound
3.3. The Algorithm
- Part I: “Improvements”: described in Algorithm 1, it includes the definition of the first and second neighborhood graph of , ; the initialization of the upper bounds for all nodes in according to Theorem 2, along all the steps these values will be updated and saved in a table ; finally, the search of improvements in the values of bounds is iteratively performed until no improvement is detected using the function bound() described in Part II. There is an improvement if the bound of at least one node in has diminished.
| Algorithm 1 Part I: Iterative improvements in the bound calculation. |
| Require: The graph , a node and a parameter . |
| Ensure: An upper bound for the local -quasi-clique community size of node . |
| 1: Define the sub-graph . |
| 2: for each node v in do |
| 3: Set (according to Equation (3) in Theorem 2). |
| 4: end for |
| 5: while there is at least one improvement do |
| 6: for each node v in do |
| 7: if then |
| 8: |
| 9: There is an improvement |
| 10: end if |
| 11: end for |
| 12: end while |
| 13: return |
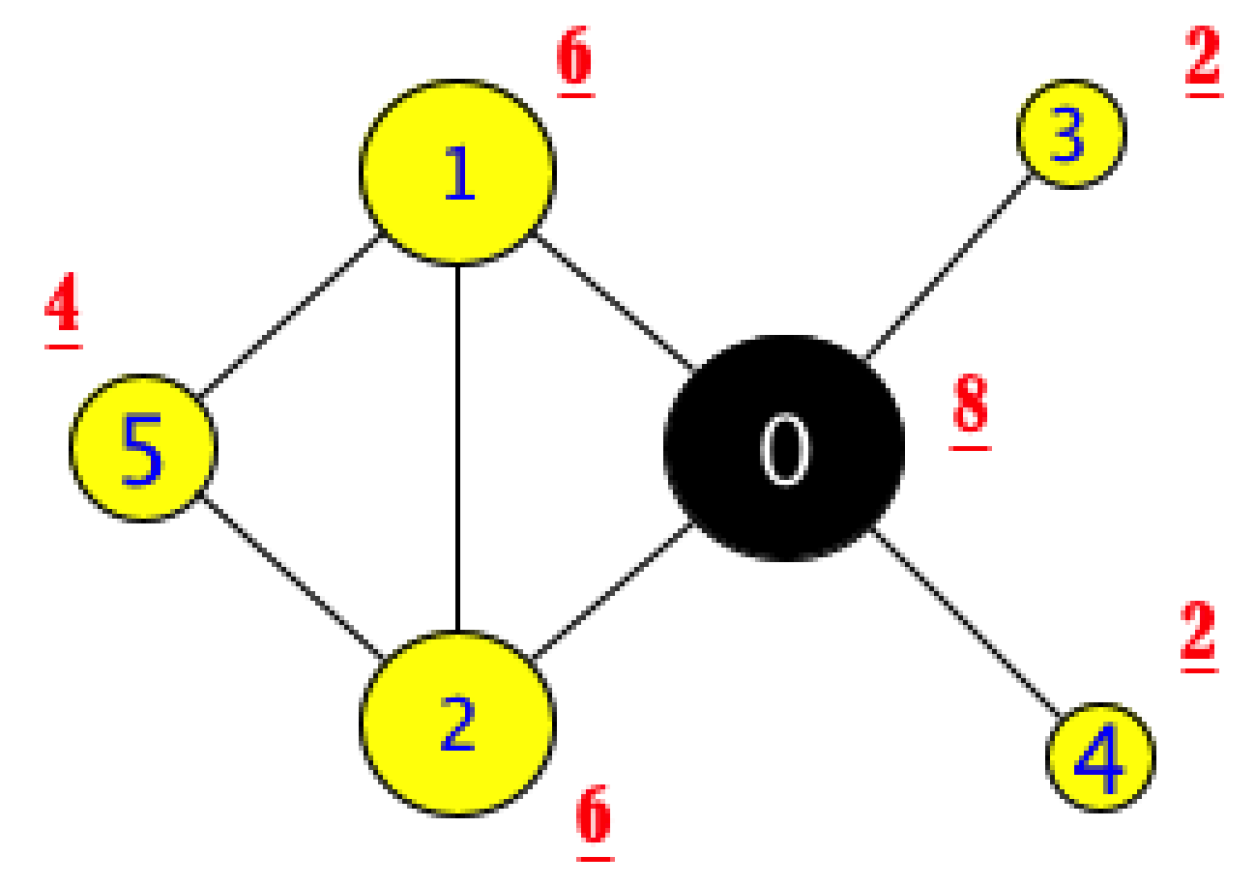
- Part II: thebound()function: described in Algorithm 2, this function calculates the bound for a given node per se taking into account the bounds of its neighbors. It takes four input parameters: the node , its neighborhood graph , the table of bounds and . First, a frequency distribution table of neighbors’ bounds is elaborated. These values are denoted and the associated frequency for i ranging from 1 to p, where p denotes the total number of different values of neighbor bounds (for instance, see Table 1 for the graph in Figure 3). Throughout the function, the bound of is denoted B and initially set to . At each iteration i, three values are updated: , , and :
- -
- is the remaining degree and corresponds to the degree (number of connections) of resulting from disregarding the neighbors having the bound smaller or equal to .
- -
- is a value of bound calculated using Theorem 2 and considering as input the remaining degree in Equation (3) instead of . That is:
- -
- is the number of neighbors that can satisfy the bound , that is, their bound is greater or equal to .
| Algorithm 2 The function bound(). |
| Require: A node , its neighborhood , the table of neighbors’ bounds and a parameter . |
| Ensure: An upper bound B for the local -quasi-clique community size of node . |
| 1: Calculate the frequency distribution of neighbors’ bounds , the resulting values |
| are denoted and the associated frequency (). |
| 2: // Initialize the iterations |
| 3: Set , , , and calculate (number of neighbors whose bound |
| is at least equal to ). |
| 4: whiledo |
| 5: i=i+1 |
| 6: Update and , calculate |
| 7: if then |
| 8: |
| 9: Break |
| 10: else |
| 11: |
| 12: end if |
| 13: end while |
| 14: returnB |
- , (after disregarding nodes 1, 2, and 3), , (nodes 10, 11 and 12). Since , then ; , then we iterate once more.
- , (after ignoring nodes 1, 2, 3, and 4), , and (nodes 10, 11 and 12). Because , then ; , we continue....
- , (after ignoring nodes 1, 2, 3, 4, 5, 6, 7, 8, and 9), , and (nodes 4, 5, 6, 7, 8, 9, 10, 11, and 12). Because , then and the algorithm exits the while loop following the break statement.
3.4. Complexity
- The calculation of the frequency table implies to sort the values of neighbors’ bounds and count the frequencies. This operation requires the necessary time to sort p values, since p is, at most, . Depending on the sorting algorithm in the worst case, this operation can perform in .
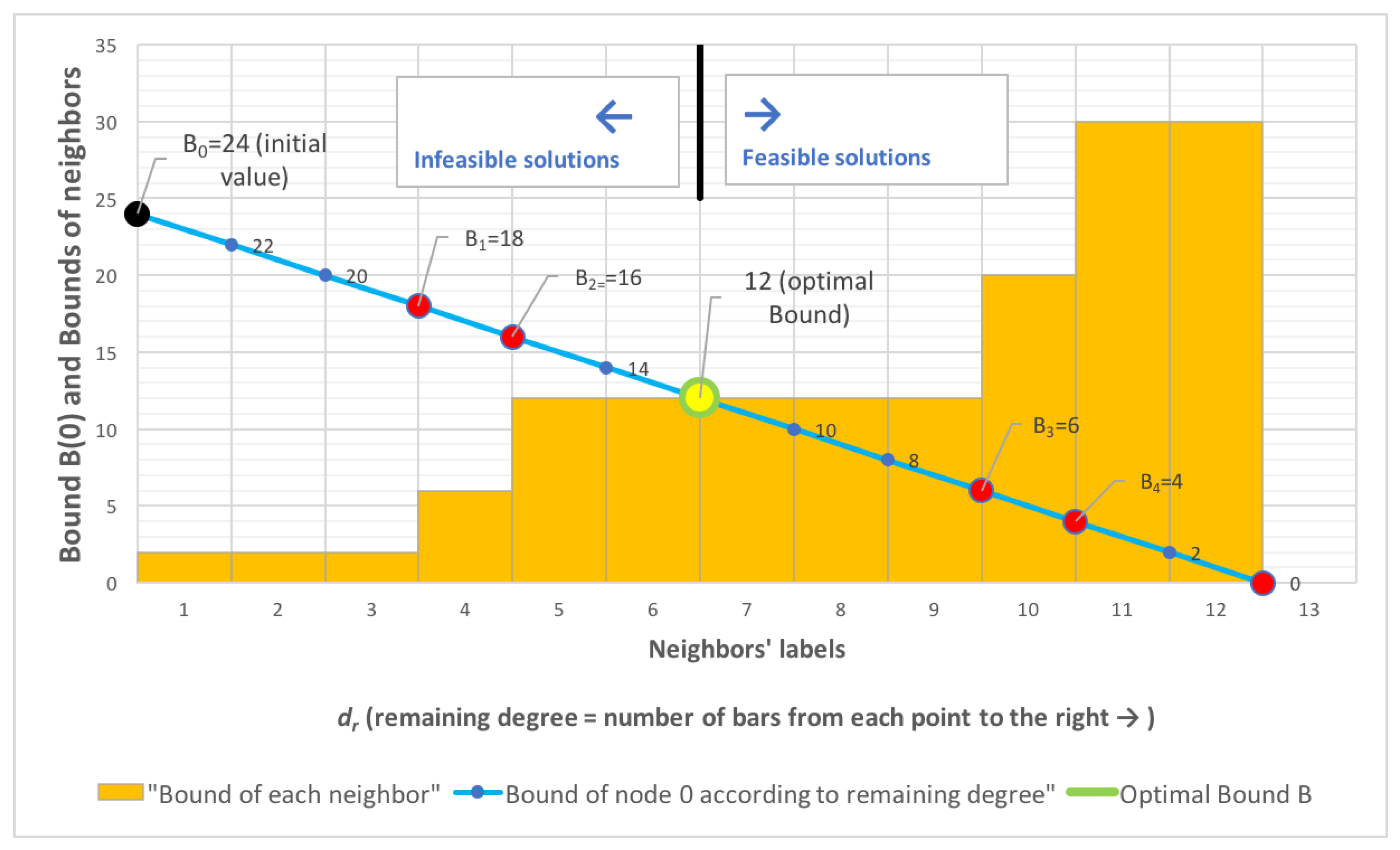
- The operations in the while loop (lines 4 to 13) to find the optimal value of bound can be executed using a binary search algorithm. Certainly, the purpose is to find a value in the frequency table of sorted neighbors’ bounds. Indeed, each row in the frequency table (see Table 1) corresponds to a step in the staircase bar chart diagram in Figure 4. The purpose is to determine the step (iteration) i, where the line intersects the bar chart. The values , and can be directly calculated from the frequency table. Given a step i with its corresponding value of , one of the following situations can take place:
- —
- implies block i is in the area of unfeasible solutions, then, the search must continue in the blocks corresponding to greater values of i (to the right following the blue line in the graphic).
- —
- implies the optimal bound is .
- —
- implies block i is in the area of feasible solutions. However, it is necessary to verify whether we are in the block of the maximal solution. If and only if , the optimal bound is ; otherwise, the search must continue in the blocks corresponding to smaller values of i (to the left following the blue line in the graphic).
- The definition of the first and second neighborhood graph which runs in . Indeed, the definition of the first neighborhood needs operations. Subsequently, to extract the second neighborhood, for each neighbor v, operations are needed.
- The calculation of the initial upper bound for all the nodes in using Equation (3) from Theorem 2 requires operations.
4. Experimental Results
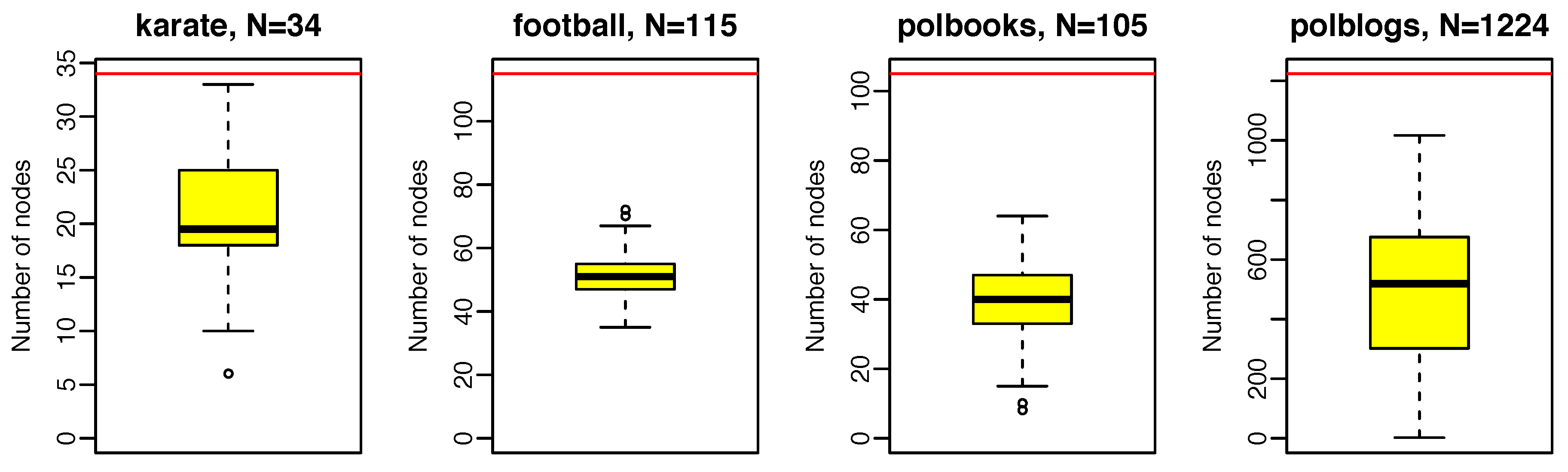
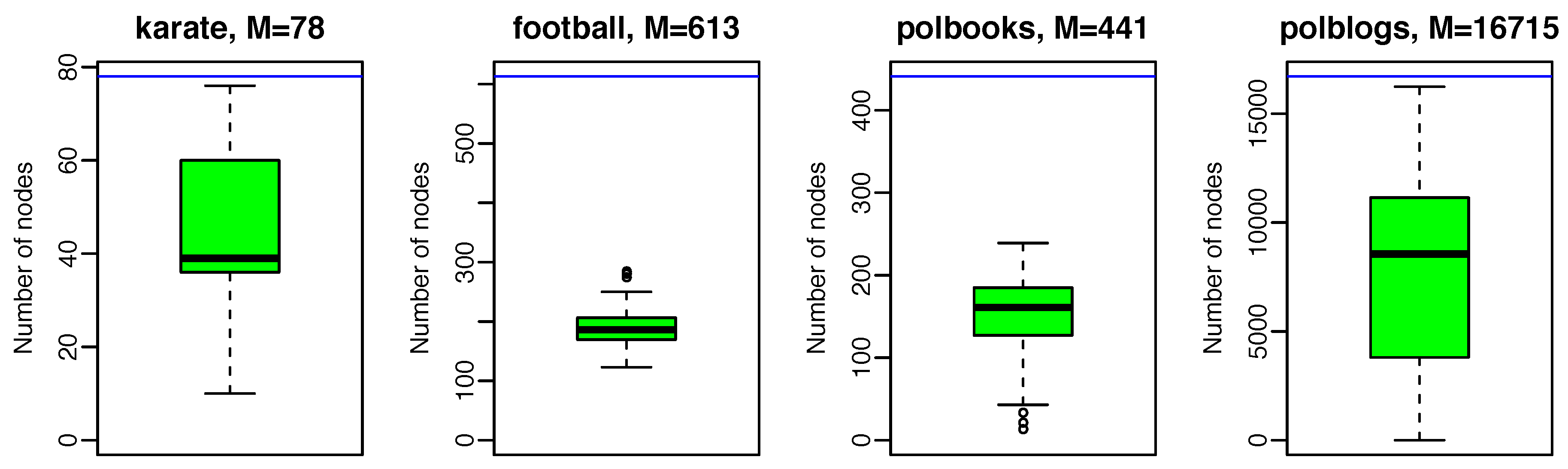
- “The Zachary Karate Club network” (karate) [30]: a network of members of a karate club at a US university in the 1970s, 34 nodes and 78 edges.
- “The American College football network” (football) [31]: a network of American football games between colleges during regular season Fall 2000, 115 nodes and 613 edges.
- “Books about US politics” (polbooks) [32]: a network of books about US politics published around the time of the 2004 presidential election and sold by the online bookseller Amazon.com. Edges between books represent frequent co-purchasing of books by the same buyers, 105 nodes and 441 edges.
- “Political blogs” (polblogs) [33]: a network of hyperlinks between weblogs on US politics, 1224 nodes and 16715 edges.
4.1. Evaluation of the Bound in a Small Real Network
4.2. Comparison of the Proposed Bound to the Baseline Version
4.3. Impact of the Iterative Improvements
5. Conclusions and Perspectives
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Fortunato, S. Community detection in graphs. Phys. Rep. 2010, 486, 75–174. [Google Scholar] [CrossRef]
- Bomze, I.M.; Budinich, M.; Pardalos, P.M.; Pelillo, M. The Maximum Clique Problem. In Handbook of Combinatorial Optimization; Kluwer Academic Publishers: New York, NY, USA, 1999; pp. 1–74. [Google Scholar]
- Lee, V.E.; Ruan, N.; Jin, R.; Aggarwal, C.C. A Survey of Algorithms for Dense Subgraph Discovery. In Managing and Mining Graph Data; Aggarwal, C.C., Wang, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 40, pp. 303–336. [Google Scholar]
- Pattillo, J.; Youssef, N.; Butenko, S. On clique relaxation models in network analysis. Eur. J. Oper. Res. 2013, 226, 9–18. [Google Scholar] [CrossRef]
- Wu, Q.; Hao, J.K. A review on algorithms for maximum clique problems. Eur. J. Oper. Res. 2015, 242, 693–709. [Google Scholar] [CrossRef]
- Newman, M.; Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E 2004, 69, 026113. [Google Scholar] [CrossRef] [PubMed]
- Fortunato, S.; Barthelemy, M. Resolution limit in community detection. Proc. Natl. Acad. Sci. USA 2006, 104, 36–41. [Google Scholar] [CrossRef] [PubMed]
- Karp, R.M. Reducibility Among Combinatorial Problems. In Complexity of Computer Computations; The IBM Research Symposia Series; Miller, R.E., Thatcher, J.W., Eds.; Plenum Press: New York, NY, USA, 1972; pp. 85–103. [Google Scholar]
- Asahiro, Y.; Hassin, R.; Iwama, K. Complexity of Finding Dense Subgraphs. Discret. Appl. Math. 2002, 121, 15–26. [Google Scholar] [CrossRef]
- Conde-Céspedes, P.; Ngonmang, B.; Viennet, E. Approximation of the Maximal α-Consensus Local Community detection problem in Complex Networks. In Proceedings of the IEEE SITIS 2015, Complex Networks and their Applications, Bangkok, Thailand, 23–27 November 2015. [Google Scholar]
- Conde-Céspedes, P.; Ngonmang, B.; Viennet, E. An efficient method for mining the Maximal alpha-quasi- clique-community of a given node in Complex Networks. Soc. Netw. Anal. Min. 2018, 8. [Google Scholar] [CrossRef]
- Conde-Céspedes, P. Local Community Detection of High Density: An Upper Bound for the Optimal Solution. Sens. Transducers 2019, 234, 37–43. [Google Scholar]
- Abello, J.; Resende, M.G.C.; Sudarsky, S. Massive Quasi-Clique Detection. In Proceedings of the 5th Latin American Symposium on Theoretical Informatics (LATIN ’02); Springer: London, UK, 2002; pp. 598–612. [Google Scholar]
- Chen, J.; Saad, Y. Dense Subgraph Extraction with Application to Community Detection. IEEE Trans. Knowl. Data Eng. 2012, 24, 1216–1230. [Google Scholar] [CrossRef]
- Pattillo, J.; Veremyev, A.; Butenko, S.; Boginski, V. On the maximum quasi-clique problem. Discret. Appl. Math. 2013, 161, 244–257. [Google Scholar] [CrossRef]
- Tsourakakis, C.; Bonchi, F.; Gionis, A.; Gullo, F.; Tsiarli, M. Denser Than the Densest Subgraph: Extracting Optimal Quasi-cliques with Quality Guarantees. In Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD ’13); ACM: New York, NY, USA, 2013; pp. 104–112. [Google Scholar]
- Brunato, M.; Hoos, H.H.; Battiti, R. On Effectively Finding Maximal Quasi-cliques in Graphs. In LION; Maniezzo, V., Battiti, R., Watson, J.P., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; Volume 5313, pp. 41–55. [Google Scholar]
- Liu, G.; Wong, L. Effective Pruning Techniques for Mining Quasi-Cliques. In Machine Learning and Knowledge Discovery in Databases; Daelemans, W., Goethals, B., Morik, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 5212, pp. 33–49. [Google Scholar]
- Chou, Y.H.; Wang, E.T.; Chen, A.L.P. Finding Maximal Quasi-cliques Containing a Target Vertex in a Graph. In DATA2015, Proceedings of 4th International Conference on Data Management Technologies and Applications—Volume 1: DATA; INSTICC, SciTePress: Setubal, Portugal, 2015; pp. 5–15. [Google Scholar] [CrossRef]
- Lee, P.; Lakshmanan, L.V.S. Query-Driven Maximum Quasi-Clique Search. In Proceedings of the 2016 SIAM International Conference on Data Mining (SDM); Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2016; pp. 522–530. [Google Scholar]
- Akoglu, L.; Mcglohon, M.; Faloutsos, C. Anomaly detection in large graphs. In CMU-CS-09-173 Technical Report; School of Computer Science, Carnegie Mellon University: Pittsburgh, PA, USA, 2009. [Google Scholar]
- Ben-Dor, A.; Shamir, R.; Yakhini, Z. Clustering gene expression patterns. J. Comput. Biol. 1999, 6, 281–297. [Google Scholar] [CrossRef] [PubMed]
- Tanay, A.; Sharan, R.; Shamir, R. Discovering Statistically Significant Biclusters in Gene Expression Data. Bioinformatics 2002, 18 (Suppl. 1), S136–S144. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Lin, H.; Yang, Z.; Wang, J. Construction of dynamic probabilistic protein interaction networks for protein complex identification. BMC Bioinform. 2016, 17, 186. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Leskovec, J. Overlapping Communities Explain Core-Periphery Organization of Networks; Technical Report; Stanford University: Stanford, CA, USA, 2014. [Google Scholar]
- De Sousa Fadigas, I.; Grilo, M.; Henrique, T.; de Barros Pereira, H.B. FIFA World Cup referees’ networks: A constant-size clique approach. Soc. Netw. Anal. Min. 2020, 10. [Google Scholar] [CrossRef]
- Matsuda, H.; Ishihara, T.; Hashimoto, A. Classifying molecular sequences using a linkage graph with their pairwise similarities. Theor. Comput. Sci. 1999, 210, 305–325. [Google Scholar] [CrossRef]
- Pei, J.; Jiang, D.; Zhang, A. On Mining Cross-graph Quasi-cliques. In Proceedings of the Eleventh ACM SIGKDD International Conference on Knowledge Discovery in Data Mining (KDD ’05), New York, NY, USA, 21–24 August 2005; pp. 228–238. [Google Scholar]
- Newman, M. Network data Site web. Available online: http://www-personal.umich.edu/~mejn/netdata/ (accessed on 30 June 2020).
- Zachary, W.W. An Information Flow Model for Conflict and Fission in Small Groups. J. Anthropol. Res. 1977, 33, 452–473. [Google Scholar] [CrossRef]
- Girvan, M.; Newman, M.E.J. Community structure in social and biological networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar] [CrossRef] [PubMed]
- Krebs, V. Books about US Politics. Available online: http://www-personal.umich.edu/~mejn/netdata/polblogs.zip (accessed on 30 June 2020).
- Adamic, L.A.; Glance, N. The Political Blogosphere and the 2004 U.S. Election. In Proceedings of the WWW-2005 Workshop on the Weblogging Ecosystem, New York, NY, USA, 21 August 2005; pp. 36–43. [Google Scholar]

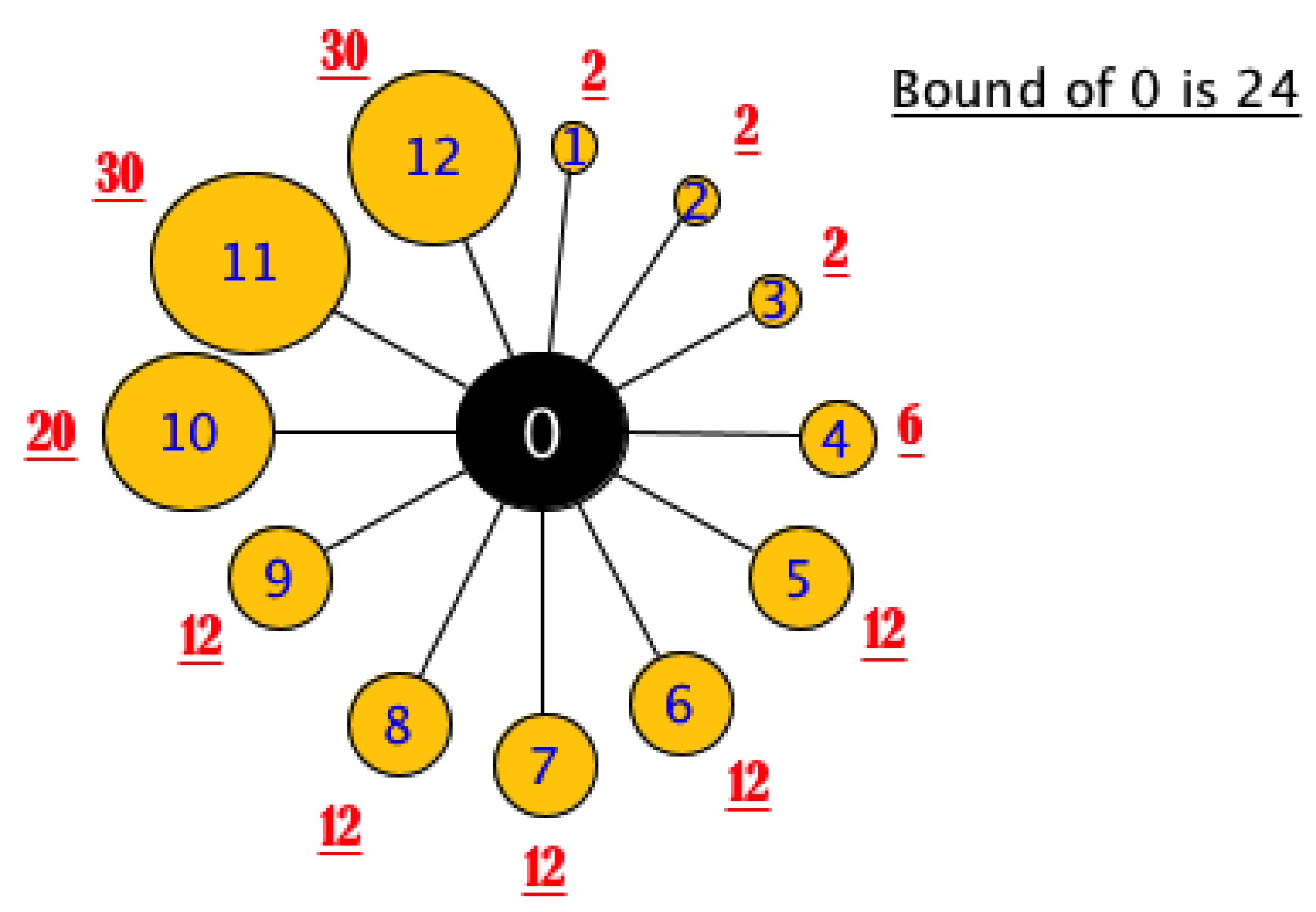
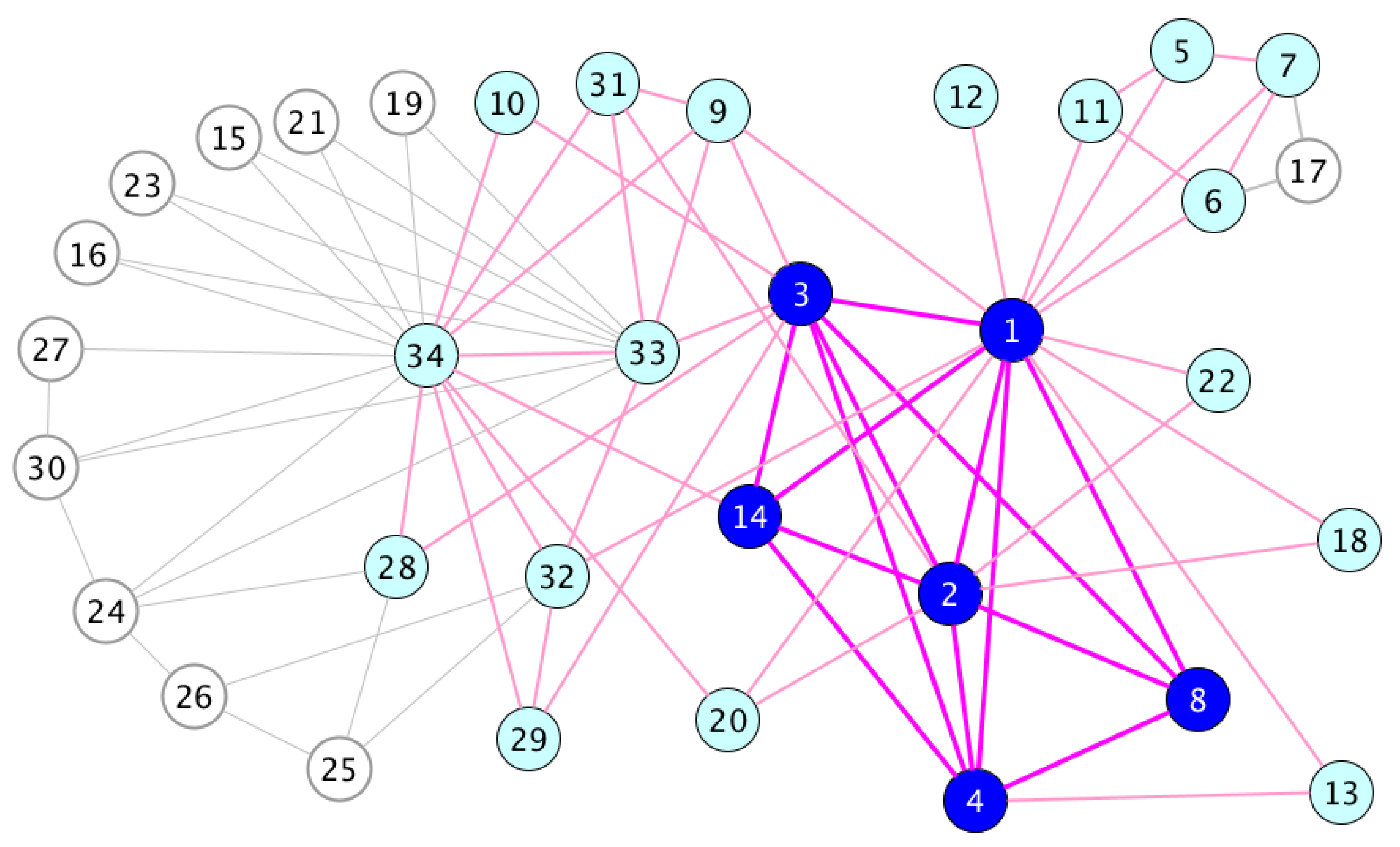
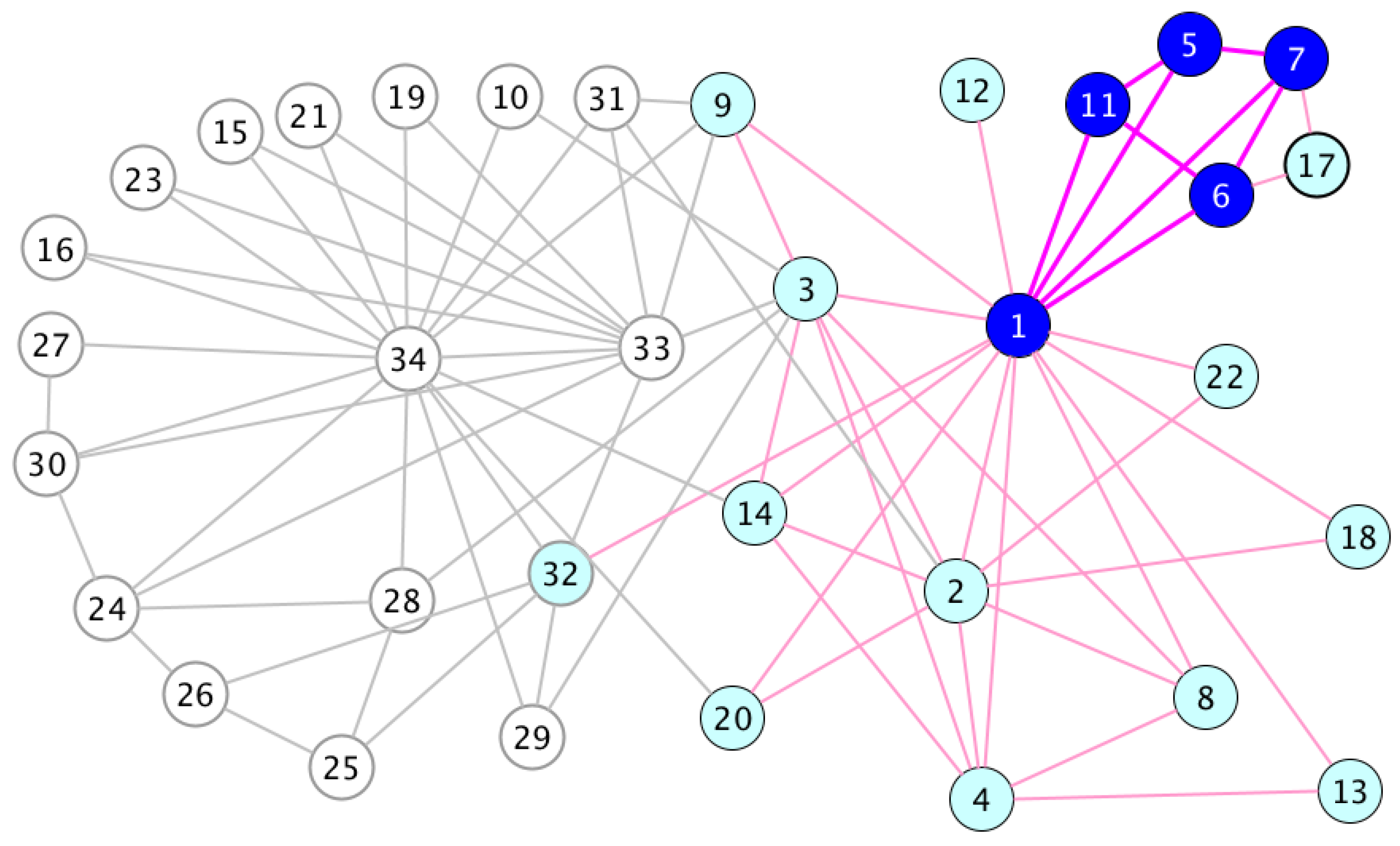

| Iteration i | Value of Bound | Frequency | Remaining Degree | Bound | Neighbors |
|---|---|---|---|---|---|
| 0 | - | - | 12 | 24 | 2 |
| 1 | 2 | 3 | 9 | 18 | 3 |
| 2 | 6 | 1 | 8 | 16 | 3 |
| 3 | 12 | 5 | 3 | 6 | 9 |
| 4 | 20 | 1 | 2 | 4 | 9 |
| 5 | 30 | 2 | 0 | 0 | 12 |
| Difference between the Bound and the Optimal Value | Number of Nodes | Percentage of Nodes | Concerning Nodes |
|---|---|---|---|
| 0 | 28 | 82 % | - |
| 1 | 4 | 12 % | 4 and 8 |
| 2 | 2 | 6% | 5, 6, 7 and 11 |
| TOTAL | 34 | 100% | - |
| karate, | football, | polblloks, | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Improvement | Improvement | Improvement | ||||||||||||||||||||
| it | 0 | 1 | 2 | TI | it | 0 | 1 | 2 | 3 | 4 | 5 | 6 | TI | it | 0 | 1 | 2 | 3 | 4 | 5 | 6 | TI |
| 1 | 100 | - | - | 0 | 1 | 100 | - | - | - | - | - | - | 0 | 1 | 100 | - | - | - | - | - | - | 0 |
| 2 | 91 | - | 9 | 9 | 2 | 49 | - | 36 | - | 12 | - | 3 | 51 | 2 | 66 | - | 25 | - | 8 | - | 2 | 34 |
| 3 | 44 | - | - | 0 | 3 | 95 | - | 3 | - | - | - | - | 3 | 3 | 80 | - | 15 | - | - | - | - | 15 |
| 4 | 33 | - | 4 | - | - | - | - | 4 | 4 | 75 | - | 1 | - | - | - | - | 1 | |||||
| 5 | 14 | - | - | - | - | - | - | 0 | 5 | 35 | - | - | - | - | - | - | 0 | |||||
| 6 | 5 | - | - | - | - | - | - | 0 | ||||||||||||||
| 7 | 2 | - | - | - | - | - | - | 0 | ||||||||||||||
| 8 | - | - | 1 | - | - | - | - | 1 | ||||||||||||||
| 9 | 1 | - | - | - | - | - | - | 0 | ||||||||||||||
| karate, | football, | polblloks, | ||||||||||||||||||||
| Improvement | Improvement | Improvement | ||||||||||||||||||||
| it | 0 | 1 | 2 | TI | it | 0 | 1 | 2 | 3 | 4 | 5 | 6 | TI | it | 0 | 1 | 2 | 3 | 4 | 5 | 6 | TI |
| 1 | 100 | - | - | 0 | 1 | 100 | - | - | - | - | - | - | 0 | 1 | 100 | - | - | - | - | - | - | 0 |
| 2 | 91 | 3 | 6 | 9 | 2 | 49 | 23 | 15 | 10 | 3 | - | - | 51 | 2 | 66 | 18 | 9 | 6 | 2 | - | - | 34 |
| 3 | 44 | - | - | 0 | 3 | 95 | 3 | - | - | - | - | - | 3 | 3 | 80 | 14 | 1 | - | - | - | - | 15 |
| 4 | 33 | 4 | - | - | - | - | - | 4 | 4 | 75 | 1 | - | - | - | - | - | 1 | |||||
| 5 | 14 | - | - | - | - | - | - | 0 | 5 | 35 | - | - | - | - | - | - | 0 | |||||
| 6 | 5 | - | - | - | - | - | - | 0 | ||||||||||||||
| 7 | 2 | - | - | - | - | - | - | 0 | ||||||||||||||
| 8 | - | 1 | - | - | - | - | - | 1 | ||||||||||||||
| 9 | 1 | - | - | - | - | - | - | 0 | ||||||||||||||
| Amount of Improvement | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| it | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 44 | TI (%) |
| 1 | 1224 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 0 |
| 2 | 819 | 113 | 62 | 48 | 45 | 21 | 24 | 11 | 24 | 17 | 7 | 9 | 5 | 5 | 3 | 2 | 1 | 2 | 1 | 1 | 2 | 33 |
| 3 | 931 | 103 | 73 | 55 | 26 | 4 | - | 1 | - | - | - | - | - | - | - | - | - | - | - | - | - | 21 |
| 4 | 1003 | 99 | 73 | 6 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 15 |
| 5 | 1019 | 110 | 7 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 10 |
| 6 | 993 | 88 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 7 |
| 7 | 932 | 60 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 5 |
| 8 | 791 | 61 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 5 |
| 9 | 706 | 7 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 1 |
| 10 | 513 | 4 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 0 |
| 11 | 355 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 0 |
| 12 | 173 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 0 |
| 13 | 60 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 0 |
| 14 | 28 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 0 |
| 15 | 17 | 1 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 0 |
| 16 | 6 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 0 |
| 17 | 5 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 0 |
| 18 | 3 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 0 |
| 19 | 1 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 0 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Conde-Cespedes, P. Approaching the Optimal Solution of the Maximal α-quasi-clique Local Community Problem. Electronics 2020, 9, 1438. https://doi.org/10.3390/electronics9091438
Conde-Cespedes P. Approaching the Optimal Solution of the Maximal α-quasi-clique Local Community Problem. Electronics. 2020; 9(9):1438. https://doi.org/10.3390/electronics9091438
Chicago/Turabian StyleConde-Cespedes, Patricia. 2020. "Approaching the Optimal Solution of the Maximal α-quasi-clique Local Community Problem" Electronics 9, no. 9: 1438. https://doi.org/10.3390/electronics9091438
APA StyleConde-Cespedes, P. (2020). Approaching the Optimal Solution of the Maximal α-quasi-clique Local Community Problem. Electronics, 9(9), 1438. https://doi.org/10.3390/electronics9091438





