Cyclostationary Impulsive Noise Mitigation in the Presence of Cyclic Frequency Offset for Narrowband Powerline Communication Systems

Abstract

Cyclostationary impulsive noise (CSIN) is the dominant source of additive noise in narrowband powerline communication (NB-PLC) systems. Frequency-shift (FRESH) filters have been applied to NB-PLC systems based on orthogonal frequency division multiplexing (OFDM) to mitigate CSIN and enhance the OFDM signals by leveraging the difference in cyclic frequency associated with CSIN and OFDM data symbols. Note that under the effects of frequency fluctuation in the mains voltage, the cyclic frequency offset associated with CSIN can degrade the performance of FRESH-filter receivers. To alleviate such an impact on the FRESH-filter receivers, this paper presents a method for the estimation of the cyclic frequency offset by observing phase variations in the coefficients of the FRESH filter. Computer simulations based on IEEE 1901.2 specifications demonstrate the effectiveness of the proposed scheme in suppressing the cyclic frequency relative error by at least 15.45 dB. Following compensation for the cyclic frequency offset, the proposed scheme achieved a bit error rate of ${10}^{-4}$ with an $E_b/N_0$ loss of only 0.7 dB, compared with the ideal case. Compared to the case without the cyclic frequency offset compensation, the proposed scheme achieved an $E_b/N_0$ gain of 2.7 dB.

1. Introduction

Narrowband powerline communication (NB-PLC) technology has wildly been applied in smart grid systems [1,2,3]. Moreover, NB-PLC can cooperate with wireless communications to gain higher receive diversity in heterogeneous networks [4]. However, multipath effects in powerline channels in the frequency band used by NB-PLC systems [5] and additive cyclostationary impulsive noise (CSIN) [6,7] can significantly degrade the performance of NB-PLC receivers [8,9]. It is possible to remove multipath effects using NB-PLC receivers based on orthogonal frequency division multiplexing (OFDM), which have been adopted as the existing standard [10], such as ITU-T G.9904 [11], ITU-T G.9903 [12], and IEEE 1901.2 [13]. Note however that despite these efforts, the performance of the NB-PLC systems can be severely degraded by additive CSIN [14,15]. Conventional filtering to deal with CSIN uses either digital adaptive filters [16] or adaptive analog nonlinear filters [17,18]. Note that CSIN as well as OFDM signals with cyclic prefix (CP) insertion can produce cyclostationarity [19,20]. Thus, frequency-shift (FRESH) filters exploit spectral correlation to extract desired information associated with a specific cyclic frequency [14,20,21,22,23]. FRESH filters are able to capture the cyclostationarity in a linear periodically time-varying (LPTV) system. By leveraging the cyclostationarity, FRESH filters are the optimal filters and could reject interference much better than a time-invariant filter. For example, the chaotic signal has a relatively flat spectrum and traditional signal processing methods are barely applicable [24]. However, it has been shown that some chaotic signals exhibit cyclostationary property and such property is possible to be exploited to encode information [25]. In Ref. [26], the authors used the cumulant-based scheme to test the presence of the cyclostationary signals and to estimate the cyclic frequencies. The authors in [20] used one set of FRESH filter with the cyclic frequency associated with the symbol rate for the reconstruction of OFDM signals. In Ref. [21], two sets of FRESH filters were used with two sets of cyclic frequency to retrieve the CSIN and OFDM signals, separately. However, it was assumed in that study that the cyclic frequency associated with the FRESH filter and the channel response of the powerline were perfectly known on the receiver side. In Ref. [22], a time-averaged least mean squared (TA-LMS) algorithm was used to train the weights of each branch of the adaptive FRESH filter for use in resolving the problem of channel estimation in NB-PLC systems. However, they lacked for considering issues pertaining to CSIN estimation or mitigation. The authors in [23] exploited spatial correlation across multiple phases at a receiving modem to enhance the performance of FRESH filters while taking into account the cyclostationarity of CSIN in order to derive an optimal solution by which to minimize the time-averaged mean square error (MSE). In our previous work [14], we proposed using an FRESH-based estimator to serve as the reference impulsive noise sources to an adaptive predictor. In such arrangement, the adaptive predictor could further refine the estimation of IN from the received signal. However, the authors did not consider the issues of cyclic frequency offset, which cause a poor estimation for the reference impulsive noise sources. Without the perfect information about the cyclic frequency associated with the CSIN, the adaptive predictor could have a worse prediction to the CSIN and could paralyze the CSIN estimation algorithm.

To the best of our knowledge, few researchers have considered the impact of cyclic frequency offset on FRESH filters. The cyclic period for CSIN is normally half the period of the mains cycle $T_{AC}$. In Taiwan, the mains frequency is generally 60 Hz, such that the typical cyclic period is 8.33 ms and the corresponding cyclic frequency is 120 Hz. However, the mains frequency is permitted to operate with a $\pm 4\%$ offset, based on regulations stipulated in Electricity Act of Taiwan [27]. In Ref. [28], the authors demonstrated that even a slight offset in cyclic frequency would be sufficient to spoil the performance of FRESH filters. In the absence of cyclic frequency offset, an adaptive FRESH filter would converge to a linear time-invariant (LTI) filter for each branch of the FRESH filter. However, when there exists a cyclic frequency offset, LTI filters behave as linear periodically time-variant (LPTV) filters. As long as the adaptation algorithm is suited to the conditions, it should be possible for an adaptive FRESH filter to track periodic variations and thereby compensate for cyclic frequency offset [28]. Nonetheless, the convergence rate of adaptive algorithms would have to be carefully selected in order to obtain reasonable results. In this paper, we present an adaptive FRESH-based receiver, mainly comprising one CSIN estimator and one signal restorer. The main contributions of this work are summarized as follows. First, we consider the imperfect information of cyclic frequency associated with the CSIN estimator and propose an estimation algorithm to estimate the cyclic frequency offset. The estimation algorithm is based on the phase variation of the tap weights of the adaptive FRESH filter over a certain observation time. In addition, we have derived the maximum observation period to avoid the phase ambiguity issue. Second, by exploiting the difference of cyclic frequency between the CSIN and the received OFDM signal, we have proposed using another adaptive FRESH filter as the signal restorer. Moreover, a practical procedure to train these two adaptive FRESH filter has been provided in this paper. Third, we have referred to the IEEE 1901.2 standard to built the simulation programs, include the channel model and CSIN model, to validate the effectiveness of the proposed adaptive FRESH-based receiver. Simulation results have confirmed that our proposed cyclic frequency offset estimation algorithm could suppress the cyclic frequency relative error by at least 15.45 dB. With the compensation of the cyclic frequency offset, the required values of the $E_b/N_0$ at bit error rate (BER) of ${10}^{-4}$ are 22.6 dB, 23.3 dB, and 25.2 dB for the ideal, compensated, and no CSIN mitigation cases, respectively, for the differential binary phase shift keying (DBPSK) modulation scheme. The remainder of this paper is organized as follows. Section 2 describes the system models considered in this study, including powerline channel and noise models. Section 3 expatiates on the proposed adaptive FRESH-filter receivers. Section 4 presents our simulation results. Conclusion and discussion are drawn in Section 5.

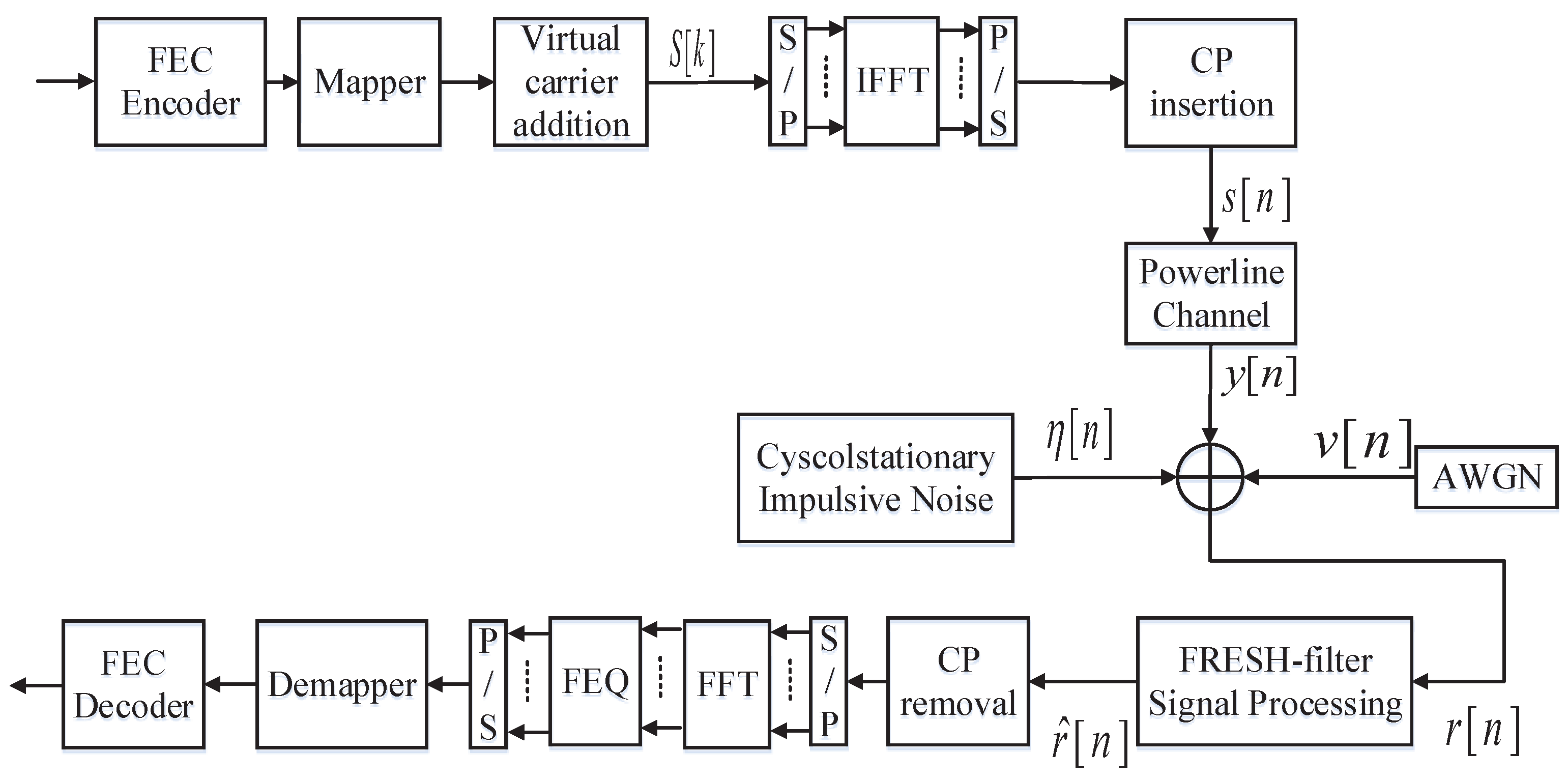
2. System Models

Figure 1 presents a block diagram of the transceiver model used in the proposed system. On the transmitting side, we parallelize the data symbols $S\left[k\right]$ by the serial-to-parallel (S/P) conversion and implement the OFDM modulation by an inverse fast Fourier transform (IFFT) with $N_{\mathrm{FFT}}$-point. The output of the IFFT block can be expressed as:

$$\begin{array}{c}\hfill s\left[n\right]=\frac{1}{\sqrt{N_{\mathrm{FFT}}}}\sum _{k=0}^{N_{\mathrm{FFT}}-1}S\left[k\right]e^{j2\pi kn/N_{FFT}},\end{array}$$

(1)

where $N_{\mathrm{FFT}}$ denotes the IFFT length, which is equal to the number of all data and null subcarriers, and $n=0,1,\dots ,(N_{\mathrm{FFT}}-1)$. Note that we assumed that the outputs of the IFFT are real numbers, which implies that we arrange the data subcarriers in Hermitian symmetric form, in the considered baseband NB-PLC systems. The data symbols $S\left[k\right]$ are produced by encoding the information bits with a forward error correction (FEC) channel encoder and then grouping the coded bits into symbols by a mapper. For the subcarriers do not intend to transmit data are called virtual carriers. Before transmitting the data symbol over a powerline, we serialize the output of the IFFT block by the parallel-to-serial (P/S) block and then prepend the CP to alleviate the multipath effects incurred by the powerline $h\left[n\right]$. On the receiving side, the received signal $r\left[n\right]$ is comprised of the output of the powerline $y\left[n\right]$, the dominant CSIN $\eta \left[n\right]$, and the background additive white Gaussian noise (AWGN) $v\left[n\right]$. We propose using a FRESH-filter based signal processing not only to remove CSIN but also to enhance the OFDM signal. Following removal of the CP from the denoised signal $\widehat{r}\left[n\right]$ and conversion to parallel form, the signal is transferred back to the frequency domain and then equalized by a frequency-domain equalization (FEQ). The equalized signals go through P/S, demapper, and FEC decoder blocks to estimate information bit stream sent from the transmitting side.

2.1. Powerline Channel Model

We chose Zimmermann’s multipath model as the powerline channel model [29], by which the frequency response of an $N_{path}$-path powerline channel can be expressed as

$$\begin{array}{c}\hfill H\left(f\right)=\sum _{i=1}^{N_{\mathrm{path}}}{\alpha }_i·e^{\left\{-(a_0+a_1{f}^{a_2})d_i\right\}}·e^{\left\{-j2\pi f{\tau }_i\right\}},\end{array}$$

(2)

where ${\alpha }_i$, $d_i$, and ${\tau }_i$ denote the weighting factor, length of powerline, and the delay time associated with the i-th path, respectively; $a_0$, $a_1$, and $a_2$ are attenuation parameters. Even the Zimmermann’s model was originally proposed to describe the complex frequency response of PLC links for the frequency range from 500 kHz to 20 MHz, it is adopted as one of the channel model for NB-PLC systems in the Annex D of IEEE 1901.2. standard. In Ref. [30], the authors have reported that the Zimmermann’s model exhibits quite accurate NB-PLC transfer functions for low voltage networks.

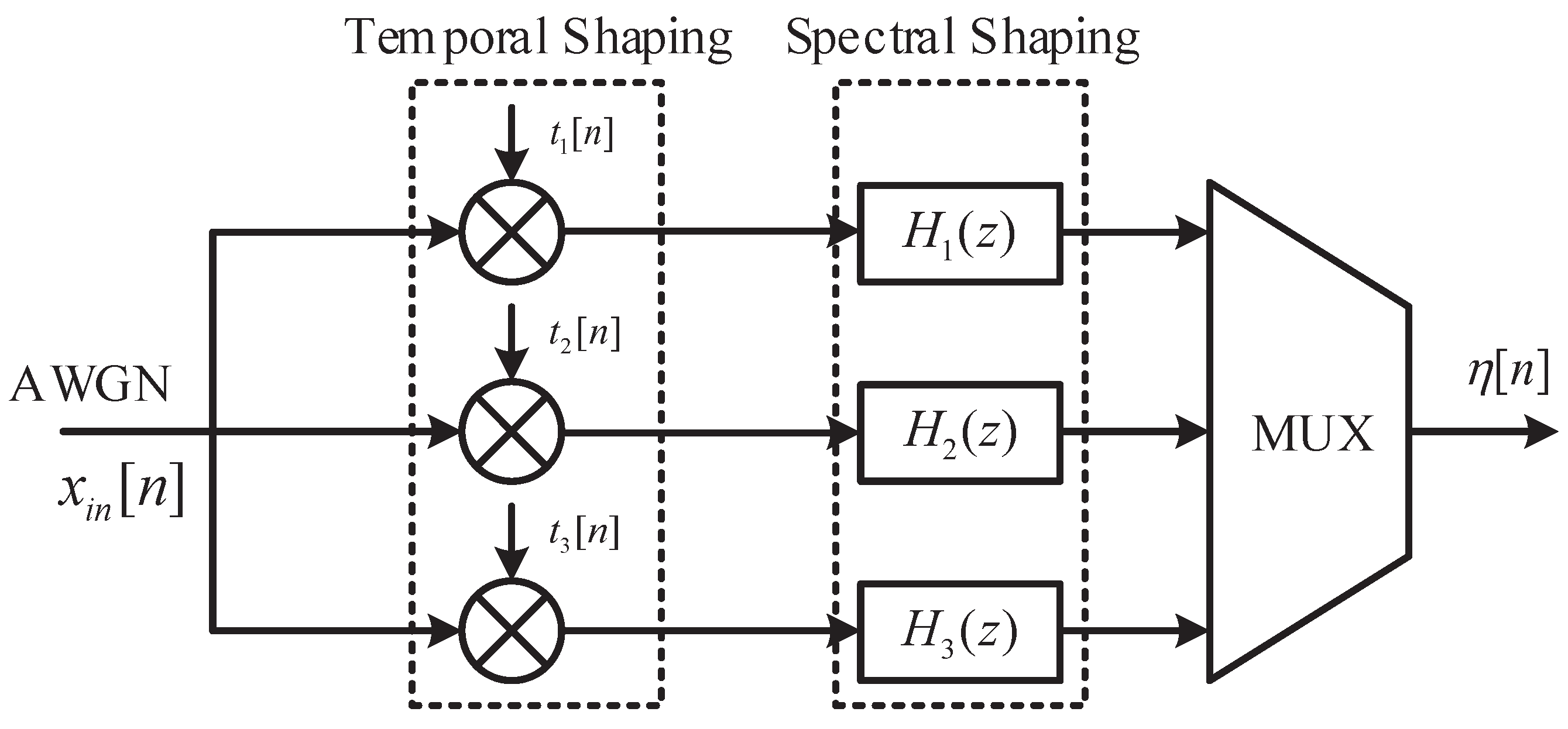
2.2. CSIN Model

According to the collected data from field measurements over powerline channels, researchers have reported that the dominant noise source in NB-PLC systems can be modeled as a cyclostationary process, which possess impulsive property and with a period equal to half the period of mains voltage [7,31,32,33,34]. The cyclostationary process is refereed to as CSIN and its sample function can be modeled by a zero-mean function and time-varying variance function ${\sigma }_{\eta }^2\left[n\right]$ Gaussian random process. Note that this variance function exhibits periodicity with period $N_{\eta }$, i.e., ${\sigma }_{\eta }^2\left[n\right]={\sigma }_{\eta }^2[n+k{N}_{\eta }]$ with $k\in \mathbb{Z}$. In the current study, we used the piecewise spectral cyclostationary Gaussian model (PSCGM) as our CSIN model, based on IEEE 1901.2 standard [13]. Figure 2 presents the block diagram of PSCGM used to generate CSIN. The multiplexer (MUX) was used to select one branch from the M regions to the output. In most cases, M falls between 2 and 4, and here we assume there are $M=3$ regions of temporal and spectral shaping functions.

The CSIN process $\eta \left[n\right]$ can be expressed as:

$$\begin{array}{cc}\eta \left[n\right]\hfill & =\sum _{\tau }h[n,\tau ]x_{in}\left[\tau \right]\hfill \\ \hfill & {\displaystyle =\sum _{i=1}^M{\mathbb{I}}_{n\in {\mathbb{R}}_i}\sum _{\tau }{t}_i\left[\tau \right]h_i\left[\tau \right]x_{in}[n-\tau ]}\hfill \end{array}$$

(3)

where $x_{in}\left[n\right]$ is the AWGN input excitation signal; $t_i\left[n\right]$ and $h_i\left[n\right]$ respectively indicate the temporal and spectral shaping functions for the i-th region of a period; ${\mathbb{R}}_i$ denotes the set of discrete time indices for the i-th region of a period; $H_i\left(z\right)$ represents the Z-transform of $h_i\left(n\right)$; ${\mathbb{I}}_n$ denotes the indicator function; $0\le n<N_{\eta }$; and $N_{\eta }=0.5f_s·T_{AC}$ is the period of the CSIN, where $T_{\mathrm{AC}}$ denotes the period of mains voltage and $f_s$ is the sampling rate of the received signal.

For a random process $\eta \left[n\right]$, the corresponding instantaneous autocorrelation function with lag m can be defined as

$$\begin{array}{c}\hfill R_{\eta }[n,n+m]=\mathbb{E}\left\{{\eta }^{*}\left[n\right]·\eta \left[n+m\right]\right\},\end{array}$$

(4)

where $\mathbb{E}\left\{·\right\}$ denotes the expectation operation and the superscript * represents complex conjugate operation of a complex number. Furthermore, the periodicity of CSIN results in the periodicity of its instantaneous autocorrelation function. Therefore, we can rewrite (4) in its Fourier series (FS) synthesis form as follows:

$$\begin{array}{c}\hfill R_{\eta }[n,n+m]=\sum _{{\alpha }_k}{R}_{\eta }[m;{\alpha }_k]e^{j2\pi {\alpha }_{k}n},\end{array}$$

(5)

where ${\alpha }_k$ is referred to as the k-th cyclic frequency connected with the FS coefficients $R_{\eta }[m;{\alpha }_k]$ (cyclic auto-correlation function), which be expressed as follows [35]:

$$\begin{array}{c}\hfill R_{\eta }[m;{\alpha }_k]=\underset{N_L\to \infty }{lim}\frac{1}{N_L}\sum _{n=-N_L/2}^{N_L/2}{R}_{\eta }[n,n+m]e^{-j2\pi {\alpha }_{k}n},\end{array}$$

(6)

where $N_L$ is the observation window size. Note also that the cyclic spectrum density (CSD) function and the cyclic auto-correlation function are Fourier transform pair. Hence, the CSD function can be expressed as follows:

$$\begin{array}{c}\hfill S_{\eta }(f;{\alpha }_k)=\sum _{m=-\infty }^{\infty }{R}_{\eta }[m;{\alpha }_k]e^{-j2\pi fm}.\end{array}$$

(7)

We also adopted a parameter referred to as the Gaussian-to-impulsive-noise ratio (GINR) to evaluate the impact of the CSIN on BER performance in NB-PLC systems as follows:

$$\begin{array}{c}\hfill \Gamma :={\sigma }_v^2/{\sigma }_{\overline{\eta }}^2,\end{array}$$

(8)

where ${\sigma }_v^2$ denotes the variance of the background zero-mean AWGN $v\left[n\right]$ and ${\sigma }_{\overline{\eta }}^2$ represents the averaged variance of the CSIN $\eta \left[n\right]$ in one period. The value of GINR indicates the strength of impulsive noise. The value of $\Gamma$ is inversely proportional to the magnitude of the impulsive noise. An exemplary value for GINR in NB-PLC applications would be 0.01 [4]. When evaluating BER performance under various values of the signal-to-noise ratio (SNR) per bit ($E_b/N_0$), the sample variance of $\eta \left[n\right]$ is calculated by ${\sigma }_{\overline{\eta }}^2={\sigma }_v^2/\mathrm{GINR}$. Thus, the magnitude of the additive CSIN in the low $E_b/N_0$ regions is larger than that in the high $E_b/N_0$ regions.

3. Proposed FRESH-Filter Receivers

Figure 3 details the signal processing blocks used in the proposed FRESH-filter receiver, which comprises one finite impulse response (FIR) filter, two FRESH filters, and one block for estimating and compensating the cyclic frequency offset associated the CSIN. We first use the pilot signals $s_p\left[n\right]$ to estimate the channel response of the powerline $h\left[n\right]$, which makes it possible to estimate the received signal without AWGN and CSIN interference. Note that the desired signal to train $h\left[n\right]$ is $r\left[n\right]$, whereas the error signal used to adapt $h\left[n\right]$ is $e\left[n\right]=r\left[n\right]-y_p\left[n\right]$, where $y_p\left[n\right]=s_p\left[n\right]\otimes h\left[n\right]$ and ⊗ denotes a convolution operation. To improve convergence results when dealing with the noisy received signals, we suggest using the recursive least-squares (RLS) algorithm to adapt $h\left[n\right]$. Note that following convergence of the adaptation process, the output of $h\left[n\right]$ is used to approximate the output of the powerline channel without additive noise; i.e., $y_p\left[n\right]\approx y\left[n\right]$. Note also that $e\left[n\right]$ could be treated as an additive noise term, including AWGN and CSIN.

Next, our objective in using an adaptive FRESH filter ${\mathbf{h}}_1\left[n\right]$ is to make predictions related to the additive CSIN signals $\widehat{\eta }\left[n\right]$. The desired signal to train ${\mathbf{h}}_1\left[n\right]$ is $e\left[n\right]$, which contains only additive noise following the convergence of $h\left[n\right]$. The error signal used to adapt ${\mathbf{h}}_1\left[n\right]$ is $e_1\left[n\right]=e\left[n\right]-\widehat{\eta }\left[n\right]$. Note that the cyclic frequency offset estimation exploits the phase rotation of the coefficients of ${\mathbf{h}}_1\left[n\right]$ in estimating the offset of the k-th branch, i.e., ${\widehat{\Delta }}_k$, of the FRESH filter (see Section 3.2).

Third, the adaptive FRESH filter ${\mathbf{h}}_2\left[n\right]$ is meant to restore the OFDM signal from the denoised signal $r_m\left[n\right]=r\left[n\right]-\widehat{\eta }\left[n\right]$. The desired signal to train ${\mathbf{h}}_2\left[n\right]$ is $y_p\left[n\right]$, whereas the error signal used to adapt ${\mathbf{h}}_2\left[n\right]$ is $e_2\left[n\right]=y_p\left[n\right]-\widehat{r}\left[n\right]$. Note that the output of ${\mathbf{h}}_2\left[n\right]$ is fed into the CP removal block for further demodulation.

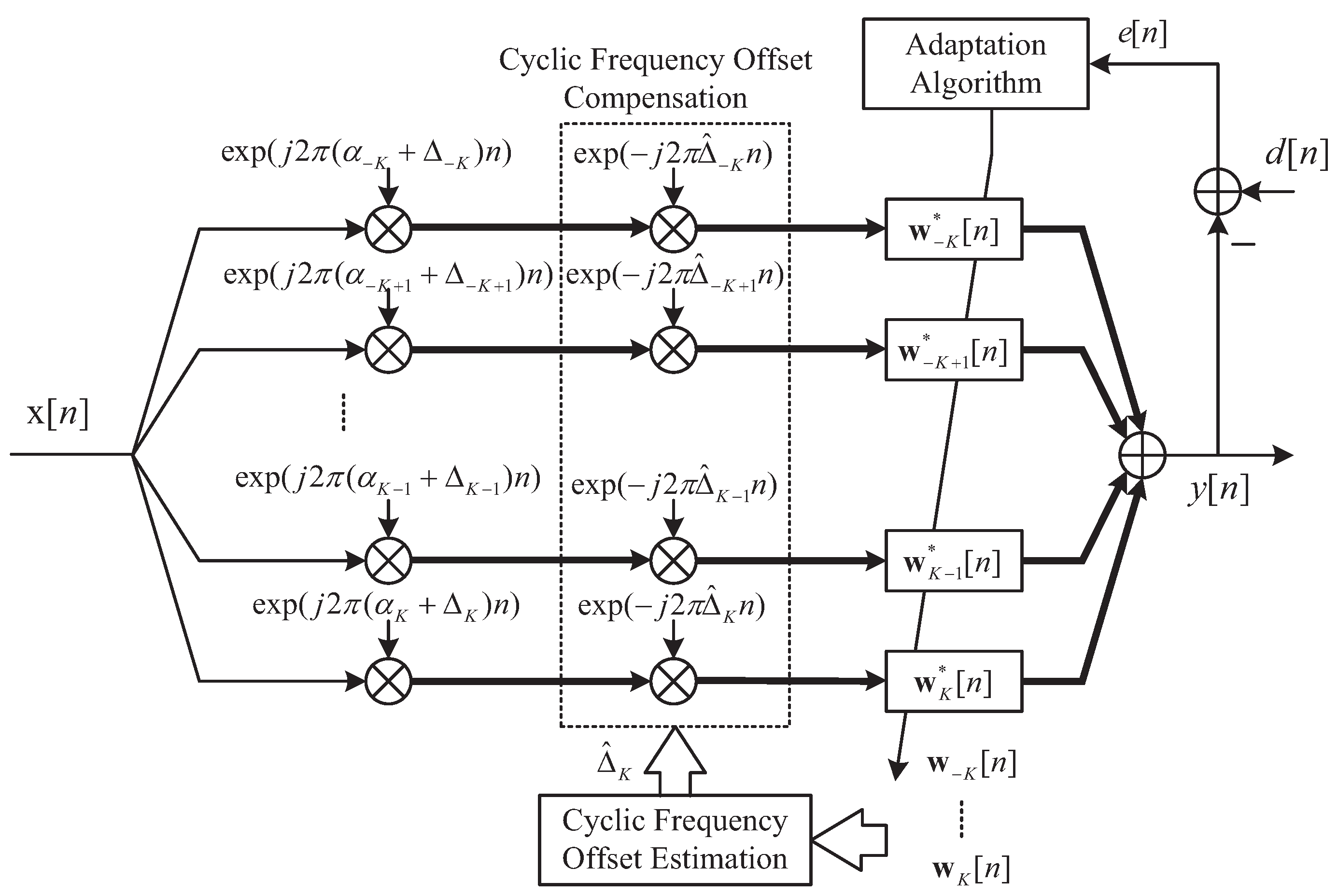
3.1. Adaptive FRESH Filter

Figure 4 presents the proposed adaptive FRESH filter with cyclic frequency offset estimation and compensation. We assumed that the input signal $x\left[n\right]$ is a real signal, and the adaptive FRESH filter includes $2K+1$ branches. The cyclic frequency corresponding to the k-th branch is ${\alpha }_k+{\Delta }_k$ for $k=\left\{0,\pm 1,\dots ,\pm K\right\}$, and ${\Delta }_k$ denotes the deviation in the cyclic frequency offset from its typical value of ${\alpha }_k$. Note that all of this is based on the assumption that only the FRESH filter ${\mathbf{h}}_1\left[n\right]$ suffers from cyclic frequency offset. For the FRESH filter ${\mathbf{h}}_2\left[n\right]$, the cyclic frequency for the k-th branch ${\beta }_k$ is determined by the length of an OFDM symbol. In the presence of sampling frequency offset in an OFDM system, ${\beta }_k$ may deviate from its typical value. A number of algorithms have been developed to compensate for the sampling frequency offset [36,37]; therefore, we assumed that ${\beta }_k$ is perfectly known by the receivers.

The authors in [38] suggested using the RLS algorithm to adapt the tap weights of the FRESH filter. The i-th element of the frequency shifted input vector associated with the k-th branch is denoted as ${\left({\mathbf{x}}_k\left[n\right]\right)}_i=x[n-i]e^{j2\pi {\alpha }_k^{\prime }(n-i)}$ for $i\in \left\{0,1,\dots ,L-1\right\}$, where ${\alpha }_k^{\prime }={\alpha }_k+{\Delta }_k$ is the cyclic frequency that considered possible offset at the k-th branch and L denotes the length of the vector. By stacking the input vector and weight vector of all branches into column vector forms, we can write the output of the FRESH filter $y\left[n\right]$ as follows:

$$\begin{array}{c}\hfill y\left[n\right]={\mathbf{W}}^H\left[n\right]\mathbf{X}\left[n\right]\end{array}$$

(9)

where $\mathbf{W}\left[n\right]={\left[{\mathbf{w}}_{-K}^T\left[n\right],{\mathbf{w}}_{-K+1}^T\left[n\right],\dots ,{\mathbf{w}}_K^T\left[n\right]\right]}^T$ and $\mathbf{X}\left[n\right]={\left[{\mathbf{x}}_{-K}^T\left[n\right],{\mathbf{x}}_{-K+1}^T\left[n\right],\dots ,{\mathbf{x}}_K^T\left[n\right]\right]}^T$. Note that $\mathbf{W}\left[n\right]$ and $\mathbf{X}\left[n\right]$ are column vectors with length $(2K+1)·L$.

The RLS adaptation algorithm can be used to update the weight vector $\mathbf{W}\left[n\right]$ as follows:

$$\begin{array}{c}\hfill \mathbf{W}\left[n\right]=\mathbf{W}[n-1]+\zeta \left[n\right]\mathbf{g}\left[n\right]\end{array}$$

(10)

where $\zeta \left[n\right]=d\left[n\right]-{\mathbf{W}}^H[n-1]\mathbf{X}\left[n\right]$ is the a priori error and $\mathbf{g}\left[n\right]$ is the gain vector, which can be expressed as

$$\begin{array}{c}\hfill \mathbf{g}\left[n\right]=\frac{\mathbf{P}[n-1]·\mathbf{X}\left[n\right]}{\lambda +{\mathbf{X}}^H\left[n\right]·\mathbf{P}[n-1]·\mathbf{X}\left[n\right]}\end{array}$$

(11)

where $\lambda$ is the forgetting factor. The matrix $\mathbf{P}\left[n\right]$ is updated by the following recursion:

$$\begin{array}{c}\hfill \mathbf{P}\left[n\right]={\lambda }^{-1}\left[{\mathbf{I}}_{(2K+1)·L}-\mathbf{g}\left[n\right]·{\mathbf{X}}^H\left[n\right]\right]·\mathbf{P}[n-1]\end{array}$$

(12)

where ${\mathbf{I}}_{(2K+1)·L}$ is an identity matrix of rank $(2K+1)·L$ Note that the initial value of $\mathbf{P}\left[n\right]$ is $\mathbf{P}\left[0\right]={\delta }^{-1}·{\mathbf{I}}_{(2K+1)·L}$, which is an identity matrix normalized by a regularization parameter $\delta$.

For the adaptive filer with length $L_R$, the computational complexity of the adaptive RLS algorithm is $\mathcal{O}\left(L_R^2\right)$ for complex-valued data. It necessitates $(4L_R^2+16L_R+1)$ real multiplications, $(4L_R^2+12L_R-1)$ real additions, and 1 real division [39]. For the adaptive FRESH filter, the length $L_R$ is $(2K+1)·L$ in total. The computational cost can be further reduced using hierarchical concept [40] or dichotomous coordinate descent iterations [41]. The data type (floating-point or fixed-point) could influence the performance on the adaptive RLS algorithm. The finite-precision error analysis related to adaptive RLS algorithm could be found in [42].

3.2. Cyclic Frequency Offset Estimation and Compensation

Ideally, the FIR filter at each branch of the FRESH filter behaves as an LPTV filter, which can be expressed as

$$\begin{array}{c}\hfill {\left({\mathbf{w}}_k\left[n\right]\right)}_i=e^{j2\pi {\Delta }_{k}n}{\left({\mathbf{w}}_{o,k}\left[n\right]\right)}_i\end{array}$$

(13)

where ${\left({\mathbf{w}}_k\left[n\right]\right)}_i$ denotes the i-th coefficient of the k-th branch of the FRESH filter and ${\mathbf{w}}_{o,k}\left[n\right]$ represents the optimal coefficients of the k-th branch of the FRESH filter when there is no cyclic frequency offset. Note that the cyclic frequency offset will induce the term $e^{j2\pi {\Delta }_{k}n}$ with the result that ${\left({\mathbf{w}}_k\left[n\right]\right)}_i$ varies periodically. We can extract offset information by calculating the following ratio:

$$\begin{array}{cc}{r}_{k,i}\hfill & =\frac{{\left({\mathbf{w}}_k\left[n_2\right]\right)}_i}{{\left({\mathbf{w}}_k\left[n_1\right]\right)}_i}\hfill \\ \hfill & =e^{j2\pi {\Delta }_k{N}_{\tau }}\hfill \\ \hfill & =cos\left(2\pi {\Delta }_k{N}_{\tau }\right)+jsin\left(2\pi {\Delta }_k{N}_{\tau }\right)\hfill \end{array}$$

(14)

where $N_{\tau }=n_2-n_1>0$ is the interval during which the phase variation of the coefficient is observed. To obtain a better estimation of ${\Delta }_k$, we can select the branch that exhibits the largest phase variation as follows:

$$\begin{array}{c}\hfill {\displaystyle {\tilde{R}}_k=\underset{k,i}{max}\left|R_{k,i}\right|}\end{array}$$

(15)

where $R_{k,i}=error\left\{r_{k,i}\right\}/error\left\{r_{k,i}\right\}=tan\left(2\pi {\Delta }_k{N}_{\tau }\right)$. Thus, the estimate of cyclic frequency offset at the k-th branch of the FRESH filter can be expressed as

$$\begin{array}{c}\hfill {\displaystyle {\widehat{\Delta }}_k=\frac{1}{2\pi N_{\tau }}{tan}^{-1}\left({\tilde{R}}_k\right)}\end{array}$$

(16)

As shown in Figure 4, estimation ${\widehat{\Delta }}_k$ can be used to compensate for the unknown cyclic frequency offset. This relaxes the required tracking ability of the adaptive FRESH filter. To quantify the effectiveness of the estimation method, we propose a performance metric called “cyclic frequency relative error” (CFRE), which is defined as follows:

$$\begin{array}{cc}{\mathrm{CFRE}}_{\mathrm{CSIN}}\hfill & =\frac{{\alpha }_1^{\prime }-{\widehat{\alpha }}_1}{{\alpha }_1^{\prime }}\times 100\%\hfill \\ \hfill & =\frac{({\alpha }_1+{\Delta }_1)-({\alpha }_1+\widehat{{\Delta }_1})}{{\alpha }_1+{\Delta }_1}\times 100\%\hfill \\ \hfill & =\frac{{\Delta }_1-\widehat{{\Delta }_1}}{{\alpha }_1+{\Delta }_1}\times 100\%\hfill \end{array}$$

(17)

where ${\alpha }_1^{\prime }$ is the fundamental cyclic frequency susceptible to cyclic frequency offset, and ${\widehat{\alpha }}_1$ is the estimate of ${\alpha }_1^{\prime }$. For the mains frequency of 60 Hz and frequency offset of 4%, the corresponding fundamental cyclic frequency ${\alpha }_1^{\prime }=120\times 1.04=124.8$ Hz, i.e., ${\Delta }_1=4.8$ Hz.

Note that observation interval $N_{\tau }$ should be selected carefully to avoid phase ambiguity caused by the arctangent function ${tan}^{-1}\left(·\right)$. Assuming that the variation in the frequency of the mains voltage is less than $ϵ$, the maximum cyclic frequency of the k-th branch is $2k(1+ϵ)/T_{AC}$. Thus, the corresponding maximum cyclic frequency offset can be expressed as follows:

$$\begin{array}{c}\hfill \left|{\Delta }_{k,max}\right|=2kϵ/T_{AC}\end{array}$$

(18)

Combining (16) with (18), we find that the maximum observation period $N_{\tau }$ must satisfy the following equation:

$$\begin{array}{c}\hfill N_{\tau }\le \left|\frac{1}{2\pi {\Delta }_{k,max}}{tan}^{-1}\left({\tilde{R}}_k\right)\right|\le \frac{T_{AC}}{8ϵk}\end{array}$$

(19)

4. Simulation Results

The major system parameters adopted in our simulation are summarized in

Table 1. Simulation parameters for the NB-PLC systems.

Parameter	Value
Modulation	Differential binary phase shift keying (DBPSK)
Forward error correction (FEC) outer encoder	Reed-Solomon coding (RS(255,239))
FEC inner encoder	Convolutional coding (r = 1/2, K = 7, $g=({171}_{octal},{133}_{octal})$)
Frequency range	35.9–90.6 kHz (CENELEC A)
Sampling rate ($f_s$)	400 kHz
Fast Fourier transform (FFT) length ($N_{FFT}$)	256
Data subcarriers	36
Null subcarriers	184
Cyclic prefix (CP) length	30

. The modulation scheme was DBPSK. The FEC encoder comprised outer as well as inner channel encoders. The outer channel encoder was Reed-Solomon $(255,239)$, which means that Reed-Solomon (RS) encoder required 239 data bytes, to which were added parity bytes to make a 255-byte codeword. The corresponding RS$(255,239)$ decoder at the receiver side was able to correct up to 8 bytes in the codeword. The inner channel encoder was a convolutional encoder with code rate $r=1/2$ and constraint length $K=7$. The generator sequences were ${171}_{octal}$ and ${133}_{octal}$.The frequency range used to transmit data was within the CENELEC A band and the sampling rate of the received signal was $f_s=400$ kHz. The length of the FFT was $N_{\mathrm{FFT}}=256$, of which 36 points were used for data carriers and 36 points were used for its conjugate parts. The remaining 184 carriers were null carriers. The first and last data carriers were placed at 35.9375 kHz and 90.625 kHz, respectively. The length of the CP was 30 points.

In accordance with (2), we used a 50-path ($N_{\mathrm{path}}=50$) powerline model with attenuation parameters $a_0={10}^{-3}$, $a_1=2.5\times {10}^{-9}$, and $a_2=1$. The resulting impulse response of the powerline channel $h\left[n\right]$ and its magnitude response $\left|H\left(f\right)\right|$ are presented in Figure 5.

The PGCSM model (see (3)) was used to produce additive CSIN according to the parameters stipulated in IEEE 1901.2 ([13], Annex D.3.1.2, LV14). The parameters provided in the Annex D.3.1.2 for modeling the CSIN were obtained by conducting field measurements in the low voltage substation and then fitting these measured data into models. Thus, even we did not collect the CSIN data by conducting real measurements, the simulation results could still reflect the situations in the real low voltage NB-PLC networks. The corresponding time-domain trace, spectrogram, and CSD plots are shown in Figure 6a–c, respectively. Note that the color bars in Figure 6b,c are used to indicate the strength of the resulting spectrogram and CSD function associated the additive CSIN at $E_b/N_0=0$ dB. In general, the resulting values of CSD function are represented in linear scale as shown in Figure 6c, which clearly reveals the fundamental cyclic frequency is about 120 Hz. The value of GINR $\Gamma$ is 0.01. Figure 7 illustrates the signal-to-interference-plus-noise ratio (SINR) at each subcarrier of the received signal when $E_b/N_0=0$ dB. Note that our data subcarriers are mainly distributed between about $0.36\times {10}^5$ to $0.9\times {10}^5$ Hz.

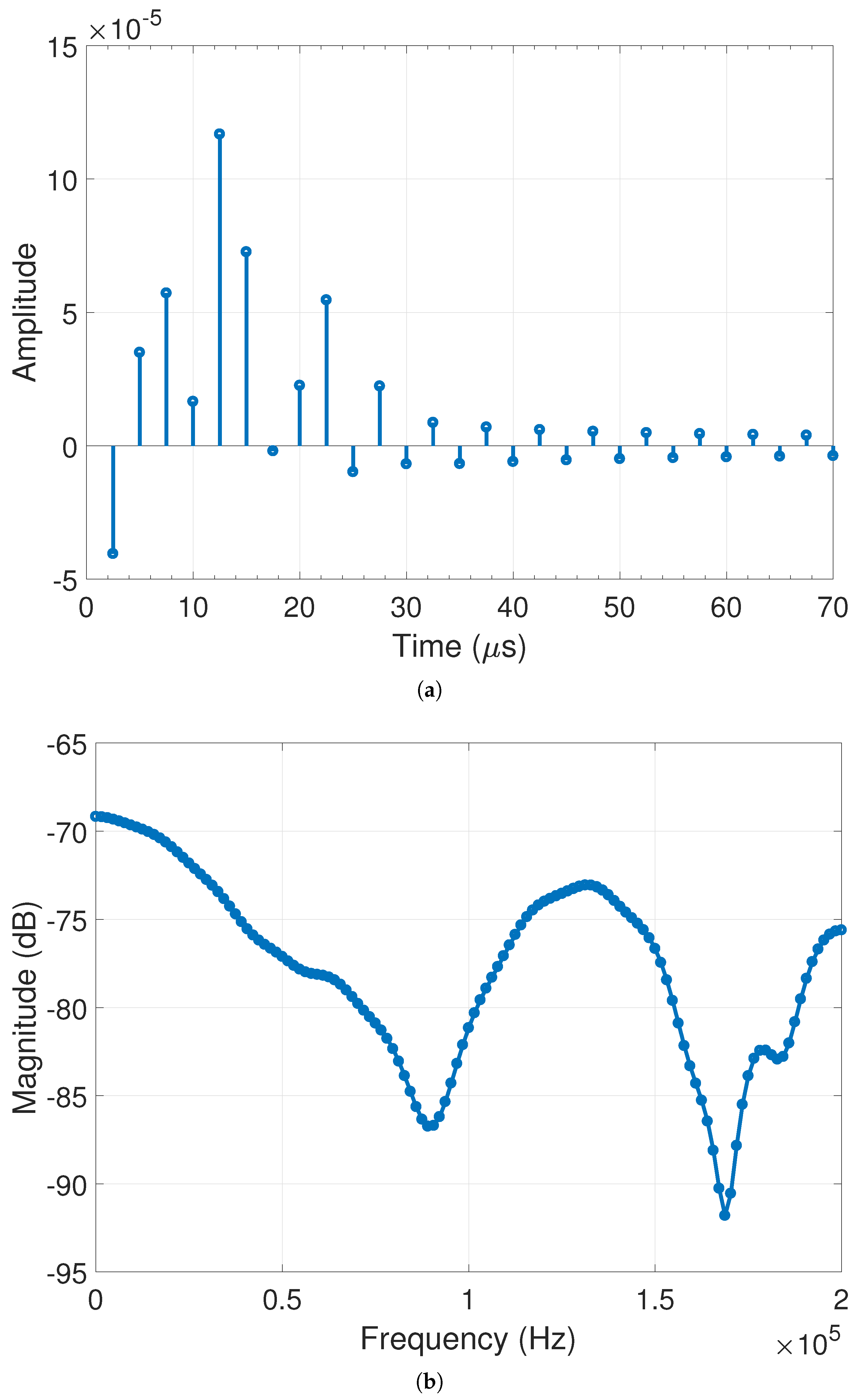
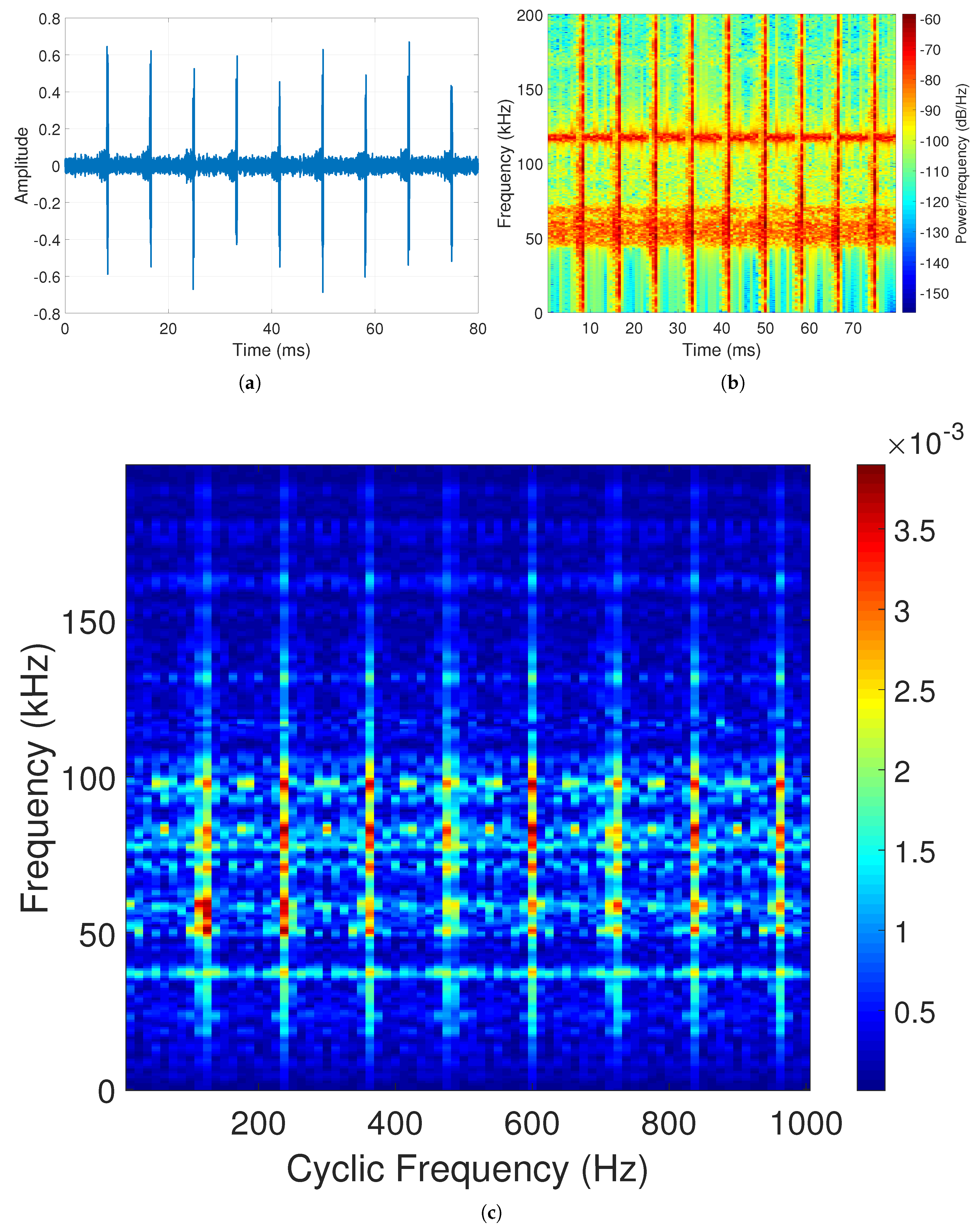
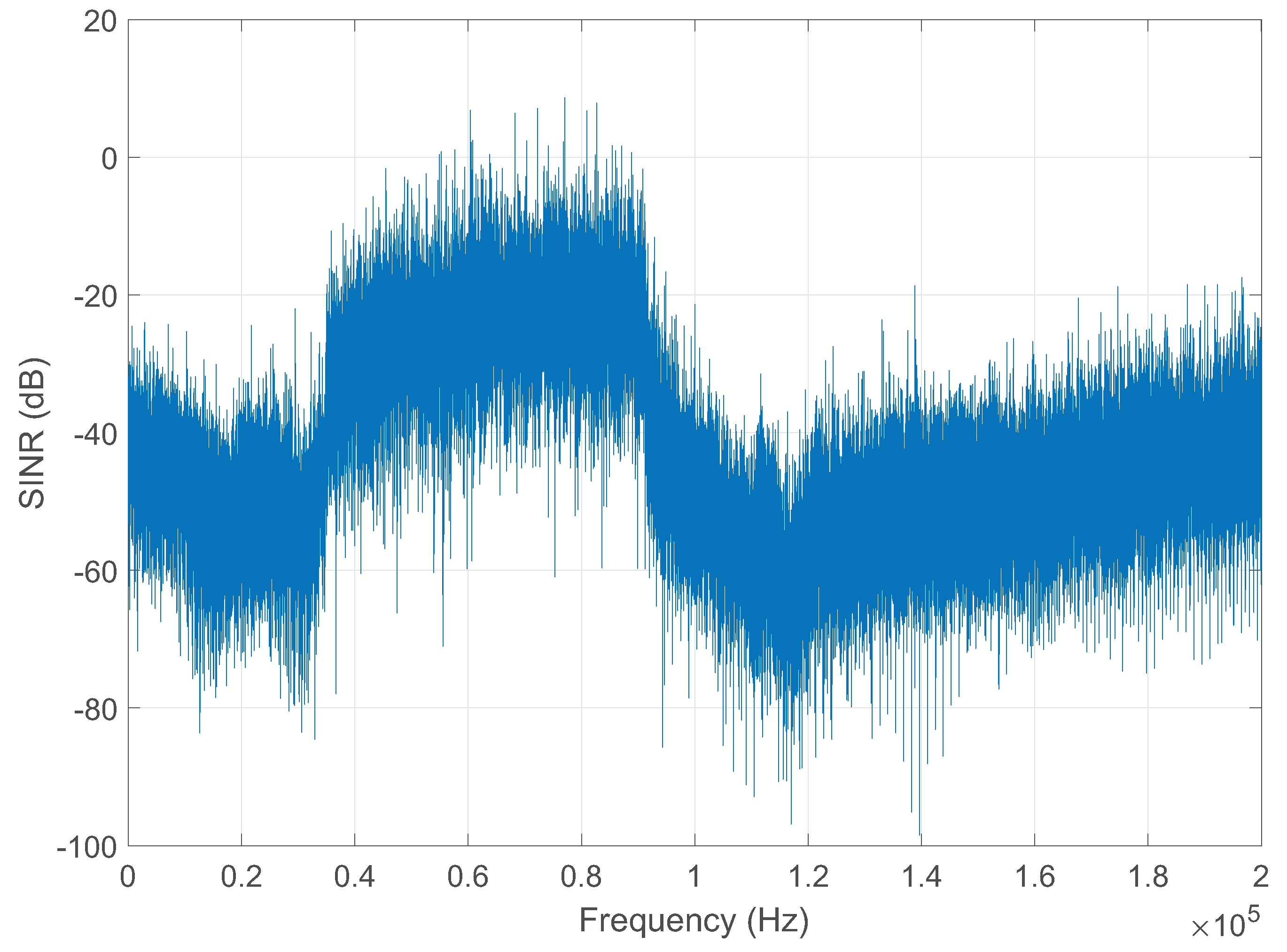
4.1. Evaluation of CSIN Estimation Module

In CSIN estimation, the number of ${\mathbf{h}}_1\left[n\right]$ branches was 15 and the FIR filter length for each branch was 16. As a performance metric, we adopted the averaged “error-to-signal power ratio” (ESR), which is defined as follows:

$$\begin{array}{c}\hfill {\displaystyle {\mathrm{ESR}}_{\mathrm{CSIN},{\mathbf{h}}_1}=10{log}_{10}\frac{{\sum }_n{\left|\eta \left[n\right]-\widehat{\eta }\left[n\right]\right|}^2}{{\sum }_n{\left|y\left[n\right]\right|}^2}}\end{array}$$

(20)

where $y\left[n\right]$ is the output signal of the powerline channel without any additive noise. Assumed the frequency offset is less than $\pm 4\%$ of the frequency of the mains voltage. Thus, we consider the cyclic frequency offset $\Delta =\pm 4.8$ Hz in our simulation. As shown in Figure 8a, $\Delta$ significantly degraded the performance of the CSIN estimation module. When the $E_b/N_0$ was less than 24 dB, the FRESH filter ${\mathbf{h}}_1\left[n\right]$ became counterproductive in terms of ESR, unless compensation for the cyclic frequency offset was provided. As shown in Figure 8b, the our proposed scheme succeeded in suppressing the value of ${\mathrm{CFRE}}_{\mathrm{CSIN}}$ to within approximately $\pm 0.65\%$. Note that the value of ${\mathrm{CFRE}}_{\mathrm{CSIN}}$ is about $3.85\%$ in the case of no compensation for the cyclic frequency offset, i.e., ${\widehat{\Delta }}_1=0$ Hz. This implies our method suppresses ${\mathrm{CFRE}}_{\mathrm{CSIN}}$ by at least 15.45 dB.

4.2. Evaluation of the BER Performance

For the signal restorer, the number of ${\mathbf{h}}_2\left[n\right]$ branches was five and the FIR filter length for each branch was 64. The resulting BER performance is shown in Figure 9. We previously demonstrated that cyclic frequency offset can significantly degrade the performance of a FRESH-filter receiver. Failure to compensate for such errors degrades BER performance to below that of the case without CSIN mitigation. At BER = ${10}^{-4}$, the $E_b/N_0$ required for the various cases was as follows: $\Delta =0$ Hz (22.6 dB), $\Delta =\pm 4.8$ Hz with cyclic frequency offset compensation (23.3 dB), without applying CSIN mitigation (25.2 dB), and $\Delta =\pm 4.8$ Hz without compensation (26 dB). These results show that the proposed method imposed a loss of only 0.7 dB, compared with the ideal case ($\Delta =0$ Hz). Note however that the proposed method enabled gains of 1.9 dB and 2.7 dB, compared with the case without CSIN mitigation and the case without cyclic frequency offset compensation. Nevertheless, the required $E_b/N_0$ to reach BER = ${10}^{-4}$ is only about 8 dB when there is no CSIN in our simulation model. This resulted from the fact that the averaged power of the CSIN is 100 times of the averaged power of the background AWGN and the CSIN cannot completely be removed by the receiver.

5. Conclusions and Discussion

This paper presents a novel FRESH-filter receiver, which exploits variations in spectral correlation among additive CSIN and received OFDM symbols aimed at mitigating the CSIN parts, while enhancing the OFDM signal parts. We also devised a method by which to estimate the cyclic frequency offset issue associated with the FRESH filter. The efficacy of the proposed scheme was verified using computer simulations with parameters conforming to IEEE 1901.2 standard. Our simulation results are summarized as follows:

(1)

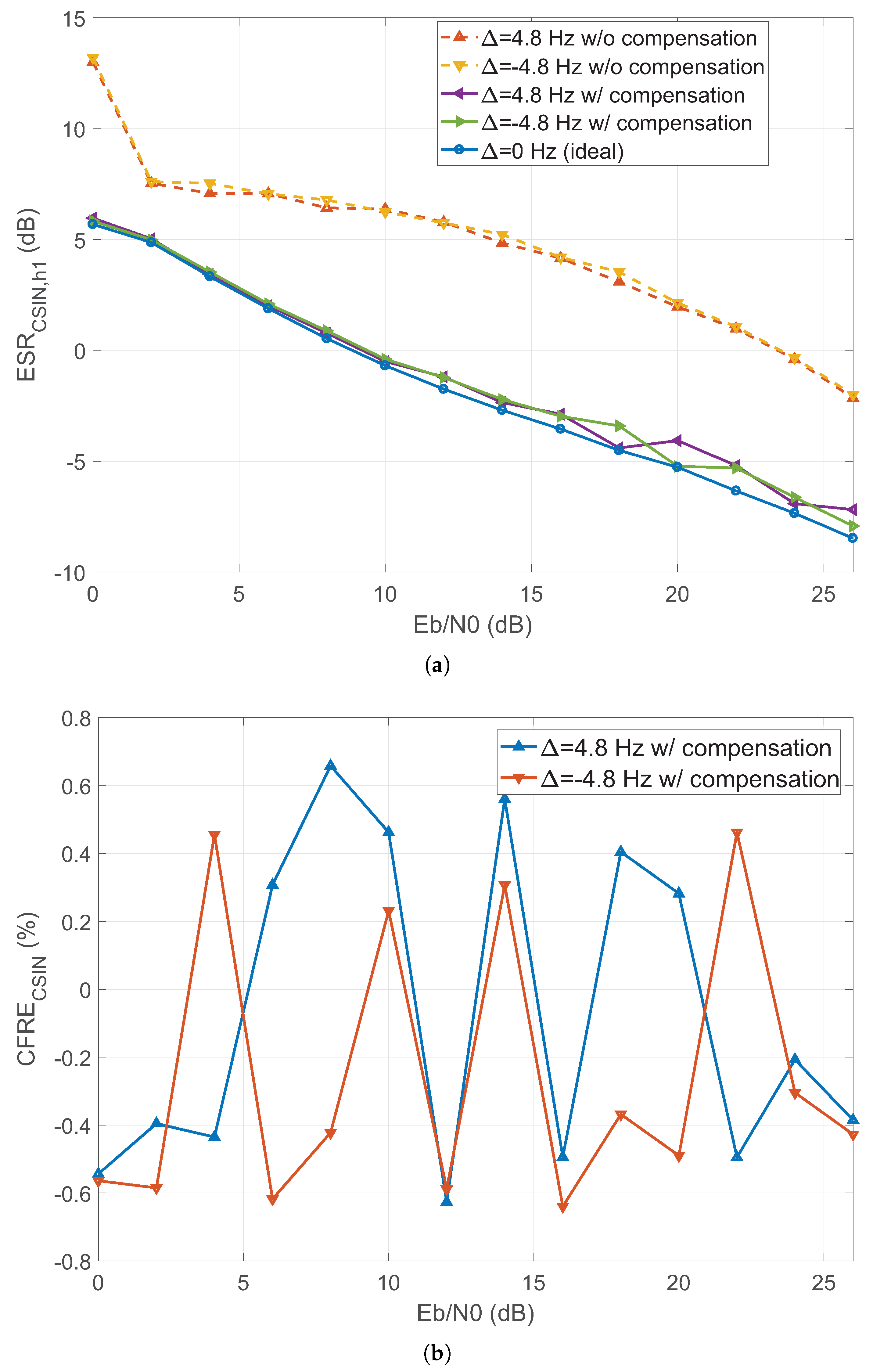
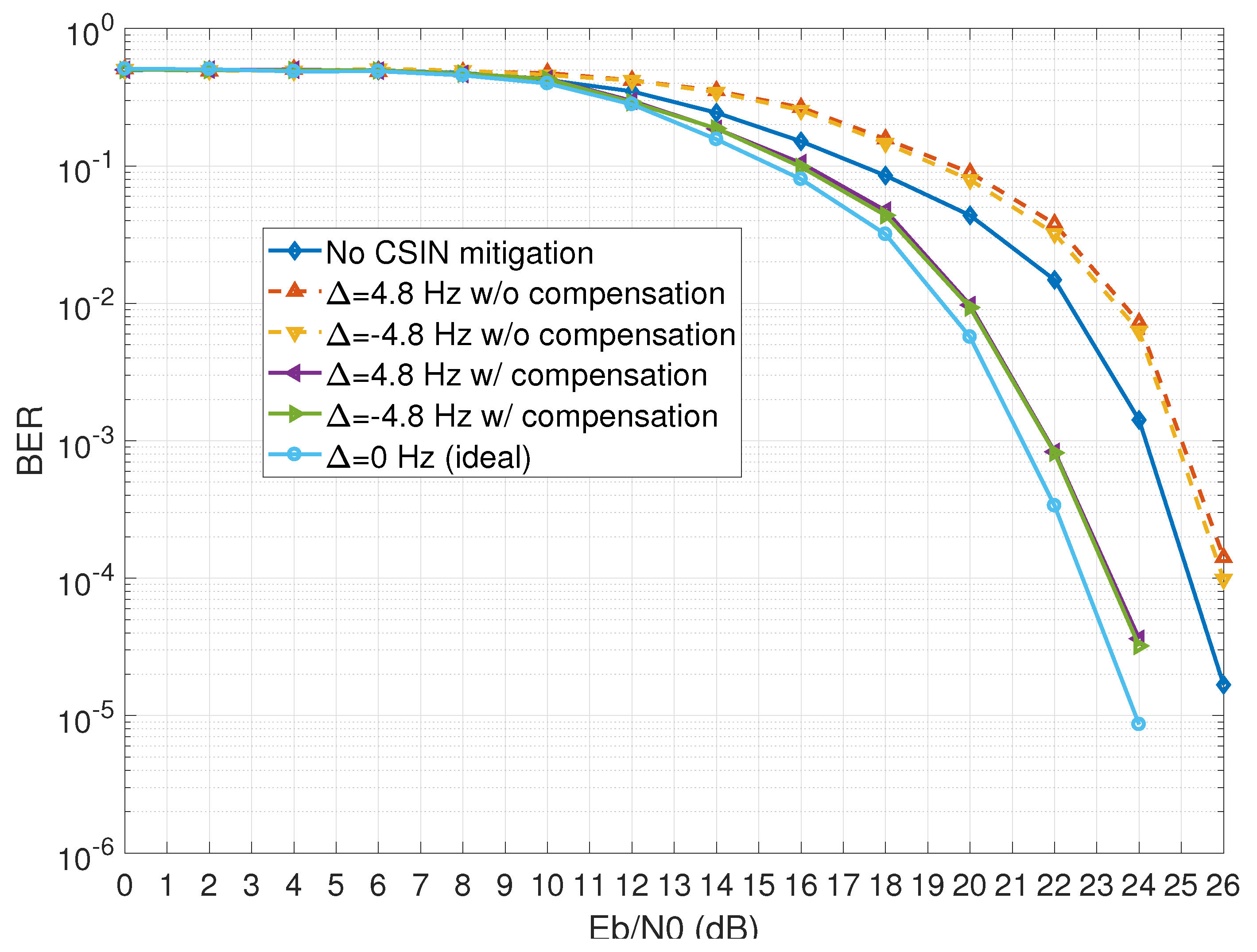
Cyclic frequency offset could degrade the performance of the FRESH-filter receiver to below that of the case without CSIN mitigation. Without the compensation for cyclic frequency offset, it could results in a loss of required $E_b/N_0$ about 0.9 dB and 3.3 dB for the case of no CSIN mitigation and the case of no cyclic frequency offset, respectively.

(2)

Our approach to estimating cyclic frequency offset by observing the phase variation of the tap weights of the FRESH filter made it possible to suppress the cyclic frequency relative error by at least 15.45 dB (from $3.85\%$ to $0.65\%$).

(3)

Following compensation for cyclic frequency offset, attaining a BER of ${10}^{-4}$ imposed an $E_b/N_0$ loss of only 0.7 dB compared with the ideal case ($\Delta =0$ Hz).

(4)

When the value of $E_b/N_0$ was fixed at 24 dB, the resulting BERs were as follows: proposed method ($3.2\times {10}^{-5}$) and the case without cyclic frequency offset compensation ($7.3\times {10}^{-3}$).

Cyclostationary signal processing and the FRESH filtering have been applied in various fields, such as non-orthogonal multiplexed cognitive radio system, spectrum sensing, and chaotic communications. However, if the FRESH filters have no perfect information of cyclic frequency associated with cyclostationary signals, the cyclic frequency offset issue should be considered. In addition, we considered the cyclic frequency offset is deterministic but unknown in this paper. In our future work, we will integrate our algorithm into a feedback loop such that the offset can be continuously tracked. Moreover, we will plan and conduct real experiments to measure the CSIN noise sources and time-varying cyclic frequency offset to further validate our proposed method on real NB-PLC communications.