Two Open Solutions for Industrial Robot Control: The Case of PUMA 560
Abstract
1. Introduction
2. Materials and Methods
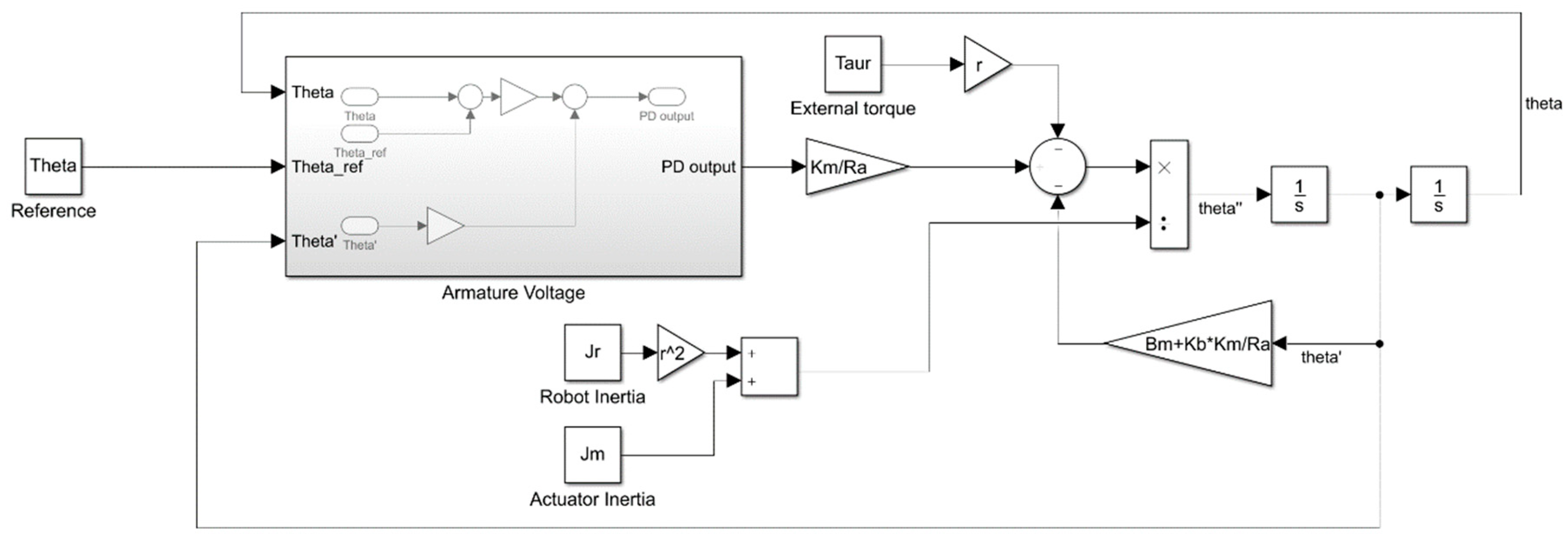
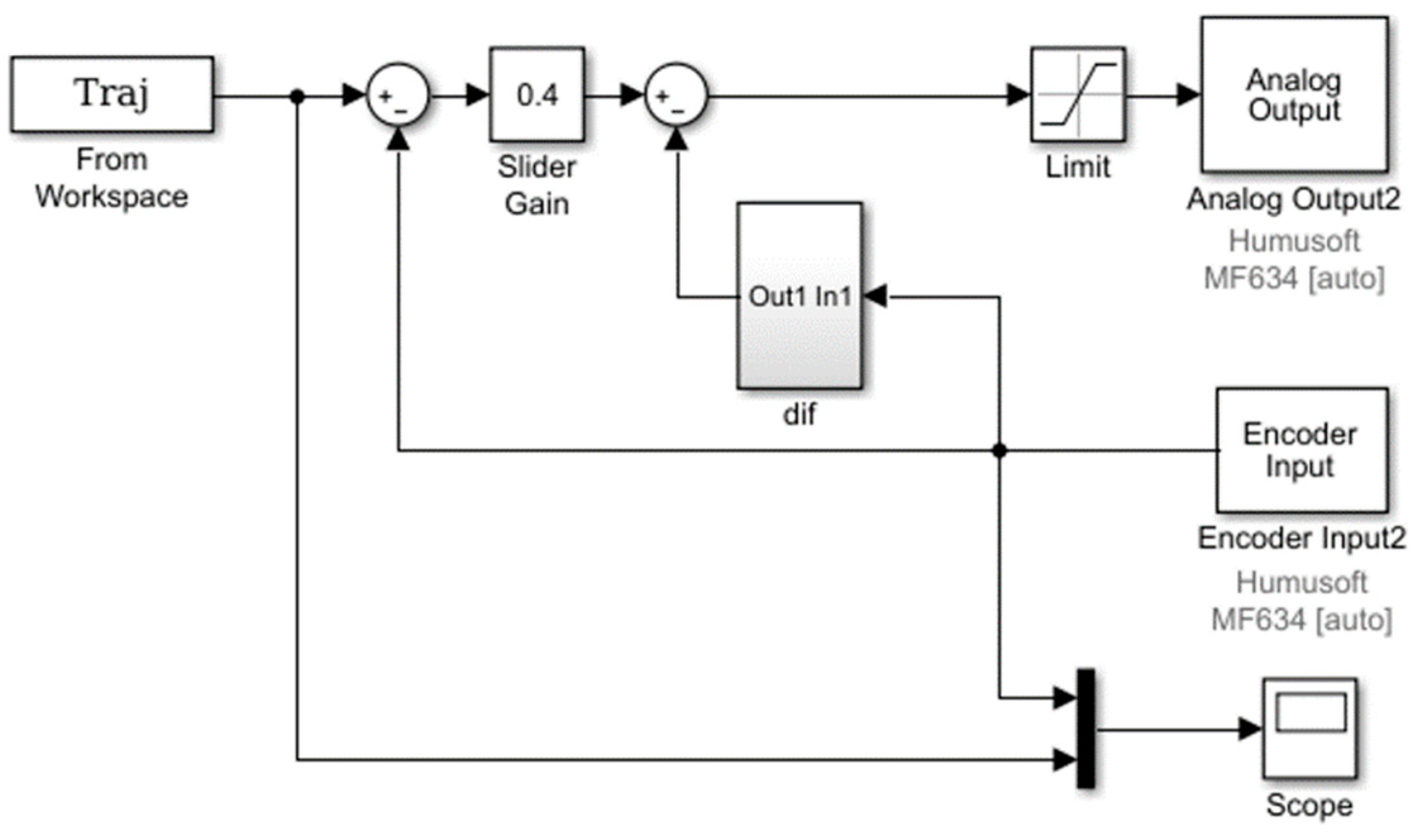
2.1. Simulation of the PUMA 560 First Robot Axis
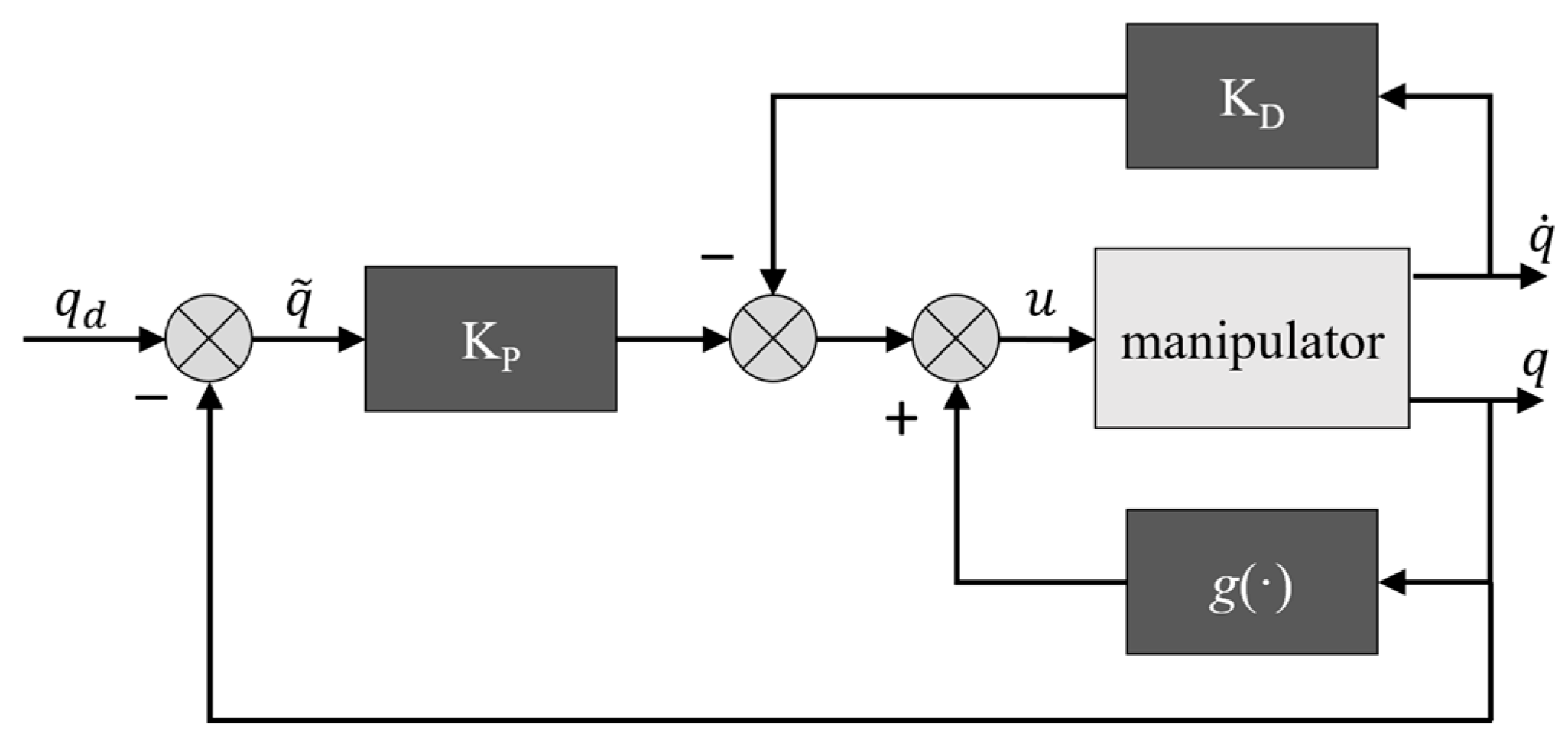
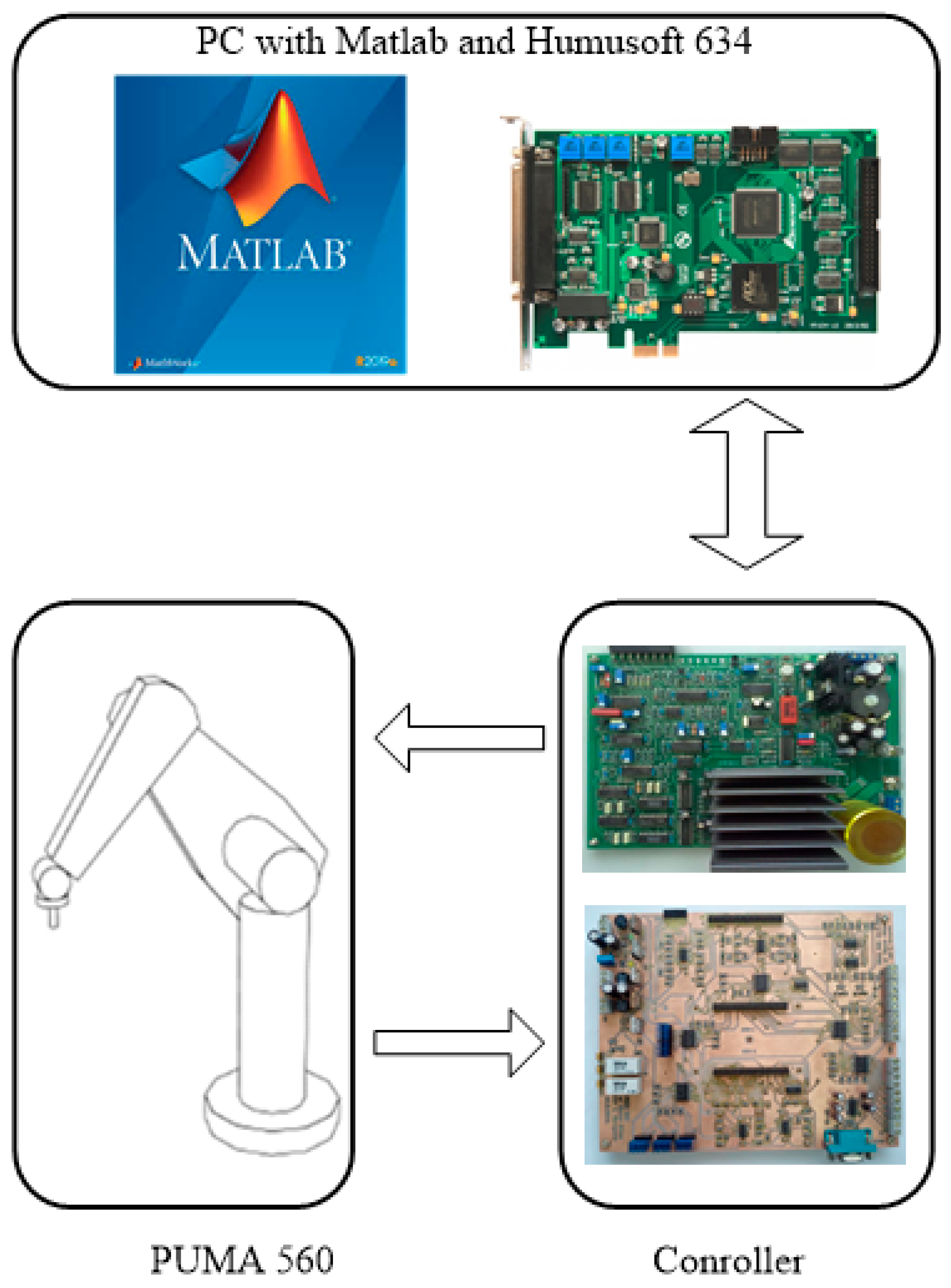
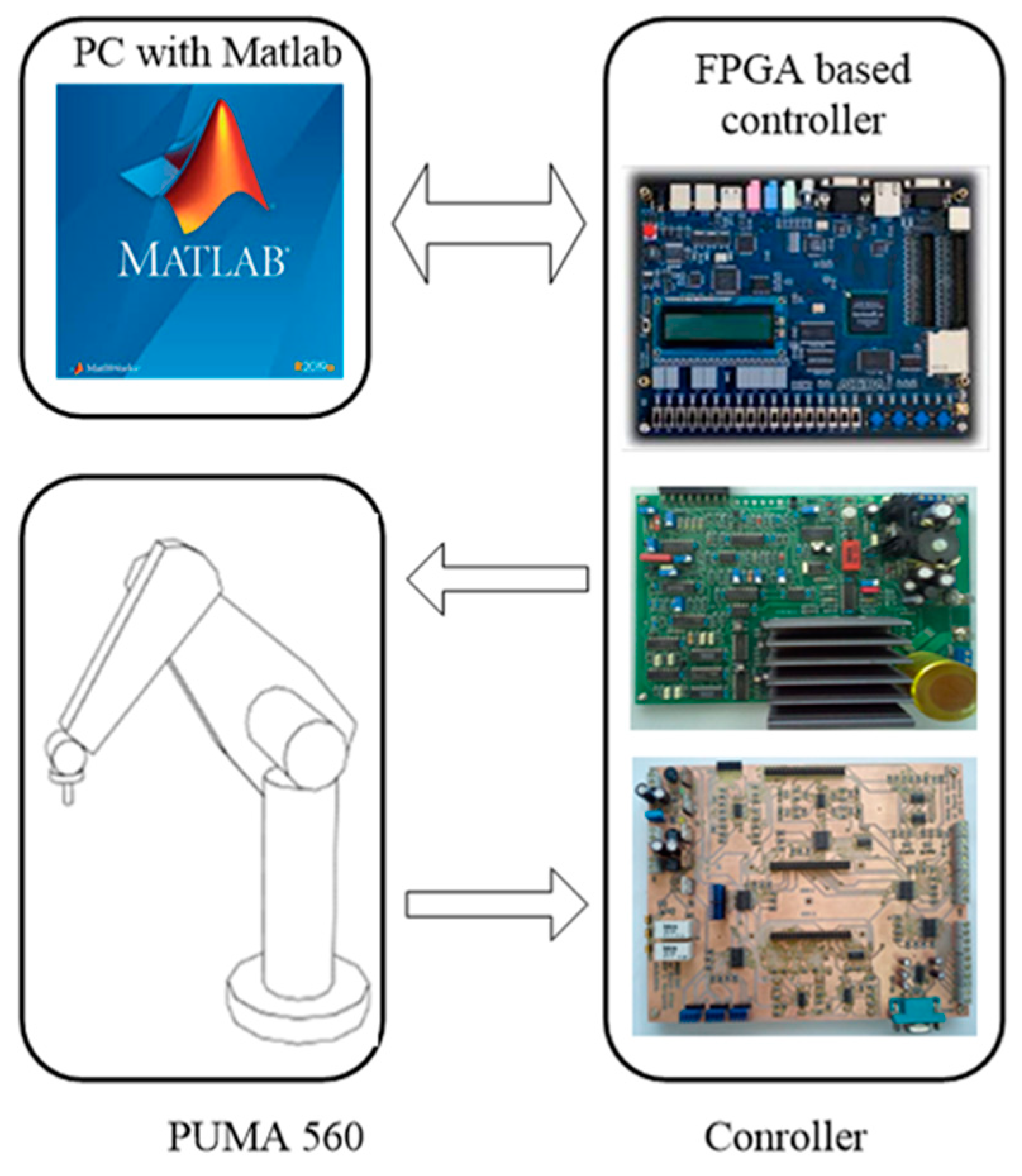
2.2. Control Scheme Using PC
2.3. Control Scheme Using FPGA
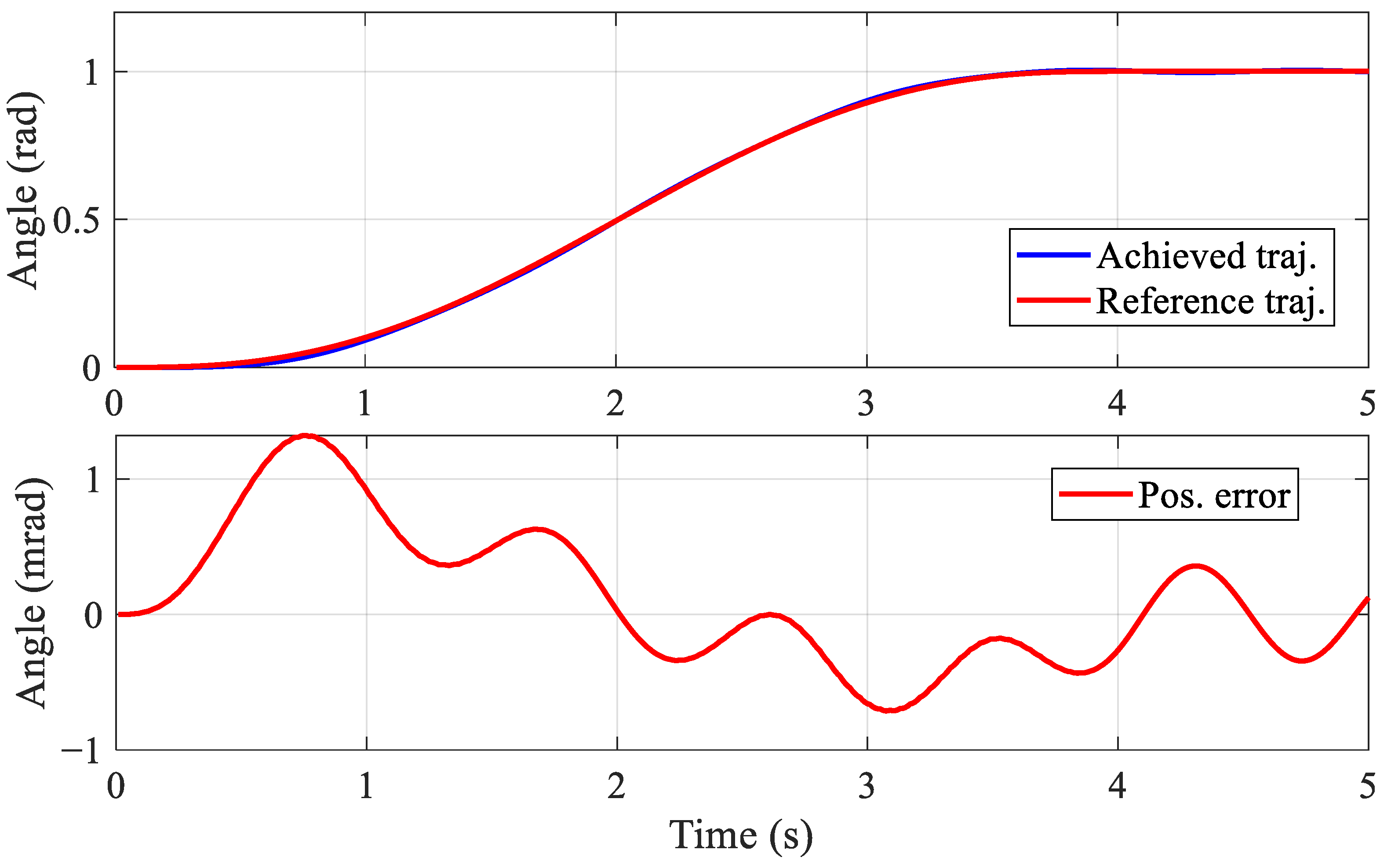
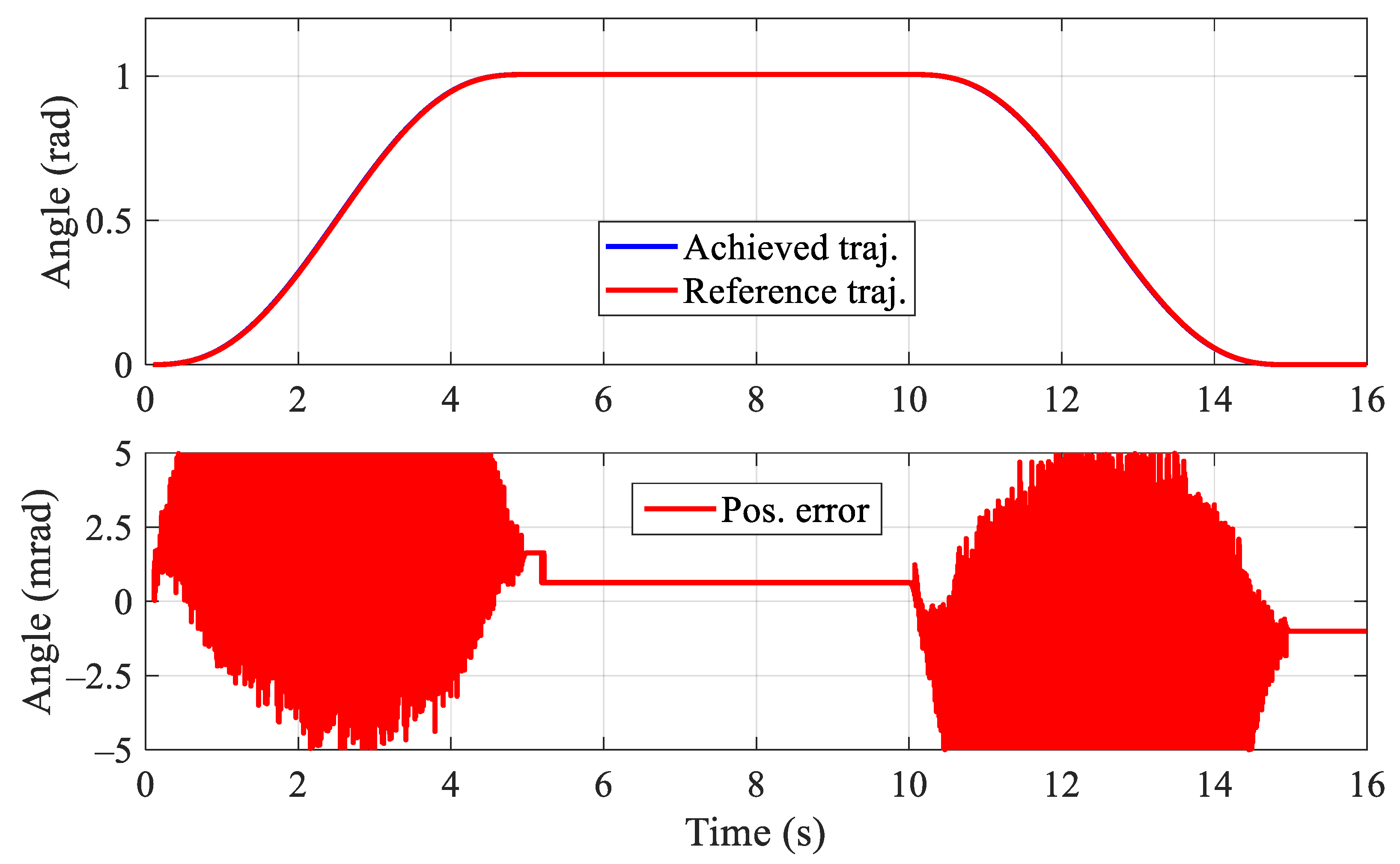
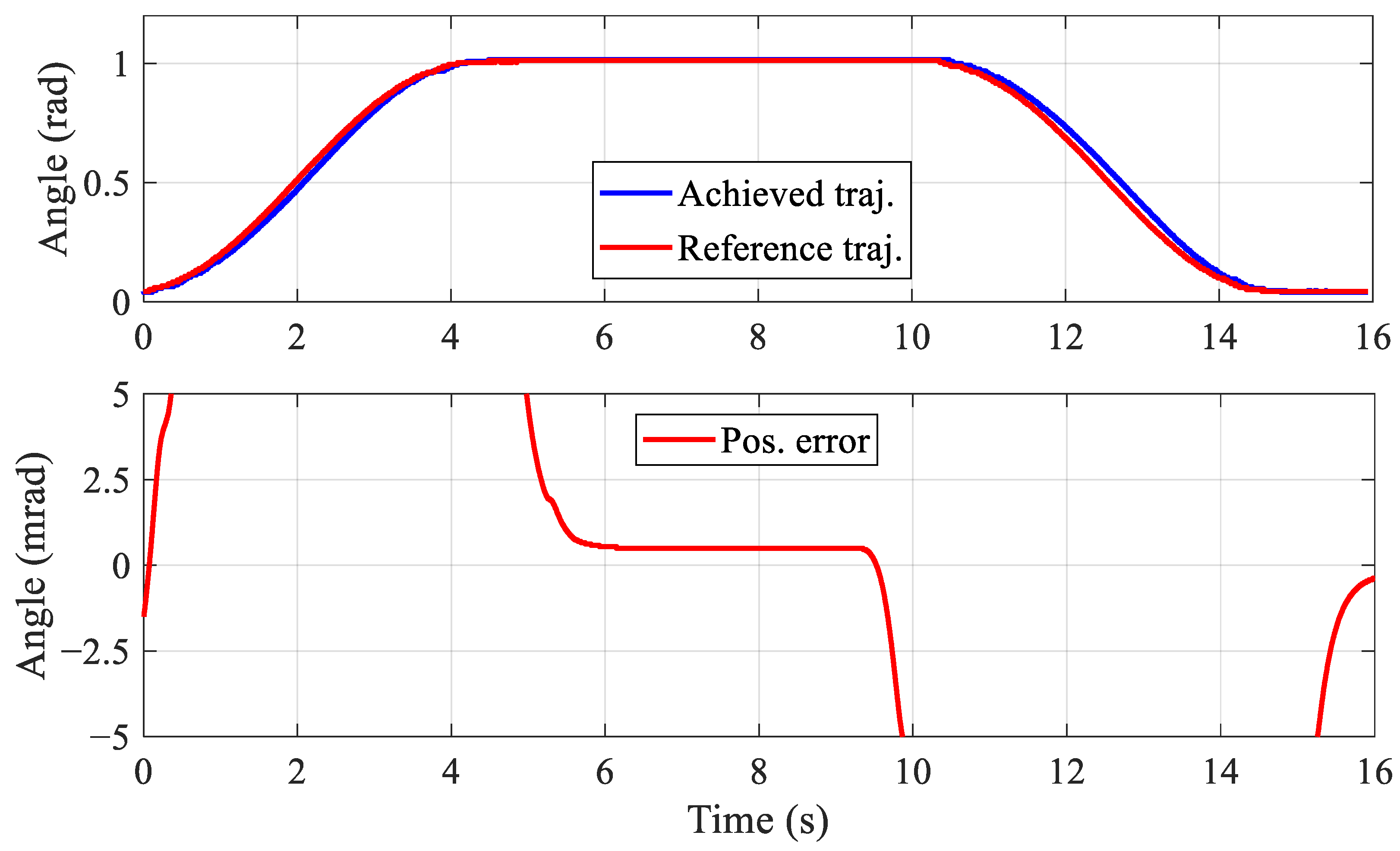
3. Results
4. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Shah, A. Can You Repair What You Own? Mech. Eng. 2018, 140, 37–41. [Google Scholar] [CrossRef][Green Version]
- Mondada, F.; Bonani, M.; Riedo, F.; Briod, M.; Pereyre, L.; Retornaz, P.; Magnenat, S. Bringing Robotics to Formal Education: The Thymio Open-Source Hardware Robot. IEEE Robot. Autom. Mag. 2017, 24, 77–85. [Google Scholar] [CrossRef]
- Corke, P.I. Robotics, Vision & Control; Springer: Cham, Switzerland, 2017; ISBN 978-3-319-54413-7. [Google Scholar]
- Farooq, M.; Wang, D.-B. Implementation of a new PC based controller for a PUMA robot. J. Zhejiang Univ. A 2007, 8, 1962–1970. [Google Scholar] [CrossRef]
- Altintas, A. A new approach to 3-axis cylindrical and cartesian type robot manipulators in mechatronics education. Elektronika ir Elektrotechnika 2015, 106, 151–154. [Google Scholar] [CrossRef]
- Plauska, I.; Lukáš, R.; Damaševičius, R. Reflections on Using Robots and Visual Programming Environments for Project-Based Teaching. Elektronika ir Elektrotechnika 2014, 20. [Google Scholar] [CrossRef]
- Becerra, V.; Cage, C.; Harwin, W.; Sharkey, P. Hardware retrofit and computed torque control of a Puma 560 Robot updating an industrial manipulator. IEEE Control Syst. Mag. 2004, 24, 78–82. [Google Scholar] [CrossRef]
- Costescu, N.; Loffler, M.; Zergeroglu, E.; Dawson, D. QRobot—A multitasking PC based robot control system. In Proceedings of the 1998 IEEE International Conference on Control Applications (Cat. No.98CH36104), Trieste, Italy, 4 September 1998; pp. 892–896. [Google Scholar]
- Piltan, F.; Sulaiman, N.; Marhaban, M.H.; Nowzary, A.; Tohidian, M. Design of FPGA based sliding mode controller for robot manipulator. Int. J. Intell. Syst. Appl. Rob. 2011, 2, 183–204. [Google Scholar]
- Martínez-Prado, M.A.; Rodríguez-Reséndiz, J.; Gómez-Loenzo, R.A.; Herrera-Ruiz, G.; Franco-Gasca, L.A. An FPGA-Based Open Architecture Industrial Robot Controller. IEEE Access 2018, 6, 13407–13417. [Google Scholar] [CrossRef]
- Ordóñez Cerezo, J.; Castillo Morales, E.; Cañas Plaza, J.M. Control System in Open-Source FPGA for a Self-Balancing Robot. Electronics 2019, 8, 198. [Google Scholar]
- Riid, A.; Preden, J.; Pahtma, R.; Serg, R.; Lints, T. Automatic Code Generation for Embedded Systems from High-Level Models. Elektronika ir Elektrotechnika 2009, 95, 33–36. [Google Scholar]
- Zhao, W.; Kim, B.H.; Larson, A.C.; Voyles, R.M. FPGA implementation of closed-loop control system for small-scale robot. In Proceedings of the ICAR ’05, Proceedings, 12th International Conference on Advanced Robotics, Seattle, WA, USA, 18–20 July 2005; pp. 70–77. [Google Scholar]
- Wang, W.-S.; Liu, C.-H. Implementation and experimental study of a multiprocessor system for real-time model-based robot motion control. IEEE Trans. Ind. Electron. 1994, 41, 163–172. [Google Scholar] [CrossRef]
- Bruno, S.; Lorenzo, S.; Luigi, V.; Giuseppe, O. Robotics—Modelling, Planning and Control; Springer: Cham, Switzerland, 2008. [Google Scholar]
- Corke, P. MATLAB toolboxes: Robotics and vision for students and teachers. IEEE Robot. Autom. Mag. 2007, 14, 16–17. [Google Scholar] [CrossRef]
- Corke, P.; Armstrong-Hélouvry, B. A search for consensus among model parameters reported for the PUMA 560 robot. In Proceedings of the 1994 IEEE International Conference on Robotics and Automation, San Diego, CA, USA, 8–13 May 1994; pp. 1608–1613. [Google Scholar]
- Arimoto, S.; Miyazaki, F. Asymptotic stability of feedback control laws for robot manipulator. IFAC Proc. Vol. 1985, 18, 221–226. [Google Scholar] [CrossRef]
- Jokic, D.Z.; Lubura, S.D.; Stankovski, S. Universal block for simple design of FPGA based controller in anthropomorphous robot configuration. IFAC-PapersOnLine 2015, 48, 135–140. [Google Scholar] [CrossRef]
- Jokic, D.; Lubura, S.; Stankovski, S. Innovative approach to programming of robot PUMA 560. In Proceedings of the XVI International Scientific Conference on Industrial Systems, Novi Sad, Serbia, 15–17 October 2014; pp. 95–100. [Google Scholar]
- Dejan, Ž.J.; Lubura, S.D.; Stankovski, S.; Jokic, D. Development of a new controller with FPGA for PUMA 560 robot. IFAC Proc. Vol. 2013, 46, 161–166. [Google Scholar] [CrossRef]
- Jokić, D.Ž.; Lubura, S.D. Comparative Analysis of the Controllers for PUMA 560 Robot. IFAC-PapersOnLine 2016, 49, 98–103. [Google Scholar] [CrossRef]
- Jokic, D.; Lubura, S.; Stankovski, S. Development of Integral Environment in Matlab/Simulink for FPGA. Adv. Electr. Electron. Eng. 2014, 12, 453–468. [Google Scholar] [CrossRef]
- Jokic, D.; Lubura, S.; Lale, S.; Lukač, D. Encoder signal processing on FPGA platform realized in Matlab/DSP Builder. In Proceedings of the 2012 20th Telecommunications Forum (TELFOR), Belgrade, Serbia, 20–22 November 2012; pp. 1044–1047. [Google Scholar] [CrossRef]
- Kelly, R. PD Control with Desired Gravity Compensation of Robotic Manipulators. Int. J. Robot. Res. 1997, 16, 660–672. [Google Scholar] [CrossRef]
- Chiacchio, P.; Chiaverini, S.; Siciliano, B. Task-Oriented Kinematic Control of Two Cooperative 6-DOF Manipulators. In Proceedings of the 1993 American Control Conference, San Francisco, CA, USA, 2–4 June 1993; Institute of Electrical and Electronics Engineers (IEEE); pp. 336–340. [Google Scholar]
- Ikeda, T.; Minami, M. Asymptotic stable guidance control of pws mobile manipulator and idynamical influence of slipping carrying object to stability. In Proceedings of the 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2003) (Cat. No.03CH37453), Las Vegas, NV, USA, 27–31 October 2003. [Google Scholar] [CrossRef]


| Joint | Parameter | Value |
|---|---|---|
| 1st joint | Gear ratio Kr | 62.61 |
| Encoder | 1000 imp/rev | |
| Accuracy | 0.101 mrad | |
| Length in Home position | 0.43 m | |
| - | Jm,1 | 2 × 10−4 kgm2 |
| Bm,1 | 6.3 Nms/rad | |
| Ra,1 | 2.1 Ω | |
| Km,1 | 0.223 Nm/A | |
| r1 | 62.61 | |
| Kb,1 | 0.26 V/rads | |
| Kp | 260 | |
| Kd | 80 | |
| All joints | PUMA 560 mass | 54.5 kg |
| Workspace | 320° |
| Features (Low, Medium, High) | Type of Controller | |
|---|---|---|
| PC-Based | FPGA-Based | |
| Reliability | Low | High |
| Vulnerable on virus | High | Low |
| Skills | Low | High (Expert) |
| Industrial oriented | Low | High |
| Educational oriented | High | Low |
| Tuning parameters | High | Medium |
| Price of hardware | Medium | Low |
| Price of software | High | Low |
| Possibility of generating an ASIC deisgn | Low | High |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jokić, D.; Lubura, S.; Rajs, V.; Bodić, M.; Šiljak, H. Two Open Solutions for Industrial Robot Control: The Case of PUMA 560. Electronics 2020, 9, 972. https://doi.org/10.3390/electronics9060972
Jokić D, Lubura S, Rajs V, Bodić M, Šiljak H. Two Open Solutions for Industrial Robot Control: The Case of PUMA 560. Electronics. 2020; 9(6):972. https://doi.org/10.3390/electronics9060972
Chicago/Turabian StyleJokić, Dejan, Slobodan Lubura, Vladimir Rajs, Milan Bodić, and Harun Šiljak. 2020. "Two Open Solutions for Industrial Robot Control: The Case of PUMA 560" Electronics 9, no. 6: 972. https://doi.org/10.3390/electronics9060972
APA StyleJokić, D., Lubura, S., Rajs, V., Bodić, M., & Šiljak, H. (2020). Two Open Solutions for Industrial Robot Control: The Case of PUMA 560. Electronics, 9(6), 972. https://doi.org/10.3390/electronics9060972







