1. Introduction
Parkinson’s Disease (PD) is a multi-systemic neurodegenerative disorder, affecting about 4% of people over the age of 80 [
1]. It causes both motor and non-motor signs and symptoms, mainly due to the death of dopaminergic neurons in the
substantia nigra pars compacta in the midbrain. The main PD motor symptoms encompass rigidity, slowness of movement (bradykinesia), impaired posture and balance, loss of automatic movements, speech and writing disability [
2]. The diagnosis of PD is mainly based on clinical observation of direct signs of the disease, thus it is conditioned to the manifestation of motor symptoms [
3]. Postural stability (PS) is typically impaired in PD patients, and worsens with disease progression [
4,
5]. The difficulty in balancing the Center of Mass (COM) makes PD patients prone to the risk of falls [
6]. However, in the initial stages of the disease, PS is often difficult to evaluate during outpatient visits, so it is seldom employed as a diagnostic criterion. On the other hand, the scoring of PS is useful to monitor the progression of the disease. In fact, a pronounced impairment in PS may denote a definite progression towards severe disease conditions.
PS is clinically assessed following the MDS–UPDRS (Movement Disorder Society–Unified Parkinson’s Disease Rating Scale) part-III recommendations [
7]. Item 3.12—”Postural Stability” contains the PS evaluation details. In brief, the retropulsion test allows the clinician to evaluate the response to the body displacement due to a quick and forceful pull on the subject’s shoulders. The evaluation is in the form of a score between 0 and 4, based on the recovery time and on the number of steps the subject takes to recover the stance position. However, it should be noticed that the retropulsion test represents a somehow invasive measure, does not exclude a risk of fall for patients, and cannot be implemented in a non-controlled environment.
The main objective of this work is to provide an automated tool, capable of accurately evaluate postural stability in PD subjects, employing a simple and safe exercise of quiet stance. Such a tool can be used to assess PS in initial stages of the disease, as well as to monitor the disease progression and risk of falls also in domestic environment [
8]. In fact, the use of commercial smartphones, a widespread and easy to use technology, can offer precious benefits to both patients and caregivers, in view of a home-monitoring system during activities of daily living.
Postural control is highly correlated to the movements of the COM [
6], and this latter concept is directly and quantitatively measurable by means of wearable (e.g., accelerometers and gyroscopes) or non-wearable (e.g., stabilometric board) sensors [
6]. Many literature studies have proven the capability of inertial sensors to quantify postural control in healthy and PD population [
6,
8]. The lumbar region has been identified as the most suitable location for data acquisition [
9]. A direct comparison between outcomes of stabilometric boards, representing the
gold standard for PS assessment, and inertial sensors yielded a sound correlation among the two measures [
10], paving the way to a possible PS assessment outside the laboratory environment. Further studies have demonstrated the possibility of discriminating PD subjects from healthy controls [
6], distinguishing patients with mild and severe disease progression [
8], detecting subjects with high risk of falls [
11] and monitoring disease progression [
8]. Most literature studies share similar inclusion criteria, clinical assessment, sample dimension, instrumentation, experimental protocol, and types of features extracted from raw inertial data. In more detail, data sets typically include subjects with diagnosis of idiopathic PD and possibly healthy controls. For example, in [
6,
8] the dataset includes 13 PD patients and 12 healthy controls. Clinical information encompasses the UPDRS-part III score, Hoeh & Yahr stage (H&Y, measure of disease progression in Parkinson’s Disease) and years from diagnosis. Most commonly employed sensors are tri-axial accelerometer and gyroscope. As for feature extraction, common measures describe COM displacement and velocity [
12]; signal variability as computed from variance, root mean square and standard deviation [
13]; movement rapidity as computed by jerkiness [
6]; spectral-domain measures, such as total power and power in specific bands [
13].
The results achieved in the present work point out that a waist-worn smartphone can be used as an automated tool to provide a picture of postural impairment in PD patients in about 30 s. This smartphone-based approach was able to distinguish subjects with optimal, slightly impaired and impaired postural control with 100% accuracy. To the best of our knowledge, no classification based on postural impairment level has been performed yet. The present study is meant to provide an easy-to-use and practical tool for the gross evaluation of postural stability in PD patients. At present, the implemented tool could be employed for a continuous and remote monitoring of postural impairment in PD patients. The rest of this work is organized as follows. In
Section 2 we describe the data included in our study, the experimental protocol and the implementation of the algorithm for PS evaluation; in
Section 3 we report the results and discuss the significance of the work and the limitations of the present study; finally, in
Section 4 we draw our conclusions, outlining a practical use of the algorithm and proposing possible future developments.
2. Materials and Methods
In this Section we describe in detail the employed dataset (
Section 2.1) as well as the experimental protocol used for data acquisition (
Section 2.2). Moreover, we provide a preliminary evaluation to assess the feasibility of this study (
Section 2.3); we describe the feature extraction task, focusing on the most relevant features (
Section 2.4). We address a novel feature selection method based on correlation between features and PS score (
Section 2.5). Finally, we discuss the selection of the final Machine Learning (ML) model and the optimization process (
Section 2.6). A schematic workflow is provided in
Figure 1.
2.1. The Dataset
Data acquisition has been carried out at the Regional Reference Center for Parkinson’s Disease and Movement Disorders, University Hospital Città della Salute e della Scienza, Turin (Italy). The study has been conducted in accordance with the Declaration of Helsinki and approved by the local Ethics Committee. Participants received detailed information on the study purposes and execution, and written informed consent for observational study was obtained. Demographic and clinical data were noted anonymously. Patients agreed to the video-taping of the procedure after receiving suitable explanations and privacy guarantees. The experiments have been carried out in hospital during the periodically scheduled outpatient visits; hence, the patients’ safety was granted by the presence of the medical staff. A total number of 42 PD patients has been recruited in the study. The inclusion criteria were: a clinical diagnosis of idiopathic Parkinson’s Disease with motor signs and symptoms; no major cognitive impairment or other conditions preventing the patient from correctly accomplishing the task; ability to keep a stance position without assistance for at least one minute; absence of dyskinesia and other comorbidities or conditions affecting balance.
Given that the experiments have been carried out during the outpatient visit, most patients were in
daily on condition, i.e., under the effect of their usual drug dose, even though a variable time interval had elapsed since the last administration. Data acquisition has also been performed on 7 young healthy subjects. The choice of a control population that does not match the PD sample for age was driven by the need of selecting some subjects with recognized optimal postural control. This allowed us to define a scale into which to position different PS levels, with controls representing the best achievable value. The number of controls was chosen in order to match that of PD patients with the worst possible postural control level. The population characteristics are summarized in
Table 1 for all PD patients and control subjects, whereas in
Table 2 are divided based on PS score.
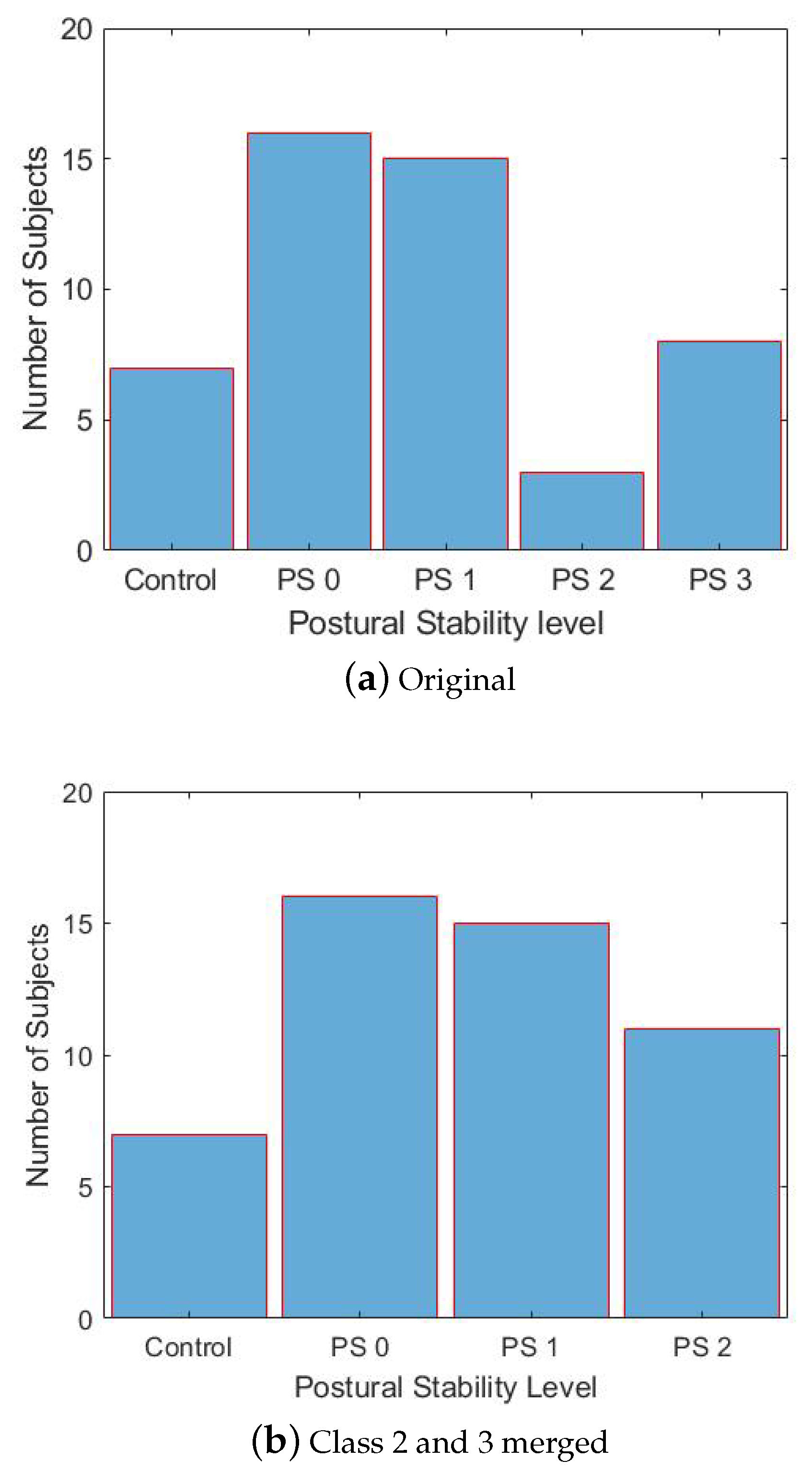
The clinical PS assessment was carried out by expert neurologists by means of the retropulsion test (MDS–UPDRS-part III, item 3.12). Neurologists assigned a score between 0 and 4, following the MDS–UPDRS recommendations. Based on this clinical score, PD subjects were divided into classes; the distribution of patients in each class, along with the control population, is reported in
Figure 2. As can be appreciated from
Figure 2a, no patient is reported in class 4, despite item 3.12 being in the range [0, 4]. This is in line with the MDS–UPDRS recommendations. In fact, a score of 4 is assigned in case the subject is largely unstable, and is unable to regain stability after it is lost. Thus, such patients usually do not perform the retropulsion test. As for patients in class 0 and 1, they take a maximum of 2 and 5 steps for recovering their balance, respectively. As for patients in class 2 and 3, they largely share a drastic deficiency of postural reflexes. Class 2 patients should be able to recover their balance taking a maximum of 5 steps backward, whereas class 3 patients should not. However, it is not common among neurologists to wait for the patient to take 5 steps backwards before grabbing them in a safe way. As a consequence, class 2 and 3 are largely overlapped, and the distinction between the two is somewhat arbitrary. Moreover, the variance
v of the data distribution computed either keeping classes 2 and 3 separated or merged together revealed a negligible difference, i.e.,
. Thus, in accordance with the expert neurologists participating in this study, we decided to merge classes 2 and 3 into a single class, named 2 in the rest of this paper. The resulting distribution is reported in
Figure 2b.
2.2. Experimental Protocol
Data acquisition was performed by means of inertial sensors, i.e., tri-axial accelerometer and tri-axial gyroscope, embedded in a commercial smartphone. The smartphone was placed inside an elastic band and secured to the patients lower back, at L3–L5 level. The smartphone recorded and locally stored inertial data by means of SensorLog, a commercial app for Android 6.0. Once collected, data were exported in CSV format and processed offline using MATLAB, version 2019b for Windows 10. We verified that the reported values were not limited by neither the Operative System nor the application employed by visual and computational analysis of the data exported in CSV files. Subjects were asked to keep a stable upright position, with their feet approximately 10 cm apart, their arms relaxed along the body, eyes open looking straight ahead. Data recording was carried out only once for at least 30 s.
2.3. Preliminary Evaluation
First of all, we investigated the technical characteristics of the employed smartphone, in terms of resolution and noise. Such specifications are very important in our context, since the experimental protocol only encompasses a stance phase, with subjects keeping a static position. Hence, small variations of the inertial sensors should be appreciated, and this requires adequate sensor resolution and noise levels. In
Table 3 we report the technical specification of the sensors embedded in the smartphone Samsung Galaxy S5 mini employed in our experiments.
We have verified that sensor noise was negligible if compared to the expected signal amplitude, performing some preliminary data acquisition tasks; this will be further discussed in
Section 3.
In order to check the feasibility of a multi-class classification problem, we performed some preliminary steps, briefly described in the rest of this Section. First of all, we verified whether significant differences arose between different classes in the frequency domain. To this end, we computed the Power Spectral Density (PSD) for each signal in the database, keeping each acceleration and angular velocity component separated, and after removing mean values and possible trends in raw signals. In more detail, a Welch periodogram was computed, setting the window length equal to the signal length (30 s) and zero window overlap, in order to achieve the highest possible frequency resolution. Then, we computed the spectrogram similarity among subjects belonging to the same class, and among those belonging to different classes. To this end, we employed a Dynamic Time Warping (DTW) approach.
The DTW is able to measure the similarity between two signals, after non-linear stretching and distortion in order to minimize the difference to the maximum possible extent. It returns two parameters: the residual Euclidean distance between the processed signals, and the so-called warping index, which takes into account the amout of interpolating samples employed. In our case, let us define the inertial data measured on patient i, , with being the number of considered subjects. encompasses six components, namely the three components of acceleration and angular velocity respectively. Given a pair of subjects and for each one of the six signal components :
The DTW is applied to the corresponding w-th dimension of and .
The Euclidean distance output by the DTW algorithm is obtained.
Once the 6 distance values
are available for all
pairs, a single parameter is obtained for each
i–th subject, as reported in Equation (
1).
We have run this algorithm on the inertial data from our population, after transforming them terms of spectrograms, having verified that DTW measures turned out more reliable in the frequency domain. We considered the DTW distances between signal pairs belonging to the same class (
intra-class distances), and signal pairs belonging to different classes (
inter-class distances). As an example,
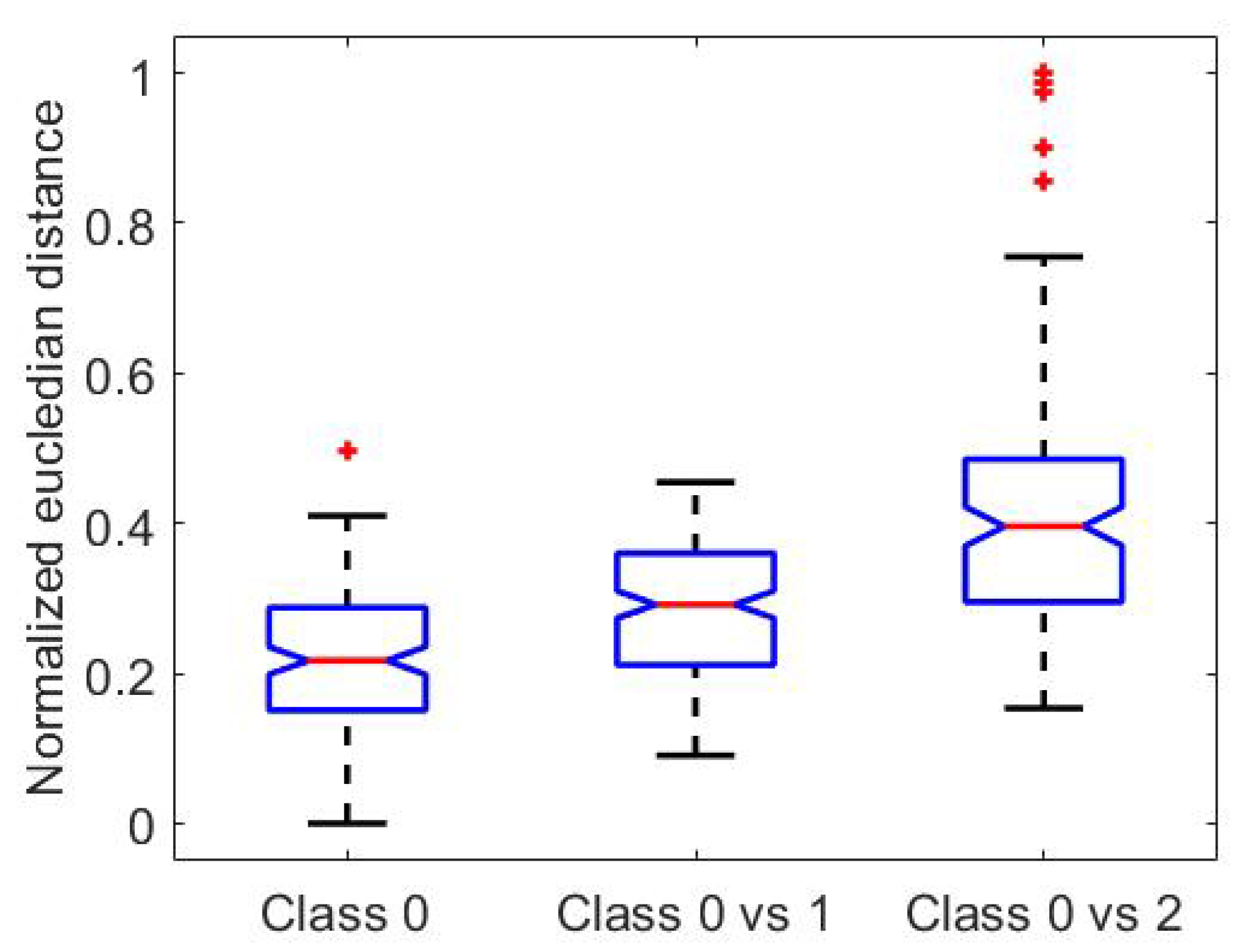
Figure 3 reports intra-class distances for class 0 and inter-class distances between classes 0–1 and 0–2, for the antero-posterior acceleration signal.
As can be appreciated from
Figure 3, median values of DTW distances exhibit an increasing trend with the distance of the considered class, while data variability is similar. Given that data was found to exhibit a continuous, non-normal distribution, we employed the Mann–Whitney U test to check whether the DTW distance data in different classes presented statistically different distributions. The test was performed on: intra-class data for class 0 and inter-class data for class 0 vs. 1; inter-class data for class 0 vs. 1 and inter-class data for class 0 vs. 2. The test outcomes confirmed that data in
Figure 3 are characterized by significantly different distributions (
p-values < 0.0001), hence can be separated by a proper algorithm. Once verified the feasibility of our classification study, we further proceeded extracting characteristics features from raw signals and selecting the most significant ones. These steps are described in the following Sections.
2.4. Feature Extraction
From our dataset, which includes 3 acceleration and 3 angular velocity components, we extracted a large set of time- and frequency-domain features. A thorough literature research, together with a visual inspection of the signals, led to the collection of 414 features (i.e., 69 features from each acceleration and angular velocity component). A list of features is reported in
Table 4, possibly along with a brief description of those features that are not self-explaining. Please notice that, for the sake of brevity, in case a feature is computed on different frequency bands (e.g., RAPP,
), it is reported only once in the table.
Some features, e.g., , amplitude, width, were selected because they are well known to be representative of the signal spectral characteristics. Other parameters, e.g., , RAPP, band, have been selected after a visual inspection of the PSD of signals grouped by class, as they are deemed significant to catch intra-class similarities and inter-class differences. For example, we found that class 3 PSD exhibits a higher peak and a broader distribution along the signal bandwidth with respect to the other classes. Specifically, in class 0 and 1 most of the signal power lies below 1 Hz, while a shift toward high frequencies (i.e., up to 5 Hz) is observed for class 2 data. Based on these observation, we defined features capable to represent the signal power in some specific frequency bands (e.g., [0–1] Hz, [1–2] Hz), the power ratio between different bands (e.g., RAPP [0–1]/[1–5] Hz), the number of spectral peaks in some specific bands (e.g., band [0–1] Hz, band [1–5] Hz). Due to the large feature set, we proceeded with feature selection, followed by a dimensionality reduction step, as discussed in the next Section.
2.5. Feature Selection
The aim of this task is to identify the most significant features, defined as those achieving the highest correlation with the clinical score. We decided to face this task using Pearson correlation r as a measure recognized to provide good selection performance. Starting from all the 414 features, we wanted to identify the smallest adequate feature subset, i.e., that containing features with high correlation with the target (most significant) and low correlation between each other (non-redundant). To this end, let us define as the vector containing all N features. We computed the Pearson correlation between all features and the target t, achieving a vector . Moreover, we computed the correlation coefficient between each feature pair: .
Given the large dimensionality of the initial dataset, we discarded features exhibiting r , this threshold representing the edge between weak and moderate correlation. Then, we removed redundant features, keeping only those ones which achieve much higher than the maximum correlation with the other features (). For the sake of clarity, the algorithm for feature selection is described below.
Algorithm 1 led to the selection of 8 features. In order to investigate whether a further dimensionality reduction was possible, we performed a Principal Component Analysis (PCA) on the resulting subset of features, after verifying the normal distribution of each feature. The first three principal components were found to explain 82% of the total variance; this is not deemed sufficient to justify a further dimensionality reduction on the feature subset. Hence, the feature selection process ended up with 8 features, reported in
Table 5, along with the original ID, source, component specification and correlation coefficient.
| Algorithm 1 Feature selection Algorithm |
| Require: | ▹ N features, target vector |
| Ensure: | ▹ M < N features |
| procedure FS() | ▹ Feature Selection function |
| while do | ▹ Iterate for each feature |
| if & | ▹ Look for significant and non-redundant features |
| select | ▹ Add to the feature subset |
| end while | |
| | ▹ End up with a subset of M features |
| end procedure | |
2.6. Classification
An a-priori selection of one among the numerous available Machine Learning (ML) algorithms is often inadequate and/or difficult to justify. For this reason, we performed the classification task using different ML models, namely: k-Nearest Neighbor (kNN), Decision Tree (DT) and Support Vector Machine (SVM). For each of them, an optimization of the relevant parameters has been heuristically performed. The very first step consisted in the decision of whether to address a binary or a multi-class classification. In our specific case, considering the simple data acquisition protocol, i.e., subjects resting in upright position with a single waist-mounted smartphone, the multi-class classification (i.e., able to distinguish control subjects and PD patients with different PS scores) is presumably very demanding. Thus, we fed all the above mentioned ML models with the addressed feature subset. In a Leave-One-Subject-Out (LOSO) validation [
17,
18], a Linear-SVM-based provided the best results, achieving accuracy equal to 70.1% and average
score equal to 67.3%. For the sake of completeness, we also investigated the performance of a Random Forest (RF) approach, as this method is one of the most popular and accurate multi-class classification methods [
19]. To this end, we have tried different ensemble methods based on DT learners, further optimizing the model parameters. The models were fed with all the initial dataset, i.e., all the features extracted from all components of subjects belonging to all classes. The Optimization procedure was based on a Bayesian approach aiming to minimize the misclassification rate; the number of iterations was set to 30. In the following we report the optimized parameters along with the eligible choice and parameters ranges: Esemble method Adaboost (Bag, Adaboost, RusBoost); Maximum number of splits 2 (1–39); Number of Learners 79 (10–100); Learning rate 0.01 (0.001–0.5). The obtained 65% accuracy and 48.6% mean F1-score for RF and the slightly superior performance of the SVM approach were not deemed satisfactory to justify the choice of a classic multi-class classification approach; hence, we abandoned the multi-class approach and followed an alternative strategy, described in the following.
The general idea is to reduce a multi-class classification problem to some binary classification tasks [
20], in order to exploit the well-known high generalization capability of SVM, used in several literature studies on Parkinson’s Disease [
21,
22,
23,
24]. We propose a new approach to face multi-class classification problems. It consists in using a first classification layer, employed to achieve a gross evaluation of postural stability. Then a second layer classification is performed.
First Layer: this classification step was meant to create a scale, whose lower and upper bounds represent subjects with opposite postural control (optimal vs. severely impaired). Given the availability of inertial data from the control population, we set up a binary classification problem, employing control subjects (i.e., people with the best possible postural control) and PD patients in class 2 (i.e., people with the worst postural control level among the considered population). We have implemented different ML models, namely SVM, KNN, DT, in order to select the one leading to the best performance. The confusion matrices of the employed models are reported in
Section 3.
Once the model was built and subject to a LOSO validation, we performed a subsequent test on PD patients belonging to classes 0 and 1. The SVM model yields an integer classification index, i.e., the label of the predicted class, as well as a soft output, i.e., a posteriori probability that a data-point belongs to either class. We computed this soft output from all the tested subjects; then, we investigated the correlation between this soft parameter and the clinical labelled classes, in order to assess the accuracy of such measure in the classification tasks. The results are reported and discussed in detail in
Section 3. The obtained correlation, although strong, was deemed not sufficient for a fine multi-class classification, thus we proceeded with a further classification step.
Second Layer: In order to go beyond the simple correlation value and perform a finer classification, we refined our algorithm by further implementing three linear-SVM classifiers, thus reducing the single initial multi-class problem to three binary classification tasks. The input of each SVM is the entire feature set, regarding only the classes to be distinguished by the specific SVM model (e.g., class 0 and 2 are input to the classifier which has to distinguish subjects in class 2 from those in class 0). These and other results will be reported and discussed in
Section 3.
3. Results and Discussion
In this Section, the main classification results of our work are reported and discussed in detail. As for the first classification layer, which is meant to classify subjects with very different postural control, the achieved results for different ML models are reported in
Figure 4 in terms of confusion matrices.
The results were obtained using a LOSO validation and extracting the discrete output from each model. As can be appreciated in
Figure 4, SVM provided the best performance in differentiating controls from PD patients with seriously impaired postural control. Thus, such a model has been used for the subsequent processing.
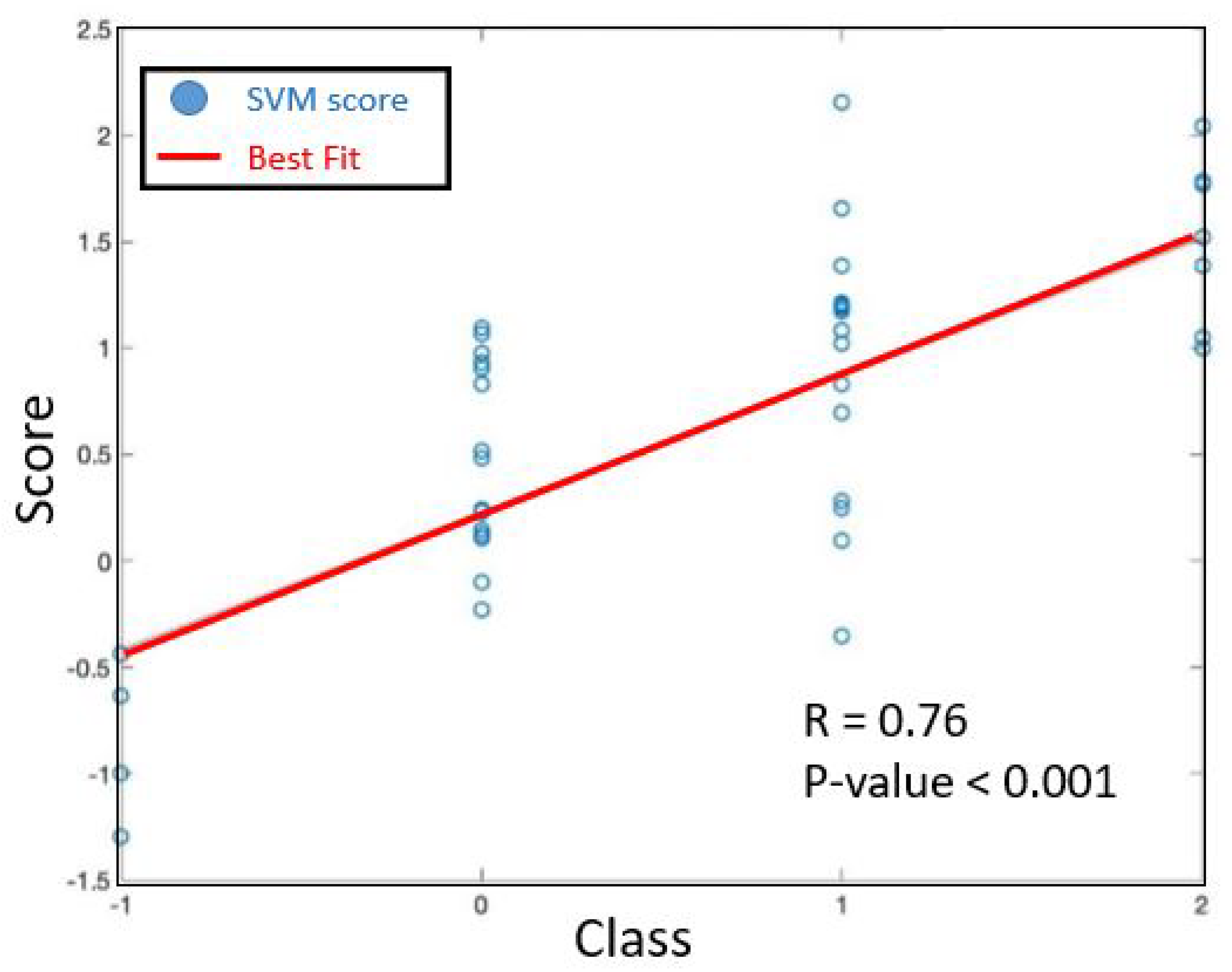
Figure 5 reports the soft output of the SVM model, together with the best-fit line, i.e., the line minimizing the mean square error. We can notice that a significant gap holds between controls and class 0 subjects. A gap is also appreciable between class 0 and class 2 subjects. Still, class 1 data are partially overlapped to both class 0 and 2 data. Nevertheless, a high Pearson correlation is achieved between the SVM soft output and the clinical score, i.e.,
with
p < 0.0001. This witnesses the potential effectiveness of our approach, given that a proper classification algorithm is addressed.
As already discussed in
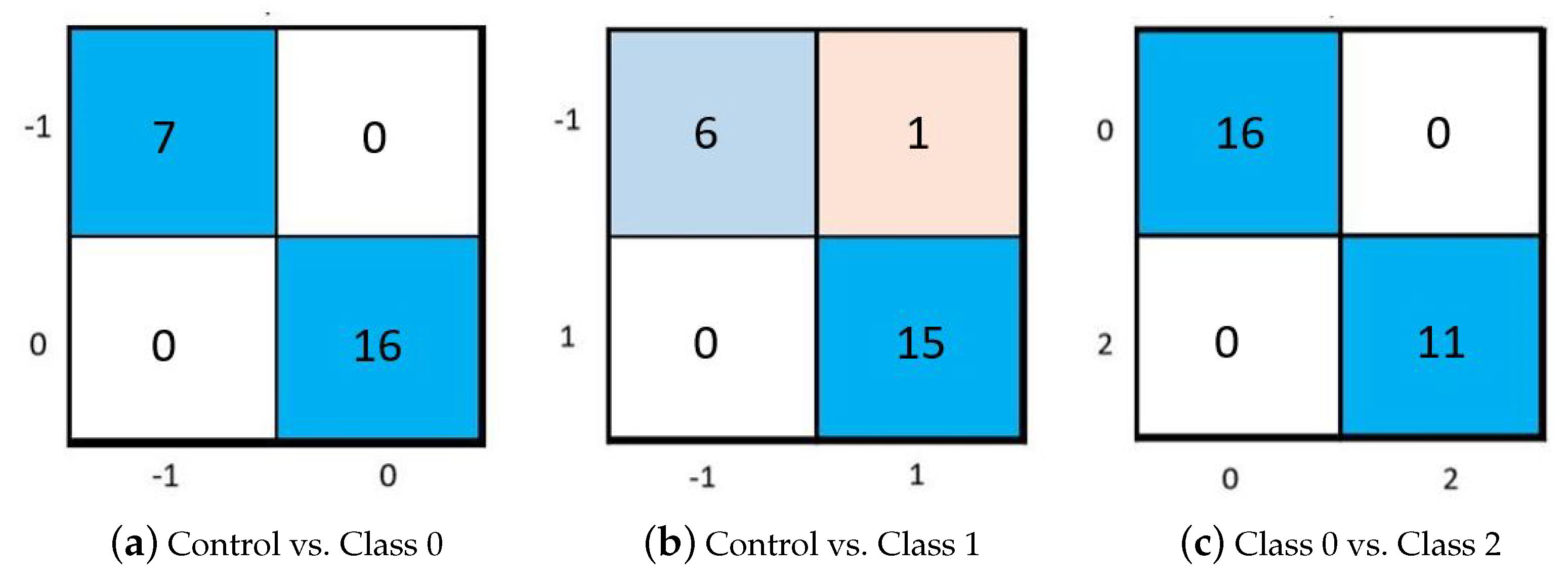
Section 2.6, a second layer classification was further implemented. The performance of the three binary SVM models is reported in
Figure 6 in terms of confusion matrices, and in
Table 6 in terms of Accuracy, Sensitivity, Specificity, Precision and
score.
As can be appreciated from
Figure 6 and
Table 6, the achieved performance are very satisfactory, achieving very high accuracy in three out of the five classification tasks. It can be appreciated that the classification task leads to impaired performance when trying to distinguish subjects belonging to adjacent classes. This can be due both to a harder classification task and to the intra- and inter-rater variability, intrinsic uncertainty of the clinical evaluation, of one class [
7,
25,
26]. This latter consideration suggests us to not rely on such fine classification, as it may provide misleading results.
It is worth noting that these results have been obtained using only 8 features and three very simple SVM models.
We deem the performance achieved in this study very promising. Satisfactory performance was obtained for multiple binary classification, allowing us to discriminate between control subjects, and patients with slight, mild and severe postural instability. As for the practical use of the algorithm, we believe that a first approach could be to use the regression model described in
Figure 5, in order to achieve a first indication of the postural control impairment entity (e.g., mild). Then, the appropriate binary SVM model can be applied to perform a finer classification. We believe this approach to be very reasonable and efficient. For the sake of completeness, having employed only 8 features and simple ML models as SVMs, and being the input a short inertial signal, processing times were found to be extremely reduced (i.e., 5 ms for data loading, 50 ms for feature extraction, 2 ms for classification). This makes us confident about a possible real-time on-board implementation of the algorithm.
It is worth noting that a simple protocol is employed, which only includes a short stance period and can safely performed during daily living. This fact, along with the use of a smartphone, has paved the way for a remote passive monitoring of PD patients in home environment. Furthermore, our term of comparison is the clinical evaluation carried out following item 3.12—“Postural Stability” of the MDS–UPDRS, i.e., the retropulsion test. This is completely different from the experimental protocol employed in this study. In fact, whereas the retropulsion test is standard in outpatient context, it is not safe in a domestic environment. This is the reason that has led to the employed, simple and safe protocol to assess postural control by means of a non-invasive and safe test. On the other hand, this choice has made the classification task more difficult.
Finally, we want to clarify that the obtained results have to be considered with caution, having employed a reduced dataset (42 PD patients, 7 Control subjects). Due to the cardinality of the classes and to the simple protocol choice, the data and the algorithm were not sufficiently adequate to perform a fine classification between adjacent classes. As for a possible implementation of the algorithm for an early detection of postural impairment in PD patients, a much larger cohort of PD patients in the early stage of the disease, together with an age-matched control population, has to be employed. As for a finer classification between adjacent classes, the cardinality of each PS class has to be increased, in order to give much more statistical meaningfulness to the results. Furthermore, due to the intrinsic intra- and inter-rater variability, the evaluation has to be performed by many neurologists, in order to employ the average clinical evaluation as the ground truth of the classification task.
4. Conclusions and Future Works
This work is part of a larger study on Parkinson’s Disease, aiming to assess both motor and non-motor symptoms associated with the beginning and progression of the disease. In [
27], we have assessed freezing of gait, i.e., a sudden non-voluntary block of gait, and the leg agility task, item 3.8 of the MDS–UPDRS, achieving promising results, using such a widespread device as the commercial smartphone. In this study, we have been focused on postural stability, as it represents one of the most troublesome motor symptom associated to PD. Moreover, it is strongly correlated with fall risk and reduced quality of life of PD patients. Thus, a non-invasive and accurate automated evaluation of postural stability would be of fundamental importance from the patient, caregiver and clinical point of view. Such automated evaluation may be devised for a home monitoring of PD subjects, employing a simple device such as a smartphone, which is nowadays the most widespread. Future developments will be in the direction of acquiring more data, in order to enlarge the dataset and achieve more sound statistical significance. Furthermore, we plan to collect more clinical information related to freezing of gait (e.g., New Freezing of Gait Questionnaire) and to fall risk (e.g., Fall Risk Questionnaire), along with a more detailed evaluation of balance (e.g., Berg Balance Scale). Finally, test–retest reliability of measure outcomes will be investigated, and differential analysis will be performed to assess postural control in different pharmacological conditions. We plan to implement this algorithm in a sort of
electronic diary, meant to collect and process data from each patient, and send the most significant information to a cloud, accessible by clinicians. This represent an urgent need, given that the outpatient visits are usually carried out once or twice a year. Thus, a large tele-monitoring system would provide objective, accurate and continuous information capable of provide a global picture of patient clinical condition.