Analog Realization of a Fractional Recursive Variable-Type and Order Operator for a Particular Switching Strategy
Abstract
1. Introduction
2. Fractional Constant-Type Variable-Order Differences
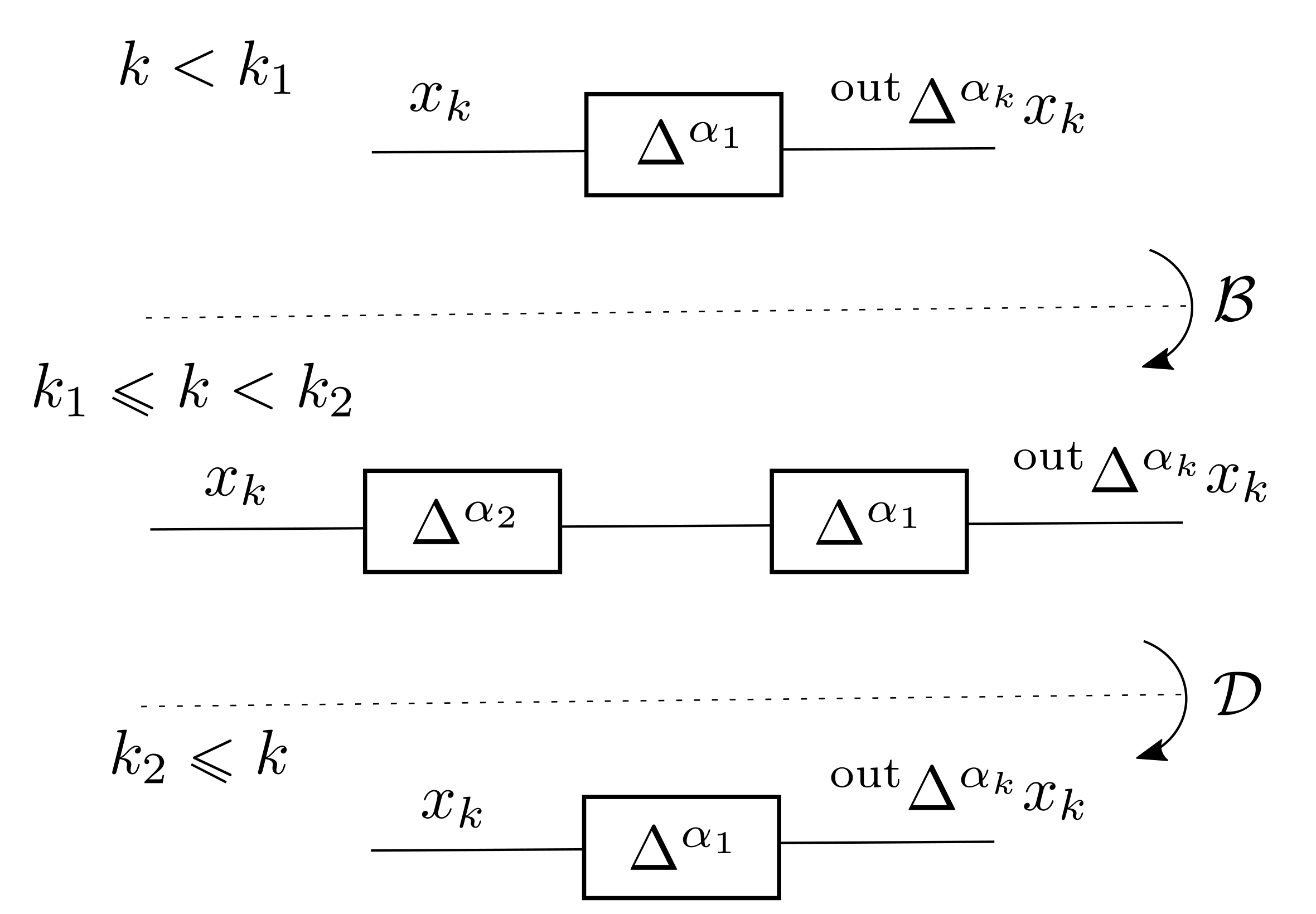
Recursive Form of Fractional, Variable-Order -Type Difference Definition
3. Fractional Variable-Type and Order Difference
3.1. Main Result—Practical Realization of -Type Variable-Type and Order Difference
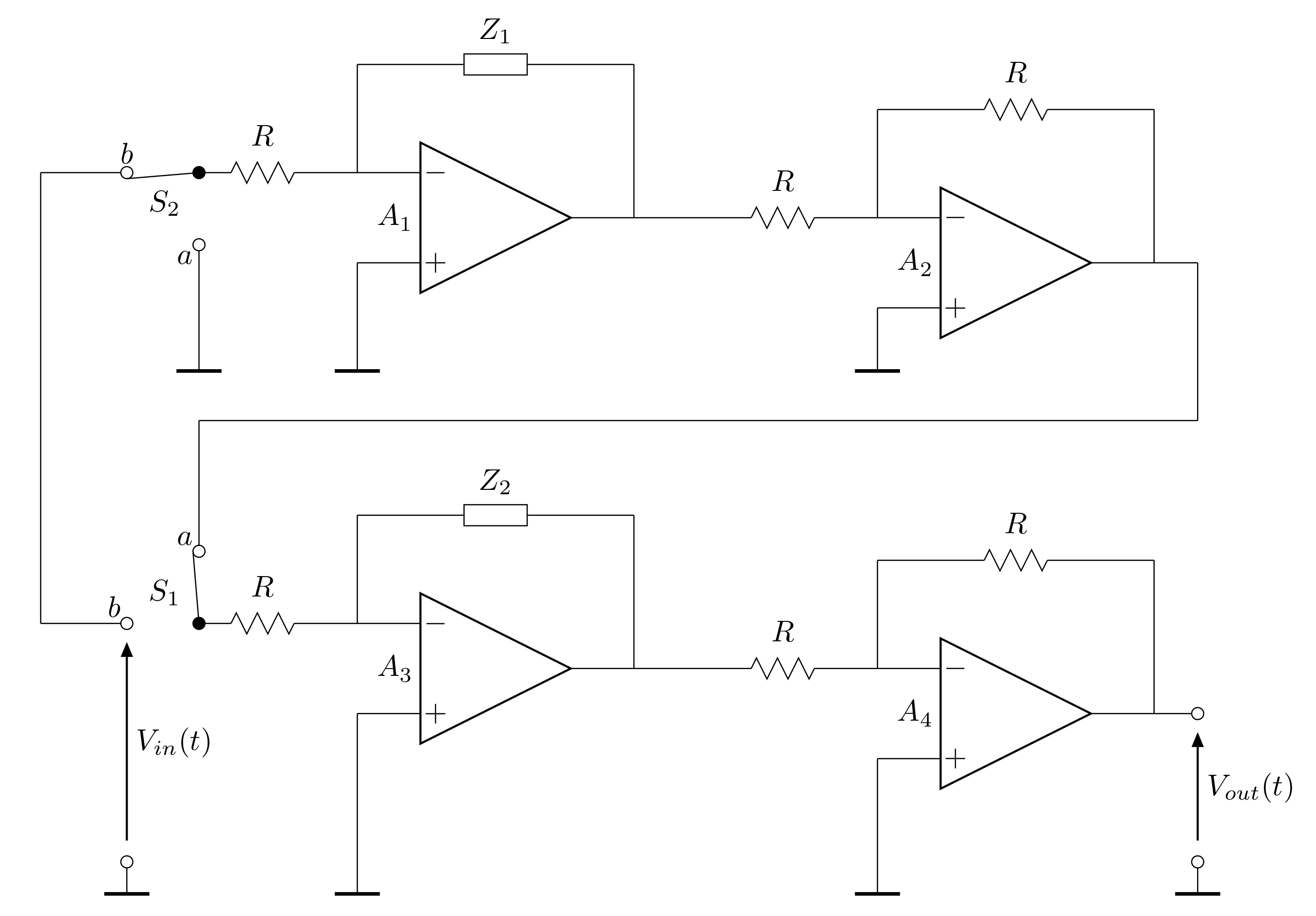
4. Analog Model of -Type Variable-Type and Order Operator
- Data acquisition card dSPACE 1104;
- Half-order impedances deeply described in [22], denoted as and ;
- Operational amplifiers TL071 denoted as and ;
- Analog switches DG303 denoted as and ;
- Resistors k.
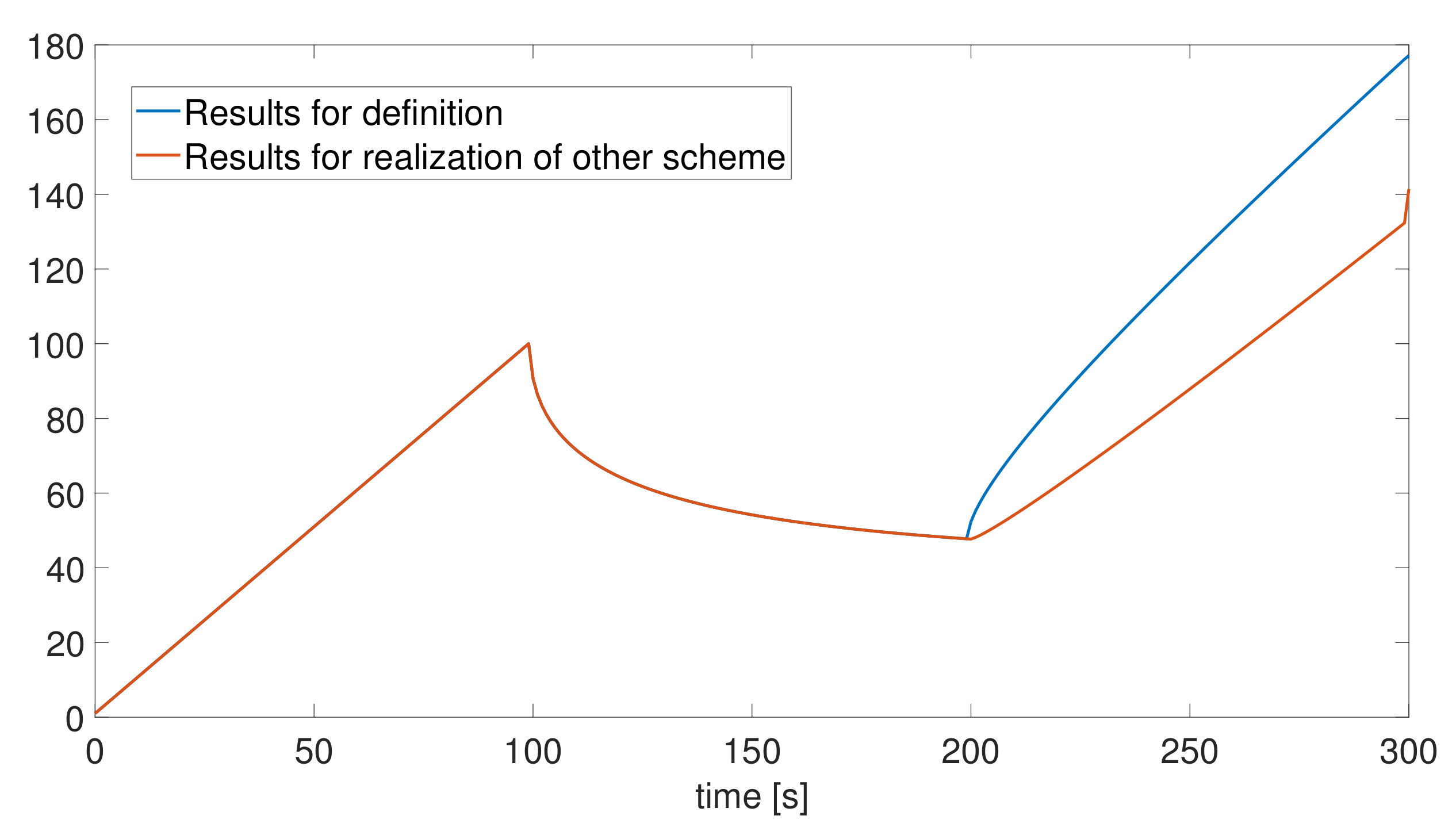
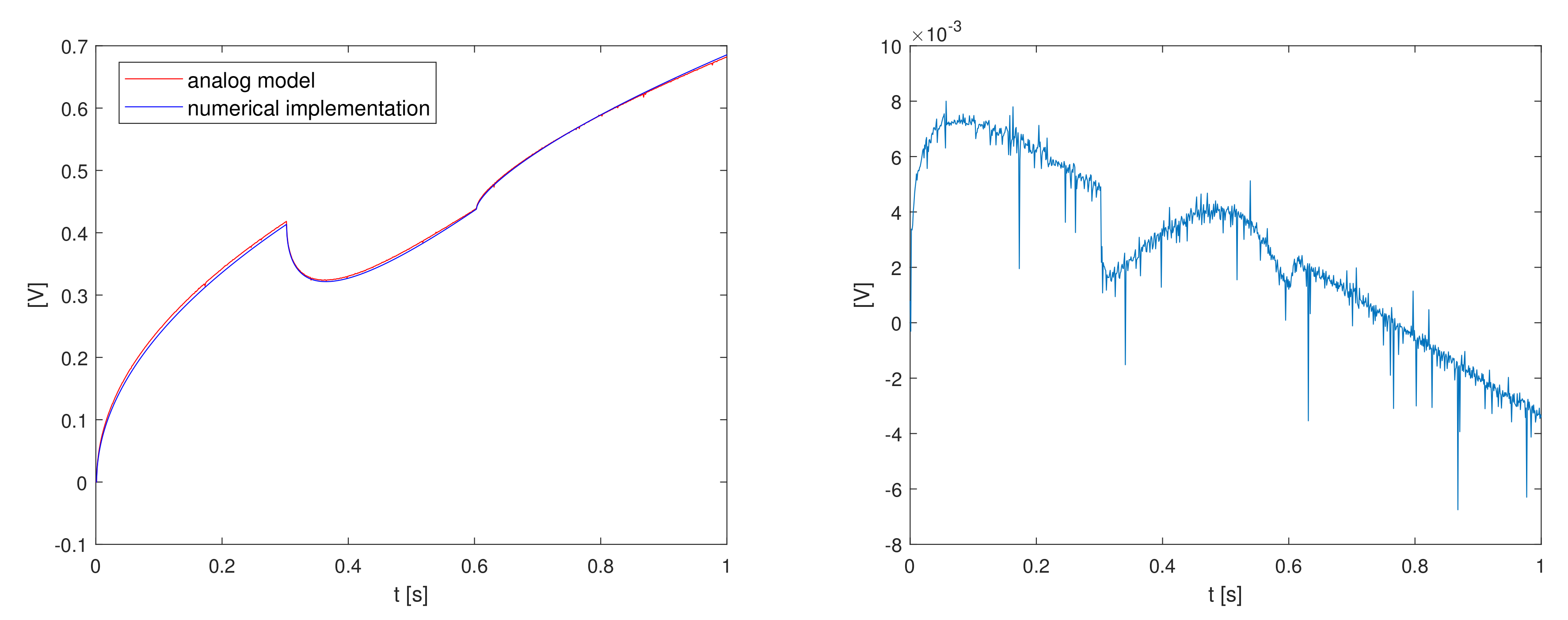
Experimental Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
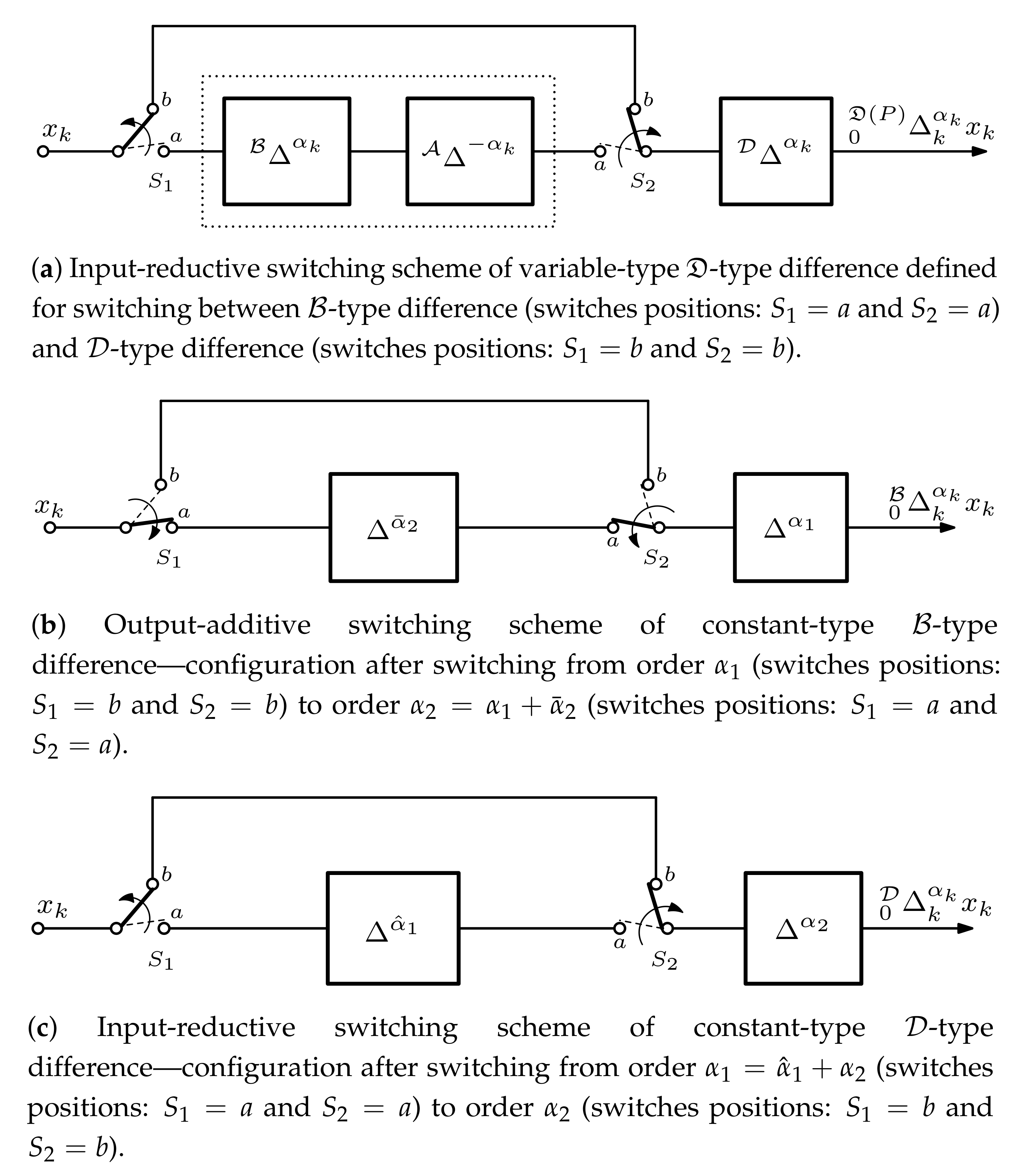
Appendix A. Other Attempts of Realization Schemes

References
- Miller, K.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differenctial Equations; John Wiley & Sons Inc.: New York, NY, USA, 1993. [Google Scholar]
- Monje, C.A.; Chen, Y.; Vinagre, B.M.; Xue, D.; Feliu, V. Fractional-Order Systems and Controls; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Magin, R.; Ortigueira, M.D.; Podlubny, I.; Trujillo, J. On the fractional signals and systems. Signal Process. 2011, 91, 350–371. [Google Scholar] [CrossRef]
- Dzieliñski, A.; Sierociuk, D. Fractional Order Model of Beam Heating Process and Its Experimental Verification. In New Trends in Nanotechnology and Fractional Calculus Applications; Baleanu, D., Guvenc, Z.B., Machado, J.A.T., Eds.; Springer: Dordrecht, The Netherlands, 2010; pp. 287–294. [Google Scholar]
- Sakrajda, P.; Wiraszka, M.S. Fractional variable-order model of heat transfer in time-varying fractal media. In Proceedings of the IEEE 2018 19th International Carpathian Control Conference (ICCC), Szilvasvarad, Hungary, 28–31 May 2018; pp. 548–552. [Google Scholar]
- Wiraszka, M.S.; Sakrajda, P. Switching Energy Loss in Fractional-Order Time-Varying Heat Diffusion Model. In Conference on Non-Integer Order Calculus and Its Applications; Springer: Berlin/Heidelberg, Germany, 2018; pp. 294–305. [Google Scholar]
- Sakrajda, P.; Sławomir Wiraszka, M. Fractional-order diffusion model for social networks. In Proceedings of the International Conference on Fractional Differentiation and its Applications (ICFDA), Amman, Jordan, 16–18 July 2018. [Google Scholar]
- Dzielinski, A.; Sarwas, G.; Sierociuk, D. Comparison and validation of integer and fractional order ultracapacitor models. Adv. Differ. Equ. 2011. [Google Scholar] [CrossRef]
- Quintana, J.J.; Ramos, A.; Nuez, I. Identification of the fractional impedance of ultracapacitors. In Proceedings of the 2nd IFAC Workshop on Fractional Differentiation and its Applications (IFAC FDA’06), Porto, Portugal, 19–21 July 2006. [Google Scholar]
- Freeborn, T.J.; Maundy, B.; Elwakil, A.S. Fractional-order models of supercapacitors, batteries and fuel cells: a survey. Mater. Renew. Sustain. Energy 2015, 4. [Google Scholar] [CrossRef]
- Sierociuk, D.; Sarwas, G.; Twardy, M. Resonance phenomena in circuits with ultracapacitors. In Proceedings of the 12th International Conference on Environment and Electrical Engineering (EEEIC), Wroclaw, Poland, 5–8 May 2013; pp. 197–202. [Google Scholar]
- Kopka, R. Changes in Derivative Orders for Fractional Models of Supercapacitors as a Function of Operating Temperature. IEEE Access 2019, 7, 47674–47681. [Google Scholar] [CrossRef]
- Kopka, R. Discrepancy between derivative orders in fractional supercapacitor models for charging and discharging cycles. In Proceedings of the 23rd International Conference on Methods and Models in Automation and Robotics (MMAR), Miedzyzdroje, Poland, 27–30 August 2018; pp. 567–572. [Google Scholar]
- Cai, W.; Wang, P.; Fan, J. A variable-order fractional model of tensile and shear behaviors for sintered nano-silver paste used in high power electronics. Mech. Mater. 2020, 145, 103391. [Google Scholar] [CrossRef]
- Zhang, Q.; Shang, Y.; Li, Y.; Cui, N.; Duan, B.; Zhang, C. A novel fractional variable-order equivalent circuit model and parameter identification of electric vehicle Li-ion batteries. ISA Trans. 2020, 97, 448–457. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Li, H.; Chen, N. An indicator for the electrode aging of lithium-ion batteries using a fractional variable order model. Electrochim. Acta 2019, 299, 378–387. [Google Scholar] [CrossRef]
- Ortigueira, M.D.; Valério, D.; Machado, J.T. Variable order fractional systems. Commun. Nonlinear Sci. Numer. Simul. 2019, 71, 231–243. [Google Scholar] [CrossRef]
- Valerio, D.; da Costa, J.S. Variable-order fractional derivatives and their numerical approximations. Signal Process. 2011, 91, 470–483. [Google Scholar] [CrossRef]
- Lorenzo, C.; Hartley, T. Variable order and distributed order fractional operators. Nonlinear Dyn. 2002, 29, 57–98. [Google Scholar] [CrossRef]
- Sierociuk, D.; Malesza, W.; Macias, M. Derivation, interpretation, and analog modelling of fractional variable order derivative definition. Appl. Math. Model. 2015, 39, 3876–3888. [Google Scholar] [CrossRef]
- Sierociuk, D.; Malesza, W.; Macias, M. On the Recursive Fractional Variable-Order Derivative: Equivalent Switching Strategy, Duality, and Analog Modeling. Circuits Syst. Signal Process. 2015, 34, 1077–1113. [Google Scholar] [CrossRef]
- Macias, M.; Sierociuk, D. An alternative recursive fractional variable-order derivative definition and its analog validation. In Proceedings of the International Conference on Fractional Differentiation and its Applications, Catania, Italy, 23–25 June 2014. [Google Scholar]
- Sierociuk, D.; Twardy, M. Duality of variable fractional order difference operators and its application to identification. Bull. Polish Acad. Tech. Sci. 2014, 62, 809–815. [Google Scholar] [CrossRef]
- Malesza, W.; Sierociuk, D. Recursive variable type and order difference, its definition and basic properties. In Proceedings of the 2016 17th International Carpathian Control Conference (ICCC), Tatranska Lomnica, Slovakia, 29 May–1 June 2016; pp. 473–478. [Google Scholar] [CrossRef]
- Sierociuk, D.; Malesza, W. On the differences of variable type and variable fractional order. In Proceedings of the 2016 European Control Conference (ECC), Aalborg, Denmark, 29 June–1 July 2016; pp. 2191–2196. [Google Scholar] [CrossRef]
- Sierociuk, D.; Malesza, W.; Macias, M. On the Output-Additive Switching Strategy for a New Variable Type and Order Difference. In Theory and Applications of Non-Integer Order Systems; Babiarz, A., Czornik, A., Klamka, J., Niezabitowski, M., Eds.; Springer: Cham, Germany, 2017; pp. 101–111. [Google Scholar]
- Sierociuk, D.; Macias, M.; Malesza, W. Analog realization of fractional variable-type and -order iterative operator. Appl. Math. Comput. 2018, 336, 138–147. [Google Scholar] [CrossRef]
- Sierociuk, D.; Malesza, W. Fractional variable order discrete-time systems, their solutions and properties. Int. J. Syst. Sci. 2017, 48, 3098–3105. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sierociuk, D.; Macias, M.; Malesza, W.; Wiraszka, M.S. Analog Realization of a Fractional Recursive Variable-Type and Order Operator for a Particular Switching Strategy. Electronics 2020, 9, 855. https://doi.org/10.3390/electronics9050855
Sierociuk D, Macias M, Malesza W, Wiraszka MS. Analog Realization of a Fractional Recursive Variable-Type and Order Operator for a Particular Switching Strategy. Electronics. 2020; 9(5):855. https://doi.org/10.3390/electronics9050855
Chicago/Turabian StyleSierociuk, Dominik, Michal Macias, Wiktor Malesza, and Michał Sławomir Wiraszka. 2020. "Analog Realization of a Fractional Recursive Variable-Type and Order Operator for a Particular Switching Strategy" Electronics 9, no. 5: 855. https://doi.org/10.3390/electronics9050855
APA StyleSierociuk, D., Macias, M., Malesza, W., & Wiraszka, M. S. (2020). Analog Realization of a Fractional Recursive Variable-Type and Order Operator for a Particular Switching Strategy. Electronics, 9(5), 855. https://doi.org/10.3390/electronics9050855





