A Low Complexity, High Throughput DoA Estimation Chip Design for Adaptive Beamforming
Abstract
1. Introduction
1.1. Related Works of DoA Estimation
1.2. Motivations and Contributions
2. Projection and Parallel Matching Pursuit Based DoA Estimation
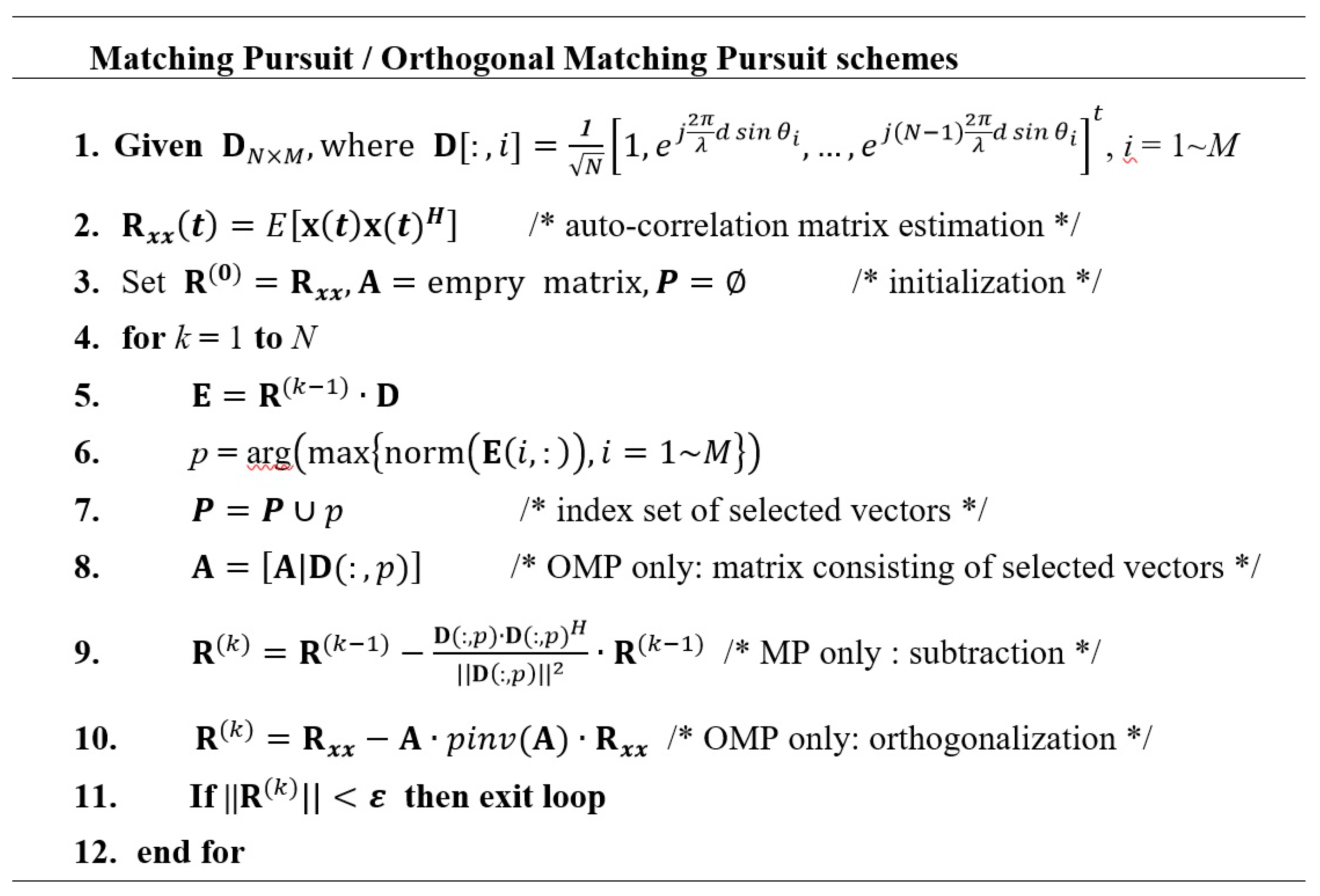
2.1. Recap of Conventional DoA Estimation Schemes
2.2. Proposed DoA Estimation Algorithm
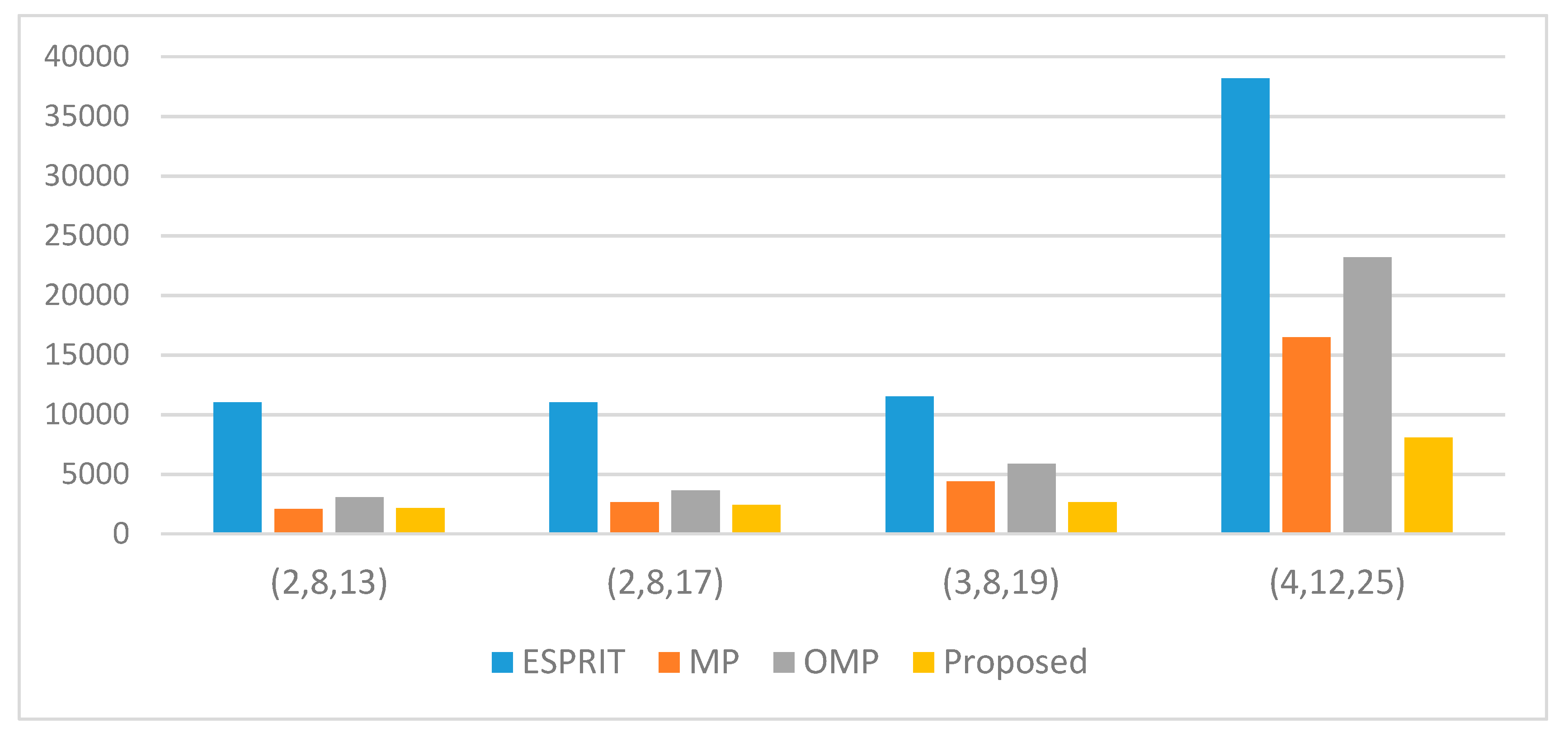
2.3. Computing Complexity Analysis
3. Simulation Results and Performance Analysis
3.1. Simulation Settings
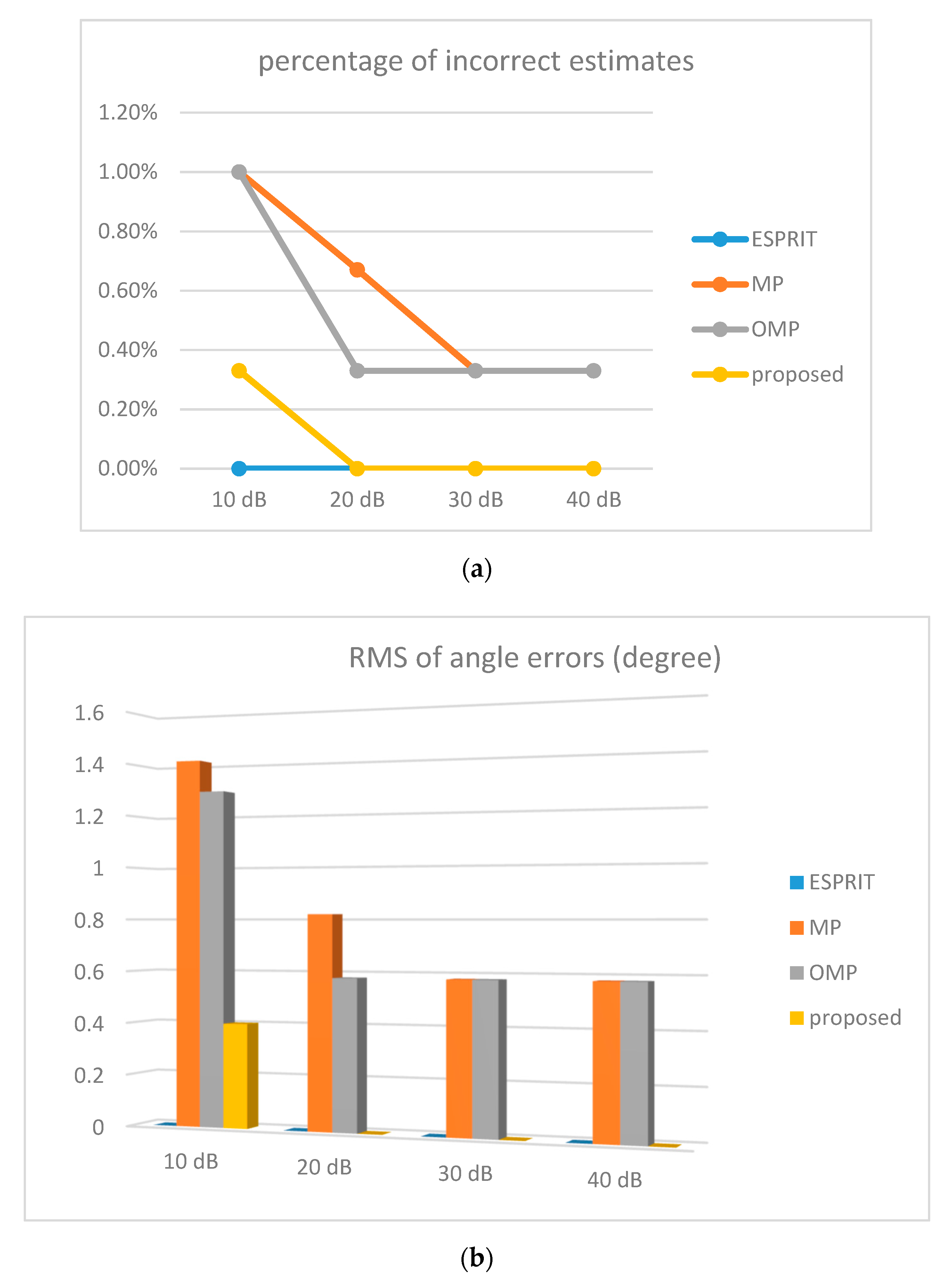
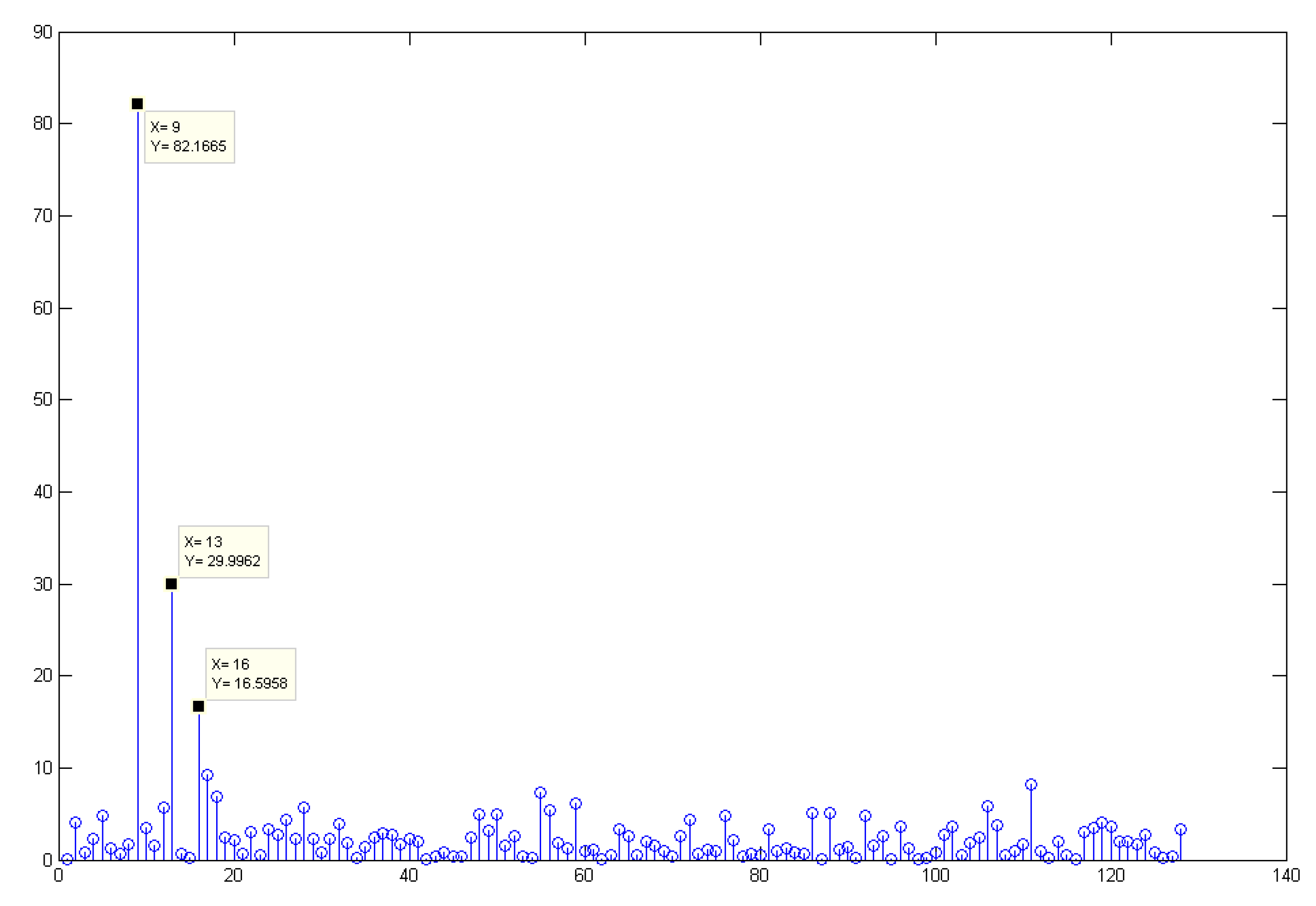
3.2. Simulation Results and Discussions
3.3. Evaluation of K Value Selection
3.4. Detection Results of FMCW Radar
4. Hardware Accelerator Design and Chip Implementation Results
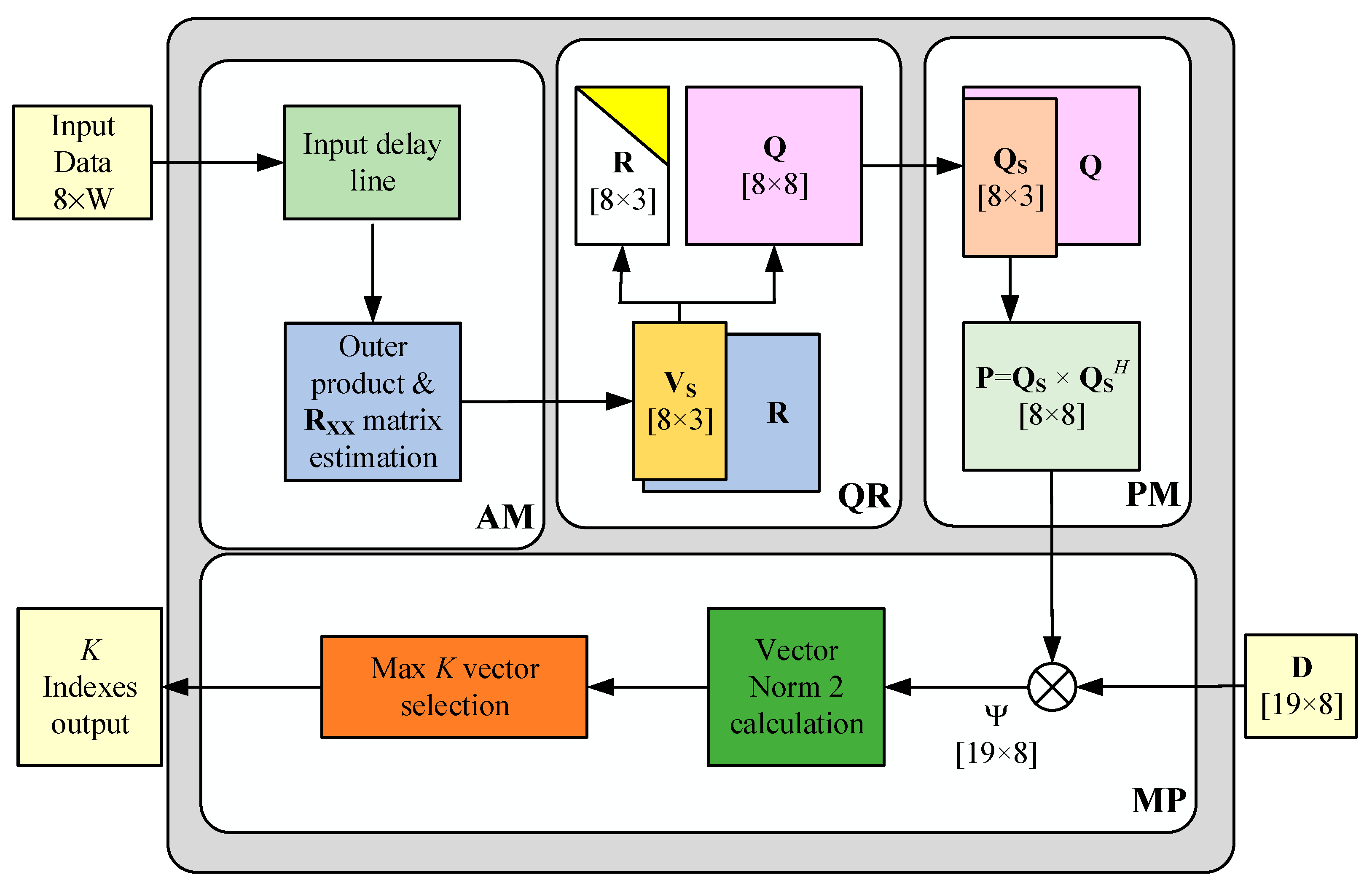
4.1. Design Specs and System Architecture
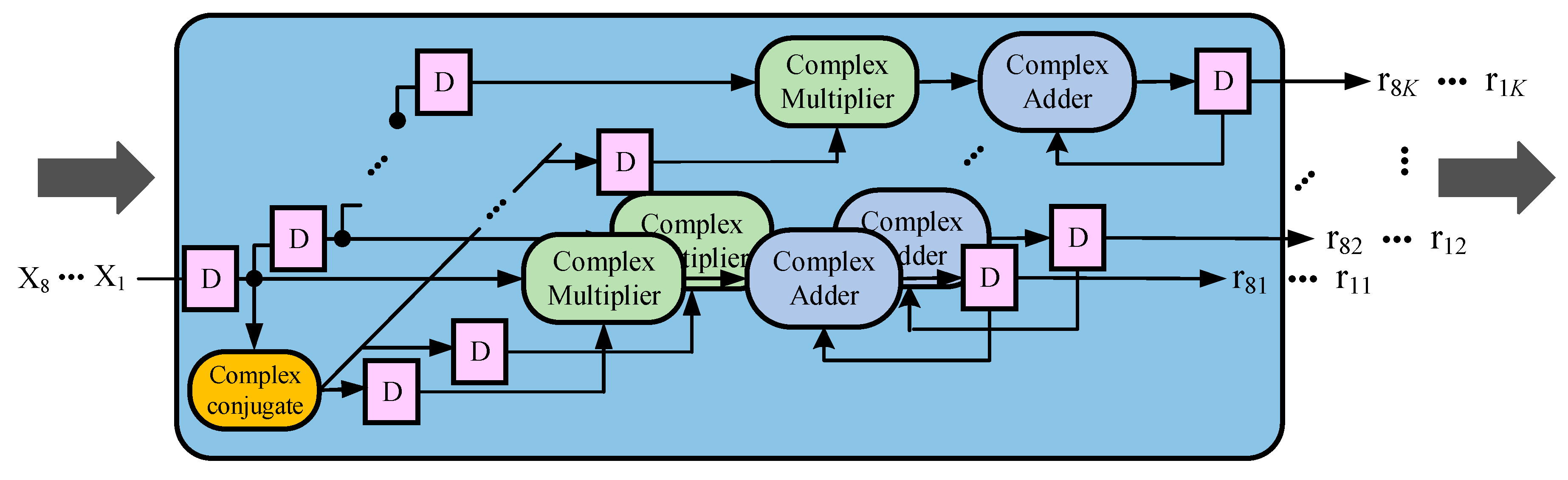
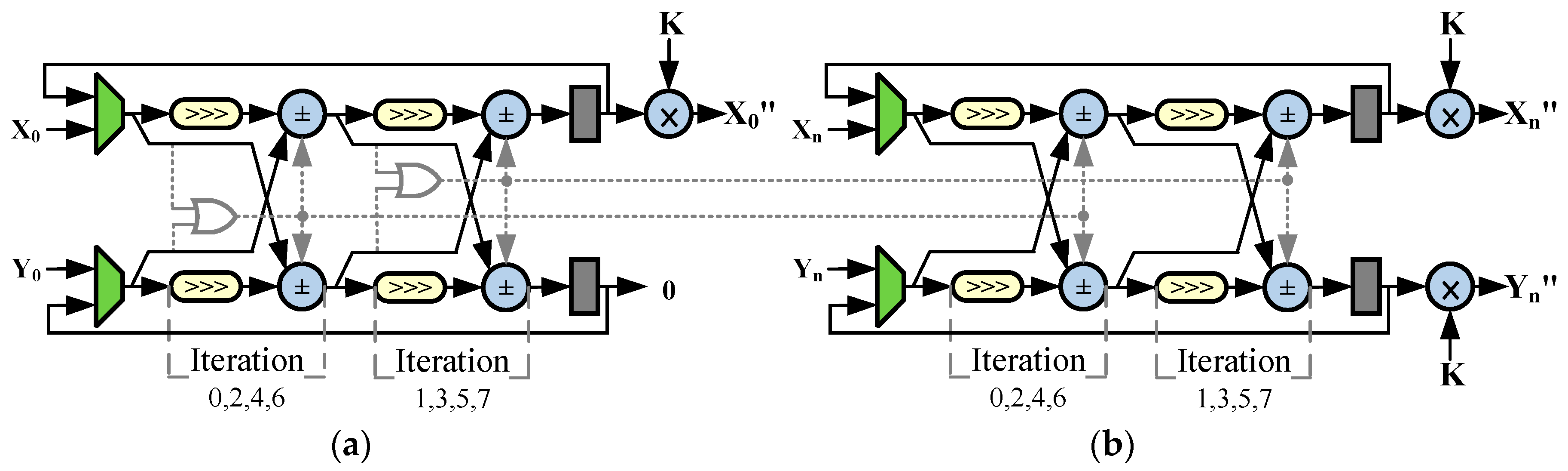
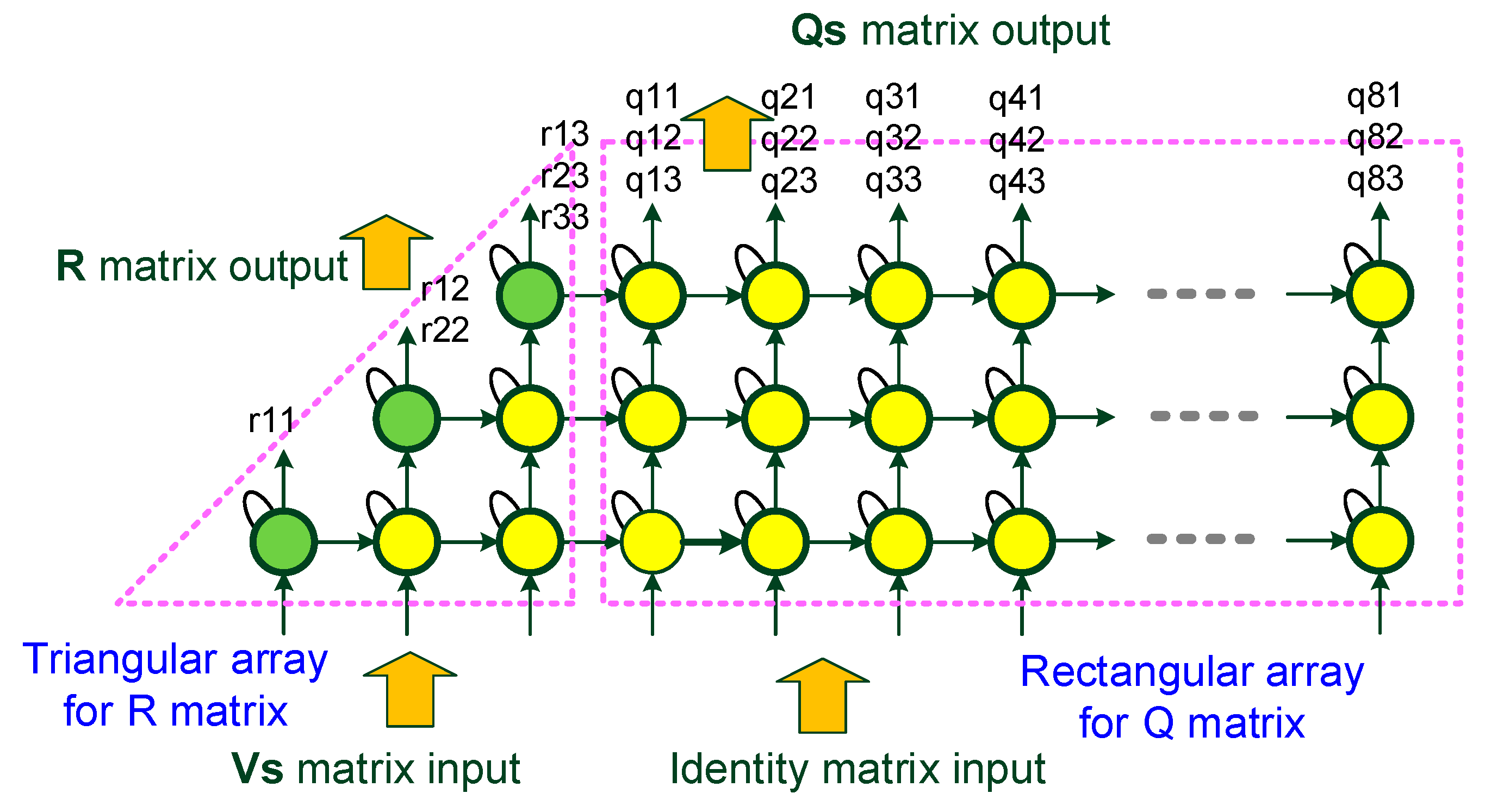
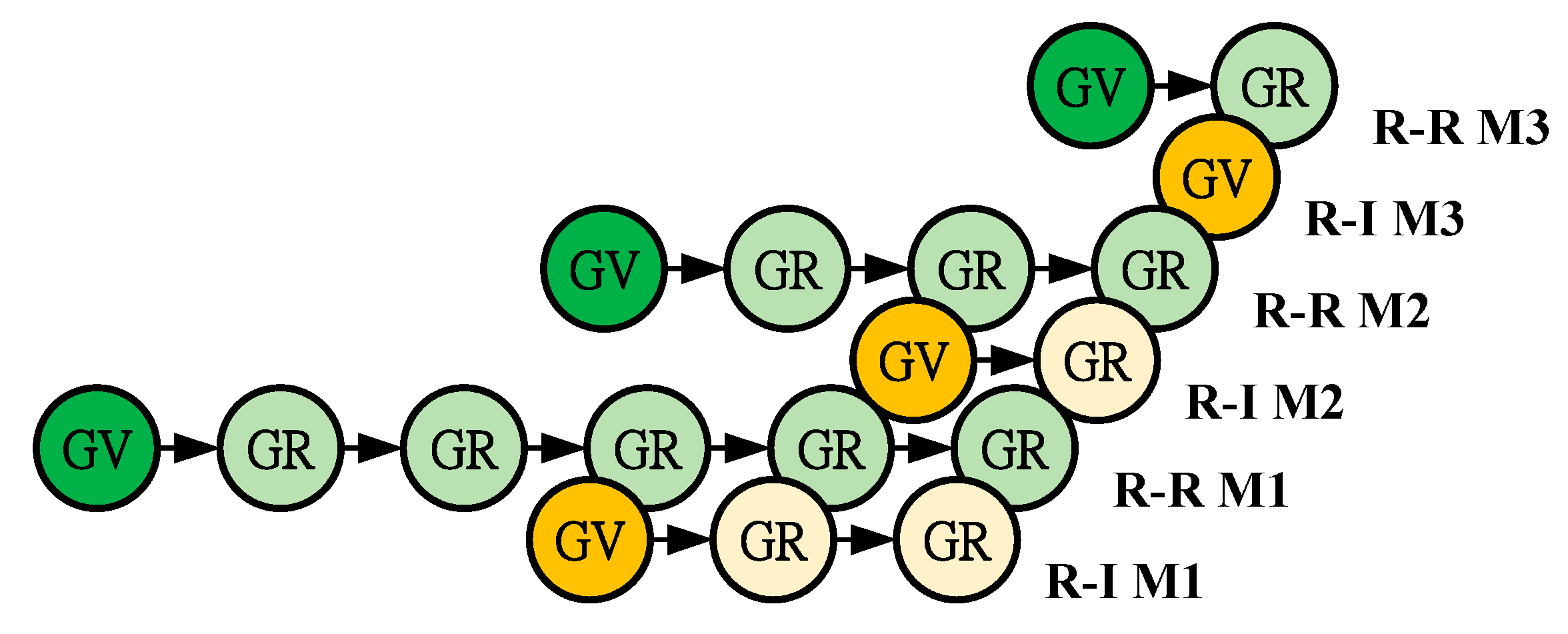
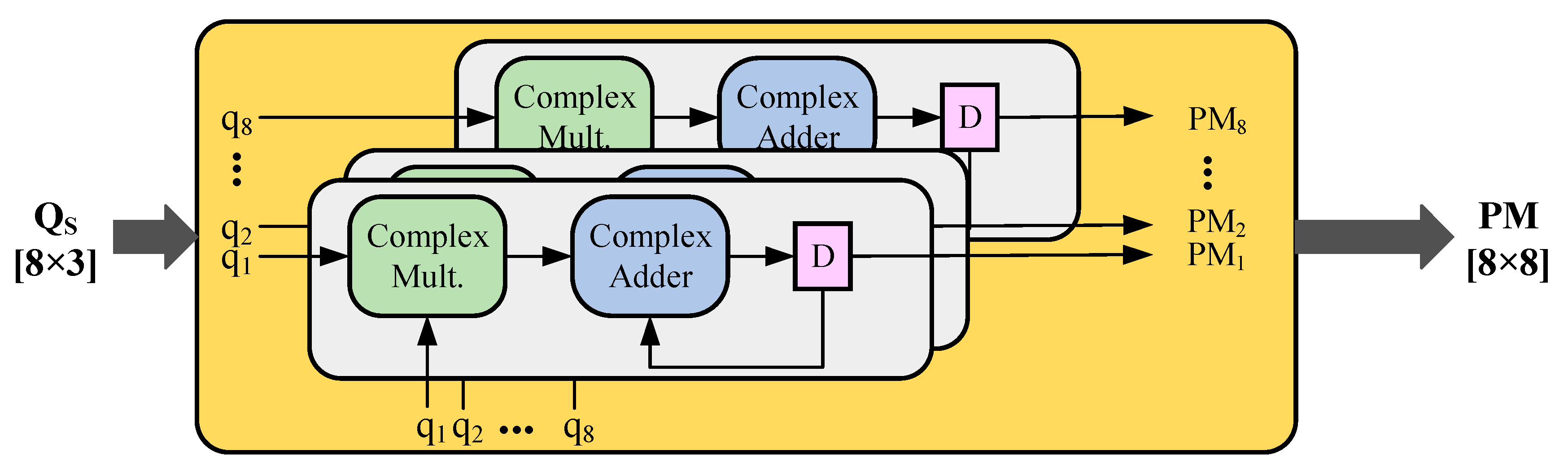
4.2. Algorithm Mapping and Module Designs
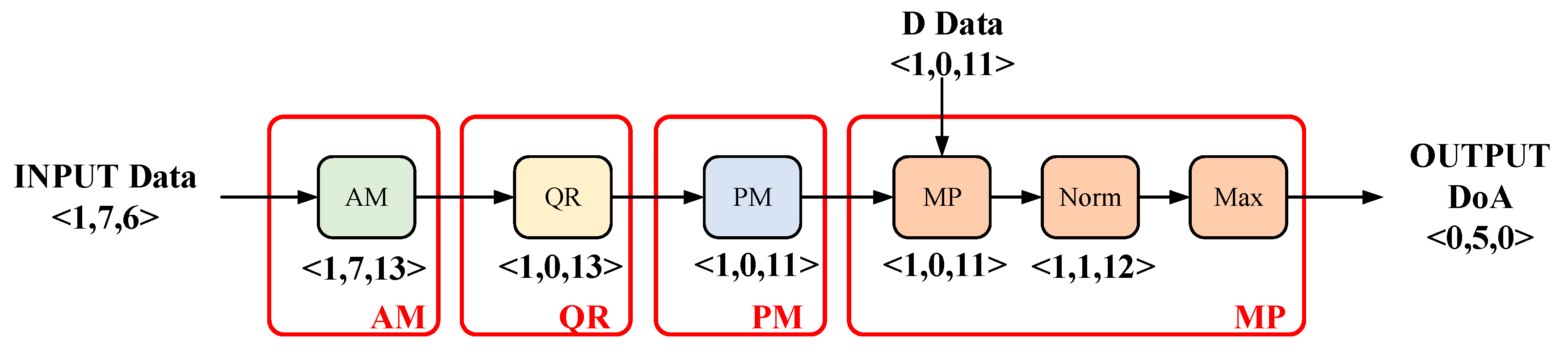
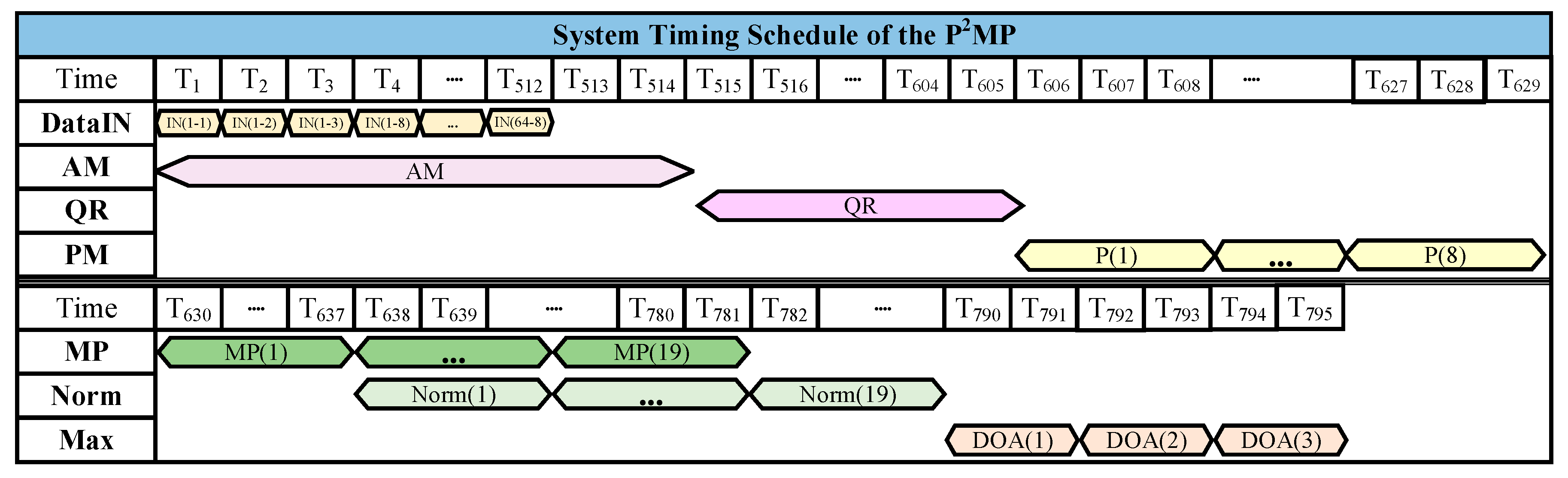
4.3. System Timing
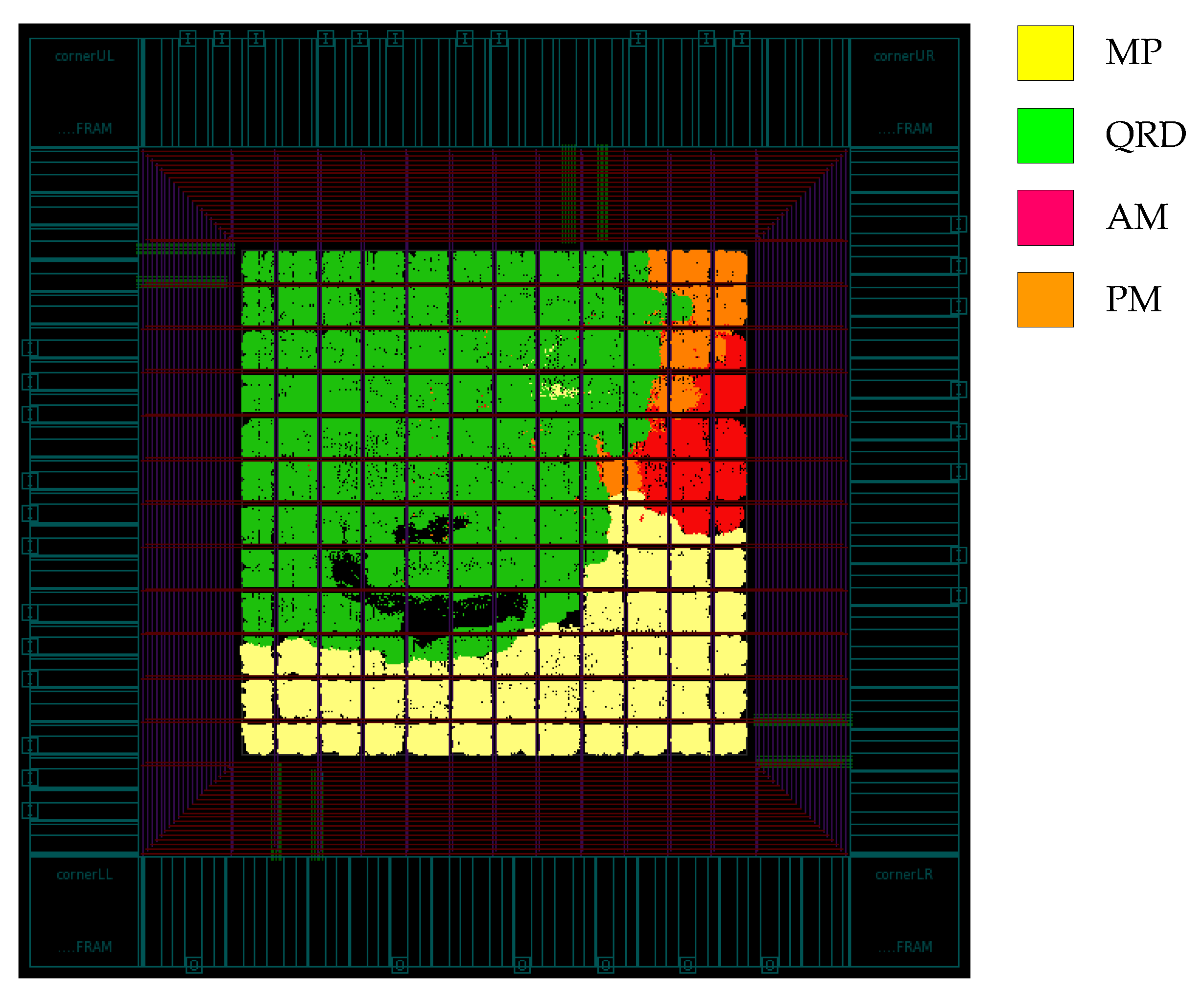
4.4. Chip Design
4.5. Comparison with Other DoA Hardware Implementation Works
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Petre, S.; Nehorai, A. MUSIC, maximum likelihood, and Cramer-Rao bound. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 720–741. [Google Scholar]
- Yan, F.; Jin, M.; Qiao, X. Low-complexity DOA estimation based on compressed MUSIC and its performance analysis. IEEE Trans. Signal Process. 2013, 61, 1915–1930. [Google Scholar] [CrossRef]
- Ali, H.; Shubair, R.M.; Salahat, E. Enhanced DOA estimation algorithms using MVDR and MUSIC. In Proceedings of the IEEE International Conference on Current Trends in Information Technology (CTIT), Dubai, United Arab Emirates, 11–12 December 2013. [Google Scholar]
- Rao, B.D.; Hari, K.V.S. Performance analysis of root-MUSIC. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 1939–1949. [Google Scholar] [CrossRef]
- Marius, P.; Gershman, A.B.; Haardt, M. Unitary root-MUSIC with a real-valued eigen decomposition: A theoretical and experimental performance study. IEEE Trans. Signal Process. 2000, 48, 1306–1314. [Google Scholar]
- Tanaka, A.; Imai, H. MUSIC-Based DoA Estimation by Oblique Projection along the signal sub-space. In Proceedings of the IEEE Workshop on Statistical Signal Processing (SSP), Gold Coast, Australia, 29 June–2 July 2014. [Google Scholar]
- Richard, R.; Kailath, T. ESPRIT-estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 984–995. [Google Scholar]
- Sylvie, M.; Marsal, A.; Benidir, M. The propagator method for source bearing estimation. Signal Process. 1995, 42, 121–138. [Google Scholar]
- Zheng, G.; Chen, B.; Yang, M. Unitary ESPRIT algorithm for bistatic MIMO radar. Electron. Lett. 2012, 48, 179–181. [Google Scholar] [CrossRef]
- Lin, J.; Ma, X.; Yan, S.; Hao, C. Time-Frequency Multi-Invariance ESPRIT for DOA Estimation. IEEE Antennas Wirel. Propag. Lett. 2016, 15, 770–773. [Google Scholar] [CrossRef]
- Zhang, W.; Han, Y.; Jin, M.; Li, X.-S. An Improved ESPRIT-Like Algorithm for Coherent Signals DOA Estimation. IEEE Commun. Lett. 2020, 24, 339–343. [Google Scholar] [CrossRef]
- Mallat, S.; Zhang, Z. Matching pursuit with time-frequency dictionaries. IEEE Trans. Signal Process. 1994, 41, 3397–3415. [Google Scholar] [CrossRef]
- McClure, M.R.; Carin, L. Matching pursuits with a wave-based dictionary. IEEE Trans. Signal Process. 1997, 45, 2912–2927. [Google Scholar] [CrossRef]
- Karabulut, G.; Kurt, T.; Yongaçoglu, A. Estimation of directions of arrival by matching pursuit (EDAMP). Eurasip J. Wirel. Commun. Netw. 2005, 2005, 618605. [Google Scholar] [CrossRef]
- Tropp, J.; Gilbert, A.C. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans. Inf. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Y.; Yuan, Y.; Jiang, T.; Yuan, Y. Low-Complexity DOA Estimation via OMP and Majorization-Minimization. In Proceedings of the 2018 IEEE Asia-Pacific Conference on Antennas and Propagation (APCAP), Auckland, New Zealand, 5–8 August 2018. [Google Scholar]
- Nasu, T.; Kikuma, N.; Sakakibara, K. Performance Improvement of DOA Estimation Using Conjugate Gradient Method with Subtraction Scheme. In Proceedings of the 2018 IEEE International Workshop on Electromagnetics: Applications and Student Innovation Competition (iWEM), Nagoya, Japan, 29–31 August 2018. [Google Scholar]
- Wang, W.; Wu, R. High Resolution Direction of Arrival (DOA) Estimation Based on Improved Orthogonal Matching Pursuit (OMP) Algorithm by Iterative Local Searching. Sensors 2013, 13, 11167–11183. [Google Scholar] [CrossRef]
- Aghababaiyan, K.; Shah-Mansouri, V.; Maham, B. High-Precision OMP-Based Direction of Arrival Estimation Scheme for Hybrid Non-Uniform Array. IEEE Commun. Lett. 2020, 24, 354–357. [Google Scholar] [CrossRef]
- Wilkinson, J.H.; Bauer, F.L.; Reinsch, C. Linear Algebra. In Handbook for Automatic Computation (2); Springer: Berlin/Heidelberg, Germany, 1971; ISBN 978-3-662-39778-7. [Google Scholar]
- Tang, C.F.T.; Liu, K.J.R.; Tretter, S.A. On systolic arrays for recursive complex Householder transformations with applications to array processing. In Proceedings of the IEEE Acoustics, Speech, and Signal Processing, Toronto, ON, Canada, 14–17 April 1991; pp. 1033–1036. [Google Scholar]
- Chung, K.-L.; Yan, W.-M. The complex Householder transform. IEEE Trans. Signal Process. 1997, 45, 2374–2376. [Google Scholar] [CrossRef]
- Lin, K.-H.; Chang, R.C.-H.; Lin, H.-L.; Wu, C.-F. Analysis and Architecture Design of a Downlink M-Modification MC-CDMA System Using the Tomlinson–Harashima Precoding Technique. IEEE Trans. Veh. Technol. 2008, 57, 1387–1397. [Google Scholar]
- Singh, C.K.; Prasad, S.H.; Balsara, P.T. VLSI Architecture for Matrix Inversion using Modified Gram-Schmidt based QR Decomposition. In Proceedings of the International VLSI Design Conference, Bangalore, India, 6–10 January 2007; pp. 836–841. [Google Scholar]
- Hwang, Y.-T.; Chen, W.-D. Design and Implementation of a High Throughput Fully-Parallel Complex-Valued QR Factorization Chip. IET Circ. Devices Syst. 2011, 5, 424–432. [Google Scholar] [CrossRef]
- Richards, M. Fundamentals of Radar Signal Processing; McGraw-Hill: New York, NY, USA, 2005. [Google Scholar]
- Zaharov, V.; Teixeira, M. SMI-MVDR beamformer implementations for large antenna array and small sample size. IEEE Trans. Circ. Syst. I Reg. Pap. 2008, 55, 3317–3327. [Google Scholar] [CrossRef]
- Unlersen, F.M.; Yaldiz, E.; Imeci, S.T. FPGA based fast Bartlett, “DoA estimator for ULA antenna using parallel computing”. Appl. Comput. Electromagn. Soc. J. 2018, 33, 450–459. [Google Scholar]
- Yan, J.; Huang, Y.; Xu, H.; Vandenbosch, G.A.E. Hardware acceleration of MUSIC based DoA estimator in MUBTS. In Proceedings of the 8th European Conference Antennas Propag (EuCAP), The Hague, The Netherlands, 6–11 April 2014; pp. 2561–2565. [Google Scholar]
- Hussain, A.A.; Tayem, N.; Butt, M.O.; Soliman, A.-H.; Alhamed, A.; Alshebeili, S. FPGA Hardware Implementation of DOA Estimation Algorithm Employing LU Decomposition. IEEE Access 2018, 6, 17666–17680. [Google Scholar] [CrossRef]
- Hussain, A.A.; Tayem, N.; Soliman, A.-H.; Radaydeh, R.M. FPGA-Based Hardware Implementation of Computationally Efficient Multi-Source DOA Estimation Algorithms. IEEE Access 2019, 7, 88845–88858. [Google Scholar] [CrossRef]






| Scheme | Complexity Formula |
|---|---|
| ESPIRIT | |
| MP | |
| OMP | |
| proposed |
| K Value | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|---|
| RMS of estimation error | SNR 20dB | 29.1° | 17.3° | 0.67° | 0.29° | 0° | 0° | 0° | 30° |
| SNR 10dB | 33.65° | 23.7° | 4.83° | 3.53° | 2.34° | 0.91° | 0.41° | 31.83° | |
| Percentage of incorrect matching | SNR 20dB | 80.3% | 58.3% | 1.7% | 1% | 0% | 0% | 0% | 90% |
| SNR 10dB | 60% | 33.3% | 12.6% | 7.3% | 3.7% | 1.3% | 0.7% | 80.3% |
| Chirp Frequency Range | 77 GHz~78 GHz | Max Beat Frequency | 3.2 MHz |
| Bandwidth | 1 GHz | Antenna array size | 8 |
| Sweep time | 20μs | FoV | 90° |
| Chirp rate | ±1 G Hz/20 μs | Sweep angle Range | −45°~45° |
| Sampling rate | 12.8 M Samples/s | Angular resolution | 5° |
| Snapshots of Number | 256 points | Codebook size | 19 |
| Maximum range | 9.6 m | FFT size | 256 |
| DoA Estimation rate | One estimate per sweep | Maximum no. of targets | 3 |
| Signal Source Number= 3, Codebook (−45°:5°:45°) Average Results Based on 500 Simulation Trials | ||||||
|---|---|---|---|---|---|---|
| SNR | 10 dB | 20 dB | ||||
| Detection rate w/o beamforming | 77.53% | 77.93% | ||||
| Detection rate for P2MP+MVDR beamforming | 90.13% | 99.13% | ||||
| False alarm rate without beamforming | 28.93% | 2.73% | ||||
| False alarm rate for P2MP+MVDR beamforming | 0.87% | 0.53% | ||||
| Prominence Simulation | signal 1 | signal 2 | signal 3 | signal 1 | signal 2 | signal 3 |
| Average prominence of detected peaks w/o beamforming | 53.71 | 23.44 | 9.44 | 53.32 | 22.65 | 9.37 |
| Average prominence of detected peaks for P2MP+MVDR beamforming | 218.71 | 85.11 | 28.97 | 204.49 | 86.21 | 46.62 |
| Item | Specification |
|---|---|
| Technology process | TSMC 40 nm CLN 40 G |
| Cell library | ARM Cell-based Design Kit |
| Voltage (Core/IO) | 0.9/3.3 V |
| Maximum clock frequency | 333 MHz |
| Minimum clock period | 3ns |
| Core Size | 0.76 |
| Die Size | 2.61 |
| IO Pad | 75 |
| Gate Count | 454.4 k |
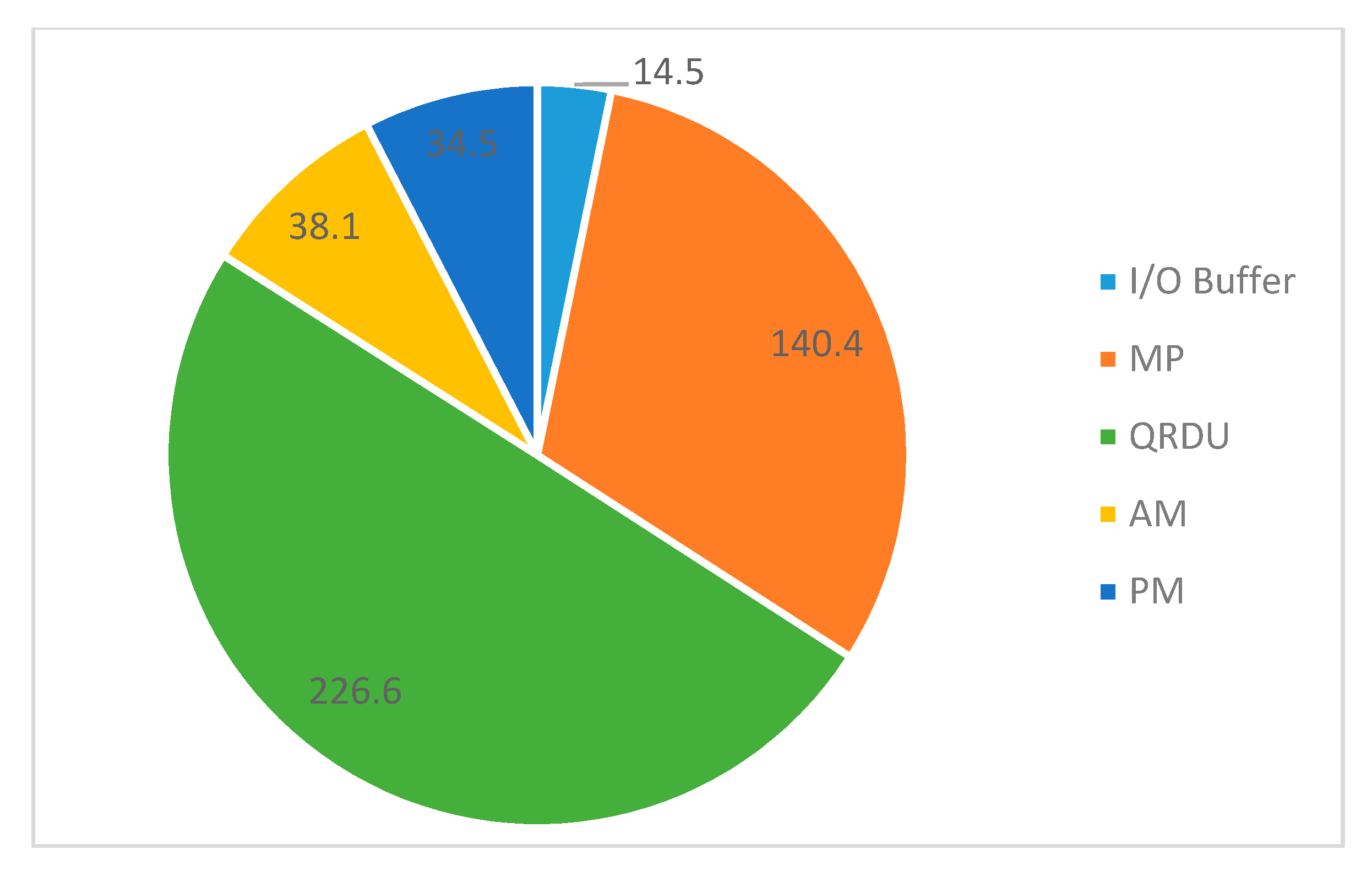
| Power (Chip/Core) | 177/83 mW |
| Latency | 512 (auto-correlation matrix) + 283 (DoA estimation) Cycles |
| Initiation interval | 1.536 μs (512clock cycles) |
| Throughput | 1.18 M estimates/sec |
| [28] | [29] | [30] | [31] | This Work | ||
|---|---|---|---|---|---|---|
| estimation scheme | Bartlett | MUSIC | LU decomp. ESPRIT | LDL decomp. | Cholesky Decomp. | Projection and parallel MP |
| Antenna array size | ||||||
| Norm. problem complexity | 1/8 | 1 | 1/8 | 1/8 | 1/8 | 1 |
| Implementation | FPGA | FPGA | FPGA | FPGA | FPGA | ASIC |
| Design effort | medium | medium | medium | medium | medium | high |
| NRE cost | medium | medium | medium | medium | medium | high |
| Unit cost | medium | medium | medium | medium | medium | low |
| Input word length | 8 bits | 16 bits | 20 bits | 20 bits | 20 bits | 21 bits |
| Clock Rate | 225 MHz | 160 MHz | 56.47 MHz | 52.5 MHz | 54.3 MHz | 333 MHz |
| Circuit complexity | NA | 54,100 LUTs 64 DSP48s | 23,438 LUTs 10 BRAMs 265 DSP48s | 21,870 LUTs 10 BRAMs 233 DSP48s | 21,956 LUTs 10 BRAMs 230 DSP48s | 454.4 k gates |
| Initiation interval | 0.804μs | 93.4μs | 2.82μs | 3.77μs | 4.05μs | 1.536μs |
| Throughput (estimates/sec) | 1.24 M | 10.7 K | 0.36 M | 0.27 M | 0.25 M | 0.65 M |
| Latency (cycles) | 181 | 14,944 | 159 | 198 | 220 | 512+283 |
| Norm. latency | 1448 | 14,944 | 1272 | 1584 | 1760 | 795 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, K.-T.; Ma, W.-H.; Hwang, Y.-T.; Chang, K.-Y. A Low Complexity, High Throughput DoA Estimation Chip Design for Adaptive Beamforming. Electronics 2020, 9, 641. https://doi.org/10.3390/electronics9040641
Chen K-T, Ma W-H, Hwang Y-T, Chang K-Y. A Low Complexity, High Throughput DoA Estimation Chip Design for Adaptive Beamforming. Electronics. 2020; 9(4):641. https://doi.org/10.3390/electronics9040641
Chicago/Turabian StyleChen, Kuan-Ting, Wei-Hsuan Ma, Yin-Tsung Hwang, and Kuan-Ying Chang. 2020. "A Low Complexity, High Throughput DoA Estimation Chip Design for Adaptive Beamforming" Electronics 9, no. 4: 641. https://doi.org/10.3390/electronics9040641
APA StyleChen, K.-T., Ma, W.-H., Hwang, Y.-T., & Chang, K.-Y. (2020). A Low Complexity, High Throughput DoA Estimation Chip Design for Adaptive Beamforming. Electronics, 9(4), 641. https://doi.org/10.3390/electronics9040641





