Abstract
The study of Current Source Matrix Converter (CSMC) static properties using the averaged state-space method for two modulation strategies Venturini and Space Vector Modulation (SVM) is the subject of this article. The converter properties for both modulation strategies have been examined and compared. The modeling approach based on the averaged state space method presented in this paper is relatively simple and requires only a small number of mathematical transformations. The averaged set equation is obtained directly from the three-phase schematic circuit, taking into account the sequences of switching patterns and modulation strategies. All the obtained results have confirmed that CSMC has some interesting properties, such as buck–boost output voltage regulation unlike the classic Matrix Converter (MC), in which the maximum voltage gain is 0.866.
1. Introduction
Frequency converters (FC) are power electronics that convert alternating current (AC) electrical energy with specified parameters into alternating current electrical energy with desired parameters [1]. One of the most desirable features of an FC is the generation of output voltage or current with arbitrary amplitude and frequency. In industrial applications, the most common are indirect PC systems with a DC energy storage in the form of an electrolytic capacitor and an output voltage inverter (Voltage Source Inverter (VSI)). Other intermediate FC solutions are systems with a DC storage in the form of a choke and an output current inverter (Current Source Inverter (CSI)) [1,2,3]. FC systems with voltage inverters are widely used in industry, mainly in electric drive [1,3], coupling renewable energy sources [2,4] and in FACTS systems [5].
There are several system solutions for voltage inverters, including multi-phase systems as well as different levels of output voltage levels, so-called multilevel inverters [1]. FC systems with current inverters have not found widespread use in industrial applications. The main problem was the implementation of the current source in the form of a choke as well as its large dimensions and weight. Switching elements used in current inverters were another technical aspect to be solved. The development of the technology of power semiconductor elements in the form of IGBT (insulated gate bipolar transistor) transistors gave new possibilities of using systems with current inverters. At the current state of technology development, several concepts of topological solutions of current inverters were created in prototype laboratory tests [2,3,6].
An alternative to indirect FC is direct FC. The best-known solution for such a system is a direct matrix converter (Matrix Converter (MC)) [7,8]. This converter is made of a matrix of bidirectional switches connected between input and output terminals. In addition, a low pass passive filter LC [9] is used to eliminate higher harmonics of the source current. The basic topology of the direct MC is powered from a voltage source and, in analogy to the indirect FC, it can be called a Voltage Source Matrix Converter (VSMC)—Figure 1a [10,11]. This type of MC configuration has a significant disadvantage in the form of low output voltage gain, which reaches a maximum value of KU max = 0.866, for undistorted load current [7,11]. This property limits or creates severe application restrictions in potential MC applications.
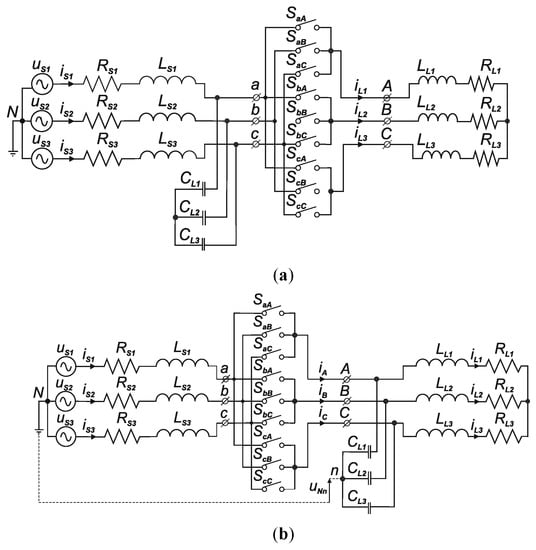
Figure 1.
Schematic diagram of the converter: (a) voltage; (b) current.
For example, when applying MC in a regulated speed electric drive, it is necessary to use motors with a lower-rated voltage or to use supply voltage boosting systems. Lack of these solutions will result in lowering the motor’s rated torque, which depends on the supply voltage. Similar to the intermediate FC, the matrix converter has several solutions including intermediate topologies (without DC storage) [7,11,12] and multi-level [13]. The configuration of power electronic switches for direct MC is symmetrical and allows the bi-directional flow of electricity from the power source to the load and from the load to the power source. The load is usually a current source (e.g., induction machine), and the power supply circuit is a voltage source. For this source configuration, MC can also be considered as a system fed from a current source with a voltage source load. The nature of the voltage source load can meet the capacitor of the output voltage filter, and the load can also be an induction machine [10,11]. Because the power grid provides us with a stable voltage source, the practical implementation of the current source is a series connection of an alternating AC voltage source with a high inductance choke [14]. The MC configured in this way is called the Current Source Matrix Converter (CSMC) (Figure 1b) [14]. MC fed a current source gives the possibility of increasing the voltage on the load terminals. The disadvantages of this solution are the need to use large input chokes and the dependence of the voltage gain characteristic on the load change [11].
To distinguish the MC topology, it should be stated that the basic topology of the direct Matrix Converter (MC) is powered from a voltage source and it can be called a Voltage Source Matrix Converter (VSMC). Furthermore, MC can also be considered as a system fed from a current source with a voltage source load, then we call such a converter a CSMC.
The available scientific literature lacks publications presenting detailed CSMC models describing the properties of the system, including the used control strategy. In articles [14,15,16] dealing with CSMC, the authors propose a control strategy that is verified in simulation studies. There is no analysis of the basic properties of the converter showing voltage gain relationships depending on various system parameters (e.g., in the form of static characteristics). In [17] the authors present the CSMC model but do not present any static characteristics. The presented property analysis is based on the presentation of time waveforms of voltage and current signals. However, the work [18] presents selected static CSMC characteristics obtained in a fairly complicated and extensive modeling process. The approach presented also does not take into account the control strategy used. In [19] authors shown only show the operating principle and general characteristics of the converter.
The modeling of CSMC presents significant challenges, due to their discontinuous switching behavior. Furthermore, given the increasing number of different modulation strategies, it is necessary to study their impact on converter properties. In order to achieve their goal, CSMC must be appropriately modeled in simulation or analytical studies. Hence it is necessary to create simple analytical models. There are several approaches to modeling switching converters. Some of them have already been used for MC analysis. The averaged state space method deserves special mention. In this method, only fundamental components of input/output voltages frequency are taking into account without higher harmonic components and power losses which are in the experimental setup. There are few methods for determining the equations of averaged state variables, e.g., the method using the theory of four terminals network [20], creating flow graphs [18] or directly creating equations using two-frequency d-q transformation [21,22].
In this paper, the average-state space method and the two-frequency d–q transformation are used to model CSMC with tow control strategy Venturini and Space Vector Modulation (SVM). The basics of modeling were taken from the article [22] and applied to the CSMC topology. The main aim of this paper is to present mathematical models of CSMC for two control strategies and analysis and comparison of static properties of the CSMC system.
2. Current Source Matrix Converter
The schematic diagram of the current PM is shown in Figure 1b [14,15], where the current source input chokes are connected to the input terminals of the switch matrix. Output capacities are connected to the load terminals to determine the nature of the load as a voltage source. Configurations of bidirectional connectors used in all systems presented in the article are presented in Figure 2. The output voltage waveform is implemented by switching bidirectional switches. These switches implement the appropriate sequence of connections between the output and input terminals in such a way that the current can flows in two directions.

Figure 2.
Main topologies for bi-directional switches: (a) common emitter IGBT, (b) common collector IGBT, (c) diode bridge and IGBT.
During matrix operation, the switches, regardless of the polarized voltage in the circuit and the direction of the flowing current, are turned off and on at a certain moment. The control function of the switches can be represented as follows [11]:
for which j ∈ {a, b, c}, k ∈ {A, B, C} where: a, b, c are the phase source terminals, while A, B, C are the output terminals of the CSMC. The switches must be controlled so that there is no short circuit of the output phases and that the current flow is always ensured in each phase of the current source (on input terminals). This is possible if only one switch will be turned on in each source phase of CSMC:

Table 1.
Allowed configurations of matrix converter depending on the states of switches.
The currents and voltages relationship in the CSMC system are determined by Equations (3) and (4). A 3 × 3 matrix system provides 27 allowed configurations of power electronic switches resulting from the limitation Equation (2). These configurations can be combined into three groups similar to VSMC but the way of connecting the input and output lines is described as follows. The first one includes three zero configurations—all three source phases are connected to the same output phase. The second group consists of active configurations. In this case, two source lines are connected to the same output line. In the third group, one input phase is connected to one output phase. The relationship between the CSMC (Figure 1b) source-side and load-side currents and voltages is described as follows [22]:
where T is the transformation matrix, - are switch state functions depending on the used modulation strategy.
It should be emphasized that the load current and voltage at the input terminals of matrix switches are shaped in the CSMC, inversely than it is the case in the classic MC. Then we adjust the voltage gain indirectly by adjusting the load current. The input power factor is also indirectly controlled by forcing the source current phase shift by setting the voltage on the input terminals of matrix switches.
3. Venturini Modulation Strategy
The classic Venturini method presented by Venturini and Alesina [23] consists in modifying the switching state function in the transformation matrix using low-frequency modulation functions. This allows you to specify the intervals for controlling the switches in the converter. The transition (transformation) function is represented by the relationship Equation (5).
where djK(t) = tjK/TPWM pulse duty factor of the state function of the switches SjK. In publication [23], Venturini and Alesina proposed the first control strategy based on two modulation matrix and . The voltage gain for this control strategy is between 0 and 0.5. It this method is possible to control the input phase shift angle in the range:. To control the input phase shift angle in the range from 0 to , then M + is used as follows:
Whereas for controlling the input phase shift angle in the range from to 0, then M− is used:
where:
- ,
- , , is the voltage gain: , , and is the pulsation of the supply and load voltage respectively, is the phase shift of current relative to voltage of at source and load terminals of MC.
In this article, only one modulation matrix was used for CSMC control without control of the source current phase shift relative to the source voltage. Then, simplified modulation functions were defined as follows [24]:
4. Space Vector Modulation of CSMC
The operation of the CSMC converter can also be described using space vector modulation - SVM. In this method, voltages and currents are represented by appropriate space vectors. The basic equation for the presentation of three-phase signals using space vector is defined by Equation (9).
in which: represent the instantaneous values of three-phase variables, while is a unitary complex rotation operator. The input voltages and output currents of CSMC can be expressed in its space phasor form as [22]:
where: αi are the phase angles of the output voltage vector, βO are the phase angles of the input current vector.
The allowed switching configuration of the current source matrix converter in the SVM algorithm is shown in Table 2. Only active and zero configurations are used in this control—a total of 18 allowed configurations. Graphic interpretation 21 configurations of switches are shown in Figure 3. Active configurations corresponding to non-zero voltage and current vectors have the following designations: (± 1, ± 2, ± 3), (± 4, ± 5, ± 6), and (± 7, ± 8, ± 9). In Figure 4 the voltage ui and current iO vectors for CSMC corresponding to the 18 active configurations are shown. The complex space vector plane is divided into six sectors Si for source voltages and six sectors SO for output current. The reference source voltage and load current space-vectors are determined by selecting 4 active configurations (vectors), applied to in a specific sequence and time intervals within the switching sequence period TSeq—Equations (12) and (13). The zero configurations are applied to complete time interval TSeq. Modulation duty cycles for switching configuration are defined as follows Equations (14)–(17). The synthesis process of source voltage and output current space-vectors for Si = 1 and SO = 1 is presented in Figure 5.
where φi is the input phase displacement angle, and are the angles of the input voltage and output current vectors measured from the bisecting line of the corresponding sectors, and are limited as follows: and .

Table 2.
Acceptable switch configurations in Space Vector Modulation (SVM) for CSMC.
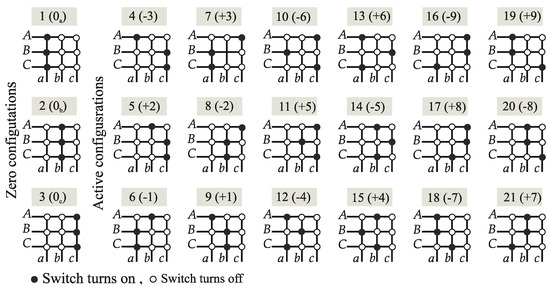
Figure 3.
Geometric interpretation of the used switch configurations in Current Source Matrix Converter (CSMC).
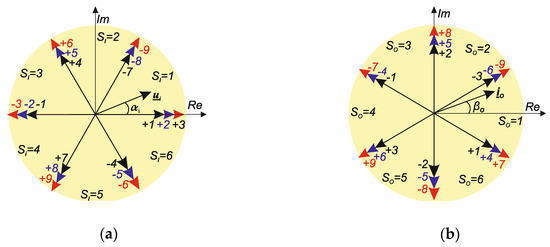
Figure 4.
Graphic interpretation of active vectors: (a) input voltage at converter; (b) output current.
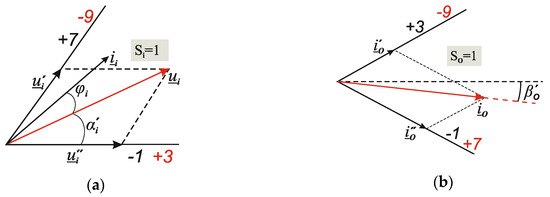
Figure 5.
Geometric interpretation of an example vector modulation: (a) of input voltage vector, (b) output current vector.
5. Modeling Theory
The local average of any time-domain function q(t) is defined by the relationship [25]:
where d(t) is the continuous duty cycle. If , then this determination is true for the next sequence periods. Then is the duty cycle in the k-th cycle. The average state-space equation is expressed by the relationship [26]:
In this equation, represents the averaged state variable vector, is the averaged matrix of state variables, is the averaged input matrix. During operation, the converter assumes different states. These states are subject to analytical combinations on which the averaging method in the space of states is based. Fig. 5 presents the idea of the average state space method related to the Current Source Matrix Converter which topology is presented in Figure 1b.
CSMC are characterized by the fact that they have 27 possible switching states. The block diagram shown in Figure 6 allows us to understand the modeling process. It is assumed that the state model is linear for each of the possible switch configurations. Each of these configurations creates a separate model. Then these models are integrated with the help of the averaged dk duty factor. Each of these configurations can be represented by the Equation:
where: x - state variable vectors, - state matrix and - input matrix for the k-th configuration of the switches. The general form of the mathematical model based on the average space equations for CSMC is described as follows:
where:
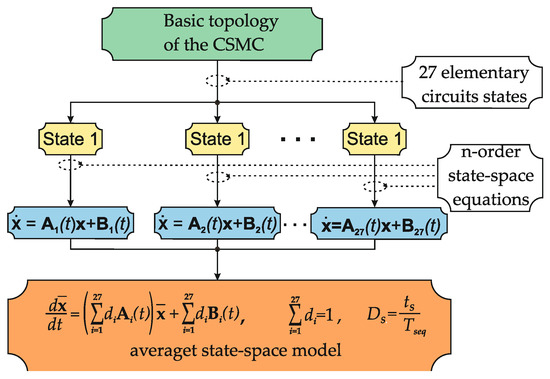
Figure 6.
Block diagram for describing the method of averaging state variables for CSMC.
The average space-space model of the CSMC presented in Equation (21) is a time-varying model. Responsible for this is the time-varying pulse duty cycle . A reduced time-invariant model of the CSMC can be realized by using two-frequency transformation matrix K described in d-q rotational coordinate frame:
In these equations, the is the d-q transformation matrix for supply voltage pulsations, while the is the d-q transformation matrix for load voltage pulsations. To get a stationary equation, substitute the expression:
in Equation (21) assuming that the frequency converter is a symmetrical system. As a result of this substitution, new state variables will appear. So Equation (21) will take the form:
where:
The solution of Equation (26) was described in [21] and have the following form:
where I is a unit matrix, while represents the vector of initial values of transformed variables. The values of averaged state variables in steady-state are represented by Equation (30) [21]:
The relationships Equations (29) and (30) can be used in the study of the operation of the CSMC presented in Figure 1b for different modulation schemes. This article will present the results of research for the simplified Venturini—described by Equation (8) and SVM—described by Equations (9)–(17).
6. Modelling of CSMC with SVM
The relationship (12) determined the relative switch-on time of the individual switch configuration—corresponding to base vectors, of the output currents and input voltages at the terminals of matrix switches for CSMC with SVM. Subsequent base vectors are turned-on with the following sequence which are defined in Table 3:

Table 3.
List of active switch (vectors) configurations assigned to of individual So and Si for appropriate d1–d4.
For the order of inclusions so adopted, the transformation matrix D, for example, Si = 1 and SO = 1 is determined by the relationship:
Finally, matrix D has the following form:
By replacing the switching times d1, d2, d3 and d4 by appropriate formulas defined by dependencies Equations (14)–(17), the matrix D takes the final form:
When constructing a mathematical model of a matrix converter with space vector modulation, it should take into account the potential difference between a grounded three-phase power point and a zero load point uNn (Figure 1b). This voltage is called the unbalance voltage and it its average value is expressed by the relationship:
Taking into account the Equation (3) the unbalance voltage is given by the formula:
Ultimately, the imbalance voltage takes the form:
where:
Taking into account Equations (9)–(39) yields the final form of the averaged state space model (20) of the CSMC with RL load (Figure 1b) with space vector modulation is defined by Equation (40). To sum up the presented analysis, we can define the following block diagram presented in Figure 7, describing the procedure of determining the model of average state-space variables for CSMC with SVM.
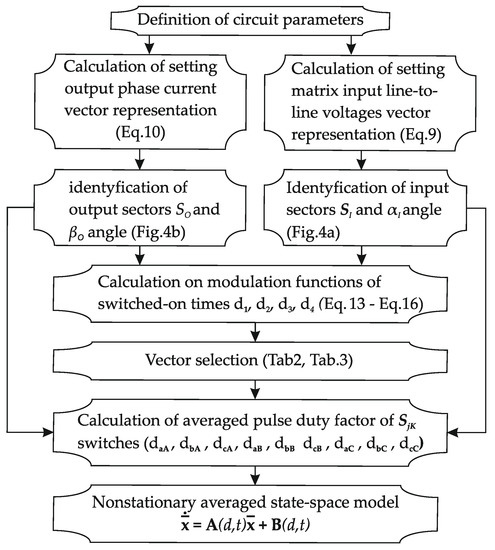
Figure 7.
Block diagram of CSMC with SVM system modeling using the average state-space model.
7. Modeling of CSMC with Venturini Modulation
Similarly to the mathematical model of CSMC with RL load using the SVM, a mathematical model with Venturini modulation [23] was constructed. This modulation is much simpler because the modulating functions are invariable for set operating conditions and defined by low-frequency modulation functions Equation (8). The average value, for the grid voltage period, of the unbalance voltage uN is zero. Then this component does not have to be included in the equations of averaged state-space variables. The mathematical model of CSMC with simplified Venturini modulation is presented in Equation (41).
8. Validation of CSMC Average Model with SVM and Venturini Modulation
Validation of the obtained models is presented for the following parameters: LS = 10 mH, RLS = 0.1 Ω, CL = 30 μF, RL= 30 Ω, LL = 1 mH. Investigations were carried out on a system consisting of an idealized power stage RSjk=0 in conduction state and RSjk=∞ in the open state.
In Figure 8, Figure 9, Figure 10 steady-state characteristics of the voltage gain, current gain and input power factor as functions of pulse duty factor q for Venturini (index (a)) and SVM (index (b)) are shown. As you can see from the presented characteristics, CSMC eliminates the VSMC disadvantage, i.e., reduced voltage at the output terminals. For CSMC, even a voltage gain of about 2.5 times for Venturini type modulation and about 3.5 times for SVM type modulation was obtained. For Venturini modulation, the current transformation characteristic is more linear than for SVM (Figure 9), while the output power factor is more beneficial for SVM control (Figure 10). All the presented characteristics from Figure 8 Figure 9 Figure 10 change slightly depending on the set frequency of the output frequency.
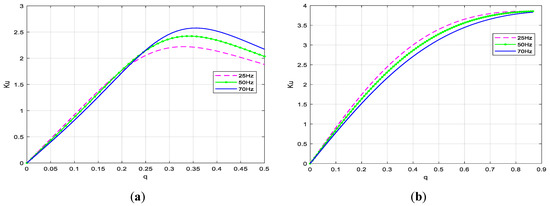
Figure 8.
Static characteristics of voltage gain: (a) Venturini modulation, (b) SVM.
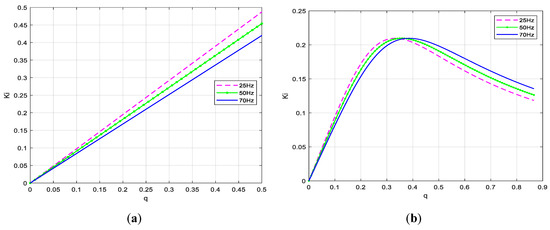
Figure 9.
Static characteristics of current gain: (a) Venturini modulation, (b) SVM.
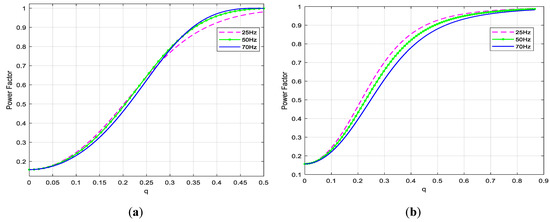
Figure 10.
Static characteristics of the input power factor: (a) Venturini modulation, (b) SVM.
The real power source, built from a serial connection of a voltage source and a high inductance choke that powers the CSMC, changes its parameters depending on the load condition. The characteristics of Figure 11 show the effect of load resistance changes on voltage gain. Increasing the load (reducing the load resistance) causes a decrease in voltage gain. However, it should be noted that for current source parameters assumed in the article, the value of voltage gain is greater than one for a load resistance of about 20 Ω. With a properly designed control system in a closed control loop, it will be possible to maintain the nominal value of the output voltage, as well as stabilize this voltage in the event of supply voltage sags. The characteristics for SVM control are more linear and for Venturini modulation, there is a decrease in voltage gain for larger values of load resistance. This is due to the phenomenon of resonance occurring between elements of the power source, output filter and load, which is more important when switching on synchronous configurations (each input phase is connected to a different output phase), which occur only in the Venturini method. Figure 12; Figure 13 show the characteristics of the current gain and input power factor depending on load changes. It should be noted that there is no significant increase in source current that would result from the phenomenon of increasing the output voltage, as illustrated by the current gain characteristics of Figure 12. A negative phenomenon is the lack of a unit input power factor (Figure 13). For SVM control it is possible to regulate it indirectly by forcing the phase shift of source current source by appropriate shaping the voltage on the input terminals of the matrix switches (ua, ub, uc). In the presented results, the phase shift value of the input voltage relative to the source current is set to zero, which does not mean that the source current will be in phase with the source voltage.
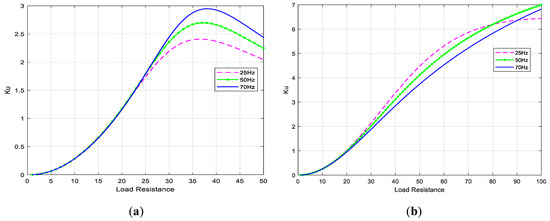
Figure 11.
Static characteristics of voltage gain as a function of load: (a) Venturini modulation for q = 0.5, (b) SVM for q = 0.866 and φi = 0.
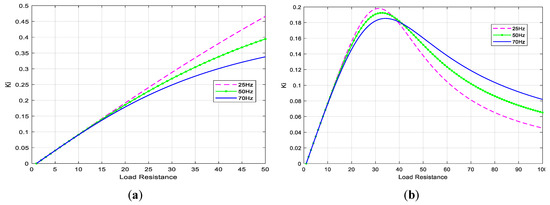
Figure 12.
Static characteristics of current gain as a function of increasing load: (a) Venturini modulation for q = 0.5, (b) SVM for q = 0.866 and φi = 0.
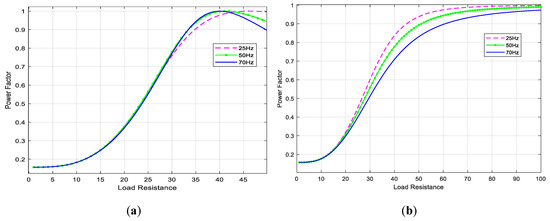
Figure 13.
Static characteristics of power factor gain as a function of increasing load: (a) Venturini modulation for q = 0.5, (b) SVM for q = 0.866 and φi = 0.
In order to investigate the impact of the given output voltage frequency and changes in load value on the voltage gain characteristics, 3D characteristics illustrating these relationships have been determined, which are shown in Figure 14. A change in the output voltage frequency has little effect on the change in voltage gain and this change is more evident in the higher load resistance. Adjustment of the converter in a closed control loop with standard controllers should handle such variability in voltage gain parameters.
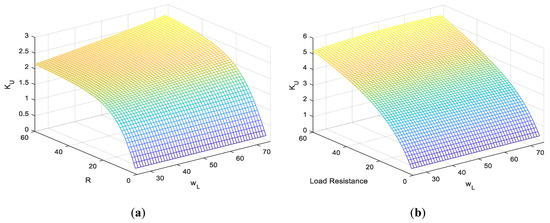
Figure 14.
Impact of the load and setting output voltage frequency on the voltage gain: (a) Venturini modulation q = 0.5, (b) SVM for q = 0.866 and φi = 0.
The summary of tests of CSMC properties presents time waveforms of load voltages obtained on the basis of simulation tests in the PSim simulation program for Venturini modulation. The waveforms shown show that when the converter is switching-on, the transient state is quite short and amounts to only half the mains voltage period (Figure 15).
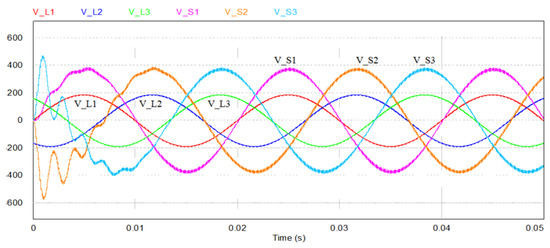
Figure 15.
Waveforms of supply voltages and amplified voltages of the system output for Venturini modulation for q = 0.5 and RL = 30 Ω.
9. Conclusions
The article presents the results of tests on the properties of a frequency converter system without a DC energy store, in which the matrix of bidirectional switches is powered from a current source (implemented by connecting a choke and a voltage source) called current source matrix converter (CSMC). A simplified strategy according to Venturini and space vector modulations (SVM) was used to control the converter connectors. The converter properties for both modulation strategies have been examined and compared. The converter properties were determined on the basis of the averaged state-space model. The equations of averaged state variables were created taking into account the relationships related to the modulation process of the converter control functions. The modeling process for Venturini strategy is much simpler than for SVM, because the modulating functions directly determine the average pulse duty ratios for individual switches. For SVM in the obtained model changes in modulating functions depending on the sectors in which the input voltage vector and the output current vector are located should be considered. In addition, the unbalance voltage between the grounding point of the sources and the star load point should be considered.
The obtained static characteristics indicate that CSMC allows increasing the output voltage in relation to the voltage of the input source. This is getting rid of the disadvantage of classic matrix converters supplied from a voltage source for which the maximum gain is 0.5 for the Venturini method and 8.66 for SVM. It should be emphasized that SVM has better regulatory properties than Venturini similar to the classic MC.
The average state-space method was used to determine the mathematical description of the CSMC properties. The obtained models are a key tool in the study of low-frequency properties, loadability margins, and control algorithm behavior. The presented modeling approach is relatively simple and requires only a small number of mathematical operations e.g., the two-frequency d–q transformation. The averaged set equation is obtained directly from the three-phase schematic circuit using Kirchhoff’s laws, taking into account the sequences of switching patterns for modulation strategies (Venturini or SVM). This method was previously presented in scientific articles for analyzing the properties of other MC-based frequency converters, and this article has been successfully implemented for CSMC analysis.
Author Contributions
Conceptualization, P.S.; validation, M.C., and P.S.; investigation, M.C. and P.S; resources, P.S. and J.K; writing—original draft preparation, M.C. and J.K; writing—review and editing, P.S. and J.K.; visualization, M.C.; supervision, P.S.; funding acquisition, J.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wilamowski, B.M.; Irwin, D.J. Power Electronics and Motor Drives. The Industrial Electronics Handbook; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Anand, S.; Gundlapalli, S.K.; Fernandes, B.G. Transformer-Less Grid Feeding Current Source Inverter for Solar Photovoltaic System. IEEE Trans. Ind. Electron. 2014, 61, 5334–5344. [Google Scholar]
- Espinoza, J.R.; Joos, G. A current-source-inverter-fed induction motor drive system with reduced losses. IEEE Trans. Ind. Appl. 1998, 34, 796–805. [Google Scholar] [CrossRef]
- Kroposki, B.; Pink, C.; DeBlasio, R.; Thomas, H.; Simões, M.; Sen, P. Benefits of power electronic interfaces for distributed energy systems. IEEE Trans. Energy Convers. 2010, 25, 901–908. [Google Scholar] [CrossRef]
- Bifaretti, S.; Zanchetta, P.; Watson, A.; Tarisciotti, L.; Clare, J.C. Advanced power electronic conversion and control system for universal and flexible power management. IEEE Trans. Smart Grid 2011, 2, 231–243. [Google Scholar] [CrossRef]
- Sahan, B.; Araújo, S.V.; Nöding, C.; Zacharias, P. Comparative Evaluation of Three-Phase Current Source Inverters for Grid Interfacing of Distributed and Renewable Energy Systems. IEEE Trans. Power Electron. 2011, 26, 2304–2318. [Google Scholar] [CrossRef]
- Kolar, J.W.; Friedli, T.; Rodriguez, J.; Wheeler, P.W. Review of three-phase PWM AC–AC converter topologies. IEEE Trans. Ind. Electron. 2011, 58, 4988–5006. [Google Scholar] [CrossRef]
- Szcześniak, P. Challenges and Design Requirements for Industrial Applications of AC/AC Power Converters without DC-Link. Energies 2019, 12, 1581. [Google Scholar] [CrossRef]
- Ferreira Pinto, S.; Fernando Silva, J. Input filter design for sliding mode controlled matrix converters. In Proceedings of the IEEE 32nd Annual Power Electronics Specialists Conference, Vancouver, BC, Canada, 17–21 June 2001; Volume 2, pp. 648–653. [Google Scholar]
- Fedyczak, Z.; Szcześniak, P.; Korotyeyev, I. New family of matrix-reactance frequency converters based on unipolar PWM AC matrix-reactance choppers. In Proceedings of the International Power Electronics and Motion Control Conference, EPE-PEMC’08, Poznań, Poland, 1–3 September 2008; pp. 236–243. [Google Scholar]
- Szcześniak, P. Three-Phase AC-AC Power Converters Based on Matrix Converter Topology. Matrix-Reactance Frequency Converters Concept; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Szcześniak, P.; Kaniewski, J.; Jarnut, M. AC-AC power electronic converters without DC energy storage: A review. Energy Convers. Manag. 2015, 92, 483–497. [Google Scholar] [CrossRef]
- Sun, Y.; Xiong, W.; Su, M.; Dan, H.; Li, X.; Yang, J. Modulation Strategies Based on Mathematical Construction Method for Multimodular Matrix Converter. IEEE Trans. Power Electron. 2016, 31, 5423–5434. [Google Scholar] [CrossRef]
- Fedyczak, Z.; Tadra, G.; Klytta, M. Implementation of the current source matrix converter with space vector modulation. In Proceedings of the 14th International Power Electronics and Motion Control Conference EPE-PEMC 2010, Ohrid, Macedonia, 6–8 September 2010; pp. T2-97–T2-102. [Google Scholar]
- Nikkhajoei, H. A Current Source Matrix Converter for High-Power Applications. In Proceedings of the 2007 IEEE Power Electronics Specialists Conference, Orlando, FL, USA, 17–21 June 2007; pp. 2516–2521. [Google Scholar]
- Castro João, P.; Pinto, S.; Fernando Silva, J. Modulation Strategy for the Boost Matrix Converter. Available online: https://fenix.tecnico.ulisboa.pt/downloadFile/844820067124290/Paper_JoaoCastro.pdf (accessed on 24 March 2020).
- Kanaan, H.Y.; Al-Haddad, K.; Rajagopalan, V. A new average modeling and control design applied to a nine-switch matrix converter with input power factor correction, EPE 2003–Toulouse. In Proceedings of the France 10th European Conference on Power Electronics and Applications, Toulouse, France, 2–4 September 2003; pp. 1–8. [Google Scholar]
- Kwon, W.H.; Cho, G.H. Analysis of static and dynamic characteristics of practical step-up nine-switch matrix converter. Proc. Inst. Electr. Eng. B 1993, 140, 139–146. [Google Scholar]
- Popov, V.; Baranov, E.; Malnev, A. Current source matrix converter. In Proceedings of the 16th International Conference of Young Specialists on Micro/Nanotechnologies and Electron Devices, Erlagol, Russia, 29 June–3 July 2015; pp. 384–386. [Google Scholar]
- Szcześniak, P.; Fedyczak, Z.; Klytta, M. Modeling and analysis of a matrix-reactance frequency converter based on buck–boost topology by DQ0 transformation. In Proceedings of the 13th International Power Electronics and Motion Control Conference, EPE-PEMC’08, Poznań, Poland, 1–3 September 2008; pp. 165–172. [Google Scholar]
- Korotyeyev, I.; Fedyczak, Z. Steady and transient states modelling methods of matrix-reactance frequency converter with buck-boost topology. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2009, 28, 626–638. [Google Scholar] [CrossRef]
- Szcześniak, P. A static and dynamic model of a space vector modulated matrix-reactance frequency converter. Electr. Power Syst. Res. 2014, 108, 82–92. [Google Scholar] [CrossRef]
- Venturini, M.; Alesina, A. The generalized transformer: A new bi-directional sinusoidal waveform frequency converter with continuously adjustable input power factor. In Proceedings of the IEEE Power Electronics Specialists Conference (PESC’80), Atlanta, GA, USA, 16–20 June 1980; pp. 242–252. [Google Scholar]
- Wheeler, P.W.; Rodriguez, J.; Clare, J.C.; Empringham, L.; Weinstejn, A. Matrix converters: A technology review. IEEE Trans. Ind. Electron. 2002, 49, 276–288. [Google Scholar] [CrossRef]
- Maksimović, D.; Stanković, A.M.; Thottuvelil, V.J.; Verghese, G.C. Modeling andsimulation of power electronic converters. Proc. IEEE 2001, 89, 898–912. [Google Scholar] [CrossRef]
- Middlebrook, R.D.; Ćuk, S. A general unified approach to modelling switching-converter power stages. In Proceedings of the 1976 IEEE Power Electronics Specialists Conference (PESC’ 76), Cleveland, OH, USA, 8–10 June 1976; pp. 73–86. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).