Cooperative Secure Transmission in MISO-NOMA Networks
Abstract
1. Introduction
- Taking multiple eavesdroppers into consideration, we investigate physical layer security in cooperative MISO-NOMA networks. We first derive an accurate closed form expression for SOP. Then, we transform the objective function in the SRM problem under certain SOP into a strictly concave function through strict mathematical proofs.
- Different from the work of [21] in which only one user was served by Alice, in this paper, we investigate cooperative secure transmission in NOMA networks where a source (Alice) intends to transmit confidential messages to one legitimate user with high-level security requirement (LU1), and serve another normal one (LU2) simultaneously. In particular, we consider the upper bound of the power Alice allocates to LU2 to guarantee the QoS constraint at LU2. In addition, we have made a comprehensive discussion and developed an adaptive approach based on different cases to obtain the optimal power allocation factor for solving the SRM problem under certain SOP.
- Numerical results are provided to verify that the proposed scheme enables dynamic transmission. Both the effectiveness and flexibility of our scheme in achieving higher secrecy performance and effective EE have also been demonstrated.
2. System Model and Problem Formulation
2.1. System Model
2.2. Problem Formulation
3. Proposed Solution for SRM Problem under Certain SOP Constraint
3.1. Solution for SOP Constraint
3.2. Power Allocation Optimization for LU1
- (a)
- . can be easily verified. Thus, we have , if ; otherwise, .
- (b)
- . Based on the characteristics of the concave function, there must exist a unique . Hence, if , we have ; otherwise, .
- (c)
- . According to (25), we have , and it is optimal for Alice to stop secure transmission, which leads to and .
| Algorithm 1 Solution to the SRM problem in (12). | |
| Input:, , , , , , , , , ; | |
| Output:; | |
| 1: | calculate according to (26); |
| 2: | if , |
| Alice stops serving LU2. In addition, the CJ scheme in [21] is carried out at Alice to guarantee secure transmission for LU1; | |
| 3: | else if , |
| the CJ scheme in [21] is implemented to solve the SRM problem in (12); | |
| 4: | else |
| the solution to obtain has been discussed in Case 3; | |
| 5: | end if |
| 6: | return; |
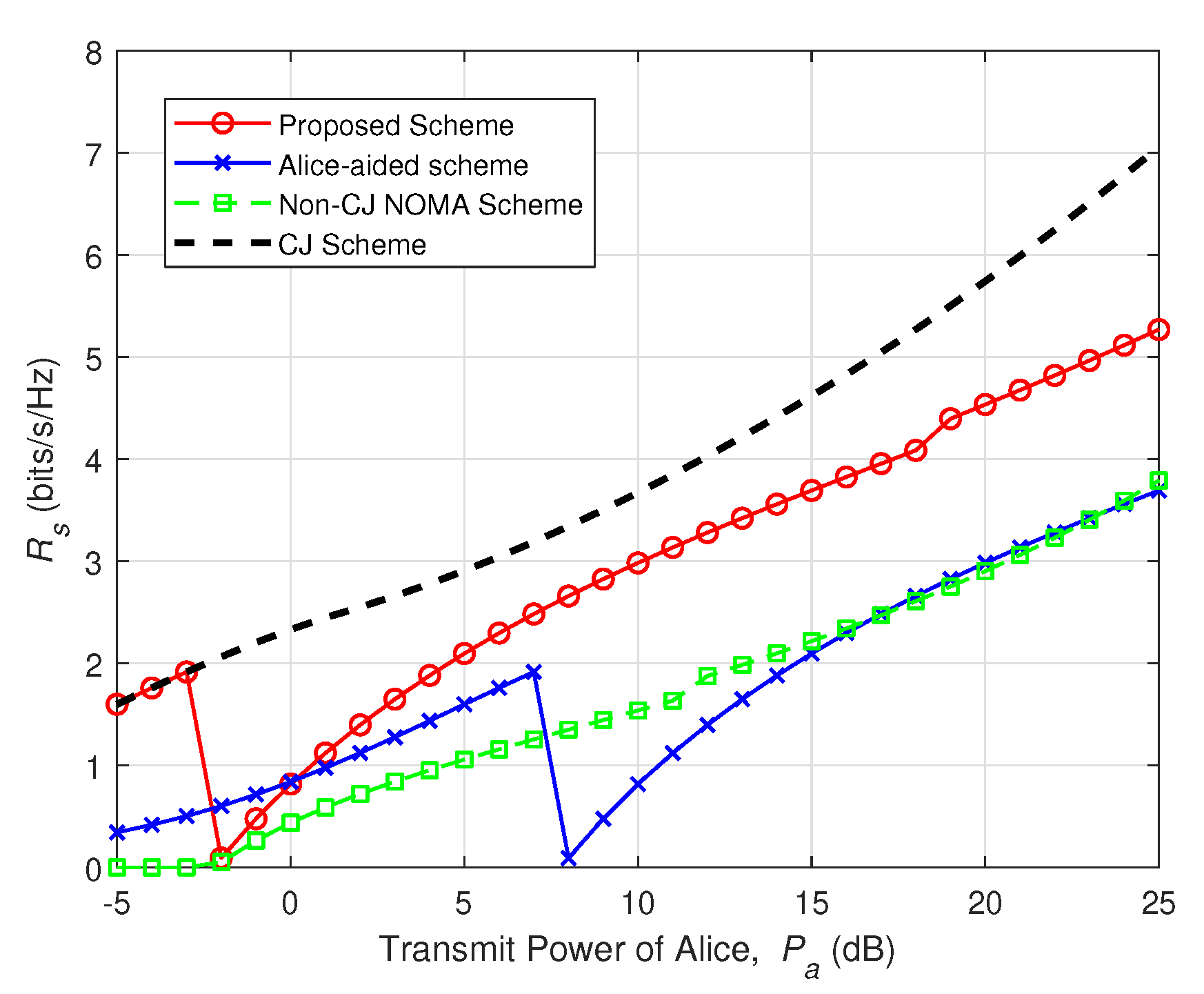
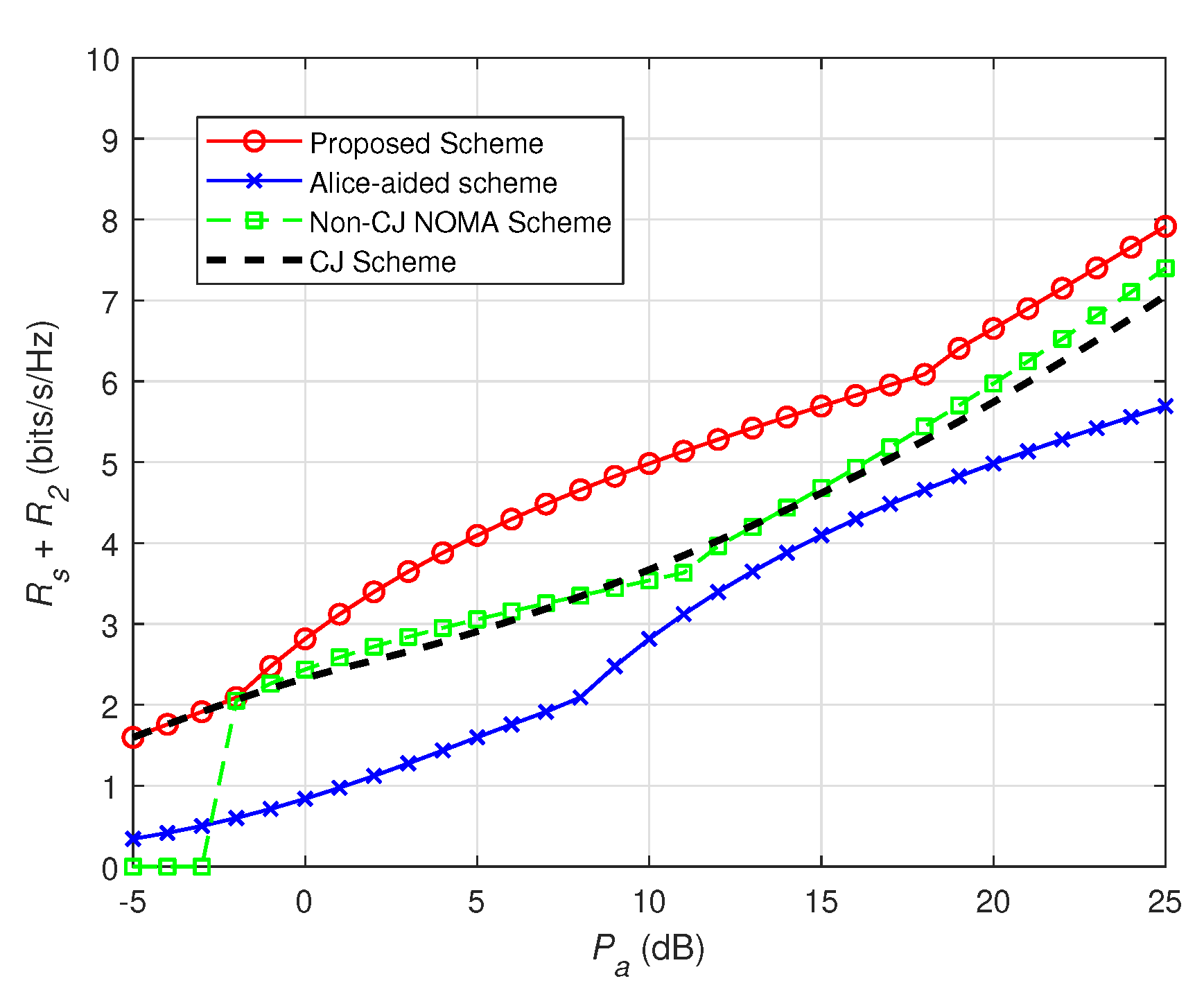
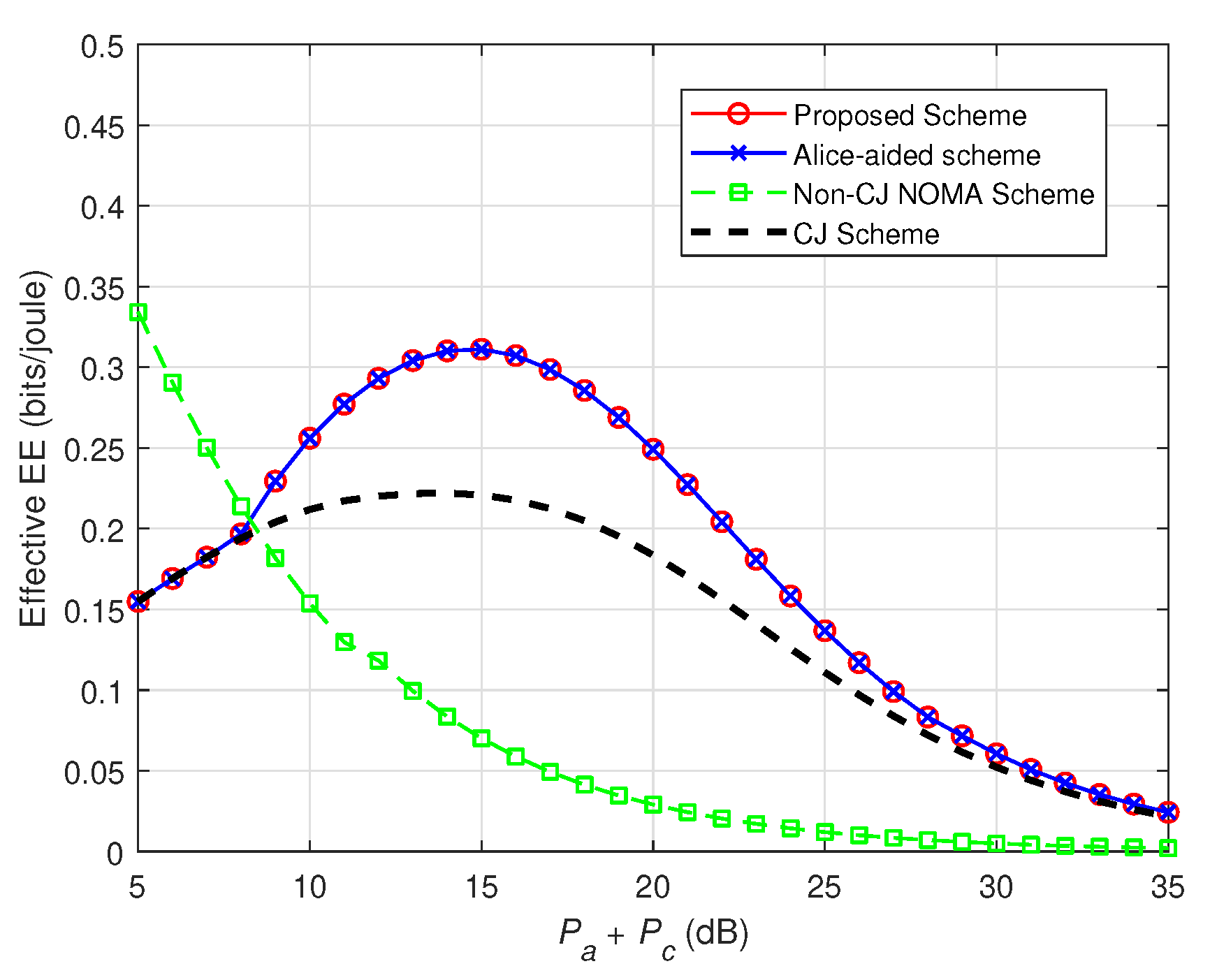
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dai, L.; Wang, B.; Yuan, Y.; Han, S.; I, C.; Wang, Z. Non-orthogonal multiple access for 5G: Solutions, challenges, opportunities, and future research trends. IEEE Commun. Mag. 2015, 53, 74–81. [Google Scholar] [CrossRef]
- Anwar, A.; Seet, B.C.; Hasan, M.A.; Li, X.J. A Survey on Application of Non-Orthogonal Multiple Access to Different Wireless Networks. Electronics 2019, 8, 1135. [Google Scholar] [CrossRef]
- Ding, Z.; Lei, X.; Karagiannidis, G.K.; Schober, R.; Yuan, J.; Bhargava, V.K. A Survey on Non-Orthogonal Multiple Access for 5G Networks: Research Challenges and Future Trends. IEEE J. Sel. Areas Commun. 2017, 35, 2181–2195. [Google Scholar] [CrossRef]
- Wang, C.; Chen, H.; Yin, Q.; Feng, A.; Molisch, A.F. Multi-User Two-Way Relay Networks with Distributed Beamforming. IEEE Trans. Wirel. Commun. 2011, 10, 3460–3471. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, Z. UAV-Aided Secure Transmission in MISOME Wiretap Channels With Imperfect CSI. IEEE Access 2019, 7, 98107–98121. [Google Scholar] [CrossRef]
- Jameel, F.; Wyne, S.; Kaddoum, G.; Duong, T.Q. A Comprehensive Survey on Cooperative Relaying and Jamming Strategies for Physical Layer Security. IEEE Commun. Surv. Tutur. 2019, 21, 2734–2771. [Google Scholar] [CrossRef]
- Ding, Z.; Peng, M.; Poor, H.V. Cooperative Non-Orthogonal Multiple Access in 5G Systems. IEEE Commun. Lett. 2015, 19, 1462–1465. [Google Scholar] [CrossRef]
- Jiao, R.; Dai, L.; Zhang, J.; MacKenzie, R.; Hao, M. On the Performance of NOMA-Based Cooperative Relaying Systems Over Rician Fading Channels. IEEE Trans. Veh. Technol. 2017, 66, 11409–11413. [Google Scholar] [CrossRef]
- Chen, B.; Chen, Y.; Chen, Y.; Cao, Y.; Zhao, N.; Ding, Z. A Novel Spectrum Sharing Scheme Assisted by Secondary NOMA Relay. IEEE Wirel. Commun. Lett. 2018, 7, 732–735. [Google Scholar] [CrossRef]
- Le, C.B.; Do, D.T.; Voznak, M. Wireless-powered Cooperative MIMO NOMA Networks: Design and Performance Improvement For Cell-Edge Users. Electronics 2019, 8, 328. [Google Scholar] [CrossRef]
- Nomikos, N.; Trakadas, P.; Hatziefremidis, A. Full-Duplex NOMA Transmission with Single-Antenna Buffer-Aided Relays. Electronics 2019, 8, 1482. [Google Scholar] [CrossRef]
- Chen, J.; Yang, L.; Alouini, M. Physical Layer Security for Cooperative NOMA Systems. IEEE Trans. Veh. Technol. 2018, 67, 4645–4649. [Google Scholar] [CrossRef]
- Feng, Y.; Yan, S.; Liu, C.; Yang, Z.; Yang, N. Two-Stage Relay Selection for Enhancing Physical Layer Security in Non-Orthogonal Multiple Access. IEEE Trans. Inf. Forensics Secur. 2019, 14, 1670–1683. [Google Scholar] [CrossRef]
- Lv, L.; Zhou, F.; Chen, J.; Al-Dhahir, N. Secure Cooperative Communications With an Untrusted Relay: A NOMA-Inspired Jamming and Relaying Approach. IEEE Trans. Inf. Forensics Secur. 2019, 14, 3191–3205. [Google Scholar] [CrossRef]
- Zhou, F.; Chu, Z.; Sun, H.; Hu, R.Q.; Hanzo, L. Artificial Noise Aided Secure Cognitive Beamforming for Cooperative MISO-NOMA Using SWIPT. IEEE J. Sel. Areas Commun. 2018, 36, 918–931. [Google Scholar] [CrossRef]
- Yu, C.; Ko, H.; Peng, X.; Xie, W.; Zhu, P. Jammer-aided Secure Communications for Cooperative NOMA Systems. IEEE Commun. Lett. 2019, 23, 1935–1939. [Google Scholar] [CrossRef]
- Yuan, C.; Tao, X.; Li, N.; Ni, W.; Liu, R.P.; Zhang, P. Analysis on Secrecy Capacity of Cooperative Non-Orthogonal Multiple Access With Proactive Jamming. IEEE Trans. Veh. Technol. 2019, 68, 2682–2696. [Google Scholar] [CrossRef]
- Cao, Y.; Zhao, N.; Pan, G.; Chen, Y.; Fan, L.; Jin, M.; Alouini, M. Secrecy Analysis for Cooperative NOMA Networks With Multi-Antenna Full-Duplex Relay. IEEE Trans. Commun. 2019, 67, 5574–5587. [Google Scholar] [CrossRef]
- Feng, Y.; Yan, S.; Yang, Z. Secure Transmission to the Strong User in Non-Orthogonal Multiple Access. IEEE Commun. Lett. 2018, 22, 2623–2626. [Google Scholar] [CrossRef]
- Lv, L.; Ding, Z.; Ni, Q.; Chen, J. Secure MISO-NOMA Transmission With Artificial Noise. IEEE Trans. Veh. Technol. 2018, 67, 6700–6705. [Google Scholar] [CrossRef]
- Hu, L.; Wen, H.; Wu, B.; Tang, J.; Pan, F.; Liao, R. Cooperative-Jamming-Aided Secrecy Enhancement in Wireless Networks With Passive Eavesdroppers. IEEE Trans. Veh. Technol. 2018, 67, 2108–2117. [Google Scholar] [CrossRef]
- Tran, T.N.; Voznak, M. Multi-Points Cooperative Relay in NOMA System with N-1 DF Relaying Nodes in HD/FD Mode for N User Equipments with Energy Harvesting. Electronics 2019, 8, 167. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, Z.; Li, Q.; Chen, H.; Ansari, N. Mitigating Intended Jamming in mmWave MIMO by Hybrid Beamforming. IEEE Wirel. Commun. Lett. 2019, 8, 1617–1620. [Google Scholar] [CrossRef]
- Yu, C.; Yu, L.; Wu, Y.; He, Y. Transmit-Power Minimization for NOMA-Enabled Traffic Offloading With Security Provisioning. IEEE Commun. Lett. 2018, 22, 986–989. [Google Scholar] [CrossRef]
- Zhao, N.; Wang, W.; Wang, J.; Chen, Y.; Lin, Y.; Ding, Z.; Beaulieu, N.C. Joint Beamforming and Jamming Optimization for Secure Transmission in MISO-NOMA Networks. IEEE Trans. Commun. 2019, 67, 2294–2305. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, H.; Hua, M.; Li, C.; Huang, Y.; Yang, L. Double Coded Caching in Ultra Dense Networks: Caching and Multicast Scheduling via Deep Reinforcement Learning. IEEE Trans. Commun. 2020, 68, 1071–1086. [Google Scholar] [CrossRef]
- Li, X.; Zhao, M.; Zhang, C.; Khan, W.U.; Wu, J.; Rabie, K.M.; Kharel, R. Security Analysis of Multi-Antenna NOMA Networks under I/Q Imbalance. Electronics 2019, 8, 1327. [Google Scholar] [CrossRef]
- Li, Y.; Yin, Q.; Sun, L.; Chen, H.; Wang, H. A Channel Quality Metric in Opportunistic Selection With Outdated CSI Over Nakagami- m Fading Channels. IEEE Trans. Veh. Technol. 2012, 61, 1427–1432. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Zhang, Z.; Li, B. Cooperative Secure Transmission in MISO-NOMA Networks. Electronics 2020, 9, 352. https://doi.org/10.3390/electronics9020352
Chen Y, Zhang Z, Li B. Cooperative Secure Transmission in MISO-NOMA Networks. Electronics. 2020; 9(2):352. https://doi.org/10.3390/electronics9020352
Chicago/Turabian StyleChen, Yang, Zhongpei Zhang, and Bingrui Li. 2020. "Cooperative Secure Transmission in MISO-NOMA Networks" Electronics 9, no. 2: 352. https://doi.org/10.3390/electronics9020352
APA StyleChen, Y., Zhang, Z., & Li, B. (2020). Cooperative Secure Transmission in MISO-NOMA Networks. Electronics, 9(2), 352. https://doi.org/10.3390/electronics9020352




