sDeepFM: Multi-Scale Stacking Feature Interactions for Click-Through Rate Prediction
Abstract
1. Introduction
- A novel structure named multi-scale stacking pooling based on different receptive fields for multi-scale feature extraction is proposed, which mines high-order and low-order features in different local information from the directions of depth and width to ensure the diversity of extraction features.
- By learning parameters using factorization, the parameters of cross-terms are no longer independent of each other. With more hidden vectors of higher-order features, the model has more samples to learn, which largely alleviates the difficulty of learning higher-order features in sparse data.
2. Methods
2.1. Problem Description
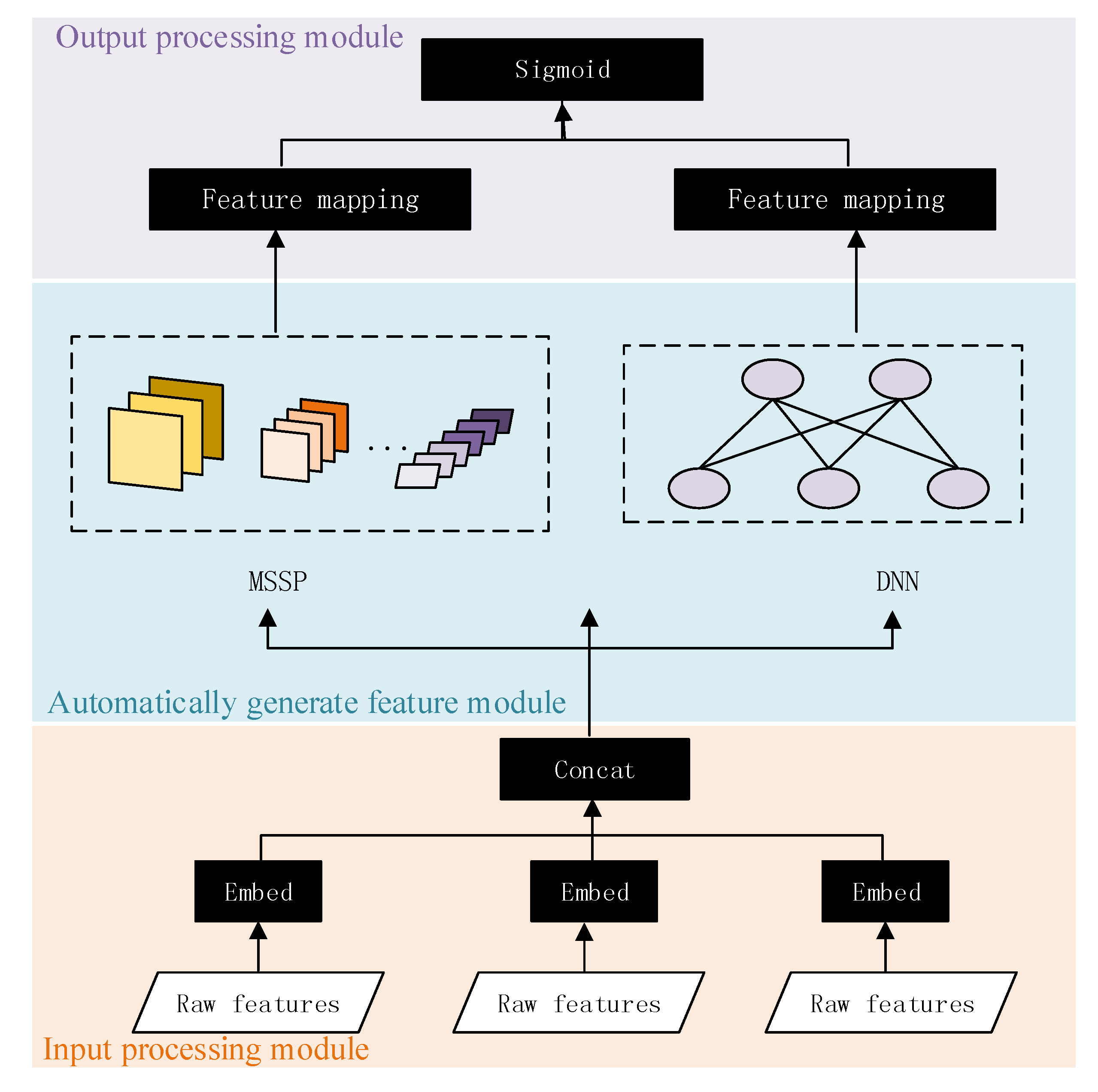
2.2. Model Description
2.2.1. The Input Processing Module
2.2.2. The Automatic Feature Interaction Module
- Multi-scale stacking pooling
- DNN component
2.2.3. The Output Processing Module
2.3. Model Learning
2.3.1. The Loss Function
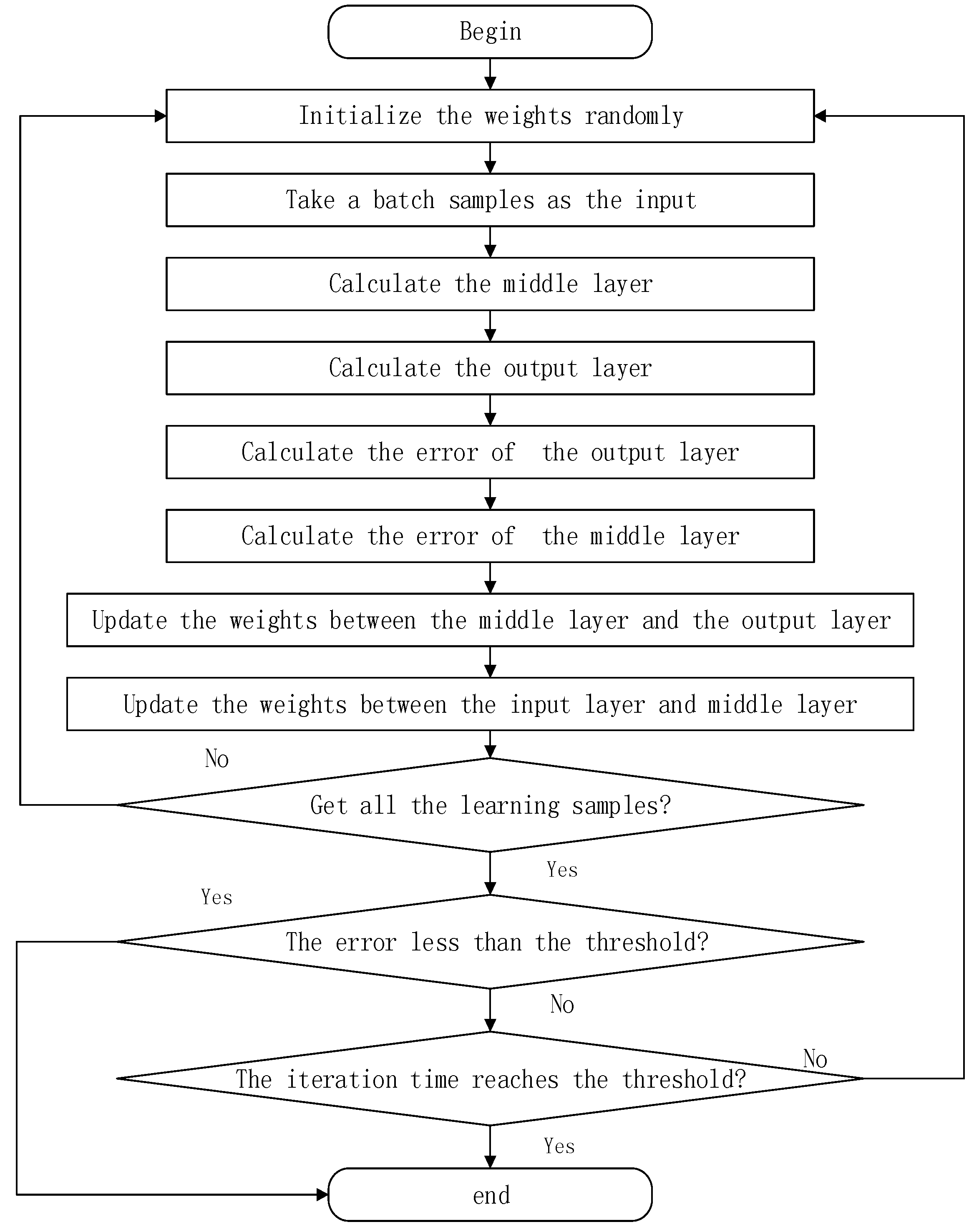
2.3.2. Training Process
2.3.3. Click-Through Rate Prediction Based on Multi-Scale Stacking Network
- The dataset is divided into a training set and a test set. There are different ways to partition different datasets. The datasets that have time can be divided by time, while the datasets without time can be divided by random sampling.
- To preprocess the dataset, we firstly classify all features with low occurrence times as the same feature while setting a threshold to reduce the dimension of features, which can prevent overfitting to some extent. Secondly, since a numerical feature with a large variance is not conducive for model learning, we carry out log transformation for values greater than 2.
- The one-hot coding transformation is applied to the classification features, and each feature after the transformation is mapped to an embedded vector with a fixed dimension. All embedded vectors corresponding to the features of a sample are spliced together as the input. The initial value of the embedded vector is set randomly.
- The MSSP structure is used to construct the high-order and low-order features in different local fields from the depth and width angles.
- The multi-scale features are fused, and then input to the last prediction layer. Finally, the model outputs the prediction results.
- The error between the predicted value and the real value is calculated, and the weight of each unit is modified by back propagation. Iterative training is continued to reduce the error until the error is less than the threshold or the iteration times reach the threshold.
- The learned model is used to predict the test set to find potential high-value customers and guide the distribution of advertisements.
3. Experiments
3.1. Dataset Description
3.2. Evaluation Metrics
3.3. Data Preprocessing
3.4. Experimental Results
3.4.1. Effect of Multi-Scale-Stacking Pooling
3.4.2. Effect of sDeepFM
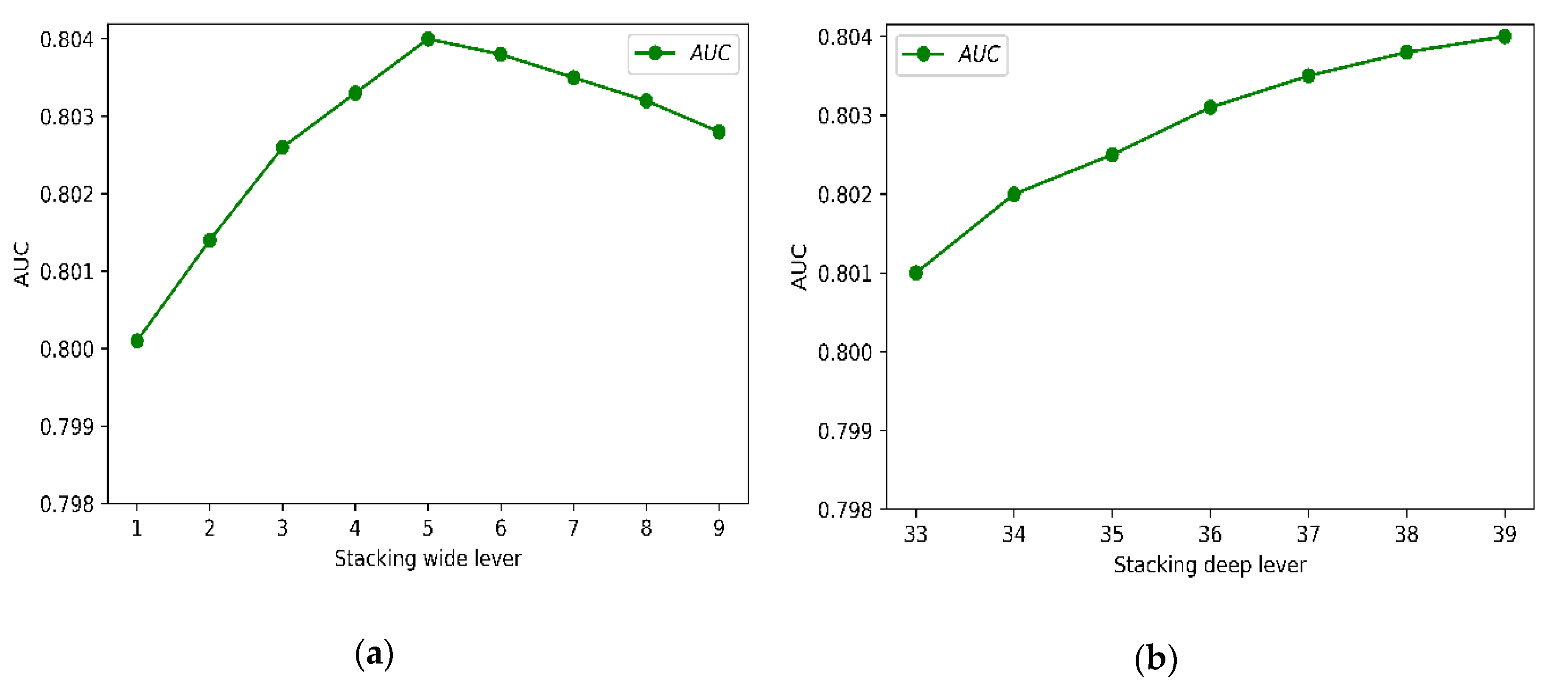
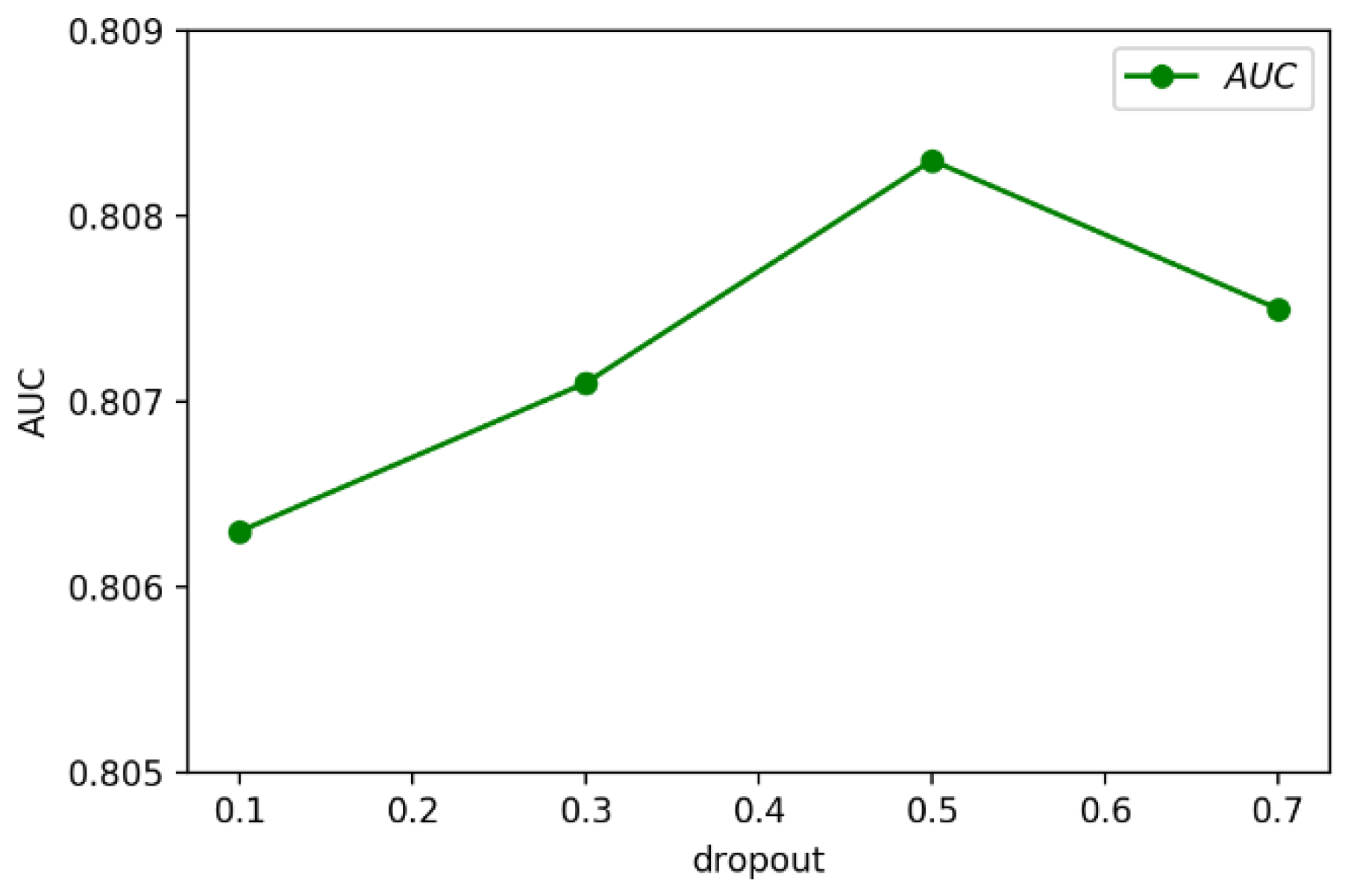
3.4.3. Effect of Hyperparameters
- Effect of stacking width and depth
- Effect of dropout
- Effect of activation function
- Effect of number of neurons
3.4.4. Discussion of Run Time Efficiency
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Covington, P.; Adams, J.; Sargin, E. Deep neural networks for Youtube recommendations. In Proceedings of the 10th ACM Conference on Recommender Systems, New York, NY, USA, 15–19 September 2016; pp. 191–198. [Google Scholar]
- He, X.; Pan, J.; Jin, O.; Xu, T.; Liu, B.; Xu, T.; Candela, J.Q. Practical lessons from predicting clicks on ads at facebook. In Proceedings of the Eighth International Workshop on Data Mining for Online Advertising, New York, NY, USA, 24 August 2014; pp. 1–9. [Google Scholar]
- Richardson, M.; Dominowska, E.; Ragno, R. Predicting clicks: Estimating the click-through rate for new ads. In Proceedings of the 16th International Conference on World Wide Web, Banff, AB, Canada, 8–12 May 2007; pp. 521–530. [Google Scholar]
- Domingos, P. A few useful things to know about machine learning. Commun. ACM 2012, 55, 78–87. [Google Scholar] [CrossRef]
- Rendle, S. Factorization machines with libfm. ACM Trans. Intell. Syst. Technol. 2012, 3, 1–22. [Google Scholar] [CrossRef]
- Shan, Y.; Hoens, T.R.; Jiao, J.; Wang, H.; Yu, D.; Mao, J.C. Deep crossing: Web-scale modeling without manually crafted combinatorial features. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 22 September 2016; pp. 255–262. [Google Scholar]
- Chang, Y.W.; Hsieh, C.J.; Chang, K.W.; Ringgaard, M.; Lin, C.J. Training and testing low-degree polynomial data mappings via linear svm. J. Mach. Learn. Res. 2010, 11, 1471–1490. [Google Scholar]
- Rendle, S.; Schmidt-Thieme, L. Pairwise interaction tensor factorization for personalized tag recommendation. In Proceedings of the Third ACM International Conference on Web Search and Data Mining, New York, NY, USA, 3–6 February 2010; pp. 81–90. [Google Scholar]
- Juan, Y.; Zhuang, Y.; Chin, W.S.; Lin, C.J. Field-aware Factorization Machines for CTR Prediction. In Proceedings of the ACM Conference on Recommender Systems, Boston, MA, USA, 15–19 September 2016. [Google Scholar]
- Wang, G.; Li, Q.; Wang, L.; Zhang, Y.; Liu, Z. Elderly fall detection with an accelerometer using lightweight neural networks. Electronics 2019, 8, 1354. [Google Scholar] [CrossRef]
- Zhang, C.; Fu, Y.; Deng, F.; Wei, B.; Wu, X. Methane Gas Density Monitoring and Predicting Based on RFID Sensor Tag and CNN Algorithm. Electronics 2018, 7, 69. [Google Scholar] [CrossRef]
- Cheng, H.-T.; Koc, L.; Harmsen, J.; Shaked, T.; Chandra, T.; Aradhye, H. Wide & deep learning for recommender systems. In Proceedings of the 1st Workshop on Deep Learning for Recommender Systems, Boston, MA, USA, 15 September 2016; pp. 7–10. [Google Scholar]
- Zhang, W.; Du, T.; Wang, J. Deep learning over multi-field categorical data: A case study on user response prediction. In Proceedings of the European Conference on Information Retrieval, Padua, Italy, 20–23 March 2016; pp. 45–57. [Google Scholar]
- Qu, Y.; Cai, H.; Ren, K.; Zhang, W.; Yu, Y.; Wen, Y.; Wang, J. Product-based neural networks for user response prediction. In Proceedings of the IEEE 16th International Conference on Data Mining, Barcelona, Spain, 12–15 December 2016; pp. 1149–1154. [Google Scholar]
- Xiao, J.; Ye, H.; He, X.; Zhang, H.; Wu, F.; Chua, T.S. Attentional Factorization Machines: Learning the Weight of Feature Interactions via Attention Networks. arXiv 2017, arXiv:1708.04617. [Google Scholar]
- Guo, H.; Tang, R.; Ye, Y.; Li, Z.; He, X.; Dong, Z. DeepFM: An end-to-end wide & deep learning framework for CTR prediction. arXiv 2018, arXiv:1804.04950. [Google Scholar]
- Lian, J.; Zhou, X.; Zhang, F.; Chen, Z.; Xie, X.; Sun, G. Xdeepfm: Combining explicit and implicit feature interactions for recommender systems. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 1754–1763. [Google Scholar]
- Walter, S.D. The partial area under the summary ROC curve. Stat. Med. 2005, 24, 2025–2040. [Google Scholar] [CrossRef] [PubMed]
- Abbas, F.; Feng, D.; Habib, S.; Rahman, U.; Rasool, A.; Yan, Z. Short term residential load forecasting: An improved optimal nonlinear auto regressive (narx) method with exponential weight decay function. Electronics 2018, 7, 432. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]

| Data | Samples | Fields | Features |
|---|---|---|---|
| Criteo | 45,840,617 | 39 | 998,960 |
| Avazu | 40,428,967 | 23 | 1,544,488 |
| Criteo | Avazu | |||
|---|---|---|---|---|
| AUC | Log Loss | AUC | Log Loss | |
| LR | 0.7810 | 0.4690 | 0.7588 | 0.3962 |
| FM | 0.7823 | 0.4688 | 0.7701 | 0.3855 |
| AFM | 0.7940 | 0.4580 | 0.7715 | 0.3853 |
| MSSN | 0.8040 | 0.4474 | 0.7744 | 0.3829 |
| Criteo | Avazu | |||
|---|---|---|---|---|
| AUC | Log Loss | AUC | Log Loss | |
| DNN | 0.8006 | 0.4520 | 0.7730 | 0.3850 |
| PNN | 0.8038 | 0.4483 | 0.7750 | 0.3827 |
| DeepFM | 0.8050 | 0.4475 | 0.7751 | 0.3829 |
| xDeepFM | 0.8069 | 0.4452 | 0.7763 | 0.3819 |
| sDeepFM | 0.8083 | 0.4436 | 0.7771 | 0.3811 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiang, B.; Lu, Y.; Yang, M.; Chen, X.; Chen, J.; Cao, Y. sDeepFM: Multi-Scale Stacking Feature Interactions for Click-Through Rate Prediction. Electronics 2020, 9, 350. https://doi.org/10.3390/electronics9020350
Qiang B, Lu Y, Yang M, Chen X, Chen J, Cao Y. sDeepFM: Multi-Scale Stacking Feature Interactions for Click-Through Rate Prediction. Electronics. 2020; 9(2):350. https://doi.org/10.3390/electronics9020350
Chicago/Turabian StyleQiang, Baohua, Yongquan Lu, Minghao Yang, Xianjun Chen, Jinlong Chen, and Yawei Cao. 2020. "sDeepFM: Multi-Scale Stacking Feature Interactions for Click-Through Rate Prediction" Electronics 9, no. 2: 350. https://doi.org/10.3390/electronics9020350
APA StyleQiang, B., Lu, Y., Yang, M., Chen, X., Chen, J., & Cao, Y. (2020). sDeepFM: Multi-Scale Stacking Feature Interactions for Click-Through Rate Prediction. Electronics, 9(2), 350. https://doi.org/10.3390/electronics9020350




