Design and Implementation of a Digital Dual Orthogonal Outputs Chaotic Oscillator
Abstract
1. Introduction
- ■
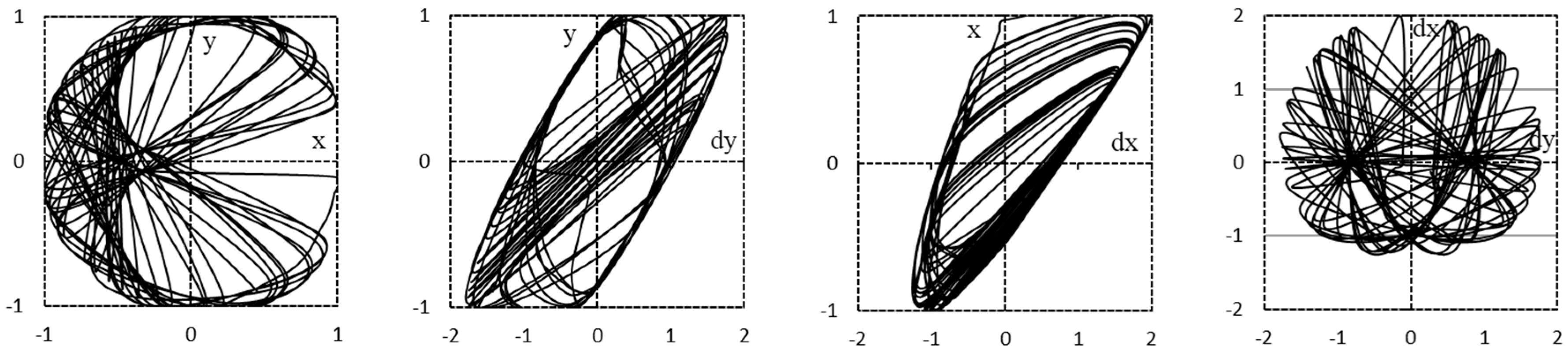
- jointly generates two orthogonal signals, i.e., the outputs are point by point in phase quadrature and constitute a unit vector.
- ■
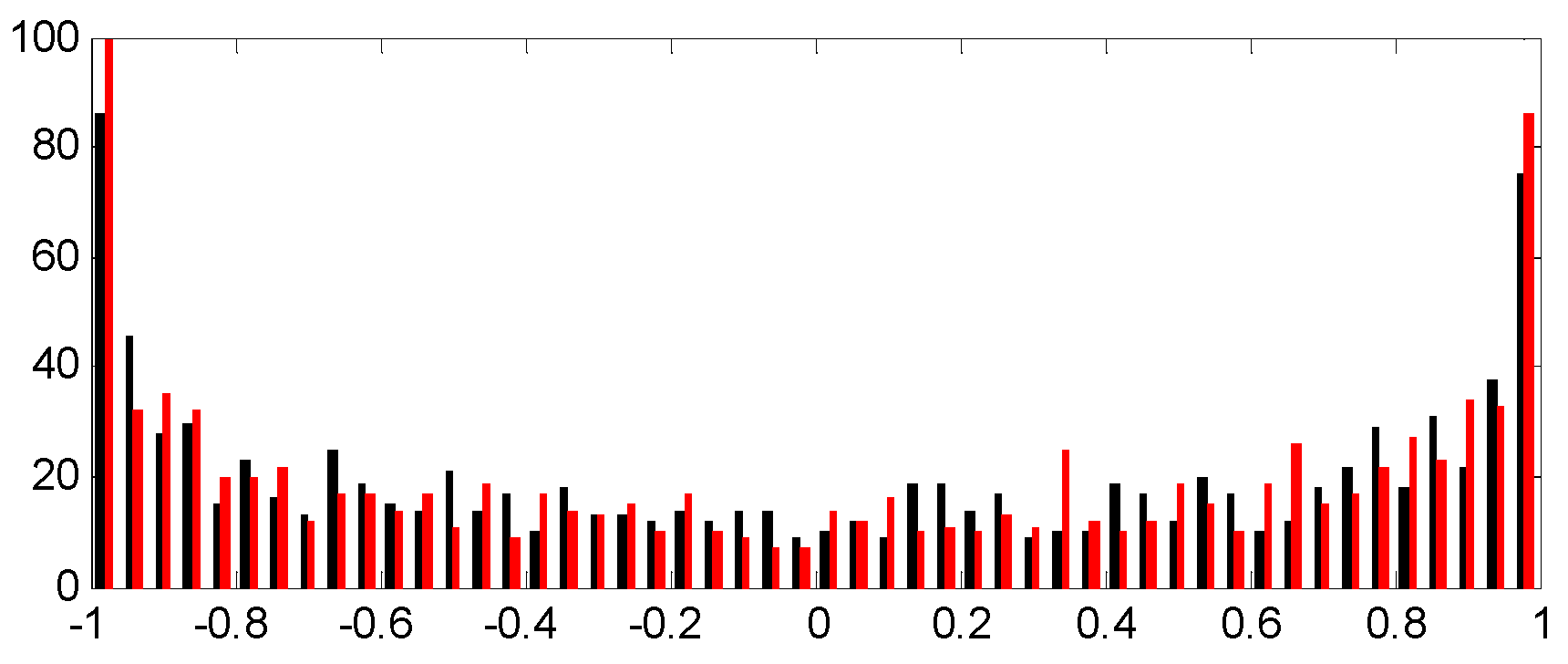
- presents statistical characteristics, such as stationary mean and standard deviation, that are also independent of the initial conditions.
- ■
- is robust when one reduces the sample quantification format.
2. Usual Digital Chaotic Sequences
2.1. Recurrence Equations
2.2. Influence of the Data Format
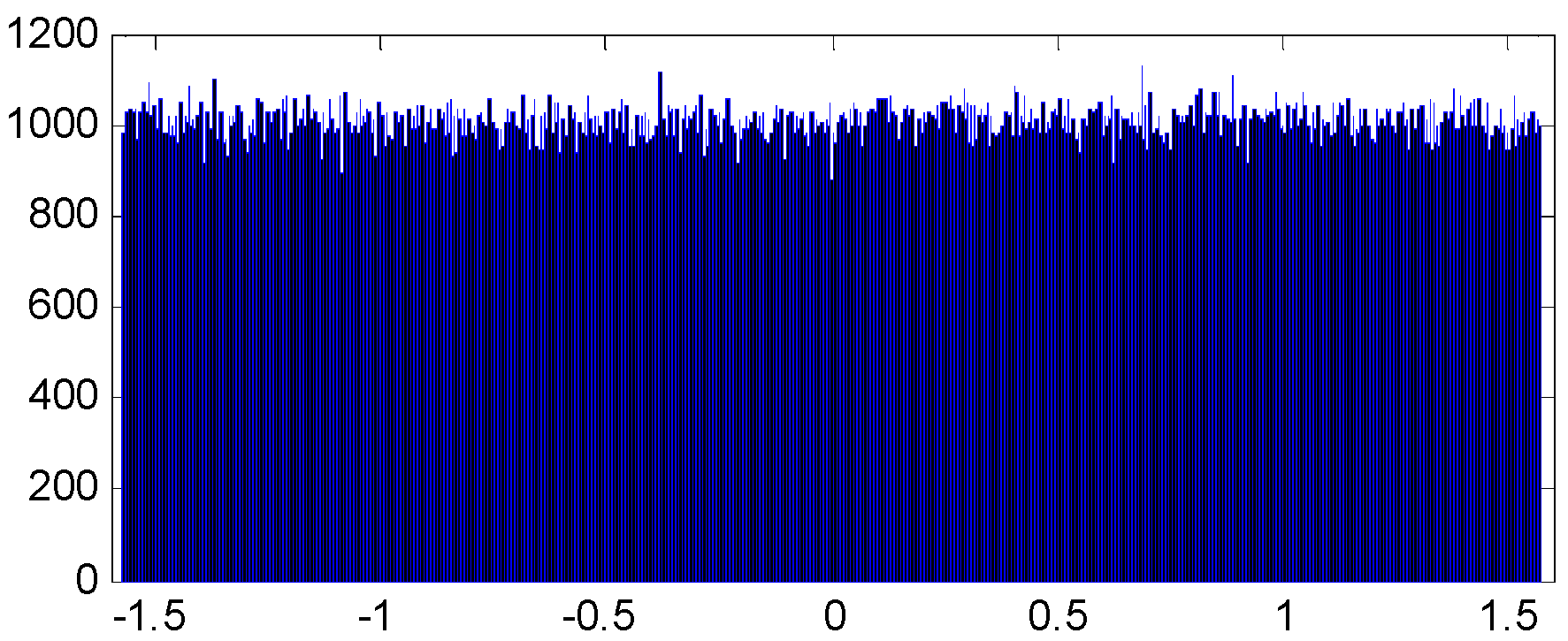
2.3. Statistical Variability
3. Proposed Orthogonal Chaotic Sequence
3.1. Theoretical Background
3.2. Normalized Recurrence Equations
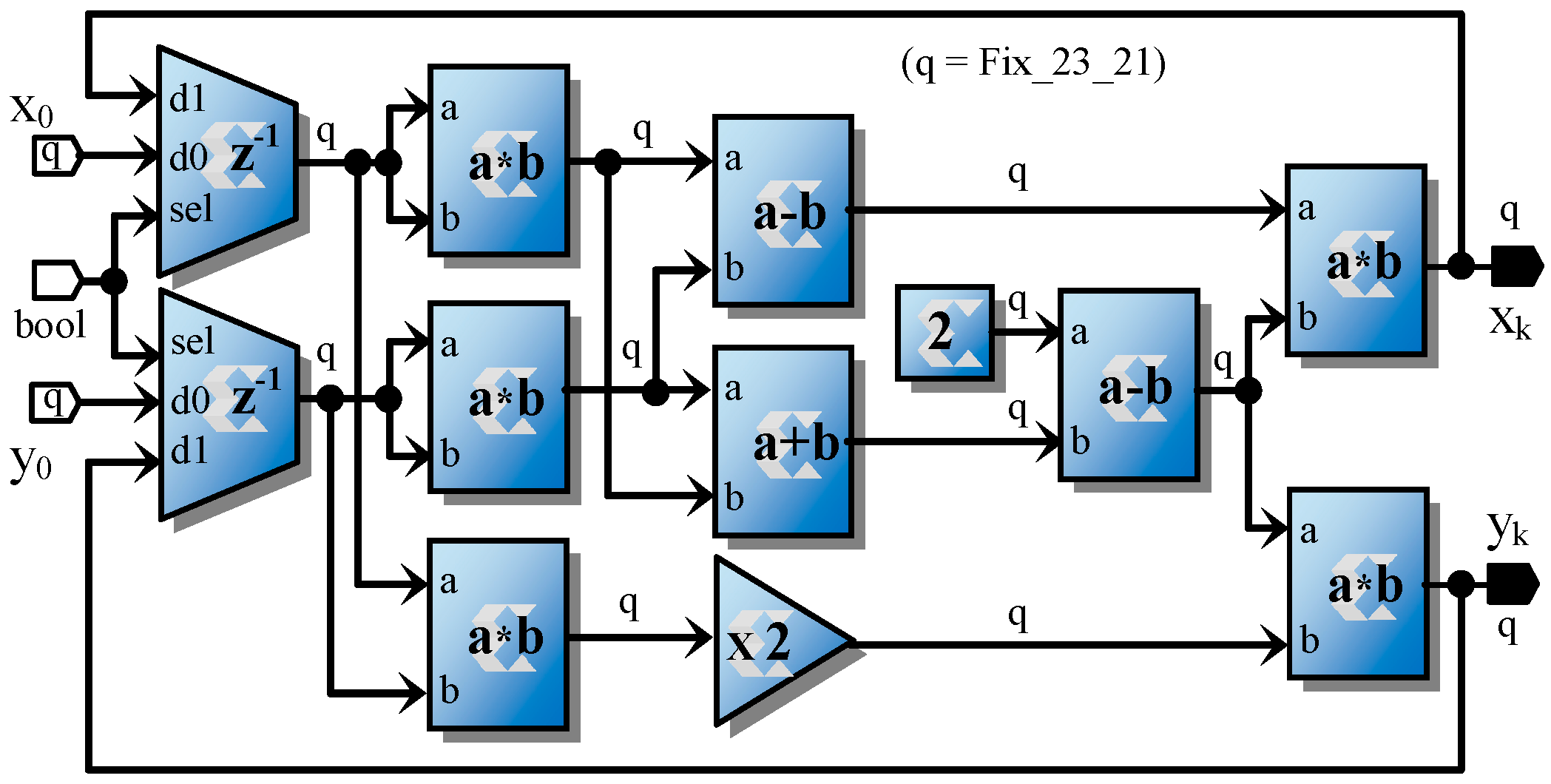
3.3. Approximation of Normalized Recurrence Equations
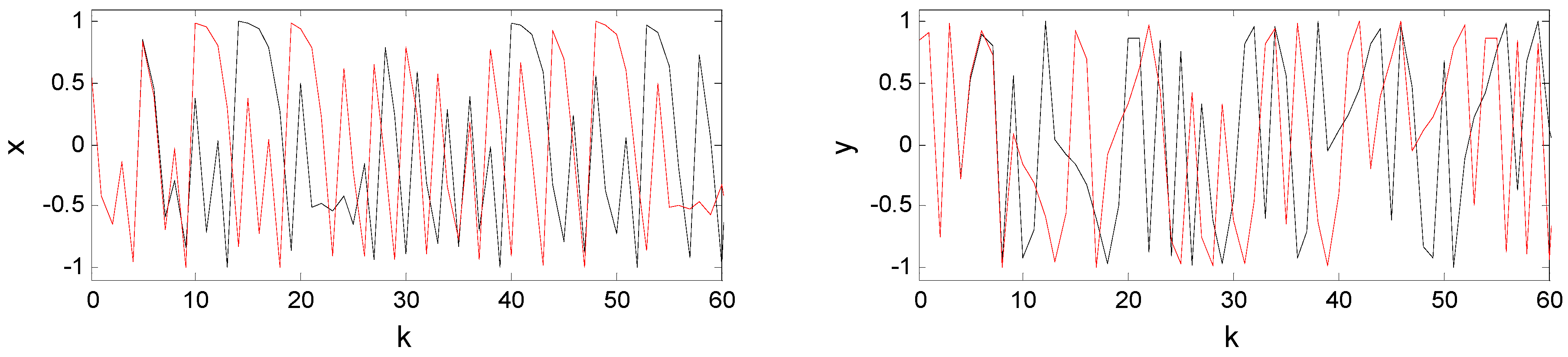
3.4. Statistic Properties of the Chaotic Oscillator
3.5. Chaotic Behavior Analysis
- ■
- λ < 0 corresponds to an orbital trajectory attracted by a stable fixed point. This situation is representative of strongly deterministic, harmonic or random sequences.
- ■
- λ very close to 0 represents a steady state close to a chaotic transition.
- ■
- λ > 0 characterizes an unstable and chaotic orbit. The larger λ, the more chaotic character is observed.
4. Hardware Implementation
5. Application to the Fast Image Encryption
5.1. Image Encryption/Decryption With Bitwise XOR Operation
- ■
- Elaboration of a sequence of N*M numerical coefficients of the chosen chaotic system in which the precise initial conditions have been introduced.
- ■
- Quantification of the coefficients in a format identical to that of the pixels of the original image (eight bits in most cases). Given the variability of the statistical characteristics of the sequence with the initial conditions, this operation can only be carried out after the computation of the entire sequence.
- ■
- Application of a bitwise XOR operation between the pixel values and the quantized coefficients.
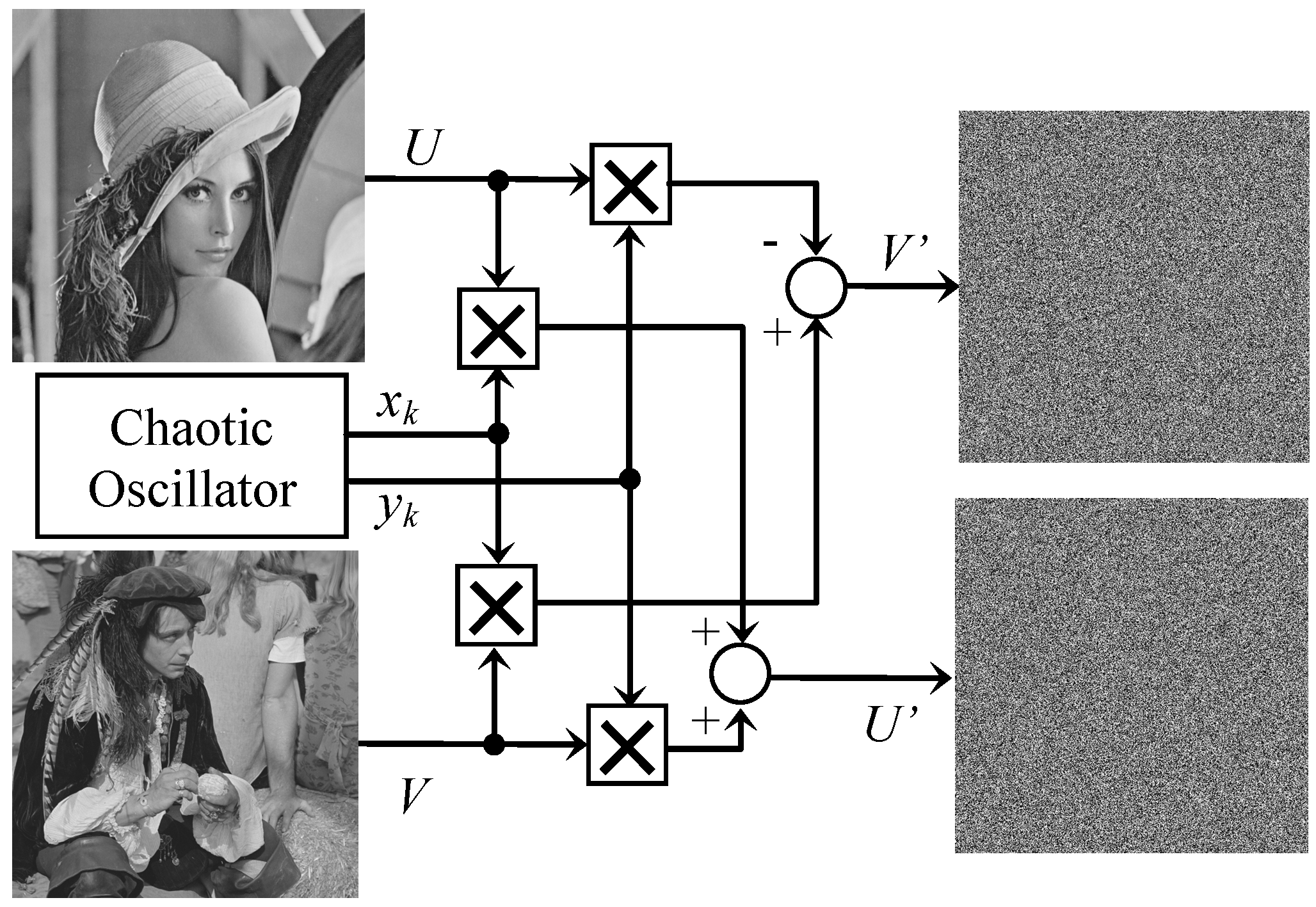
5.2. Simultaneous Images Mixing Encryption/Decryption
- Step 1:
- Read the two original images with size N*M, then convert them into one dimensional arrays U and V, and assign the initial conditions x0 and y0.
- Step 2:
- For each pair (uk and vk), compute the following:
- Step 3:
- Convert the two arrays U’ and V’ into two images with the size N*M.
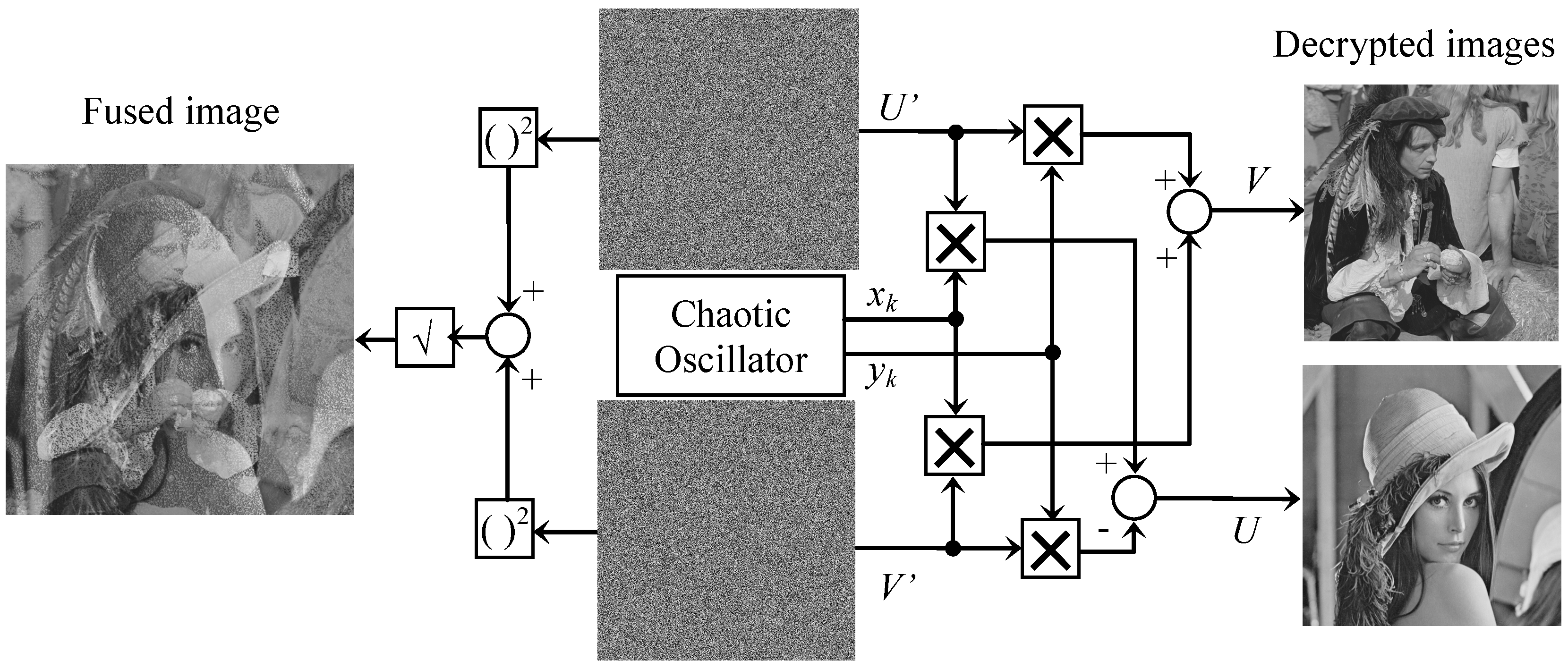
- Step 1:
- Read the two encrypted images with size N*M, then convert them into one-dimensional arrays U’ and V’, and assign initial conditions x0 and y0.
- Step 2:
- For each pair (u’k and v’k), compute the following:
- Step 3:
- Convert the two arrays of U and V into two images with the size N*M.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Leonov, G.; Kuznetsov, N. On differences and similarities in the analysis of Lorenz, Chen, and Lu systems. Appl. Math. Comput. 2015, 256, 334–343. [Google Scholar] [CrossRef]
- Koyuncu, I.; Özcerit, A.T.; Pehlivan, I. Implementation of FPGA-based real time novel chaotic oscillator. Nonlinear Dyn. 2014, 77, 49–59. [Google Scholar] [CrossRef]
- Sambas, A.; Vaidyanathan, S.; Tlelo-Cuautle, E.; Zhang, S.; Guillen-Fernandez, O.; Hidayat, Y.; Gundara, G. A Novel Chaotic System with Two Circles of Equilibrium Points: Multistability, Electronic Circuit and FPGA Realization. Electronics 2019, 8, 1211. [Google Scholar] [CrossRef]
- Chen, S.L.; Hwang, T.; Chang, S.M.; Lin, W.W. A fast digital chaotic generator for secure communication. Int. J. Bifurcation Chaos 2019, 20, 3969–3987. [Google Scholar] [CrossRef]
- Liao, T.-L.; Wan, P.-Y.; Chien, P.-C.; Liao, Y.-C.; Wang, L.-K.; Yan, J.-J. Design of High-Security USB Flash Drives Based on Chaos Authentication. Electronics 2018, 7, 82. [Google Scholar] [CrossRef]
- Li, W.; Wang, C.; Feng, K.; Huang, X.; Ding, Q. A multidimensional discrete digital chaotic encryption system. Int. J. Distrib. Sens. Netw. 2018, 14, 1–8. [Google Scholar] [CrossRef]
- Alroubaie, Z.M.; Hashem, M.A.; Hasan, F.S. FPGA Design of Encryption Speech system using Synchronized Fixed-Point Chaotic Maps Based Stream Ciphers. Int. J. Eng. Adv. Technol. 2019, 8, 2249–8958. [Google Scholar]
- Zhang, W.; Zhu, Z.; Yu, H. A Symmetric Image Encryption Algorithm Based on a Coupled Logistic–Bernoulli Map and Cellular Automata Diffusion Strategy. Entropy 2019, 21, 504. [Google Scholar] [CrossRef]
- Liu, H.; Kadir, A.; Sun, X. Chaos-based fast colour image encryption scheme with true random number keys from environmental noise. IET Image Process. 2017, 11, 324–332. [Google Scholar] [CrossRef]
- Zhang, Q.; Guo, Y.; Li, W.; Ding, Q. Image encryption method based on discrete lorenz chaotic sequences. J. Inf. Hiding Multimed. Signal Process. 2016, 7, 575–586. [Google Scholar]
- Rohith, S.; Bhat, K.H.; Sharma, A.N. Image encryption and decryption using chaotic key sequence generated by sequence of logistic map and sequence of states of Linear Feedback Shift Register. In Proceedings of the 2014 International Conference on Advances in Electronics Computers and Communications, Bangalore, India, 10–11 October 2014; pp. 1–6. [Google Scholar]
- Kennedy, M.P.; Kolumbán, G.; Kis, G. Chaotic Modulation for Robust Digital Communications over Multipath Channels. Int. J. Bifurc. Chaos 2000, 10, 695–718. [Google Scholar] [CrossRef]
- Babu, S.B.S.; Kumar, R. 1D-Bernoulli Chaos Sequences Based Collaborative-CDMA: A Novel Secure High Capacity CDMA Scheme. Wirel. Pers. Commun. 2017, 96, 2077–2086. [Google Scholar] [CrossRef]
- Liu, L.; Yang, P.; Zhang, J.; Ja, H. Compressive sensing with Tent chaotic sequence. Sensors Transducers 2014, 165, 119–124. [Google Scholar]
- Yu, L.; Barbot, J.P.; Zheng, G.; Sun, H. Compressive Sensing With Chaotic Sequence. IEEE Signal Process. Lett. 2010, 17, 731–734. [Google Scholar]
- Linh-Trung, N.; Minh-Chinh, T.; Tran-Duc, T.; Le, H.V.; Do, M.N. Chaotic compressed sensing and its application to magnetic resonance imaging. J. Electron. Commun. 2013, 3, 84–92. [Google Scholar] [CrossRef]
- Ren, H.-P.; Bai, C.; Liu, J.; Baptista, M.S.; Grebogi, C. Experimental validation of wireless communication with chaos. Chaos: Interdiscip. J. Nonlinear Sci. 2016, 26, 083117. [Google Scholar] [CrossRef]
- Venkatesh, P.R.; Venkatesan, A.; Lakshmanan, M.; Ramadass, V.P. Implementation of dynamic dual input multiple output logic gate via resonance in globally coupled Duffing oscillators. Chaos: Interdiscip. J. Nonlinear Sci. 2017, 27, 083106. [Google Scholar] [CrossRef]
- Ikeda, K. Multiple-valued stationary state and its instability of the transmitted light by a ring cavity system. Opt. Commun. 1979, 30, 257–261. [Google Scholar] [CrossRef]
- Zhu, S.; Wang, G.; Zhu, C. A Secure and Fast Image Encryption Scheme based on Double Chaotic S-Boxes. Entropy 2019, 21, 790. [Google Scholar] [CrossRef]
- Ogras, H.; Turk, M. A secure chaos-based image cryptosystem with an improved sine key generator. Am. J. Signal Process. 2016, 6, 67–76. [Google Scholar]
- Alawida, M.; Samsudin, A.; Teh, J.S.; AlShoura, W.H. Digital Cosine Chaotic Map for Cryptographic Applications. IEEE Access 2019, 7, 150609–150622. [Google Scholar] [CrossRef]
- Rochberg, R. The equation (i-s)g = f for shift operators in Hilbert space. Proc. Am. Math. Soc. 1968, 19, 123–129. [Google Scholar]
- Ben Saïda, A. Noisy chaos in intraday financial data: Evidence from the American index. Appl. Math. Comput. 2014, 226, 258–265. [Google Scholar]
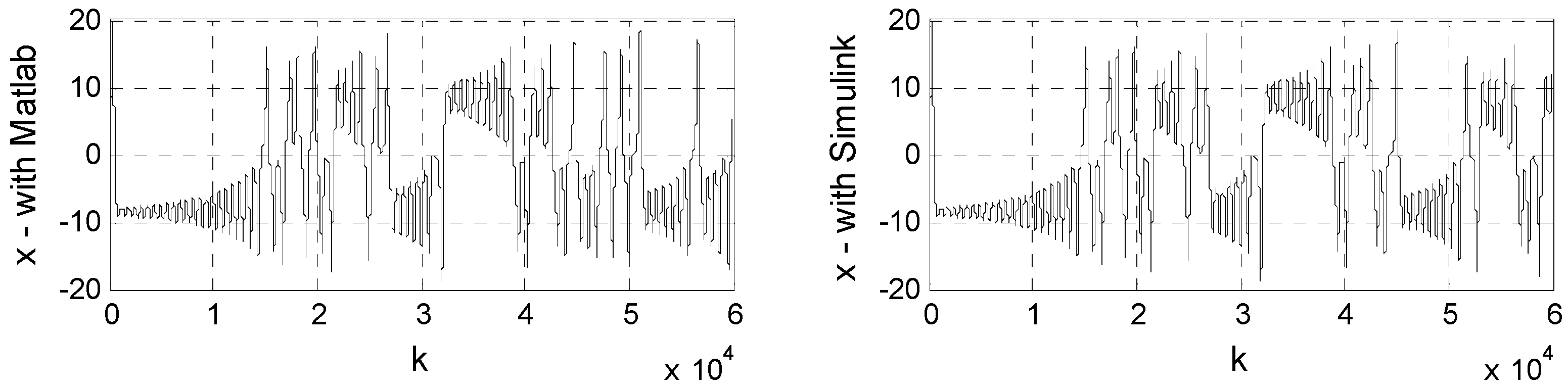


| Dim. | Model | Recursive Equations | Chaos Conditions |
|---|---|---|---|
| 1D | Logistic | ||
| 1D | Bernoulli | ||
| 2D | Hénon | a = 1.4 b = 0.3 | |
| 3D | Lorenz discrete (Euler approx. dt = h) | h < 0.025 |
| x0; y0; z0 | 0.1; 0.1; 0.1 | 0.5; 0.5; 0.5 | 1; 1; 1 | 2; 2; 2 |
|---|---|---|---|---|
| m | −2.19 | −0.64 | −1.00 | −1.44 |
| std | 7.72 | 8.00 | 7,94 | 7.86 |
| Case | Initial Magnitude | Convergence | Behavior | Examples |
|---|---|---|---|---|
| 1 | Chaotic Transient |  | ||
| 2 | Chaotic steady state | 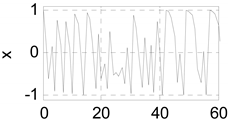 | ||
| 3 | or | Chaotic Transient or Steady state | ➔ transient ➔ steady state | |
| 4 | Divergence |  |
| Logistic | Hénon | Proposed Chaotic Oscillator | |
|---|---|---|---|
| μ = 3.8 = 0.2 | a =1.4; b = 0.3 = 1; | ||
| λx = 1.29 | λx = 0.89 λy = 1.21 | λx = 2.14 λy = 0.30 | λx = 1.63 λy = 0.68 |
| Data Format | LUT | FF | DSP | Dyn. Power | fs max |
|---|---|---|---|---|---|
| Float 64 | 2999 | 128 | 40 | 35 mW | 33 MHz |
| Float 32 | 1453 | 64 | 17 | 20 mW | 50 MHz |
| Fix 23_21 | 33 | 32 | 6 | 6 mW | 100 MHz |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berviller, Y.; Tisserand, E.; Poure, P.; Rabah, H. Design and Implementation of a Digital Dual Orthogonal Outputs Chaotic Oscillator. Electronics 2020, 9, 264. https://doi.org/10.3390/electronics9020264
Berviller Y, Tisserand E, Poure P, Rabah H. Design and Implementation of a Digital Dual Orthogonal Outputs Chaotic Oscillator. Electronics. 2020; 9(2):264. https://doi.org/10.3390/electronics9020264
Chicago/Turabian StyleBerviller, Yves, Etienne Tisserand, Philippe Poure, and Hassan Rabah. 2020. "Design and Implementation of a Digital Dual Orthogonal Outputs Chaotic Oscillator" Electronics 9, no. 2: 264. https://doi.org/10.3390/electronics9020264
APA StyleBerviller, Y., Tisserand, E., Poure, P., & Rabah, H. (2020). Design and Implementation of a Digital Dual Orthogonal Outputs Chaotic Oscillator. Electronics, 9(2), 264. https://doi.org/10.3390/electronics9020264






