Analysis of Symmetric Dual Switch Converter under High Switching Frequency Conditions
Abstract
1. Introduction
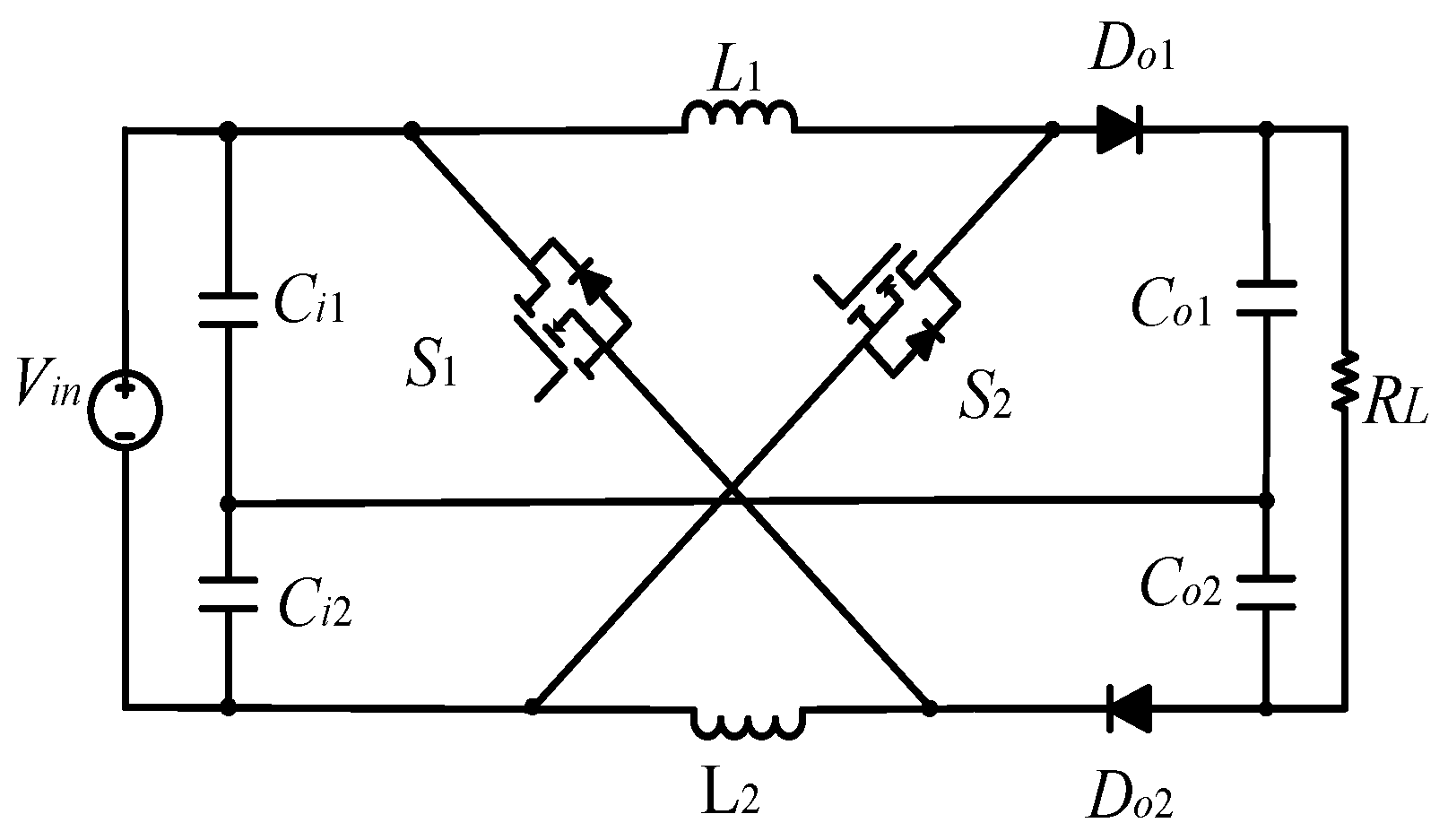
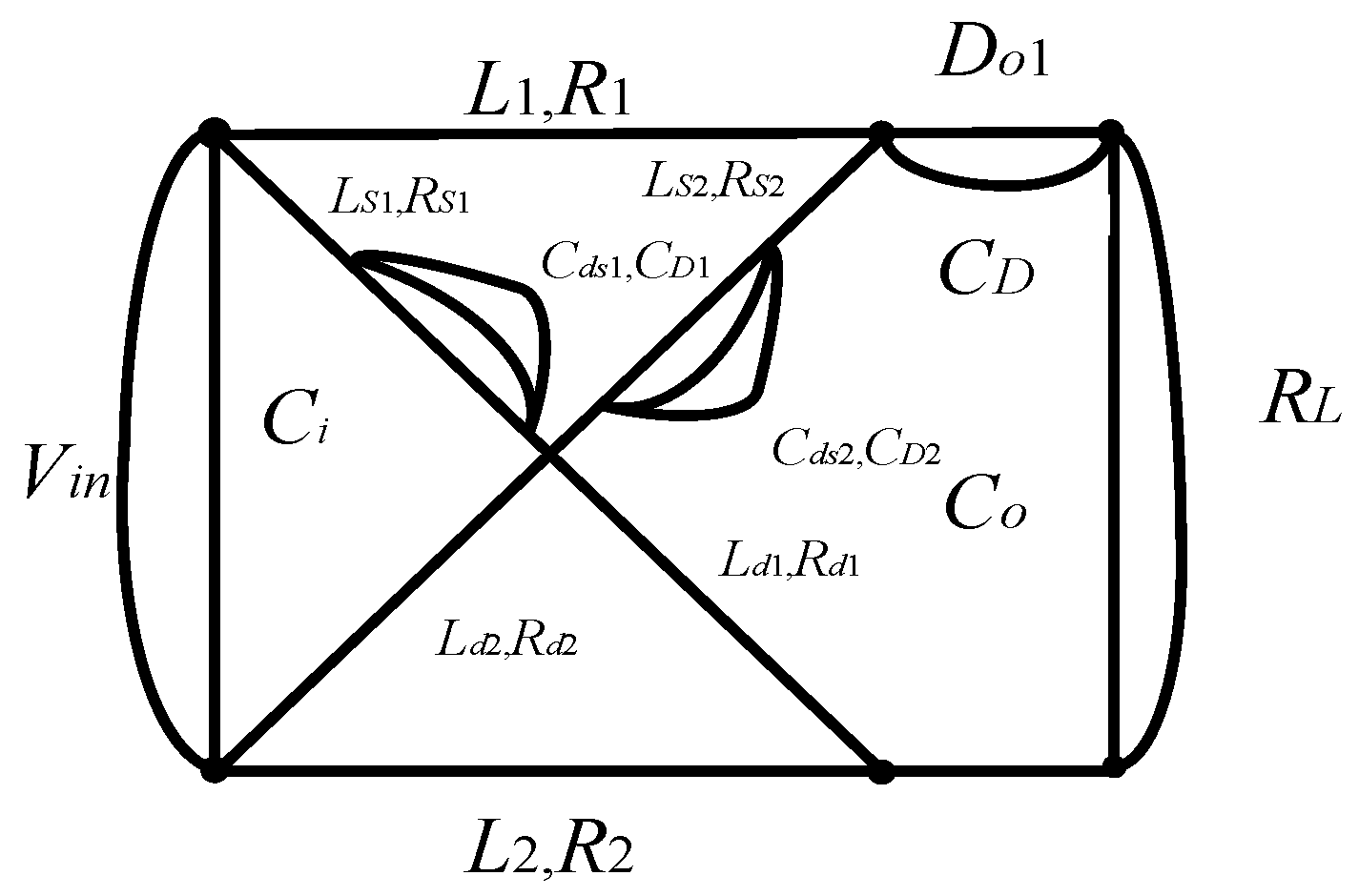
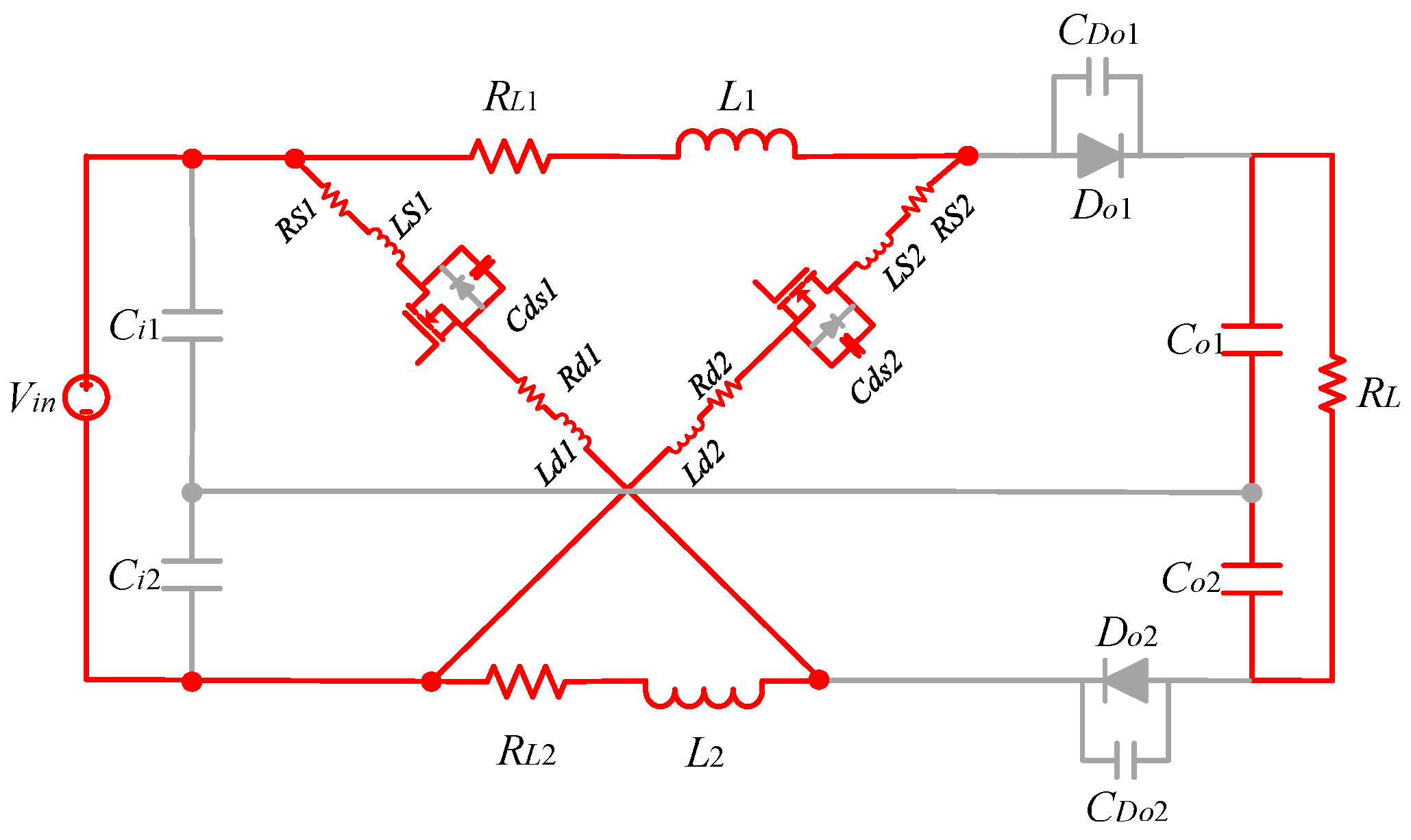
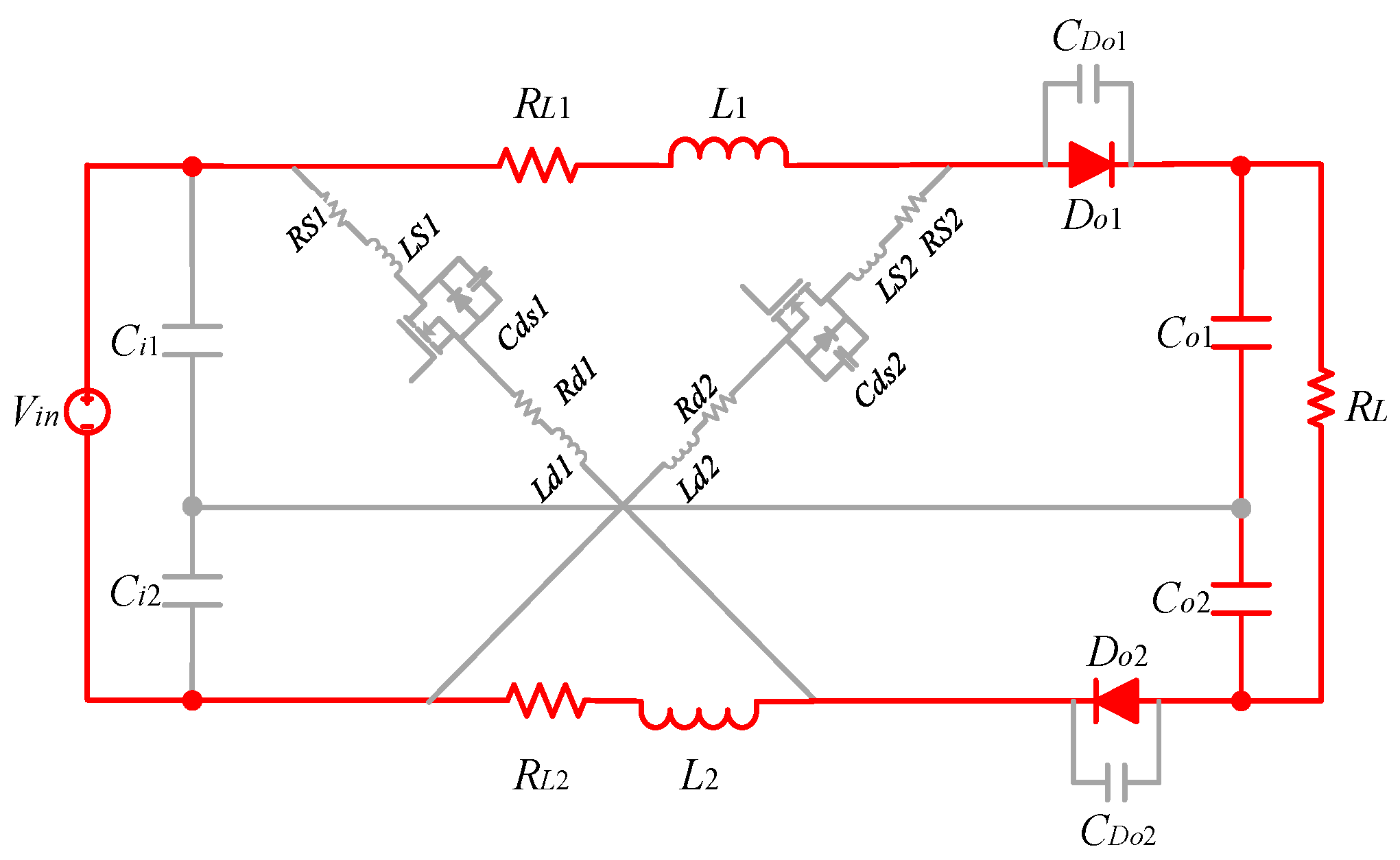
2. Analysis of Sneak Circuit of Dual-Switch Converter with Parasitic Parameters
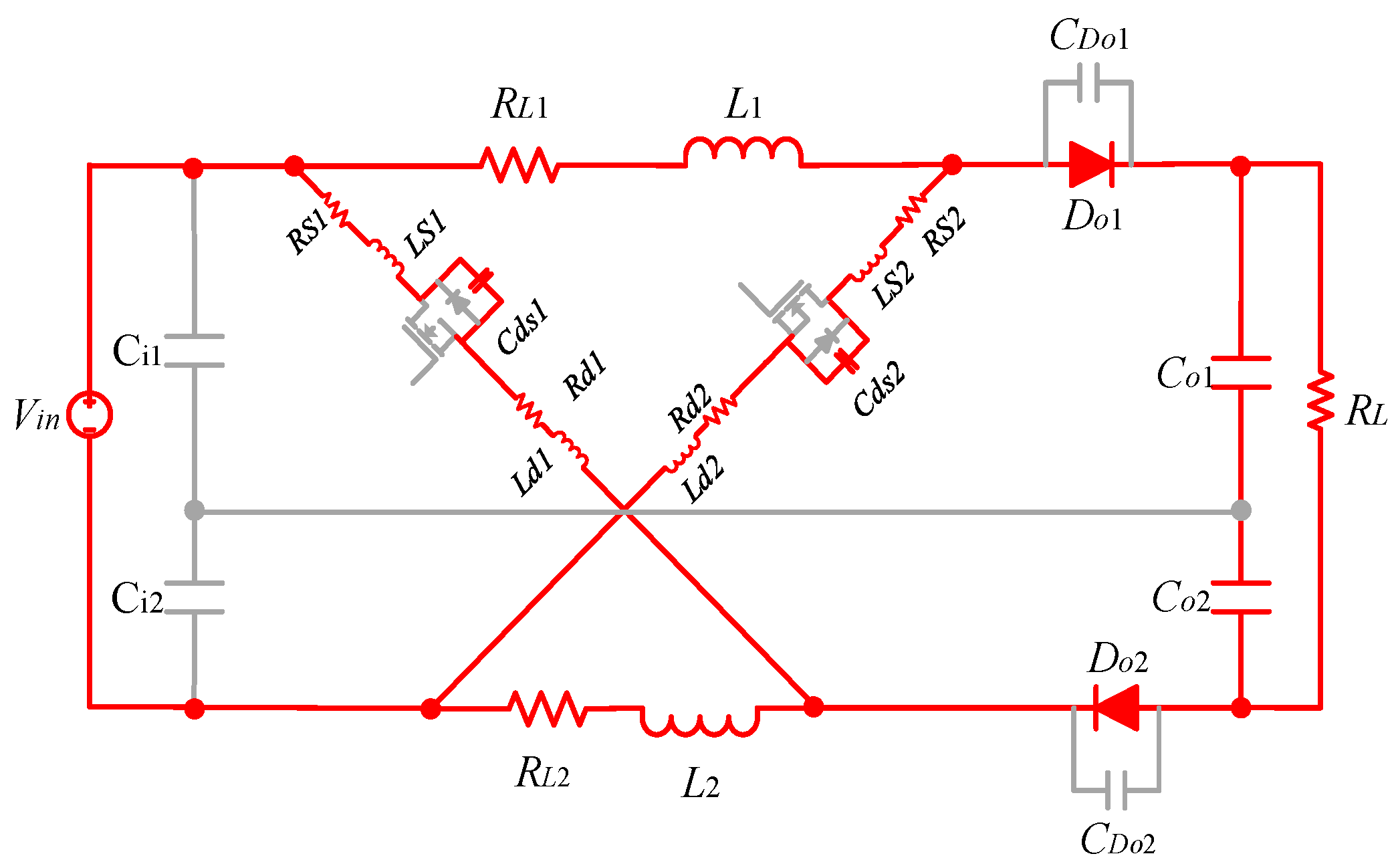
2.1. Analysis of Normal Modes
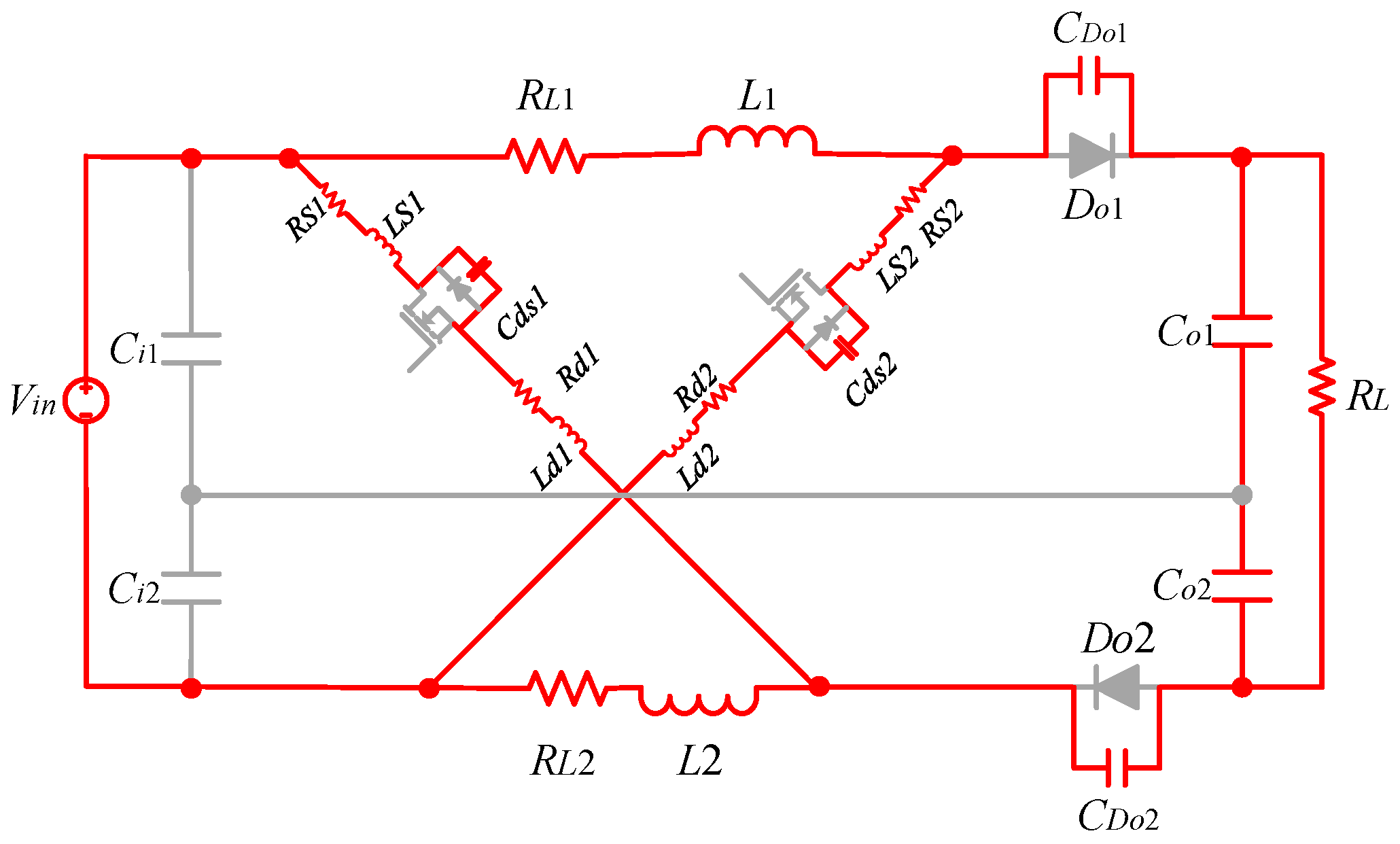
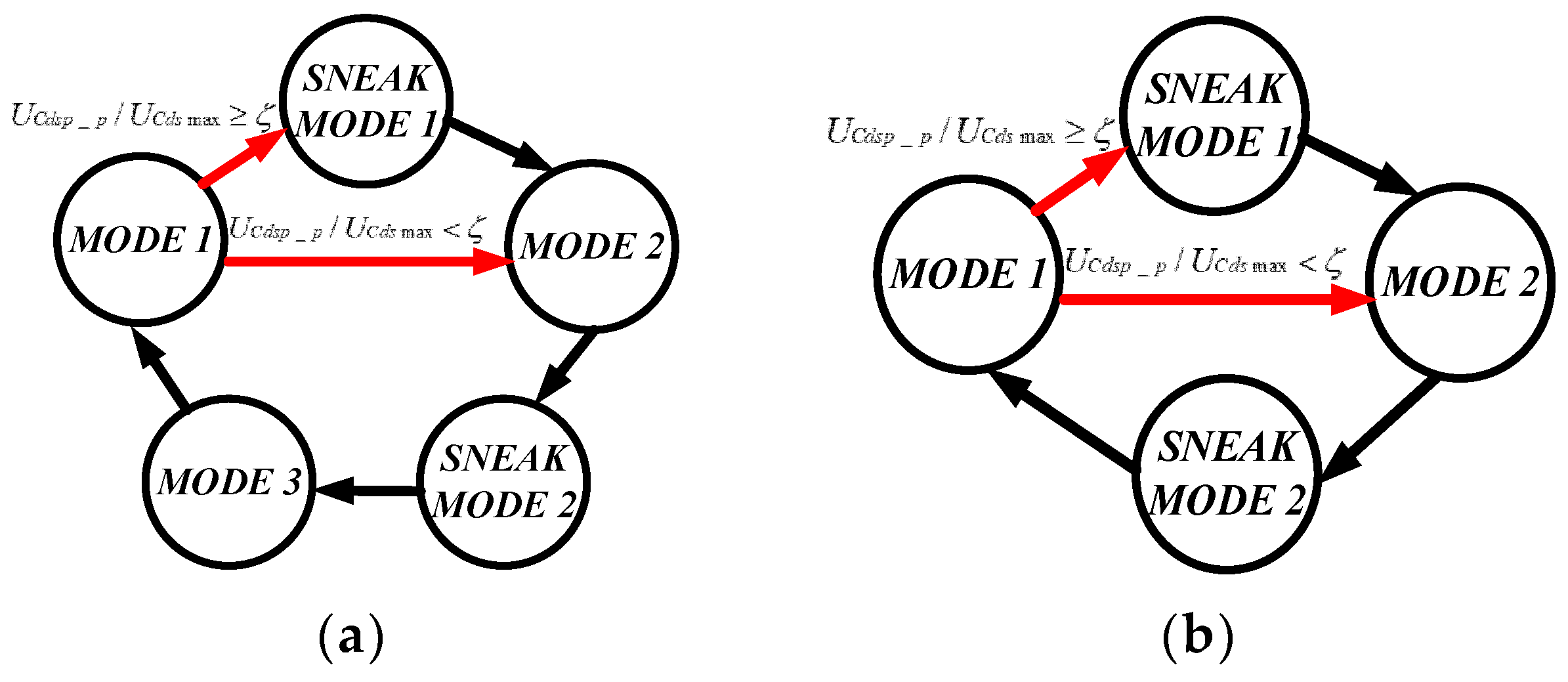
2.2. Analysis of Sneak Modes
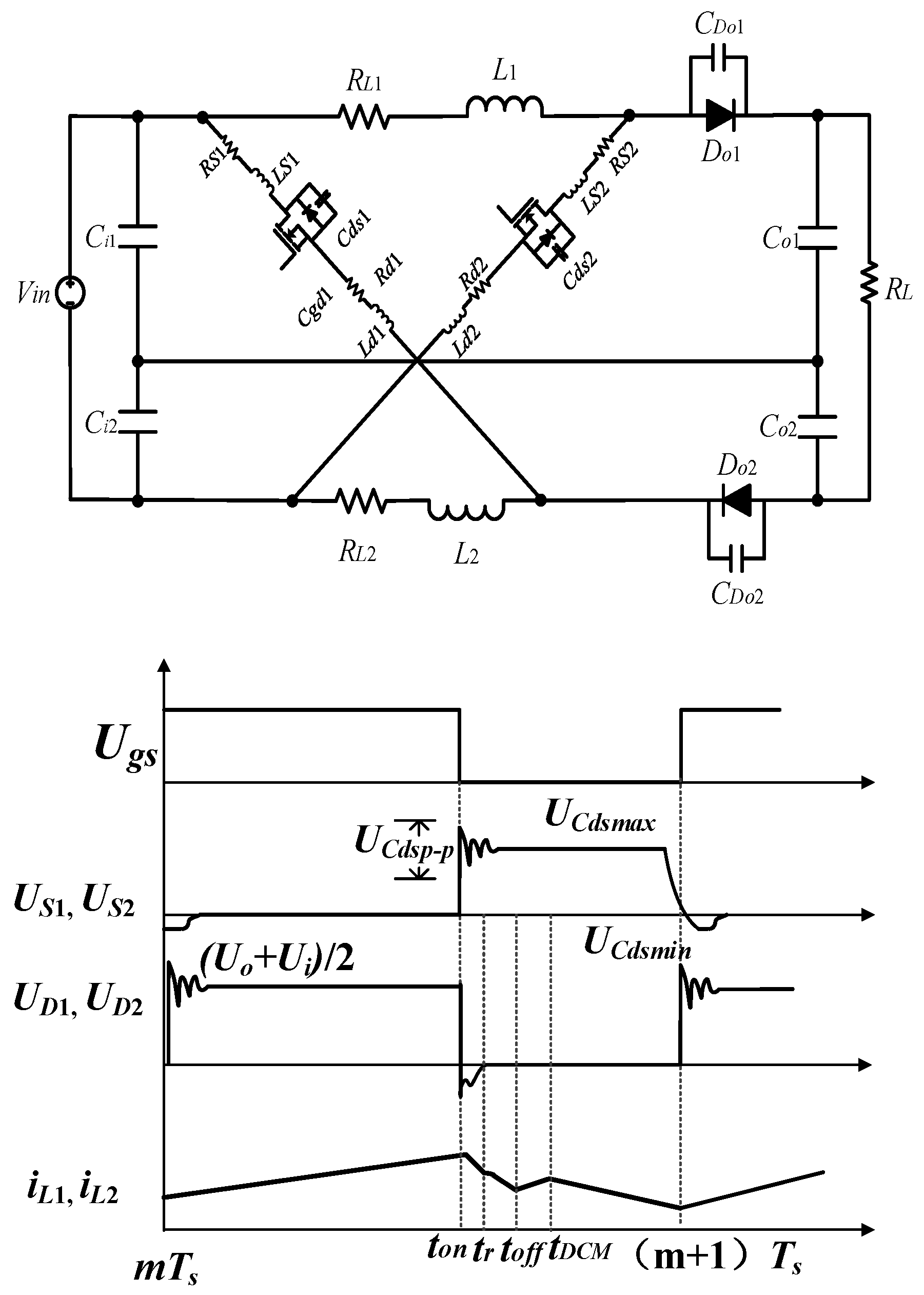
3. Considering the Influences of Parasitic Parameters on Converter Characteristic
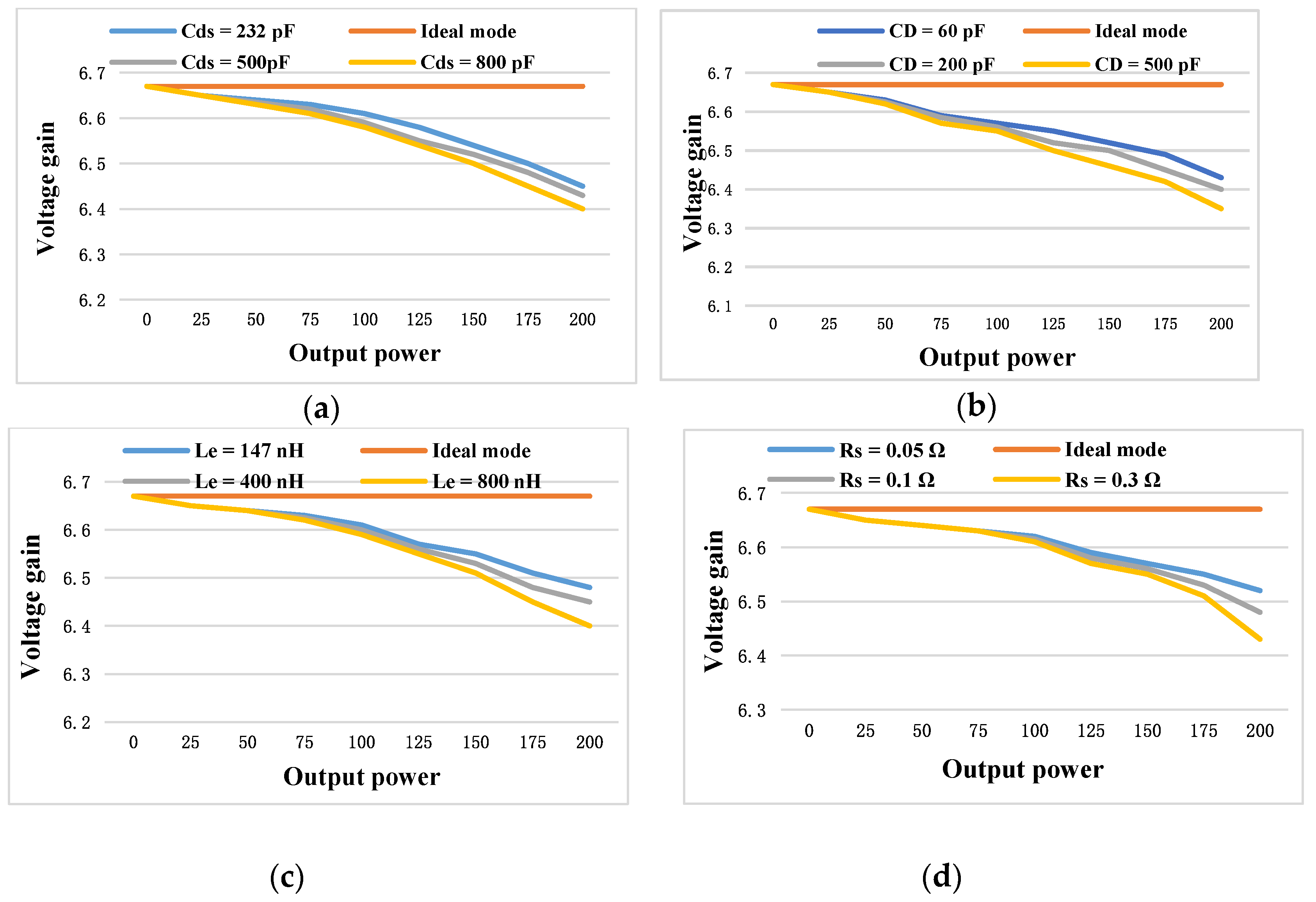
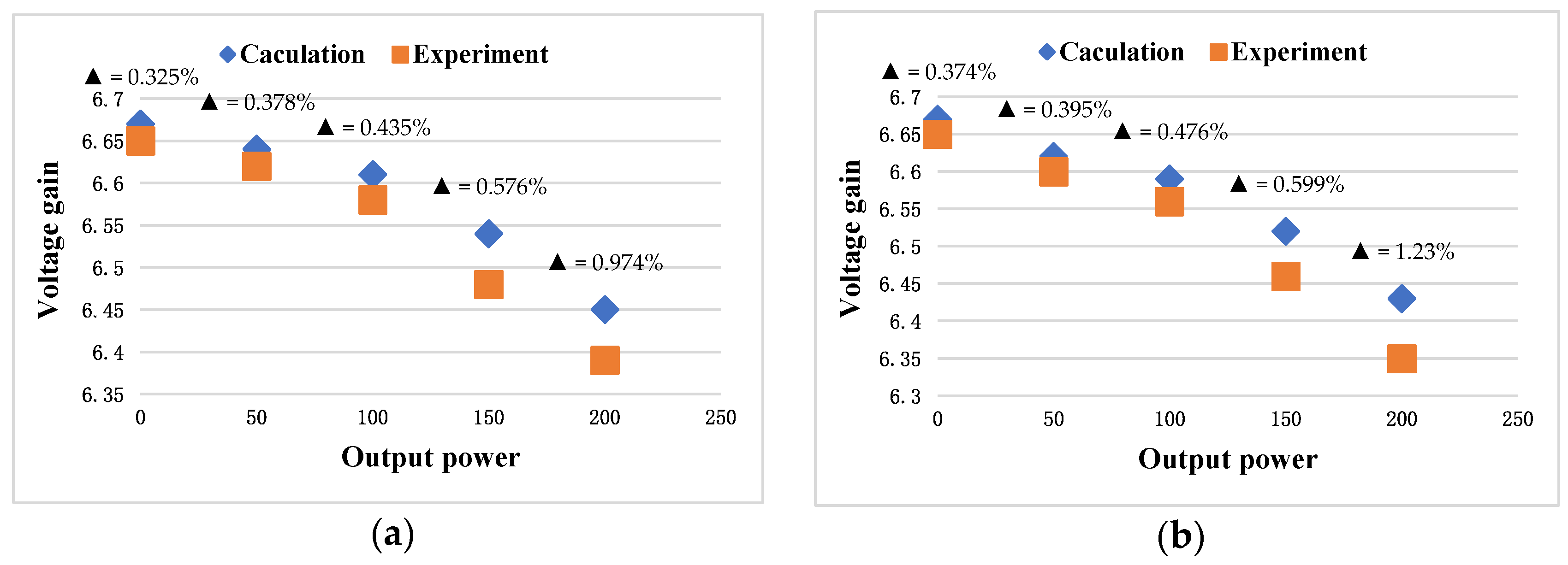
3.1. Effects of Parasitic Parameters on Voltage Gain
- In the Ideal Case
- 2.
- Considering Parasitic Parameters
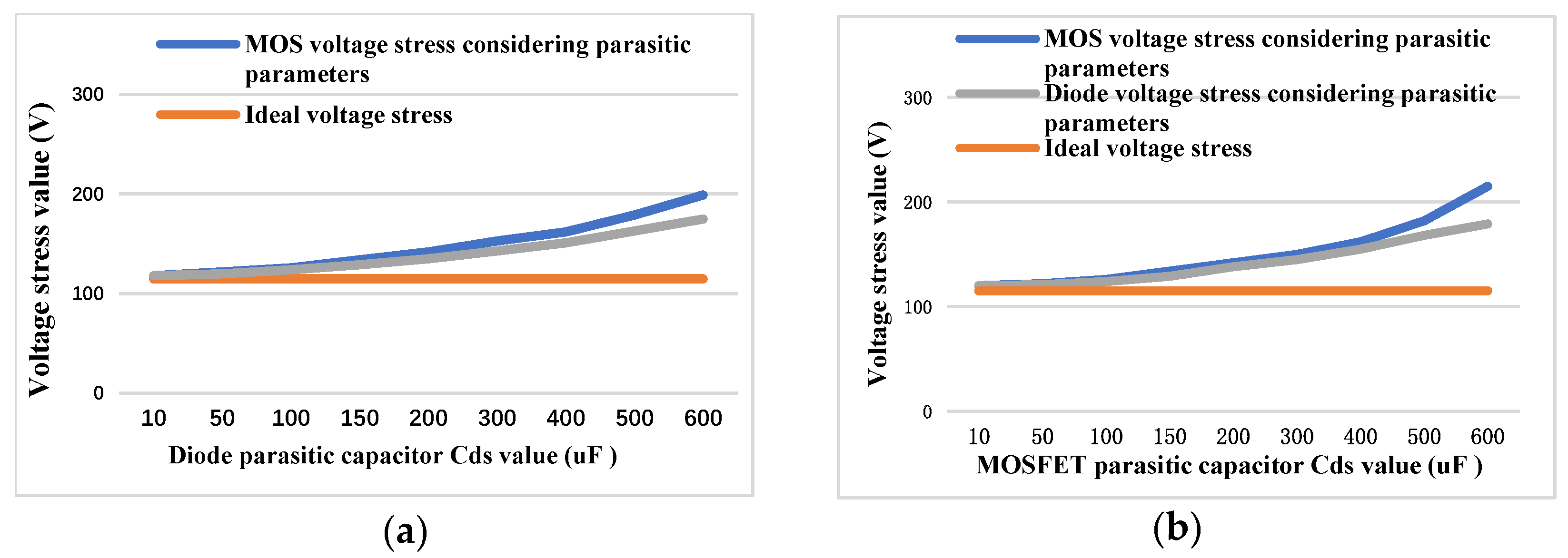
3.2. Effects of Parasitic Parameters on Switch Stress
- Ideal conditions
- Conditions considering parasitic parameters
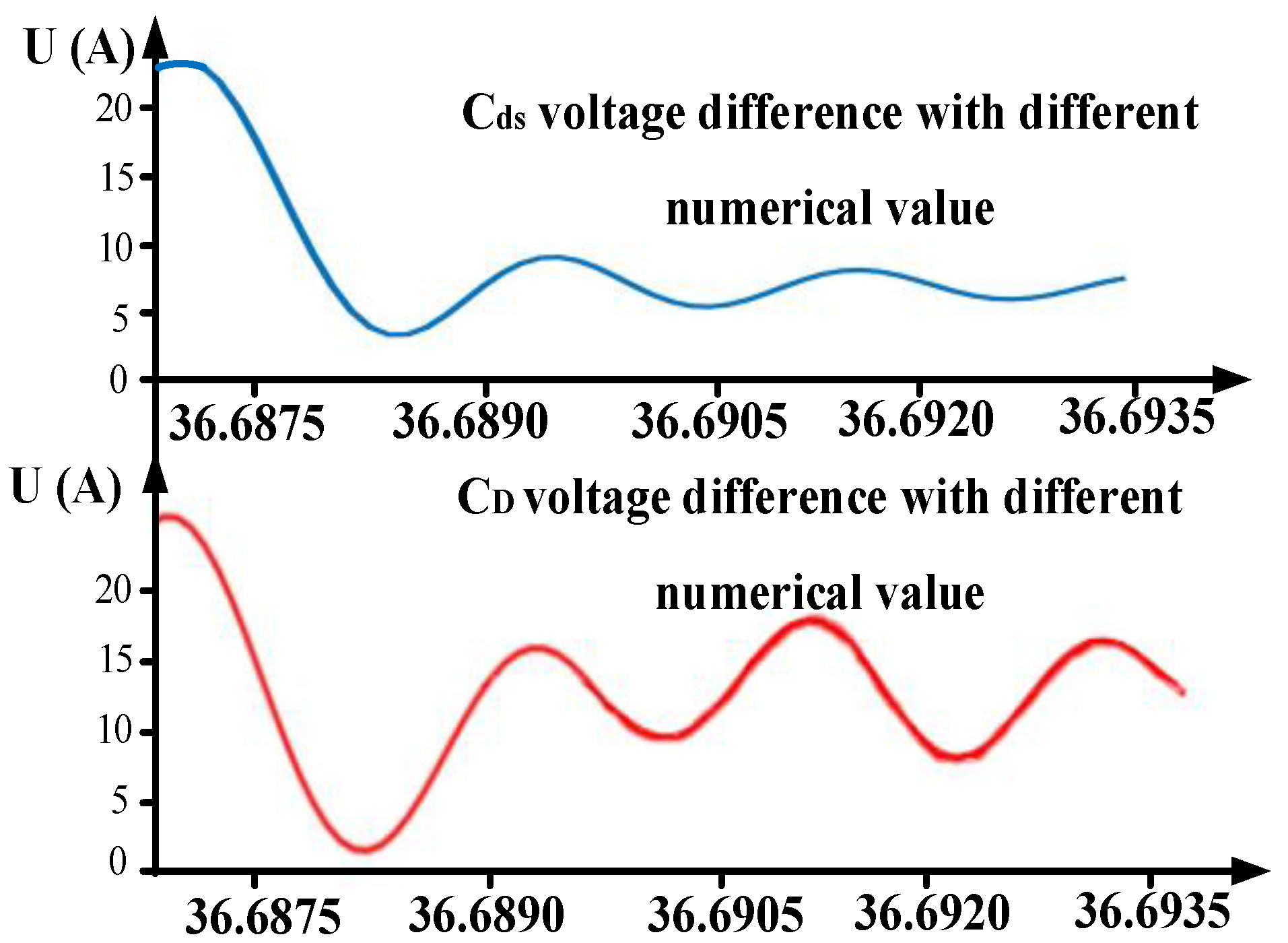
3.3. Influence of Parasitic Parameters Asymmetry on Circuit
4. Simulations and Experiment Verification
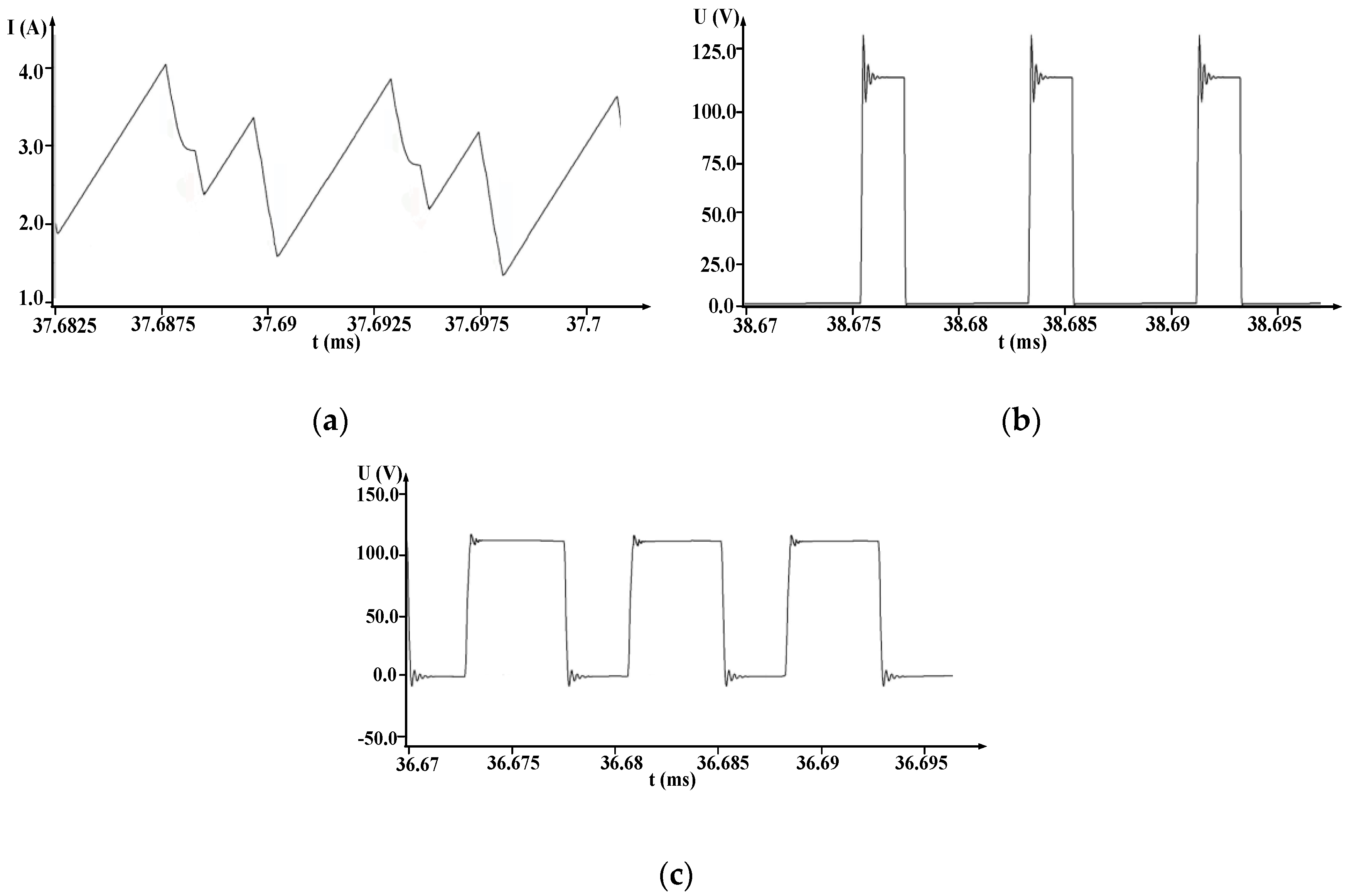
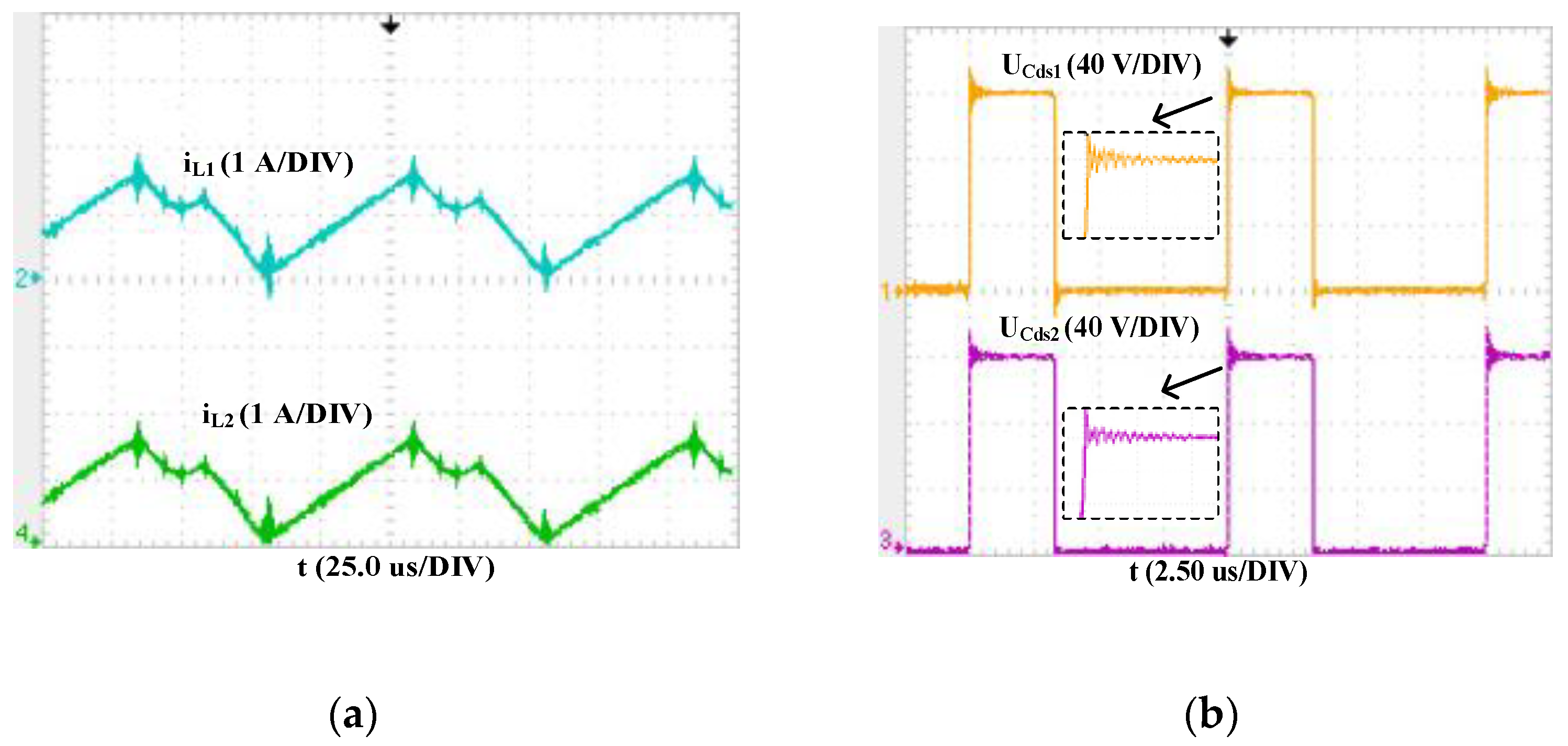
4.1. Simulations in Saber
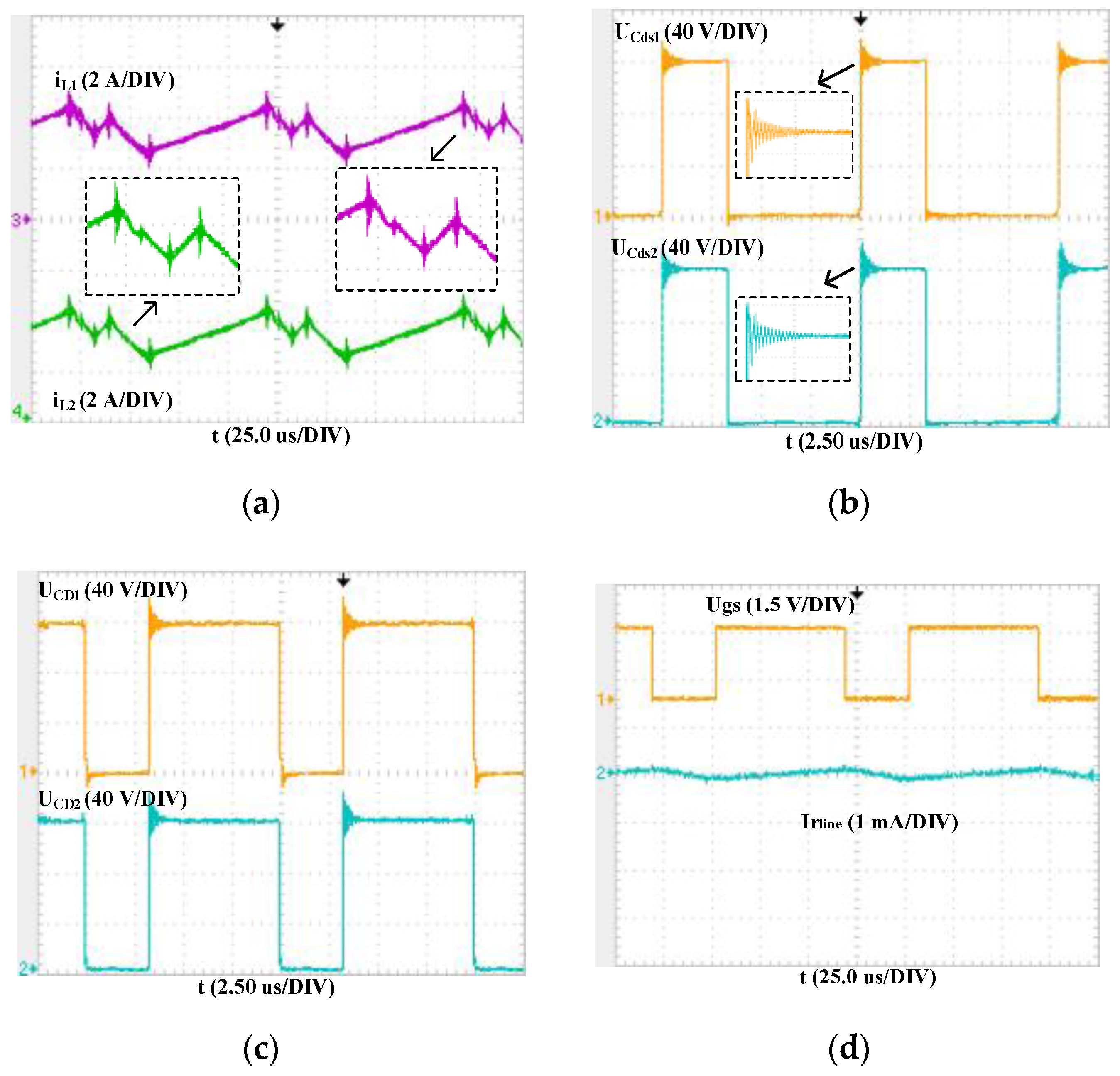
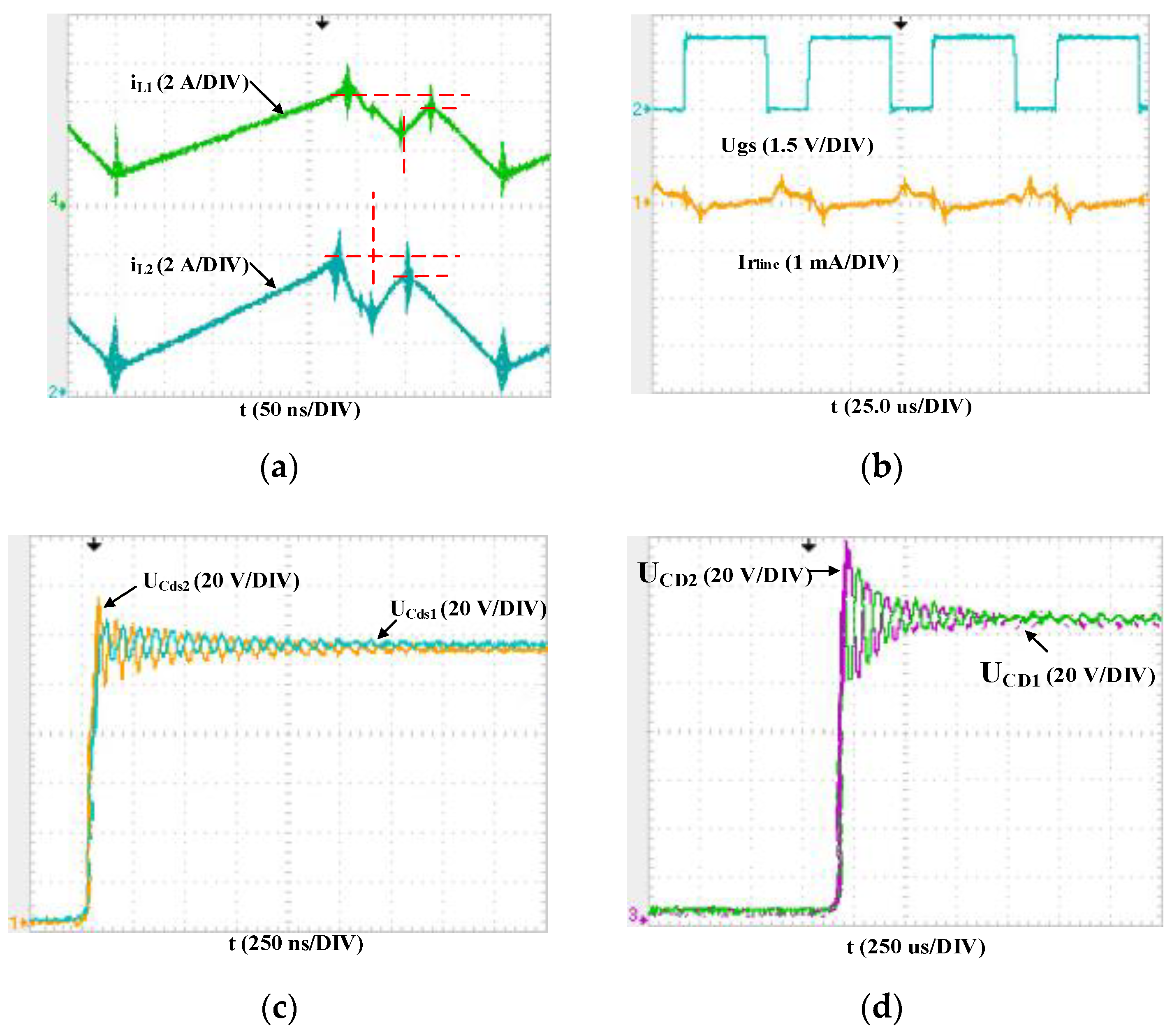
4.2. Experimental Verification
4.3. Comparative Analysis of Simulation and Experimental Waveforms
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Han, J.; Gu, X.; Yang, Y.; Tang, T. Dynamic Improvement with a Feedforward Control Strategy of Bidirectional DC-DC Converter for Battery Charging and Discharging. Electronics 2020, 9, 1738. [Google Scholar] [CrossRef]
- Zhang, B.; Qiu, D. Sneak circuits in power converters: Concept, principle and application in CPSS Transactions on Power Electronics and Applications. CPSS Trans. Power Electron. Appl. 2017, 2, 68–75. [Google Scholar] [CrossRef]
- Hongchen, L.; Li, F. Novel High Step-Up DC-DC Converter with Active Coupled-Inductor Network for a Sustainable Energy System. IEEE Trans. Power Electron. 2015, 30, 6476–6482. [Google Scholar]
- Liu, G.; Zhao, P.; Zhao, M.; Yang, Z.; Chen, H. Electromagnetic Disturbed Mechanism of Electronic Current Transformer Acquisition Card under High Frequency Electromagnetic Interference. Electronics 2020, 9, 1293. [Google Scholar] [CrossRef]
- Li, M.; Zhang, B.; Qiu, D. Sneak circuit analysis of Boost converter considering parasitic parameters. In Proceedings of the Applied Power Electronics Conference & Exposition, IEEE, Fort Worth, TX, USA, 16–20 March 2014. [Google Scholar]
- Tang, Y.; Wang, T.; He, Y.; Fu, D. Study of a high step-up voltage gain DC/DC converter with passive lossless clamp circuit. In Proceedings of the IEEE IECON, Vienna, Austria, 10–13 November 2013; pp. 1308–1313. [Google Scholar]
- Shen, C.-L.; Chen, L.-Z.; Chen, H.-Y. Dual-Input Isolated DC-DC Converter with Ultra-High Step-Up Ability Based on Sheppard Taylor Circuit. Electronics 2019, 8, 1125. [Google Scholar] [CrossRef]
- Zhao, B.; Song, Q.; Li, J.; Liu, W.; Liu, G.; Zhao, Y. High-Frequency-Link DC Transformer Based on Switched Capacitor for Medium-Voltage DC Power Distribution Application. IEEE Trans. Power Electron. 2016, 31, 4766–4777. [Google Scholar] [CrossRef]
- Zhang, B.; Qiu, D.Y. Sneak Circuits of Power Electronic Converters; Wiley: New York, NY, USA, 2015. [Google Scholar]
- Zhaksylyk, Y.; Halvorsen, E.; Hanke, U.; Azadmehr, M. Analysis of Fundamental Differences between Capacitive and Inductive Impedance Matching for Inductive Wireless Power Transfer. Electronics 2020, 9, 476. [Google Scholar] [CrossRef]
- Rogina, M.R.; Rodríguez, A.; Vázquez, A.; Lamar, D.G.; Hernando, M.M. Event-Focused Digital Control to Keep High Efficiency in a Wide Power Range in a SiC-Based Synchronous DC/DC Boost Converter. Electronics 2020, 9, 2154. [Google Scholar] [CrossRef]
- Ansari, S.A.; Moghani, J.S. A Novel High Voltage Gain Noncoupled Inductor SEPIC Converter. IEEE Trans. Ind. Electron. 2018, 66, 7099–7108. [Google Scholar] [CrossRef]
- Ragab, K.; Kozak, M.; Sun, N. Thermal Noise Analysis of a Programmable-Gain Switched-Capacitor Amplifier with Input Offset Cancellation. IEEE Trans. Circuits Syst. II Express Briefs 2013, 60, 147–151. [Google Scholar] [CrossRef]
- Muhammad, M.; Armstrong, M.; Elgendy, M.A. A Nonisolated Interleaved Boost Converter for High-Voltage Gain Applications. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 352–362. [Google Scholar] [CrossRef]
- Gutsmann, B.; Mourick, P.; Silber, D. Exact inductive parasitic extraction for analysis of IGBT parallel switching including DCB-backside eddy currents. In Proceedings of the 2000 IEEE 31st Annual Power Electronics Specialists Conference, Galway, Ireland, 23 June 2000. [Google Scholar]
- Chen, Z.; Boroyevich, D.; Burgos, R. Experimental parametric study of the parasitic inductance influence on MOSFET switching characteristics. In Proceedings of the 2010 International Power Electronics Conference-ECCE ASIA, Sapporo, Japan, 21–24 June 2010. [Google Scholar]
- Xiong, F.; Zhang, J.M.; Qian, Z.M. Effect of parasitic parameters on current distortion of boost PFC circuit. Proc. CSEE 2010, 30, 40–47. [Google Scholar]
- Li, M.; Zhang, B.; Qiu, D.; Zhang, G. Sneak Circuit Phenomena in a DCM Boost Converter Considering Parasitic Parameters. IEEE Trans. Power Electron. 2017, 32, 3946–3958. [Google Scholar] [CrossRef]


| Components | Parameter Values |
|---|---|
| Ui/Uo | 30–50 V/200 V |
| FS | 200 kHz |
| S1, S2 | IRFP250 |
| D | SF24 |
| CD | 126 pF |
| Ld1, Ld2 | 135 nH |
| Ls1, Ls2 | 12 nH |
| Cds1, Cds2 | 232 pF |
| RL, Rd | 0.05 Ω |
| Rs1, Rs2 | 0.1 Ω |
| CD01, CD02 | 60 pF |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, Y.; Kong, D.; Tong, H. Analysis of Symmetric Dual Switch Converter under High Switching Frequency Conditions. Electronics 2020, 9, 2183. https://doi.org/10.3390/electronics9122183
Tang Y, Kong D, Tong H. Analysis of Symmetric Dual Switch Converter under High Switching Frequency Conditions. Electronics. 2020; 9(12):2183. https://doi.org/10.3390/electronics9122183
Chicago/Turabian StyleTang, Yu, Dekai Kong, and Haisheng Tong. 2020. "Analysis of Symmetric Dual Switch Converter under High Switching Frequency Conditions" Electronics 9, no. 12: 2183. https://doi.org/10.3390/electronics9122183
APA StyleTang, Y., Kong, D., & Tong, H. (2020). Analysis of Symmetric Dual Switch Converter under High Switching Frequency Conditions. Electronics, 9(12), 2183. https://doi.org/10.3390/electronics9122183




