1. Introduction
The future of society is digital; how to transfer the physical society’s relationships to money, law, and even lifestyle and culture into digital relationships in the virtual world is a big challenge in IT technologies. The notion of the smart contract (SC) is one of the basic concepts to solve the code contract proposed by Nick Szabo in 1994, in the paper, “Formalizing and Securing Relationships on Public Networks” [
1]. Szabo gave an algorithmic specification of a car loan scenario: if the lender fails to pay its loan, the smart contract would automatically withdraw his digital car keys. It is obvious that car dealers will find this automatic contract attractive. Smart contracts utilize protocols and user interfaces to facilitate all steps of the contracting process, which almost obviates the ambiguity of contractual clauses in text or their implementation. Smart contracts aim to reduce transaction costs imposed by principals, third parties, or the tools of transactions. Smart contracts are one of the pillars of tomorrow’s digital society.
Szabo’s smart contracts theory and the Internet (world wide web) are invented almost at the same time. However, Szabo had no clear idea to make it real. Hence, the application has been far behind the theory. Two problems exist mainly. First, there is no way to control the physical property effectively. Vending machines can control the ownership of goods by storing goods in boxes. However, it is challenging to manage real-world assets such as industrial products, agricultural produce, etc. Second, there is no trustworthy execution environment for smart contracts, where the contractors can observe and verify the performances of other contract parties. Blockchain [
2] is an effective way to solve these problems. It is not only a safely distributed ledger to store the contract code but also a distributed execution environment to control the digital asset directly. The blockchain nodes will execute the contract code in a distributed way, which is similar to the law and regulation executor of commercial transactions. Combined with blockchain, smart contracts can help companies to fulfill corporate social responsibility [
3], easily supervised by the government and the public, reduce transaction costs, and improve business performance.
However, there are still many problems with smart contracts.
The smart contract is the executable code, and it should adapt to the reliable mass software production; The smart contract has higher requirements for its correctness. Hence, it requires a way to generate a credible contract code; The smart contracts will likely replace the contract’s text in the future. Therefore, it is necessary to keep conformance with the regulations in law texts.
In this paper, the concept of “smart contract engineering” is proposed, which aims to guide the code generation of smart contracts so that we can obtain legal and correct smart contract software. It will be the integration of the theory of software engineering (SE) [
4], Formal Methods [
5,
6], intelligent methods, and computational law [
7]. It aims to reduce the potential errors during the contract development process, improve the efficiency of the development of contracts, and promote the standardization of contract development.
The main contributions of this paper are as follows:
The concept and method of smart contract engineering are proposed in
Section 4;
The formal description and formal model of the smart contract are proposed in
Section 5;
Model-driven verification methods corresponding to smart contracts’ features are presented in
Section 6, including iterative road map: modeling, model transformation, model verification, automatic code generation, and runtime verification;
Conformance testing is applied to verify the conformance of smart contracts code, and contract texts are described in
Section 7;
This paper is structured as follows:
Section 2 presents a general review of smart contracts;
Section 3 discusses related techniques and works;
Section 4 introduces smart contract engineering;
Section 5 proposes the formal description of smart contracts and describes model, transaction, and attributes of smart contracts;
Section 6 shows the formal methods in SCE;
Section 7 shows the conformance testing methods applied to smart contracts;
Section 8 presents a case study of formal verification to illustrate the advantages of formal methods; Finally,
Section 9 reports the conclusion.
2. Smart Contracts
Smart contracts utilize protocols and user interfaces to facilitate all steps of the contracting process. To make it widely used with soundness and completeness, we define the following eight basic attributes that smart contracts should satisfy: legality, probativeness, consistency, customizability, observability, verifiability, self-enforceability, and access-controlling.
The main features are as follows:
Legality: The code complies with legal regulations. The controlled assets have ownership, and they are valid.
Probativeness: Process data and scenarios must be securely stored, and they can be used for legal evidence.
Consistency: Smart contracts should be consistent with the existing law text. Before publishing the smart contract, it should be reviewed by professional law persons to assure that the contract will not contradict the existing laws.
Customizability: Smart contracts are customizable. Multiple basic contracts can be combined into complex or complicated contracts.
Observability: Smart contracts require interfaces to observe the state of contracts, including the contract itself, its performance, and everything about the contract.
Verifiability: The records about the smart contracts can be verified. The working logic and the correctness of the execution of smart contracts are verifiable.
Self-enforceability: It needs enforcement to protect against breach and third parties which do not rely on law enforcement. Cryptographic contracts would give control by the cryptographic keys to operate the property for persons who rightfully own the property in terms of the contract.
Access-controlling: The information of contracts, such as knowledge, control, and performance, must be only accessible for contract-related persons. Unless when a conflict occurs, these properties of the contract will be exposed to the third parties.
To satisfy the above properties and solve the problems of smart contracts, we can learn from business contract architecture [
8,
9,
10,
11,
12] to design the role-based architecture of blockchain-based smart contracts system (as shown in
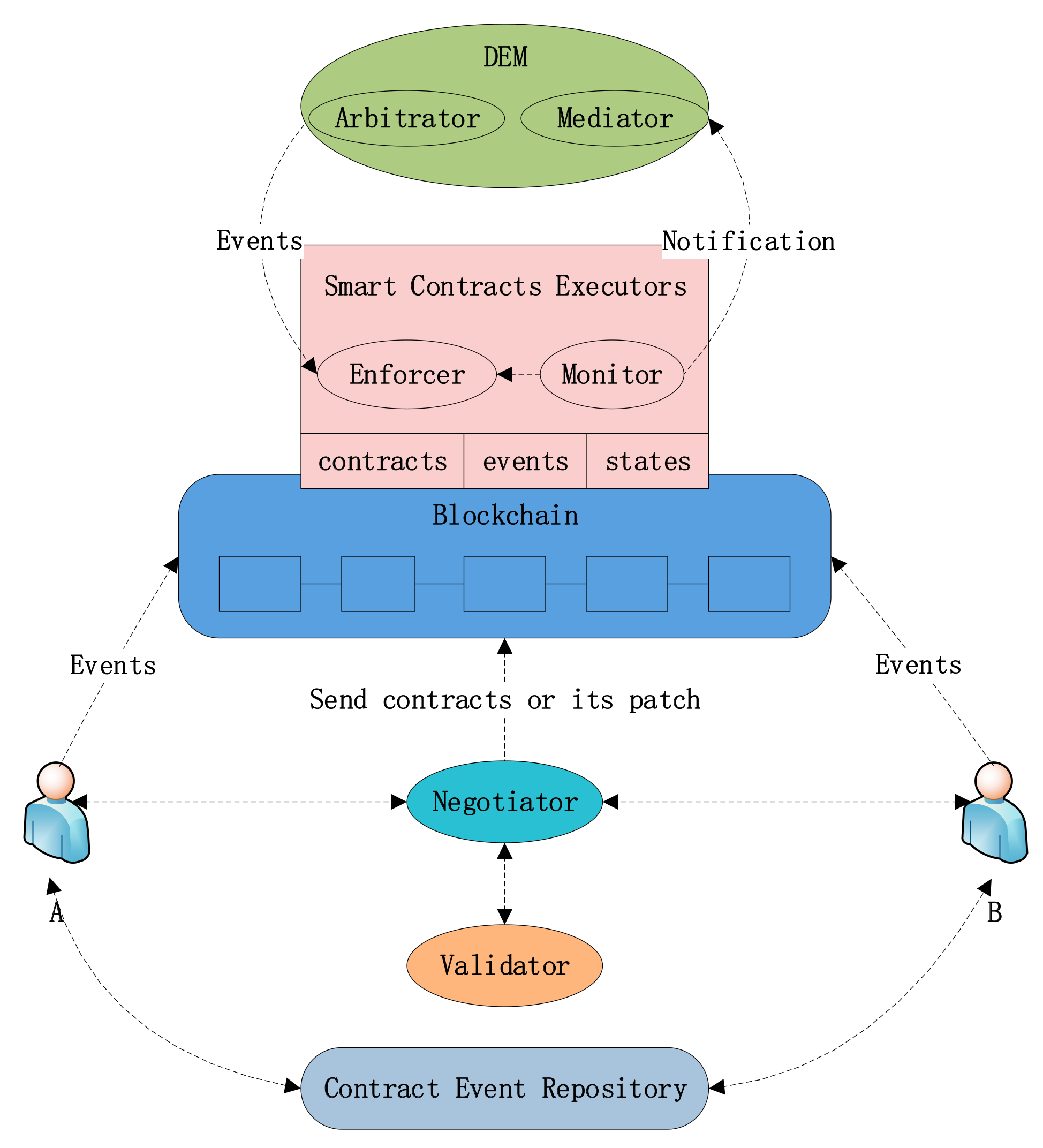
Figure 1). In this architecture, there are a variety of roles played in the contract establishing, implementing, and trust mechanism.
- (1)
Roles Supporting Contract Establishment
The following roles are supporting the process of establishing a contract.
Negotiator mediates the negotiation process (alternatively, this can be carried out by the parties themselves). During this phase, parties can exchange contract instances. Contract instances will be submitted for checking validity. Then the negotiator will send the signed contract instances to the blockchain and the same for the contract patches.
Validator uses formal methods to verify the logical correctness of the contract itself.
The blockchain is a safely distributed database to store contract instances. Such contract instances can be later used as evidence of agreement in the contract monitoring and enforcement activities [
2].
Contract events repository provides storage and access to standard contract templates in different contractual scenarios. Parties can use predefined contract templates to trigger contract execution.
- (2)
Roles Supporting Contract Execution
The following roles support discretionary and non-discretionary contract enforcement during the performance of a contract.
Smart contracts executors are pieces of code run by blockchain nodes; it may take the following specific roles for the events from outside of the blockchain.
Monitor enables participants to monitor the activities of parties, measure their performance, and record the relevant events. It evaluates the policies for these events against the agreements that are stored in the blockchain and signal a contract noncompliance event to the Enforcer. The monitor is subscribed to contract significant events and when these occur.
Enforcer applies to enforce actions directly for the parties to ensure that some specific behavior conforms to the contract.
Notifier implements various notification mechanisms needed to send warning messages to contract parties. For simplicity, the Notifier is not shown in
Figure 1.
Discretionary enforcement moderator (DEM) forms an opinion about the extent of deviation by the non-performing parties. It forms its opinions on the basis of evidence about the deviation of the non-performing parties, which is provided by the evidence stored on the blockchain, external advisers, and possibly additional recommendations from agents representing the parties, in a spirit similar to a (human) judge’s process to arrive at his ruling.
During this process, the DEM component may take the following specific roles:
Mediator initiates a settlement leading to the success of an amended transaction or decides the failure of mediation leading to the invocation of arbitration;
Arbitrator will not only take enforcement measures according to the results of settlements, the advice from external advisors, and the recommendations from agents representing the parties but also has the power to arbitrate, that is, to decide himself if the parties are unable to reach an amicable settlement of their dispute. An arbitrator may initiate the enforcement of corrective measures by sending events to the Contract Enforcers.
At present, the technology of smart contracts on the blockchain is still in the early stage. It is immature, unsafe, and unskilled. The technology does not form a theoretical system and cannot meet the needs of large-scale applications. For example, the DAO contract was attacked on 17 June 2016 due to the loopholes of DAO’s smart contracts. This accident resulted in the loss of 60 million dollars from the account [
13]. Moreover, in April 2018, the BEC blockchain platform was exposed to security vulnerabilities and was attacked by hackers with the BatchOverFlow vulnerability in the ERC-20 smart contract of Ethereum, causing an immense price crash. Although there are already some contract management systems, such as Selectica [
14], Novatus [
15], and Apttus [
16], these systems provide only the role of management contracts, and they cannot enforce to execute the terms of the contract.
The current research of smart contracts is still in its infancy. The application is also very simple, even fabled. The development and application of smart contract need to consider solving the following:
The problem of external information: If smart contracts retrieve some information from an external source and the information source is outside blockchain, so, there is no guarantee that each node will receive the same information. Once the consensus is broken, the entire blockchain system will be paralyzed.
The problem of the business model: How to build a model for the different real business phenomenon in the right way? How to build a large number of business modeling tools in software engineering is the key to support user’s applications.
The problem of credible contract: Is there no bug in the program? If the contract is in favor of the one contract party, obviously, how to fix it? How to verify the logic of the contract is correct, and how to eliminate the loopholes in the contract? Hence, far, the formal method is a powerful tool to transform concepts, judgment, reasoning in the contract into specific formal language for eliminating ambiguity and non-commonality of natural language.
The problem of contract execution: When multiple contracts need to be triggered at a certain time, who will manage and send the triggering events? If multiple contracts are executed at the same time, it will bring complex access control, synchronization concurrency, and consistency issues.
The problem of contract custom: How to develop a good template for the smart contract? Customizing different contracts depending on the different scenes and combining multiple contracts to form a composite contract. Further, we can model, analyze, validate, and generate contract code automatically by the formal method for the smart contract.
The problem of legality: Does the smart contract has the same power of law as a “real” contract? If the result of a smart contract breaks the law, or the court finds that the smart contract has a conflict with contract law, how to solve it? The study of computational law will give a breakthrough on the technical and legal aspects. Common Accord [
17] generates a new idea based on a smart contract in the legal documents and generating code automatically.
The problem of contract security: Contract cryptography, evidence, and information security will always be important research directions. Increasing complex contract procedures consume much computing power (such as forming an infinite loop) for a computing node, and how should we avoid such a situation?
The problem of contract performance: Combining the consistency of the smart contract state with the blockchain consistency process may increase the production time of the block. For example, the construction time of the block in Ethereum includes the processing time of the transaction in the block, and thus the speed of building the block is getting slower. How should we speed up the implementation of the contract efficiency?
The problem of non-intelligent: The current common approach is basically to use the fixed contract templates. Who will write, test, and dynamically modify smart contracts is a new model. Moreover, combining with artificial intelligence technology is the research trend. The smart contract is more like a third party who has the ability of analysis to perform the contract by the method of artificial intelligence.
This paper proposes the concept of smart contract engineering (SCE) in order to solve these problems.
3. Related Work
Early work on smart contracts has been done by Szabo [
1], who proposed the initial concept and principles of smart contracts and analyzed the possibilities and advantages of constructing smart contracts by using computers, the Internet and other new technologies. In 2000, Mark S. Miller [
18] designed a system E based on Szabo’s contract basis, which is a secure distributed persistent language for capability-based smart contracting.
Smart contracts, as a new technology in computational law, have very important features: when certain conditions are met, contracts will execute appropriate actions automatically. However, this feature has been applied in similar technology in other applications. For example, knowledge-based systems had this feature in the 1980s. The first one is the rule-based systems. When certain conditions are met, the corresponding rule will be triggered. If more than two rules are triggered at the same time, there will be a corresponding resolution mechanism to coordinate the execution of these rules. The second one is the blackboard architecture. Multiple agents are monitoring simultaneously. When a specific condition is met, the corresponding agent will activate its own rule and execute the relevant process. The different point from the rule-based system is that these agents can be grouped, and these agents who are in the same group will be on the same platform and share the same information. The third one is the database trigger. When a change in the data in the database satisfies the conditions for the database trigger, the corresponding program will be activated to perform. The last one is the service-oriented system. When the service caller meets a certain condition, the system will provide the corresponding service to the service caller.
The development of smart contracts has been slow because there was no trust execution environment to meet the need for observable, verifiable and self-enforced. Before the blockchain, the contracting party is unable to observe and verify the performance of other contract parties directly. It often involves trusted third parties, who are involved in the performance phase of contracting, which is the most expansive part. Hence, we need a contract machine which deals with contract processing automatically according to the performance of contract parties, but the machine cannot be affected by any one of them. The blockchain is a secure distributed database; anything in blockchain cannot be changed by any one of them but can be checked by all of them [
19]. Ethereum [
3] significantly promoted the development of smart contracts to meet the basic requirements of Nick Szabo smart contracts.
Contract states in blockchain cannot be changed without correct transactions, and each change of state on it needs to go through the blockchain’s consistency algorithm. Ethereum stores the contract itself and its status in the blockchain; when the terms and conditions of the contract are satisfied, the contract code stored in the blockchain will be executed. Since distributed nodes complete the execution of smart contracts in Ethereum, so there is no single point failure, and the smart contracts’ execution will be immutable and verifiable. Therefore, there is much room for development to combine smart contracts and blockchain. Many companies focus on the research on blockchain and smart contracts, such as Codius, SmartContract, IBM and Eris, etc.
Smart contracts need to be embedded into software, hardware to be executed automatically, so the language of smart contracts should be paid attention to. But a programming language is not like the language in everyday life, which is rich in semantics. The more semantically rich language of the contract, as the efficiency of the programming language, will be reduced. What’s more, complex and high-level languages are accompanied by potential security threats, vulnerabilities, and various other issues. Many partial solutions have been proposed to address specific security issues, but there is a lack of systematic research on smart contracts. Singh et al. [
20] analyzed the current formalization approaches for smart contracts in great detail and identified open issues with possible solutions to mitigate these issues. Huang et al. [
21] proposed a software lifecycle perspective to solve the smart contract security issues by dividing reviewed research into four development phases. Compared to previous works, this paper proposed the concept of SCE more extensively and systematically with a combination of software engineering, formal methods, and computational law to promote the standardization of contract design methodologies.
Learning from protocol engineering [
22], contract engineering will be used to facilitate smart contracts’ generation. To reduce the potential errors during the contract development process, this paper has used a formal verification method to verify the logical correctness of the contract itself. Formal verification techniques have been developed with three main approaches: model checking, deductive verification, and equivalence checking:
This approach [
23,
24] exhaustively explores concerned property in a model. It is possible for finite models, but also for some infinite models where infinite sets of states can be effectively represented finitely by using abstraction or taking advantage of symmetry. Usually, this consists of exploring all states and transitions in the model by using smart and domain-specific abstraction techniques to consider whole groups of states in a single operation and reduce computing time. Implementation techniques include state space enumeration, symbolic state space enumeration, abstract interpretation, symbolic simulation, and abstraction refinement. The properties to be verified are often described in temporal logics, such as linear temporal logic (LTL) or computational tree logic (CTL). The significant advantage of model checking is that it is often fully automatic; its primary disadvantage is that it does not work in general scale to large systems; symbolic models are typically limited to a few hundred bits of state, while explicit state enumeration requires the state space being explored to be relatively small. VerX [
25] uses temporal logic and model checking to automatically prove the temporal safety properties of Ethereum smart contracts. PROMELA [
26] was used for describing smart contracts, which were later verified with the SPIN model checking tool.
- (2)
Deductive verification
It consists of generating from the system and its specifications (and possibly other annotations) a collection of mathematical proof obligations, the truth of which imply conformance of the system to its specification, and discharging these obligations using either interactive theorem provers (such as HOL, ACL2, Isabelle, or Coq), automatic theorem provers, or satisfiability modulo theories (SMT) solvers. This approach has the disadvantage that it typically requires the user to understand in detail why the system works correctly and to convey this information to the verification system, either in the form of a sequence of theorems to be proved or in the form of specifications of the system components (e.g., functions or procedures) and perhaps sub-components (such as loops or data structures) [
27]. Theorem proving is used by researchers to propose KEVM [
28], an executable formal specification of the EVM’s bytecodes stack-based language built with the K framework. It was designed to provide support for rigorous formal analysis of smart contracts. B. Spitters et al. [
29] have modeled a vulnerable contract, faithful to the real DAO, and showed that by modeling it by Coq in a natural way, one could have caught this vulnerability.
- (3)
Equivalence checking
This is a form of semi-technical words, with the first two verify the correctness of the different technologies; it is the consistency of design verification, namely, whether the design of the different design stages the same functions and symbols commonly used in this art methods and incremental approach [
30].
Code generation can help to improve the automation level of software development, shorten the software development cycle and reduce manual workload and the possibility of encoding error.
Early automatic code generation technology refers specifically to translate the parse tree (parse tree) or an abstract syntax tree (abstract syntax tree) into an intermediate language (intermediate language) technology in a high-level programming language compiler back end. However, now, it refers to all kinds of programming language code generation technologies, such as graphical user interface (GUI) to generate high-level programming language code, and transition between different high-level programming language, and model-based high-level programming language automatic code generation.
The model-based automatic code generation concept stems from model-driven architecture (MDA). Model to code generation and model-to-model transformations are a subset of the MDA transformation. MDA is a software development framework that is proposed by the object management group (OMG) in 2001. The following describes the automatic generation of technology and analysis the tools of model-based code generation.
- (a)
PIM-based and PSM-based code generation
According to the results of the evolution of MDA development, it can be divided into the platform-independent model (PIM) code generation and platform-specific model (PSM) code generation. PIM describes the system but does not involve the knowledge of the final implementation platform and implementation technology; PSM describes the system and includes the knowledge of the implementation platform and related technology. PIM code generation includes PIM to PSM, PSM to code generation in two parts [
31]. PSM to code generation transit predefined PSM into the code; it can be divided into relational PSM code generation, EJB code generation and web code generation. Their difference is that relational PSM code generation’s input is the ER model, EJB code generation’s input is the EJB-UML model, and Web code generation’s input is the Web-UML model.
According to the Hierarchical modeling language representation system, it can be divided into structural model code generation and behavior model code generation. The structure model describes the static structure of the system, and the behavior model describes the dynamic behavior of the system. Static model generation is relatively fixed and only makes the appropriate translation. The behavioral model describes the system’s dynamic logic includes internal control flow, state transition, the interaction between objects, and so on. Dynamic logic makes these models own the properties of applications, but also it increases the complexity of implementation.
According to the way of processing model during the code generation, it can be divided into a rule-based engine code generation and template code generation. The rule engine is used to judge whether it can match the real-time runtime conditions for the implementation of predefined operations. A template is a file of the static text and placeholders; static text will be directed to a text code file; the placeholder will be replaced with the information which will be put into the code file. Templates are actually coding conversion rule carriers.
4. Smart Contract Engineering (SCE)
A smart contract is a piece of code that performs the contract text written in a specific computer algorithm. The contract parties agree with, sign, and fulfill contracts according to contract code.
However, there are still many problems in smart contracts, as we mentioned in the introduction. Traditional software engineering methods cannot meet the requirements of smart contracts mass production. Hence, a new concept is proposed: smart contract engineering, to standardize the generation process of smart contracts to produce the legal contract code effectively.
Definition 1.Smart contract engineering (SCE) is a systematized, modularized, and judgmental process for the smart contract that is based on development, maintenance, and execution, and that integrates with software engineering, intelligent methods as well as legal code technology.
SCE can significantly reduce development costs, and eliminate the repeated low-level development work, and bring advantages of conformance and maintainability. People can rapidly get a new contract by modifying the old model. In the early analysis and verification, system design can find potential errors as soon as possible; the use of formal methods for analysis and verification of the model also has a higher level of reliability. SCE maintains all steps of contract development to reduce the potential errors during the contract development process, improve the efficiency of development contracts, and promote the standardization of contract development.
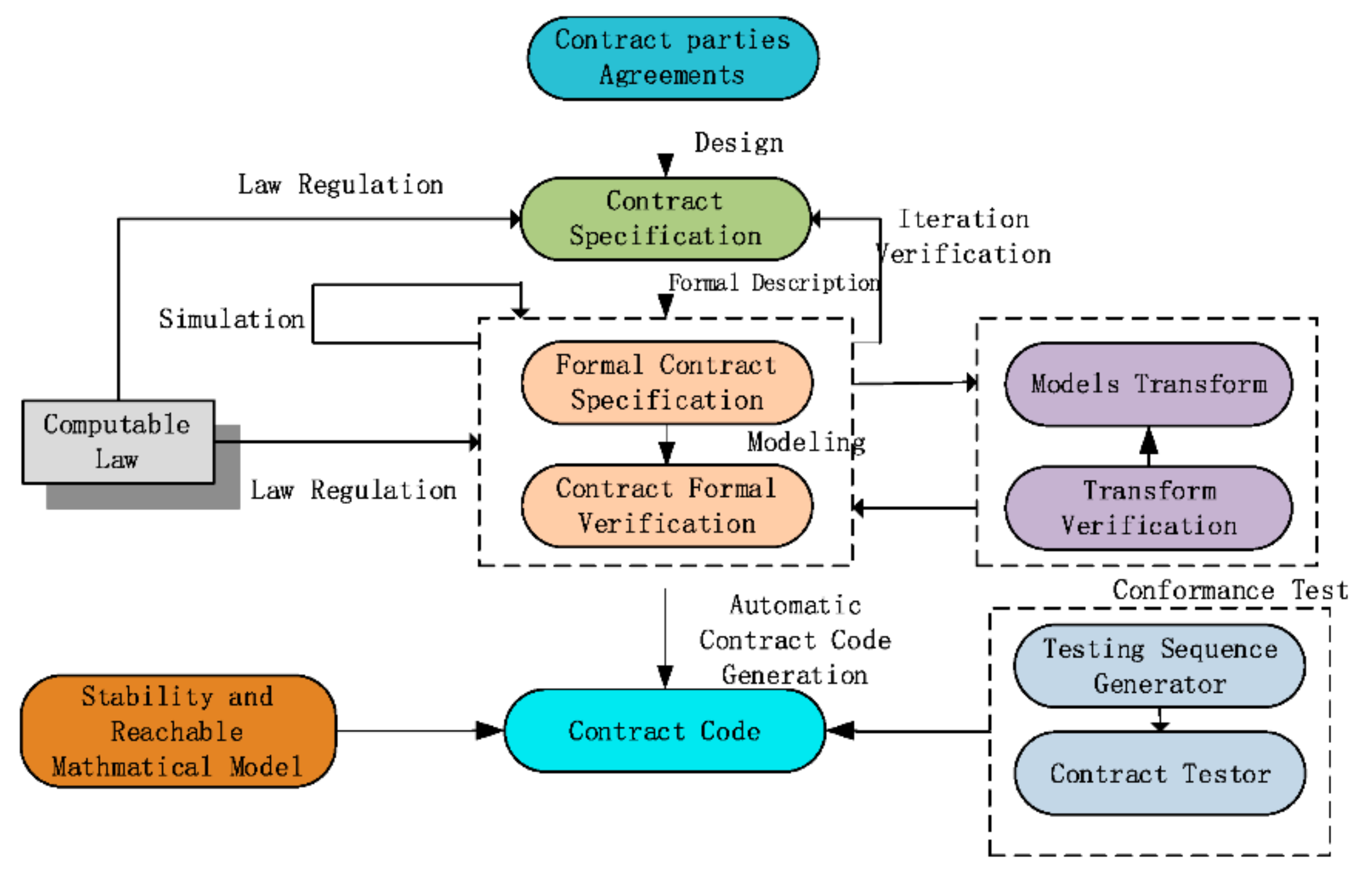
In the framework of SCE (as depicted in
Figure 2), the contract code generation includes design, description, verification, automatic code generation, performance analysis, and conformance testing, etc. [
27]. In general, three major technologies are integrated. The first one is the traditional theoretical method of software engineering, where the formal method is an effective method for deterministic high-level verification of contracts. We transform contracts’ definitions, judgments, and reasoning into formal descriptions, which can eliminate the ambiguity and incompatibility of natural language. Then we use formal tools to model, analyze, and verify smart contracts and automatically generate the verified contract codes [
32,
33] in a cyclic process. The second is the use of intelligent methods in the production process of smart contracts, making it easier for users to understand, write, deploy, and implement supervision. For example, natural language recognition, cognitive theory, and machine-learning methods make it possible to more accurately and automatically convert complex contract rules into smart contract code. The third is that smart contracts require regulation at the legal level. Computational law studies how computer technology can be used to implement the expression and automatic execution of legal documents such as laws, regulations, contracts, and constitutions in electronic media to ensure that the contract codes are consistent with statutory rules in the real world.
The key parts of contract engineering are as follows:
Contract design will construct informal contract specifications according to contract parties’ agreements. It directly decides whether the contract meets users’ demands.
Contract formal Description is used to describe contracts without ambiguity. It is the most critical part of SCE to link all other steps.
Contract law regulation will normalize the format of contract parties’ performance and make the contract consistent with the existing law. In this way, the records on the blockchain can be electronic evidence in judicial proceedings. Judicial proceedings can serve as a back-up solution whenever the self-execution of a smart contract is not successful, e.g., due to a technical fault, or when a new dispute arises between the parties to the contract after it was put into operation.
Contract model transformation as an engineering practice of the formal method, model-driven engineering (MDE) [
34] aims to raise the level of abstraction in program specification and improve automation in program development. The idea promoted by MDE is to use models at different levels of abstraction to develop systems, thereby raising the level of abstraction in program specification. MDE can support smart contract’s whole life, from modeling, verification to code generation [
35].
Contract verification Techniques are used to verify the logical correctness of the contract itself.
Stable and reachable mathematical model is used for modeling the relationship among the contract entities and for contract code generation.
Automatic contract code generation aims at automatically generating the executable code from the formal specification.
Conformance testing detects whether new contract code implementation meets all the requirements in the formal specification.
In this paper, we will mainly focus on techniques related to formal methods to give several aspects that can be applied in the verification of smart contracts.
5. Formal Description of Smart Contract
5.1. Smart Contract Model
The formal model of smart contracts is constructed by FSM called automata [
22] as follows:
Definition 2.Smart contracts can be modeled by automata.
Contract
includes contract parties’ information
,
means the information about the contracting party
, there are m contract parties joining the contract; contract automata
and contract execution automata set
. Contract automata
equals to the combination of contract execution automata set
. Contract automata
is a quintuple:
Among them,}. is the set of all states of contract execution automata, is the contract execution background, is contained in the state set of the contracting party , ; is the set of all input events; is the set of all the transition functions, ; is the initial state, ; is the set of termination states, .
Moreover,
is the contract execution automata of the contracting party
, which is a quintuple:
Among them, is the set of all execution states of ; is the set of all input events; is the set about the transition functions of , ; is the initial state, ; is the set of termination states, . Contract automata and the combination of contract execution automata set share the same events set .
5.2. Transaction Description
The data that needs to be processed by the smart contract system is collectively referred to as the “transaction”.
5.2.1. Transaction Model
The transaction includes both real transfer transactions and data that require consensus and storage and need to be sent to the blockchain. On the blockchain model, it is generally to operate for a list of transactions, and the transaction stored in a block is also a list. This paper uses the symbol T to represent the transaction list, and the symbol T represents the transaction.
The address is the source and destination of a transaction in the system. The address indicates the user’s attribution of value or data, and the lowercase “a” represents the address. A user can own multiple addresses, for example, , which represents the user owns address. In order to protect the user’s privacy, this paper draws on the public blockchain model, which uses a string of 20 bytes hash as the address, that is, , where refers to the character sequence, refers to 20 characters sequence.
In order to meet the needs of most transaction types, the transactions defined in this paper include the following fields:
from: the sender of value or data is a 20-byte address; for normal data, this field is empty. This field is represented by , so or.
to: the recipient of the value or data is also a 20-byte address; this field is also empty for an ordinary transaction or transaction that is created by a smart contract. This field is represented by , so, or .
type: the type of transaction, an 8-bit binary positive integer. This field is represented by , so , where represents a positive integer and represents an n-bit binary positive integer, that is .
nonce: the transaction number that the sender has sent to identify the order. This field is a 32-bit binary positive integer, denoted by , so .
value: the value of the transfer transaction is a 64-bit binary positive integer, indicated by , so, .
result: the result of the execution of the transaction, success or failure, etc. An 8-bit binary positive integer, denoted by , so .
timestamp: the timestamp of the transaction, indicated by .
data: the transaction data, if a smart contract creates the transaction, it is the smart contract byte stream code. This field has no length limit and is represented by .
Therefore, a transaction
can be represented:
and
and
and
When performing transactions on every node, we need to modify and update a global state and then hash the transaction to generate a Merkle tree. Whether it is a transfer transaction or normal data, a transaction needs to have a transaction’s ACID characteristics, namely, atomic, consistency, isolation, and durability. Therefore, when executing a transaction, we need to ensure its business characteristics.
The execution of a transaction is the most complicated part of a smart contract: it defines the state transition function . It is assumed that any transactions executed first pass the initial tests of intrinsic validity. These include:
- (1)
The transaction is well-formed RLP, with no additional trailing bytes;
- (2)
The transaction signature is valid;
- (3)
The sender account balance contains at least the cost v0, required in up-front payment;
- (4)
The other transaction parameters are valid.
Formally, we consider the state transition function γ. σ represents the state of the system; σ’ is the post-transactional state; T represents the transaction.
5.2.2. TStatus
The status of the transaction is called TStatus, and represented by T, which is a tuple:
S is the finished set, which includes a set of accounts that will be abandoned when the transaction is completed. L is the log memory, which includes the log records of the VM execution and the smart contract’s status. R is the contract balance, and it always keeps the balance of the contract’s account. Expenditure and income always keep equal.
The empty sub-state is defined
to have no finished set, no logs and a zero balance:
5.3. Attribute Description
The attribute of model checking has two main parts; its description is as follows:
5.3.1. Functional Attributes Description
Functional descriptions detail the operating attributes. Operating attributes define the entire behaviors of a service, such as defining how to invoke a service and where to invoke services. Functional descriptions describe the syntax of the message and how to configure the network protocol for sending messages.
For example, checking whether the model can run. If it cannot run, then there is a lexical or grammatical error, there is a need to modify the model to run.
5.3.2. Non-Functional Attributes Description
The non-functional description is mainly about service quality attributes, such as service cost, performance, response time, accuracy, security, authentication, authorization, attribute (transaction) integrity, reliability, scalability and availability.
Validation of the model, the most important content is to check whether the contract meets specified contractual clauses in nature. Under normal circumstances, the properties of the contract include the following:
Verifying the accessibility between the contract states [
36]. Some properties can be represented as follows in some elements in Equation (2).
represents the time length of a period of a contract. Function min () represents the minimum value of a number, and function max () represents the maximum value of a number.
represents a certain moment.
No deadlock. The most typical deadlock is that all entities on the contract are in wait.
No livelock. Livelock refers to the contract is in death in an infinite loop, and nothing can do to free the contract from the loop.
Boundedness. Verifying the capacity of certain ingredients or test parameters of the contract is bounded.
Recoverability of self-synchronization. When an error occurs, the contract can return to the normal state in the limited steps to execute.
Stateless ambiguity. A process at a time only allows a stable state.
Termination or progress. That refers to the service that the contract provides must be completed within a limited time.
There are still some other attributes in a smart contract, as follows:
Mutually exclusive. The exclusive contract refers that some actions cannot be executed simultaneously by multiple users.
No redundant description. Contract specification has no useless and redundant description.
Fairness. Every contract entity should have equal opportunity to access to execution, no matter what the other contract entities do what they want to do.
6. Smart Contract Verification
The verification for smart contracts is an essential process that includes modeling, model transformation, model verification, and automatic code generation. Formal methods run throughout the entire life cycle of SCE; it is a unique technology based on mathematics; it is suitable to describe, develop, and verify software and hardware.
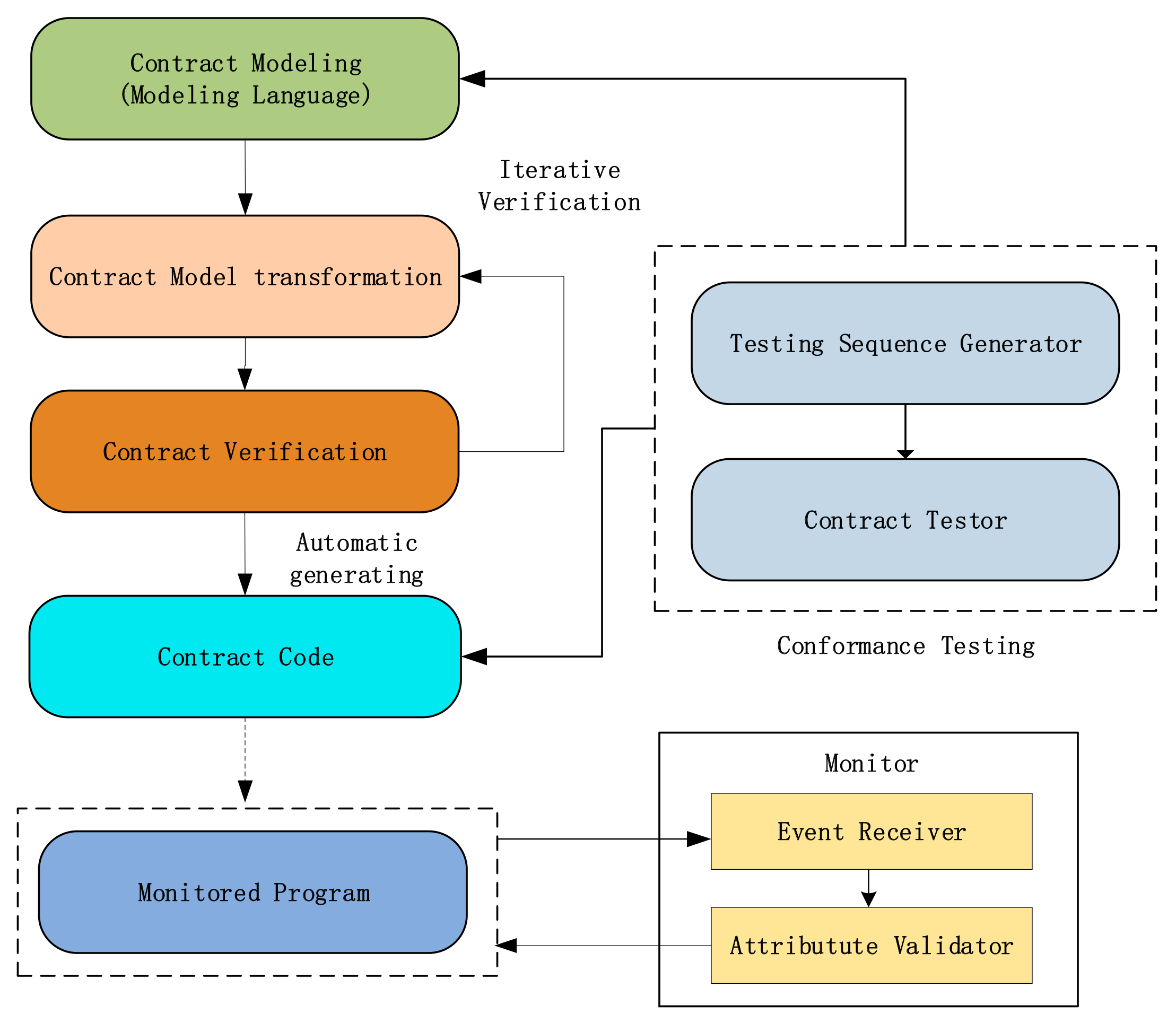
We now propose a framework of smart contracts verification in
Figure 3. The first step is contract modeling, which use the formal specification to build a smart contract. In particular, we use the mathematical description to overcome the shortcomings of natural language description, such as ambiguity; the second step is model transformation, and it can transform a contract model to another contract model to verify the richer properties of the contract. During this process, we need to verify the consistency between the two models. The third step is formal verification, it is basically the model verification, and it can check whether there are logical errors in the contract models. Moreover, it can do reachability analysis, invariance analysis, equivalence analysis, symbol execution, and simulation. The next step is automatic code generation. A tool can be made to automatically convert the verified contract to the executable contract code; then, we can use runtime verification to monitor the running programs after obtaining the contract code. The final step of formal methods is conformance testing, which can ensure that the generated contract code is consistent with the initial contract specification.
6.1. Formal Description Techniques
The formal description technique (FDT) is the most important step in Smart contract engineering because it not only provides a way to describe the contracts without ambiguity but also supports all steps of contract engineering implementation and automation.
Based on different theoretical bases like process algebra, state-transition system, set theory, and others, we analyzed the existing formal description technologies of smart contracts.
Process algebra [
37] is a family of mathematical approaches used to describe distributed or parallel systems with interacting concurrent processes. Li et al. [
38] translate the public functions of solidity to process notations defined in communicating sequential processes (CSPs), and the actions of a smart contract and its users are presented by CSP events as well as changes in a smart contract state implemented via shared variables. A state-transition system is an effective and common way to describe the behaviors of smart contracts, and there are many options in modeling smart contracts as state-transition systems. For instance, Markov decision processes, colored Petri Net, finite state machine, and timed automata are available to describe the time, probabilistic, state transition, and multi-agent interactive properties of the smart contracts.
Set-based modeling language Event-B can model the behaviors of solidity contracts and specify the properties using first-order logic [
39]. Moreover, we took Event-B as an example to demonstrate the verification process in
Section 8. There are also other formal description methods. For example, Bhargavan K [
40] used F*, which is a functional programming language, to model the solidity contract and its virtual machine called EVM. Here we summarized the key features which a good formal description technique should meet, hoping to guide the new formal description technologies.
The complete syntax and semantic definitions;
Easy-expressiveness for the contract’s architecture, functionality and contract itself;
Easy-verification for the contract’s important properties;
Support for the combination of the basic contract;
Support for complex contract management;
Support for the methods of refining contract step by step;
Abstraction mechanisms for implementation independence;
Support for all steps of contract generation, including verification, implementation and conformance testing;
Support for automated or semi-automated ways for contract design, verification, implementation and maintenance.
6.2. Model Transformation
In some cases, describing and verifying a contract model in one formal description language is not enough because the capability of the contract description language and verification tools is limited. For smart contracts, it is necessary to use the model transformation technology to convert the model into another formal description language so that we can apply the other verification tools to verify the contract better [
41]. At the same time, the properties of the contract must be consistent at different models.
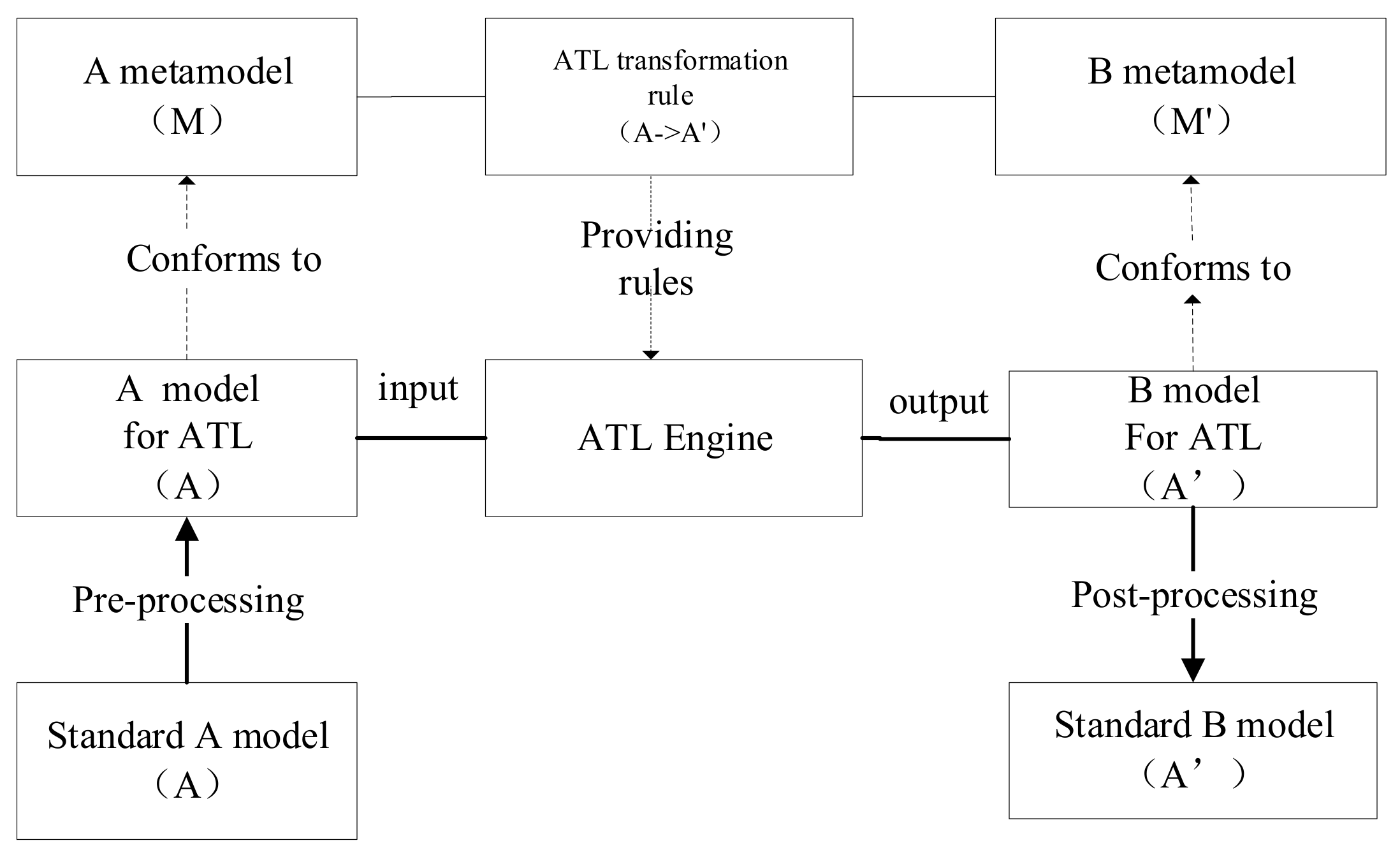
Therefore, the main research is the transformation rules, the transformation methodologies, and the transformation tools, which transform from one model to another model on the target platform. As shown in
Figure 4, the ATL transformation [
10] is used to implement the mapping between the two models. ATL is a specialized language for model transformations proposed and implemented by the ATLAS INRIA and LINA research team. ATL is a hybrid language descriptive and imperative. The excellent way is just to write a descriptive statement that can be converted to express the relationship between source and targeted model elements clearly. Compared with the traditional manual conversion, it can implement automatic conversion easily and have high reusability. For example, when the corresponding user’s PROMELA model is generated, the model checker tools, such as SPIN, can be used to verify various software properties.
The meta-models of the A model and the B model and the ATL transformation are needed for the transformation. Meta-model describes the abstract syntax of language while the ATL transformation, usually as the ATL file, defines the mapping rules between the source model and the target model. The preprocessing and postprocessing parts are the complements of the transformation. The method includes the following steps (transform standard A model to standard B model): (1) Make the ATL transformation rules between A meta-model and B meta-model; (2) get A model for ATL which conforms to the A meta-model from standard A model; (3) output the target B model for ATL which conforms to the B meta-model through the ATL engine; (4) finally, obtaining the standard B model from B model for ATL before.
Model transformation is the core of model-driven architecture (MDA) and one of the key techniques for model evolution and reconstruction. Model transformation must follow certain constrained rules to maintain some properties of the model, such as the property of external behavior, interface, etc. This transformation constraint is generally called property preservation constraint, which is mainly used to ensure that the model transformation does not destroy some properties of the model. The contract can be described in a formal language, and its formal semantics and properties can also be given. Moreover, theorem proving can also prove whether a transformation maintains the semantics or properties of the contract [
42,
43].
Especially just as shown in definition 2, smart contracts can be described as automata. It always changes the system from one state to another state for various transactions by some events. Moreover, we can define the mode change of smart contracts as follows:
Definition 3.Mode transition = < M, m0, Event, Transition >, where,
M is the set of smart contract operation mode (SCOM)
m0 M is the initial mode
Event is the set of events which trigger the smart contract mode change
Transition = M × Event × Mis the set of mode changes.
6.3. Formal Verification
During the smart contract development process, formal verification is used for proving the correctness or incorrectness of the smart contracts’ formal models concerning a certain formal specification or property. There are many techniques, tools, and frameworks that are employed for the verification of the smart contract models described in
Section 6.1 and
Section 6.2. According to the principle of verification, we can divide them into model checking and deductive verification.
Model-checking technology is an automatic verification technology for verifying a system model against its specification based on an exhaustive enumeration of states. Importantly, the verified smart contract should be modeled with appropriate abstraction techniques to avoid the state explosion problem. Usually, we use model checking tools to verify smart contract models. For example, the SPIN model checker is applied to verify the smart contract, which is modeled by Promela, which supports modeling of a synchronous distributed system as non-deterministic automata. Properties of the smart contract are expressed as Linear temporal logic (LTL) formulas [
44]. Bai et al. [
26] used this technology to verify smart contracts’ common properties like deadlock—and livelock—freedom.
Deductive verification technology consists of generating a collection of mathematical proof obligations from the smart contracts’ specifications and discharging these obligations using either proof assistant like Coq or automatic theorem prover like SMT solver. In our case study, we modeled the solidity contracts using Event-B and defined the properties like “the user’s balance should be non-negative” as invariants in the model. Then the proof obligations generated are discharged using Event-B provers.
6.4. Automatic Code Generation
Smart contracts should be applied for mass production in the future digital society. It is essential to be able to generate and combine contract code automatically and efficiently. Automatic code generation will utilize the formal model above to generate the contract code to run in the real machine.
Automatic code generation is based on the model from (model-driven architecture (MDA) [
45], which is a software development framework. MDA can analyze and verify the contract as soon as possible and generate code from the verified model. In terms of the model to automatically generate the code, including three aspects to study: code generating rules from model to executable code, methods, and tools.
In addition, the specific research content includes using a template-based technology to generate code automatically and making the template as the carrier of the rule to transform code automatically. The template is easy to modify and customize; therefore, for different platforms, developing appropriate rules and implement suitable transformation templates to generate the target code on the appropriate platform is important.
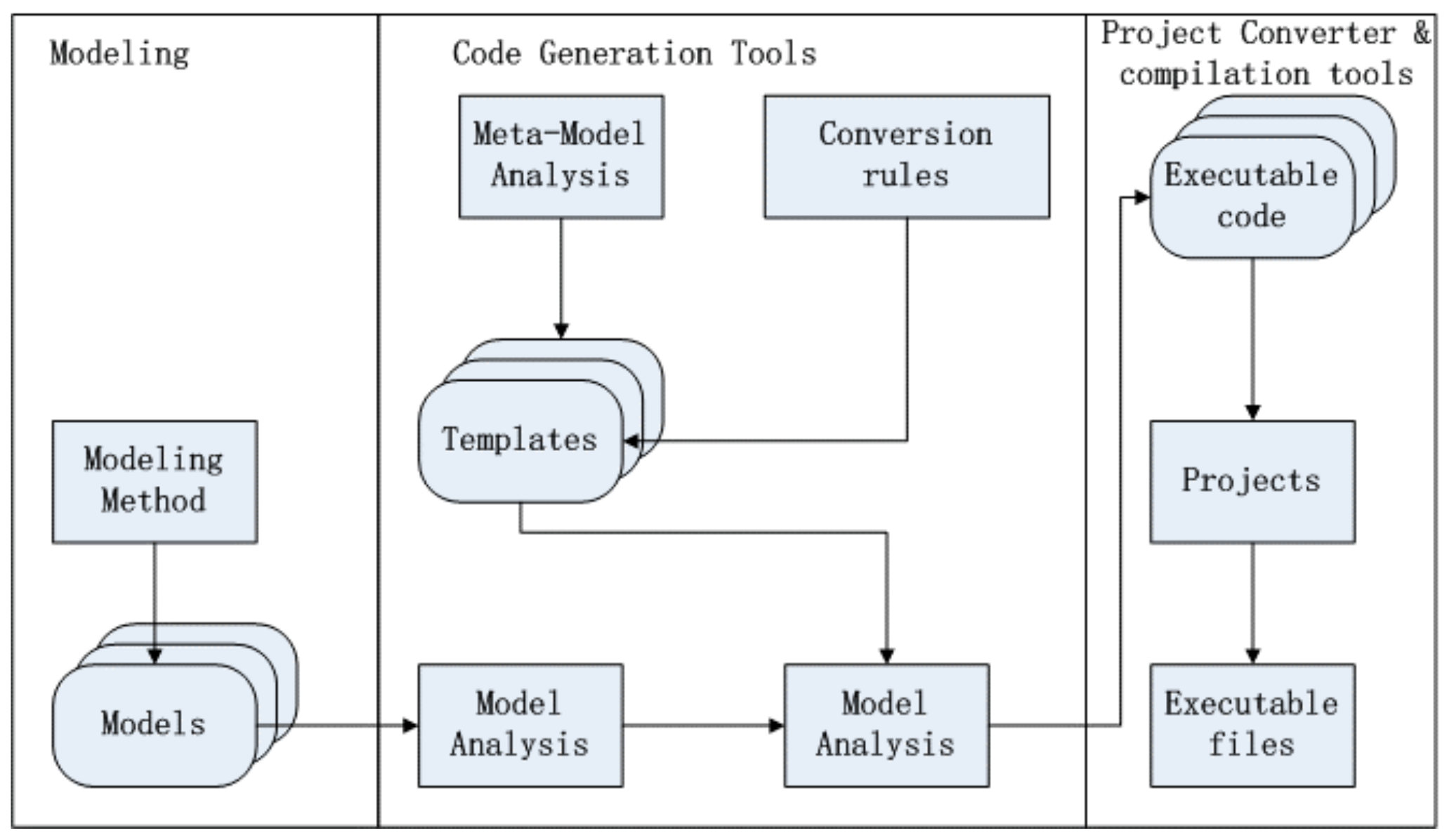
In
Figure 5, First, we should build up the models using formal description language and modeling methods. Models are the foundations for the subsequent formal validation and code generation; second, according to the describing language features, we should design the conversion rules between model and the target platform code; again, according to the conversion rules and the Meta-model design to design code templates; and finally by analyzing the models, we should extract and package the model information, model information and templates will be used to generate the target platform code by the conversion engine.
6.5. Runtime Verification
Runtime verification is a lightweight verification technique that detects the operation of the system and determines whether the system conforms to given attributes or specifications. Different from the formal verification techniques mentioned in
Section 6.4, runtime verification is applied to the generated code running in the virtual machine or other environments. In particular, the running code can be a sequence of instructions executed by the virtual machine, while it can also refer to a sequence of events emitted by a smart contract. As shown in
Figure 3, the module that detects the program under testing is called a monitor. The monitor receives the traces of the program and determines whether the program’s behavior satisfies these given attributes.
Because Rice’s theorem [
46] states that there is no perfect static analysis for a recursively enumerable language and the smart contract language is Turing-complete, that is, recursively enumerable language. Therefore, In the process of formal verification of smart contracts, false positives may occur. The advantage of using runtime verification is that we can judge whether the execution is correct according to the actual input, so if the monitor in
Figure 3 finds an error, it must be wrong! Moreover, runtime verification can provide a reactive defense against vulnerabilities or violation of correctness at runtime. For example, Solythesis [
47] is a source-to-source runtime validation tool that allows users to specify critical safety invariants of smart contracts. Taking a potentially insecure smart contract and the specified invariants as inputs, Solythesis verifies the solidity contract with runtime checks to enforce the invariants. The verified contract is guaranteed to nullify all transactions that cause the contract to violate the specified invariants. Moreover, it demonstrated that runtime validation for smart contracts could have negligible overhead.
7. Conformance Testing
One of the SCE objects is to ensure consistency between contract code and contract text. Here we give the general conformance testing methods to solve it.
Conformance testing is a kind of black test which is used to test the conformance between implementation and specification. A formal test description language can create an abstract model of a real system under test and describe the action during the execution of various tests [
48]. This section will present the general method of conformance testing for smart contracts.
7.1. Test Sets
Test sets are the basis of testing conformance, which consists of the most basic testing events sequence and defines the behavior between the testing system and contract entity. Hence, there is a need to use a formal language to define the behavior of the testing system and implementation under test (IUT).
7.2. Test Sequence Generation Algorithms
There is a variety of testing sequence generation algorithms currently, which are all based on a formal description model, such as based on FSM, Petri net and so on. The common conformance sequence generation method that is based on the finite state machine model includes Transition Tour and the special interaction sequence method.
The special interaction sequence method is the most common method, including characterizing set, referred to as W method [
49]; distinguishing sequences, referred to as D method [
50]; unique input/output sequences referred to as UIO method [
51].
The thought of the D method is that we enter the same sequence of events to each state of the protocol state machine and determine the current state according to distinguishing output event sequences. We can uniquely determine the state because the output event sequences of different states are different. The advantage is that the produced test sequence has an excellent ability of error checking and can check out the input and conversion errors roundly; the disadvantage is that the generated test sequence length is longer than others, and there are no DS (distinguishing sequence) sequences, which are necessary for the method in many actual protocol FSMs.
The W method is an extension of the D method, and it uses the set of feature sets, W-set, instead of the DS series. W-set is a set including k input events. For each state of the protocol state machine, W-set is the same. However, output models that are made up of output events from different states are different. Thus, people could determine the state according to different output models. The advantage is that it can be used more generally; the disadvantage is the process of generating the sequence is too complex.
UIO method is based on the thought of UIO sequence. Each state of protocol state machine corresponds to one or more UIO sequences. UIO sequence consists of a series of I/O operations; other states in the protocol state machine cannot work on the same I/O behavior. Thus this UIO sequence can uniquely identify this state. Generally speaking, the UIO sequence is relatively easy to get. The error detection ability of the UIO method is relatively strong, and the length of the generated test sequence is relatively short. UIO method is the most commonly used test sequence generation algorithm.
A UIO-based algorithm is given for conformance testing of the smart contract. Currently, for the UIO method, there are several specific implementation algorithms. There is a common UIO algorithm in this paper. The thought of the algorithm is: for each state conversion (si, sj; i/o), we can construct a corresponding test subsequence, e (si, sj, st; i/o) = {i/o, UIO (sj)}, si is the initial state of test subsequence, sj is the state after performing i/o conversion, st is the terminal state following Seka-characteristic sequence UIO (sj), that is the terminal state of test subsequence. The FSM in the protocol is directed graph G = (V, E), V is the set of nodes, and E is the set of conversion. Constructing graph G’ = (V, E’), E’ is the set of test subsequence; then constructing directed symmetrical graph G* based on the graph G and graph G’, and finally we can obtain test sequence of the protocol by Euler Tour. Specific steps are as follows:
Calculating the shortest UIO sequence of each state in FSM;
For each conversion i/o in the graph, finding out test subsequence e (si, sj, st; i/o) = {i/o, UIO (sj)};
Constructing G’ = (V, E’), E’ is the set of test subsequence e(si, sj, st;i/o);
Changing graph G’ into directed graph G* = (V, E*), E* = E ∪ E’, that is adding several arcs taken from E between node i and node j in the graph G’ to change G’ into symmetric graph G*;
Constructing Euler Tour ET from an initial node as a starting node in the graph G*, that is the last generated test sequence TS.
7.3. The Process of Conformance Testing
Contract conformance testing generally includes the following steps: determining test purpose, generating test sets, test implement, test execution and assessing results.
- (1)
Determining test purpose
Common conformance testing purpose includes the following: ability test; behavioral test of correct behavior; behavioral test of syntax error; behavioral test of inappropriate behavior; test of necessary behavior in the protocol; test that sending interacts with receiving; test that is associated with implementation options.
- (2)
Generating test sets
A set of test cases of a particular protocol is called the test set. The event that is used to describe test tasks of a given contract or action sequence is called test cases; thus, the test sequence is the basis to generate a test case. Generating the test set includes three aspects: generating test sequences, generating test data, combining test sequences with test data to generate and describing the test set.
- (3)
Test implementation
Based on the related test tools, describing test sets with formal description language.
- (4)
Test execution
In the test tool, execution of the test case for the tested protocol implementation, observation and recording of external behavioral responses of the tested protocol implementation.
- (5)
Test assessment
Assessing and analyzing conformance testing results, determining whether it can pass the conformance testing. If the tested protocol does not pass the test, people need to find out the reasons for feedback.
7.4. Conformance Testing Method
The conformance testing method determines the generation of test sets and the structure of the described method and test execution system. ISO9646 defines four standard abstract test methods: local test method, distributed test method, coordination test method and remote test method. In addition, for the four test methods, there are some variants, such as the ferries test method, the multi-test method and so on.
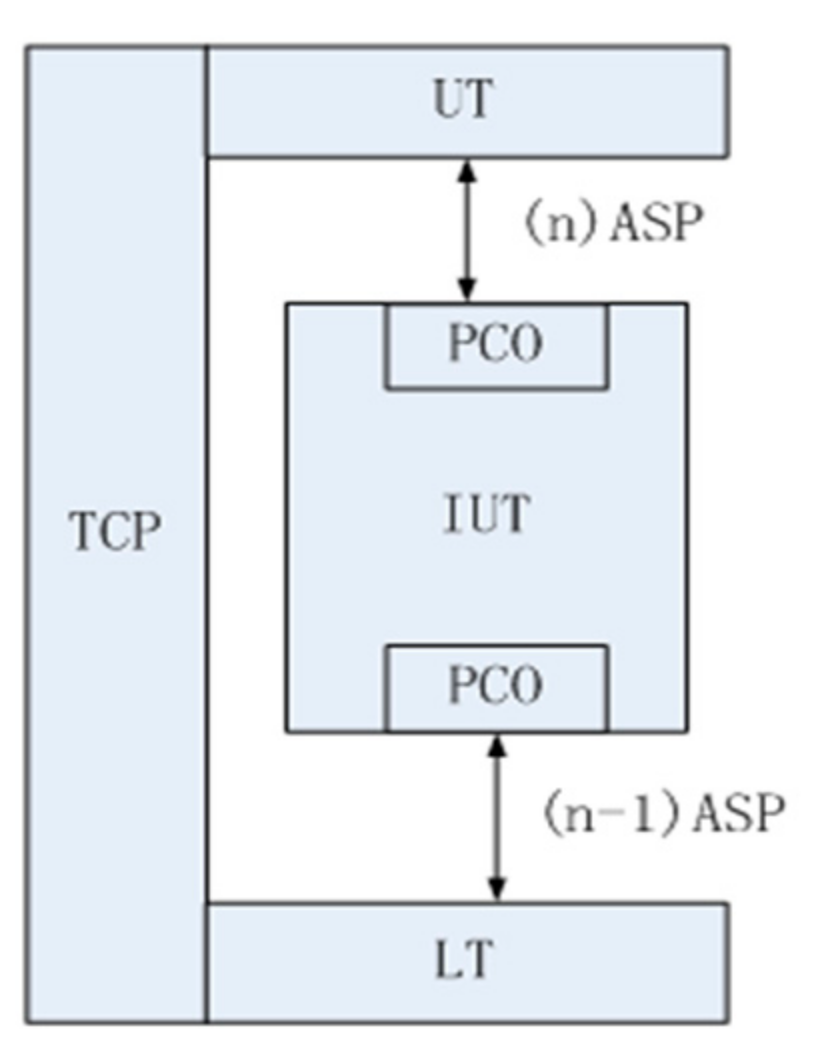
The local test method is the most common method to use, as shown in
Figure 6 [
52]. In this method, UT is the upper tester, LT is the lower tester, PCO is the point of control and observation, TCP (test coordinate procedure) is used to coordinate the operation of the UT and LT, IUT is the tested system (implementation under test). The test system carries out input incentives to IUT by PCO and observes output responses of IUT. Then the system makes the test determine according to the protocol description. UT and LT observe the behavior of IUT at the top and bottom interface of IUT by exchanging test events. In this method, LT, UT and IUT are in the same machine, and tests do not need support from the underlying communication systems; thus, the test is relatively easy to implement.
8. A Case Study
We apply the smart contract verification part of SCE to verify a specific smart contract. The process of smart contract verification consists of five parts: contract modeling, contract model transformation, contract verification, automatic contract code generation, and conformance testing. In this case study, we first establish an abstract Event-B model [
53] of the solidity contract called safe remote purchase, then we refine the abstract model to a more precise model to verify its properties. The key to the modeling process is translation rules from solidity to Event-B, and we can realize the translator tool to automatically generate codes. Below, we give a detailed introduction of formal verification of solidity contracts in Event-B.
Safe Remote Purchase
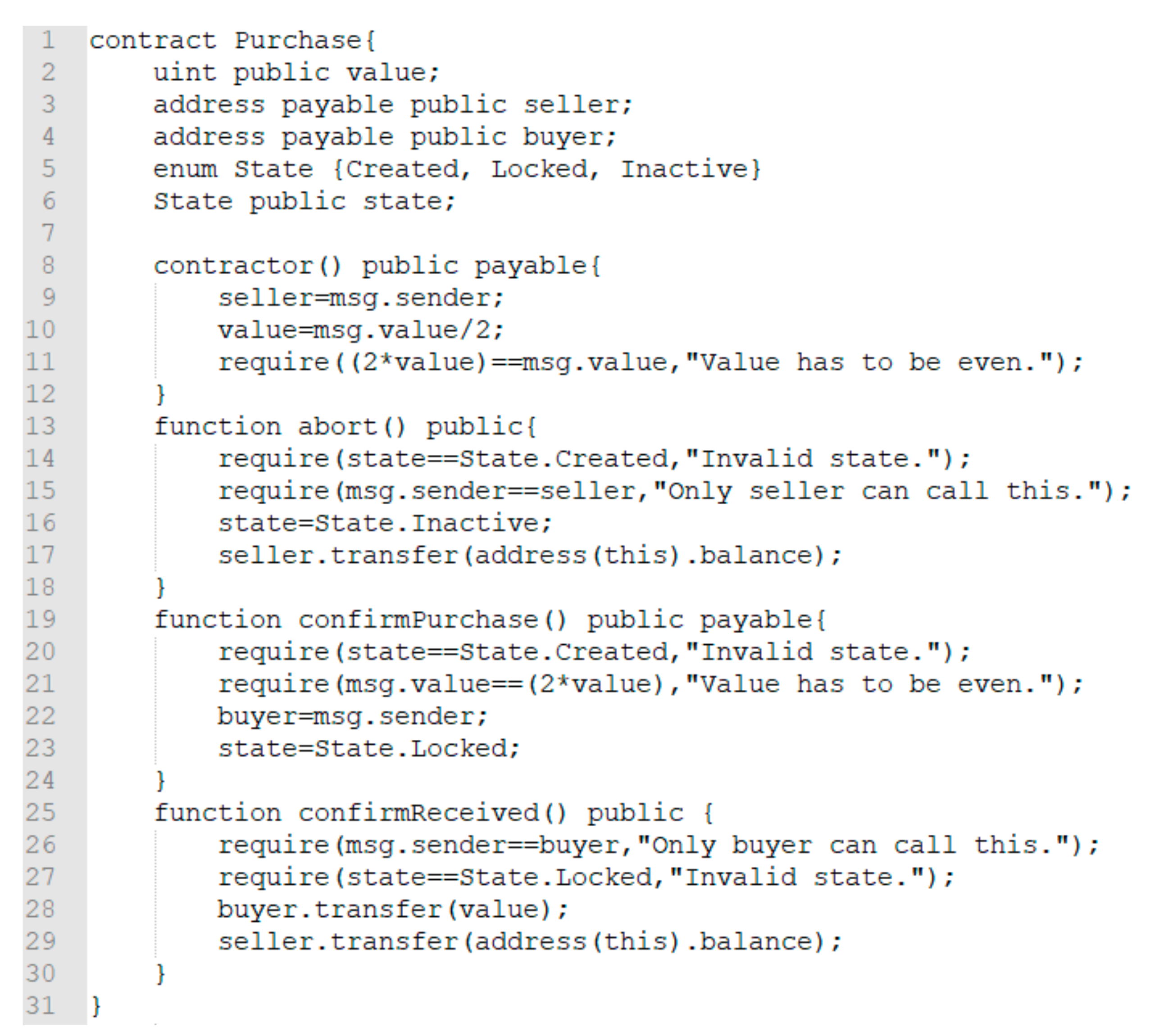
We take a concrete smart contract called “safe remote purchase” as an example, whose source code is on the solidity official website [
54]. Its source codes are shown in
Figure 7, which was simplified by removing some useless information in our verification process. Its operating mechanism is applicable to online shopping by the smart contract. To ensure the transaction go smoothly, it divides the entire process into three states, corresponding to three events:
abort (): When the merchant thinks that the pricing needs to be modified, it is called to withdraw funds and redeploy the contract;
confirmPurchase (): This is left to the buyer to confirm the order, at that time, contract status is set to locked (locked status), which can only be unlocked after the buyer receives the goods;
confirmReceived (): This occurs after the buyer confirms the receipt, then he unlocks the account and completes the transaction transfer.
Event-B consists of two components: contexts and machines. A context is made of constants linked to some properties that define axioms and sets that define data types. A machine has variables associated with invariants and events. An event consists of a guard and an action. The guard denotes the enabling condition of the event, and the action denotes the way the event modifies the state. Key features of Event-B are the use of set theory as a modeling notation and the use of mathematical proof to verify consistency between refinement levels, which permit to verify the validity of the properties of the smart contract, is guaranteed by mathematical proof obligations.
We should first establish a semantical map between solidity contracts and Event-B language.
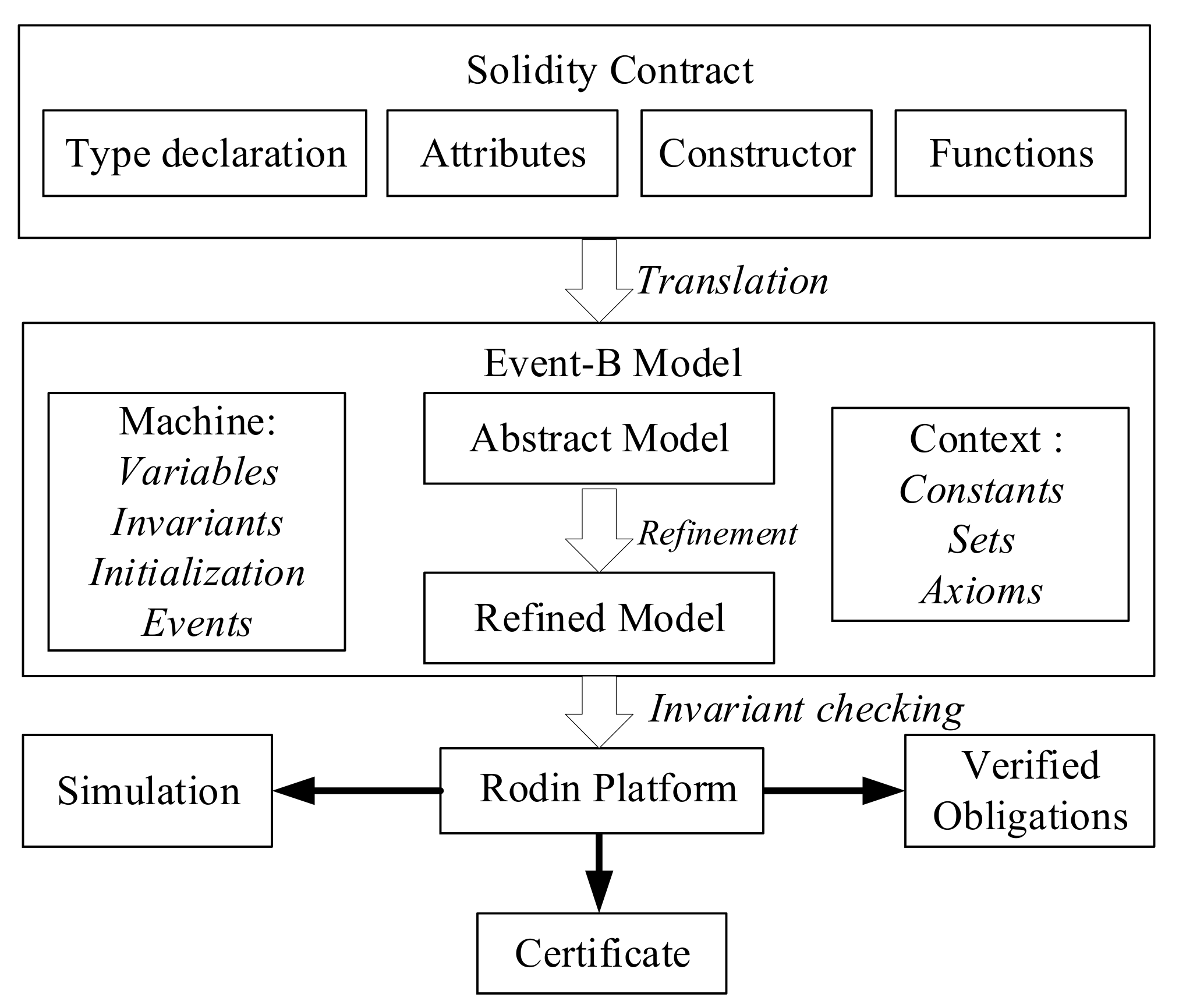
Figure 8 outlines the framework to analyze and formally verify solidity contracts using the Event-B method [
39]. Once we have the solidity contract translated to the Event-B model, its correctness is established by proof obligations for the invariants, where each event, including the initialization event, should preserve these invariants. Event-B guards are used to define preconditions that should hold before the event can be executed. The guard and the action of an event define a relation between variables before the event holds and after. Properties related to the correct operations of the solidity contract are modeled as Event-B invariants. Rodin platform [
55] is used to check these invariants and validate the correct functionality of events using simulation, as shown in
Figure 8. Once the contract’s properties are verified, we can obtain a certificate for our smart contracts and deploy them. If one of the proof obligations cannot be verified, it will help us locate the problem which originates in the failure to prove the required invariants.
Based on the translation rules given in [
39], we have modeled a data entity in
Table 1, where we define a set called “ADDRESS” to be used for the source of unique identifiers for different addresses. Moreover, the “state” set is defined to show three different states of the smart contract, which contains “created”, “locked” and “inactive”. “seller1” represents the seller determined by the constructor function in the solidity contract, which owns the balance “seller1account”. “value” represents the price of the merchandise, “this” represents the account of the solidity contract, and “buyer1” the initial value of the variable buyer in the Event-B machine, which owns the balance “buyer1account”. Moreover, from
@axm1 to
@axm11, we have defined the relations between these constants and sets by means of axioms. For example,
@axm7 states that the balance of the buyer should be sufficient for the payment.
In the event abort, as shown in
Table 2, we define a parameter “msg_sender”, which represents any user contract who invokes this function. Here we define three guards, where
@grd1 requires the state of the contract to be created.
@grd2 guarantees the property of
msg_sender, and
@grd3 requires that only the seller can invoke this function. Then we define two actions:
@act1 means that the seller can abort the transaction and get its money back, and
@act2 means the state of the contract will be inactive after having invoked this function.
In the event confirmPurchase, as shown in
Table 3, we have defined again “msg_sender” and “msg_value” as the parameters, where the “msg_value” represents the amount to transfer. Then we have defined six guards to restrain the parameters and the variables. For example,
@grd1 requires the state of the contract to be created, and
@grd2 requires that the value to transfer should be twice the constant value. Here we have defined three actions:
@act1 states that the user contract should be a buyer,
@act2 states that the buyer should pay deposits and the contract account will get the deposits, and
@act3 states that the state of the contract will be locked after having confirmed the purchase.
Finally, we have modeled the event “confirmReceive,” as shown in
Table 4, of which the guard and the parameter are similar to before. Here we have defined two actions: @act1 states that the buyer can recover half of the deposit and the seller can get all the balance of the smart contract, and @act2 states that the state of the contract will be inactive.
When the smart contract is deployed, there are some basic properties that should be satisfied to maintain the operation of the contract. These properties are modeled as Event-B invariants and must hold for the contract to be correct. Each generates a number of proof obligations in Rodin. These proof obligations are proven one by one, some are automatically proved using the tool, and some need to be proven interactively. In the following, we state four important properties for illustration purposes.
The first property states that the balance of each account should be strictly positive or zero.
Prop. 1balance of ∈ address_tem→ℕ
The next property states that the balance of the contract account should be thrice the value when the state of the contract is locked.
Prop. 2state = Locked ⇒ balance of (this) = 3* value
A similar property states that the balance of the contract account should be the value when the state of the contract is created.
Prop. 3state = Created ⇒ balance of (this) = value
The last property states that the balance of the contract account should be zero when the state of the contract is inactive.
Prop. 4state = Inactivebalance of (this) = 0
These properties are all defined as invariants in the Rodin platform, and the tool generates proof obligations, which should be successfully proved using Event-B proof control.
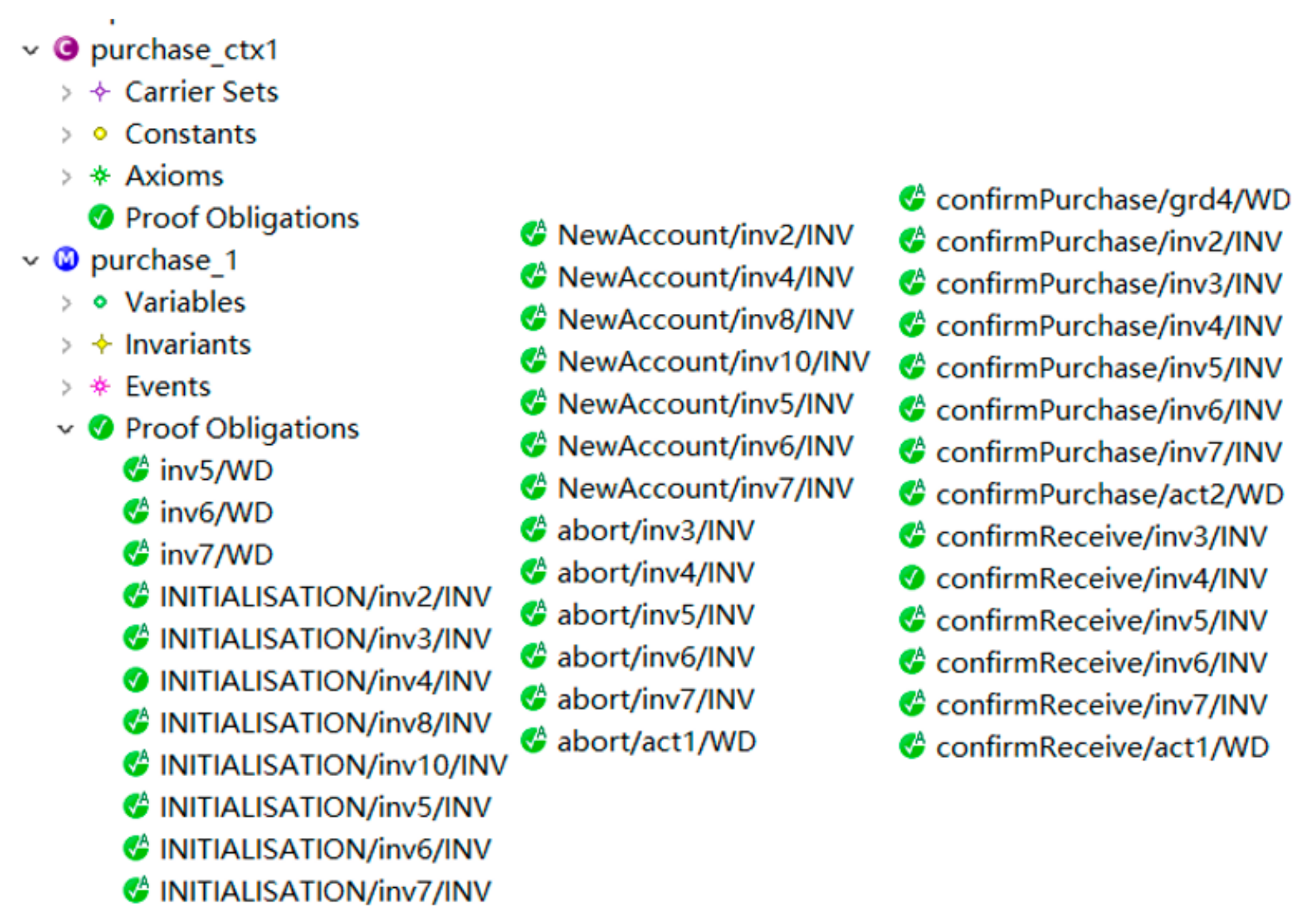
Figure 9 shows all proof obligations of this Event-B model, which are all verified indicated with a green checkmark.
In conclusion, we have used Event-B languages to formally describe the solidity contract, which is the first step of the smart contracts verification process in
Figure 3. Then we propose several basic properties that should be satisfied by the solidity contracts and model them using the Event-B invariants. Rodin generates proof obligations, which are all proved; the smart contracts are therefore verified strictly. If more complex properties need to be verified, we can iteratively use contract model transformation in
Section 6.2. For Event-B, it is to continuously refine the model, which is too abstract to include concrete properties of the solidity contract. Moreover, we found that Event-B is more suitable to detect logical vulnerability, but it is not convenient to find code-level vulnerabilities such as integer overflow. It is not possible to use one method to verify all the properties and detect all the vulnerabilities, we need to iteratively verify the model by applying different formal methods and construct different formal models before generating the contract code, and running verification can monitor the running program and react to the running errors.
9. Conclusions
This paper summarizes the features of smart contracts completely and proposes the concept and framework of smart contract engineering (SCE) to meet the requirements of large-scale smart contract software production and verification in the future. The roadmap of formal methods for smart contracts is described in detail, including its main steps: from modeling to model transformation, to verification, to automatic code generation, and to conformance testing. The corresponding methods are given to meet smart contract features. We took the verification process of a solidity contract in Event-B for example; the result shows that formal methods can be applied to verify critical properties in the value transfer process, which can mitigate the huge economic losses caused by the smart contract vulnerabilities. We have reasons to believe that the SCE method will be widely used for the design and development of large-scale smart contracts.
In future work, we will improve the combination of smart contracts and computational law by designing a legal-oriented smart contract language, which can strengthen the legal supervision of smart contracts. Moreover, we also plan to develop a tool that automatically detects the conformance between the contract code and models, including the natural language context. It will speed up the extension and development of smart contract engineering.