Abstract
For almost one decade, the academic community has been working in the design and analysis of new lightweight primitives. This cryptography development aims to provide solutions tailored for resource-constrained devices. The U.S. National Institute of Standards and Technology (NIST) started an open process to create a Lightweight Cryptography Standardization portfolio. As a part of the process, the candidates must demonstrate their suitability for hardware implementation. Cost and performance are two of the criteria to be evaluated. In this work, we present the analysis of costs and performance in hardware implementations over five NIST LWC Round 2 candidates, COMET, ESTATE-AES/Gift, LOCUS, LOTUS, and Oribatida. Each candidate’s implementation was adapted to the Hardware API for Lightweight Cryptography for fair benchmarking of hardware cores. The results were generated for Xilinx Artix-7 xc7a12tcsg325-3. The results indicate that it is feasible to achieve the reduction of each solution below 2000 LUTs and 2000 slices where some of them (the variants of ESTATE-AES/Gift) are below 850 LUTs and 600 FF when they are included in the LWC CryptoCore.
1. Introduction
Every day, more communication scenarios use devices with hardware-constrained conditions. These communication scenarios include tasks designed for applications such as RFID tags, sensor nodes networks, healthcare, the Internet of Things (IoT), and Cyber-Physical Systems. Typically, these devices are present in wireless environments, where the sensible nature of the type of data exchanged among them demands the implementation of security services such as confidentiality, integrity, and authentication. Being unfeasible using public-key cryptography due to these hardware restrictions, the efficient and high-performance way to provide the listed services is by implementing an algorithm of authenticated encryption with associated data (AEAD), which reduces resources and eliminates potential security vulnerabilities. However, the standard cryptographic algorithms to provide these services are not suitable for these devices due to the same hardware restrictions.
About these hardware restrictions, there are several drawbacks that should be overcome regarding the area usage and power consumption, mainly. Compared to the elements that typical wired computer networks have, in wireless environments, the availability of a permanent power source is not possible. Each wireless device is fed by a battery (or another power source) that has a limited amount of stored energy, thus reducing its duty cycle to a limited amount of time. Besides, these devices are used in heterogeneous places where the area is reduced, thus their footprint should be minimum. For instance, there are very limited power and area resources in RFID environments, limiting the use of traditional cryptographic primitives. The main goal is that the battery (or the converter that holds the received energy for passive RFID tags) should maintain working the entire device as long time as possible, i.e., the battery or the power source should last for a reasonable time to allow the device performing its duties before being idle or turned off. Additionally, other tasks (such as the data exchange) would have a higher priority to use the available energy. Similar issues are also considered for the area because other tasks may have a higher priority to use resources (storage if available and data exchange), leaving few area resources remaining for cryptographic primitives. Similar constraints are presented in the other devices mentioned above (IoT, wireless sensor networks, etc.)
The main goal is that a cryptographic primitive may use the lowest possible hardware resources with low power consumption without adding more hardware complexity in terms of resources dedicated to other critical tasks in the device where sensible information is generated.
In August 2018, the U.S. National Institute of Standards and Technology (NIST) initiated a process to solicit nominations from any interested party for candidate algorithms to be considered for lightweight cryptographic (LWC) standards suitable for use in constrained environments, where the performance of current NIST cryptographic standards exceeds the hardware limits of the devices to be protected. Fifty-six candidates qualified for Round 1. For Round 2, 32 candidates were selected.
As a part of the evaluation criteria for the NIST LWC competition, each candidate is evaluated in several aspects, including security evaluation of the algorithms against known attacks, side-channel and fault attack resistances, cost, performance, third-party analysis, and suitability for hardware and software implementations. The Hardware API for Lightweight Cryptography by George Mason University (GMU LWC) was established as the interface to perform the hardware evaluation process. This work aims to contribute to the analysis of five candidates of NIST LWC in terms of the established criteria of cost, performance, and suitability for hardware implementations. In this way, these extensive evaluation processes open for anyone who wants to participate guarantee that the proposed cryptographic solutions are reliable for their use in constrained hardware environments, without degrading the main security features that a typical cryptographic primitive should hold, i.e., high-security features with a low footprint.
To be part of these extensive evaluation processes, in this paper, we present the hardware implementation for five NIST LWC candidates: COMET [1], ESTATE [2], LOCUS [3], LOTUS [3], and Oribatida [4]. All of these hardware implementations were done in the FPGA Xilinx Artix-7 xc7a12tcsg325-3, with area restrictions, where we present a medium-scale study of these five NIST LWC Round 2 candidates. The number of slices, FFs, LUTs, frequency, and throughput are the main aspects to be presented in this manuscript to determine which is the best option, how they were adapted to LWC conditions, the different datapath-size implemented for some of these candidates, and their pros and cons. We performed extensive behavioral benchmarking that guaranteed their correctness. Our implementations will be open-source available.
The contributions of this work can be summarize as: We provide the first implementations of five NIST LWC candidates compliant with the GMU LWC interface. All our designs hold the restrictions on resources utilization in the official FPGA benchmark. Our implementation compared with the ones published in the unique existing work [5] are smaller as we present implementations with small datapaths, 32 and 8 bits.
The organization of this paper is as follows. In Section 2, we provide a background where we talk about the Encrypted Authentication and the GMU LWC interface. In Section 3, we introduce each candidate selected and we present their implementation, summarizing their critical hardware-oriented design decisions. Then, a comprehensive discussion about the resources and performance of the candidates is presented in Section 4. Finally, the conclusions of the paper are in Section 5.
2. Background
2.1. Authenticated Encryption with Associated Data
Privacy and authentications are requirements to establish secure communication. Privacy means that only authorized entities can understand the message. Authentication guarantees that the entity sending a message is the expected by using a secret key previously agreed, and ensures data integrity distinguishing any change in the message.
Block ciphers are cryptographic primitives used to provide privacy, and, when they are used in a mode of operation, they can provide privacy and authentication, as well. NIST has recommended Electronic Codebook (ECB), Cipher Block Chaining (CBC), Cipher Feedback (CFB), Output Feedback (OFB), and Counter (CTR) as secure modes for encryption [6]. On the other hand, MESSAGE AUTHENTICATION CODES (MACs) are modes of operations that provide authentication and data integrity. Two widely known MACs are CBC-MAC [7] and PMAC [8].
Authenticated encryption algorithms offer privacy, authentications, and data integrity. The simple way to construct an AE is by implementing an Online Encryption (OE) mode and a MAC independently.
Sometimes, the messages could include supplemental information that cannot be encrypted but must be authenticated; this supplemental information is called associated data. Some examples of associated data are the header of a network packet, which has to remain as plaintext, but its integrity should be preserved. A typical example is the TCP/IP protocol, where there are several flags that indicate how the rest of the content in the packet should be decoded and presented. To provide authentication to these kinds of data, an extended algorithm of authenticated encryption was proposed to handle associated data; it is called Authenticated Encryption with Associated Data (AEAD).
In recent years, AEAD algorithms have received particular attention after the call submissions of Competition for Authenticated Encryption: Security, Applicability, and Robustness (CAESAR) and the NIST LWC. According to NIST LWC, an AEAD algorithm is defined by two operations: authenticated encryption and verified decryption. Both operations need to input a public message number (nonce), a secret key K, and an associated data . Particularly for encryption, the plaintext is an input, and the outputs are , , ciphertext , and tag T. In authenticated decryption, the specific inputs are and T and the outputs are the and the tag verification. A local is computed and checked if it is equal to the tag provided in the input, and releases the messages if and only if . For authenticated encryption and authenticated decryption, , , and can be zero-length.
2.2. GMU LWC Interface
The Hardware API for Lightweight Cryptography (LWC) was proposed [9] to guarantee the fairness of benchmarking and compatibility among implementations of the same algorithm by different designers. The interface defines two types of data, secret and public. The key input is the unique secret data; the public data are message blocks, AD blocks, ciphertext blocks, and verification Tag. For the outputs, they are all public, ciphertext, decrypted message, and the tag.
There are three possible sizes for the input/output buses, 8, 16, and 32 bits. This small size-bus allows the implementation of the final AEAD core in low-end FPGA devices and is compatible with more common processors and micro-controllers used in IoT technology. The input/output data are handled by preprocessing and postprocessing components that define a communication protocol to communicate with the developed cores. All signal names related to the key have sdi as a prefix, the signals in the public bus have the prefix pdi, and the name signals in the output bus use the prefix do.
The API has a component called CryptoCore. CryptoCore is the starting point for hardware designers; in this part, the cryptographic implementation is integrated into the LWC API. The block diagram of the LWC core is shown in Figure 1. The block two-pass FIFO and its input/output signals (denoted as , , , , , , , , , , , and ), as well as and signals, are optional as they are used only when the implemented cipher is two passes, i.e., when the AEAD authenticates the AD and the message before encrypts. The communication protocol organizes the input blocks as segments; the valid segments are shown in Table 1. GMU LWC Interface also includes segments for hash functions; however, this functionality is not used for the present implementations.
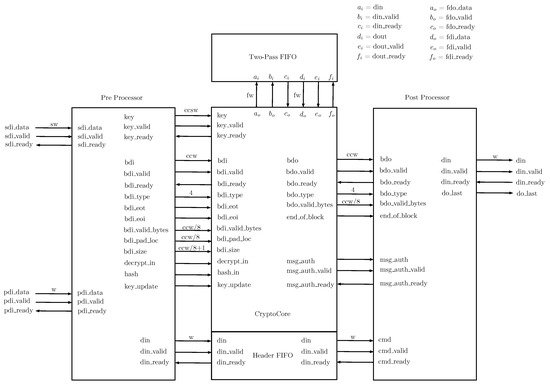
Figure 1.
Top-level block diagram of LWC core (based on the scheme found at [9]). sw, external key width; w, external data width; ccsw, internal key width; ccw, internal data width.

Table 1.
Valid segments in LWC API communication protocol.
The communication protocol does not accept all the possible combinations of segments; in general, all ciphers receive the sequence of the segments as , , as input and gives as output , T for encryption. In decryption, the input is , , T, and the output is . For double pass algorithms, it is necessary to decrypt the message before performing the authentication, so the tag T needs to be received before . We have done some modifications to allow the LWC interface to handle the order of segments as , , T, for decryption.
When the last block of AD or message is incomplete, it is necessary to pad it. For each authenticated cipher or hash function, it is necessary to define their own padding rule. To know when a block does or does not need padding, the LWC interface provides specific signals bdi_valid_bytes, bdi_pad_loc and bdi_size. Similarly, for the output, we need to indicate to the LWC interface if the last block of CT or PT is incomplete and for that it provides the signal .
3. Implemented Authenticated Ciphers
This section summarizes each candidate, and then describes and analyzes their respective hardware implementation.
3.1. Preliminaries
Along this manuscript, we refer the input message as message blocks or PT blocks. When the input is an encrypted message, we use encrypted message blocks or CT blocks and AD blocks for associated data blocks. The term Npub and nonce are equivalent in our descriptions. All the n-bit binary strings are considered as elements of the field and the addition is defined as a logical XOR denoted as ⊕, and the product as polynomial multiplication modulo and irreducible polynomial of degree n. The circular shift bit-wise operation is denoted as ⋙ or ⋘ depending of the direction.
3.2. Hardware Design Principles
For the next sections of this manuscript, we refer as CryptoCore to the particular implementation of a candidate algorithm. The register-transfer level implementation design abstraction is used for all the implementations; our designs use only synchronous registers and multiplexers. All the CryptoCore implementations were adapted to the Hardware API LWC. The inputs and outputs are compatible with the API. For each implementation in CryptoCore, a 32-bit datapath is presented, but some also have an 8-bit datapath.
3.3. LOTUS and LOCUS
LOTUS and LOCUS are authenticated ciphers that provide Release Unverified Plaintext (RUP) security. Both were presented in the NIST competition [3] and then an extended version with detailed security analysis was published by Chakraborti et al. [10]. LOTUS and LOCUS are a construction based on a tweakable block cipher, in this case tweGift-64.
The main goal of its design is to provide high-performance capability and suitability for low-end and memory-constrained devices. The high performance can be reached with parallel implementations. The structure followed by LOTUS and LOCUS is based on OTR [11] and OCB [8]. However, two in a row block ciphers are used instead of just one. Such structures allow constructing a parallel authenticated cipher.
For both AEAD, the initialization phase, the Associated Data processing (ADP), and the tag generation (TAG) are the same. Figure 2 shows the graphical representation for ADP and TAG. ADP is based on a variant of the hash layer of parallelizable MAC (PMAC), for which it is possible to make the parallelization. TAG aims to provide RUP security, and thus the checksum of all intermediate outputs and the output of each AD block is used to calculate the checksum.
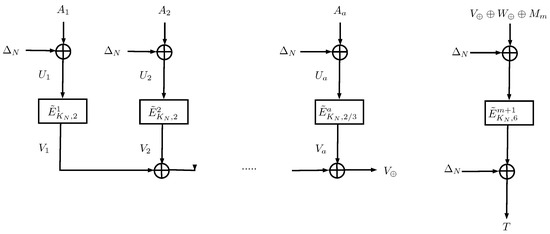
Figure 2.
Block diagram for associated data processing and Tag generation for LOCUS and LOTUS.
Both LOTUS-AEAD and LOCUS-AEAD in encryption mode defines as inputs an encryption key , a nonce , an associated data , and a message ; as outputs the ciphertext ; and a tag . With fixed , .
The dependent keys and tweak schedules are an integral part of these AEAD modes. The key and tweak change for each block cipher call. During the initialization phase, is ciphered with K to obtain T; K is XORed with N for generating the nonce-dependent key ; and the nonce-dependent masking key is computed by cipher Y with . The dependent keys are computed by -, , where ; the multiplication is reduced using the irreducible polynomial . The tweak changes depending on the type of data that is processing and is defined where .
The CrytoCore for LOTUS/LOCUS hardware implementation of 32-bit datapath is shown in Figure 3. The main components are a tweGift-64, registers, and multiplexers. The register are , , , , and . stores the nonce-dependent; stores the checksum of the output for processed AD blocks and the intermediate outputs of the di-block; and stores every block message XORed with , which is because, in the bus bdi, the message is no longer available when the output of the last cipher is. The control is not displayed, but it is implemented by using a Finite State Machine (FSM) with 11 states.
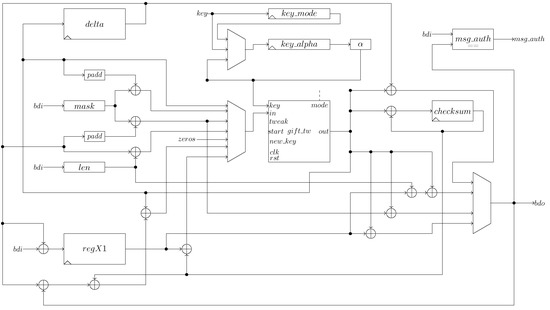
Figure 3.
LOTUS/LOCUS hardware architecture.
The key schedule is the most expensive part of the mode, in area terms. and are registers of 128-bit length. The first one stores K, since it can be used to encrypt several messages. It needs four clock cycles to be loaded entirely and rotated with 32-bit. implements the dependent keys when there is a new key, and when the key is ready, the register is loaded by 32-bit each clock cycle, as same as .
In addition, is updated with the value of the nonce-dependent key during the initialization phase; later, it is updated with each dependent key, i.e., the result of the -. This task is done in one clock cycle because the result is loaded in parallel. Finally, where there is a new message to process, and there is no new key, the register is updated with the content of , and a parallel charge also performs it.
3.4. LOTUS
Using a block cipher only in encryption mode, this kind of constructions are known as inverse free. Particularly, LOTUS was inspired by OTR [11]; data are parsed into 2n-bit di-blocks. Figure 4 presents the block diagram of LOTUS mode, similar to a two-round Feistel, but with two successive block ciphers in both layers.
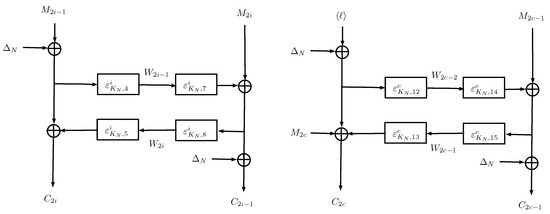
Figure 4.
Block diagram of LOTUS mode for encryption.
The tweakable block cipher is instantiated four times for each two message blocks. A new dependent key is calculated for di-block, i.e., the same key for four block ciphers. However, the tweak changes depending on the layer: the upper layer tweak is 0100, and the bottom layer one is 1101. For the last di-blocks, the tweaks are 1100 and 1101, respectively.
3.5. LOCUS
LOCUS is published along with LOTUS in [3,12]. It also uses tweGift-64 as an underlying block cipher, but LOCUS requires the inverse function of tweGift-64. Figure 5 presents the block diagram of LOCUS mode. In general, LOCUS in based on OCB.
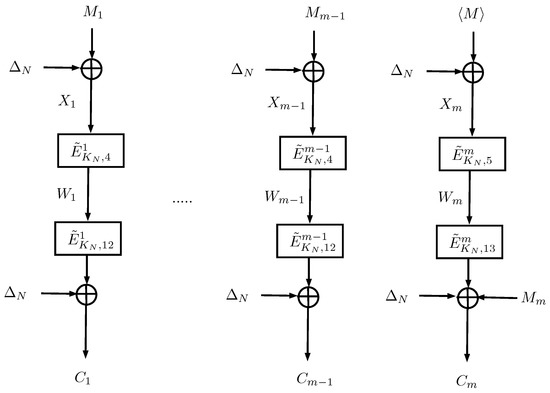
Figure 5.
Block diagram of LOCUS mode for encryption.
The message is parsed into n-bit blocks. For each block, a mask with the nonce-dependent is applied, then it is encrypted by two successive tweGift-64, and masked again. Similar to LOTUS, the intermediate outputs are used for calculating the checksum. For the last message block, the input is the message length, and the output is XORed with the final message block. The key is updated by before each block processing and tweak = 4 and tweak = 5 for non-final and final blocks, respectively.
Brief Description of tweGift-64
Gift is a lightweight block cipher introduced by Banik et al. [13]. It is a Substitution-Permutation- Network (SPN) with the option to handle 64-bit or 128-bit as block length. The substitution layer is performed using a 4-bit S-box, the permutation layer is bit-wise, and a key addition phase is performed at the end of each round. The key schedule is linear, i.e., it is based on shift registers. The tweaked version of Gift called tweGift was presented by Chakraborti et al. [12], where a 4-bit tweak is injected in Gift and AES in order to enhance the output space of the ciphers paying a small cost.
The datapath designed for tweGift-64 is shown in Figure 6. A serial implementation was done with a 32-bit datapath to make the tweGift-64 core cheap in area. However, although the design is focused toward low-end devices, we add some extra registers that allow efficient processing of the tweGift-64 core. The core allows simultaneous entry of the key and the message.
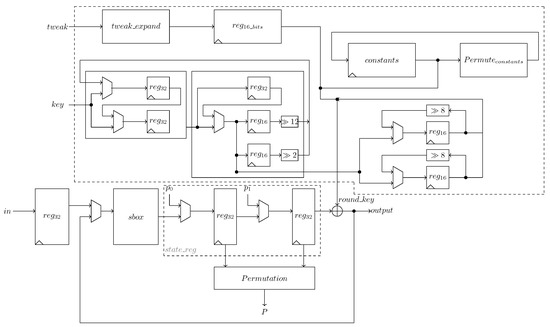
Figure 6.
tweGift-64 design implementation, for a 32-bit datapath.
For encryption, the 32-bit input is divided into chops of 4-bit, and an S-box is applied to each chop. Its output is loaded into the status register of 64-bit implemented as two registers of 32-bit in a row. Then, when both registers are loaded, the control commands parallel loading of the value resulting from the permutation; then, the information is shifted, and the output of the register is XORed with the corresponding round key. This process is done for the 28 rounds stated in the cipher algorithm.
The core has two inputs to calculate the round key, a 64-bit and a 4-bit . The input is stored in the register. The is extracted from the 32 least significant bits of the K. In particular, our design has a copy of these 32 bits; it allows that, after the first block output, the core can admit a new M and K.
The tweak is connected to component, and its output is stored in a shift register of 16-bit length. performs the function of and tweak using a linear code described below:
Finally, Gift algorithm uses round constants calculated by an affine LFSR.
3.6. ESTATE
ESTATE is a deterministic authenticated encryption (Mac-then-encrypt AE mode) constructed using tweGift-128 and tweAES-128 as underling tweakable block ciphers. It was presented in the NIST competition in the specification document [14] and then published with security proofs by Chakraborti et al. [2]. ESTATE follows the design of Sundae cipher [15]. It combines the MAC algorithm based on classic mode cipher block chaining (CBC) and encryption algorithm based on output feedback (OFB). The authentication tag T is generated by FOCB receiving as input the AD and M blocks; then, the generated tag is used as IV of OFB mode to encrypt the message. T depends on all the message blocks; we have to go through all message blocks to authenticate the message and store each message block in external memory for the encryption processing. The external memory is implemented as FIFO by the LWC interface, and it is external to the CryptoCore design; hence, it does not add additional cost in area.
It is important to note the simplicity of the ESTATE algorithm: all the tweakable block ciphers calls use the same key, and it does not include multiplication by 2 or as Sundae, which saves two inputs to the multiplexer in the input of the tweakable block cipher. The tweak is a 4-bit value as in LOCUS and LOTUS. When the nonce is processed and there are no message and AD blocks, tweak = 8; otherwise, tweak = 1. For the AD and message blocks, tweak = 0, except for the last blocks. Besides the padding rule, if the block is complete, tweak = 2, otherwise tweak = 3. For the last message block, tweak = 4 if it is complete or tweak = 0 if it is not. For the special case when the message is empty, the tweak to process the last message change to tweak = 4 when it is complete and tweak = 5 when it is incomplete. Figure 7 illustrates the operations performed by ESTATE when there are AD blocks and M blocks.
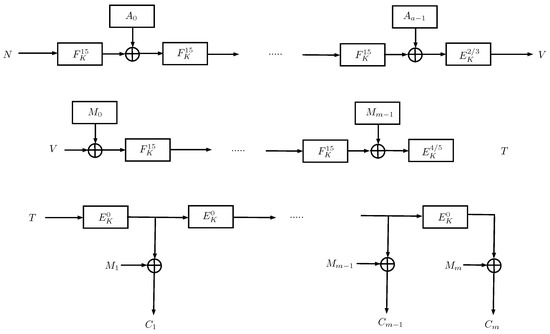
Figure 7.
ESTATE deterministic authenticated cipher.
sESTATE is a variant of ESTATE that reduces the latency of the mode; it uses a round-reduced variant of the tweakable block cipher to process the AD blocks except the last. In this study, we only implement ESTATE since sESTATE uses almost the same area, and latency reduction is not part of the scope of this article, where we examine the area of different NIST LWC Round 2 candidates.
We implement ESTATE using tweAES-128 and tweGift-128. We present two architectures using 32-bit and 8-bit datapaths for both underlying tweakable block ciphers. In Figure 8, we show the implemented architecture for ESTATE.
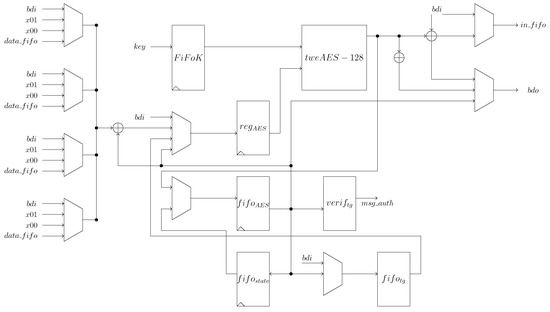
Figure 8.
Architecture for ESTATE.
In this case, the tweAES-128 block cipher was implemented with 32-bit datapath. Because its output must be fed back, a FIFO to store the output is needed (labeled as ). The padding layer is implemented using four multiplexers with three 8-bit inputs, where the first one is the input value bdi from LWC interface, the second one is the padding byte 01, and the last one is byte 00. When all the input values in bdi are valid, the four multiplexers select the first value. For instance, if only the first byte in bdi is valid, only the first multiplexer selects its first input, the second selects the padding byte 01, and the other two selects 00. After padding, the inputs are XORed to the feedback from tweAES-128. As the authentication tag is computed before start to encrypt, the component stores the tag and gives it as output after all the encrypted message is computed.
Changes for Decryption: For authenticated decryption, it is necessary to decrypt the message first and then compute the authentication tag. We modify the order of segments to the following order: , , T, /. For decryption, the first step is to process AD blocks and store the value in in the register . Just after the last AD block is loaded, the tag for verification is loaded and stored in . With the tag stored in , the message inputs from bdi port are decrypted, and the output to the bdo port is taken as valid decrypted message, while, in parallel, all the outputs blocks are also stored in the external FIFO and later they are used to compute the authentication tag. The verification process is done by the component , where such component is a comparator. It receives as inputs the tag store in and the output from tweAES-128. The control unit is a finite state machine. It generates all the control bits needed by the components in the architecture.
The four implementations of ESTATE reported in this work use the same architecture, and the only change is the AES core, where it could be tweAES-128 with 8-bit datapath or tweGift-128 with either 8-bit or 32-bit datapath.
Brief Description of AES
The Advanced Encryption Standard (AES) [16] is the standard for encryption defined by NIST in 2001. Its original name is Rijndael. It is a SPN computed in rounds, where each round includes four transformations: SubstitutionBytes (S-box), ShiftRows, MixColumns, and AddRoundKey. A key schedule function generates the round keys. ESTATE uses the tweaked version of AES with a key length of 128-bit, thus rounds are executed; hence, ten round keys are also computed. Our implementation of tweAES-128 with 8-bit datapath is based on the implementation of AES presented in [17]. Such design needs a permuted input, and it gives a permuted output, which was done to save some multiplexers as the design was implemented for ASIC technology.
FPGAs multiplexes, from two to four inputs, can be implemented using only one LUT per byte, so we modified the original architecture to avoid the permuted input and output; this change in FPGAs is for free. For the 32-bit datapath architecture, our design is based on the architecture presented in [18], which uses Tboxes to avoid the matrix multiplication of MixColums, by combining SubstitutionBytes and MixColumns in a large table. As we attempt to avoid BRAMs, we compute TBoxes using four Sboxes (implemented using LUTs) and the matrix multiplication for MixColumns.
Below, we explain the latency of our implementations of tweAES and tweGift-128. All the implementations computes the round keys on-the-fly and have registers to store the key or the actual value in the round. Such registers are called key state and state, respectively.
- tweAES-8: The version of tweAES with 8-bit datapath uses eight clock cycles to compute the AddRoundKey and SubstitutionBytes, ShiftRows takes one clock cycle, and finally MixColums is performed in four clock cycles. Thus, the latency per round is 21 clock cycles, and ten rounds take 210 clock cycles and 16 additional clock cycles to output the encrypted block, giving a total latency of 226 clock cycles. This architecture uses only one Sbox. As the last round does not include the MixColumns transformation, to maintain the uniformity of the design, the state register is disabled, avoiding compute the MixColums in the 10-th round.
- tweAES-32: The computation of the round is column-wise, so each round takes four clock cycles as the ShiftRows and MixColumns are performed in parallel, only selecting the correct bytes from the state to compute the MixColums. Four additional clock cycles are used to give the output. Thus, the total latency of tweAES is 44 clock cycles. This implementation uses four Sboxes.
- tweGift-128: Both implementations, 8-bit datapath and 32-bit datapath, use the same architecture; the only changes are that for 32 bits it uses eight Sboxes (4-bit Sbox) while for 8 bits only two Sboxes are used. The permutation step takes one clock cycle for both cases and the computation of the round is 5 and 17 clock cycles for 32-bit datapath and 8-bit datapath, respectively. Gift-128 executes 40 rounds in 32 bits, so the total latency is 204 clock cycles, and for 8 bits it is 696 clock cycles.
For tweAES, the tweak is expanded from four bits to eight bits using the same linear code as in tweGift-64; in the case of tweAES the tweak is injected, making a XOR with the least significant bit of each byte in the top two rows of the state matrix. The injection of the tweak is performed every two rounds.
For the tweGift-128, the tweak is expanded using the same linear code to a 32-bit value; then, it is XORed to the bits in position for of the state register. Such operation is applied every five rounds.
3.7. COMET
COMET was presented by Shay et al. [1] as an authenticated encryption algorithm that combines Counter encryption mode and Beetle authenticated cipher [19] using AES as underlying block cipher. Its basic operations are and , where is used to update the AES key while combines the input AD or message blocks with feedback from the AES cipher and generates the ciphertext blocks. receives as input a 128-bit string and performs multiplication by 2 of the low half part of the input key ; as , the multiplication is reduced using the irreducible polynomial . The function takes as input two 128-bit strings and outputs two 128-bit strings: one is taken as the input of the block cipher, and the other is taken as ciphertext if required. Internally performs a shuffle of four 32-bit words of the feedback input, first X is split as and then shuffle as . The value is XORed to the padded input blocks and fed to the block cipher. The input is truncated to the ciphertext generation’s input block length and XORed to the value. The key is XORed with 6-bit constant words called control words. The first is , and it is the XORed key just after the nonce’s encryption. If the last AD block is incomplete, then the key is XORed with . Before the first message block is processed, the key is XORed with the value , and then, if the last message block is incomplete, the key is XORed with . Finally, when the tag is computed, the key is XORed with . In Figure 9, COMET algorithm is illustrated.
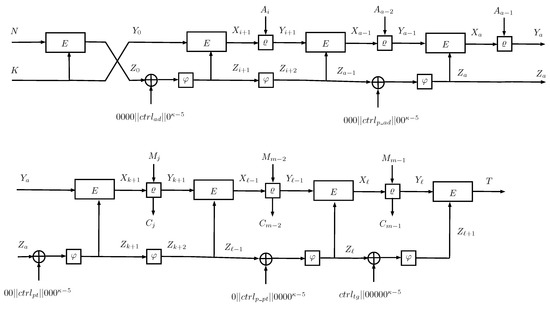
Figure 9.
Block diagram for COMET.
COMET can be instantiated using three different block ciphers: AES, CHAM, and Speck. In this work, we present the implementation of COMET only with AES.
We implement COMET using the architecture in Figure 10 for 8-bit datapath and 32-bit datapath. Two dedicated components were developed to compute shuffle and permute operations; the shuffle component computes and stores , and stores also its original input X as it is needed to compute the feedback input to the AES. The permute component only computes the operation permute explained above; it consists only of a 128-bit register capable of multiplying by 2 its 64 low bits. The output bdo is selected by a multiplexer between tag produced directly by the block cipher, plaintext, or ciphertext, which comes from the function . The register mkey stores the secret key loaded from the LWC interface as many messages can be encrypted with the same key; the key is updated only if the interface requests it. The registers Y_reg and Z_reg are used to store the outputs of functions and , respectively. The register adptct stores the data input, and the register ptctr allows computing the ciphertext or plaintext. Finally, the authentication is done by the component that is only a word-wise comparator; the word size can be 8 or 32 depending on the size of the datapath. The control signals are generated using a finite state machine.
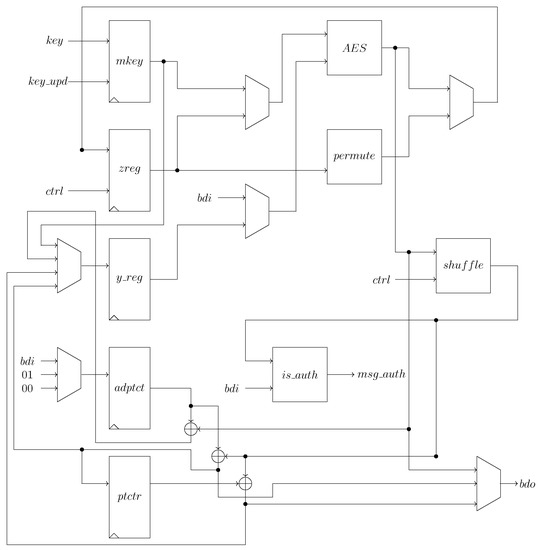
Figure 10.
COMET architecture for 8 bit and 32 bit.
The data flow for encryption and decryption is the same; the order of the processing of the blocks is the following: , , , T.
3.8. Oribatida
Oribatida is an authenticated cipher based on a sponge function, and it uses a public permutation simP based on block cipher Simon [20]. There are two Oribatida versions, one with a permutation size of 192 bit and the other one with 256 bit [4]. In this manuscript, we implement only the 256-bit version; it is denoted as Oribatida-256. Oribatida-256 manages a 128-bit message (M) and AD (A) blocks. The key and nonce size are also of 128 bits. SimP performs 34 rounds twice (P’) or four times (P) depending on which type of data is processing.
In Figure 11, the Oribatida mode of operation is shown, where Figure 11a shows the nonce/AD stage. First, the nonce (N) and the key (K) are concatenated and used as the starting values to generate the seed that helps to process the received AD, i.e., and . Then, there are a stages to process the respective a blocks of 128-bit that form A, where the first are computed with and the last one is computed with P. Every output coming from or P is XORed with the respective . The last block is padded if needed before being processed by P. For Figure 11b, M is encrypted. To obtain the ciphertext C, each 128-bit block of M is XORed with and , i.e., (just the 64 LSB of ) and then each is used as input for P together with . The last block is padded before being processed by P and the is just of the size of . With the last P for M, the tag T is computed by extracting the MSB places of the output of P. An additional note should be done regarding to the domains , , and , where each one is XORed against , and , respectively. These domains help to indicate if A or M is padded or not. Regarding the pad for the and , the remaining empty bytes are filled with the sequence with . In addition, in Figure 11, observe that each block of the ciphertext is masked using the capacity part of the permutation, which allows Oribatida to offer RUP security.
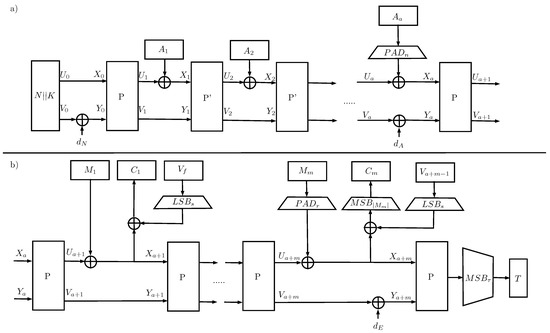
Figure 11.
Encryption version of Oribatida AEAD Algorithm, where (a) is the nonce/AD stage and (b) is the encryption stage (scheme based on the one found in [4]).
Now, to be compliant with the LWC contest specifications, our implementation of Oribatida-256 supports any M/A size. That means A and M are conveyed in a packet that can be authenticated and encrypted regardless of their size or if they are not included in that packet. Figure 12 describes the implemented architecture for Oribatida-256; a sequential architecture was adopted to save area. Due to the nature of this architecture, the current input block must be fully processed before processing the next one. The blocks (), , and are XORed with a domain of 4-bit. The domain is chosen depending on if A or M should be padded or not. Special attention deserves the decryption operation when is processed, because here (as well as pad) obtained from is used as a new frame to obtain the respective with an encryption operation, otherwise will not be computed correctly.
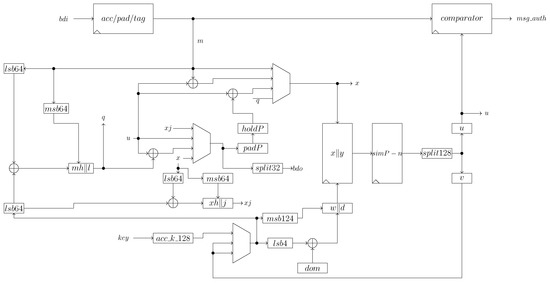
Figure 12.
LWC architecture for Oribatida AEAD.
The input and output of the LWC interface work with 32-bit inputs. We implement a component to pre-process the input blocks labeled as for A, M, and T; meanwhile, receives the four 32-bit key frames and constructs K from these frames. The pad is XORed to and if necessary. On the other hand, the output blocks are split into 32-bit blocks and sent to LWC interface by the component .
The block simP-n computes the permutation-based on Simon, where it executes P (for n = 4) and P’ (for n = 2) operations. Here, n is the number of times that the permutation simP is executed. The permutation simP-n receives X and Y in a concatenated way X||Y as input, and generates U||V as output. Details about SimP-n can be found in [4]. The architecture uses three multiplexer components, two to select the input X||Y to simP-n, and the other selects the correct output, i.e., which value is sent to the component . The verification tag is done using a 128-bit comparator with two inputs, one comes from that contains the verification tag, and the second input comes from the output U of the simP-n. The control unit is a finite state machine; it generates the signals to follow the correct operation flow of the Oribatida algorithm and generates the values of the domain depending on if there are of not A and M blocks or if the last block of them is complete or not.
4. Results
In this section, we present the result of the implementation process of the developed architectures. We used Xilinx Vivado version 2020.1 with the target FPGA Artix 7 xc7a12tcsg325-3, with 8000 LUTs, 16,000 FFs, 40 18Kbit BRAMs, 40 DSPs, and 150 I/O. All the utilized resources and times were obtained after place and route. In Table 2, we show the area in LUTs, Flip Flops (FF), and slices; we add a column for the number of clock cycles used to produce each block of ciphertext as we used it to compute the throughput. For each implemented AEAD, its datapath size is appended to its name.

Table 2.
Utilization of resources, throughput and TPA for implemented architectures on the xc7a12tcsg325-3 FPGA.
Table 2 has a comparative abstract of the implementation results in terms of utilization resources, throughput, and TPA. The utilization resources are in terms of LUT, FFs, and slices. As these implementations aim to be feasibly implemented in restricted devices, the best results are using fewer resources. The throughput metric is the rate of process one complete block message and is calculated by
. Finally, TPA is a useful metric to evaluate the performance/area tradeoff, it is computed by Throughput/Area.
The results in Table 2 show that COMET_32 is the fastest, followed by ESTATE-AES_32. In comparing these two implementations, their frequency is very close as both use the same AES implementation. The throughput of COMET_32 is better because it uses fewer clock cycles per block than ESTATE-AES_32, 70 vs. 88. ESTATE-AES_32 is a double pass algorithm so that it uses two calls to AES per input block, and it offers RUP security; hence, it is more secure than COMET_32. In terms of utilized resources, COMET_32 is more significant as it needs more additional registers than ESTATE-AES_32.
The biggest design is LOCUS_32; even though it uses tweGift-64 as a core, the large multiplexers it needs for input and key of tweGift-64 make the area increase. It is the same with LOTUS_32 as it also needs large multiplexers to feed tweGift-64. Comparing with ESTATE-Gift_32, which uses Gift-128, LOCUS_32 and LOTUS_32 are both more significant, the main reason being that the definition of ESTATE is straightforward as it uses the same key for all the block cipher calls and needs only four inputs to the underlying tweakable block cipher.
For 8-bit datapath architectures, ESTATE-AES_8 is the smallest, even compared to ESTATE-Gift_8, in the number of LUTs and FFs. Regarding the speed, ESTATE-Gift_8 is faster, but, as it needs more clock cycles per block, its throughput is lower than ESTATE-AES_8, which is reflected in better TPA for ESTATE-AES_8. Particularly, it is important to note an incrementation in area around 70% for ESTATE-AES between the 8-bit and 32-bit datapath architectures; in addition, the throughput increase is more than 500%. In ESTATE-Gift, the increase in area between the architecture of 8-bit datapath and the one with 32-bit datapath is around 28%, and the increase in throughput is 307%. Oribatida-256 with permutation simP takes 137 clock cycles, which is much more than AES implemented with 32-bit datapath, almost the same as Gift128. Oribatida-256 is smaller than LOCUS_32, LOTUS_32, and COMET_32, in the number of LUTs, but smaller in the number of FFs only for the last one.
The best in TPA is COMET_32 as its throughput is the best, while its area is not too much bigger than ESTATE-AES_32. The worst in TPA is ESTATE-Gift_8 as it requires 1392 clock cycles per block while ESTATE-AES_8 requires 552 clock cycles.
In Table 3, we show the real overhead introduced by the LWC interface, i.e, how much of the resources correspond to the implementation of the AE algorithm and how much to the LWC interface. To get such results, we implement the entity CryptoCore as the top entity. The overhead is shown in both LUTs and FFs. For all the presented cases, the number of FFs and LUTs are below 2000 which is one of the conditions for hardware components that the LWC contests suggest to use, even with the inclusion of the overhead of the extra components that LWC uses to complement CryptoCore for each evaluated solution. In summary, the overhead is below 300 LUTs and 250 FFs if we consider the worst cases for each feature (ESTATE-AES_32 with 294 LUTs and ESTATE-Gift_32 with 244 FFs). Along with the LUTs and FFs for the complete design, we put the percentage of utilization of such resources. We can see that our biggest design, LOCUS, occupies 23.07% and 6.28% of available LUTs and FFs and the smallest ESTATE-AES_8 9.96% and 2.60% of available LUTs and FFs, respectively. With this information, we can see that the available resources to develop an application using any of our designs as a security component is at least around 74%. An example of an application could be a wireless transmitter, using LOCUS to encrypt and authenticated the network packets. Almost 74% of resources are left over to implement the rest of the components to achieve the functionality.

Table 3.
Overhead in resources for complete design (LWC + CryptoCore) compared with CryptoCore alone. %Usage is the percentage of utilization of available resources on the xc7a12tcsg325-3 FPGA.
The more significant overhead in FFs is introduced to the ESTATE_32; as ESTATE is a double pass cipher, it needs an extra FIFO to store the plaintext or decrypted message. To communicate with such FIFO, 64 ports should be added to the LWC core. However, there are not enough input/output ports available on the target FPGA xc7a12tcsg325-3 (150); thus, we implement a wrapper to convert 32-bit vectors to 16-bit vectors, which allowed us to fit the design in the target FPGA but increased the number of utilized FFs.
Table 4 shows the results obtained in this work against those previously reported in the literature. First, we need to clarify that these solutions are different from those included in this manuscript. They were implemented using iterated full path round strategy; in our study, only the implementation for Oribatida-256 follows such strategy. All the ciphers implemented in [20] are single pass, and they offer more security compared with COMET but not compared to LOCUS, LOTUS, STATE, and Oribatida-256, which provides RUP security as is expected, using a full datapath for AES results in better throughput and more area. For example, our implementation of COMET_32 is almost 1000 LUTs smaller than the one presented in [20] but nearly four times slower. Gift-COFB in [20] is implemented with a 128-bit datapath while our implementation of ESTATE-Gift_32 uses a 32-bit datapath, the reduction in area is almost 50%, and the reduction in throughput is almost eight times as ESTATE is a double-pass cipher, i.e., it needs two block cipher calls per message block. As our implementation needs more clock cycles to encrypt one 128-bit block, Gift-128 uses 40 rounds, and our 32-bit approach uses 204 clock cycles, 5 per round, and finally 408 per message block, causing a low throughput.

Table 4.
Comparison of our LWC implementations regarding to the existing literature.
Despite the difference in the compared architectures, it may help to determine if the solutions here tested to have a better performance against those obtained in [20], by considering that this is a contest that evaluates if a solution is better than the others. At first sight, with the LUTs parameter, the winner in this ranking is ESTATE-AES_8 (ranked as 1, because it is the solution with the fewest LUTs, 797), followed by ESTATE-Gift_8 and COMET_8. Additionally, the number of LUTs occupied by the solutions presented in [20] is larger than those shown in this manuscript, with the notorious exception of SpoC (ranked as 5 for LUTs, with a value of 1172), which is better than the following solutions here presented: LOCUS, LOTUS, ESTATE-AES_32, COMET_32, and Oribatida-256_256 (ranked as 10, 8, 6, 9 and 7, respectively). The worst case is Schwaemm, with 4313 LUTs.
Now, comparing among all the solutions in terms of throughput, ASCON-AEAD is the best because it has the largest throughput value (1683.2 Mbps), followed by COMET-AES and Gift-COBF (2 and 3, respectively). About the solutions here presented, COMET_32 is the first with the best ranking (ranked as 5, with a value of 427.40 Mbps), followed by ESTATE-AES_32, COMET-CHAM, and Oribatida-256_256 (ranked as 6, 7, and 8, respectively). The worst case is ESTATE-Gift_8, with a throughput of 23.88 Mbps.
Nonetheless, for a fair comparison among all the presented solutions, it is necessary to consider the TPA that belongs to each candidate. For the sake of clarity, the content of Table 4 is sorted by TPA, from the largest to the lowest value. Then, ASCON-AEAD (0.887) and COMET-AES (0.584) have the best TPA record. However, the number of LUT components for the last one exceeds the 2000 allowed units (see Column 2). From the solutions presented, COMET_32 arises as the best candidate (ranked as 4, with 0.246), followed by ESTATE-AES_32 and Oribatida-256_256. The worst case is ESTATE-Gift_8, with a TPA of 0.029. Additionally, Gift-COFB (0.329) is better than any solution in the group of the candidates evaluated in this manuscript. ESTATE-AES_32 (0.216) and Oribatida (0.161) are better than SpoC (0.132), COMET-CHAM (0.128) and Schwaemm (0.121).
Discussion of Results
By considering the results shown in Table 3 and Table 4, the designs here presented are competitive when compared to those found in [5]. According to Table 3, when the solutions are synthesized in FPGA xc7a12tcsg325-3 (8000 LUTs and 16000 FFs available) with the use of the LWC CryptoCore, considering the number of LUTs, the biggest solution is LOCUS, with 23.07% usage, being ESTATE-AES_8 the lowest one with 9.96%. If FFs are considered, Oribatida is the biggest with 8.24% and ESTATE-AES_8 is the lowest with 2.60%. Then, ESTATE-AES_8 has lower area usage in general terms, with either LUTs or FFs. Nevertheless, it is interesting to see that, when the solution and overhead are analyzed individually, LOCUS has a lower overhead than ESTATE-AES_8 (195 LUTs and 52 FFs vs. 209 FFs and 72 FFs); meanwhile, with Oribatida, only the number of LUTs is lower (209 vs. 184). It is important to highlight that all the tested solutions in this manuscript are below 2000 LUTs and 2000 FFs, which is a recommendation to be followed when a new solution is proposed and implemented.
By considering the number of LUTs presented in Table 4 for those solutions found in [5], the third column helps us to choose just those solutions that can be a reference to determine which percentage is used before comparing against to the solutions presented in this manuscript. Only SpoC (ranked as 5) can be used as the best one among those presented in [5], with 1172 LUTs (or 14.65% resource usage), which is better than LOCUS and Oribatida, but worse than ESTATE-AES_8. The worst case in [5] is Schwaemm, with 4313 (or 53.91%), which is more than 50% of the total number of LUTs available. Unfortunately, the numbers of FFs and slices, as well as an analysis of overhead when using LWC CryptoCore from [5] are not available to determine the additional use of resource in the FPGA to make a more accurate comparison.
Now, by analyzing the throughput (sixth column) shown in Table 4, ASCON-AEAD (first), COMET-AES (second), Gift-COMB (third), Schwaemm (fourth), and COMET_32 (fifth) are the winners, but only ASCON-AEAD, Gift-COFB and COMET_32 have fewer LUTs than 2000 (1898, 1932, and 1737, respectively). Thus, these solutions are suitable for the recommended restrictions, while COMET-AES and Schwaemm are discarded as infeasible solutions. If we compare ASCON-AEAD against Gift-COFB, ASCON-AEAD is 2.6499 times more efficient. Now, if we compare ASCON-AEAD against COMET_32, ASCON-AEAD is 3.9382 times more efficient. The worst solution is ESTATE-Gift_8, with 23.88 Mbps, even when in terms of LUTs it is the second best solution (821).
Finally, by analyzing the TPA (eighth column) shown in Table 4 with the consideration that the number of LUTs should be lower than 2000, ASCON-AEAD (first), Gift-COMB (third) and COMET_32 (fifth) are the winners, being ASCON-AEAD more efficient than Gift-COMB and COMET_32 by 1.5188 and 2.6960 times, respectively. The worst solution is again ESTATE-Gift_8, with 0.029.
Regarding the potential scenarios to be applied, having in mind the restrictions of 2000 LUTs and 2000 FFs, if the user needs high throughput, ASCON-AEA (first), Gift-COFB (third), and COMET_32 (fifth) are the best options, being the first the best one. If the user needs lower area usage in terms of LUTs regardless of the throughput, ESTATE-AES_8 (first), ESTATE-Gift_8 (second), and COMET_8 (third) are the best choices, notwithstanding ESTATE-Gift_8 has the worst throughput among all the evaluated solutions (0.029). Then, ESTATE-AES_8 and COMET_8 become feasible solutions because they also have an acceptable tradeoff in terms of TPA (0.072 and 0.088, respectively).
5. Conclusions
This work is another effort to help in the evaluation of the NIST LWC Contest by implementing our architectures, with some of the existing candidate solutions using the adopted LWC-API. This was done to have a fair comparison between implementations. We present the implementation of some authenticated ciphers which offer RUP security, and we show that they can be implemented using similar resources as traditional authenticated ciphers. All the presented solutions fit into the FPGA of reference xc7a12tcsg325-3 (8000 LUTs and 16,000 FFs available), being the largest tested solution LOCUS, with 23.07% LUTs and Schwaemm with 53.91%.
The main goal regarding to the area usage has been covered because each implemented solution has fewer than 2000 LUTs and 2000 FFs. For that reason, Schwaemm has been discarded as feasible solution. The TPA for ESTATE-AES_32 (0.216) and Oribatida (0.161) (which offers RUP security), as well as COMET_32 (0.246), are competitive when compared to those presented in [5]. Nevertheless, ASCON-AEAD (0.887) and Gift-COFB (0.329) have better TPA, where their respective ratio is 1.5188 times in favor of ASCON-AEAD. Taking COMET_32 as reference, the ratio against to ASCON-AEAD is of 2.6960.
One of the goals of this work was to find solutions that reduce the area usage as low as possible, as shown in the cases of ESTATE-AES_8 (797 LUTs), ESTATE-GIFT_8 (821 LUTs) and COMET_8 (1052 LUTs). Even when ESTATE-GIFT_8 has low LUTs usage, their TPA is the worst among all the evaluated solutions (0.029). Then, ESTATE-AES_8 (0.072) and COMET_8 (0.088) are considered as feasible ones. Nonetheless, if the throughput is not relevant at all, ESTATE-GIFT_8 can be considered as feasible.
The next steps in these efforts are the implementation of additional architectures that help to reduce the area usage by trying the minimization of the TPA, i.e., few area usage with high throughput. Another future task will be the implementation of another set of lightweight solutions to determine the full features that they have (LUTs, slices, FFs, and throughput, among others) to do more accurate comparisons.
Author Contributions
Conceptualization, B.O.-M., C.M.-L., A.F.M.-H. and J.A.B.-G.; methodology, L.-J.S.-A. and J.G.-M.; hardware, B.O.-M., C.M.-L., A.F.M.-H. and J.A.B.-G.; validation, B.O.-M., C.M.-L., A.F.M.-H. and J.A.B.-G.; formal analysis, B.O.-M., C.M.-L., A.F.M.-H. and J.A.B.-G.; investigation, B.O.-M., C.M.-L., A.F.M.-H. and J.A.B.-G.; resources, B.O.-M., C.M.-L., A.F.M.-H. and J.A.B.-G.; data curation, B.O.-M., C.M.-L., A.F.M.-H. and J.A.B.-G.; writing—original draft preparation, B.O.-M., C.M.-L., A.F.M.-H. and J.A.B.-G.; writing—review and editing, J.G.-M., D.G.-T., J.-C.B.-C., and P.-J.G.-V.; visualization, B.O.-M., C.M.-L., A.F.M.-H. and J.A.B.-G.; supervision, B.O.-M., C.M.-L., A.F.M.-H. and J.A.B.-G.; project administration, B.O.-M., C.M.-L., A.F.M.-H. and J.A.B.-G.; funding acquisition, B.O.-M., C.M.-L., A.F.M.-H. and J.A.B.-G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Council of Science and Technology of Mexico, with the grant number 313572.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shay, G.; Ashwin, J.; Mridul, N. COMET: COunter Mode Encryption whith Authentication Tag. 2019. Available online: https://csrc.nist.gov/Projects/lightweight-cryptography/round-2-candidates (accessed on 11 November 2020).
- Chakraborti, A.; Datta, N.; Jha, A.; Mancillas-López, C.; Nandi, M.; Sasaki, Y. ESTATE: A Lightweight and Low Energy Authenticated Encryption Mode. IACR Trans. Symmetric Cryptol. 2020, 2020, 350–389. [Google Scholar] [CrossRef]
- Chakraborti, A.; Datta, N.; Jha, A.; Lopez, C.M.; Nandi, M.; Sasaki, Y. LOTUS-AEAD and LOCUS-AEAD. Lightweight Cryptography, Round 2 Candidates. 2019. Available online: https://csrc.nist.gov/CSRC/media/Projects/Lightweight-Cryptography/documents/round-1/spec-doc/lotus-aead-and-locus-aead-spec.pdf (accessed on 11 November 2020).
- Bhattacharjee1, A.; List, E.; López, C.M.; Nandi, M. The Oribatida Family of Lightweight Authenticated Encryption Schemes. 2019. Available online: https://csrc.nist.gov/CSRC/media/Projects/lightweight-cryptography/documents/round-2/spec-doc-rnd2/oribatida-spec-round2.pdf (accessed on 11 November 2020).
- Rezvani, B.; Coleman, F.; Sachin, S.; Diehl, W. Hardware Implementations of NIST Lightweight Cryptographic Candidates: A First Look. Cryptology ePrint Archive, Report 2019/824. 2019. Available online: https://eprint.iacr.org/2019/824 (accessed on 11 November 2020).
- Dworkin, M.J. SP 800-38A 2001 Edition. In Recommendation for Block Cipher Modes of Operation: Methods and Techniques; Technical Report; NIST: Gaithersburg, MD, USA, 2001. [Google Scholar]
- Dworkin, M.J. SP 800-38B. In Recommendation for Block Cipher Modes of Operation: The CMAC Mode for Authentication; Technical Report; NIST: Gaithersburg, MD, USA, 2005. [Google Scholar]
- Rogaway, P. Efficient Instantiations of Tweakable Blockciphers and Refinements to Modes OCB and PMAC. In Advances in Cryptology—ASIACRYPT 2004, Proceedings of the 10th International Conference on the Theory and Application of Cryptology and Information Security, Jeju Island, Korea, 5–9 December 2004; Lee, P.J., Ed.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2004; Volume 3329, pp. 16–31. [Google Scholar] [CrossRef]
- Kaps, J.P.; Diehl, W.; Tempelmeier, M.; Homsirikamol, E.; Gaj, K. Hardware API for Lightweight Cryptography. Tech. Report Oct 2019. 2019. Available online: https://cryptography.gmu.edu/athena/LWC/LWC_HW_API.pdf (accessed on 11 November 2020).
- Chakraborti, A.; Datta, N.; Jha, A.; Mancillas-López, C.; Nandi, M.; Sasaki, Y. INT-RUP Secure Lightweight Parallel AE Modes. IACR Trans. Symmetric Cryptol. 2019, 2019, 81–118. [Google Scholar] [CrossRef]
- Minematsu, Kazhuhiko. AES-OTR v3.1, Cited September 2020. Available online: https://competitions.cr.yp.to/round3/aesotrv31.pdf (accessed on 11 November 2020).
- Chakraborti, A.; Datta, N.; Jha, A.; Lopez, C.M.; Nandi, M.; Sasaki, Y. Elastic-Tweak: A Framework for Short Tweak Tweakable Block Cipher. Cryptology ePrint Archive, Report 2019/440. 2019. Available online: https://eprint.iacr.org/2019/440 (accessed on 11 November 2020).
- Banik, S.; Pandey, S.K.; Peyrin, T.; Sasaki, Y.; Sim, S.M.; Todo, Y. GIFT: A Small Present—Towards Reaching the Limit of Lightweight Encryption. In Cryptographic Hardware and Embedded Systems—CHES 2017, Proceedings of the 19th International Conference, Taipei, Taiwan, 25–28 September 2017; Fischer, W., Homma, N., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2017; Volume 10529, pp. 321–345. [Google Scholar] [CrossRef]
- Chakraborti, A.; Datta, N.; Jha, A.; Lopez, C.M.; Nandi, M.; Sasaki, Y. ESTATE. Lightweight Cryptography, Round 2 Candidates. 2019. Available online: https://csrc.nist.gov/CSRC/media/Events/lightweight-cryptography-workshop-2019/documents/papers/estate-authenticated-encryption-mode-lwc2019.pdf (accessed on 11 November 2020).
- Banik, S.; Bogdanov, A.; Luykx, A.; Tischhauser, E. SUNDAE: Small Universal Deterministic Authenticated Encryption for the Internet of Things. IACR Trans. Symmetric Cryptol. 2018, 2018, 1–35. [Google Scholar] [CrossRef]
- Daemen, J.; Rijmen, V. The Design of Rijndael: AES—The Advanced Encryption Standard; Information Security and Cryptography; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar] [CrossRef]
- Moradi, A.; Poschmann, A.; Ling, S.; Paar, C.; Wang, H. Pushing the Limits: A Very Compact and a Threshold Implementation of AES. In Advances in Cryptology—EUROCRYPT 2011, Proceedings of the 30th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Tallinn, Estonia, 15–19 May 2011; Paterson, K.G., Ed.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6632, pp. 69–88. [Google Scholar] [CrossRef]
- Rouvroy, G.; Standaert, F.; Quisquater, J.; Legat, J. Compact and Efficient Encryption/Decryption Module for FPGA Implementation of the AES Rijndael Very Well Suited for Small Embedded Applications. In Proceedings of the International Conference on Information Technology: Coding and Computing (ITCC’04), Las Vegas, NV, USA, 5–7 April 2004; IEEE Computer Society: Washington, DC, USA, 2004; Volume 2, pp. 583–587. [Google Scholar] [CrossRef]
- Chakraborti, A.; Datta, N.; Nandi, M.; Yasuda, K. Beetle Family of Lightweight and Secure Authenticated Encryption Ciphers. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2018, 2018, 218–241. [Google Scholar] [CrossRef]
- Beaulieu, R.; Shors, D.; Smith, J.; Treatman-Clark, S.; Weeks, B.; Wingers, L. The SIMON and SPECK lightweight block ciphers. In Proceedings of the 52nd Annual Design Automation Conference (DAC), San Francisco, CA, USA, 7–11 June 2015; pp. 1–6. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).