Abstract
Backstepping is a control technique based on Lyapunov’s theory that has been successfully implemented in the control of motors and robots by several nonlinear methods. However, there are no standardized methods for tuning control gains (unlike the PIDs). This paper shows the tuning gains of the backstepping controller, using Genetic Algorithms (GA), for an Unmanned Aerial Vehicle (UAV), quadrotor type, designed for autonomous trajectory tracking. First, a dynamic model of the vehicle is obtained through the Newton‒Euler methodology. Then, the control law is obtained, and self-tuning is performed, through which we can obtain suitable values of the gains in order to achieve the design requirements. In this work, the establishment time and maximum impulse are considered as such. The tuning and simulations of the system response were performed using the MATLAB-Simulink environment, obtaining as a result the compliance of the design parameters and the correct tracking of different trajectories. The results show that self-tuning by means of genetic algorithms satisfactorily adjusts for the gains of a backstepping controller applied to a quadrotor and allows for the implementation of a control system that responds appropriately to errors of different magnitude.
1. Introduction
Nowadays, Unmanned Aerial Vehicles (UAV) enjoy great popularity in activities where video or photo shots are required, particularly quadrotor models (with four rotors). Due to their configuration [1], quadrotors can perform tasks that previously had to be performed from a helicopter or airplane by highly qualified personnel, which implies a high cost in terms of the vehicle (helicopter) and personnel (pilot and cameraman); furthermore, the risk to human life is eliminated with UAV. Current UAV can develop different activities such as exploration, transportation, mapping, reconnaissance, environmental monitoring, construction monitoring and surveillance [2,3,4,5,6,7] in civil, police or military activities [8,9]. The advances in robotics, mechatronics, and microelectronics facilitated the development of hardware at a low cost, coupled with the development of real-time processing for navigation. Quadrotors have very simple mechanics since the control of their position is determined by the changes in speed in their motors and they are used when high maneuverability is required, since they are capable of moving in any direction or flying at low speeds. Due to the complexity of the system, different algorithms have been developed to achieve autonomous control in Unmanned Aerial Vehicles, using techniques from linear control methodologies with PID [10,11], to nonlinear control techniques such as Feedback Linearization control, model predictive control, adaptive control approaches [12], fail-safe methodologies based on sliding mode control theory and backstepping control [13,14], combinations such as Adaptive Sliding Backstepping Control [15,16,17], diffuse control in the proposal of Geometric Control [18,19], Nonlinear Dynamic In-version (NDI) Control [20], the Robust Generalized Dynamic Inversion (RGDI) Quadcopter Control System [21] and the Neural Network Control System of UAV Altitude Dynamics [22,23,24,25]; most of these state-of-the-art nonlinear and adaptive control techniques for quadrotors were discussed by Hongwei and Ghulam.
The mathematical model of the system to be controlled must have a solid basis to be able to perform the controller design process in a safer and more reliable way, which are critical qualities within the aviation industry. UAV systems have been studied as a whole or in subsystems (for example, tilt control). The challenge of these vehicles is that they are nonlinear, subacted, and multivariable systems, subject to unpredictable disturbances such as the interaction of the rotor flow with the quadrotor chassis or atmospheric turbulence [26,27,28,29,30,31,32,33,34,35,36,37,38,39], so that classic control (linear and invariant over time) has limited results where instabilities can occur when the system moves away from equilibrium.
Genetic algorithms have been used to tune the best solution in different control models, from the classic PID control and in fields as diverse as industrial processes and finite element analysis thanks to its versatility and adaptability. Genetic algorithms are based on stochastic optimization techniques that emulate biological evolution and its genetic‒molecular basis, inspired by Charles Darwin’s theory of evolution whereby the fittest prevails. It starts with a randomly generated population and evaluates the objective function with these values, organized in the form of vectors. Those that generate a greater margin of error are discarded; in the next generation, new values are proposed as a combination of those that obtain better results and random values within a predetermined range, emulating the mechanisms of reproduction, crossing, mutation, and so on for a certain number of generations or until the values of the gains obtain results within the values established as acceptable [40].
Since there is no standard for tuning the gains of a backstepping type controller, some reports indicated that the gains were tuned manually, while others proposed automatic tuning using fuzzy methods. That is why, in this work, we propose a tuning of the gains using genetic algorithms, which gives greater possibilities to obtain an optimal tuning to control the system response. This work contributes with an option to the lack of automatic tuning proposals with an automatic tuning for the gains of the backstepping controller using genetic algorithms. This paper presents the tuning using genetic algorithms for a nonlinear dynamic model with a backstepping control structure, tuned to find the most appropriate control gains of a quadrotor-type unmanned aerial vehicle. In Section 2, by analyzing the operation of the quadrotor, the kinematic equations and dynamic equations are obtained using the Newton‒Euler methodology for the Tait‒Bryan navigation angles. Section 3 describes the design of backstepping control based on Lyapunov’s theory. Finally, in Section 4, tuning is performed using genetic algorithms. Section 3 shows the validation of the proposed control through simulations of the controller’s response to different preplanned paths, and the results are discussed. Finally, conclusions and proposals for improvement of future work are presented in Section 4.
2. Materials and Methods
2.1. Mathematical Model of A Six-Degrees-of-Freedom Air Vehicle
The aerial vehicle on which this work is based is a Draganflyer IV, which has the configuration of four coplanar rotors (quadrotor), as shown in Figure 1. The movement of the quadrotor originates from the speed changes of the rotors. Each rotor consists of a direct electric current motor, a gear mechanism, and a blade rotor. To achieve movement on an axis, a speed difference must be created in the rotors corresponding to that axis. The yaw movement is obtained from the difference in torque between each pair of rotors—that is, it accelerates the two rotors clockwise while decelerating the rotors counterclockwise, and vice versa.

Figure 1.
Unmanned Aerial Vehicle (UAV), quadrotor type, model: Draganflyer IV. The equations proposed in this paper for modeling UAV are based on [41].
If the vehicle is considered as a rigid solid, the system has six degrees of freedom: three of them define the position of a reference point in the body (the center of mass), and the other three define the orientation of the body, so that, to obtain the model, the quadrotor is supposed to be a rigid body in space, subject to a main force and three moments, which together represent the control inputs of the system. This work will use the Tait‒Bryan navigation angles (Figure 2) to describe the rotation of the system in three-dimensional space.
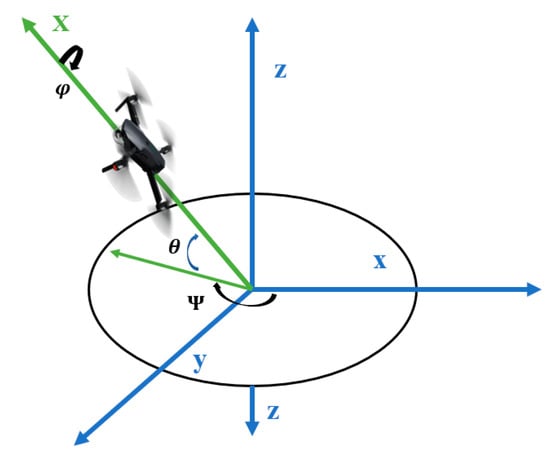
Figure 2.
Navigation angles defined by Tait‒Bryan. angles for an aircraft. The fixed frame has been moved backwards from center of gravity (preserving angles) for clarity.
The navigation angles, known in mathematics as Tait‒Bryan angles, are a set of three angles that describe the orientation of a rigid body—in this case, the drone—with reference to a fixed system. We considered two vector sets of a right-handed trihedron that belong to a fixed reference system and a body . The body initially allows rotation about the axis through angle ; the other axes, and , are carried along with the body, keeping their orthogonality. Now the drone rotates around axis about angle . As before, the two axes and are carried along with the body. Finally, the drone rotates about axis through angle such that axes and are carried along with the body. In each rotation, the other two axes are carried along with the body, so that the set of axes around which the rotations occur () are not orthogonal. However, the orientation of the drone can now be described using the Tait‒Bryan angle set .
This sequence is the preferred one to define the dynamics of air vehicles, and is defined with the transformation (1), where s means sine and c means cosine.
Each rotation sequence defines a unique orientation of the drone. To solve for these angles, we must place the angles in the correct quadrant. These angles are limited to the range described in Equation (6):
To end the kinematic analysis, Equation (2) shows the matrix that relates to the angular velocities, where , and are the angular velocities in the fixed coordinate system in three-dimensional space.
Considering the above and using the Newton‒Euler formulation, the forces and acting moments are established with respect to the established coordinate system (Figure 3). The equations that describe the dynamics of a rigid solid in space are as follows:
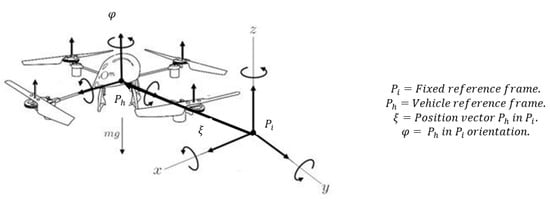
Figure 3.
Reference frames and forces. The position and speed of the quadrotor are evaluated with respect to an inertial frame located at a fixed station.
Given the following vectors:
Since the vehicle is held with the pushing force, the angles must be bounded, that is:
From the previous equations, it is clear that is the translational velocity vector with respect to the fixed reference frame, is the angular velocity, m is the mass of the vehicle, represents the vector of forces acting on the vehicle, represents the torques applied to the system, and is the inertia matrix. Using Newton’s second law, , we obtain:
where represents the transformation matrix between reference frames and represents the external forces applied to the body of the vehicle, which can be represented by:
where is the force that occurs due to gravity, represents the gravity constant (), and is defined as the aerodynamic force:
where is a diagonal matrix that expresses the friction parameters. Knowing that is the force produced by the thrust of the propellers, it can be represented by the vector shown in Equation (10), which contains the forces , which are the thrust forces generated by each motor and are determined by:, where is the air density, is the thrust coefficient, is the area of the rotor disk, the radius of the propeller, and is the angular velocity of each motor; since all values are constant with the exception of , the constant can be defined as .
Substituting the corresponding values and using the correct vector operation in the previous equation, we obtain:
Torques applied to the vehicle are obtained with a similar procedure, considering as the external torque applied to the system that can be represented as follows:
where represents the aerodynamic torques and is determined by the expression:
Given represents torque’s friction coefficients produced by the motors, is a matrix with the torques generated on each axis and is determined by Equation (14)
where represents the torques generated by each of the four engines and is represented by the following expression: . Once the above equations have been determined, it is possible to represent the dynamic behavior of the system through the following set of equations:
Operating and simplifying Equation (15), we reach:
The procedure for obtaining angular accelerations is similar to that used to obtain the equations that describe linear behavior, obtaining:
Equation (16) represents the translational dynamics of the vehicle, while Equation (17) represents the rotational dynamics of the vehicle; these equations provide a model that allows for studying and simulating the dynamics of the system.
When we try to control a system, the first step is to develop a mathematical model that is simple enough to be able to represent it, but as close to reality as possible; the more real variables we consider, the more complex the proposed mathematical model will be. When the system is too complex or time-variant, it is difficult to develop a mathematical model that can represent it. In this case, there are intelligent control techniques such as fuzzy control or neural networks, among others. Fuzzy control builds on the experience of an operator to propose a set of rules that can help control the system, and neural networks adjust to system changes regardless of the initial conditions. When there is the possibility of mathematically modeling a system, different algorithms can be developed and tested by means of simulations in software, which allows us to fine-tune the algorithm coefficients, thus increasing the probability of success in field testing with software and hardware under real conditions. This methodology has been tested in various investigations using specific software such as BikeSim, TruckSim, or CarSim for specific simulations of motor vehicles [42], or HARFANG 3D Framework for modern multimedia applications such as virtual reality [43], with MATLAB the most commonly used software for general process simulations, including autonomous guided vehicles (AGV) [44] and aerial autonomous guided vehicles (UAVs) [45,46,47].
2.2. Backstepping Control
Backstepping is a recursive control procedure based on Lyapunov’s theory and is useful in the design of feedback control; it allows for the control of a nonlinear dynamic system and shows high performance in the face of parametric uncertainties, which is why this technique has been selected for the development of a controller that allows the quadrotor to track a preplanned path.
As a first step, the system is rewritten in state space , Considering the vector of system states as .
By substituting the relationships described in Equation (18) into Equations (16) and (17) and neglecting the gyroscopic effects of the quadrotor, the system can be expressed as follows:
where
The basis of the backstepping control strategy, like most control techniques, is based on reducing the system error. Control signal will be based on the system position error on the axis x:
With its derivative being:
A candidate function for Lyapunov is proposed; considering that it must be defined and positive and its derivative with respect to time must be semidefined and negative, it is proposed as follows:
The derivative of Equation (23) is:
To achieve the stabilization of , a virtual control input must be proposed:
Given represents a control gain, taking the value of from Equation (25), we can rewrite Equation (21) as follows:
We guarantee that the derivative of the proposed Lyapunov function is negative and semidefined. Substituting Equation (25) into Equation (22), we have:
Solving of Equation (25) and substituting it into Equation (28) we reach:
So that it can be modified in the previous equation, the expression of the initial system error has been increased; to stabilize the new terms without modifying the previous system, the following variable change is made:
With its derivative being:
To cancel this new error function, an increased Lyapunov function is proposed:
We derive Equation (32) as follows:
Substituting Equations (29) and (31) into Equation (33) and clearing the value of from Equation (30), we obtain:
Considering Equation (16), we obtain the value of as follows:
where:
Substituting Equation (32) into Equation (31) and assuming the acceleration reference has a null value (since it is assumed that the vehicle starts from a resting state), we obtain:
Considering Equation (30) and satisfying , a control signal is proposed to guarantee it, thus obtaining:
If the control signal proposed in Equation (34) is replaced, we obtain:
This guarantees compliance with the Lyapunov criteria, a fact that establishes the expression obtained for the control signal as appropriate. The same procedure is performed to obtain the control signals , which is related to and ; , which stabilizes error and ; and , related to and ; therefore, the expressions defining said control signals are:
Equation (17) defines the movement of the vehicle on the x‒y plane, and it can be seen that the only force that it depends on is the thrust . So and will be control signals used to calculate the warping and pitch angle necessary to move the drone in the x‒y plane and the and signals must satisfy the condition , where and , and where and , respectively, to ensure system stability. Following the same methodology that was followed to obtain the control signal , we obtain:
Equations (34)–(37) represent the control signals necessary for path tracking. On the other hand, Equations (38) and (39) are used to determine the warping and pitch angles necessary for tracking the reference. The only value that remains unknown is , so tuning of the controller is required.
2.3. Tuning the Backstepping Controller Using Genetic Algorithms
The response of a controller depends largely on the values of its gains; for PID-type controllers, there are tuning methods that allow attainment of the values of , and , in order to obtain the desired response. However, there is no established method for tuning the gains of a backstepping controller, which is due to one of the options being the so-called metaheuristic algorithms, within which are the genetic algorithms, so named because they are bio-inspired by the way in which nature selects the strongest genes.
Genetic algorithms will be used because they have greater capacity and adaptability as a universal optimization method; due to their random nature, it is difficult to compare metaheuristic algorithms, but some studies show that GA has a better speed‒performance relationship [43], which is important in the development of this work due to the computational weight of the simulations.
The algorithm used is the Fixed-state Genetic Algorithm, which uses a generational scheme like that of mammals and other long-lived animals, where parents and their descendants coexist; however, in the long run, competition between them is generated. In this model, two parents must be selected, and certain members of the previous population must be eliminated to make space for the descendants, so that, after each crossing, the new descendants are immediately available for reproduction. This allows the model to use the characteristics of a promising individual as soon as it is created. The algorithm is based on the flowchart shown in Figure 4 and is basically divided into the following functions: create population, selection, reproduction, mutation, and reintegration into the population.
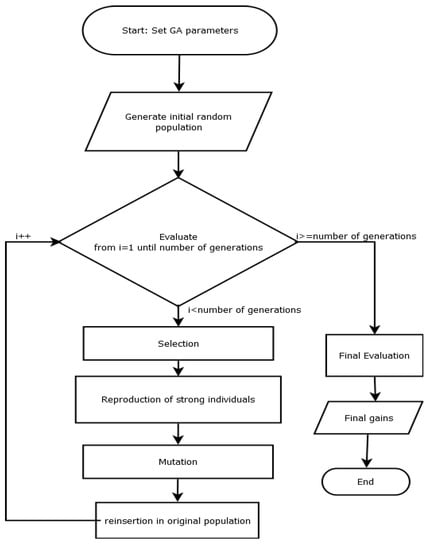
Figure 4.
Flowchart of the genetic algorithm used.
The process shown in Figure 4 is the overall method of this paper. First, a random population is proposed and the genetic algorithm selects the strongest genes (through reproduction and mutation) for a predetermined number of iterations; then, final values are proposed. The first stage of the implementation consists of defining the parameters used to search for profits. Using this algorithm, these parameters are summarized in Table 1.

Table 1.
Parameters of the genetic algorithm.
The parameter “size of the population” provides genetic diversity, so a large number is desired; however, if the number is very large, the computational cost and the algorithm execution time also increase. With this in mind, the parameter was chosen as 100 initial individuals; this number provides adequate genetic variation without increasing the algorithm run time.
The parameter “generations” is eight and was selected experimentally, since when this number of generations elapsed, it was found that most of the population complied with the genetic model. The parameter “range” is the range of the gains and must by definition be greater than 0, so only an upper limit must be defined; for this work it was 30, because with higher numbers a saturation is observed in the torque.
The mutation probability was fixed at 20% because a very high number causes the algorithm to take longer to converge and a very low number causes stagnation. On the other hand, the biological pressure was set to 30%, which allows 30% of individuals to reproduce and eliminates 30% of the worst original population; this value allows for rapid convergence in each generation.
Finally, the strongest genes selected are those with the best fitness. This value was obtained by calculating the Euclidean distance between the value and the ts obtained by the evaluated genes and the values provided by the genetic model. For evaluation, the system is divided into three subsystems, one for each axis: the subsystem has four associated α gains , the subsystem has four associated gains , and the subsystem has four gains too ; this association is due to the displacement in the axis caused by the roll angle; the movement in the axis is caused by the pitch angle. So, the tuning is done in every subsystem, evaluated under the step input as a reference. As in the design of control laws, the system is not tuned globally; instead, it takes advantage of the natural subdivision of the system. Therefore, the tuning of the X axis subsystem corresponds to the control law U2, which depends on the speed of rotors 1 and 3. The tuning of the Y axis subsystem corresponds to the control law U3, which depends on rotors 2 and 4. Finally, the subdivision of the Z axis system corresponds to the control laws U3 and U4, which depend on the speed of the four rotors—that is why they are tuned together.
3. Results
In this section, numerical results are provided to facilitate the performance evaluation of the tuning backstepping controller using genetic algorithms.
This algorithm was subjected to different tasks, which were split into two main sections. The first one refers to ideal conditions—that is, disturbances were not included. In the second study, random disturbances were considered to simulate the wind current effects.
Simulations were performed on Matlab/Simulink in order to test the validity of the proposed controller. An accurate dynamic model for the four-rotor rotorcraft was used, and the model was developed on the base of the Draganflyer. In addition, due to the inclusion of realistic effects on simulations, the calculation of parameters such as inertia, propeller pitch, maximum rotor speeds, and others was performed, and the information from the drone data sheet was used.
Parameters:
, and moments of inertia ; ; , length from the rotor to drone center .
A set of solutions obtained by the genetic algorithm is shown to show the performance of the tuned controller. The selection was performed by means of the numerical simulation of the control law and the drone dynamics. The results are summarized in Table 2.

Table 2.
Results of the genetic algorithm.
3.1. Experimental Validation
Using these gains, the final step response of the movements in the , and axes was simulated. The responses obtained determine if the tuning fulfills the parameters of the genetic model.
For a validation of the controller performance tuned by the proposed method, the UAV was subjected to a step input on each axis—that is, the system was subjected to the following reference inputs:
- To prove axis
- To prove axis
- To prove axis
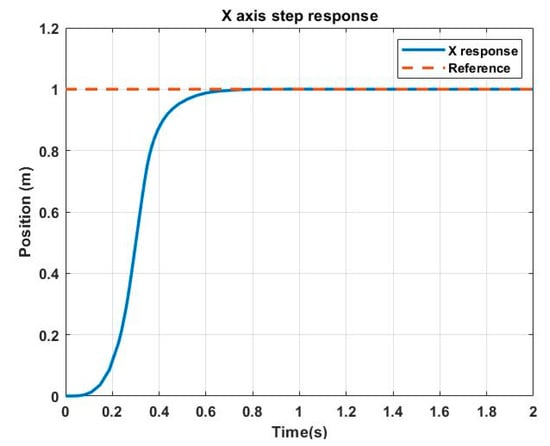
Figure 5.
System response in axis.
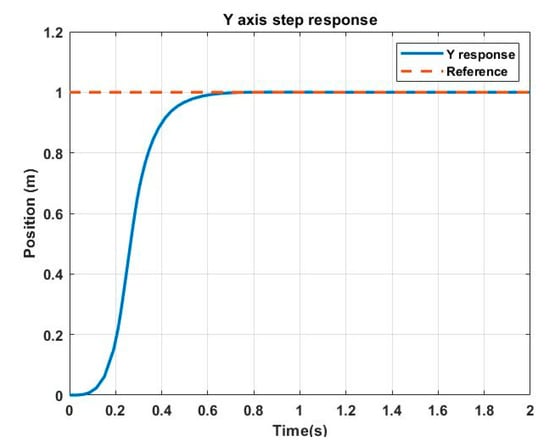
Figure 6.
System response in axis.
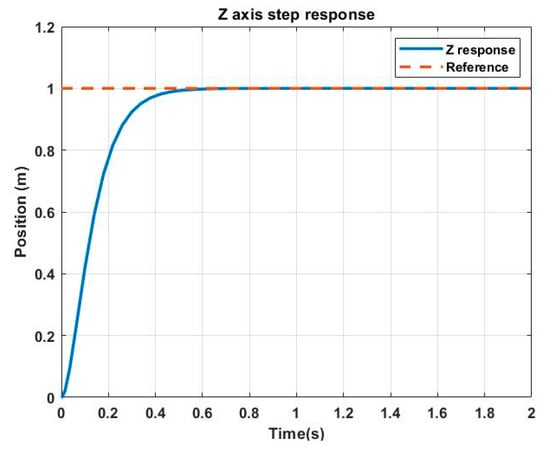
Figure 7.
System response in axis.
Table 3 shows the numeric results, considering as the time necessary for the system response to not vary by more than of the final value.

Table 3.
Numeric results for step response.
Remembering that the genetic model is and , we can observe that the values obtained by the GA fulfill these parameters for a step input. Subsequently, the system was tested with various trajectories, obtaining favorable results in each of the tests. The most relevant results are as follows:
Task 1:
Task 2: with random disturbances (simulation of wind effects).
Task 1. The system was tested with a clover-shaped reference. In this test, the quadrotor starts with an initial error of 1 m in position as shown in Figure 8, which is a challenge given the characteristics of the vehicle.
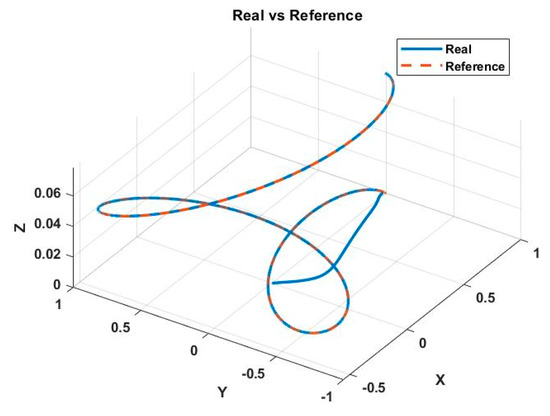
Figure 8.
Real trajectory () vs. desired trajectory ().
The results obtained as a response of reference from task 1 show that the tracking reference is appropriate. Figure 9, Figure 10 and Figure 11 show the behavior of the drone in each axis.
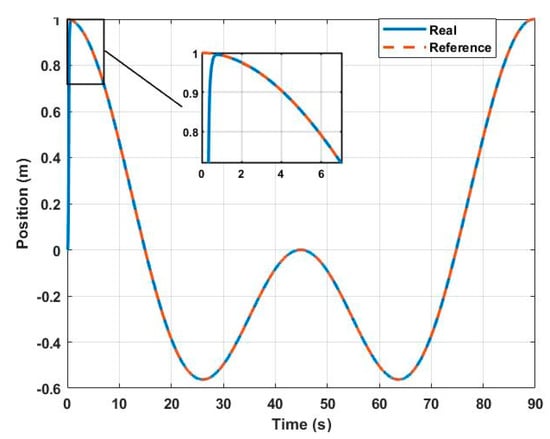
Figure 9.
real () vs. () desired.
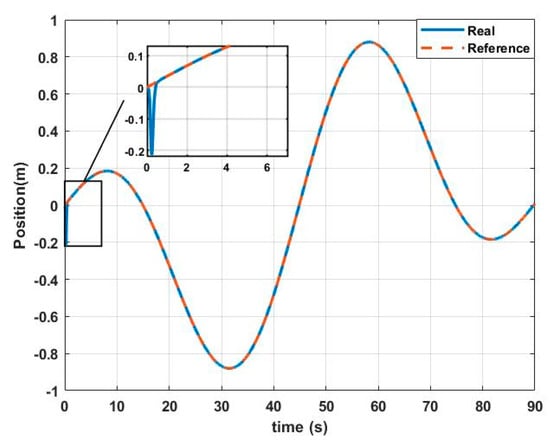
Figure 10.
real () vs. () reference.
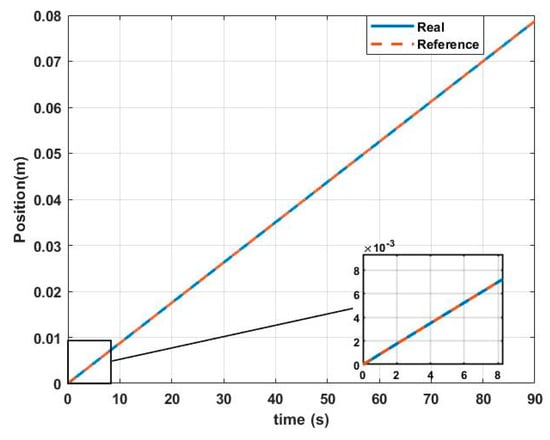
Figure 11.
() real vs. () desired.
The functioning of the system can be analyzed by observing the tracking errors in position and orientation, shown in Figure 12 and Figure 13, respectively.
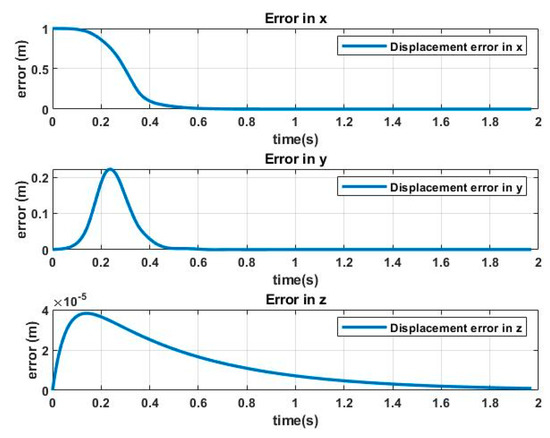
Figure 12.
Relative displacement errors vs. time from task 1.
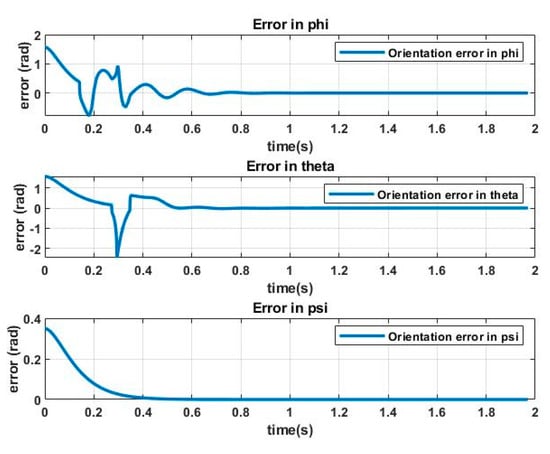
Figure 13.
Relative orientation errors vs. time from task 1.
As can be seen, the errors of the position and orientation tracking tend to 0 quickly and remain at that value throughout the 90 s of the analysis.
Task 2. Helical-type trajectory in which the quadrotor starts at an initial error of 0; additionally, a random perturbance was added during the simulation, t starting at 4.5 s and finishing at 9 s; the disturbance has random components that change in value during the disturbance. The biggest disturbance in simulation has components of 6.17 m/s, 5.97 m/s, and 3.45 m/s for x, y, and z, respectively, and a magnitude of 9.25 m/s. Through additional tests, it was determined that the designed backstepping controller is capable of rejecting a disturbance with a maximum magnitude of 10.1 m/s, as long as no component of the disturbance is greater than 6.6 m/s. The results of the controller under perturbation are shown in Figure 14, Figure 15, Figure 16, Figure 17, Figure 18 and Figure 19 The effect of the disturbance can be observed from 4.5 s onward. It can be seen that the controller tuned with the gains in Table 2 is able to return to the desired trajectory once the disturbance disappears.
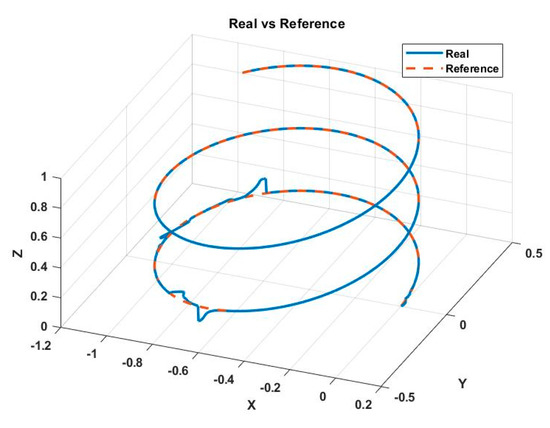
Figure 14.
Helicoidal trajectory with perturbance. Real () vs. desired ().
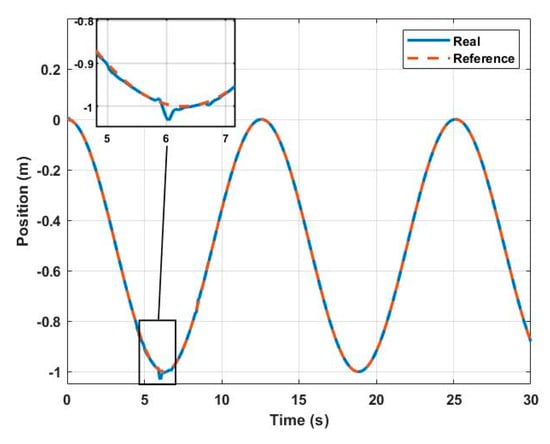
Figure 15.
X real () vs. X() desired with perturbance.
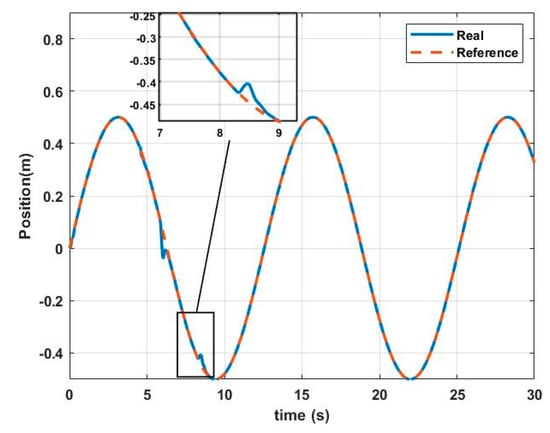
Figure 16.
Y () real vs. Y desired with perturbance.
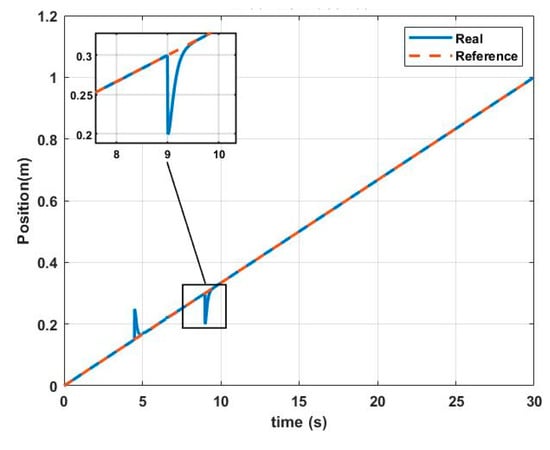
Figure 17.
Z () real vs. Z desired with perturbance.
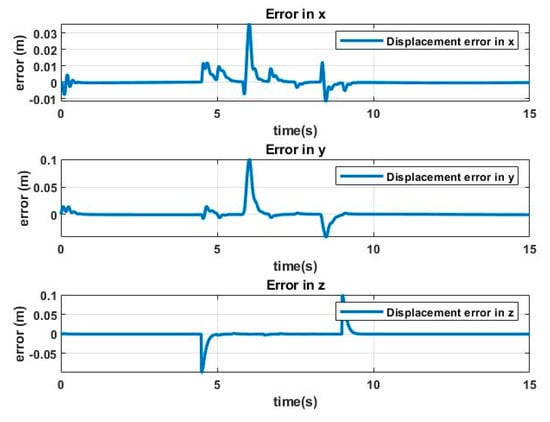
Figure 18.
Relative displacement errors vs. time from task with perturbance.
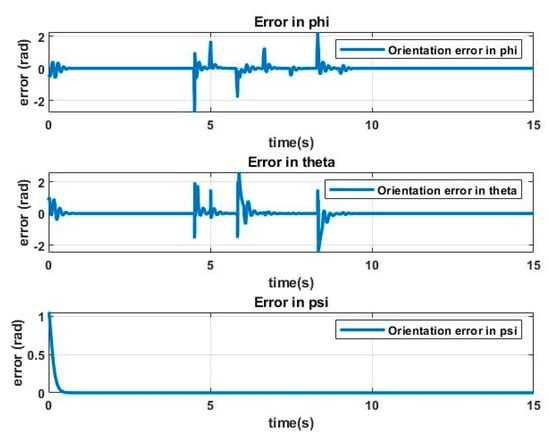
Figure 19.
Relative orientation errors vs. time from task with perturbance.
The helical path used can be seen in Figure 14. The performance of the controller in each of the axes of the fixed inertial system is shown in Figure 15, Figure 16 and Figure 17 and the response of the system is compared against the reference path.
Finally, the errors in position and orientation, respectively, are shown in Figure 18 and Figure 19. Note the effect of the disturbance and the correction of the controller when disturbance disappears.
Tests show that the controller is capable of following trajectories even in the presence of initial errors or random disturbances, such as those that can cause air currents in a flight. The system correctly manages the added error within a short response time because of the correct tuning of the controller; due to the lack of standardized methods, the application of the genetic algorithm shows appropriate results for field tests.
3.2. PID Controller
For comparison purposes, a PID-type controller was developed that allows for tracking a trajectory; in this way, the performance of the proposed backstepping controller can be compared. The control signal U(t) in a PID is represented by the sum of the value of the proportional, integral, and derivative components, which depend on the error; that is:
The values of the constants Kp, Kd, and Ki determine the behavior of the PID. For the control of the AUV, six control signals of the PID type were implemented; again, the control signals in the xy plane will be used to determine the roll and pitch reference angles, and the four control signals (U1, U2, U3, and U4) will be applied to their corresponding degree of freedom. The values of the control constants used for the PID controllers can be seen in Table 4.

Table 4.
PID gains used in this work.
With the constants shown in Table 4, the drone is able to follow a trajectory, as shown in Figure 20.
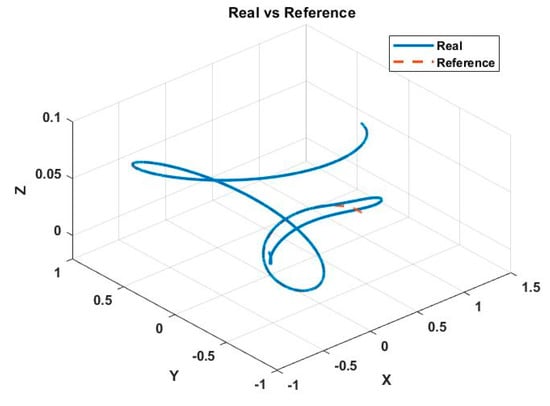
Figure 20.
Tracking trajectory with PID.
For a comparison with the backstepping controller, the design parameters ts and Mp will be considered. For this reason, it is necessary to evaluate the PID controller against step inputs such as trajectories a, b, and c. Figure 21, Figure 22 and Figure 23 show the results of the PID controller.
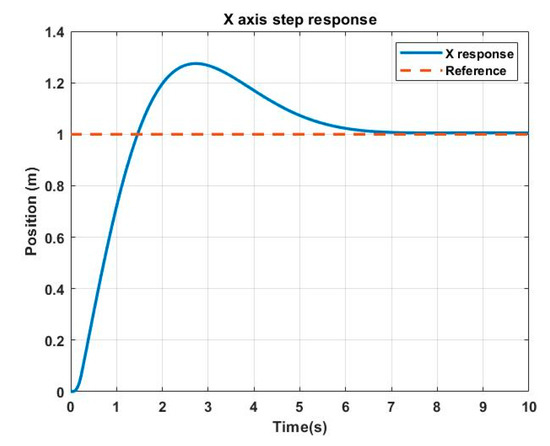
Figure 21.
PID step response in X axis.
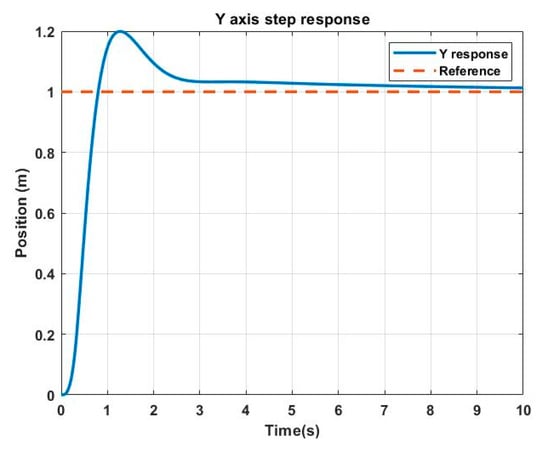
Figure 22.
PID step response in Y axis.
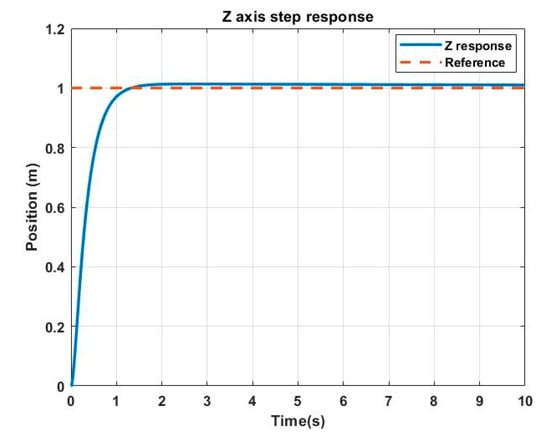
Figure 23.
PID step response in Z axis.
Table 5 shows the numerical results from the PID controller.

Table 5.
PID numerical results and comparison with backstepping.
From Table 5, we see that the PID controller does not meet the required design parameters, even though, overall, it is able to track a path satisfactorily. Finally, the PID controller was tested against the same disturbances that the backstepping controller was subjected to, but it did not reject the disturbances.
4. Conclusions
In this article, we deal with backstepping controller gain tuning for a quadrotor using genetic algorithms. First, the dynamics of the quadrotor were developed using the Newton‒Euler method. Then the equations of the rotational and translational dynamics of the system are presented. Subsequently, the setback control system, which is a recursive control procedure based on Lyapunov’s theory, is presented; this control system shows high performance in the face of parametric uncertainties, as is clear from the time of establishment (0.5 s) and the maximum impulse (<5%) on different reference inputs and errors of different magnitudes. The stability analysis based on Lyapunov’s theorem showed that the control proposal implemented by the self-adjustment of the gains leads to the error of the quadrotor having stability asymptotically. This is reflected in the comparison with other implemented methods; it can even be appreciated in the angles and perturbations implemented to test the method.
Compared with other backstepping controllers such as those presented by Amjad (2019), the present work obtains better results in terms of the error establishment time (less than 0.5 s) compared to the 3 s of the backstepping control proposed by Amjad. Although the systems are different, the controller is still the backstepping type.
Compared with the systems proposed for unmanned aerial vehicles, such as the one reported by Tennakoon and Munasinghe (2008), the present work has better results for the error settlement time, less than 0.5 s.
The present control proposal had satisfactory results in the simulations carried out in MatLab software, leaving as future work its physical implementation in a drone and the carrying out of real flight tests.
Author Contributions
Conceptualization O.R.-A., R.H.-A. and A.F.R.; methodology, O.R.-A., J.M.G.-G., R.H.-A., A.F.R. and C.F.-S.; software, O.R.-A. and R.H.-A.; validation, O.R.-A. and R.H.-A.; formal analysis, O.R.-A., J.M.G.-G., R.H.-A. and A.F.R.; investigation, O.R.-A., J.M.G.-G., R.H.-A. and A.F.R.; resources, J.M.G.-G. and R.H.-A.; data curation, J.M.G.-G. and R.H.-A. writing—original draft preparation, all authors; writing—review and editing, O.R.-A. and R.H.-A.; visualization, O.R.-A., J.M.G.-G., R.H.-A., A.F.R. and C.F.-S.; supervision, O.R.-A., J.M.G.-G., R.H.-A., A.F.R. and C.F.-S.; project administration, all authors; funding acquisition, O.R.A., A.F.R. and C.F.-S. All authors have read and agreed to the published version of the manuscript.
Funding
The authors would like to acknowledge the financial support of Universidad Politecnica de Queretaro in the production of this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Xin, J.; Zhong, J.; Yang, F.; Cui, Y.; Sheng, J. An Improved Genetic Algorithm for Path-Planning of Unmanned Surface Vehicle. Sensors 2019, 19, 2640. [Google Scholar] [CrossRef] [PubMed]
- Giernacki, W.; Horla, D.; Baca, T.; Saska, M. Real-Time Model-Free Minimum-Seeking Autotuning Method for Unmanned Aerial Vehicle Controllers Based on Fibonacci-Search Algorithm. Sensors 2019, 19, 312. [Google Scholar] [CrossRef] [PubMed]
- Castano, F.; Beruvides, G.; Villalonga, A.; Haber, R.E. Self-Tuning Method for Increased Obstacle Detection Reliability Based on Internet of Things LiDAR Sensor Models. Sensors 2018, 18, 1508. [Google Scholar] [CrossRef] [PubMed]
- Zemmour, E.; Kurtser, P.; Edan, Y. Automatic Parameter Tuning for Adaptive Thresholding in Fruit Detection. Sensors 2019, 19, 2130. [Google Scholar] [CrossRef]
- Espinoza, K.; Valera-Martínez, D.L.; Torres, J.A.; López-Martínez, A.; Molina-Aiz, F. An Auto-Tuning PI Control System for an Open-Circuit Low-Speed Wind Tunnel Designed for Greenhouse Technology. Sensors 2015, 15, 19723–19749. [Google Scholar] [CrossRef]
- Tang, J.; Zheng, J.; Wang, Y.; Yu, L.; Zhan, E.; Song, Q. Self-Tuning Threshold Method for Real-Time Gait Phase Detection Based on Ground Contact Forces Using FSRs. Sensors 2018, 18, 481. [Google Scholar] [CrossRef]
- Lee, C.; Chen, R. Optimal Self-Tuning PID Controller Based on Low Power Consumption for a Server Fan Cooling System. Sensors 2015, 15, 11685–11700. [Google Scholar] [CrossRef]
- Besada, J.A.; Bergesio, L.; Campaña, I.; Vaquero-Melchor, D.; Lopez-Araquistain, J.; Bernardos, A.M.; Casar, J.R. Drone Mission Definition and Implementation for Automated Infrastructure Inspection Using Airborne Sensors. Sensors 2018, 18, 1170. [Google Scholar] [CrossRef]
- Hamza, M.; Jehangir, A.; Ahmad, T.; Sohail, A.; Naeem, M. Design of surveillance drone with X-ray camera, IR camera and metal detector. In Proceedings of the 2017 Ninth International Conference on Ubiquitous and Future Networks (ICUFN), Milan, Italy, 4–7 July 2017; pp. 111–114. [Google Scholar]
- Pedro, J.O.; Dangor, M.; Kala, P.J. Differential evolution-based PID control of a quadrotor system for hovering application. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016; pp. 2791–2798. [Google Scholar]
- Zheng, H.; Zeng, Q.; Chen, W.; Zhu, H.; Chen, C. Improved PID control algorithm for quadrotor based on MCS. In Proceedings of the 2016 IEEE Chinese Guidance, Navigation and Control Conference (CGNCC), Nanjing, China, 12–14 August 2016; pp. 1780–1783. [Google Scholar]
- Mo, H.; Farid, G. Nonlinear and Adaptive Intelligent Control Techniques for Quadrotor UAV—A Survey. Asian J. Control. 2019, 21, 989–1008. [Google Scholar] [CrossRef]
- Pervaiz, M.; Khan, Q.; Bhatti, A.I.; Malik, S.A. Dynamical Adaptive Integral Sliding Backstepping Control of Nonlinear Nontriangular Uncertain Systems. Math. Probl. Eng. 2014, 2014, 1–14. [Google Scholar] [CrossRef]
- Knöös, J.; Robinson, J.W.C.; Berefelt, F. Nonlinear Dynamic Inversion and Block Backstepping: A Comparison. In Proceedings of the AIAA Guidance, Navigation, and Control Conference 2012, Minneapolis, MN, USA, 13–16 August 2012. [Google Scholar] [CrossRef]
- Koshkouei, A.; Zinober, A. Adaptive Sliding Backstepping Control of Nonlinear Semi-Strict Feedback form Systems. In Proceedings of the 7th IEEE Mediterranean Control Conference, Haifa, Israel, 28–30 June 1999. [Google Scholar]
- Koshkouei, A.; Burnham, K.J. Adaptive backstepping sliding mode control for feedforward uncertain systems. Int. J. Syst. Sci. 2011, 42, 1935–1946. [Google Scholar] [CrossRef]
- Koshkouei, A.J.; Mills, R.E.; Zinober, A.S.I. Adaptive Backstepping Control. In Variable Structure Systems: Towards the 21st Century; Yu, X., Xu, J.-X., Eds.; Lecture Notes in Control and Information Sciences; Springer: Berlin/Heidelberg, Germany, 2002; Volume 274, pp. 129–153. ISBN 978-3-540-45666-7. [Google Scholar]
- Gao, Y.; Tian, D.; Wang, Y. Fuzzy Self-tuning Tracking Differentiator for Motion Measurement Sensors and Application in Wide-Bandwidth High-accuracy Servo Control. Sensors 2020, 20, 948. [Google Scholar] [CrossRef] [PubMed]
- Lee, T.; Leok, M.; McClamroch, N.H.; Leoky, M. Geometric tracking control of a quadrotor UAV on SE (3). In Proceedings of the 49th IEEE Conference on Decision and Control (CDC 2010), Atlanta, GA, USA, 15–17 December 2010; pp. 5420–5425. [Google Scholar]
- Das, A.; Lewis, F.; Subbarao, K. Sliding Mode Approach to Control Quadrotor Using Dynamic Inversion. Chall. Paradig. Appl. Robust Control 2011, 3–24. [Google Scholar] [CrossRef]
- Sieberling, S.; Chu, Q.; Mulder, J.A. Robust Flight Control Using Incremental Nonlinear Dynamic Inversion and Angular Acceleration Prediction. J. Guid. Control. Dyn. 2010, 33, 1732–1742. [Google Scholar] [CrossRef]
- Ansari, U.; Bajodah, A.H. Robust generalized dynamic inversion based control of autonomous underwater vehicles. SAGE J. 2017. [Google Scholar] [CrossRef]
- Muliadi, J.; Kusumoputro, B. Neural Network Control System of UAV Altitude Dynamics and Its Comparison with the PID Control System. J. Adv. Transp. 2018, 2018, 1–18. [Google Scholar] [CrossRef]
- Kusumoputro, B.; Priandana, K.; Wahab, W. System identification and control of pressure process rig® system using backpropagation neural networks. ARPN J. Eng. Appl. Sci. 2015, 10, 7190–7195. [Google Scholar]
- Hernández-Alvarado, R.; García-Valdovinos, L.G.; Salgado-Jiménez, T.; Gómez-Espinosa, A.; Fonseca-Navarro, F. Neural Network-Based Self-Tuning PID Control for Underwater Vehicles. Sensors 2016, 16, 1429. [Google Scholar] [CrossRef] [PubMed]
- Reyad, M.; Arafa, M.; Sallam, E.A. An optimal PID controller for a qaudrotor system based on DE algorithm. In Proceedings of the 11th IEEE International Conference on Computer Engineering and Systems (ICCES), Cairo, Egypt, 20–21 December 2016; pp. 444–451. [Google Scholar]
- Mellinger, D.; Kumar, V. Minimum snap trajectory generation and control for quadrotors. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 2520–2525. [Google Scholar]
- Tesch, D.A.; Eckhard, D.; Guarienti, W.C. Pitch and Roll control of a Quadcopter using Cascade Iterative Feedback Tuning. In Proceedings of the 4th IFAC Symposium on Telematics Applications TA 2016, Porto Alwegre, Brasil, 6–9 November 2016. [Google Scholar]
- Jokar, A.; Godarzi, A.A.; Saber, M.; Shafii, M.B. Simulation and optimization of a pulsating heat pipe using artificial neural network and genetic algorithm. Heat Mass Transf. 2016, 52, 2437–2445. [Google Scholar] [CrossRef]
- Li, Y.; Song, S. A survey of control algorithms for Quadrotor Unmanned Helicopter. In Proceedings of the Fifth International Conference on Advanced Computational Intelligence (ICACI 2012), Nanjing, China, 18–20 October 2012; pp. 365–369. [Google Scholar]
- Yu, G.; Doukhi, O.; Fayjie, A.R.; Lee, D.J. Intelligent Controller Design for Quad-Rotor Stabilization in Presence of Parameter Variations. J. Adv. Transp. 2017, 2017. [Google Scholar] [CrossRef]
- Sadeghzadeh, I.; Abdolhosseini, M.; Zhang, Y. Payload Drop Application of Unmanned Quadrotor Helicopter Using Gain-Scheduled PID and Model Predictive Control Techniques. Lect. Notes Comput. Sci. 2012, 7506, 386–395. [Google Scholar]
- D’Amato, E.; Di Francesco, G.; Notaro, I.; Tartaglione, G.; Mattei, M. Nonlinear Dynamic Inversion and Neural Networks for a Tilt Tri-Rotor UAV. IFAC-PapersOnLine 2015, 48, 162–167. [Google Scholar] [CrossRef]
- Davoudi, B.; Taheri, E.; Duraisamy, K.; Jayaraman, B.; Kolmanovsky, I. Quad-Rotor Flight Simulation in Realistic Atmospheric Conditions. AIAA J. 2020, 58, 1992–2004. [Google Scholar] [CrossRef]
- Lee, J. Optimization of a modular drone delivery system. In Proceedings of the 2017 Annual IEEE International Systems Conference (SysCon), Montreal, QC, Canada, 24–27 April 2017; pp. 1–8. [Google Scholar]
- Berning, A.W.; Taheri, E.; Girard, A.; Kolmanovsky, I. Rapid Uncertainty Propagation and Chance-Constrained Trajectory Optimization for Small Unmanned Aerial Vehicles. In Proceedings of the 2018 Annual American Control Conference (ACC), Milwaukee, WI, USA, 27–29 June 2018; pp. 3183–3188. [Google Scholar]
- Ventura Diaz, P.; Yoon, S. High-Fidelity Computational Aerodynamics of Multi-Rotor Unmanned Aerial Vehicles. In Proceedings of the 2018 AIAA SciTech Forum, American Institute of Aeronautics and Astronautics, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar]
- Mishra, A.; Davoudi, B.; Duraisamy, K. Multiple-Fidelity Modeling of Interactional Aerodynamics. J. Aircr. 2018, 55, 1839–1854. [Google Scholar] [CrossRef]
- Lim, S.P.; Haron, H. Performance comparison of Genetic Algorithm, Differential Evolution and Particle Swarm Optimization towards benchmark functions. In Proceedings of the 2013 IEEE Conference on Open Systems (ICOS 2013), Kuching, Malaysia, 2–4 December 2013; pp. 41–46. [Google Scholar]
- Winiczenko, R.; Górnicki, K.; Kaleta, A.; Janaszek-Mańkowska, M. Optimisation of ANN topology for predicting the rehydrated apple cubes colour change using RSM and GA. Neural Comput. Appl. 2018, 30, 1795–1809. [Google Scholar] [CrossRef] [PubMed]
- McKerrow, P. Modelling the Draganflyer four-rotor helicopter. In Proceedings of the 2004 IEEE International Conference on Robotics and Automation, New Orleans, LA, USA, 26 April–1 May 2004; Volume 4, pp. 3596–3601. [Google Scholar] [CrossRef]
- Yim, S. Comparison among Active Front, Front Independent, 4-Wheel and 4-Wheel Independent Steering Systems for Vehicle Stability Control. Electronics 2020, 9, 798. [Google Scholar] [CrossRef]
- Kong, W.; Zhou, D.; Yang, Z.; Zhao, Y.; Zhang, K. UAV Autonomous Aerial Combat Maneuver Strategy Generation with Observation Error Based on State-Adversarial Deep Deterministic Policy Gradient and Inverse Reinforcement Learning. Electronics 2020, 9, 1121. [Google Scholar] [CrossRef]
- Zhang, C.; Zhou, L.; Li, Y.; Fan, Y. A Dynamic Path Planning Method for Social Robots in the Home Environment. Electronics 2020, 9, 1173. [Google Scholar] [CrossRef]
- Wei, Y.; Hong, T.; Kadoch, M. Improved Kalman Filter Variants for UAV Tracking with Radar Motion Models. Electronics 2020, 9, 768. [Google Scholar] [CrossRef]
- Trujillo, J.-C.; Munguía, R.; Urzua, S.; Grau, A. Cooperative Visual-SLAM System for UAV-Based Target Tracking in GPS-Denied Environments: A Target-Centric Approach. Electronics 2020, 9, 813. [Google Scholar] [CrossRef]
- Masood, K.; Molfino, R.; Zoppi, M. Simulated Sensor Based Strategies for Obstacle Avoidance Using Velocity Profiling for Autonomous Vehicle FURBOT. Electronics 2020, 9, 883. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).