1. Introduction
It is challenging to ascertain the domain of attraction (DA) for a point in equilibrium in a non-linear dynamical system. DA represents those initial conditions where the system state converges to equilibrium asymptotically [
1,
2]. Incorporating DA in the design specifications is crucial while working on control synthesis to ensure system stability [
3,
4]. Specifically, it would be helpful to gauge the optimal Lyapunov function that maximises the DA [
5,
6,
7]. Consequently, it is vital to determine the shape of this region every time one has to scrutinise the system’s stability [
7]. For this reason, we use the fundamental theory regarding Lyapunov stability (see [
1,
8,
9]). As a matter of fact, for a specific Lyapunov, the biggest estimated area of asymptotic stability may be characterised as the largest set of the function, which is in the area where the derivate is negative [
10,
11].
It is widely understood that it is non-trivial to study the DA. Considering the nonlinear system, several methods have been suggested for calculating inner estimates, see e.g., [
12,
13]. For instance, some classical approaches like the Zubov method [
14], La Salle method [
15] and the trajectory reversing method are studied in [
16]. Typically, such techniques use Lyapunov functions and yield inner estimates for the domain of attraction by providing a set of sublevels for a Lyapunov function. These estimates are confirmed mathematically by validating those sets as invariant.
For nonlinear polynomial systems, several techniques have been suggested to handle this step. A majority of these may be used only with this category of system, e.g., Sum of Square (SOS) relaxation-based techniques, which cause a Linear Matrix Inequality (LMI) [
17], Bilinear Matrix Inequality (BMI) techniques [
18], SOS programming [
19], and methods employing simulations and those based on Chebychev points [
20]. The interest in enlarging the stability and robustness domain for nonlinear optimal control systems with parametric and structural uncertainties is attractive and well justified for practical process implementation [
21,
22].
This paper further assesses the potential benefits of using the stability theory for approximating DA using a simpler shape for estimation. A Lyapunov function is used to describe the shape, and it is typically a quadratic function. For a specific Lyapunov function, the calculation of an optimal DA estimate (which is the biggest estimate for the selected shape) is equivalent to solving a non-convex distance problem.
Considering this context, a problem of significant importance is the choice of quadratic LF (QLF). The selected LF for estimating the DA significantly affects the volume of the optimal estimate. It is obvious that the optimal quadratic LF (OQLF) is that which designates the function that provides for maximum volume. Discouragingly, the calculation of the OQLF is akin to solving a non-convex optimisation [
23]. The Largest Estimate of DA (LEDA) must be calculated for a given QLF after which the OQLF may be determined.
Our study uses the enlargement synthesis technique substantiated in [
24] and extends it to use an evolutionary approach in order incorporate an estimator of a candidate Lyapunov function [
6]. The problem of optimising the DA is converted to a generalised eigenvalue problem (GEVP). It is assumed that the Lf describing the form of the largest estimation of the attraction region is a polynomial. Using identified relaxations that have been established around the polynomial sum of square, it is revealed that a lower bound of the largest attainable attraction region can be computed through a generalised eigenvalue problem. This later is considered to be a quasi-convex LMI optimisation where the solution can be computed efficiently.
In this paper, an original strategy aiming to enlarge domains of attraction of stable equilibriums based on maximal Lyapunov functions is developed. The key idea consists in searching the coefficients of the best level set of a Lyapunov function. This latter is supposed to be fully enclosed in the region of negative definiteness of its time derivative. A heuristic optimisation methodology is established, which involves a tangency constraint between the level sets and requirements on the sign of the Lyapunov function. Such constraints help in evading a large number of potential local solutions of the nonlinear optimisation routine. In a first step, a CPSO [
25] algorithm is implemented to estimate the maximal Lyapunov function coefficients. Subsequently, an iterative technique based on GEVP is set up for the resultant LF, which provides the maximal estimate for the DA.
The largest varieties of stabilising control methods considered for nonlinear systems are effective only within a definite domain of the state variables space, titled the attraction domain. The calculation of this domain is generally a delicate task and is time-consuming. This paper offers an efficient computational CPSO approach that is validated to estimate the region of stable equilibrium points for the class of nonlinear polynomial systems.
The main objective of this work consists of designing a swift optimising Lyapunov-based technique that allows the identification of the Lyapunov function coefficients. Subsequently, it exploits the resultant function in a heuristic optimising algorithm to maximise the region of attractions for the class of nonlinear polynomial systems. The synthesised technique is computationally valid and is efficient for real-time applications. In this technique, after a Lyapunov function candidate is computed, a CPSO algorithm estimates the maximal sublevel set of the Lyapunov function such that the time derivative is negative definite through the defined sublevel set. The proposed technique is implemented to estimate the attraction region of numerous benchmark nonlinear systems, which have been previously examined in the related literature, to confirm its aptitude in an analytical study in comparison with pre-existing approaches.
The motivation of this work is to develop an evolutionary synthesised technique that will be appropriate for estimating enlarged DAs of polynomial nonlinear systems. Unlike most existing works, the designed algorithm is running with non-fixed LF. Indeed, the CPSO is currently optimising the LF coefficients and continuously running a quasi-convex LMI optimisation problem. Moreover, the GEVP is considered to be the objective function for the CPSO, which is an original technique of estimation where a meta-heuristic approach is combined with a deterministic technique.
As a matter of fact, it is necessary to synthesise a computationally operative algorithm that converges to a maximised DA in a significantly reduced time. Regardless of the benefit of contributing in a better enlarged accurate DA at less time, CPSO can be very useful for real-time control problems. It is likewise valuable for the control strategies using online sequential composition formalism as described in the literature. For assessing these algorithms, certain benchmark functions are deployed. The simulation results highlight that applying the quadratic Lyapunov function rather than using random sequences enhances the performance of evolutionary algorithms.
After this introduction, the paper is organised as follows. In
Section 2, we give a general description of the class of systems deliberated and recall some fundamental notions. In
Section 3, we set up the LMI-based iterative algorithms to devise the Lyapunov function which maximises the DA estimate.
Section 4 discusses the CPSO-based parameter selection approach.
Section 5 presents the simulation outcomes of a renowned numerical example. A comparative study with other methods and a results analysis and discussion technique will be established to evaluate the efficiency of the synthesised strategy in
Section 6. A brief conclusion is offered in
Section 7.
Standard notation has been used in this paper, where represents the set of real numbers, denotes the transpose of the real matrix ; positive definite (semi-definite) matrix; is the identity matrix ; represents the determinant of A; refers to the Kronecker product of matrices and ; s.t. is used to denote subject to.
3. Estimating the Asymptotic Region Using Parametric Lyapunov-Based Techniques
Calculating Lower Bounds Dependent Parameter
The initial step towards determining the domain of attraction is the introduction of a parameterisation for the square Lyapunov form representing the system origin Equation (2). The conditions ensuring that is a LF for the system origin can be stated as:
is radially unbounded and positive definite;
is negative definite locally.
For a homogenous Lyapunov function, the square matricial representation (SMR) is expressed as
where
is a vectorial function comprising all monomials wherein the degree
in
and
is a symmetric matrix comprising the parametric coefficient of the Lyapunov function.
where
represents the weighting coefficients for the Lyapunov function.
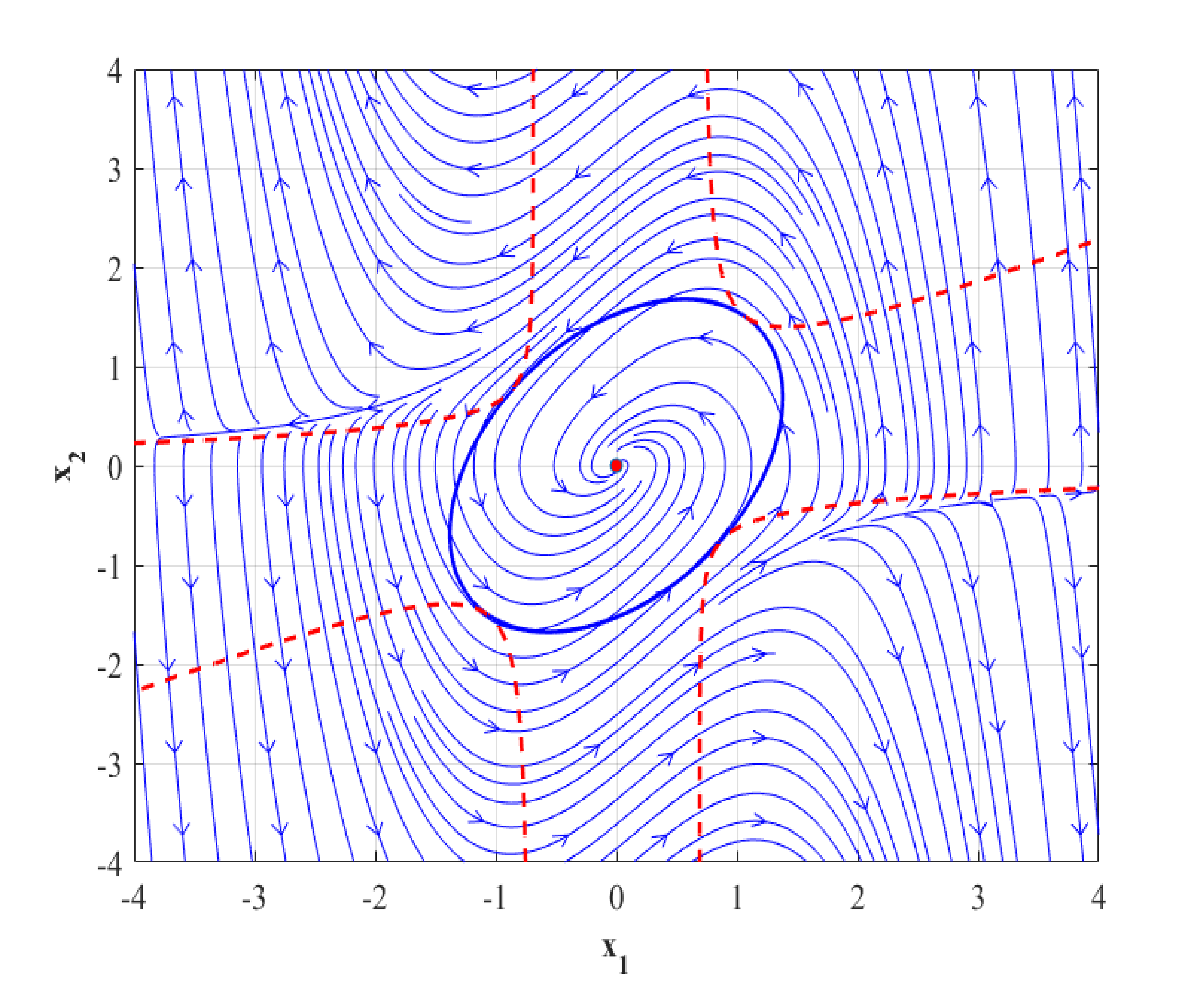
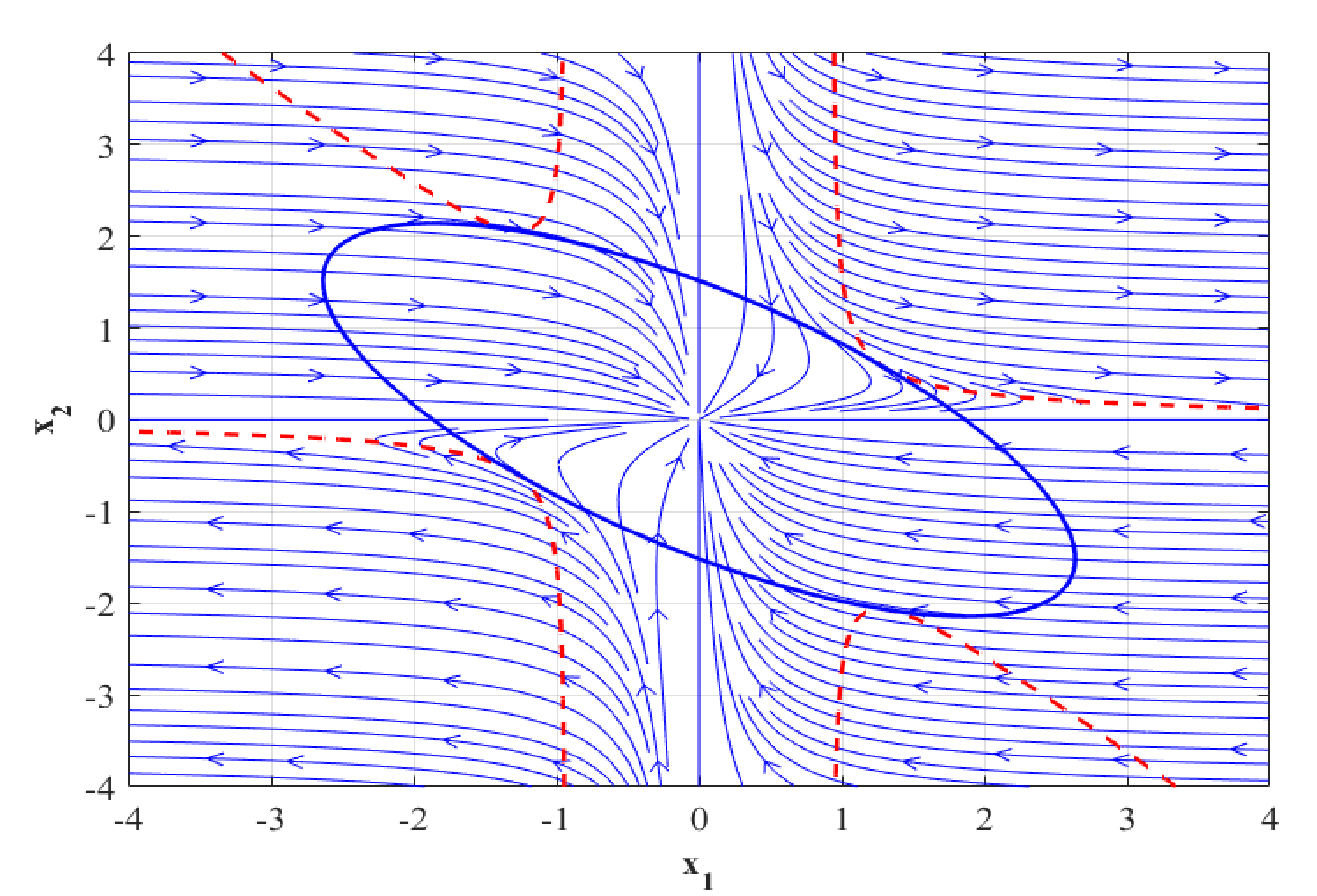
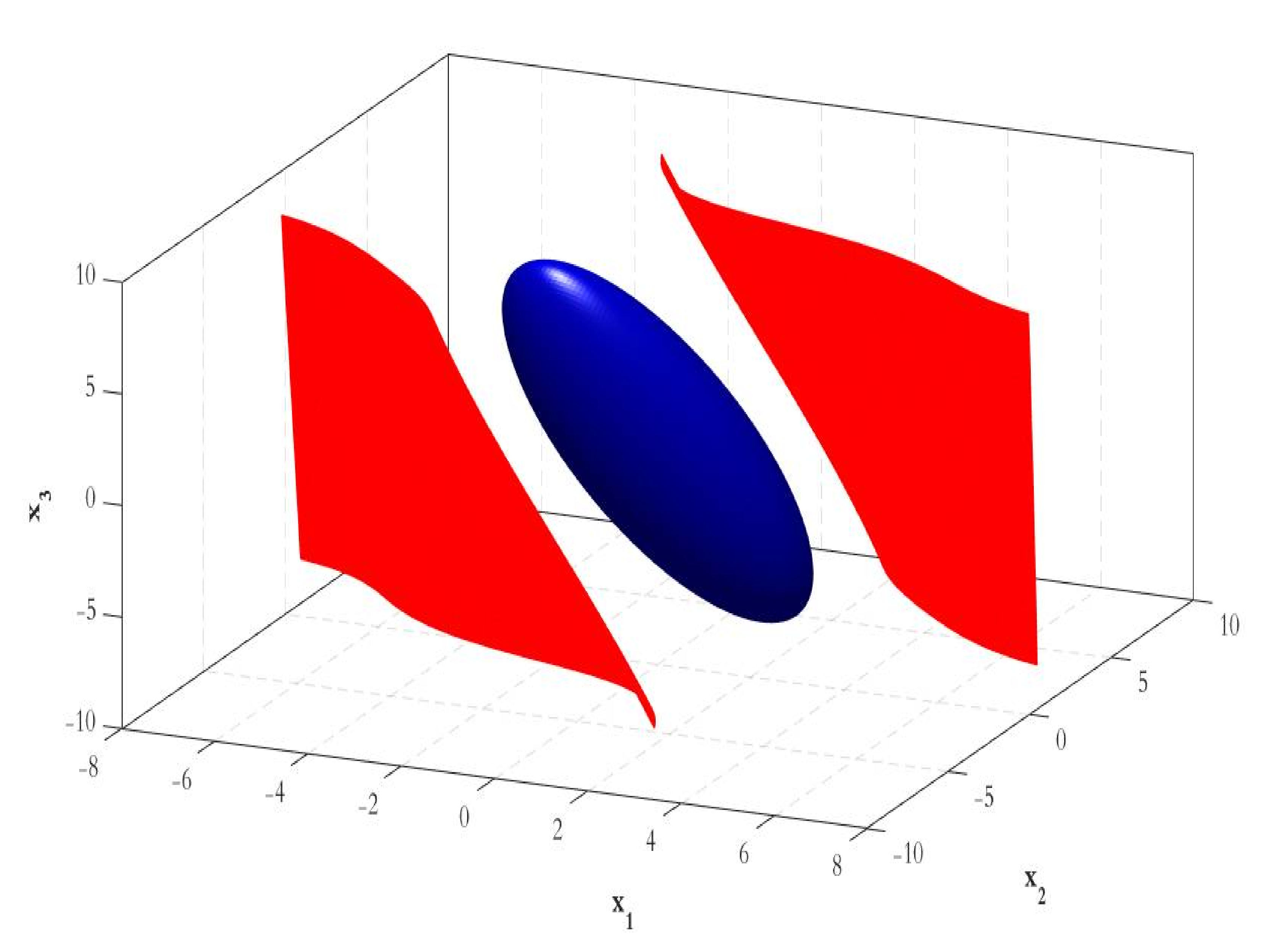
Let the ellipsoidal set associated with the positive definite QLF be defined as
while the negative time derivative region is defined as
Then, under that condition that , it can be said that is an ellipsoidal estimate of the DA.
To handle the estimation problem, it should first be converted to an optimisation problem, where the LEDA should be minimised and is represented by
where
This note considers that the problem is the calculation of the largest achievable LEDA in the considered matrix .
Definition 1 Considering a feasible positive definite QLFfor system (2), the corresponding LEDA of the origin is stated by The optimal positive definite QLF is described as the QLF that maximises the DA volume.
Definition 2 [
17]
For system (2), specifies the optimal positive definite QLF whereand It may be observed that the calculation of optimal positive definite QLF is akin to solving a double non-convex optimisation problem. In fact, , which represents the volume function, reveals not only the local maxima, but also the global, which is represented by . Additionally, even the evaluation of necessitates the computation of , which refers to the solution for the non-convex distance problem (17).
To be able to address (19), it is evident that a specified scalar
is a lower bound of
, i.e.,
is easily provable if
This condition can also be outlined in the following lemma.
Lemma 1: Letbe a given scalar and define the polynomialwhereis any positive definite polynomial, then To check the condition in Lemma 1, the following polynomials are introduced
The polynomial degrees of
and
are
and
respectively. If we choose
degree to be
such that
Then the polynomial has a degree of , which is also the degree of , where .
To get an appropriate form of the optimisation problem, we use the complete square matricial representation (CSMR) and the square matricial representation (SMR) of the polynomials [
24]. This implies that
, and
may be written using the SMR with regards to the vectors
,
, and
, that do not have the constant term, that is
where
,
and
denote symmetric matrices having suitable dimensions. The matrix
is specified as
where
denotes the CSMR matrix for
, while
and
represent any SMR matrices of,
and
, respectively
Then
Since in , multiplies the parameters of , (28) leads to a non-convex problem. To move past this difficulty, (29) is reformulated in a GEVP. To proceed, the following preliminary result is required.
Lemma 2 [
24].
Suppose that there exists a polynomialwhere is a scalar and the SMR matrix is specified below: Theorem 2 [
24].
Let denote a specified Lyapunov Function having and let denote any scalar. The lower bound in (29) is specified aswhere is the solution of the GEVP. Using this GEVP technique, we can establish a domain of attraction. Nevertheless, this technique is usually limited to systems and arbitrary Lyapunov functions that can be expressed by polynomial equations. This paper presents an alternative by employing the evolutionary approach to estimate the optimal Lyapunov function.
4. Main Results
This section presents a strategy for choosing good parameters for the optimal positive definite QLF. The fundamental idea is to determine the matrix , which maximises the volume of an ellipsoid having a fixed shape and is included in in (16), which denotes the negative time derivative area. It is reasoned that to maximise the size of the LEDA, an appropriate strategy is to broaden the set , which itself contains the LEDA.
4.1. Computation of Optimal Positive Definite QLF: Evolutionary Approach
Let denote a specified ellipsoid domain. The volume of the ellipsoid specified by is proportional to , and therefore the optimisation problem (17) searches for the biggest ellipsoid inside the region for some feasible QLF matrix .
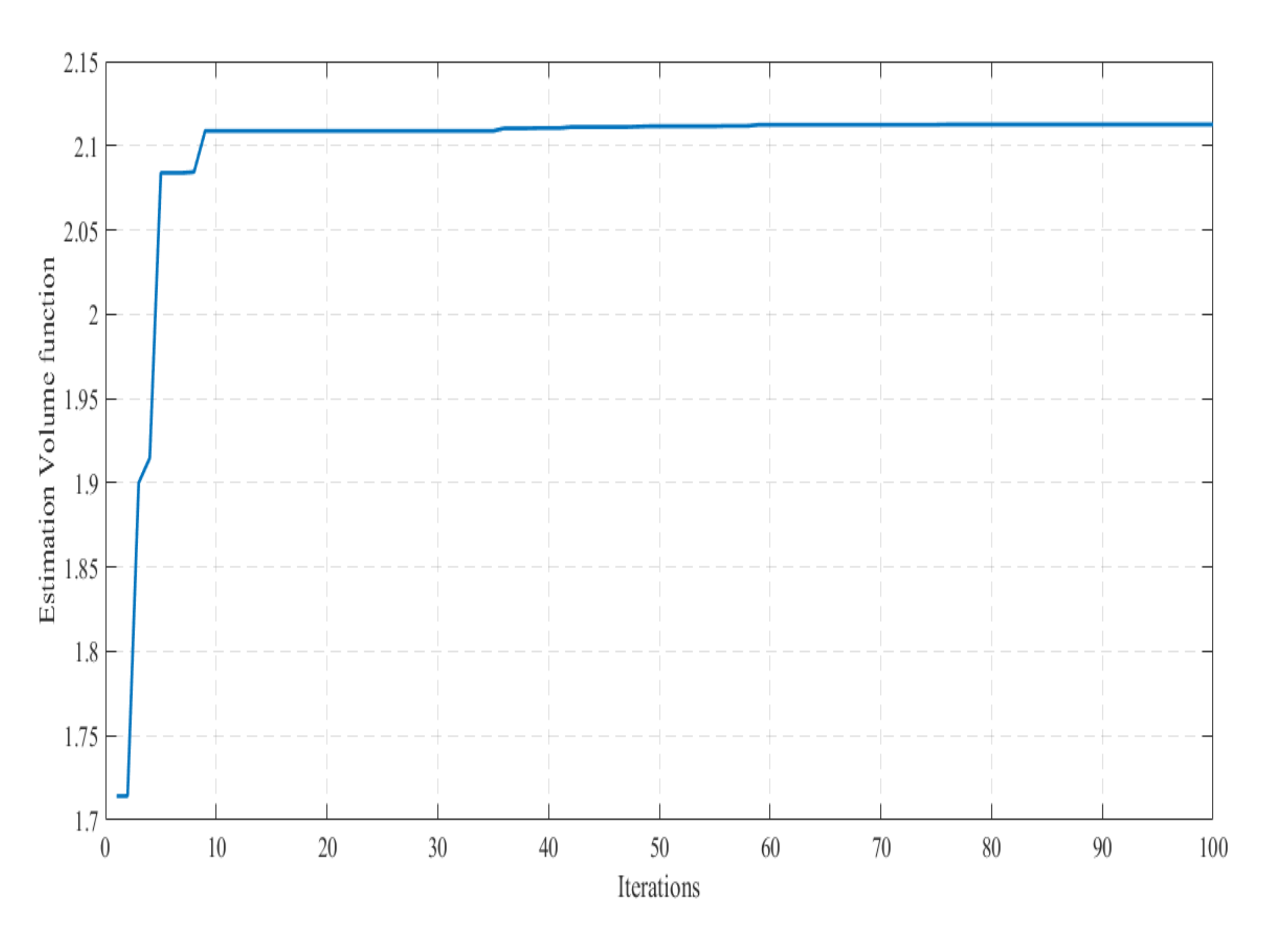
The coefficients for parameters of the Lyapunov function are evaluated using evolutionary techniques. The user-defined candidate Lyapunov function, as well as the corresponding domain and the condition specified by Theorem 1, are validated for being positive and being negative. In the case that these conditions are not met, GEVP (34) optimisation is not feasible; hence, we estimate repeatedly the coefficients for the Lyapunov function until the GEVP optimisation has a solution. The basis for this criterion is that to obtain a large optimal estimate of the parameters using Evolutionary Algorithms, the volume should be maximal. Considering the evolutionary algorithms, we specifically used swarm optimisation and chaotic particle swarm optimisation.
The algorithm begins with being initialised as the initial domain.
Our algorithm relies on determining the matrix G that maximises the volume of a fixed-shape ellipsoid whose boundary falls inside the negative time derivative region (16).
4.2. Particle Swarm Optimisation
4.2.1. Motivation on PSO Methods
Swarm intelligence is a crucial subject of evolutionary computing research. It investigates the mutual natural behaviour of distributed, self-organised processes. The stimulation often originates from natural, biological organisms [
27]. An interesting example of swarm intelligence is the PSO.
This latter is a meta-heuristic global optimisation technique that is now one of the most commonly used optimisation methods.
In this paragraph, a short comprehensive exploration of PSO is presented. As an efficient optimising technique, PSO has seen several rapid advances, such as fuzzy PSO, chaotic PSO, hybridisation with genetic algorithm, artificial bee colony, discrete optimisation, extensions to multi-objective optimisation, etc. [
27].
One of the most promising fields in which PSO has been implemented is in automation and controlled systems. The PSO algorithm has been adopted by each research domain that follows a definite scheme and has approved swarm intelligence methods for attaining optimal performance. Several proposed control schemes have been based on linear matrix inequalities with parameters that are tuned by PSO [
28].
Numerous research subjects have been fully addressed in the literature [
29], including supply chain management, floor planning design, weapon target assignment issues, strategic industrial coordination and symbolic regression analysis.
Many other works investigate analytical analysis problems in control theory. It is essentially a matter of solving nonlinear problems that are difficult to address with conventional analytical techniques. The objective of the remaining part of this paper is to pave the way in order to implement a hybrid estimating technique merging between CPSO and an LMI technique.
4.2.2. Definition
PSO optimisation is a population-based technique. The method’s computational efficiency and simplicity are the reason it has seen widespread use in several fields, especially for parameter optimisation [
30]. In PSO, the individual agents are referred to as “particles”. “Position” refers to a vector of the candidate solutions and is associated with every particle. Additionally, a “velocity” operator regulates the approach to a globally optimal solution [
31]. The literature shows that PSO is one of the most efficient methods for solving non-smooth global optimisation problems. The key advantages of such a method can be summarised as follows:
It is a derivative-free technique, unlike comparable meta-heuristic optimisation methods.
It is simple in its coding implementation and fundamental concept compared to other heuristic optimisation methods.
It is less sensitive to the features of the objective function when compared to the conventional analytical techniques and other heuristic approaches.
Compared with other heuristic optimisation techniques, PSO has a limited number of parameters: the acceleration coefficients and the inertia weight factor. Equally importantly, the sensitivity of parameters to the optimal solutions is considered to be less delicate compared to other heuristic algorithms.
PSO appears to be less dependent on a set of initial points when evaluated with other evolutionary methods, including that the algorithm convergence is robust.
PSO methods can engender high-quality solutions within a shorter calculation time and with more stable convergence features than other stochastic techniques.
Based on the above characteristics, we opted to merge CPSO technique with an LMI-based method to obtain more accurate DA in less time. This can be very beneficial for real-time control problems. It is similarly constructive for control techniques using online sequential composition concepts. A comprehensive presentation of the PSO algorithm, variants of the algorithm, algorithm convergence analysis, and parameter tuning is specified in the references [
32,
33,
34,
35], and references cited therein. “Position” refers to a vector of the candidate solutions and is associated with every particle. Additionally, a “velocity” operator regulates the approach to the globally optimal solution.
In the case pertaining to this study, it is only necessary to ensure that a connection exists between the “Stability world” and the "PSO world” using the position of a particle [
36]. The decision variables that represent the parameters to be evaluated are specified as the position vector of the
ith particle, as presented below:
where
is the swarm size (number of particles).
In every iteration
, the velocity for every particle in the swarm is updated, and the positions are calculated using the following equations:
denotes the current candidate solution encoded using the position of the
ith particle during iteration
and
denotes the updated particle position.
where
and
denote the lower and upper bounds for the
dimension, respectively.
and
are the velocities possessed by the new and old particles, respectively.
denotes the best position, also called the “personal best”, which the
ith particle attained in the past.
denotes the best position between the neighbours of every particle and is also referred to as the “global best”.
and
denote two random numbers in the range (0, 1) and
and
denote the coefficients of acceleration, which regulate how far a particle will reach during a single generation. The inertia weight
determines the effects of the previous particle velocity on its current velocity.
defines the maximum number of iterations. Generally, the weight of inertia is decreased in a linear sense from 0.9 to 0.4 during the progression of the exploration. This is done to appropriately balance the global and local searching of the swarm capabilities. The corresponding equation for inertia weight
can be specified as:
In Equation (39), and have values of 0.9 and 0.4, respectively. Iteration max refers to the maximum iterations permitted.
4.2.3. PSO Stability
The conditions necessary and sufficient for swarm stability were derived in [
34] and are stated below
and
Such conditions ensure that the system converges to a stable equilibrium. Nevertheless, it cannot be said with absolute certainty that the proposed solution would be the global optimum.
4.2.4. Computation of Fitness Function
The fitness function computation is the primary operation that needs to be conducted while executing a PSO algorithm. Accordingly, the evaluation of the particle quality is done using the volume of the domain of attraction.
is the objective function that needs to be maximised. Given the position
for the
ith particle, the domain of attraction
, and the matrix
, the process specified in Algorithm 1 may be used to evaluate the fitness function for the
ith particle.
| Algorithm 1 Evaluation of the fitness function |
| Require:,
,
|
| 1. Initialise:
,
,
|
| 2.Fordo |
| 3.
Form the CSMR matrix of the homogeneous form in (27);
|
| 4.
Run an GEVP feasibility test to compute the domain of attraction .
|
| 5.
if then |
| 6.
|
| 7.
|
| 8.
Store in |
| 9.
end if |
| 10.
|
| 11.
end for |
| 12.
return:
|
4.3. Fundamentals of Chaotic PSO (C-PSO)
In the PSO technique, the varying parameters
and
are the crucial features influencing the characteristics of the algorithm convergence [
37]. The weight of inertia regulates the steadiness between local searchability and global examination. While a larger inertia weight favours global exploration, a smaller weight of inertia favours local searchability. Therefore, the search process typically involves decreasing linearly the weight of inertia, starting at 0.9 and ending at 0.4. Given the fact that the logistic maps are the often-used chaotic behaviour maps, chaotic sequences may be rapidly created and easily saved. Additionally, there is no requirement to store long sequences [
38]. The CPSO technique comprises sequences produced by the logistic maps which update randomised parameters
and
in PSO.
The logistic map modifies the parameters
and
as per the specified Equation (37), such that
will be substituted by
where:
will be substituted by:
At the value of
, Equation (42) outputs a chaotic sequence, having a value between 0 and 1. In Equation (42), for every independent run,
is generated randomly.
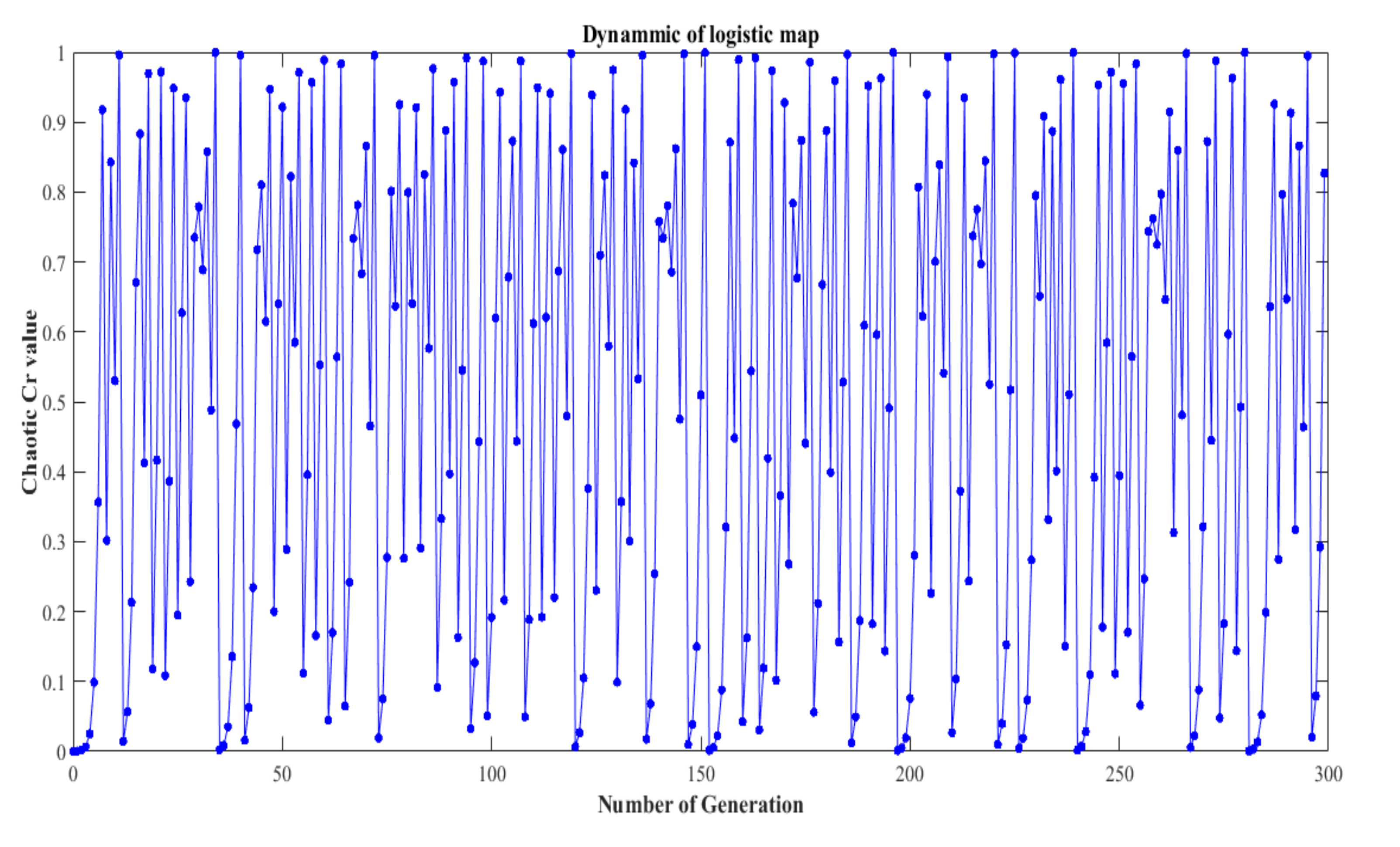
Figure 1 depicts the chaotic value
generated through a logistic map with
and 300 iterations.
For CPSO, the velocity update formula may be specified as:
The following pseudo-code describes the computational process for calculating the domain of attraction in a polynomial system by using the proposed Chaotic-PSO-based algorithm.
| Algorithm 2 Pseudo-code of the Chaotic-PSO |
01: Start
02: Initialise the particles swarm in a random way
03: Create randomly
04: while (the ending criterion is not obtained or iteration number is performed)
05: Assess the particle swarm fitness criterion
06: for to particles’ number
07: Determine
08: Determine
09: for till particle dimension number
10: Refresh the chaotic value as described by Equation (42)
11: Refresh the particles position as defined by Equations (37) and (38)
12: Increment
13: Increment
14: Refresh the value of the inertia weight given by Equation (39)
15: Increment generation till stopping criterion is satisfied
16: end
17: end
18: end |
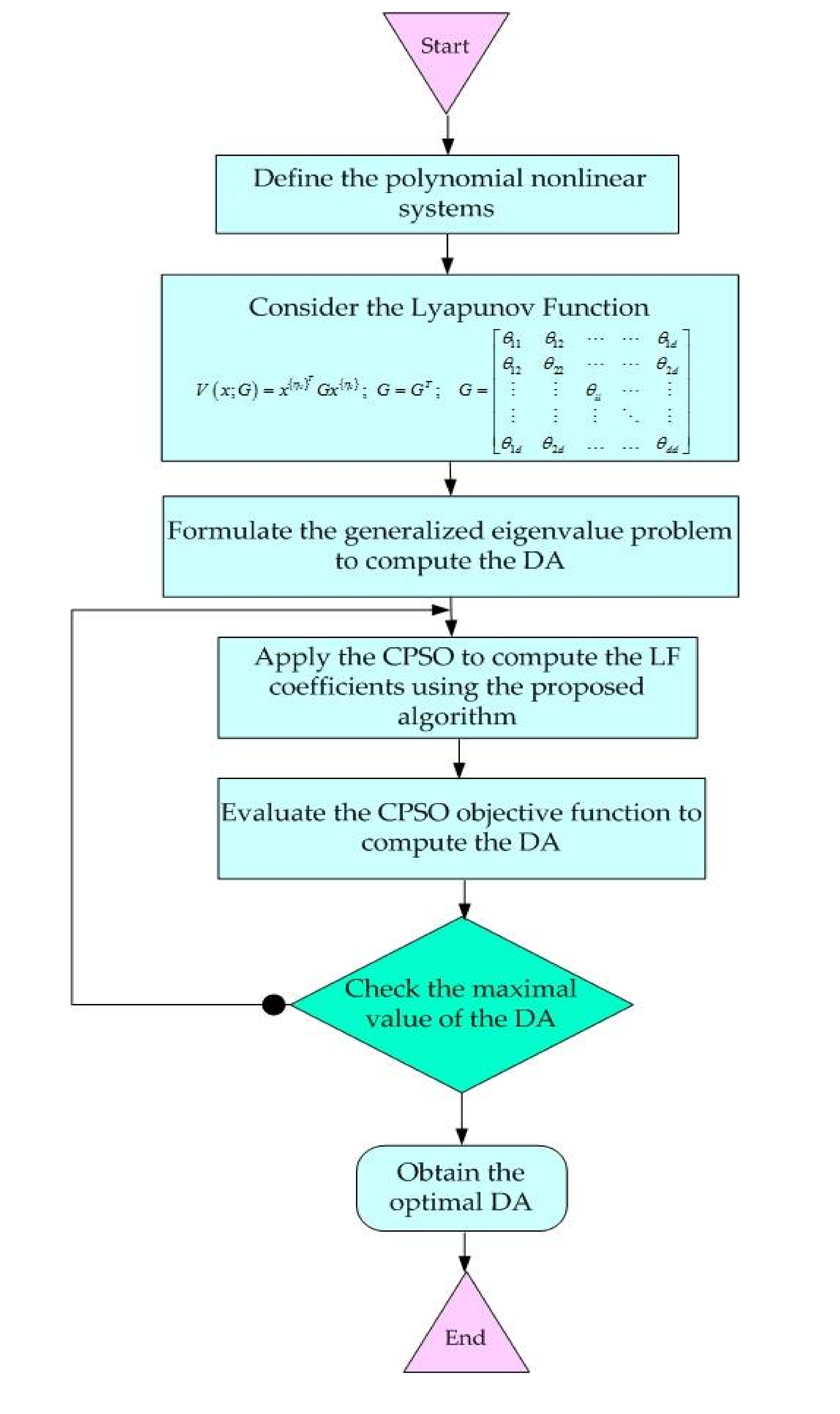
The flowchart describing the developed strategy is described by
Figure 2.
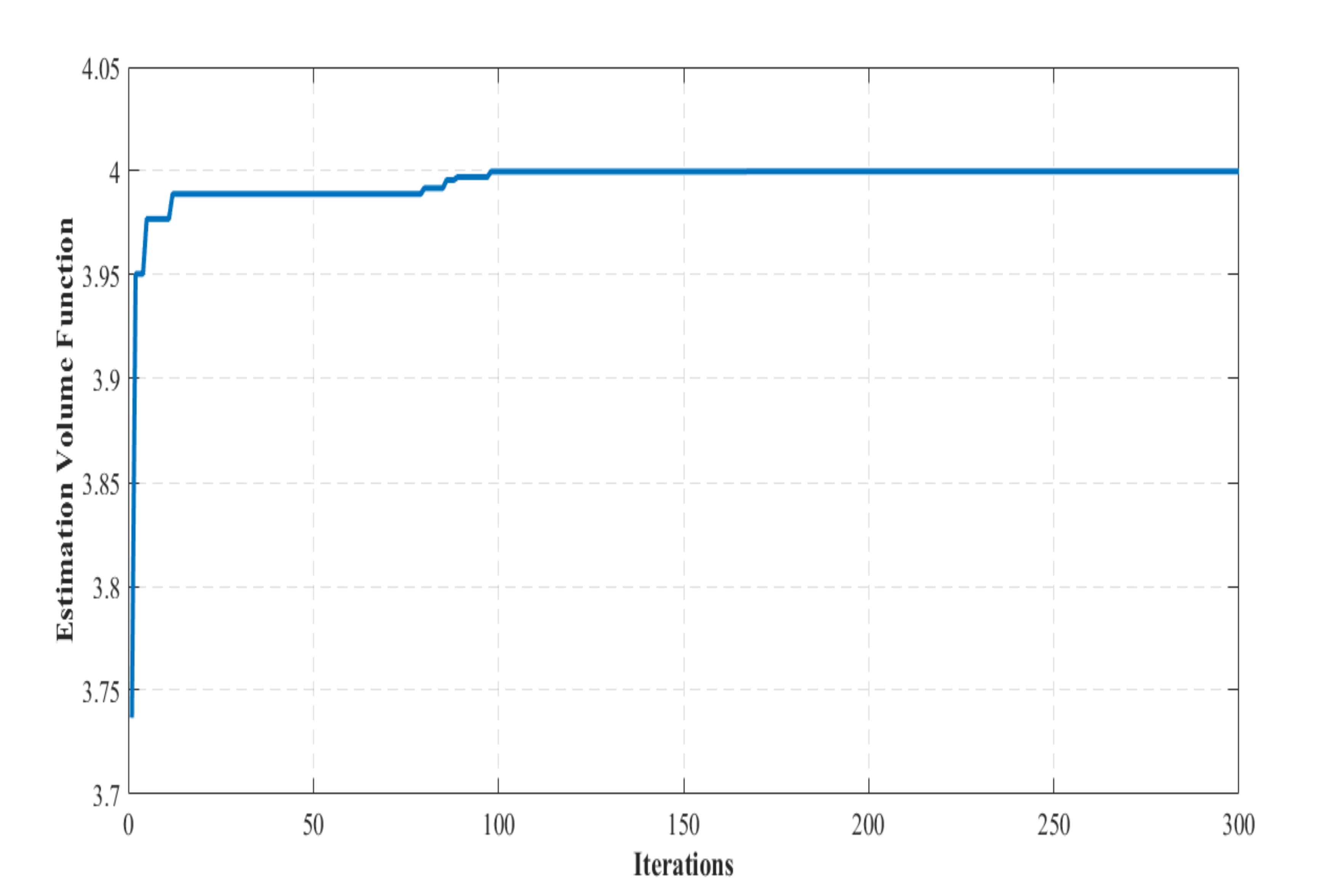
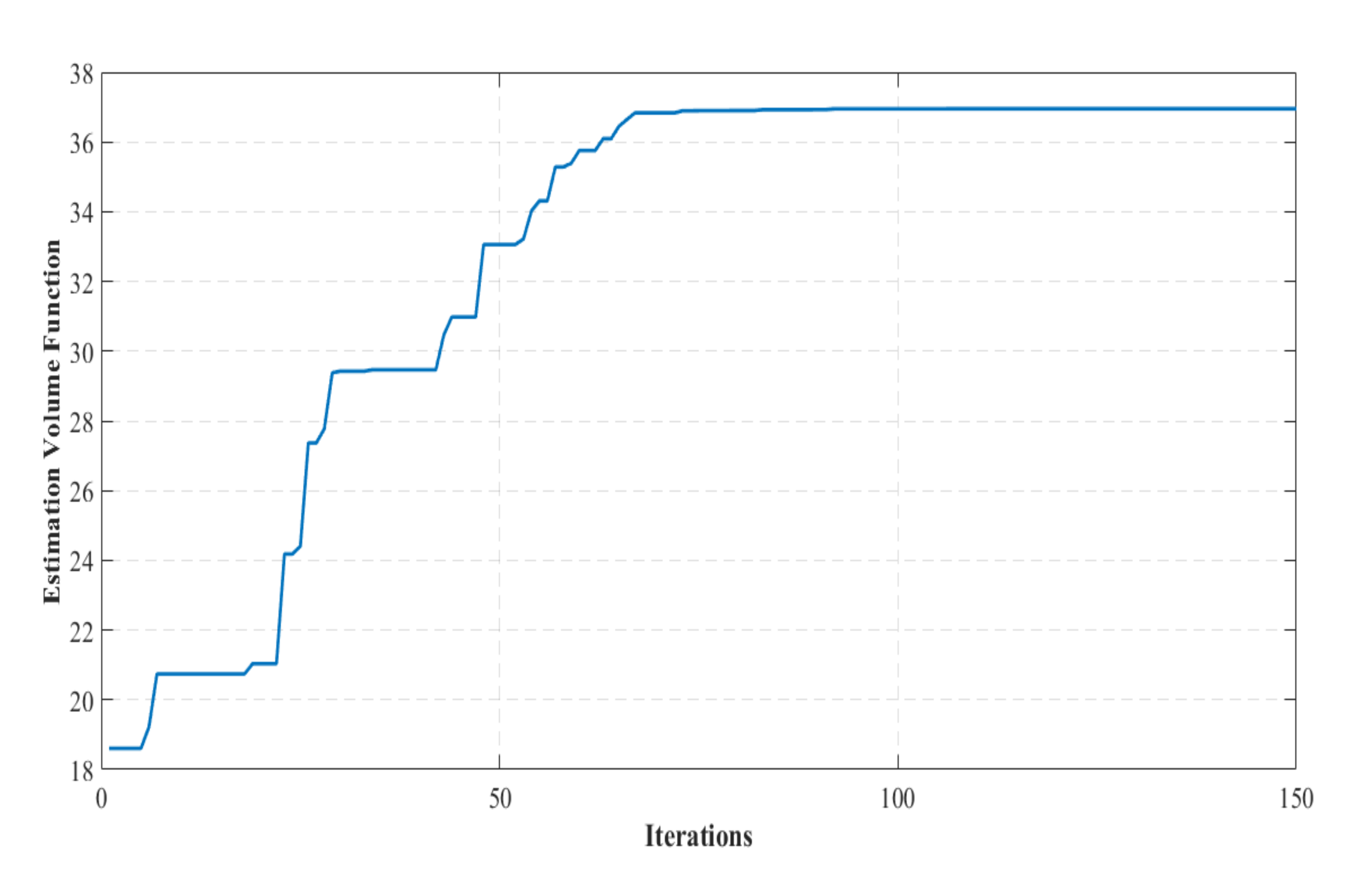
6. Results Analysis and Discussion
This section is dedicated to an evaluative comparative analysis between the synthesised CPSO estimation strategy in this paper and another peer reviewed technique [
26].
Table 1 provides the estimated DA features for three dynamical nonlinear systems with quadratic LF(s) taken from the literature [
39,
40]. The selected examples are presented in their nonlinear polynomial form. Examples E1 [
39] and E2 [
40] are second-order systems. However, example E3 [
39] is a third-order nonlinear polynomial model. Please note that the main evaluation criterion is the domain volume. The obtained results are quite satisfactory in terms of the value of the domain volume. Moreover, the designed strategy provides a complete solution starting from defining the optimal LF and finishing with providing the maximal domain volume. This result is achieved for all studied examples with an easy implementation concept and low consuming time.
A second step was performed to evaluate the performance of the CPSO strategy, consisting of investigating the domain volume for the three examples based on the same LF that was reported in [
26,
39,
40].
For each example, the maximum possible value of
is computed by the CPSO method and compared with the outcomes obtained by a peer optimisation-based technique, reported in the literature [
26]. It appears obvious in
Table 2 that for the three investigated examples, the estimated volumes of the DA(s) attained by the CPSO technique are significantly better than the estimates resulting from optimisation-based approaches. For the case of example E3, the performance of the CPSO scheme is even larger and more accurate.
Likewise, it can be concluded that the developed CPSO procedure is appropriate for estimating enlarged DA of polynomial nonlinear systems. As a matter of fact, it is computationally operational and converges to the optimal DA estimate in a significantly reduced time. Despite the benefit of offering more accurate DA in less time, CPSO can be very useful for real-time control problems. It is likewise valuable for control strategies that use online sequential composition formalism as described in [
26]. Finally, we should emphasise the fact that the work presented in [
26] is based on a random procedure that characterises the evolution of the designed algorithm. This means that an intensive simulation study should be performed each time to obtain the optimal solutions. This fact is the main disadvantage for the described approach. For the CPSO strategy, the final estimated domain is the same independent of the simulation settings.