A Novel Switched-Capacitor Multilevel Inverter Topology for Energy Storage and Smart Grid Applications
Abstract
1. Introduction
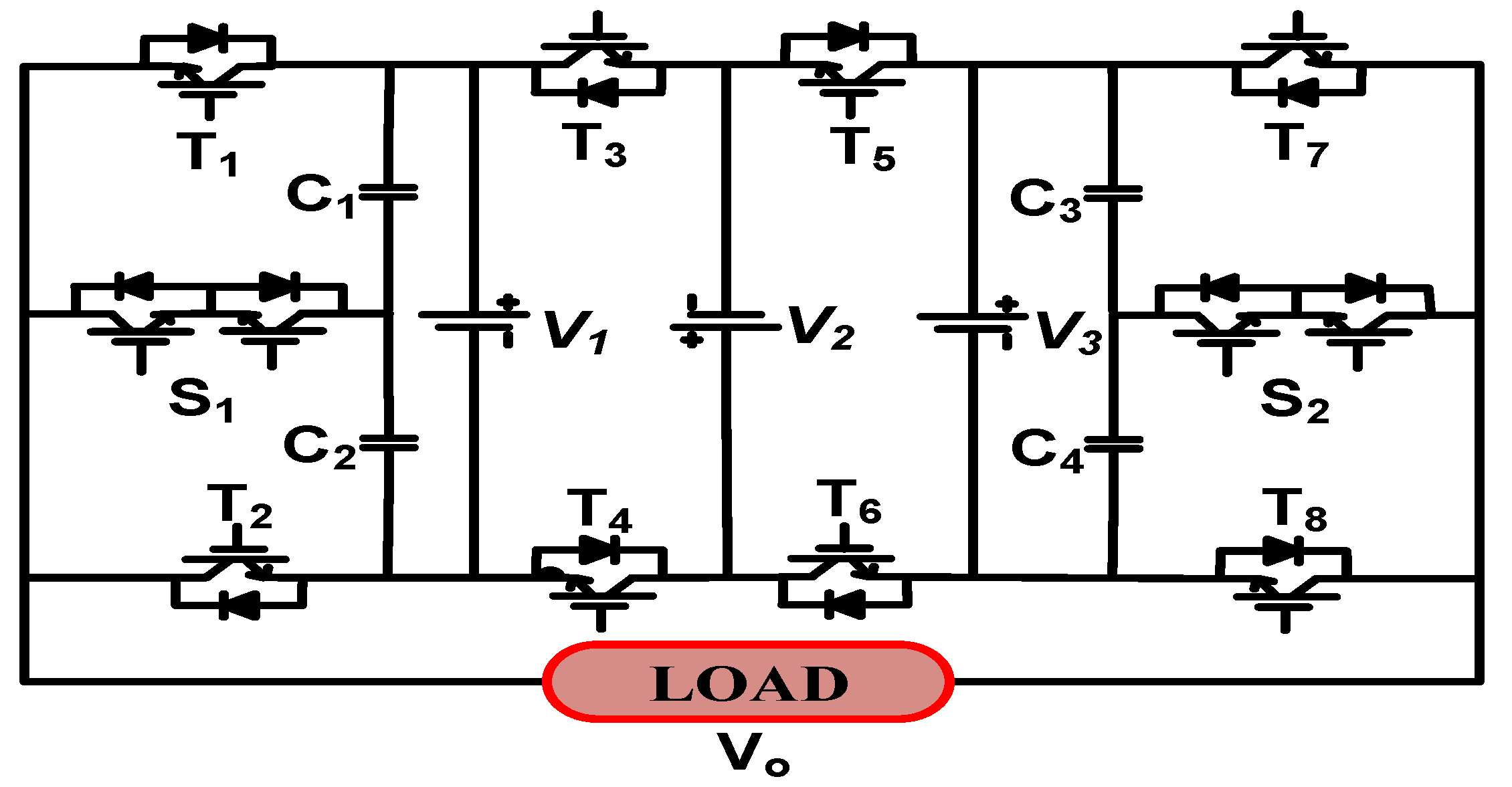
2. Proposed Topology
2.1. Symmetrical Configuration
2.2. Asymmetrical Configuration
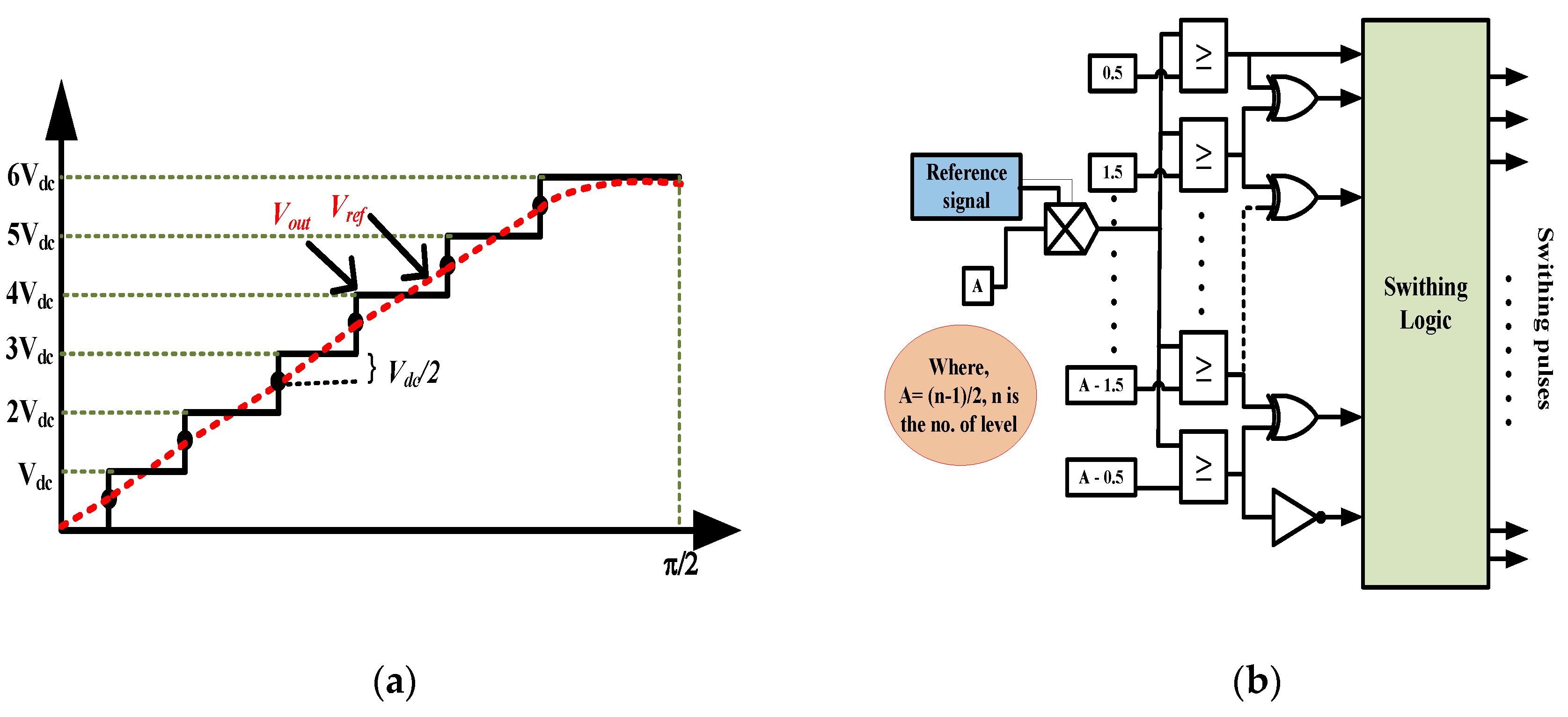
3. Nearest Level Control
4. Comparative Analysis
4.1. Comparision with a Single Source and Symmetric Topologies
4.2. Comparison with a Symmetric Topologies
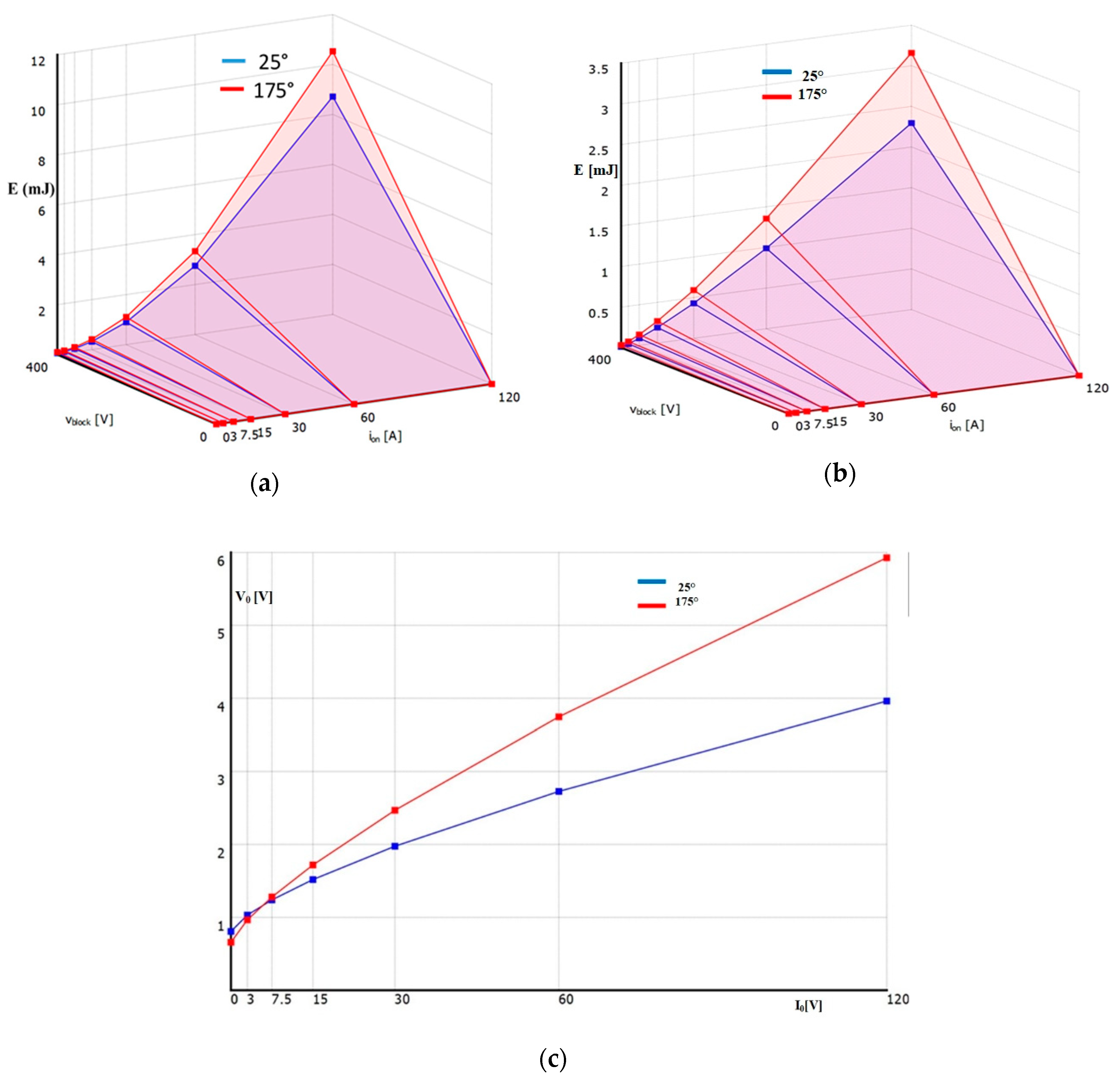
5. Power Loss Analysis
5.1. Switching Losses
5.2. Conduction Losses ()
5.3. Capacitor Ripple Losses ()
6. Results and Discussions
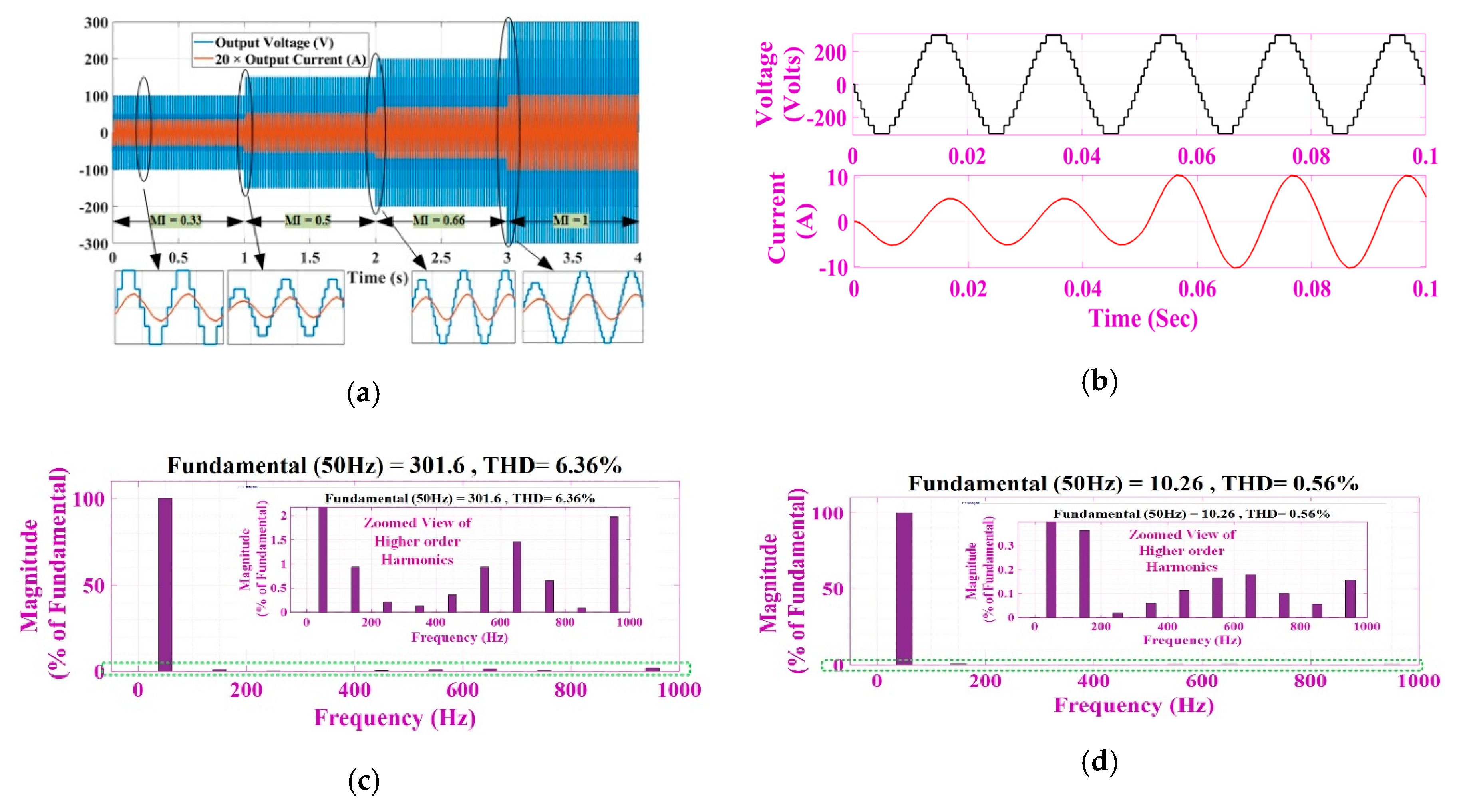
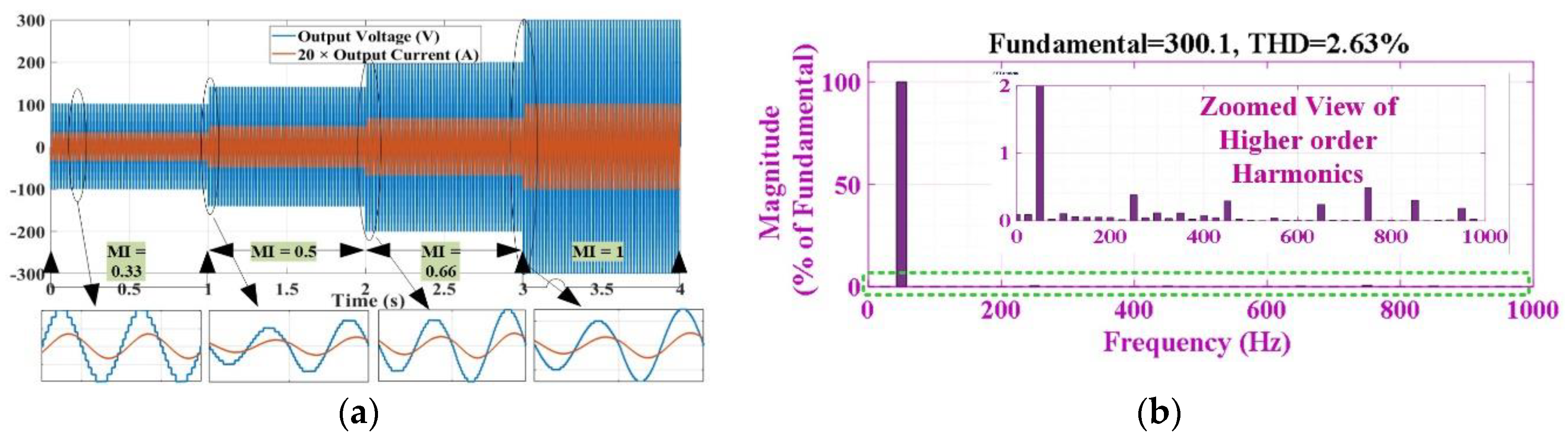
6.1. Simulation Results
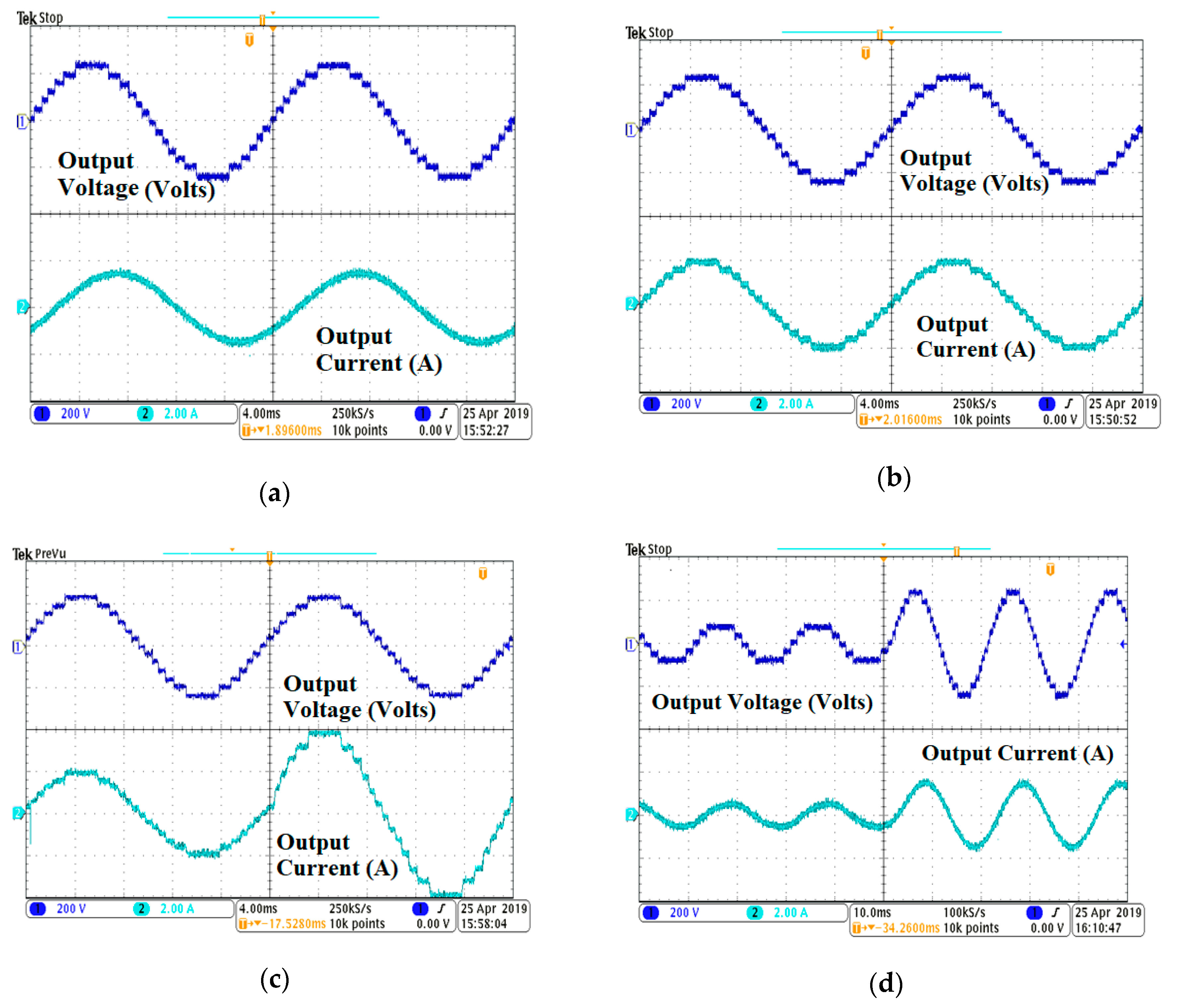
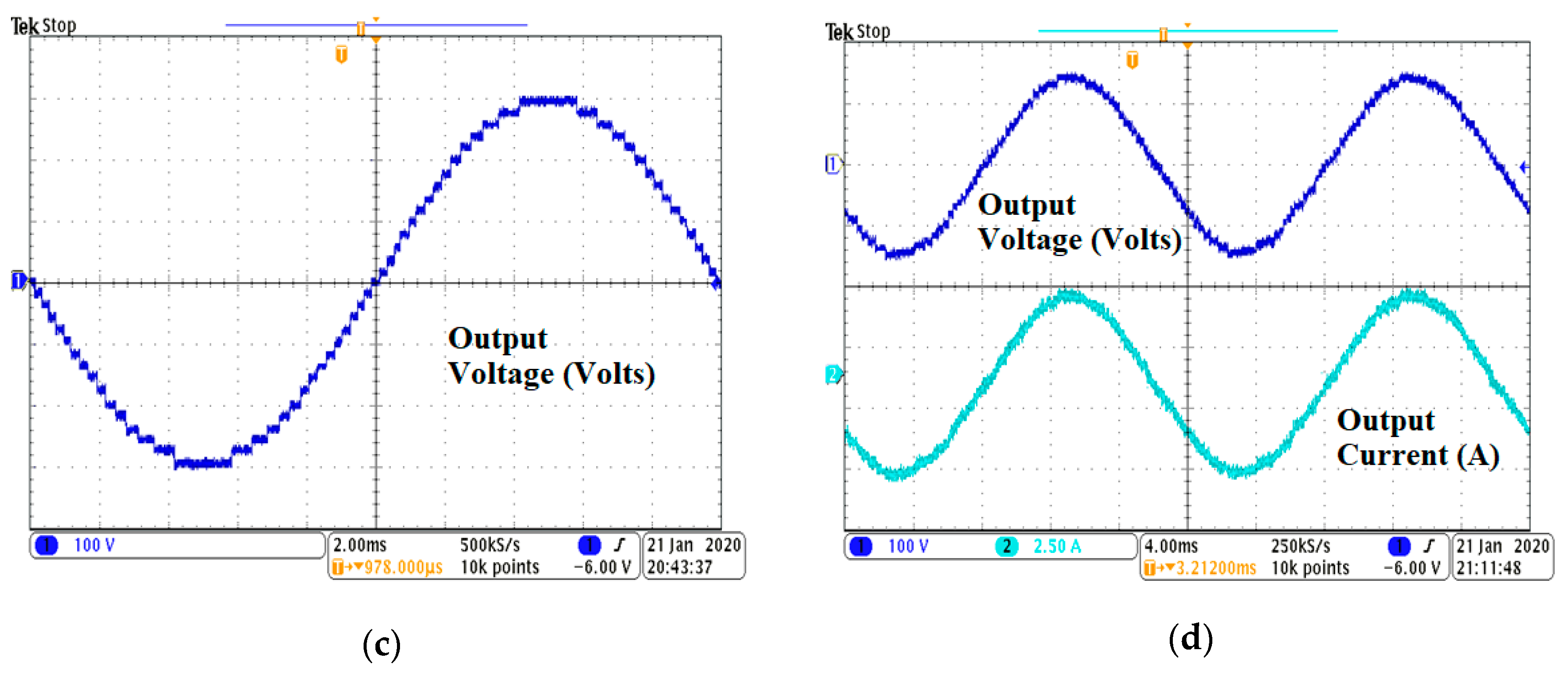
6.2. Experimental Results
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rodríguez, J.; Leon, J.I.; Kouro, S.; Portillo, R.; Prats, M.A.M. The age of multilevel converters arrives. IEEE Ind. Electron. Mag. 2008, 2, 28–39. [Google Scholar]
- Wang, C.; Zhu, Y.; Shi, W.; Chang, V.; Vijayakumar, P.; Liu, B.; Mao, Y.; Wang, J.; Fan, Y. A Dependable time series analytic framework for cyber-physical systems of IoT-based smart grid. ACM Trans. Cyber-Phys. Syst. 2018, 3, 1–18. [Google Scholar] [CrossRef]
- Otuoze, A.O.; Mustafa, M.W.; Larik, R.M. Smart grids security challenges: Classification by sources of threats. J. Electr. Syst. Inf. Technol. 2018, 5, 468–483. [Google Scholar] [CrossRef]
- Saeedian, M.; Hosseini, S.M.; Adabi, J. Step-up switched-capacitor module for cascaded MLI topologies. IET Power Electron. 2018, 11, 1286–1296. [Google Scholar] [CrossRef]
- Gupta, K.K.; Ranjan, A.; Bhatnagar, P.; Sahu, L.K.; Jain, S. Multilevel inverter topologies with reduced device count: A review. IEEE Trans. Power Electron. 2016, 31, 135–151. [Google Scholar] [CrossRef]
- Chakraborty, C.; Iu, H.H.C.; Lu, D.D.C. Power converters, control, and energy management for distributed generation. IEEE Trans. Ind. Electron. 2015, 62, 4466–4470. [Google Scholar] [CrossRef]
- Barzegarkhoo, R.; Moradzadeh, M.; Zamiri, E.; Madadi Kojabadi, H.; Blaabjerg, F. A new boost switched-capacitor multilevel converter with reduced circuit devices. IEEE Trans. Power Electron. 2018, 33, 6738–6754. [Google Scholar] [CrossRef]
- Siddique, M.D.; Mekilef, S.; Shah, N.M.; Memon, M.A. Optimal design of a new cascaded multilevel inverter topology with reduced switch count. IEEE Access 2019, 7, 24498–24510. [Google Scholar] [CrossRef]
- Dargahi, V.; Sadigh, A.K.; Abarzadeh, M.; Eskandari, S.; Corzine, K. A new family of modular multilevel converter based on modified flying-capacitor multicell converters. IEEE Trans. Power Electron. 2014, 30, 138–147. [Google Scholar] [CrossRef]
- López, I.; Ceballos, S.; Pou, J.; Zaragoza, J.; Andreu, J.; Kortabarria, I.; Agelidis, V.G. Modulation strategy for multiphase neutral-point-clamped converters. IEEE Trans. Power Electron. 2015, 31, 928–941. [Google Scholar] [CrossRef]
- Zhang, Y.; Adam, G.P.; Lim, T.C.; Finney, S.J.; Williams, B.W. Hybrid multilevel converter: Capacitor voltage balancing limits and its extension. IEEE Trans. Ind. Inform. 2013, 9, 2063–2073. [Google Scholar] [CrossRef]
- Malinowski, M.; Gopakumar, K.; Rodriguez, J.; Perez, M.A. A survey on cascaded multilevel inverters. IEEE Trans. Ind. Electron. 2010, 57, 2197–2206. [Google Scholar] [CrossRef]
- Mathew, R.; Agarwal, S. Modified reduced switch symmetrical multilevel inverter. In Proceedings of the IEEE International Conference on Circuit, Power and Computing Technologies, ICCPCT 2017, Kollam, India, 20–21 April 2017; pp. 1–8. [Google Scholar]
- Lee, S.S.; Sidorov, M.; Idris, N.R.N.; Heng, Y.E. A symmetrical cascaded compact-module multilevel inverter (CCM-MLI) with pulsewidth modulation. IEEE Trans. Ind. Electron. 2018, 65, 4631–4639. [Google Scholar] [CrossRef]
- Saha, D.; Roy, T. A new symmetrical three phase multilevel inverter using switched capacitor basic units for renewable energy conversion systems. In Proceedings of the 2018 International Conference on Control, Power, Communication and Computing Technologies (ICCPCCT), Kannur, India, 23–24 March 2018; pp. 368–374. [Google Scholar]
- Salem, A.; Ahmed, E.M.; Ahmed, M.; Orabi, M. Stand-alone three-phase symmetrical multi-level inverter. In Proceedings of the 2015 IEEE International Telecommunications Energy Conference (INTELEC), Saka, Japan, 18–22 October 2015; pp. 1–6. [Google Scholar]
- Salem, A.; Ahmed, E.M.; Orabi, M.; Ahmed, M. New three-phase symmetrical multilevel voltage source inverter. IEEE J. Emerg. Sel. Top. Circuits Syst. 2015, 5, 430–442. [Google Scholar] [CrossRef]
- Siddique, M.D.; Alamri, B.; Salem, F.A.; Orabi, M.; Mekhilef, S.; Shah, N.M.; Sandeep, N.; Mohamed Ali, J.S.; Iqbal, A.; Ahmed, M.; et al. A single DC source nine-level switched-capacitor boost inverter topology with reduced switch count. IEEE Access 2020, 8, 5840–5851. [Google Scholar] [CrossRef]
- Samadaei, E.; Salehi, A.; Iranian, M.; Pouresmaeil, E. Single DC source multilevel inverter with changeable gains and levels for low-power loads. Electronics 2020, 9, 937. [Google Scholar] [CrossRef]
- Wang, J.; Wang, J.; Xiao, B.; Gui, Z.; Jiang, W. Full range capacitor voltage balance PWM strategy for diode-clamped multilevel inverter. Electronics 2020, 9, 1263. [Google Scholar] [CrossRef]
- Siddique, M.D.; Mekhilef, S.; Shah, N.M.; Sarwar, A.; Iqbal, A.; Tayyab, M.; Ansari, M.K. Low switching frequency based asymmetrical multilevel inverter topology with reduced switch count. IEEE Access 2019, 7, 86374–86383. [Google Scholar] [CrossRef]
- Siddique, M.D.; Mustafa, A.; Sarwar, A.; Mekhilef, S.; Shah, N.B.M.; Seyedamahmousian, M.; Stojcevski, A.; Horan, B.; Ogura, K. Single phase symmetrical and asymmetrical design of multilevel inverter topology with reduced number of switches. In Proceedings of the 2018 IEEMA Engineer Infinite Conference (eTechNxT), New Delhi, India, 13–14 March 2018; pp. 1–6. [Google Scholar]
- Siddique, M.D.; Mekhilef, S.; Shah, N.M.; Sarwar, A.; Iqbal, A.; Memon, M.A. A new multilevel inverter topology with reduce switch count. IEEE Access 2019, 7, 58584–58594. [Google Scholar] [CrossRef]
- Almakhles, D.J.; Ali, J.S.M.; Padmanaban, S.; Bhaskar, M.S.; Subramaniam, U.; Sakthivel, R. An original hybrid multilevel DC-AC converter using single-double source unit for medium voltage applications: Hardware implementation and investigation. IEEE Access 2020, 8, 71291–71301. [Google Scholar] [CrossRef]
- Lee, S.S. A single-phase single-source 7-level inverter with triple voltage boosting gain. IEEE Access 2018, 6, 30005–30011. [Google Scholar] [CrossRef]
- Ye, Y.; Cheng, K.W.E.; Liu, J.; Ding, K. A step-up switched-capacitor multilevel inverter with self-voltage balancing. IEEE Trans. Ind. Electron. 2014, 61, 6672–6680. [Google Scholar] [CrossRef]
- Liu, J.; Wu, J.; Zeng, J. Symmetric/Asymmetric hybrid multilevel inverters integrating switched-capacitor techniques. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 1616–1626. [Google Scholar] [CrossRef]
- Roy, T.; Bhattacharjee, B.; Sadhu, P.K.; Dasgupta, A.; Mohapatra, S. Step-up switched capacitor multilevel inverter with a cascaded structure in asymmetric DC source configuration. J. Power Electron. 2018, 18, 1051–1066. [Google Scholar]
- Raghu Raman, S.; Cheng, K.W.E.; Ye, Y. multi-input switched-capacitor multilevel inverter for high-frequency AC Power distribution. IEEE Trans. Power Electron. 2018, 33, 5937–5948. [Google Scholar] [CrossRef]
- Fong, Y.C.; Raman, S.R.; Ye, Y.; Cheng, K.W.E. Generalized topology of a hybrid switched-capacitor multilevel inverter for high-frequency AC power distribution. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 2886–2897. [Google Scholar] [CrossRef]
- Zeng, J.; Wu, J.; Liu, J.; Guo, H. A quasi-resonant switched-capacitor multilevel inverter with self-voltage balancing for single-phase high-frequency AC microgrids. IEEE Trans. Ind. Inf. 2017, 13, 2669–2679. [Google Scholar] [CrossRef]
- Axelrod, B.; Berkovich, Y.; Ioinovici, A. A cascade boost-switched-capacitor-converter two level inverter with an optimized multilevel output waveform. IEEE Trans. Circuits Syst. Regul. Pap. 2005, 52, 2763–2770. [Google Scholar] [CrossRef]
- Liu, J.; Cheng, K.W.E.; Ye, Y. A cascaded multilevel inverter based on switched-capacitor for high-frequency AC power distribution system. IEEE Trans. Power Electron. 2014, 29, 4219–4230. [Google Scholar] [CrossRef]
- Alishah, R.S.; Hosseini, S.H.; Babaei, E.; Sabahi, M.; Zare, A. Extended high step-up structure for multilevel converter. IET Power Electron. 2016, 9, 1894–1902. [Google Scholar] [CrossRef]
- Roy, T.; Sadhu, P.K.; Dasgupta, A. Cross-switched multilevel inverter using novel switched capacitor converters. IEEE Trans. Ind. Electron. 2019, 66, 8521–8532. [Google Scholar] [CrossRef]
- Babaei, E.; Kangarlu, M.F.; Mazgar, F.N. Symmetric and asymmetric multilevel inverter topologies with reduced switching devices. Electr. Power Syst. Res. 2012, 86, 122–130. [Google Scholar] [CrossRef]
- Taghvaie, A.; Adabi, J.; Rezanejad, M. A self-balanced step-up multilevel inverter based on switched-capacitor structure. IEEE Trans. Power Electron. 2018, 33, 199–209. [Google Scholar] [CrossRef]
- Wu, D.; Peng, L. Characteristics of nearest level modulation method with circulating current control for modular multilevel converter. IET Power Electron. 2016, 9, 155–164. [Google Scholar] [CrossRef]
- Kouro, S.; Bernal, R.; Miranda, H.; Silva, C.A.; Rodríguez, J. High-performance torque and flux control for multilevel inverter fed induction motors. IEEE Trans. Power Electron. 2007, 22, 2116–2123. [Google Scholar] [CrossRef]
- Saeedian, M.; Adabi, M.E.; Hosseini, S.M.; Adabi, J.; Pouresmaeil, E. A novel step-up single source multilevel inverter: Topology, operating principle, and modulation. IEEE Trans. Power Electron. 2019, 34, 3269–3282. [Google Scholar] [CrossRef]
- Gautam, S.P.; Kumar, L.; Gupta, S. Hybrid topology of symmetrical multilevel inverter using less number of devices. IET Power Electron. 2015, 8, 2125–2135. [Google Scholar] [CrossRef]
- Babaei, E.; Gowgani, S.S. Hybrid multilevel inverter using switched capacitor units. IEEE Trans. Ind. Electron. 2014, 61, 4614–4621. [Google Scholar] [CrossRef]
- Alishah, R.S.; Hosseini, S.H.; Babaei, E.; Sabahi, M. Optimal design of new cascaded switch-ladder multilevel inverter structure. IEEE Trans. Ind. Electron. 2017, 64, 2072–2080. [Google Scholar] [CrossRef]
- Taheri, A.; Rasulkhani, A.; Ren, H.-P. An asymmetric switched capacitor multilevel inverter with component reduction. IEEE Access 2019, 7, 127166–127176. [Google Scholar] [CrossRef]
- Zamiri, E.; Vosoughi, N.; Hosseini, S.H.; Barzegarkhoo, R.; Sabahi, M. A new cascaded switched-capacitor multilevel inverter based on improved series-parallel conversion with less number of components. IEEE Trans. Ind. Electron. 2016, 63, 3582–3594. [Google Scholar] [CrossRef]
- Barzegarkhoo, R.; Kojabadi, H.M.; Zamiry, E.; Vosooghi, N.; Chang, L. Generalized structure for a single phase switched- capacitor multilevel inverter using a new multiple DC link producer with reduced number of switches. IEEE Trans. Power Electron. 2016, 31, 5604–5617. [Google Scholar] [CrossRef]
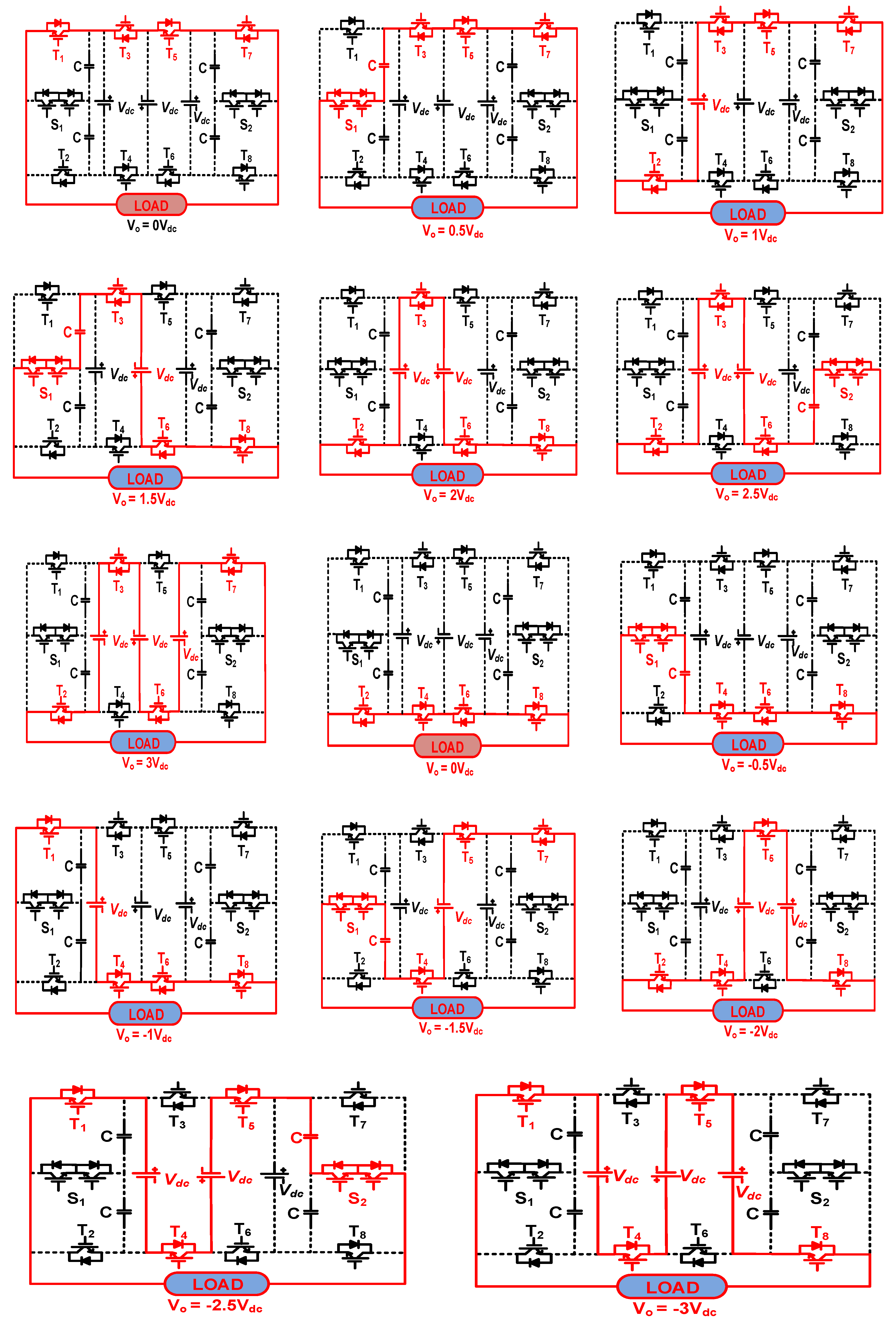






| S1 | S2 | T1 | T2 | T3 | T4 | T5 | T6 | T7 | T8 | Vo |
|---|---|---|---|---|---|---|---|---|---|---|
| OFF | OFF | ON | OFF | ON | OFF | ON | OFF | ON | OFF | 0 |
| ON | OFF | OFF | OFF | ON | OFF | ON | OFF | ON | OFF | 0.5 |
| OFF | OFF | OFF | ON | ON | OFF | ON | OFF | ON | OFF | |
| ON | OFF | OFF | OFF | ON | OFF | OFF | ON | OFF | ON | 1.5 |
| OFF | OFF | OFF | ON | ON | OFF | OFF | ON | OFF | ON | 2 |
| OFF | ON | OFF | ON | ON | OFF | OFF | ON | OFF | OFF | 2.5 |
| OFF | OFF | OFF | ON | ON | OFF | OFF | ON | ON | OFF | 3 |
| OFF | OFF | OFF | ON | OFF | ON | OFF | ON | OFF | ON | 0 |
| ON | OFF | OFF | OFF | OFF | ON | OFF | ON | OFF | ON | |
| OFF | OFF | ON | OFF | OFF | ON | OFF | ON | OFF | ON | |
| ON | OFF | OFF | OFF | OFF | ON | ON | OFF | ON | OFF | |
| OFF | OFF | ON | OFF | OFF | ON | ON | OFF | ON | OFF | |
| OFF | ON | ON | OFF | OFF | ON | ON | OFF | OFF | OFF | |
| OFF | OFF | ON | OFF | OFF | ON | ON | OFF | OFF | ON |
| S1 | S2 | T1 | T2 | T3 | T4 | T5 | T6 | T7 | T8 | Vo |
|---|---|---|---|---|---|---|---|---|---|---|
| OFF | OFF | OFF | ON | OFF | ON | OFF | ON | OFF | ON | 0 |
| OFF | OFF | ON | OFF | ON | OFF | OFF | ON | OFF | ON | |
| OFF | OFF | OFF | ON | OFF | ON | OFF | ON | ON | OFF | |
| OFF | OFF | ON | OFF | ON | OFF | OFF | ON | ON | OFF | |
| ON | OFF | OFF | OFF | ON | OFF | ON | OFF | OFF | ON | |
| ON | ON | OFF | OFF | ON | OFF | ON | OFF | OFF | OFF | |
| ON | OFF | OFF | OFF | ON | OFF | ON | OFF | ON | OFF | |
| ON | OFF | OFF | OFF | ON | OFF | OFF | ON | OFF | ON | |
| ON | ON | OFF | OFF | ON | OFF | OFF | ON | OFF | OFF | |
| ON | OFF | OFF | OFF | ON | OFF | OFF | ON | ON | OFF | |
| OFF | OFF | OFF | ON | ON | OFF | ON | OFF | OFF | ON | |
| OFF | ON | OFF | ON | ON | OFF | ON | OFF | OFF | OFF | |
| OFF | OFF | OFF | ON | ON | OFF | ON | OFF | ON | OFF | |
| OFF | OFF | OFF | ON | ON | OFF | OFF | ON | OFF | ON | |
| OFF | ON | OFF | ON | ON | OFF | OFF | ON | OFF | OFF | |
| OFF | OFF | OFF | ON | ON | OFF | OFF | ON | ON | OFF | |
| OFF | OFF | ON | OFF | ON | OFF | ON | OFF | ON | OFF | 0 |
| OFF | OFF | OFF | ON | OFF | ON | ON | OFF | ON | OFF | |
| OFF | OFF | ON | OFF | ON | OFF | ON | OFF | OFF | ON | |
| OFF | OFF | OFF | ON | OFF | ON | ON | OFF | OFF | ON | |
| ON | OFF | OFF | OFF | OFF | ON | OFF | ON | ON | OFF | |
| ON | ON | OFF | OFF | OFF | ON | OFF | ON | OFF | OFF | |
| ON | OFF | OFF | OFF | OFF | ON | OFF | ON | OFF | ON | |
| ON | OFF | OFF | OFF | OFF | ON | ON | OFF | ON | OFF | |
| ON | ON | OFF | OFF | OFF | ON | ON | OFF | OFF | OFF | |
| ON | OFF | OFF | OFF | OFF | ON | ON | OFF | OFF | ON | |
| OFF | OFF | ON | OFF | OFF | ON | OFF | ON | ON | OFF | |
| OFF | ON | ON | OFF | OFF | ON | OFF | ON | OFF | OFF | |
| OFF | OFF | ON | OFF | OFF | ON | OFF | ON | OFF | ON | |
| OFF | OFF | ON | OFF | OFF | ON | ON | OFF | ON | OFF | |
| OFF | ON | ON | OFF | OFF | ON | ON | OFF | OFF | OFF | |
| OFF | OFF | ON | OFF | OFF | ON | ON | OFF | OFF | ON |
| SCMLI Presented in | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| γ = 0.5 | γ = 1.5 | ||||||||
| [7] sym | 9 | 10 | 1 | 8 | 2 | 1 | 6.00 | 2.70 | 3.33 |
| [7] asym | 17 | 18 | 2 | 14 | 4 | 2 | 6.00 | 4.82 | 5.52 |
| [33] | 13 | 18 | 3 | 18 | 3 | 3 | 5.00 | 10.27 | 11.42 |
| [34] | 13 | 14 | 2 | 14 | 4 | 4 | 5.30 | 5.95 | 6.76 |
| [35] | 13 | 16 | 2 | 16 | 4 | 2 | 5.60 | 6.27 | 7.13 |
| [36] | 13 | 14 | 6 | 14 | 0 | 0 | 4.70 | 13.11 | 16.20 |
| [37] | 13 | 29 | 1 | 29 | 5 | 0 | 4.83 | 5.03 | 5.40 |
| [40] | 9 | 8 | 1 | 8 | 4 | 4 | 4.00 | 2.90 | 3.33 |
| [41] | 17 | 14 | 4 | 14 | 4 | 8 | 4.25 | 9.91 | 10.91 |
| [42] | 17 | 10 | 2 | 10 | 2 | 4 | 5.50 | 3.38 | 4.03 |
| Proposed multilevel inverters (MLI) | 13 | 12 | 3 | 10 | 4 | 0 | 2.17 | 6.08 | 6.75 |
| SCMLI Presented in | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| γ = 0.5 | γ = 1.5 | ||||||||
| [34] | 31 | 14 | 2 | 14 | 4 | 4 | 5.33 | 2.49 | 2.83 |
| [35] | 31 | 16 | 2 | 16 | 4 | 2 | 5.67 | 2.63 | 3.00 |
| [42] | 25 | 12 | 2 | 12 | 2 | 2 | 5.00 | 2.44 | 2.84 |
| [43] | 31 | 14 | 6 | 10 | 0 | 0 | 5.33 | 5.16 | 6.19 |
| [23] | 25 | 12 | 4 | 10 | 0 | 0 | 5.00 | 3.92 | 4.72 |
| [34] | 49 | 18 | 2 | 18 | 6 | 6 | 5.50 | 2.07 | 2.30 |
| [44] | 25 | 14 | 2 | 10 | 4 | 0 | 5.83 | 2.47 | 2.94 |
| Proposed MLI | 31 | 12 | 3 | 10 | 4 | 0 | 5.87 | 2.80 | 3.37 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hussan, M.R.; Sarwar, A.; Siddique, M.D.; Mekhilef, S.; Ahmad, S.; Sharaf, M.; Zaindin, M.; Firdausi, M. A Novel Switched-Capacitor Multilevel Inverter Topology for Energy Storage and Smart Grid Applications. Electronics 2020, 9, 1703. https://doi.org/10.3390/electronics9101703
Hussan MR, Sarwar A, Siddique MD, Mekhilef S, Ahmad S, Sharaf M, Zaindin M, Firdausi M. A Novel Switched-Capacitor Multilevel Inverter Topology for Energy Storage and Smart Grid Applications. Electronics. 2020; 9(10):1703. https://doi.org/10.3390/electronics9101703
Chicago/Turabian StyleHussan, Md Reyaz, Adil Sarwar, Marif Daula Siddique, Saad Mekhilef, Shafiq Ahmad, Mohamed Sharaf, Mazen Zaindin, and Muhammad Firdausi. 2020. "A Novel Switched-Capacitor Multilevel Inverter Topology for Energy Storage and Smart Grid Applications" Electronics 9, no. 10: 1703. https://doi.org/10.3390/electronics9101703
APA StyleHussan, M. R., Sarwar, A., Siddique, M. D., Mekhilef, S., Ahmad, S., Sharaf, M., Zaindin, M., & Firdausi, M. (2020). A Novel Switched-Capacitor Multilevel Inverter Topology for Energy Storage and Smart Grid Applications. Electronics, 9(10), 1703. https://doi.org/10.3390/electronics9101703









