Abstract
This work deals with circuit modeling of noise mode conversion due to system asymmetry in a three-phase motor drive system. In fact, it is well-known that in case of system asymmetry (e.g., slightly asymmetrical LC filter parameters), differential-mode noise can convert into common-mode noise, resulting in increased level of conducted electromagnetic interference. This phenomenon has been observed with measurements and reported in previous works, but a clear and rigorous analytical description is still a challenging point. The main novelty proposed in the paper is a rigorous analytical description of differential-to-common-mode noise conversion based on the Clarke transformation and the eigenvalue analysis. In particular, the magnitude and the frequency location of the differential-mode resonances injected into the common-mode circuit are derived in closed form. Moreover, since system asymmetry is usually uncontrolled (e.g., component tolerance and parasitic elements), a statistical analysis is also presented by treating the parameters of the LC filter as random variables. Thus, a second contribution proposed in the paper is the analytical derivation in closed form of the probability density function, the mean value, and the standard deviation of the random frequency location of the resonance peaks injected into the common-mode circuit. The importance of the analytical results derived in the paper is two-fold. First, a deep theoretical understanding of the phenomenon in terms of circuit theory concepts is achieved. Second, the impact of differential-to-common-mode noise conversion is described in quantitative terms. Thus, the obtained analytical results can be used to predict or explain the noise conversion impact on the frequency-domain measurements of common-mode currents. Theoretical derivations are validated through a time-domain Simulink implementation of a three-phase motor drive system, and a frequency-domain analysis through the discrete Fourier transform.
1. Introduction
Technical literature concerning three-phase motor drive systems is very wide and rich in contributions investigating several aspects related to that kind of systems. A first set of contributions is related to functional issues such as, for example, the control strategies for three-phase inverters (e.g., [1]). A second set of contributions is related to circuit modeling and measurement techniques of conducted electromagnetic interference (EMI) [2,3,4,5,6,7,8,9,10,11,12]. This point is crucial in modern power systems due to the widespread and pervasive use of power electronics. EMI modeling, indeed, is essential for both analysis and EMI mitigation techniques.
As far as the EMI issue is considered, several approaches have been used to model the high-frequency behavior of power converters. Time-domain and frequency-domain approaches have both several disadvantages, such as long computational time and system oversimplification, respectively. Such drawbacks are potentially overcome by a further approach consisting in the behavioral modeling of power converters, based on the extraction of Thevenin or Norton equivalents from EMI measurements [6].
In all the approaches mentioned above, conducted EMI are modeled as the superposition of differential-mode (DM) and common-mode (CM) noise. Such separation is essential in EMI modeling and filter design [13,14,15,16,17,18]. It is well-known; however, that such sharp separation between DM and CM noise is possible only under the assumption that the converter is perfectly symmetrical with respect to the ground. In fact, system asymmetries lead to DM–CM noise transformation (i.e., noise conversion between the two noise components) [6,19].
Several papers can be found about this point when single-phase converters are considered [19,20]. As an example, Figure 1 shows measured DM–CM noise transformation due to asymmetries in an EMI filter [19]. As far as three-phase converters are studied, however, few analytical contributions are available in the literature. Nevertheless, mode conversion in three-phase converters is well documented by experiments. For example, the experimental results reported in [21] show clearly that the three-phase LC filter is a critical component. In fact, in case of slight filter asymmetry, the DM resonances can be measured as resonances in the CM current. As an example, Figure 2 shows the amplitude spectrum of the measured CM current in the three-phase motor drive system reported in [21]. The blue curve was measured without filter, whereas the green and the magenta curves were measured for two different values of the DM inductances (i.e., 3.5 and 2.5 μH, respectively) of a DM–CM LC filter. The resonances of the DM circuit (i.e., 380 and 450 kHz corresponding to the two values of the DM inductance, and 50 nF capacitance) were clearly measured in the spectrum of the CM current. This is a clear experimental evidence of DM-to-CM noise conversion. Recognizing this point is crucial for a proper filter design. In fact, if DM-to-CM noise conversion is not recognized, unnecessary overdesign of the CM filter could be implemented.
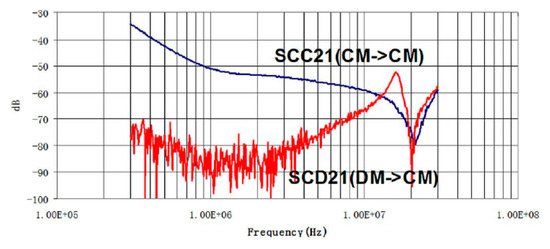
Figure 1.
Measured S parameters of an EMI filter [19]. The transmission coefficient (mixed-mode S parameter) provides CM response with DM excitation and it is due to filter asymmetries. It is compared with measured with CM excitation and CM response. is even higher than above 13 MHz.
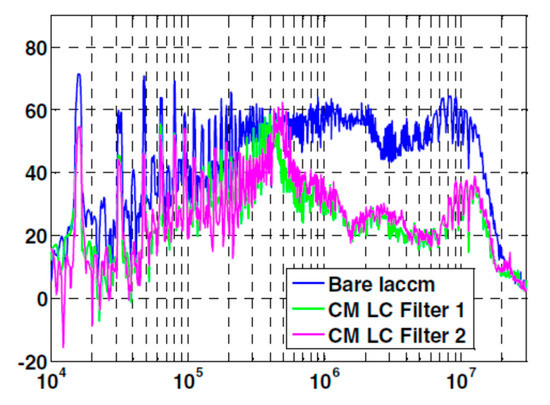
Figure 2.
Measured amplitude spectrum of AC-side CM current without filter (blue curve), CM LC filter with 3.5 μH DM inductance (green curve) and with 2.5 μH DM inductance (magenta curve) [21]. The corresponding DM resonances, with 50 nF DM capacitance, are 380 and 450 kHz, respectively. The DM resonances are clearly observed in the CM current spectrum due to DM-to-CM noise conversion.
Although the general idea of noise mode conversion due to three-phase asymmetry is well established, to the Author’s knowledge a rigorous analytical description of differential-to-common-mode noise conversion in three-phase systems is still a challenging point. The main novelty introduced in this paper is the mathematical derivation and explanation of differential-to-common-mode noise transformation in asymmetrical three-phase systems by resorting to the Clarke transformation and the eigenvalue analysis. In particular, differential-to-common-mode noise conversion due to a slightly asymmetrical LC filter will be investigated. The proposed methodology, however, has general validity. Thus, the analytical results derived in the paper can be used to describe the impact on the CM circuit of any three-phase asymmetry (e.g., asymmetrical cable parameters). It will be shown that, in case of three-phase asymmetry, the CM circuit is affected by the DM circuit on the whole frequency axis, but the main impact is due to the DM resonances injected into the CM circuit. Thus, the spectral lines corresponding to the DM resonances appear in the amplitude spectrum of the CM current with shifted frequency. The proposed analytical derivations provide the magnitude and the frequency location of the CM current peaks due to noise conversion, as functions of the filter asymmetry.
A second novelty introduced in the paper is a statistical analysis based on the assumption that, due to component tolerances, the filter parameters can be treated as random variables. Randomness in the filter parameters results in randomness in the frequency location of the CM current peaks due to differential-to-common-mode noise conversion. A complete statistical characterization of the frequency shift of the CM current peaks due to noise conversion is derived in terms of probability density function, mean value, and variance.
The relevance of the analytical results derived in the paper can be summarized in two points. First, the differential-to-common-mode noise conversion in an asymmetrical three-phase system is rigorously described in terms of theoretical properties and circuit equivalents. Second, the derived models allow quantitative prediction and explanation of the impact of noise conversion on frequency-domain measurements of CM currents.
The paper is organized as follows. In Section 2 the Clarke transformation is recalled, and its relationship with the well-known symmetrical component transformation in the frequency-domain is clarified. In Section 3 the impact of asymmetrical parameters of the LC filter on the differential-to-common-mode noise conversion in a three-phase motor drive system is described in analytical terms. To this aim, the equations in terms of Clarke variables are decoupled through the eigenvalue analysis. The magnitude and frequency location of the CM current spectral lines due to DM resonances are provided in closed form. In Section 4, specific three-phase motor drive system is implemented in Simulink to provide numerical validation of the analytical results. Section 5 is devoted to the statistical analysis of differential-to-common-mode noise conversion. In particular, by treating the asymmetrical parameters of the LC filter as random variables, the probability density function, the mean value, and the standard deviation of the frequency location of the CM current peaks from noise conversion are derived in closed form. Finally, conclusions are drawn in Section 6.
2. The Clarke Transformation
The analytical derivations proposed in the next Sections are based on the well-known Clarke transformation, which is a mathematical transformation broadly used in the analysis of three-phase power converters [22]. In fact, under the common assumption of circuit symmetry between the three phases, the Clarke transformation allows the introduction of voltage/current space vectors able to provide a compact and meaningful description of the three-phase system.
The Clarke transformation operates on a triplet a, b, c, of time-domain phase variables (e.g., phase voltages and currents) to obtain a triplet of transformed variables named α, β, and 0. For example, by considering phase currents, the Clarke transformation operates as:
It is worth noticing that the transformation defined in (1) is in its rational form (i.e., the transformation matrix T is orthogonal ()). This property guarantees power conservation across the transformation and allows consistent derivation of equivalent circuits in the transformed domain.
In case of circuit symmetry between the three phases, the transformation matrix T operates diagonalization of parameter matrices. For example, by considering the inductance matrix L of a three-phase component with symmetrical phases:
Similar results can be obtained for capacitance/resistance matrices. Matrix diagonalization is a crucial point since it results in decoupled equations in the transformed variables. Notice that α and β parameters in the transformed matrix take the same values (i.e., in (2)). This means that the α and β equations have the same structure and the same parameters. Therefore, the α and β circuits can be treated as a single circuit with the α and β variables combined to form complex space vectors. Each space vector has a real part given by the α component and imaginary part given by the β component. Thus, the current space vector corresponding to (1) is defined as:
where . Notice that since the Clarke transformation operates in the time domain, it can be used to analyze three-phase systems under transient conditions. However, when distorted steady-state conditions are considered, the same transformation in (1) operates on the phasor quantities at each frequency. In this case, the Clarke transformation can be put in relation with the well-known symmetrical component transformation [23]. The following relationship between phasors can be readily derived:
where , , and are the positive, negative, and zero-sequence phasor components, respectively. Notice that from (4) we obtain that the α component is proportional to the sum of the positive-sequence and negative-sequence components, whereas the β component is proportional to the difference between the same quantities. The zero-component of the Clarke transformation equals the zero-sequence component . Thus, the α and β components can be identified as the common mode (CM) and the differential mode (DM) of the pure three-phase system, respectively, whereas the zero-component can be identified as the conventional CM resulting from the interconnection of a three-phase circuit with a single-phase circuit. That is the usual condition of a three-phase inverter where the so-called CM current circulates in a single-phase circuit consisting mainly in the system parasitic elements.
Finally, it is worth highlighting that the diagonalization property (2) of the Clarke transformation holds only in case of circuit symmetry between the three phases. In case of asymmetrical phases, the straightforward use of (2) leads to a full matrix (i.e., to circuit coupling between the Clarke variables α, β, 0) [24]. In particular, since the zero components correspond to the conventional CM variables, asymmetrical phases result in injection of α and β component currents into the CM circuit. The theoretical investigation of such phenomenon is presented in the next Sections where the spectral lines of the CM current due to phase asymmetry are characterized in analytical and statistical terms.
3. Differential-to-Common-Mode Conversion Due to LC Filter Asymmetry
Let us consider the three-phase motor drive system represented in Figure 3 and consisting in a dc-fed three-phase inverter, a line impedance stabilization network (LISN), a dc-link capacitor, a CM/DM LC filter, a shielded cable, and an induction motor. The LC filter is realized by means of a CM choke whose leakage inductance provides DM filtering, and three star-connected grounded capacitors [21]. The following derivations, however, have general validity and can be readily adapted to different filter realizations. The cable is represented by a lumped RLC circuit, whereas each motor phase is represented by a series RL connection and a parallel capacitor to take into account high-frequency effects of windings.
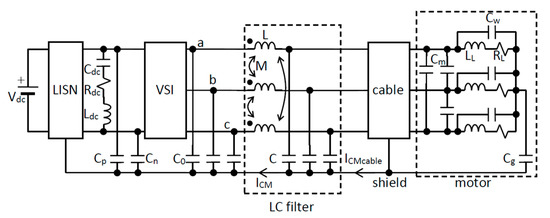
Figure 3.
The structure of the three-phase motor drive system, including the main parasitic elements, analyzed in this paper.
The main parasitic elements are also included in the model, that is, the series resistance and inductance of the link capacitor , the capacitances and from the dc-bus to the ground, the three capacitances from each inverter phase to the ground, the motor input capacitances , and the capacitance between motor windings and frame.
The following analysis considers the impact of asymmetrical values of the LC filter parameters on the differential-to-common-mode noise conversion. The proposed methodology, however, can be readily used to investigate the impact on noise conversion of other asymmetrical parameters (e.g., the three-phase cable parameters).
3.1. Circuit Modeling and Analytical Derivations
The three-phase system depicted in Figure 3 can be analyzed through the Clarke transformation recalled in Section 2. In case of ideal circuit symmetry between the three phases, the α and β circuits show the same topology and the same parameter values (see Figure 4a). To this aim it is worth recalling that the topology of α and β circuits follows the same rules as the positive- and negative-sequence circuits for the symmetrical components, that is, a short circuit connects all the star centers of the three-phase system (notice that the delta-connected capacitors can be first transformed into star connected capacitors ) [23]. As far as the zero-component circuit is considered, however, a different circuit topology is obtained (see Figure 4b). In fact, by following the same rules valid for the zero-sequence component in the symmetrical components framework, the interaction between the three-phase and the single-phase parts of the system must be taken into account. In particular, in previous works it was shown that a single-phase circuit connected to the star centers of a three-phase circuit can be moved, with unchanged topology, to the three-phase side through a multiplication by 3 of single-phase impedances and by of single-phase voltage sources, and division by of single-phase current sources [23,24].
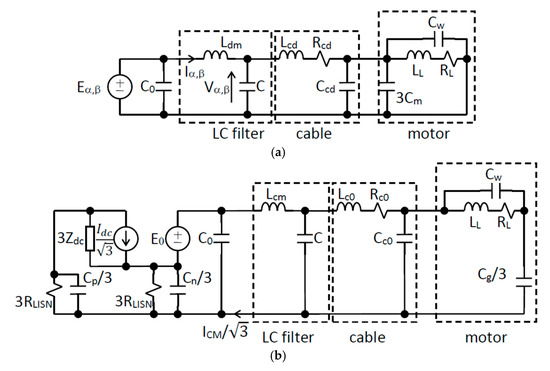
Figure 4.
Clarke equivalent circuits of the three-phase motor drive system represented in Figure 3. The α and β circuits have the same topology (a), whereas the zero-component circuit (b) takes into account the interconnection of the three-phase circuit with the single-phase part of the system.
In case of circuit symmetry between the three phases, the α, β, and zero circuits are uncoupled. In particular, the resonances of the α and β circuits have no impact on the zero circuit. It can be easily observed that the main resonance in the α and β circuits is given by the filter components. In fact, the low-level impedance corresponding to the large filter capacitance is only slightly affected by the high-level cable and motor impedances due to capacitances much smaller than . Thus, the differential-mode inductance of the filter can be approximately considered in series with the filter capacitance . The resulting series resonance is located at the frequency . In case of asymmetrical filter components, it is expected that such resonance is injected into the zero-component circuit (i.e., the CM circuit). The impact of asymmetry in filter capacitances and inductances on the CM circuit is analyzed in the following Subsections.
3.1.1. Asymmetrical Filter Capacitors
As far as the filter capacitors are considered, the simple case of a small perturbation of the capacitance connected to the phase a is first investigated. The voltage–current relationship for the phasor Clarke components is given by [25]:
After simple algebra the following equations can be obtained from (5):
where it is apparent that the β circuit is not affected by the capacitance perturbation.
The interaction between α and 0 circuits can be investigated by introducing two reasonable approximations in (6a) and (6c). First, under normal conditions the zero-component variables are much smaller than the α and β variables. Moreover, the impact of α and β circuits on the zero-component circuit is large around the resonances of α and β circuits. Therefore, in (6a) it is reasonable to assume (i.e., no feedback is assumed from the zero to the α circuit). Second, the small perturbation assumption allows for neglecting the term in (6c). Therefore, the approximate versions of (6a)–(6c) are given by:
From (7a) we observe that the equivalent α capacitance is changed by the additive term . As a consequence, the resonance in the α circuit is shifted to the value
Such resonance has impact on the zero-component circuit through (7c):
Thus, the resonance in the α circuit is injected into the CM circuit. The frequency location of the corresponding spectral line is given by (8), and both the frequency location shift and the magnitude of the spectral line are proportional to the capacitance deviation .
The above analytical results hold in the case of capacitance deviation of the phase a. It is expected that similar results hold in case the capacitance deviation is placed on the phase b or c. By writing (5) for or , however, the equations corresponding to (6a)–(6c) do not allow a straightforward interpretation as in the case of because a further coupling is introduced between α and β variables. Moreover, from both theoretical and practical viewpoint, the general case of simultaneous deviation of all the three parameters , , and would be of interest. To this aim, a more general analytical approach is derived.
In case of simultaneous deviation of the three capacitances with respect to the nominal value , the Clarke transformation:
provides the three equations:
By introducing the same approximation used above (i.e., negligible feedback from the zero-component circuit to the α and β circuits), for the α and β variables we obtain the following approximate expressions:
In matrix form:
Therefore, the problem can be reformulated as the diagonalization of a matrix:
where:
It can be readily shown that the eigenvalues of A are given by:
By substituting (15) into (16), after simple algebra we obtain the eigenvalues of the full matrix in (13):
It is worth noticing that in (17) the term in the first bracket is the mean value of the capacitance deviations, whereas the square-root term represents the root mean square value of the capacitance deviations.
The matrix P of the eigenvectors, corresponding to the eigenvalues (17), when applied to (13) leads to transformed variables:
and matrix diagonalization:
Therefore, we obtain decoupled equations in the transformed variables:
The fundamental result in (20) provides two different shift values to the nominal capacitance in case of distinct eigenvalues (17). This means that under the general condition of two or three capacitance deviations, two different resonances are generated in the α and β circuits, and they are coupled into the zero-component circuit through (11c). The frequencies of the two resonances are given by:
Notice that in the special case of only one capacitance deviation (i.e., any phase, a, b, or c), one of the two eigenvalues (17) is zero, whereas the second is given by . Null eigenvalue means no circuit interaction (i.e., only the resonance corresponding to is injected into the zero-component circuit). Therefore, only one spectral line due to mode conversion is present in the CM current in case of one capacitance deviation, whereas two spectral lines are expected in case of two or three capacitance deviations.
Finally, in case of equal capacitance deviations from (17), we have one double eigenvalue, but from (11c) there is no interaction with α and β circuits. This is consistent with the fact that means symmetrical capacitance values.
3.1.2. Asymmetrical Filter Inductors
A CM choke can be modeled as a coupled three-phase inductor according to (2). In the symmetrical case the DM inductance is , and the CM inductance . Notice that small asymmetrical self-inductances can result in large relative deviations of the DM inductance , because usually and take close values.
By assuming simultaneous deviations of the three self-inductances with respect to the nominal value , the Clarke transformation:
provides the following equations:
By introducing the same approximation used in the previous Subsection (i.e., negligible feedback from the zero circuit to the α and β circuits), for the α and β variables we obtain the following approximate expressions in matrix form:
The full matrix in (24) has the same structure as (14). Therefore, the matrix diagonalization can be obtained by using the same results already shown in Section 3.1.1. In particular, from (16) we obtain the eigenvalues:
Thus, the corrected values of the inductance in the α and β circuits are given by and . The corresponding frequencies of the resonances injected into the zero-component circuit are given by:
The same remarks already highlighted for (21) hold for (26). In particular, it is worth noticing that, in general, two spectral lines are generated in the CM circuit, and the frequency displacement with respect to the ideal location depends on .
Finally, the case of asymmetrical mutual inductances can be included into the above derivations. Starting from the Clarke transformation of a completely asymmetrical inductance matrix:
by simple algebra and by using the approximation of no-feedback from the zero-component circuit to the α and β circuits we obtain:
The eigenvalues of the full matrix in (28) can be still evaluated through (16). Explicit expressions are not reported here for the sake of simplicity. Also in this case the eigenvalues result, in general, in two inductance shifts and , and the related resonance frequencies injected into the zero-component circuit.
4. Numerical Validation
The three-phase motor drive system represented in Figure 3 was implemented in Simulink. The three-phase voltage source inverter (VSI) was controlled with pulse width modulation (PWM) with 50 Hz modulating frequency and 1650 Hz carrier frequency (i.e., the frequency-modulation ratio was 33), whereas the amplitude-modulation ratio m was 0.95. was 100 V, , and the dc-link capacitor was represented by a high-frequency equivalent circuit consisting in the series connection of , , and . The VSI parasitic capacitors were and . The LC filter was implemented by a CM choke with and , and star-connected capacitors with [21]. Thus, the DM and CM cutoff frequencies were and , respectively. The shielded cable was represented by a lumped equivalent circuit (see Figure 4) with , , , and . Thus, the DM and CM cable resonance frequencies were and , respectively. The motor phases were represented by , , and , whereas the motor parasitic capacitances were and .
The time-domain simulations were performed with sampling frequency , and the samples of the CM current (see Figure 3) were processed through the fast Fourier transform (FFT) to obtain the amplitude spectrum within the frequency range. Figure 5 shows the amplitude spectrum of the CM current (limited to , according to the conducted emissions standards [21]) in case of filter symmetry. The impact of the CM filter with cutoff frequency is clearly apparent. Moreover, no resonance frequencies can be identified (i.e., no peaks), even in proximity of the DM resonance located at . This means that, according to the theory, in case of symmetrical parameters there is no interaction between DM and CM circuits.
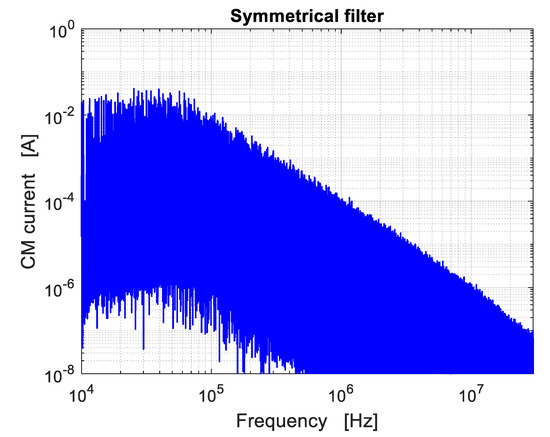
Figure 5.
Amplitude spectrum of the CM current in case of filter with symmetrical components.
Figure 6 shows the effect of a deviation of the filter capacitance with respect to its nominal value . According to (8), a negative deviation results in a positive relative increase in the resonance frequency of the α circuit. Moreover, according to (9) such resonance is injected into the CM circuit with increasing magnitude with the deviation . This is confirmed in Figure 6, where three different percent values of were selected (i.e., , , and ). The corresponding shift in the DM resonance frequency (i.e., ) are given by , , and , respectively. According to the eigenvalue analysis derived in Section 3.1.1, similar results can be obtained when the asymmetrical capacitance is either or .
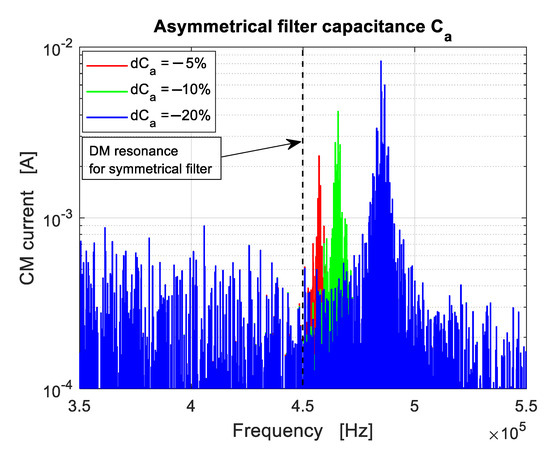
Figure 6.
Resonance peaks in the CM current amplitude spectrum due to three different percent values of (i.e., , , and ). Negative deviations result in resonance peaks with increased frequency with respect to the nominal value (i.e., the DM resonance frequency in case of symmetrical filter, represented by the dashed vertical line).
Figure 7 shows the case of two simultaneous deviations and . The deviation was selected such that . According to (17) and (21), the two eigenvalues are , and the two resonance frequencies . Thus, the two peaks have frequency separation . Three different percent values were assumed for (i.e., , , and ). The corresponding frequency separation of each couple of peaks are 13 kHz, 26, kHz, and 52 kHz. This point is confirmed by Figure 7. Notice that for the two peaks (blue line) are not perfectly symmetrical with respect to . This is because the formula is approximate, and it provides better results for small values of .
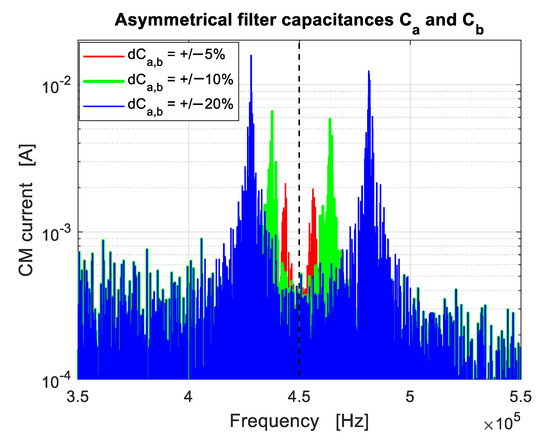
Figure 7.
Amplitude spectrum of the CM current in case of asymmetrical filter capacitances and . Opposite deviations between a and b were assumed (i.e., ). Three different percent values for the relative deviations were considered (i.e., , , and ).
Figure 8 shows the case of simultaneous deviations of the inductances and . By selecting, as in the previous case, , according to (25) and (26), the two eigenvalues are , and the two resonance frequencies . Thus, the two peaks have frequency separation . Three different percent values were assumed for (i.e., , , and ). The corresponding frequency separation of each couple of peaks are 13, 26, and 52 kHz. This point is confirmed by Figure 8. The same remark mentioned in the previous case holds for the location of peaks when .
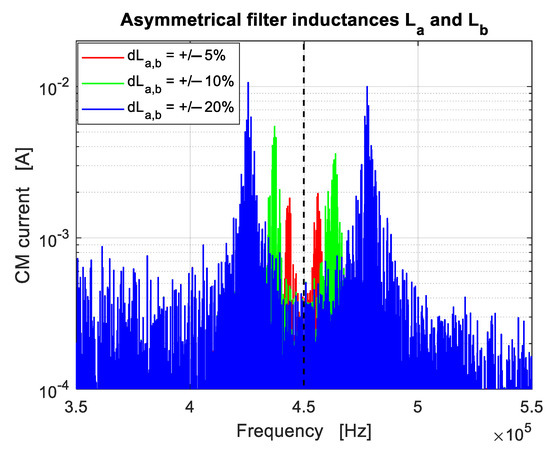
Figure 8.
Amplitude spectrum of the CM current in case of asymmetrical filter inductances and . Opposite deviations between a and b were assumed (i.e., ). Three different percent values for the relative deviations were considered (i.e., , , and ).
Figure 9 shows the impact of simultaneous deviations of both filter inductances and capacitances. Two cases can be put into evidence. First, the deviations of components a (i.e., and ) have the same sign (i.e., ), as well as the deviations of components b (i.e., ). In this case, the two peaks are reinforced by the two filter components. In the second case, the deviations of components a have opposite sign (i.e., ), as well as the deviations of components b (i.e., ). In this case, the action of the two filter components are in the opposite directions, resulting in a contrast to the frequency shift of the peaks. To highlight this phenomenon, a first simulation was performed with and (green curve). The effect of each deviation is doubled. In particular, the frequency separation between the two peaks is doubled with respect to Figure 8. A second simulation (blue curve) was performed by doubling the relative deviations (and keeping the same signs as before). The frequency separation of the two peaks is doubled with respect to Figure 8. Finally, a simulation with opposite sign was performed (red curve) (i.e., and ). Since the deviations of the two filter components act in opposite directions, the result is only one peak with small magnitude and negligible frequency shift.
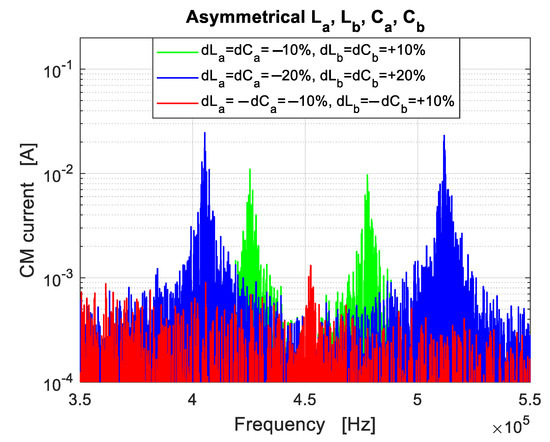
Figure 9.
Amplitude spectrum of the CM current in case of asymmetry in the filter inductances and capacitances. The green and blue curves show the cases of deviations resulting in a decrease in and , and increase in and . The red curve shows the case of and changing in the opposite direction (same for and ). In this case the asymmetries tend to compensate each other.
Figure 10 shows the amplitude spectrum of the cable CM current (see in Figure 3) for different deviations of the cable self-inductances. This set of simulations was performed to show how the DM circuit can inject current into the CM circuit at any system asymmetry (i.e., not only the LC filter). In case of cable asymmetry, the DM resonance involving the cable leads to current injection into the cable CM circuit. According to Figure 4a, the cable is responsible of a DM resonance corresponding to its DM inductance (i.e., the difference between the self and the mutual inductances) and the total capacitance consisting in the sum of the cable capacitance and the parasitic capacitances and (in fact, at high frequencies the branch can be ignored). Thus, the frequency of the DM resonance is given by . The self-inductance deviations were selected such that , and three different values were selected for (i.e., , , and ). According to the corresponding frequency separation of each couple of peaks were 300 kHz, 600 kHz, and 1.2 MHz. This is confirmed by Figure 10, where another spectral line can be clearly seen at 6.9 MHz. Such spectral line is independent of cable asymmetry since it is related to the resonance of the CM circuit (see Figure 4b): , where .
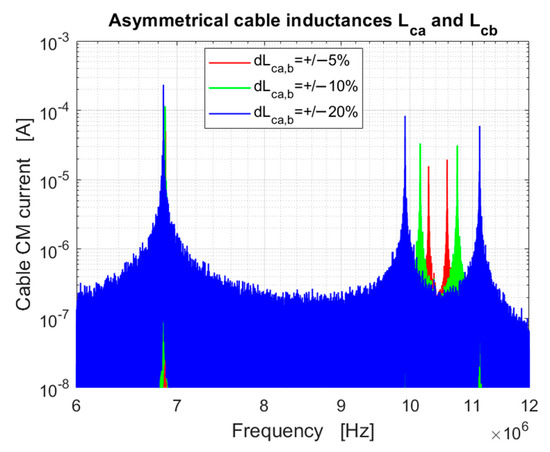
Figure 10.
Amplitude spectrum of the cable CM current in case of cable with asymmetrical self-inductances. The spectral line at 6.9 MHz is not affected by cable asymmetry since it is due to the CM circuit resonance.
5. Statistical Analysis
Analytical results derived in Section 3 allow accurate evaluation of DM resonances injected into the CM circuit in case of known asymmetrical values of the filter components. When we are interested in the effects of component tolerance, however, a statistical approach is more suited to the objective. The statistical analysis of the eigenvalues (17) and (25), and the related resonance frequencies (21) and (26), will be derived in this Section by treating all the deviations (i.e., and ) as random variables. Two cases will be investigated, corresponding to two different statistical distributions for the random variables : Gaussian and Uniform distributions. In order to obtain unitary and normalized results, the following transformation of random variables will be investigated:
where , , for capacitances, and , , for inductances. The corresponding normalized resonance frequencies are given by:
5.1. Gaussian Distribution
Let us assume as uncorrelated Gaussian random variables with zero mean and variance . The transformation (29) requires first the analysis of the random variable:
By taking into account that , for the mean value and the variance of we obtain [26]:
Therefore, the mean value and the variance of can be approximated as:
where the approximations through the first and second order derivatives were used (i.e., the Taylor series approach) [26,27].
From (29) and (33) the mean values and the variance of are given by:
Notice that since and are defined as the sum of uncorrelated random variables, their distribution can be approximated as a Gaussian distribution with mean values and variance given by (34).
Finally, the mean value and variance of the normalized resonance frequencies (30) can be approximated as:
The probability density function (PDF) of (30) can be obtained through the theorem of the transformation of random variables [26]. By taking into account that, as mentioned before, can be approximated by Gaussian random variables, the PDF of the two normalized resonance frequencies are given by:
where and are given by (34).
Figure 11 shows the behavior of the two PDFs (36) for three values of (i.e., 0.05, 0.10, and 0.20). The analytical curves corresponding to (36) (solid curves) are compared with numerical results obtained by repeated run analysis (dotted curves). Notice that for each the two PDFs show one peak on the left and one peak on the right side of the normalized frequency 1. By increasing , the two peaks decrease in magnitude and move away from 1, whereas the PDF spread increases. For the left resonance can decrease till about , whereas the right resonance can increase till about . For 0 the left resonance can decrease till about , whereas the right resonance can increase till about . For the left resonance can decrease till about , whereas the right resonance can increase till about .
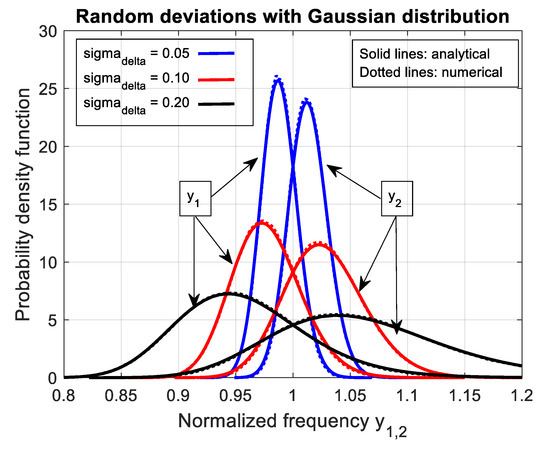
Figure 11.
Probability density functions of the normalized resonance frequencies of the DM current injected into the CM circuit. The normalized deviations of the filter parameters (i.e., capacitances or self-inductances) are treated as random variables with zero-mean Gaussian distribution and normalized standard deviation equal to 0.05, 0.10, and 0.20. Analytical results (solid lines) are compared with numerical repeated-run results (dotted lines).
5.2. Uniform Distribution
Let us assume as uncorrelated Uniform random variables with zero mean and variance , where is the range of each random variable (i.e., the interval ).
By taking into account that , for the mean value and the variance of we obtain:
Therefore, the mean value and the variance of can be approximated as:
where the approximations through the first and second order derivatives were used [26,27].
From (29) and (33) the mean values and the variance of are given by:
Notice that since and are defined as the sum of uncorrelated random variables, their distribution can be approximated as a Gaussian distribution with mean values and variance given by (39). In this case, however, a worse approximation is obtained with respect to the Gaussian case because Uniform distributions have limited range.
Finally, the mean value and variance of the normalized resonance frequencies (30) can be approximated as:
Figure 12a,b shows the behavior of the mean value and the standard deviation of as functions of (red lines). Analytical results (40) (solid lines) are compared with numerical results obtained through repeated runs (dashed lines). The same figure shows the behavior of the mean value and the standard deviation of in the Gaussian case (35) (blue lines) for in the same range of . Gaussian distribution results clearly in larger spread of the resonance frequencies.
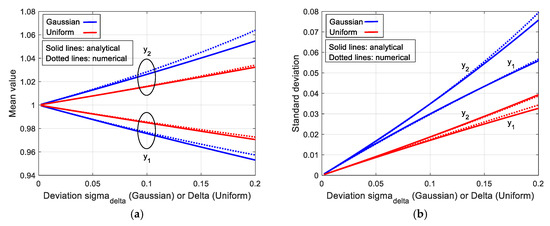
Figure 12.
Mean value (a) and standard deviation (b) of the normalized resonance frequencies as functions of (Gaussian case) and (Uniform case) of the random deviations . Analytical results (solid lines) are compared with numerical repeated-run results (dotted lines).
The PDF of (30) could be readily obtained through the theorem of the transformation of random variables as in the Gaussian case. By taking into account that can be approximated by Gaussian random variables, the PDF of the two normalized resonance frequencies are given by (36), where and are given by (40).
6. Conclusions
DM-to-CM-noise conversion in a three-phase system was investigated in the frequency-domain by deriving in analytical form the interaction between the α, β, and zero circuits of the Clarke transformation due to phase circuit asymmetries. In particular, the frequency location of DM resonances injected into the CM circuit was derived in closed form as function of the asymmetry in the LC filter parameters. Usually, engineers are aware about this phenomenon because it can be observed in frequency-domain measurements of CM current, but a theoretical and quantitative description was still missing in the literature concerning three-phase systems. Since circuit asymmetry is usually due to component tolerances, a statistical analysis was also derived in the paper by treating the filter parameters as random variables. Selection of proper probability distributions of input parameters can be made on the basis of available information for the specific problem under analysis. The complete statistical characterization of the frequency location of CM current peaks due to DM-to-CM noise conversion was derived in analytical form in terms of probability density function, mean value, and standard deviation. Future work will be devoted to the analysis of more general three-phase systems and the related impact of further system asymmetries on noise conversion.
Funding
This research received no external funding.
Conflicts of Interest
The author declares no conflict of interest.
References
- Hamed, S.A. Performance evaluation of three-phase variable-speed DC drive systems with uniform PWM control. IEEE Trans. Power Electron. 1997, 12, 228–242. [Google Scholar] [CrossRef]
- Skibinski, J.L.; Kerkman, R.J. EMI emissions of modern PWM ac drives. IEEE Ind. Appl. Mag. 1999, 5, 47–81. [Google Scholar] [CrossRef]
- Jettanasen, C.; Costa, F.; Vollaire, C. Common-mode emissions measurements and simulation in variable-speed drive systems. IEEE Trans. Power Electron. 2009, 24, 2456–2464. [Google Scholar] [CrossRef]
- Wang, S.; Maillet, Y.Y.; Wang, F.; Boroyevich, D.; Burgos, R. Investigation of hybrid EMI filters for common-mode EMI suppression in a motor drive system. IEEE Trans. Power Electron. 2010, 25, 1034–1045. [Google Scholar] [CrossRef]
- Zhu, C.; Hubing, T.H. An active cancellation circuit for reducing electrical noise from three-phase AC motor drivers. IEEE Trans. Electromagn. Compat. 2014, 56, 60–66. [Google Scholar]
- Bishnoi, H.; Mattavelli, P.; Burgos, R.; Boroyevich, D. EMI behavioral models of DC-fed three-phase motor drive systems. IEEE Trans. Power Electron. 2014, 29, 4633–4645. [Google Scholar] [CrossRef]
- Moreau, M.; Idir, N.; Le Moigne, P. Modeling of conducted EMI in adjustable speed drives. IEEE Trans. Electromagn. Compat. 2009, 51, 665–672. [Google Scholar] [CrossRef]
- Ran, L.; Gokani, S.; Clare, J.; Bradley, K.J.; Christopoulos, C. Conducted electromagnetic emissions in induction motor drive systems. II. Frequency-domain models. IEEE Trans. Power Electron. 1998, 13, 768–776. [Google Scholar] [CrossRef]
- Revol, B.; Roudet, J.; Schanen, J.L.; Loizelet, P. EMI study of three-phase inverter-fed motor drives. IEEE Trans. Ind. Appl. 2011, 47, 223–231. [Google Scholar] [CrossRef]
- Koyama, Y.; Tanaka, M.; Akagi, H. Modeling and analysis for simulation of common-mode noises produced by an inverter-driven air conditioner. IEEE Trans. Ind. Appl. 2011, 47, 2166–2174. [Google Scholar] [CrossRef]
- Meng, J.; Ma, W. A new technique for modeling and analysis of mixed mode conducted EMI noise. IEEE Trans. Power Electron. 2004, 19, 1679–1687. [Google Scholar] [CrossRef]
- Jin, M.; Weiming, M.; Qijun, P.; Zhihua, Z.; Lei, Z. Noise source lumped circuit modeling and identification for power converters. IEEE Trans. Ind. Electron. 2006, 53, 1853–1861. [Google Scholar]
- Lee, S.; Lim, J.; Oh, S.; Kim, Y.; Oh, D.; Lee, J. Differential-To-Common-Mode Conversion Suppression Using Mushroom Structure on Bent Differential Transmission Lines. IEEE Trans. Compon. Packag. Technol. 2019, 9, 702–711. [Google Scholar]
- Huang, Y.; Cheng, C.; Wu, T. A Synthesized Method for Common-Mode Noise Suppression Filters with Specified Common-Mode and Differential Mode Response. IEEE Trans. Electromagn. Compat. 2019, 61, 893–902. [Google Scholar] [CrossRef]
- Chen, S.; Lee, W.; Wu, T. Balanced-to-Balanced and Balanced-to-Unbalanced Power Dividers with Ultra-Wideband Common-Mode Rejection and Absorption Based on Mode-Conversion Approach. IEEE Trans. Compon. Packag. Manuf. Technol. 2019, 9, 306–316. [Google Scholar] [CrossRef]
- Brovont, A.D. Generalized Differential-Common-Mode Decomposition for Modeling Conducted Emissions in Asymmetric Power Electronic Systems. IEEE Trans. Power Electron. 2018, 33, 6461–6466. [Google Scholar] [CrossRef]
- Ohn, S.; Zhang, X.; Burgos, R.; Boroyevich, D. Differential-Mode and Common-Mode Coupled Inductors for Parallel Three-Phase AC–DC Converters. IEEE Trans. Power Electron. 2019, 34, 2666–2679. [Google Scholar] [CrossRef]
- Niyomsatian, K.; Vanassche, P.; Gyselinck, J.J.C.; Sabariego, R.V. Active-Damping Virtual Circuit Control for Grid-Tied Converters with Differential-Mode and Common-Mode Output Filters. IEEE Trans. Power Electron. 2020, 35, 7583–7595. [Google Scholar] [CrossRef]
- Wang, S.; Lee, F.C. Investigation of the Transformation Between Differential-Mode and Common-Mode Noises in an EMI Filter Due to Unbalance. IEEE Trans. Electromagn. Compat. 2010, 52, 578–587. [Google Scholar] [CrossRef]
- Qu, S.; Chen, D. Mixed-mode EMI noise and its implications to filter design in offline switching power supplies. IEEE Trans. Power Electron. 2002, 17, 502–507. [Google Scholar] [CrossRef]
- Xue, J.; Wang, F.; Guo, B. EMI noise mode transformation due to propagation path unbalance in three-phase motor drive system and its implication to EMI filter design. In Proceedings of the 2014 IEEE Applied Power Electronics Conference and Exposition (APEC), Fort Worth, TX, USA, 16–20 March 2014; pp. 806–811. [Google Scholar]
- Bellan, D.; Superti-Furga, G. Space-vector state-equation analysis of three-phase transients. J. Electr. Syst. 2018, 14, 188–198. [Google Scholar]
- Bellan, D.; Pignari, S.A.; Superti-Furga, G. Consistent circuit technique for zero-sequence currents evaluation in interconnected single/three-phase power networks. J. Electr. Syst. 2016, 12, 230–238. [Google Scholar]
- Bellan, D. Symmetrical-Component Approach for Circuit Modeling of EMI Emissions in Three-Phase Inverters. In Proceedings of the 11th IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Macao, China, 1–4 December 2019; pp. 1–5. [Google Scholar]
- Bellan, D. Mode transformation of EMI noise due to unbalanced filter capacitors in three-phase motor drive systems. In Proceedings of the IECON 2017—43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 7024–7027. [Google Scholar]
- Papoulis, A.; Pillai, S.U. Probability, Random Variables and Stochastic Processes, 4th ed.; McGraw-Hill: New York, NY, USA, 2002. [Google Scholar]
- Bellan, D.; Gaggelli, A.; Pignari, S.A. Noise Effects in Time-Domain Systems Involving Three-Axial Field Probes for the Measurement of Nonstationary Radiated Emissions. IEEE Trans. Electromagn. Compat. 2009, 51, 192–203. [Google Scholar] [CrossRef]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).