1. Introduction
The desire of mobile users for high quality wireless connections imposes tremendous pressure on a wireless service provider to improve the service quality. The traffic requirements of mobile users are also becoming prominent and the requirements of such users are increasing rapidly. To respond to such requirements and to satisfy users, different methods have been applied. One such method that has been studied quite frequently and can be applied for such applications is the use of the cooperative relay. From research that has been conducted in recent years and also from communication theory, the presence of a relay on a weak wireless link could improve quality of service (QoS) of the link. In typical circumstances, the relay overhears the source signal and forwards the data to the desired destination in case the direct link fails or to provide link diversity. The cooperation among relays could use two, three or more hops and such cooperative relay protocol in effect establishes a virtual antenna array among geographically dispersed relays, even those that have been placed randomly. The selection of the best relay in cooperative wireless networks has been a topic of research for some time. Different relay selection methods have been proposed. For instance, in [
1] the power and signal-to-noise ratio (SNR) auction method is proposed for power allocation and relay selection. In [
2] it has been proved that a good channel condition determines the best selection of dual hop relay. In [
3] the relay selection problem using OFDM in a multi-access network for relay selection has been explored. The issue of fairness and data transmitting speed among relays is shown in [
4]. In [
5] a simplified form of single relay selection for decode and forward (DF) protocol has been studied. A two-stage strategy for relay selection to achieve the minimal outage probability was studied in [
6]. In [
7], a relay is selected to transfer an end to end signal only if it successfully decodes the source signal. Each relay stores information about the successfully decoded source signal.
The unpredictable behavior of the channel gain due to Rayleigh fading and its implications on the performance of the cooperative relay network needs to be more fully studied. Previous works on selection of relays have placed little emphasis on the fade duration as a relay selection criteria. This is unfortunate because fade duration may have the biggest effect on user experience and the performance of channel and source coding. Long fade durations can cause enough packet drops to noticeably degrade audio and video streaming. One study [
8] has shown a duration of longer than 30 ms causes significant problems with professional live audio performances. Long fades can also cause channel coding schemes to fail, resulting in groups of dropped packets since channel coding cannot handle too long a burst of errors. Therefore, this paper focuses on this issue to make use of fade duration to find the best relay selection decisions. In this paper, relay selection based on the average fade duration (AFD) over Raleigh faded channels is presented. Paths are found for two hop and three hop cooperative wireless relay networks. The selection method is based on the analysis of the second order statistics for level crossing rate (LCR) and AFD over multiple relay hops. We derive the closed form expression of AFD over a DF cooperative network. We also consider the selection of relays and a relay path based on the fade duration outage probability (FDOP), which is the probability that a fade duration would exceed a given time duration threshold.
Some of the contributions of this paper are as follows.
Proposal of cooperative relay techniques among source and destination pairs through one or two designated relays (i.e, two or three hop relay paths) to improve the received signal. The three hop path is more costly to the network (which we emulate through a cost penalty), but it can produce a better QoS.
Usage of the fade duration outage probability (FDOP) technique to analyze the quality of each end-to-end path and to apply the optimization method to select a designated relay.
Proposal of relay selection based on the average fade duration (AFD) method.
Simulation study for comparing relay selection with the traditional SNR method versus our fade duration methods. SNR based optimization frequently chooses different relay paths, as low as only 63% of the same relay paths as FDOP or AFD optimizations. Since the fade duration approach more accurately reflects the true quality of a signal, this work shows the value of moving away from SNR methods to fade duration methods.
The article is presented in four parts. In
Section 2, the system model is presented.
Section 3 discusses threshold based relay selection for two and three hop cooperative relay networks.
Section 4 provides validation through optimization, simulation, and numerical analysis.
Section 5 provides real-world practical application of the concepts of this paper.
Section 6 provides final conclusions.
2. System Model
Cellular wireless networks allocate orthogonal divided channels to transmitting terminals. Due to insufficient isolation between TX and RX, a full-duplex system is not considered in this paper, but rather a half-duplex allocation.
The channel model for the cooperative relay network is characterized by using time division notation where
,
and
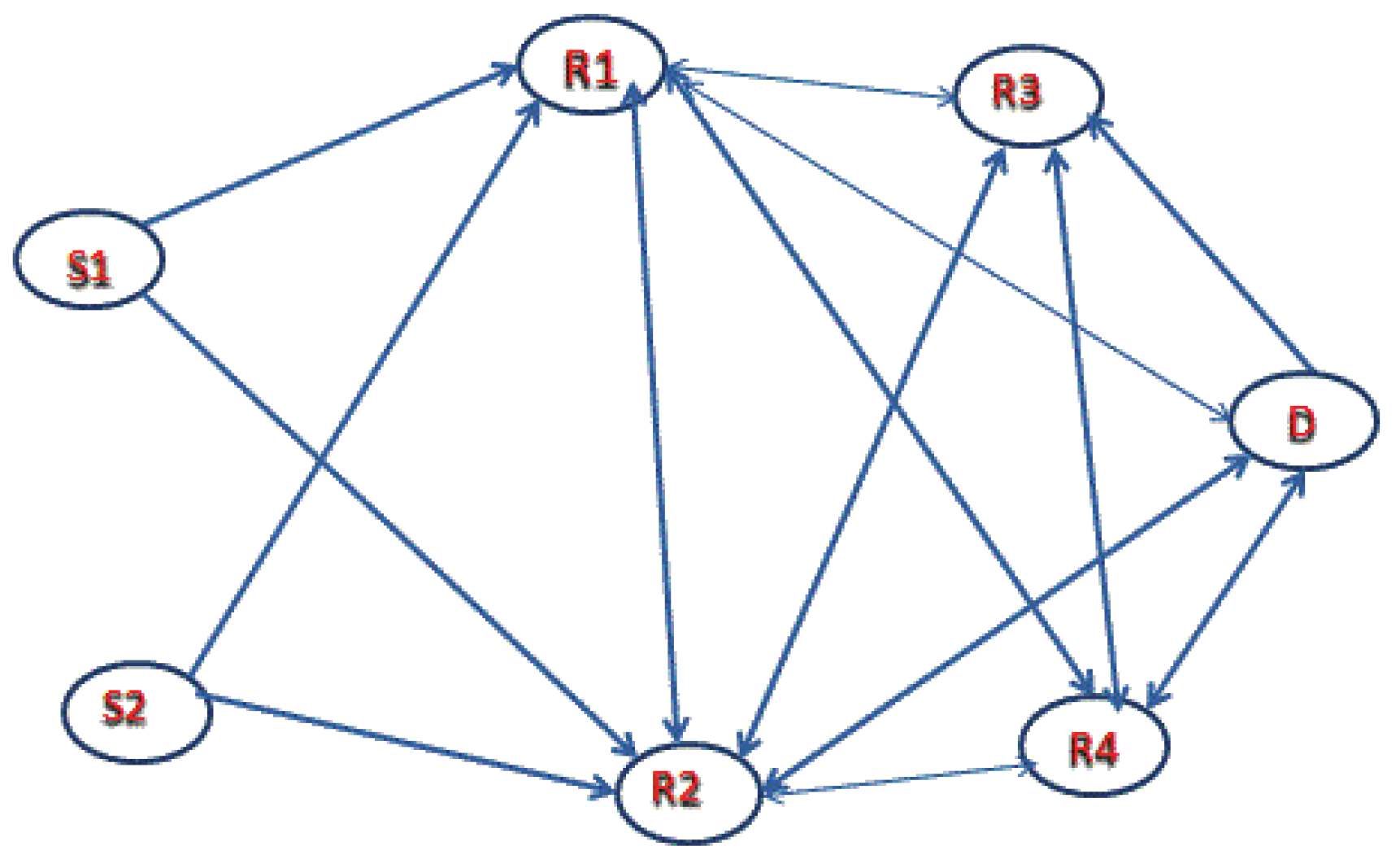
represent the source, the relay, and the destination terminals. In this paper, we study the up/down communication among the source/destination pairs through the designated relay. As depicted in
Figure 1, we consider that relays are deployed randomly between the source and destination. The main purpose of the relay is to enhance source nodes’ capacity through source–relay cooperation.
At a given time, relay cooperation is possible if there exists a relay that is capable of retransmitting data from the source and able to transfer to the final destination. The designated relay will be able to help receive the source signal. As shown, the system model is composed of a two hop and three hop cooperative relay system that consists of the source (S), relay (R), and the destination (D). The network contains S sources and R relays. The model is based on the DF protocol over the half-duplex sub-channel of S–R–D for for two hop and S–R–R–D for a three hop relay cooperative network. There is an assumption that the direct link between the source and the destination is weak and each sub-channel experiences independent, flat, frequency non-selective Rayleigh fading. The fading is assumed to have the same stochastic characteristics within each time slot. For a two hop network, the time slot is subdivided into two sub-time slots. In the first time sub-slot, S transmits while R and D listen, and in the second sub-slot R transmits and D listens. An important part of this work is consideration of the three hop relay network. A simple example illustrates. Suppose there are two sources, S and S, and two relays, R and R. Moreover, suppose the link from R to the destination is very poor. In a two hop relay network, the sources would send to the relays in the first sub-time slot and then each relay would send to the destination in the second sub-time slot. The data from R to destination would be severely degraded or lost. In a three hop case, however, relay R could send data from one source in the second sub-time slot, say using the path S–R–D. Moreover, in the third sub-time slot would send data from the other source using path S–R–R–D. The three hop path option provides more opportunity for good communication. It does, however, require the network to use the third sub-time slot, which is a cost to the network; this cost is incorporated into the models in this work.
In this paper the signal transfer can be chosen to either use a single relay or multiple relays, based on the optimum path that is found, based on AFD, FDOP, or SNR. These include the paths which minimize the sum of total path AFDs, maximize the sum of total path SNRs, minimize the sum of total path FDOPs, minimize the maximum link AFDs on a path, maximize the minimum link SNRs on a path, or minimize the maximum link FDOPs on a path.
2.1. Direct Transmission
For direct transmission the channel can be modeled as
The mutual information for the direct transmission by independent identical distribution zero mean Gaussian distributions is described as
where
is the channel gain on the source-destination link. In terms of
and the fading coefficient for spectral efficiency R, the outage event occurs when
, for the direct transmission the outage in terms of channel gain is given as
Replacing SNR with the received signal and noise powers; the above equation can be represented as:
For outage probability in Rayleigh fading,
follows an exponential distribution with parameter
given by
2.2. Two Hop Relay Network
In a single hop system, a relay is selected to transfer the received signal to the destination. The information per bit of the received signal is denoted by
where SNR and
H represent signal to noise ratio and channel gain, respectively. Due to Rayleigh fading, the mutual information
may drop below a certain level. Assuming the minimum acceptable spectral efficiency to be
then
The received signal will be decoded successfully as the mutual information exceeds
. The channel amplitude can be represented in terms of
as
2.2.1. AFD Based Analysis
An outage occurs with probability
. During such event the received signal amplitude
R crosses the threshold value
and the number of times the crossing occurs per unit time determines the level crossing rate (LCR). The average fade duration (AFD) depends on the LCR value. The channel gain
is a random process and the probability a going and staying below the threshold value of
is determined by the time correlation as captured by the LCR and the AFD. The AFD is the average time the received signal remains below
and is defined as [
9]
where LCR as a function of
is determined by the Rice equation as given by [
10], Equation (
5):
Now we derive the fade duration equation for multiple links. The two links between source to relay and relay to destination are represented as
and
, respectively, are each distributed according to the Rayleigh PDF as
The cumulative distribution function CDF for
is obtained as
where for link
. The value of
could be obtained as
and
where
is denoted as the average squared amplitude or the average power. In terms of
, the probability that one of the links is below the threshold value (hence the two hop amplitude
R is below
) is given by
From the Rayleigh fading calculation
and also
then
If
happens to be true, Equation (
16) can be simplified as
From the Rice equation, the joint probability of
R and
is expressed as
where
denotes the PDF of
when
is a time differentiation of R when it crosses the threshold value of
. Then applying Equation (
18) to the Rice equation for the entire two hop relay network we obtain the LCR
.
The LCR for individual links in terms of
as their respective thresholds is represented as
where
and
denote the Doppler shift values for each link and
represents the value of
R normalized to the RMS.
is expressed in terms of the received signal as
Similarly,
can be expressed as
Rearranging Equation (
19) using the above two equations where
q and
s links are identical yields
Using Equations (22) and (23) and applying them to Equation (
19), the AFD in Equation (
9) can be formulated as
Thus Equation (
25) represents the closed form of the average fade duration for path
k over links
q and
s in a two hop cooperative relay network. The selection of the best relay easily relies on the value of the AFD value observed during the selection period.
If
and
have similar values, the AFD in Equation (
25) can be simplified as
2.2.2. SNR Based Analysis
The outage probability for Rayleigh fading occurs when the probability of the mutual information is below a certain rate
.
where
In terms of SNR, the outage probability can be equally shown as
Assuming that on the S-D link there is no direct line of sight
. Then for Rayleigh fading from Equation (
17)
and also
resolving the above equations for the two hop relay path yields
2.3. Three Hop Relay Network
2.3.1. AFD Based Analysis
Referring to
Figure 1, the three hop relay path has three links in order to reach the final destination. If two relays are involved, the time slots to get from the source to the destination consists of three sub-time slots. In the first sub-time slot, the source sends the data to the relay and destination, and in the remaining two sub-time slots the selected two relays use those sub-time slots to reach to the destination. Therefore the information is expressed as
. The probability that R on any given link will be less than the threshold value,
, is given by
If
, similar to Equation (
17), Equation (
33) simplifies as
The LCR for
,
is expressed as
From there the three hop relay AFD can be formulated as
To select the best relay for a three hop cooperative network, the closed-form of Equation (
38) could be applied.
If
=
=
, and applying Equation (
19) for the three hop relay, yields
In this case, the closed form of AFD can be simplified as
2.3.2. SNR Based Analysis
In a three hop relay network as shown in
Figure 1, the data received from the source can be represented in terms of the channel gain as
whereas in the second time slot the data received at the second relay and the destination can be denoted as
In the third time slot the relay that detects the signal from the other relay transmits to the destination. Then
Here, we are assuming that S-D link unreachable and no direct line of sight. Then the outage can be computed as
since there is no direct link then
. For the source–relay link
for
link
and to the destination
Considering three hop relay for the equation above and resolving for link S-R1, R1-R2, R2-D yields
2.4. Fade Duration Outage Probability
Due to Rayleigh fading, the received signal is usually affected by how long it remains in a fading dip. While the received signal remains in a fading dip, an ‘outage’ occurs. To select a relay based on the frequency of dips and to minimize outages, it is important to compute fade duration outage probability (FDOP), and ensure the FDOP < FDOP. The amount of time the signal remains in a fading dip characterizes its quality. The longer it remains in a fading dip the more distorted the signal will be.
The fade duration outage probability (FDOP) is based on several works including the initial work on the fade duration distribution (FDD) by Rice in [
10]. Subsequent efforts extended this work include [
11], where Mandayam, Chen, Holtzman derived asymptotic approximations for FDD to determine what they call the minimum duration outage. We believe the term fade duration outage probability is a better understood name. This was extended by Lai and Mandayam [
12] and simplified by Nadarajah and Kotz [
13]. More recently, Ohmann and Fettweis showed interest in fade duration outages in [
14] by approximating FDD models using an exponential model, making it tractable and manageable to include multiple links. References [
15,
16,
17,
18,
19,
20,
21,
22,
23] provide other foundational contributions in cooperative relaying.
The probability that the amplitude of a received signal remains below the threshold value
for more than
is denoted by Rice’s asymptotic approximation in [
10]
where
is a modified Bessel function order one. The PDF of the fade duration can be obtained as shown in ([
12], Equation (
18)) as:
where
, the PDF of the outage duration can be denoted for
. As shown in [
12] Equation (
19)
The fade duration outage probability is computed as
where as
is the outage rate. After putting all the components together and simplifying, the FDOP can be finally denoted as (this is from [
13], Equation (
6), and our own simplifications)
where
To determine the relay path with minimum fade duration outage probability for a particular source relay path, it is important to compute the fade duration outage probability of each relay path and select the minimum FDOP for each source relay path. The issue gets more challenging and complicated as the number of involved relays and sources gets bigger. To deal with such challenging issue and to obtain an optimal solution, we propose two optimization methods of relay selection based on FDOP. The analysis and the selection criteria along with AFD and SNR methods is shown in
Section 3.
3. Optimal AFD/SNR/FDOP Threshold Based Relay Selection
In an effort to study the value and comparisons between fade duration based (either AFD or FDOP) and SNR based selection methods, we have conducted the following research. First of all, we devise several optimization approaches that would choose the best sets of relays. These are link-by-link and path based approaches that use SNR, AFD, and FDOP. Then we conduct extensive simulations to see when and where AFD, FDOP, and SNR optimizations choose the best paths. Of particular interest are cases when relay path choices are different. Since we assert that fade duration approaches approximate user expectations more effectively, we see that SNR approaches fail to choose the same paths as FDOP and AFD methods in several situations, resulting in lower performance. Such optimizations, however, would likely only be used in limited situations due to their computational complexity. As we conclude the paper, we present methodologies for implementation of relay selection in today’s coming 5G networks. In real situations, the number of available relays would not be very large. Individual sources would seek out possible macro cell and relays path using fade duration based metrics.
The traffic demand and the maximum allowable data loss that can be tolerable during wireless communication differs from one application to the other. For instance, a video signal will lose the picture synchronization if the data loss is more than a certain number of frames. During deep Rayleigh fading, as the length of the fade duration becomes longer and deeper, the more data gets lost before reaching the BS. Such loss will be hard to recover. To avoid such issues, relay selection based on the AFD and FDOP is proposed. To better correlate with quality of service for real applications, we also compare with SNR based relay selection to see where SNR based relay selection would choose relay paths with worse AFD and FDOP performance.
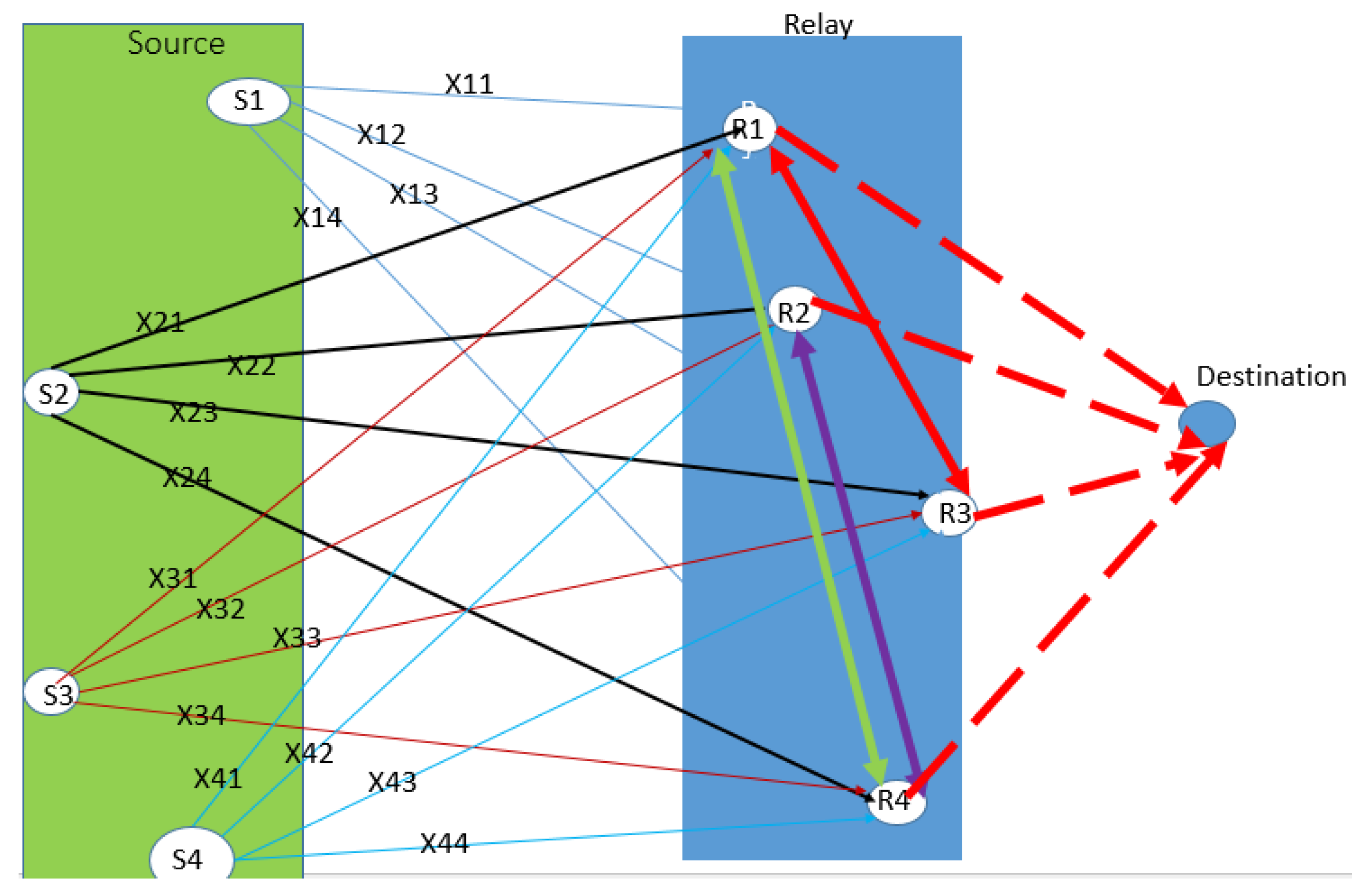
As seen in
Figure 2, the selection process needs to determine which relay path performs better in order to satisfy the selection criteria. The cooperative relay selection problem has been formulated to facilitate the best relay selection among
R available relays for
S number of sources. To determine the best relay choices, two different path selection methods are formulated, which are path-by-path (total path) and link-by-link optimization. In the former, we compute the total path metrics and find the best combination of paths. In the latter, we compute metrics for each link and then use max–min or min–max formulations to find the best paths.
3.1. Path-By-Path (Total Path) Optimization
3.1.1. AFD Based Optimization
The AFD based optimization method selects the best path on the basis of the AFD value. The path with the least AFD value exhibits less loss of data and a strong source signal reaches the final destination. In this type of optimization, the end-to-end optimization computes the path with the least sum of the AFD values for all of the paths to be the best paths for end to end connections.
To determine the AFD value, we apply the derived closed forms of AFD as shown in Equations (25) and (38). AFD represents AFD for source j, first relay i, and last relay l. If , only one relay is used. P represents the penalty value to the three hop path network for using an extra time slot in comparison to the two hop relay network. No penalty is imposed on a two hop relay. Penalty values are examined extensively in the simulations.
The optimization can be formulated as
subject to
where
is a binary variable that indicates the path chosen. If
, then the path is from source
j to relay
i and then straight to the destination. Otherwise,
l is the second relay.
is computed from Equations (25) and (38).
Equation (58) is a linear programming optimization. Equation (59) states that one and only one source must be associated with only one relay. Equation (60) ensures the first relay i can only be used at most once. The relay selected could not be used by any other source in that particular time slot. Equation (61) ensures that a path goes from one relay to another relay or goes direct to the destination. A relay link is bidirectional and can only be used in one direction at a time, which is enforced by Equation (62). Equation (63) enforces that each link AFD value remain below the threshold value.
3.1.2. SNR Based Optimization
This method the selection of relay to transfer the data from source to destination is based on the path with possible higher SNR than the remaining paths. The objective is to find the maximum sum of the SNRs for the chosen paths. This method is similar to the AFD selection method except in this method the highest sum of SNR values is selected whereas in the AFD selection method the path with minimum AFD value is preferred.
subject to
and the Equations (59) through (62). SNR
comes from Equations (32) and (51).
3.1.3. FDOP Based Optimization
The main task of this optimization is to locate those relays that minimize the total sum of fade duration outage probabilities based on the following
subject to
and Equations (59) through (62). The total path FDOP is computed as follows for two or three relays.
The optimization shown above is a simple LP optimization where Equation (67) states that the FDOP also needs to be less than the threshold value FDOP.The selection of a relay based on this criteria will minimize the outage rate and increase the performance of the cooperative relay network.
3.2. Link-By-Link Optimization
In these methods, the metrics are computed for each link and optimization occurs to find the best combinations of links.
3.2.1. AFD Based Optimization
In this method the AFD value of link by link (source–relay, relay–relay, relay–destination) is optimized and the min–max method is applied to select the best relay. In each scenario, the AFD value of each link should be below the threshold value to be considered as a potential path.
The objective is first to select the link with the maximum average fade duration from the source to the destination through each two hop or three hop relay path. Then select the min of the selected values to find the best path. The optimum solution
subject to
where X
is a binary variable that indicates the link from source
j to relay
i; Y
is a binary variable that indicates the link from relay
i to relay
l. If such a link is chosen, a penalty P
is multiplied to that link AFD. Z
is a binary variable that can indicate either a link from relay
i to relay
l and then to the destination, or if
a link directly from the relay to the destination without going to the second relay. Each AFD is computed from Equation (
9), AFD
from source to relay, AFD
relay–relay, and AFD
to the destination.
In this linear programming optimization, Equations (70) and (71) state that each source will be served at least by one relay and each relay will be served from at most one source. From the relay, the packet must then go directly to the destination or to another relay, as enforced by Equation (72). A relay link is bidirectional and can only be used in one direction at a time, as in Equation (73). In Equation (74), once a relay–relay link is used then the packet goes to the destination. Equation (75) enforces that each link AFD value remain below the threshold value.
3.2.2. SNR Based Optimization
The SNR based optimization is similar to the above method with the exception of the objective function and the threshold value.
subject to
and the same Equations (70) through (74). SNR optimization is a max–min optimization in this case.
3.2.3. FDOP Optimization Method
In case of FDOP based optimization, we use the following
subject to
and again the same Equations (70) through (74). FDOP optimization is a min–max optimization.
4. Simulation Results
A series of simulations were conducted regarding the link-by-link min–max (AFD and FDOP) and max–min (SNR) optimizations. A 1000 by 1000 m area was used. The source nodes were uniformly randomly placed in the leftmost 400 by 1000 m area, relays in next 400 to 700 by 1000 m, and a single destination in the rightmost 700 to 1000 by 1000 m area. A Friis’ pathloss model was used with pathloss exponent 3.0, carrier frequency 1.8 GHz, transmit power 40 dBm, omnidirectional transmit and receive antennas, and background noise of −90 dBm. AFD and FDOP simulations used maximum Doppler shift Hz, minimum received power dBm (min SNR of 0 dB), and for FDOP maximum fade duration ms.
4.1. Verfication
The first step was to verify the correctness of the optimizations and simulations.
Table 1 shows details of a two source and two relay simulation. The separate AFD, FDOP, and SNR tables show each parameter from source nodes to relays, between relay nodes, and from relays to the destination. The penalty parameters used were
for AFD and FDOP, and
for SNR. The logic of using these penalty choices was that a relay–relay transmission would add an extra timeslot to transmit to the destination, increasing from two to three slots.
The results show that all cases make use of a relay to relay transmission. Looking first at the AFD results, the maximum AFD for all links was the R1–D AFD of 0.001647. Therefore, both paths chose to use the R2–D link, with the S1–R1–R2–D path including a link between R1 and R2. Now let’s consider the effect of the penalty value. Since the relay–relay link had an AFD of , the adjusted AFD including the penalty would be , less than the 0.001647. If however, a penalty of were used, then the adjusted AFD would be , making the relay–relay link increase the objective of the min–max optimization. The optimization would then chose to use paths S1–R1–D and S2–R2–D, avoiding use of the relay–relay link. The FDOP results also avoided the R1–D link when using . For the FDOP case, for , the optimization avoids the relay–relay link, since the ratio between the R1–D link and the R1–R2 link is . Only when the penalty for FDOP is much larger than the AFD penalty (29.55 compared to 2.45) would FDOP avoid the use of relays. We investigate this effect further in the next subsection.
The SNR optimization is a max–min optimization, so the penalty value needs to reduce the adjusted SNR of the relay–relay link to possibly make that link undesirable. If at first using the 1.5 penalty value for AFD and FDOP, but in this case using
, the results are seen in
Table 1. Again the worst link is R1-D, here with the lowest SNR of 6.8 (not in dB). Here a lower penalty value of
would make the routes become S1-R1-D and S2-R2-D, where the
P value threshold comes from
.
Table 2 provides some results for four scenarios with four sources and four relays.
Table 2 shows four scenarios where the results are different between the AFD, FDOP, and SNR methods. Those routes which are highlighted are different from the other two methods, and for scenarios 3 and 4, the three methods produce three different results. As we will see in the next section, with the P values equal to 1.5 and 0.667 as above, FDOP and AFD use different sets of paths 70.0% of the time, FDOP and SNR methods use different paths 75.7% of the time, and SNR vs. AFD are different 72.1% of the time.
4.2. Penalty Value Comparisons
This subsection provides a comparison of the effects of varying the penalty parameters. As seen above for the two-by-two cases, penalty values can be quite different to cause the avoidance of using a relay–relay path, such as for AFD and in those examples. The goal here is to vary penalty values in the range of values over which the we see the full effects of the penalty value. Greater than some large penalty values for AFD and FDOP and less than small penalty values for SNR, relay–relay hops would stop being used completely.
Before finding optimizations with relays, we first determined the maximum and minimum values of AFD, FDOP, and SNR that were found in the simulations, then determined the maximum values of P that were needed. These were found to be P, P, and P. When conducting the simulations, we varied P from 1 to on a linear log scale, then varied P and P along linear log scales from 1 to their maximums or minimums. For example, P.
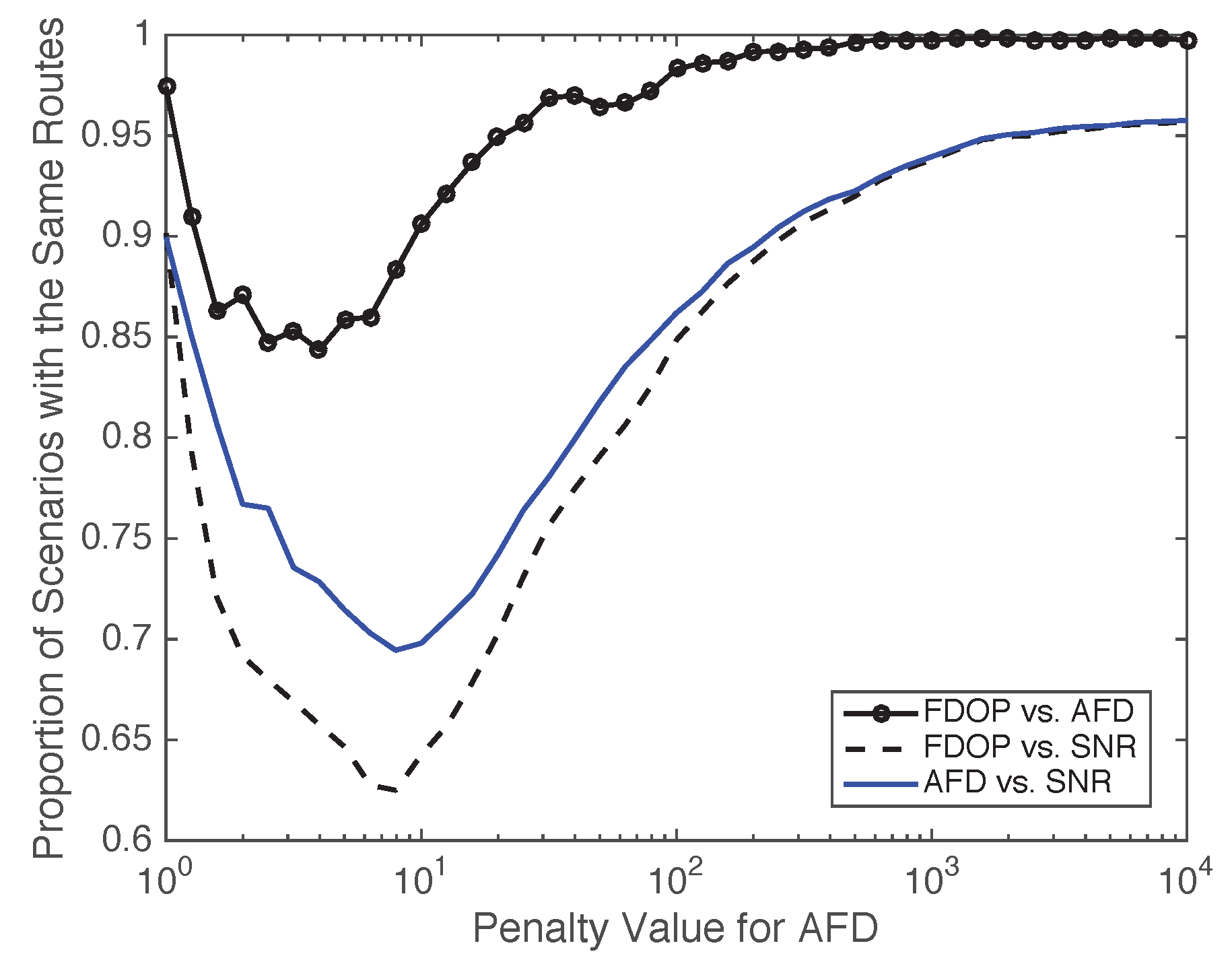
Figure 3 shows the results of variations compared with penalty values. The three curves provide pairwise comparisons between the three optimization criteria. Each sample point is the result of randomly generating 2000 scenarios and determining when the simulation results were the same or different. Optimizations were conducting using the AMPL tool using the CPLEX solver.
These results are most useful if a particular parameter is chosen to be the most relevant. For ultra-reliable ultra-low latency (URLLC) traffic, the FDOP metric might be most important. FDOP might also be most important for other types of critical traffic. AFD might be most useful for voice and video streaming, since this would help find the proportion of the streaming signals that might be degraded and SNR would be useful for more traditional uses. In 5G and beyond be a machine to machine communication or any other form of communication, the most important point is reliable and error free network. The communication network should provide closer to 100% reliability. Such type of communication could not be achieved just by adjusting the SNR value, but instead by providing a tool that creates a conducive environment for reliable and error free network. FDOP could be useful tool for such mission. We believe SNR will be the least useful for emerging 5G and machine-to-machine traffic types.
Regardless of the choice, the extent to which that choice is better than other choices can be pronounced. Take the traditional use of the SNR metric. When P
as seen in
Figure 3, this corresponds to P
and P
. In this case, the similarity in routes between FDOP and SNR is only 70% and similarity between AFD and SNR is only 63%. So the SNR choice can frequently produce routes that are not as useful for FDOP. The most important observation is that the AFD and FDOP optimizations share the same routes much more often than FDOP vs. SNR or AFD vs. SNR. Since we believe fade duration based metrics are most important, this shows that it is very important to actually use fade duration metrics instead of SNR when choosing one or two relays.
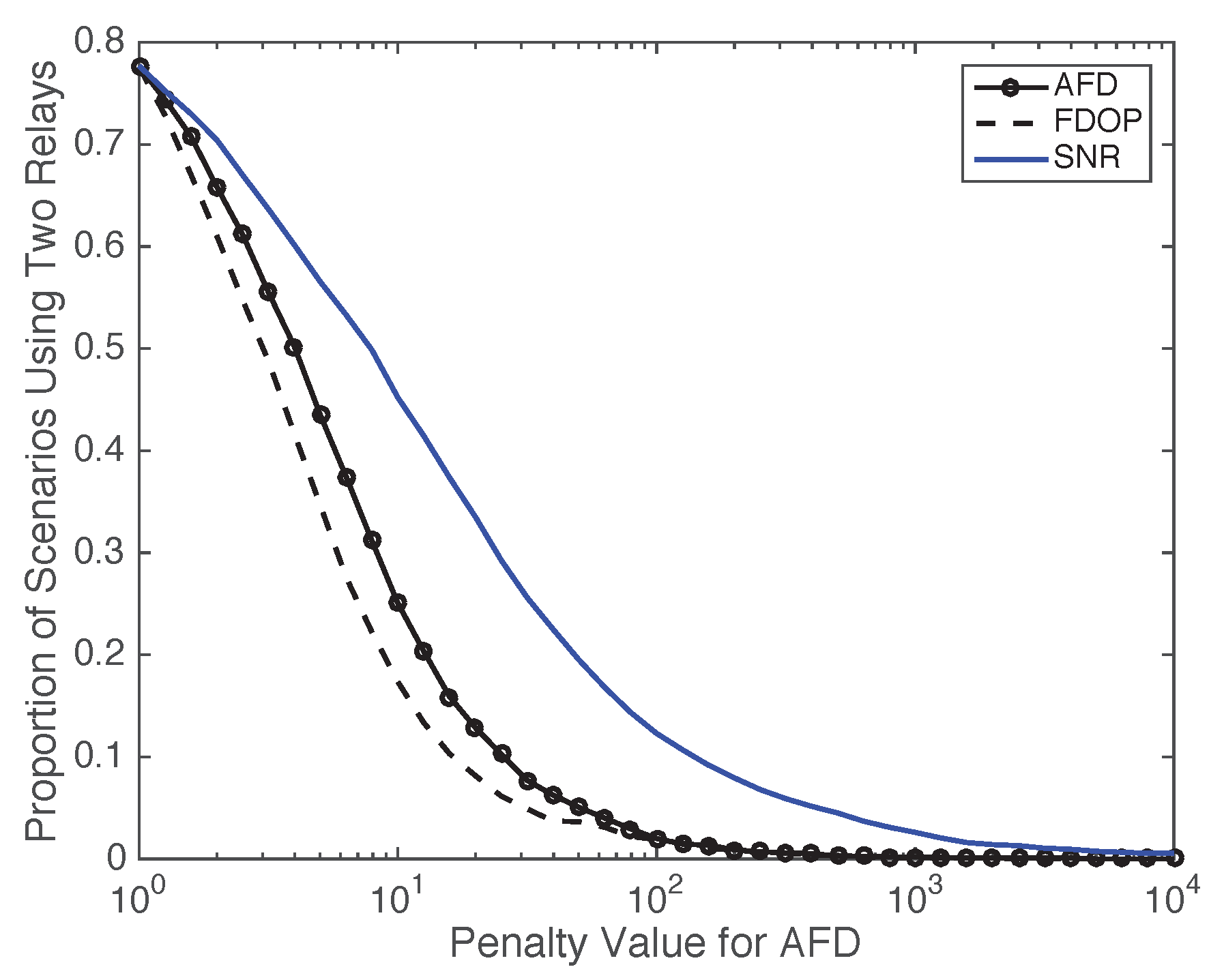
Figure 4 provides some insight into how often relays are used. Again the AFD penalty is used for the x-axis, but the other metrics also range from their minimum to maximum accordingly. When all penalty values are 1 (i.e., no penalty), all three methods used relays in 78% of the scenarios. Then as the impact of penalty values increases,
Figure 4 shows how the use of relays diminishes. Penalty values cause AFD and FDOP to limit uses of relays much sooner than SNR as the penalty values increase.
4.3. Doppler Spreading
A parameter that has a significant impact on AFD and FDOP equations is the maximum Doppler shift,
. The amount of time in a fade is certainly dependent on the rate of change of the fading effects.
Figure 5 shows the differences in choices of relay routes as
varies from 2 to 200 Hz. It is anticipated that the differences in relay routes would exist between SNR and either FDOP or AFD. This is confirmed with the AFD vs. SNR curve, although it is interesting to see that the proportion is always around 79%. Differences in relay routing for either metric compared to FDOP do indeed vary significantly versus
. However, above approximately 60 Hz, there are no additional significant changes in those differences.
5. Practical Implementation
In real-world practical application of the concepts of this paper, it is important to understand deployment issues of relays in today’s and future networks. Today’s real-world practical application of relay deployment is extensive and varies based on the cellular operator’s available resources, users’ demands for better service, traffic analysis, and collected key performance indicators such as drop call rates, data rates, low data rate thresholds, etc. The geographical landscape of the area where a macro station is intended to cover is also another factor to consider for the use a relay. These factors may compel an operator to deploy a relay to facilitate users’ traffic in a seamless way and to improve the coverage.
We do not suggest always deploying the optimizations in
Section 3 and
Section 4 due to the computational complexity of the optimizations when there are many sources and relays. The purpose of those sections was to compare and show the benefits of AFD and FDOP relay path selection compared with SNR based selection. Rather we suggest that source nodes work individually to find best paths. Cellular networks help sources find the best relays when communication is requested. We have shown in previous sections that fade duration (AFD or FDOP) based methods have the best correlation with the performance expected by end users. During relay selection, throughput and reliable link selection becomes the main focus in selection of the best relay or multihop relay path. Throughput on some occasions could be compromised due to relay placement and the distance between relay and the macro station. When choosing relay paths, a source would need to query the network about the relays available, relay locations, link quality between relays and macro stations, and link quality between relays. From our analysis, these link quality metrics should be related to AFD and FDOP computations.
Various cellular operators apply the relay concept in various forms using labels such as “UE relay,” “repeater,” “magic box,” etc. Such equipment can handle more than one user at a time, so we are not limited to one user per relay as we used in the optimizations. The user also has a choice to connect either to the nearby macro cell or to the relay. The focus in our case was on situations where there is a bad link between the user and the macro site, so the user needs to connect to one of the nearby relays. We assume the main propose of the relay is to provide coverage to the badly covered area that is away from or in an obstructed location from the macro site. The placement of relays should have minimal overlap of each other’s coverage areas to avoid possible interference and to provide the best use of resources such as available bandwidth.
There are cases, however, when our optimization frameworks may be useful, when the number of relays available for a single user at a time is limited. This is usually the case in today’s networks, but more relays are being deployed over time. In our case we assumed only four sources and four relays, this took very little computation time to find a solution. However, even if there is a case of 100 sources and 100 relays, we completed the computation on a general purpose computer that took 5.3 sec. This was accomplished using AMPL with the CPLEX solver.
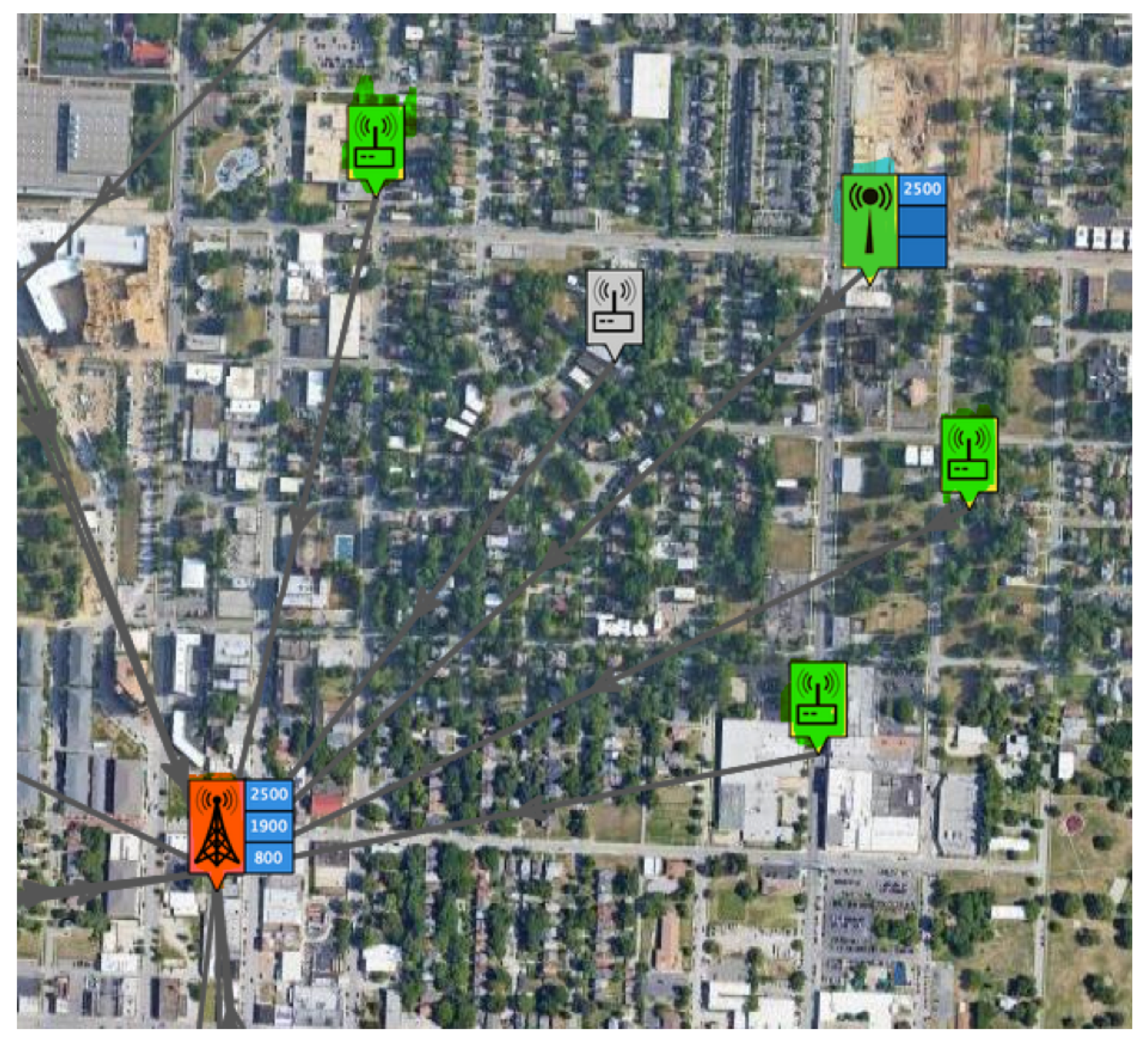
Figure 6 shows an instance of relay deployments from a cellular carrier where UE relays connect to macro sites and provide coverage for users not reachable by the macro station. The red labeled symbol is a macro station with a capability of three bands in 800, 1800, and 2500 MHz. The ones with the green labels are UE relays with different capacities of user connections than the macro stations. The furthest relay is located about 800 m from the main station and the distance between each UE relay is between 150 and 400 m. The one labeled in gray is a non- active relay. The purpose of
Figure 6 is just to show one typical example of relay deployment in a practical environment, but not necessarily every relay deployment should follow this type of deployment. The user that is located far from the macro station may have a maximum of four UE relays to choose from. Based on our suggestion in this paper the user may connect to the one with a better FDOP for the best customer experience, and multihop relay paths may provide even better benefit.
6. Conclusions
Several unique as well as reliable relay selection methods have been proposed which can achieve the best performance for wireless networks. Depending on service requirements, fade duration outage probability, average fade duration, or SNR can be used to determine the best wireless channels and relay links. We have argued that fade duration metrics are increasingly important for today’s streaming and IoT URLLC traffic. We have also shown that simply using SNR metrics to choose relay paths would frequently result in different paths than would have been chosen if fade duration metrics were used directly. Moreover, we have shown how to use those metrics. Future work could be to extend routes to allow more than two relays, but we posit that diminishing benefits would be gained from more relay hops, especially considering the penalty values. Relay networks keep being more widely deployed, and this work takes advantage of them, especially with more substantial possibilities for connections between relays. Fade duration metrics will best serve the traffic that is emerging.