1. Introduction
Over the past few years, Internet of Things (IoT) technologies have been applied for a variety of fields ranging from industrial applications, such as smart grids, intelligent transportation systems, smart security, and others, to personal applications, such as access cards and bus cards. IoT devices in many fields refine a vast amount of raw data that comes from surrounding environment into meaningful and extracted information, and constantly exchange data with other IoT devices via the Internet. One of the important issues in the IoT networks is the collision problem that occurs when two or more IoT devices access the medium at the same time [
1]. To tackle this problem that comes from multiple access, a variety of MAC protocols have been proposed. In Reference [
2], Framed-Slotted ALOHA protocols resources in time domain are divided into slots. And it assigns the slots to each of devices. In Reference [
3], ALOHA-based anti-collision algorithms were introduced with Dynamic Framed-Slotted ALOHA (DFSA) algorithm that estimates the number of devices. These protocols have contributed to increase throughput by reducing the frequency of collision occurrence.
MAC protocols are categorized into Contention-Based MAC Protocol (CBP) and Contention Free MAC Protocols (CFP) [
4]. In CBP, all nodes have their own discretion to access the channel to transmit data. A node listens to the shared channels when it wants to access them without collision. If the channel is not busy, the node sends packets to the channel for data transfer, otherwise it waits until the channel becomes idle. Representative examples of CBP are ALOHA and Carrier Sense Multiple Access (CSMA). When a sender receives an ACKpacket from the peer node, ALOHA protocol starts sending the data. If a sender does not receive an ACK packet from the peer node, it tries to send packets again after backoff time to avoid collisions. In CSMA protocol, the sender observes the shared channel by short control packets or tone-based monitoring to see whether the channel is in use or not. If the channel is busy, the sender sends packets after a while. However, CBP cannot fully resolve the collision issue. CFP utilizes channel more efficiently. Multiple access schemes are classified by certain criteria, in which Frequency Division Multiple Access (FDMA) partitions the frequency of a channel, Code Division Multiple Access (CDMA) encodes a signal allows access to a channel, and Time Division Multiple Access (TDMA) divides the channel into fixed interval time. These allow nodes to access the shared channels without collision. Each divided channel is assigned to a node. Only the node that is allocated for the channel can transmit data by using the channel. For this operation, a large amount of information exchange between nodes is required. And it generates lots of overhead for scheduling resources, which results in performance degradation.
Reinforcement learning can reduce the required time that takes to communicate for resource allocation in MAC protocols. In cognitive radio networks, a reinforcement learning enables efficient channel usage, while reducing signaling overhead [
5]. In Reference [
6], a reinforcement learning algorithm is applied to scheduling collision-free shared channel by using only ACK packets in wireless network environments. The reinforcement learning algorithms used in [
5,
6] are developed based on Q-learning [
7]. The number, location, and traffic characteristic of nodes keep changing in IoT networks. Therefore, the reinforcement learning can be an adequate solution for MAC protocol of IoT networks because it is adaptable to changing environment in distributed manner without any control message overhead. In this paper, we propose a low complexity algorithm for anti-collision that can be applied for CBS protocols to find a suitable transmission time by using a collaborative Q-function which is obtained by the shared channel observation.
2. Methods
An IoT device is regarded as an agent in this reinforcement learning framework. An IoT network is composed of multiple agents. The slotted ALOHA protocol is employed in the system model. Firstly, an agent chooses its initial slot in a random manner in a frame. After all transmission in a frame ends, the agent chooses its next slot by reinforcement learning methodology for determining appropriate transmission time.
The purpose of reinforcement learning is to know the interrelationships between actions and consequences during the interaction of agents and the environment by determining future behavior learned from the prior experiences. In reinforcement learning, the agent learns the appropriate action strategy in any state of the environment only through trial and error [
8]. Action of agent according to the present state is represented by numeric value, which is called a Q-value. All of the actions for all states have Q-values, which are the expected future reward for taking a specific action of the agent in a state. Q-value is denoted as Equation (
1).
is a Q-value of action a in state s at time t, is the reward as a result of taking action a of agent in the state at time k. Here, the action of the agent is the choice of its next transmission slot and the state represents current selected slot of the agents. is a discount factor(). T is the total number of time steps until the end of the learning.
values are stored in the two-dimensional arrangement, known as the Q-table. In Reference [
9], Q-table is represented by only actions in a multi-agent environment and considered to a 1-dimensional Q-table. The stateless Q-learning algorithm is simpler and uses much smaller memory space because it only estimates a single reward for each action. The stateless Q-value in 1-dimensional Q-table at time
t,
, can be derived as expected Q-table with respect to state space, which is defined as Equation (
2).
In the proposed MAC protocol, the stateless Q-learning is used as an action selection strategy for anti-collision. The shared medium for data transmission between agents is divided into slots with respect to time. A frame is composed of a fixed number of slots. Each agent has a 1-dimensional Q-table consisting of
for every slot in the frame. The
in the Q-tables are initialized to random value between 0 and 1, so all agents start learning with random choice among all available slots. At each frame after beginning, every agent selects a slot using
, which indicates the preference of slots. The Q-table is updated by transmission results, success or failure due to the collisions. The recursive update equation is as follows.
where
is the Q-value of action
a at time
t, and
is a discount factor (
). The
is the learning rate parameter, which weighs recent experience with respect to previous the Q-values,
, is the reward associated with a result of transmission at time
t,
is the collaborative Q-value for selecting the appropriate slot in the next frame, taking into account the transmission strategies of all agents in the current frame. Each agent should choose empty slot that other agents are not accessing. Since every agent has its own
at time
t, it has its own policy that selects an access slot determined by
. If an agent knows other agents’ strategy, it could find its own access slot faster. Here, a new Q-value function
is proposed that combines all transmission trials in action
a of the frame at time
t so that the agent can consider other agents’ policy derived from their value functions. That is to say, Equation (
3) updates a value function of the agent by considering other agents collaboratively.
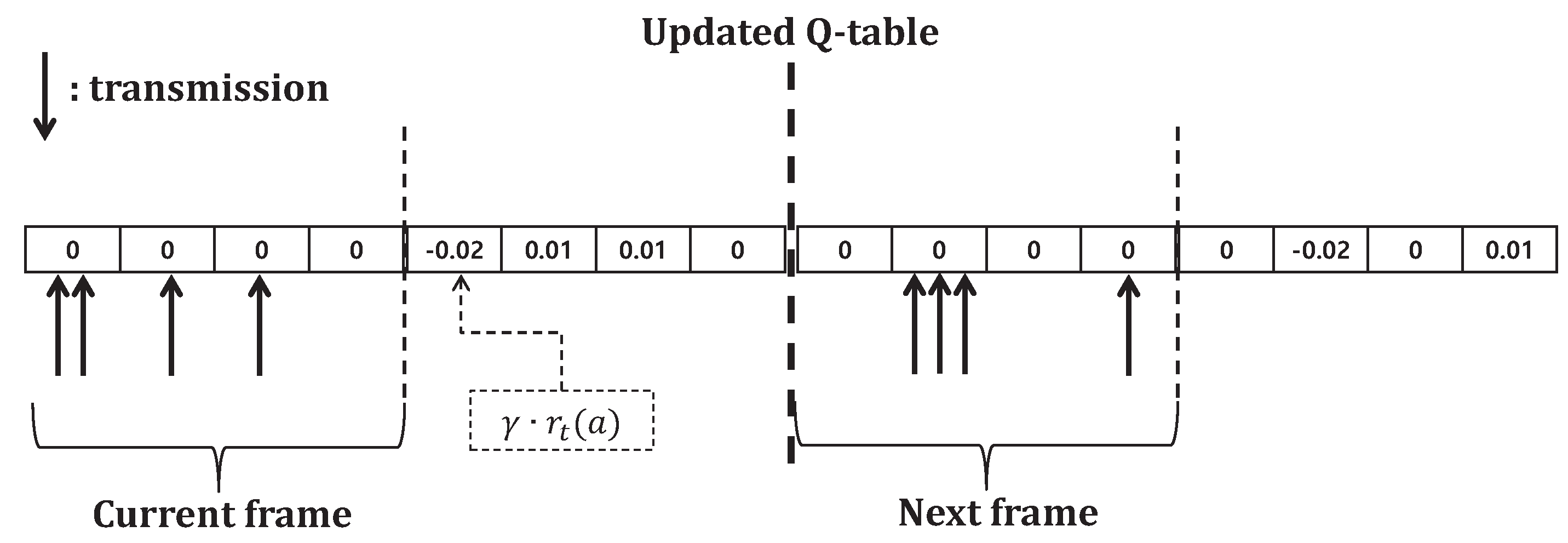
Figure 1 shows the calculation process of consequences of transmission in environment assumed that four agents in IoT networks transmit data in a frame comprising of four slots when
,
. The frame is a row vector with 1 by the number of slots. In the current frame, two agents select 1st slot for data transmission and the transmission result (−0.02) is stored in 1st slot. The next frame is reset to zero after the Q-table is updated. For the next slot, three agents select 2nd slot but the agents can only know whether there was collision or not. In practice, since agents cannot perfectly estimate the number of collided agents, every agent in this system regards this 2nd slot as doubled negative rewards due to the collision. Then,
can be calculated as Equation (
4), where
is the reward of agent
m chooses action
a at time
t.
Each agent refers to its Q-table to select a slot. Equation (
5) is the simple methodology of finding an access slot which selects the largest Q-value in the Q-table. The method of selecting an action
according to a given condition has called a policy, and the method of selecting an action like (
5) is called a greedy-policy.
On the other hand, since greedy-policy control provides a locally optimal policy, rather than an global optimal strategy, two exploration-based policies are used in this paper. Firstly, Equation (
6) is an
-greedy policy control that follows random choices with a probability
and follows greedy-policy with a probability 1
when the number of possible action in a state is
.
The proposed protocol takes decaying
-greedy policy, which decreases the value of
over time, for increasing the probability of using greedy policy.
The second policy control scheme is a softmax strategy. In Equation (
7), the
k-th action
is chosen by probability
. The agent selects a slot with probability
.
A is a set of actions that the agent can access.
is a parameter which determines the amount of exploration. That is to say, as
, the agent randomly selects a slot, and as
the agent follows the greedy policy.
In this algorithm, agents choose strategies which do not have the largest Q-value with small probability. This makes agents to explore other strategies not to fall into locally optimal solution. However, as time spends, the amount of exploration,
and
, decreases to converge global optimum. Since each agent randomly accesses slots at the beginning, using
-greedy policy and softmax strategy, agents can have efficient experiences to get optimal policy [
10]. Through these slot selection strategies, all agents can achieve globally optimal steady-state conditions that all agents have unique slots.
4. Results
In this section, the performance of the proposed protocol is verified by numerical simulation results and compared with ALOHA-Q, which is considered for the conventional scheme that employed Q-learning for ALOHA protocol [
6]. The update equation of ALOHA-Q is as follows.
Different from our proposed Scheme (
3), ALOHA-Q does not take into account the collaborative Q-value
. We consider a wireless network with
N IoT nodes that are allowed to transmit one packet per frame that consists of
M slots (
). The convergence time is represented by the number of frames used until all nodes have approached the steady-state, in which each node has a unique slot not to collide. The convergence time of the proposed protocol is evaluated in networks in which quality of service is prioritized and deprioritized. The prioritized service, such as VoIP and ultra low latency communication, needs to access earlier than other nodes to a shared medium. The deprioritized service, such as best effort data transmission, does not concern latency so that it does not matter whenever they can transmit in a frame. Nodes learn the expected reward to determine their behavior. In the deprioritized network that only provides deprioritized services, since all nodes have an equal priority, they receive same rewards according to the results of their transmission (success: +1, failure: −1). In the network where some nodes require the access to the shared channel earlier, they have an order of the channel use and receive different rewards. Those prioritized nodes receive better reward when they transfer data at the preferred slot (success: +2, failure: −1); in contrast, they receive worse reward when they transfer data at the undesirable slot (success: +1, failure: −2).
Here,
Table 1 provides the parameter setting of the reinforcement learning algorithms used for the simulation. Reward
r is set to
or
according to the simulation scenarios. The values of learning rate
and discounting factor
is fixed for every iteration of the simulations. Exploration parameters for policy control schemes,
and
, are initialized to a fixed number at the beginning of the simulation, as simulation goes along, those values converge to zero.
f is the number of frame,
is the value of
at frame
f, and
is the value of
at frame
f.
The purpose of the prioritized services is to provide high quality of service to specific nodes, such as VoIP traffic, that tend to transfer data earlier, which results in low latency.
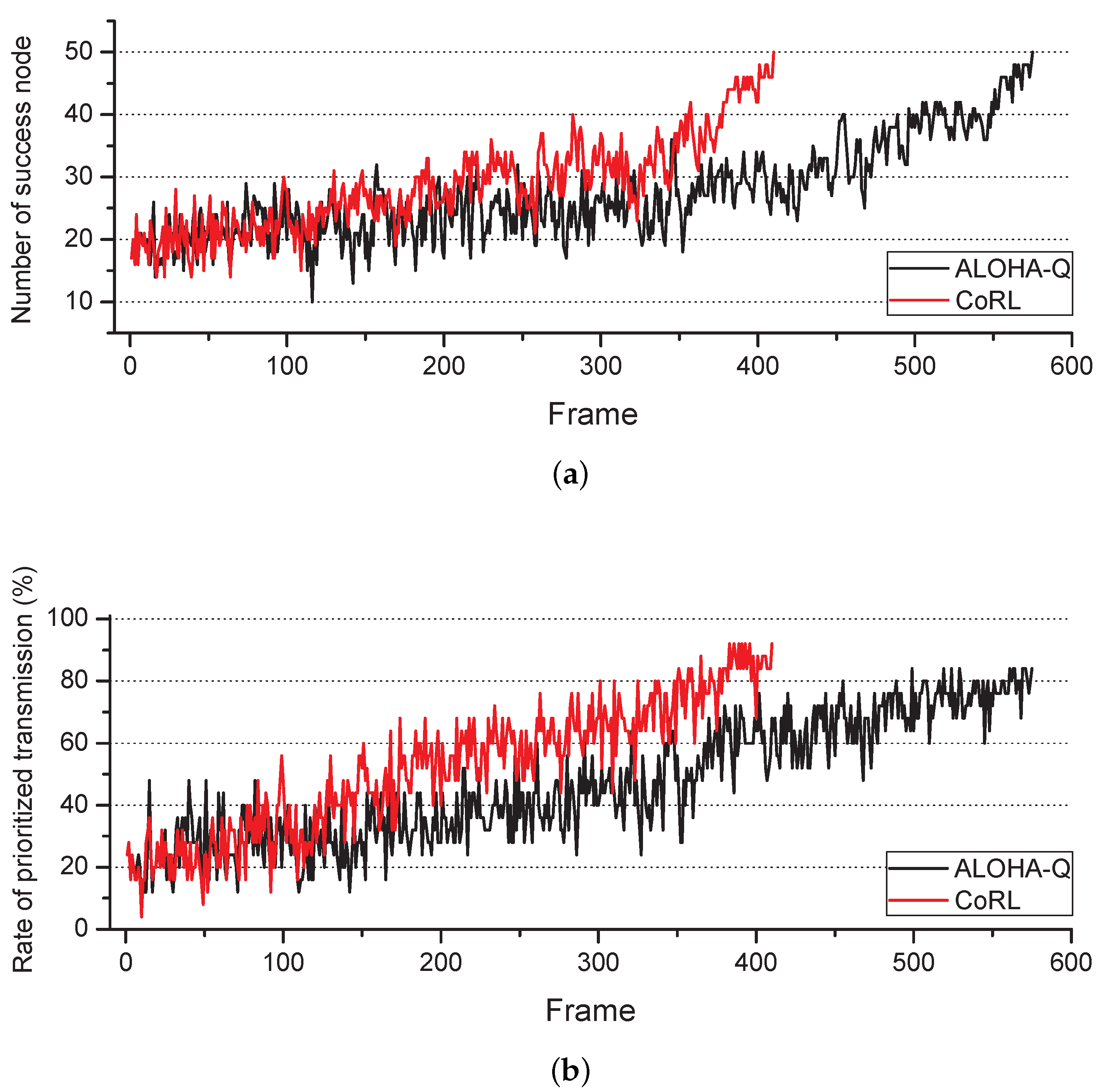
Figure 2 shows the transient results of success transmission of prioritized nodes. In this simulation, the network contains 50 nodes and the frame is divided into 50 slots, 25 nodes are the prioritized nodes and the other nodes serve deprioritized service packet. We assumed that a new packet of a node is repeatedly generated at the beginning of each frame. Latency of the packet is defined as time spent from the beginning of the frame to the successful transmission of the packet. The prioritized nodes that succeed packet transmission between 1st and 25th slots, they receive the reward +2. If the prioritized nodes failed the transmission in the front half of the frame, they receive the reward −1. When the prioritized nodes transmit packets from 26th to 50th slot, they receive the reward +1. If the prioritized nodes fail to transmit due to collision in the latter slots of the frame, they receive the reward −2. The deprioritized nodes receive the reward as opposed to the prioritized nodes. This distinct reward affect actions of all nodes in the network.
As a result of learning by the proposed algorithm, the prioritized nodes have tendency to select the front slot of the frame. On the other hand, the deprioritized nodes learn to select the back slot of the frame.
Figure 2a shows the number of nodes which have succeeded transmission without collision in former slots of the frame. The convergence time of our proposed scheme is 410 frames and ALOHA-Q is 575 frames.
Figure 2b represents the ratio of the number of prioritized nodes which successfully transmit data at the former slots of the frame to the number of all nodes. As shown in
Figure 2b, 92% of the prioritized nodes could successfully transmit data earlier with our proposed scheme, on the other hand, only 82% of the prioritized nodes succeeded prioritized transmission with ALOHA-Q. When we consider the energy consumption of IoT devices of
Figure 2, it can be derived as below [
11].
where
is the transmit power, and
is the receive power in case of
k bit transmission and reception, respectively. The experimental parameter in [
11] was
nJ/bit,
pJ/(bit × m
), and
p was set to 2. The network region was 500 m by 500 m. When those parameters are applied, the average transmit power is 12.55
J/bit and the receive power is 50 nJ/bit. Now, we can measure the power consumption of a transmission case as depicted in
Figure 2. For numerical evaluations, we assumed that the packet size is the same and the idle power and control message overhead is regardless. The transmit power of a node until convergence is 7.216 mJ for both schemes. Total number of frames until convergence of ALOHA-Q is 575 frame. On the other hand, since convergence time for CoRL is 410 frame, 1.005 mJ is consumed as the receive power. Then, the power consumption for ALOHA-Q and CoRL is 7.216 mJ and 8.221 mJ, respectively. The power consumption is increased when our proposed scheme is applied. However, when we consider energy efficiency, the number of successful transmission until 510 frame is 15,787 and 19,998 for ALOHA-Q and CoRL, respectively. The power consumption for a successful transmission is derived as 22.855
J, 20.554
J for ALOHA-Q and CoRL, respectively. That is to say, our proposed scheme consumes slightly smaller power for achieving the same throughput.
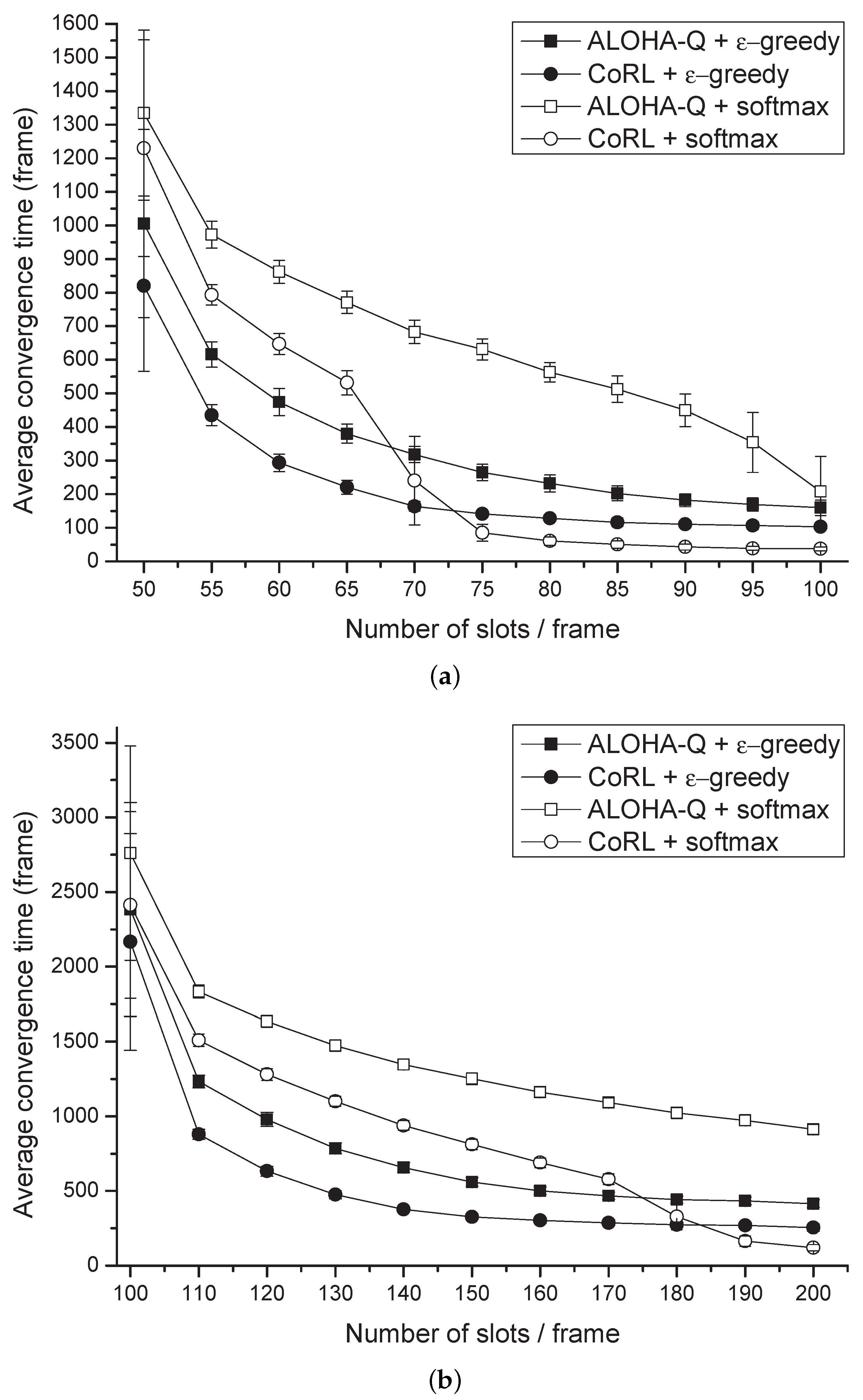
Figure 3 shows the average convergence time with respect to the number of slots in a frame for the deprioritized services. Each marker represents the convergence time averaged for 100 simulations with varying number of slots per frame. The average convergence time has been determined by the number of nodes approaching the steady-state in the networks. Here, the value of
and
is proportional to
, where
f is the number of frames spent. As shown in the
Figure 3, the average convergence time decreases with increasing number of slots per frame, because when the number of slots increases, possible choices for the node also enlarge. In
Figure 3a, the number of frames for convergence of the proposed CoRL has been spent about 228 frames less than that of the ALOHA-Q and as shown in
Figure 3b, proposed scheme have reduced 374 frames compared with ALOHA-Q. For both results, when the number of slots per frame is small CoRL with
-greedy policy control was the fastest model compared with other models. However, as the number of slots per frame increases, CoRL with softmax policy control showed better performance compared with other models.
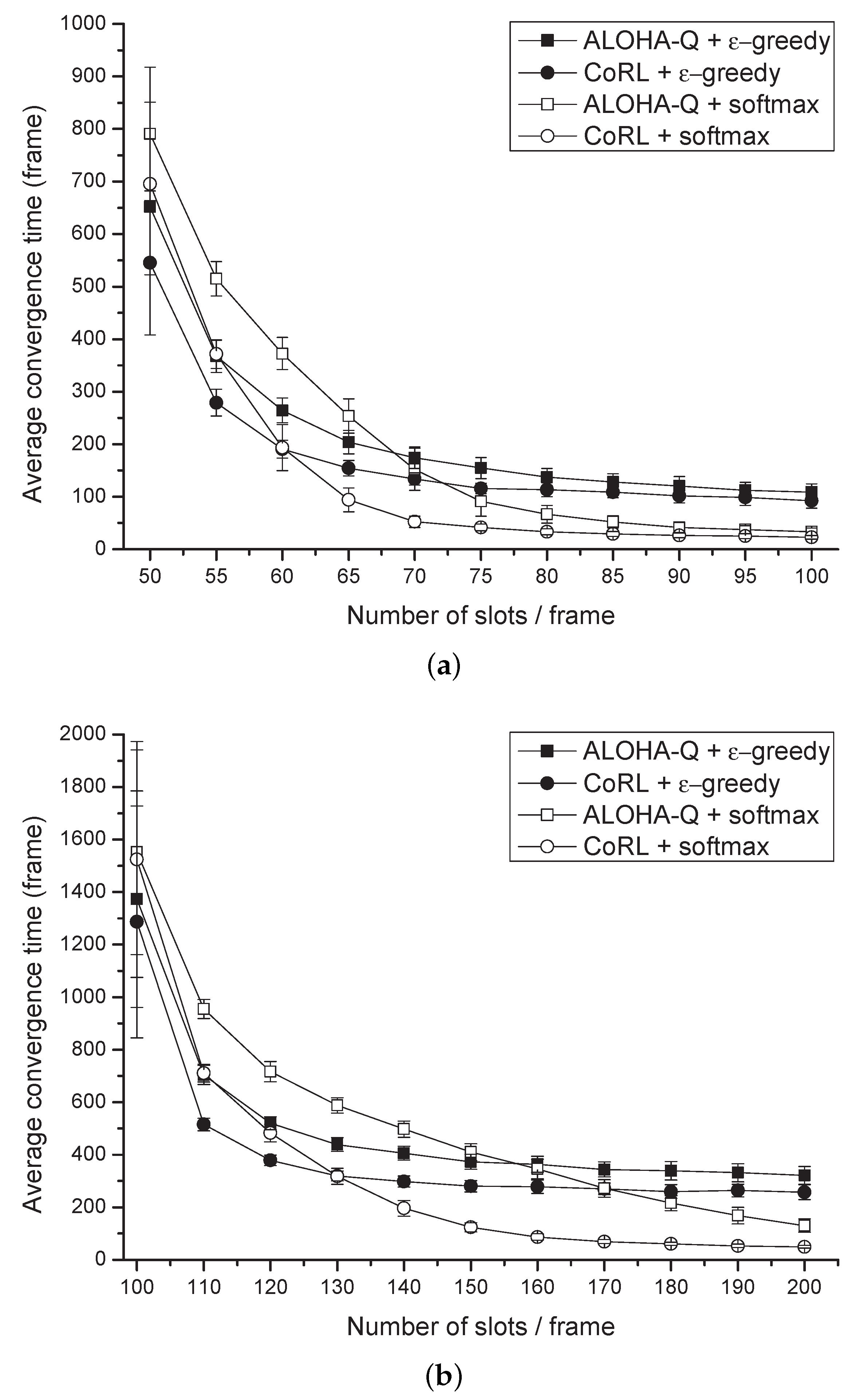
Figure 4 shows the average convergence time with different number of slots per frame with the prioritized services. The results were averaged for 100 different simulations with variable number of slots per frame. In these networks, half of nodes provide prioritized service, the others are deprioritized nodes. As shown in
Figure 4a, the convergence time of our proposed scheme have been spent 58 frames less than that of the ALOHA-Q. In
Figure 4b, the reduced convergence time was 154 frames in average. Our proposed scheme showed an improvement of convergence in all regions. In these networks, when the number of slots per frame is small,
-greedy based policy control showed better performance compared with softmax based policy control, but
-greedy based policy control shows poor performance when the number of slots per frame becomes bigger. We can see that softmax based policy control provides better exploration strategy at the prioritized networks with high number of slots per frame. Because of different reward to selecting slot of nodes with different services, the searching space of nodes is narrow. As a result, the average convergence time of models in prioritized networks is faster than that of deprioritized networks.
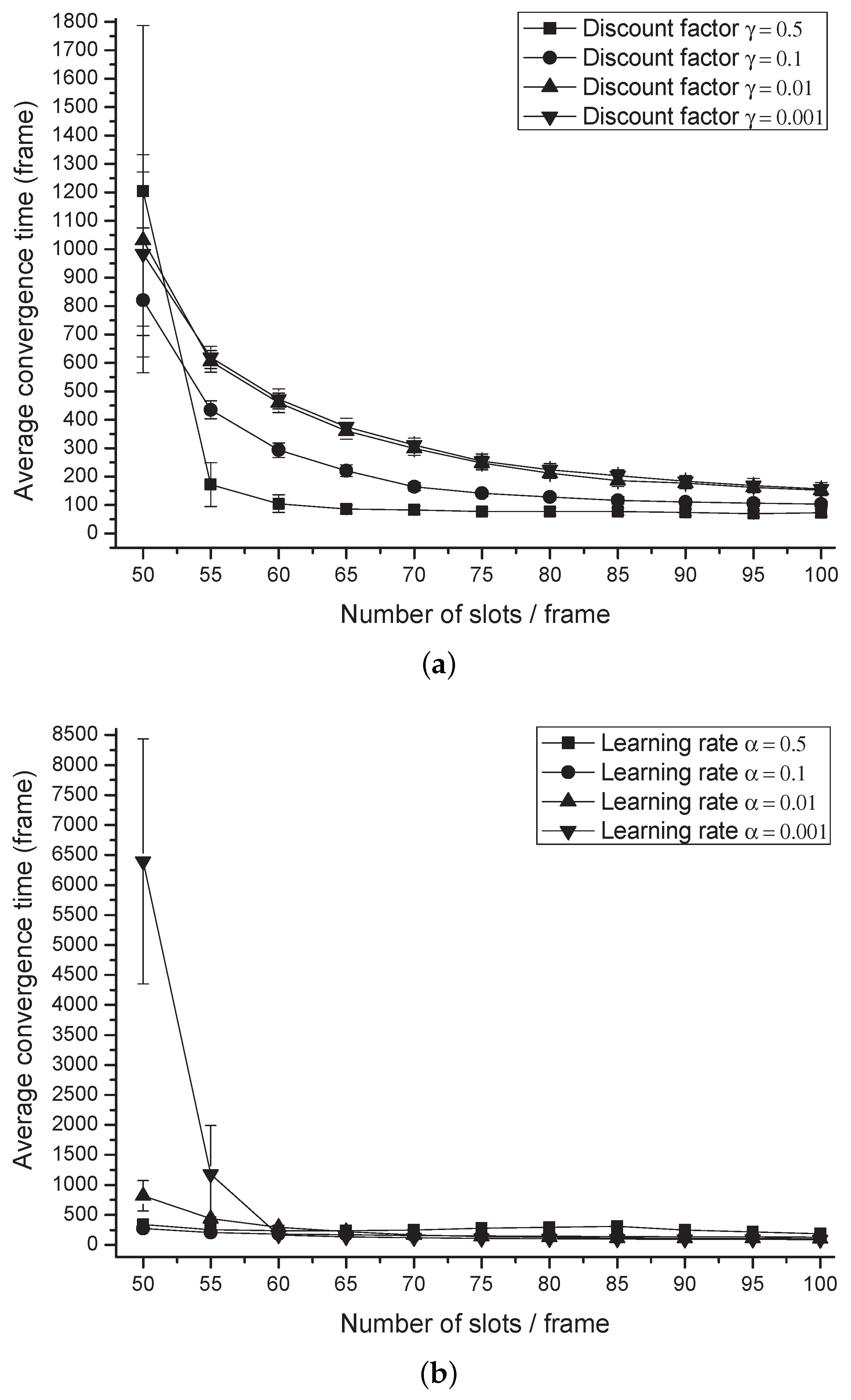
Figure 5 shows the average convergence time of CoRL with
-greedy policy control according to the change of reinforcement learning related parameters. The networks consisting of five nodes provide the deprioritized service. The number of slots that each frame can contain is ranged from 50 to 100. Different learning rate
and discount factors
are applied in these simulations to examine the impact of these parameters on the performance of the proposed protocol. When we consider discount factor as depicted in
Figure 5a,
achieves 32.7% reduced convergence time compared with the case of
on average. Large discount factor results in fast convergence performance, as we can see in the simulation results. In addition, algorithm convergence time was affected by the learning rate and the number of slots per frame as shown in
Figure 5b. In the case that the learning rate is 0.5, the convergence time increases as the number of slots per frame increases. As the number of slots per frame decreases, performance degradation increases in the case of relatively small learning rates. On the other hand, the smaller learning rate shows better and stable performance when the searching candidates expand.