Secondary Control for Storage Power Converters in Isolated Nanogrids to Allow Peer-to-Peer Power Sharing
Abstract
1. Introduction
- Grid-forming DERs, i.e., those DERs responsible for keeping proper and stable frequency and voltage values within the microgrid, are connected (either directly or through radial feeders) to the same Point of Common Coupling (PCC), where the loads are also connected [13]. In this case, voltage setpoint is the same for every DER and virtual impedance is usually required to decouple Active Power-Frequency and Reactive Power-Voltage dependence relationships.
- Power sharing obeys to individual energy ratings, thus avoiding circulating currents among DERs. Therefore, power interchange due to economic agreements is usually discarded in isolated mode.
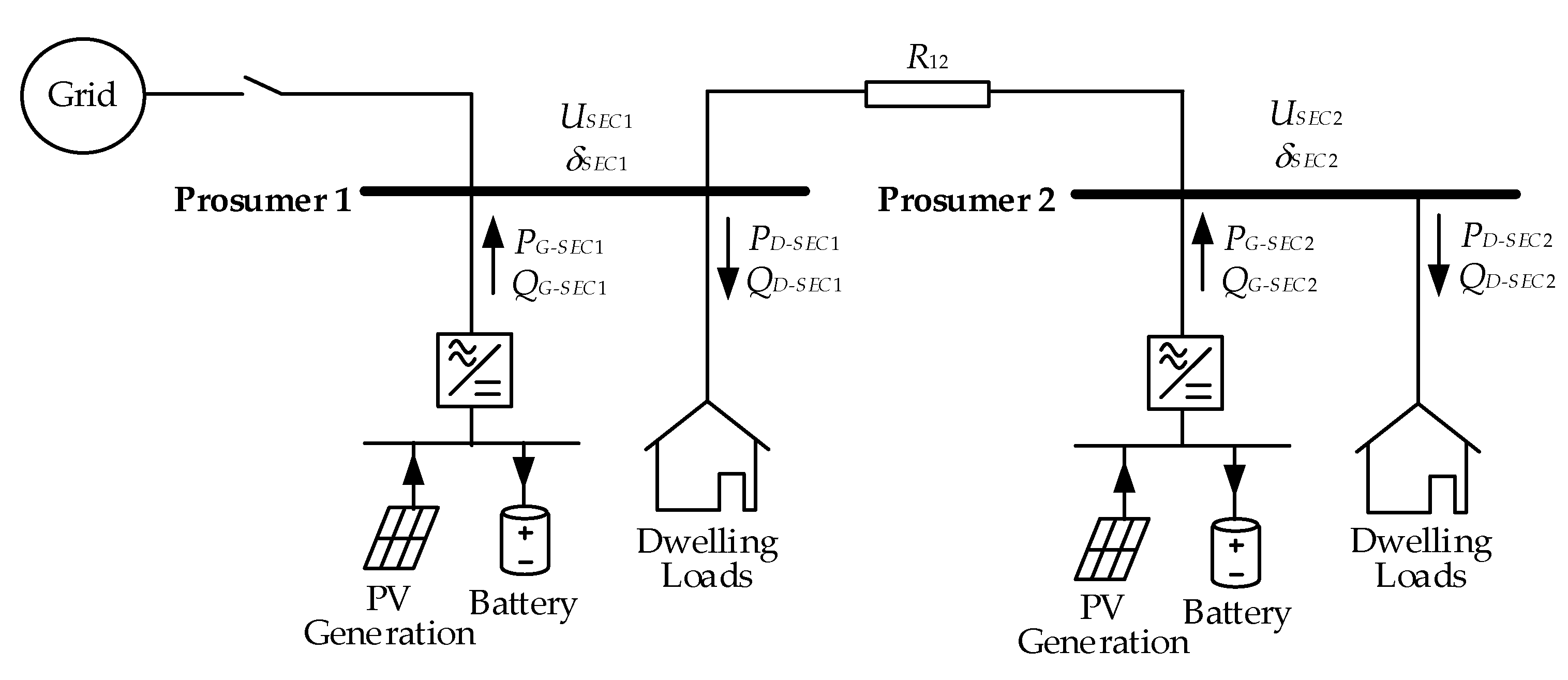
- P2P energy trading between prosumers is addressed in islanded microgrids, from the point of view of the voltage and power setpoint generation and how the DER converter can follow them. Power flow among prosumers is guaranteed due to different voltage setpoint in each prosumer’s load bus.
- A novel secondary control based on power flow algorithm in microgrids is proposed to reach classical secondary control target as well as allow energy interchange between DERs.
- A residential nanogrid is simulated with all the necessary control loops to perform hierarchical control, starting from previously mentioned setpoints.
2. Proposed Control Strategy
- Tertiary control aims to optimize the energy use inside the nanogrid. Starting from generation and demand forecasting, demand and storage systems are managed at this stage to match power and energy balance in the isolated nanogrid with optimal resource exploitation. Energy interchange among the resources within the nanogrid presents a clear importance when it is grid-connected, with the aim of obtaining economic advantages and improving self-consumption and self-sufficiency. Another scenario for this tertiary control is P2P energy interchange, which schedules energy sharing under agreement in both grid-connected and isolated situation.
- Secondary control determines the electrical magnitude setpoints for the DERs. In the context of isolated nanogrids, the target of this stage is usually to restore the voltage and the frequency in a unique PCC, with a power-sharing strategy that aimed at using the available resources to keep secure and stable electrical conditions, without considering the economic or agreement-based energy interchange among DERs. In this paper, the P2P energy interchange concept is taken into account at this control stage to allow for complying with economic or energy agreements among different prosumers.
- Primary control acts automatically to obtain stable frequency and voltage magnitudes when power balance mismatching occurs due to unexpected changes in demand or generation. A decentralized droop control is the most frequently used strategy for this stage, whose formulation strongly depends on the resistive/inductive character of the system.
2.1. Nanogrid Tertiary Control
- PG-TERCi: hourly average active power setpoint for tertiary control (W)
- QG-TERCi: hourly average reactive power setpoint for tertiary control (VAr)
- PGi: hourly average forecasted PV generation power, once curtailed (W)
- PBi: hourly average scheduled battery power (positive values when charging, negative when discharging) (W)
- QDi: hourly average forecasted reactive power demanded by load in bus i (VAr)
2.2. Nanogrid Secondary Control
- There is no slack bus in microgrids, as there is not a bus with a powerful generation capacity that assures stable frequency and provides power losses. Two kind of buses are usual in microgrids: PQ (load or grid-following generation buses) and droop buses (this is a new kind of bus, which shares the responsibility to keep stable and proper frequency values).
- Frequency value of the system is not guaranteed, but it is a variable of the problem.
- Active and reactive power generation is governed by droop rules.
2.2.1. Element Modelling for Power Flow Algorithm
- Rij: line resistance (Ω)
- Xij: line reactance (Ω)
- Lij: line inductance (H)
- f: nanogrid frequency (Hz)
- PD-SECi: active power demand estimation for secondary control (W)
- QD-SECi: reactive power demand estimation for secondary control (VAr)
- Ui: RMS value of the voltage in bus i (V)
- Un: rated voltage (230 V in low-voltage single-phase systems)
- fn: rated frequency (50 Hz)
- α, β: active and reactive exponents
- kpf, kqf: sensitivity factors of active and reactive power to frequency (pu/pu)
- PG-SECi: active power setpoint for the converter output, for secondary control (W)
- QG-SECi: reactive power setpoint for the converter output, for secondary control (VAr)
- mp, mq, kp, kq: droop coefficients
2.2.2. Power Flow Algorithm Formulation
- USECi, δSECi: RMS value (V) and phase angle (rad) of i-bus voltage
- Yik, γik: magnitude (S) and phase angle (rad) of ik-element of Ybus admittance matrix
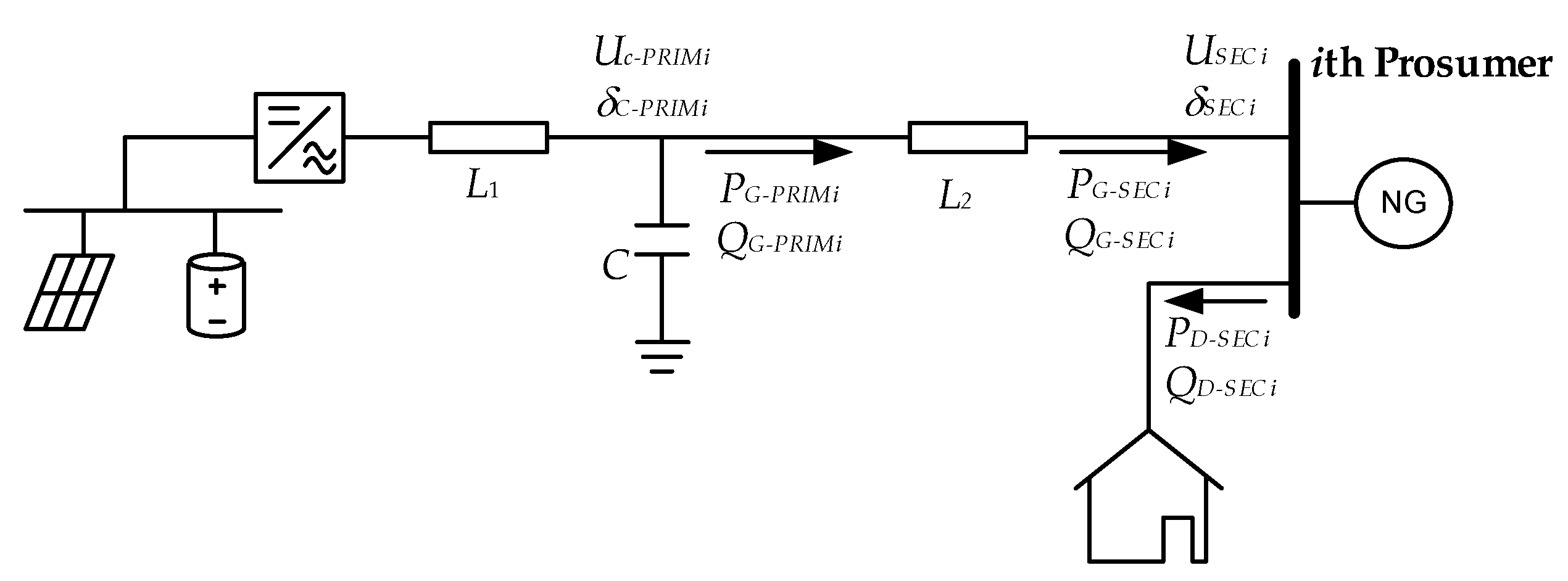
2.3. Nanogrid Primary Control
- uci-ref: reference voltage signal in the filter capacitor of the ith converter
- Uci-ref: RMS value of uci-ref (V)
- θci-ref: angle signal of uci-ref
- Pi: measured active power in the filter reactance L2 of the ith converter (W)
- Qi: measured reactive power in the filter reactance L2 of the ith converter (VAr).
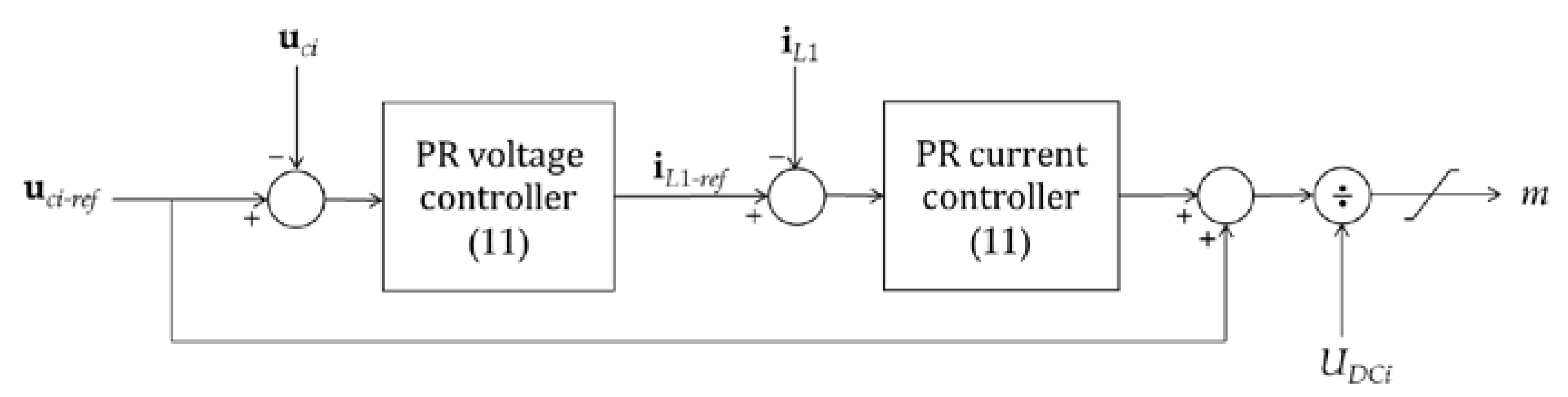
2.4. Power Converter Inner Voltage and Current Control Loops
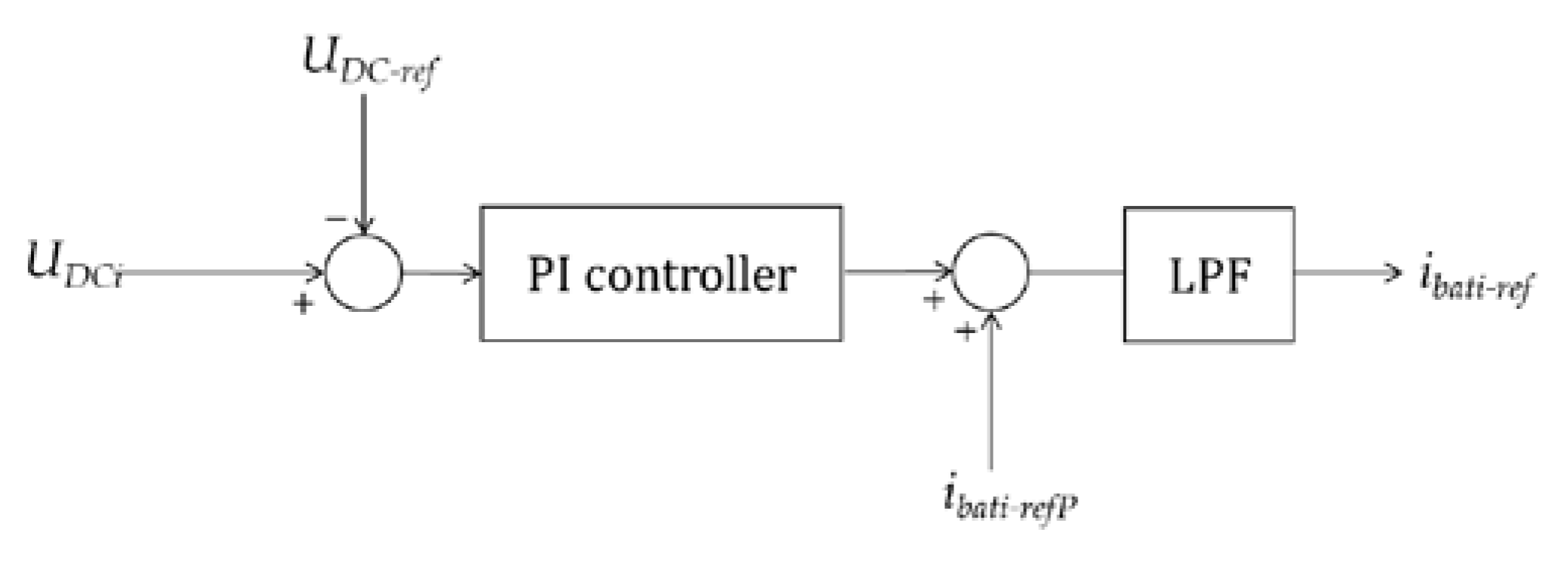
2.5. Battery DC/DC Converter Control Loop
- ibati-ref: reference charging current for the ith battery (A)
- ibati-refP: power-reference charging current for the ith battery (A)
- UDC-ref: reference value for the DC-link voltage of the ith converter (V)
- UDCi: measured value for the DC-link voltage of the ith converter (V)
- ipvi: measured value for the ith PV generator current (A)
- ubati: measured value for the battery voltage (V)
- dbati: duty cycle for the ith battery DC/DC converter
- ibati: measured value for the battery current (A)
- Lbat: filter inductance (H)
- Rbat: filter resistance (Ω)
- Ts: sampling period (s)
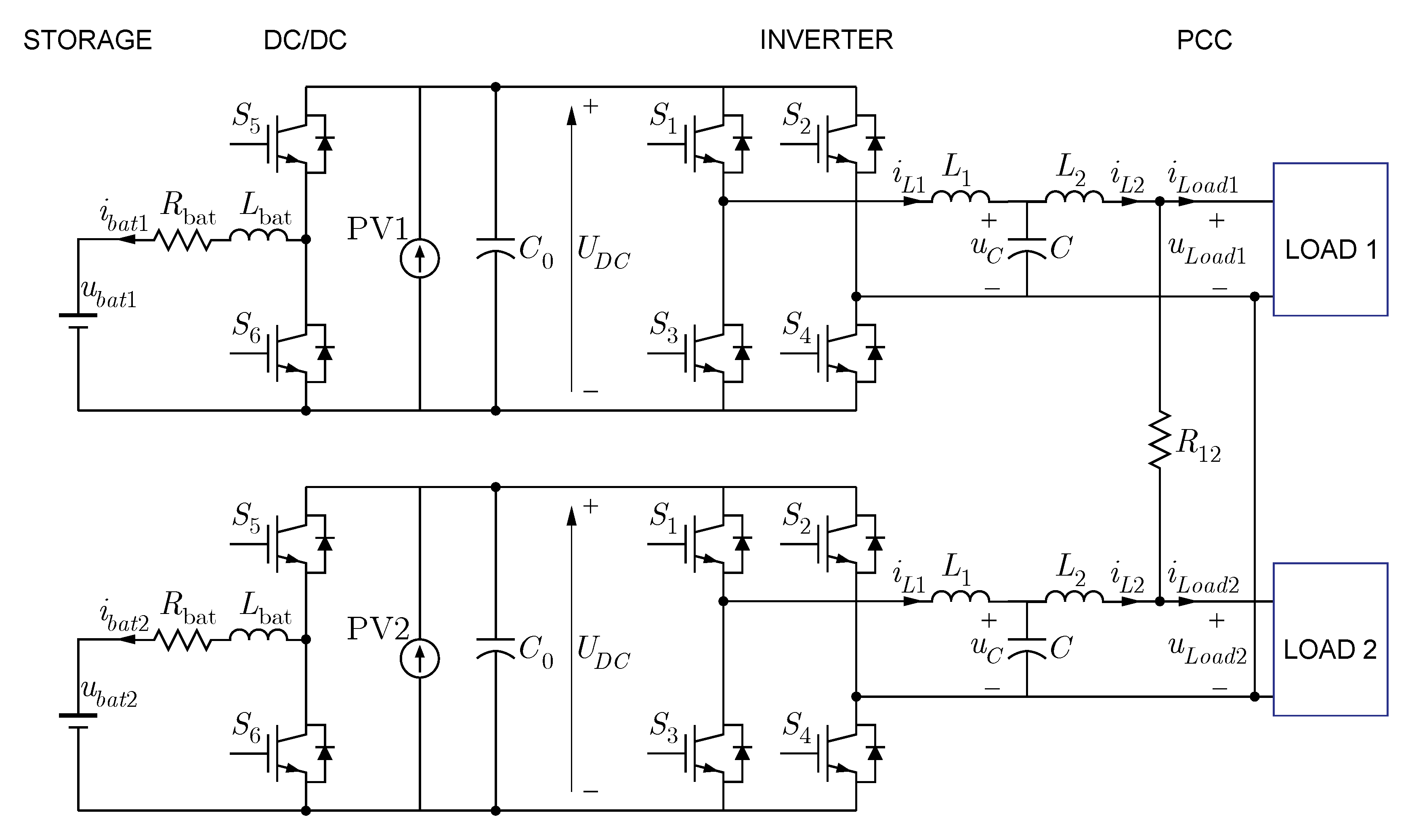
3. Case Study and Simulation Parameters
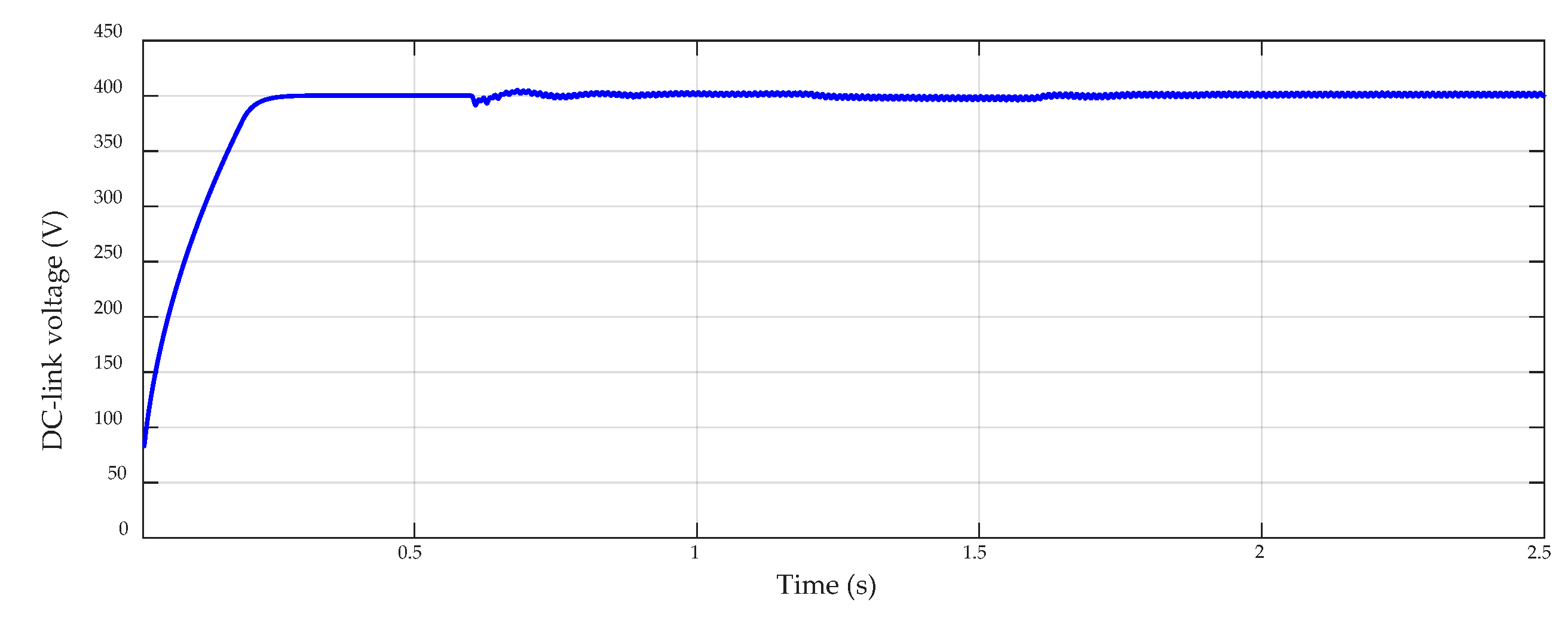
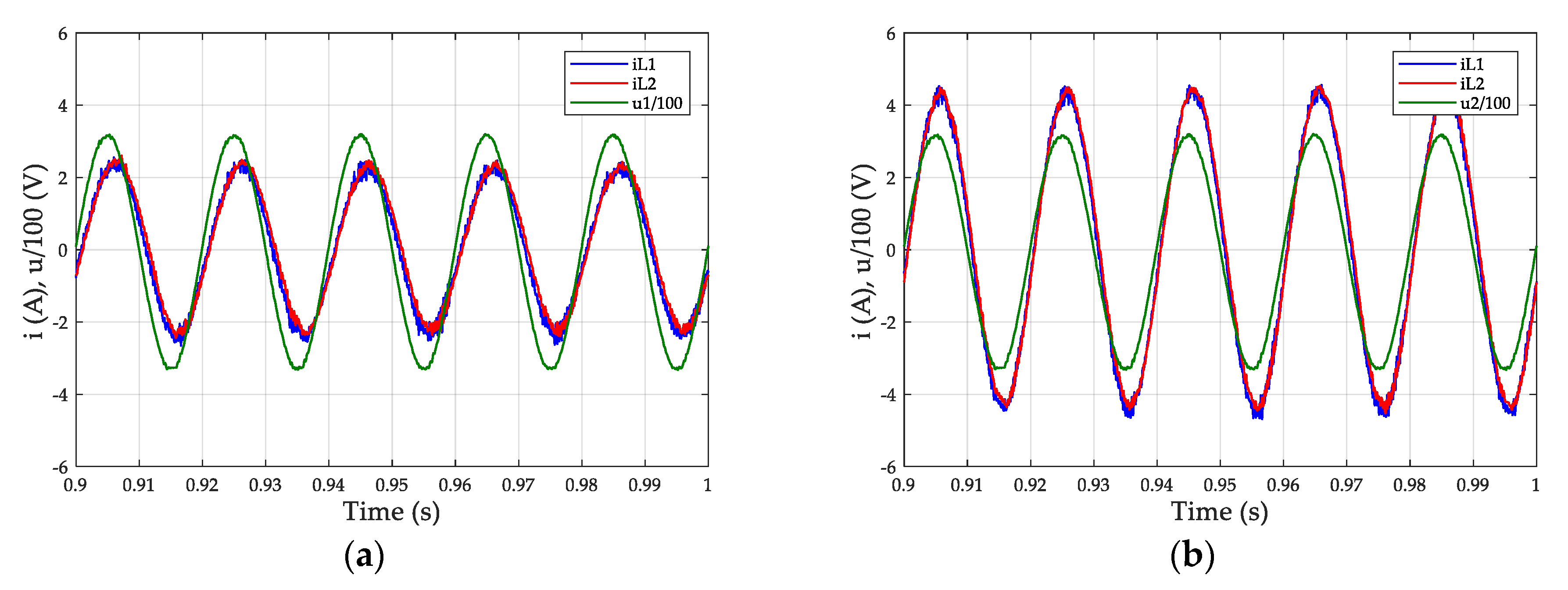
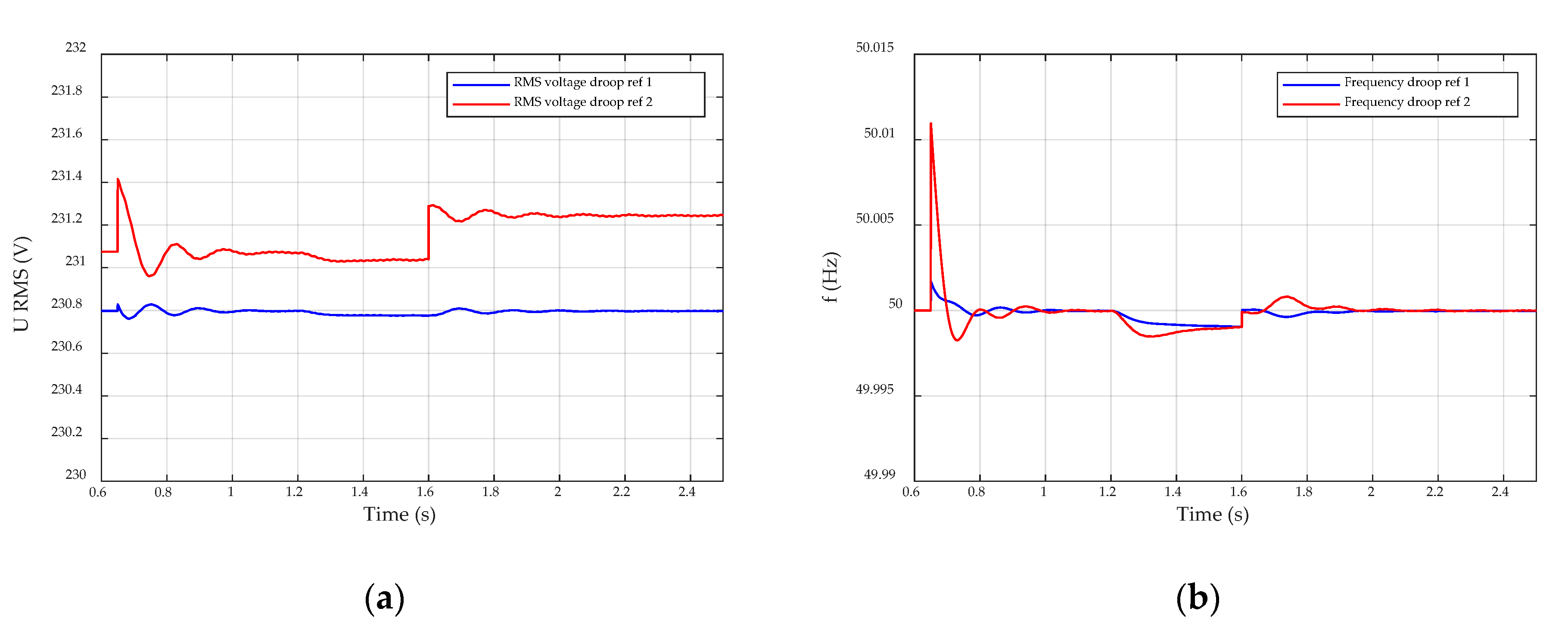
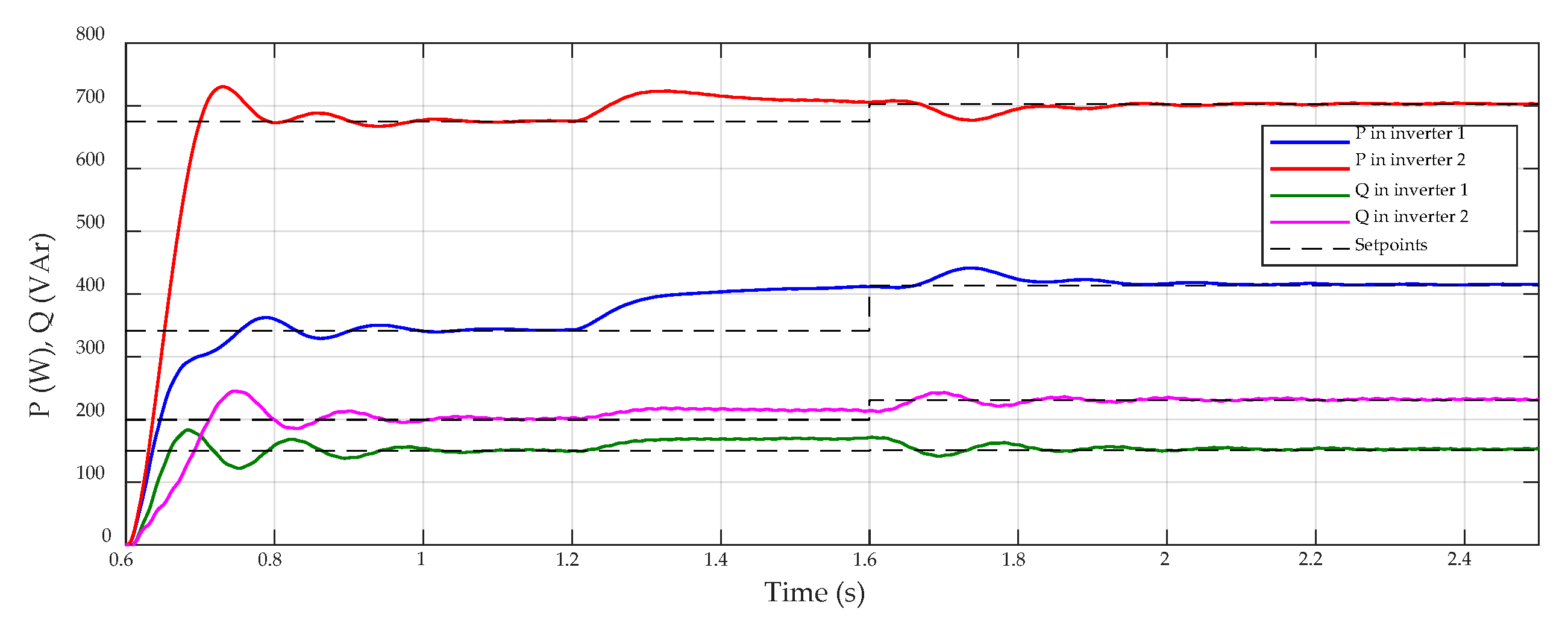
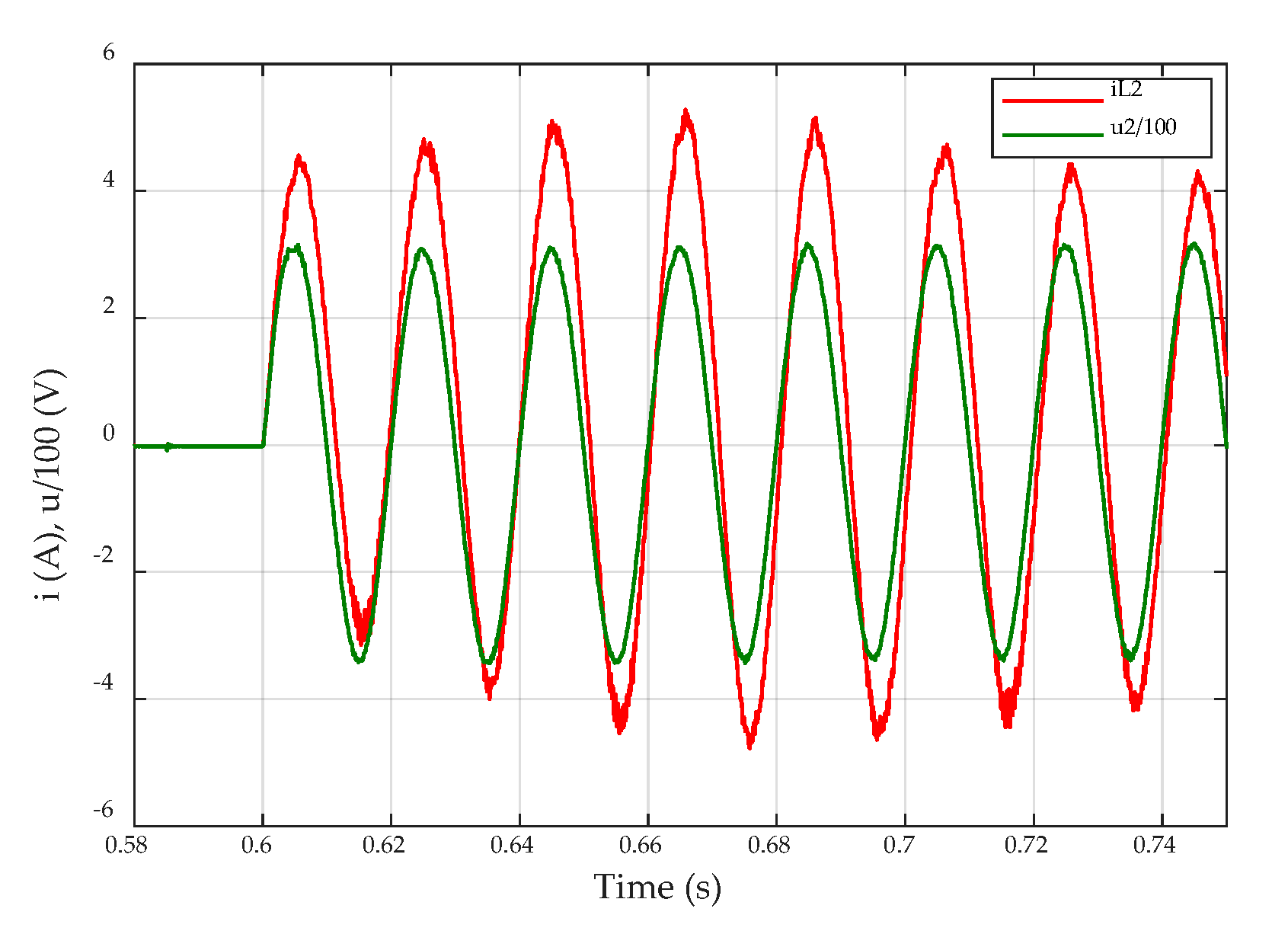
4. Simulation Results and Discussion
5. Conclusions and Future Works
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Acronyms | |
| DER | Distributed Energy Resource |
| DG | Distributed Generation |
| DSM | Demand Side Management |
| EMS | Energy Management System |
| ESS | Energy Storage System |
| MPP | Maximum Power Point |
| PCC | Point of Common Coupling |
| PR | Proportional-Resonant |
| PV | Photovoltaic |
| PWM | Pulse Width Modulation |
| RPP | Reference Power Point |
| SoC | State of Charge |
| Variables | |
| C | Capacitance of the LCL Filter |
| C0 | Capacitance of the DC-link capacitor |
| dbati | Duty Cycle of the ith Prosumer’s Battery Converter |
| f | Frequency |
| fn | Rated Frequency |
| ibati | Charging Current of the ith Prosumer’s Battery |
| ibati-ref | Reference Charging Current of the ith Prosumer’s Battery |
| ibati-refP | Power-Reference Charging Current of the ith Prosumer’s Battery |
| iL1 | Current Signal in the Inner Filter Reactance of the ith Prosumer |
| iL1-ref | Reference Current Signal in the Inner Filter Reactance of the ith Prosumer |
| iL2 | Current Signal in the Outer Filter Reactance of the ith Prosumer |
| ipvi | Current of the ith Prosumer’s PV Generation System |
| kp | P-U Droop Coefficient |
| kpf | Sensitivity Factor of Active Power Load to Frequency |
| kP-PR | Proportional-Term Constant of Proportional-Resonant Controllers |
| kq | Q-f Droop Coefficient |
| kqf | Sensitivity Factor of Reactive Power Load to Frequency |
| kR-PR | Resonant-Term Constant of Proportional-Resonant Controllers |
| L1 | Converter-Side Inductance of the LCL Filter |
| L2 | Grid-Side Inductance of the LCL Filter |
| Lbat | Inductance of the Battery Filter |
| Lij | Line Inductance of Feeder Between ith and jth Prosumers |
| mp | P-f Droop Coefficient |
| mq | Q-U Droop Coefficient |
| PB0i | 1 Minute-Resolution Interpolation of PBi |
| PBi | Charging Power of the ith Prosumer’s Battery |
| PD0i | Last-Minute Measured Active Power Demand of the ith Prosumer |
| PDi | Hourly Average Active Power Demand Forecasting of the ith Prosumer |
| PD-SECi | Active Power Estimation of the ith Prosumer’s Demand, for Secondary Control |
| PG0i | Last-Minute Measured Power PV Generation of the ith Prosumer |
| PGi | Hourly Average Power PV Generation Forecasting of the ith Prosumer |
| PG-PRIMi | Active Power Setpoint for the ith Converter Output, in Primary Control |
| PG-SECi | Active Power Setpoint for the ith Converter Output, in Secondary Control |
| PG-TERCi | Active Power Setpoint for the ith Converter Output, in Tertiary Control |
| Pi | Measured Active Power in the Outer Filter Reactance of the ith Converter |
| PSECi | Net Injected Active Power in the ith bus, in Secondary Control |
| QDi | Hourly Average Reactive Power Demand Forecasting of the ith Prosumer |
| QD-SECi | Reactive Power Estimation of the ith Prosumer’s Demand, for Secondary Control |
| QG-PRIMi | Reactive Power Setpoint for the ith Converter Output, in Primary Control |
| QG-SECi | Reactive Power Setpoint for the ith Converter Output, in Secondary Control |
| QG-TERCi | Reactive Power Setpoint for the ith Converter Output, in Tertiary Control |
| Qi | Measured Reactive Power in the Outer Filter Reactance of the ith Converter |
| QSECi | Net Injected Reactive Power in the ith bus, in Secondary Control |
| Rbat | Resistance of the Battery Filter |
| Rij | Line Resistance of Feeder Between ith and jth Prosumers |
| SG-PRIMi | Complex Power Setpoint for the ith Converter Output, in Primary Control |
| SG-SECi | Complex Power Setpoint for the ith Converter Output, in Secondary Control |
| t | Time |
| Ts | Sampling Period |
| ubati | Voltage of the ith Prosumer’s Battery |
| uci | Voltage Signal in the Filter Capacitor of the ith Converter |
| Uci | RMS Value of the Voltage in the Filter Capacitor of the ith Converter |
| uci-ref | Reference Voltage Signal in the Filter Capacitor of the ith Converter |
| Uci-ref | Reference RMS Value for the Voltage in the Filter Capacitor of the ith Converter |
| Uc-PRIMi | RMS Value of the Voltage Signal in the Filter Capacitor of the ith Converter, in Primary Control |
| uc-PRIMi | Voltage Signal in the Filter Capacitor of the ith Converter, in Primary Control |
| Udci | Voltage in DC-Bus of the ith Converter |
| Udc-ref | Reference Voltage of DC-Bus |
| Ui | RMS Value of the Voltage in the ith bus |
| ui | Voltage Signal in the ith bus |
| Un | Rated Voltage |
| uSECi | Reference Voltage Signal in the ith bus, in Secondary Control |
| USECi | RMS Value of the Voltage in the ith bus, in Secondary Control |
| Xij | Line Reactance of Feeder Between ith and jth Prosumers |
| Yik | Module of the ik-element of the system admittance matrix |
| Zij | Line Impedance of Feeder Between ith and jth Prosumers |
| α | Sensitivity exponent of Active Power Load to Voltage |
| β | Sensitivity exponent of Reactive Power Load to Voltage |
| δc-PRIMi | Phase Angle of the Voltage in the Filter Capacitor of the ith Converter, in Primary Control |
| δSECi | Phase Angle of the Voltage in the ith bus, in Secondary Control |
| γik | Phase Angle of the ik-element of the system admittance matrix |
| θci-ref | Reference Angle Signal of the Voltage in the Filter Capacitor of the ith Converter |
| ωn | Reference Angular Frequency |
References
- Vasquez, J.C.; Guerrero, J.; Miret, J.; Castilla, M.; De Vicuna, L.G. Hierarchical Control of Intelligent Microgrids. IEEE Ind. Electron. Mag. 2010, 4, 23–29. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Vasquez, J.C.; Matas, J.; De Vicuña, L.G.; Castilla, M. Hierarchical control of droop-controlled DC and AC microgrids—A general approach towards standardization. IEEE Trans. Ind. Electron. 2011, 58, 158–172. [Google Scholar] [CrossRef]
- Hou, X.; Sun, Y.; Lu, J.; Zhang, X.; Koh, L.H.; Su, M.; Guerrero, J.M.; Hai, K.L. Distributed Hierarchical Control of AC Microgrid Operating in Grid-Connected, Islanded and Their Transition Modes. IEEE Access 2018, 6, 77388–77401. [Google Scholar] [CrossRef]
- Khayat, Y.; Guerrero, J.M.; Bevrani, H.; Shafiee, Q.; Heydari, R.; Naderi, M.; Dragicevic, T.; Simpson-Porco, J.W.; Dorfler, F.; Fathi, M.; et al. On the Secondary Control Architectures of AC Microgrids: An Overview. IEEE Trans. Power Electron. 2019. [Google Scholar] [CrossRef]
- European Commission. The Strategic Energy Technology (SET) Plan. At the Heart of Energy Research & Innovation in Europe. Available online: https://setis.ec.europa.eu/publications/set-plan-implementation-progress-reports/strategic-energy-technology-set-plan-heart-of (accessed on 29 November 2019).
- Gao, C.; Xu, D.; Miao, L.; Yu, X. A redundant parallel control strategy of multiple PCS (power conversion system) for microgrid in islanded operation. In Proceedings of the 2014 International Conference on Power System Technology, Chengdu, China, 20–22 October 2014; pp. 3147–3151. [Google Scholar]
- Gregoratti, D.; Matamoros, J. Distributed energy trading: The multiple-microgrid case. IEEE Trans. Ind. Electron. 2015, 62, 2551–2559. [Google Scholar] [CrossRef]
- Wang, H.; Huang, J. Incentivizing energy trading for interconnected microgrids. IEEE Trans. Smart Grid 2018, 9, 2647–2657. [Google Scholar] [CrossRef]
- Long, C.; Wu, J.; Zhang, C.; Thomas, L.; Cheng, M.; Jenkins, N. Peer-to-peer energy trading in a community microgrid. In Proceedings of the 2017 IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017; pp. 1–5. [Google Scholar]
- Baez-Gonzalez, P.; Rodriguez-Diaz, E.; Vasquez, J.C.; Guerrero, J.M. Peer-to-peer energy market for community microgrids [Technology leaders]. IEEE Electrif. Mag. 2018, 6, 102–107. [Google Scholar] [CrossRef]
- Neagu, B.C.; Grigoraş, G.; Ivanov, O. An efficient peer-to-peer based blockchain approach for prosumers energy trading in microgrids. In Proceedings of the 2019 8th International Conference on Modern Power Systems (MPS), Cluj Napoca, Romania, 21–23 May 2019; pp. 1–4. [Google Scholar]
- Paudel, A.; Beng, G.H. A hierarchical peer-to-peer energy trading in community microgrid distribution systems. In Proceedings of the 2018 IEEE Power & Energy Society General Meeting (PESGM), Portland, OR, USA, 5–9 August 2018; pp. 1–5. [Google Scholar]
- Ramos-Ruiz, J.A.; Enjeti, P.; Xie, L. Peer-to-peer energy transaction in microgrids with power electronics enabled angle droop control. In Proceedings of the 2018 IEEE Electronic Power Grid (eGrid), Charleston, SC, USA, 12–14 November 2018; pp. 1–6. [Google Scholar]
- Yang, X.; Du, Y.; Su, J.; Chen, X.; Chang, L. An optimal secondary voltage control strategy for islanded microgrid. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 22–26 May 2016; pp. 2880–2885. [Google Scholar]
- Hashmi, K.; Khan, M.M.; Xu, J.; Shahid, M.U.; Habib, S.; Faiz, M.T.; Tang, H. A quasi-average estimation aided hierarchical control scheme for power electronics-based islanded microgrids. Electronics 2019, 8, 39. [Google Scholar] [CrossRef]
- Barrero-González, F.; Miñambres-Marcos, V.; Guerrero-Martínez, M.A.; Romero-Cadaval, E.; Milanes-Montero, M.; González-Romera, E. Photovoltaic converter with smart grid functions. In Proceedings of the 2016 IEEE 16th International Conference on Environment and Electrical Engineering (EEEIC), Florence, Italy, 6–8 June 2016; pp. 1–6. [Google Scholar]
- Garrido-Zafra, J.; Moreno-Munoz, A.; Gil-de-Castro, A.; Palacios-Garcia, E.J.; Moreno-Moreno, C.D.; Morales-Leal, T.A. Novel direct load control testbed for smart appliances. Energies 2019, 12, 3336. [Google Scholar] [CrossRef]
- Ruiz-Cortés, M.; González-Romera, E.; Amaral-Lopes, R.; Romero-Cadaval, E.; Martins, J.; Milanés-Montero, M.I.; Barrero-González, F. Optimal charge/discharge scheduling of batteries in microgrids of prosumers. IEEE Trans. Energy Convers. 2019, 34, 468–477. [Google Scholar] [CrossRef]
- Abdelaziz, M.M.A.; Farag, H.E.; El-Saadany, E.F.; Mohamed, Y.A.I. A novel and generalized three-phase power flow algorithm for islanded microgrids using a newton trust region method. IEEE Trans. Power Syst. 2013, 28, 190–201. [Google Scholar] [CrossRef]
- Price, W.W.; Casper, S.G.; Nwankpa, C.O.; Bradish, R.W.; Chiang, H.-D.; Concordia, C.; Staron, J.V.; Taylor, C.W.; Vaahedi, E.; Wu, G. Bibliography on load models for power flow and dynamic performance simulation. IEEE Trans. Power Syst. 1995, 10, 523–538. [Google Scholar]
- Arguence, O.; Raison, B.; Cadoux, F. Comments on “Impact of Load Frequency Dependence on the NDZ and Performance of the SFS Islanding Detection Method”. IEEE Trans. Ind. Electron. 2017, 64, 7277–7279. [Google Scholar] [CrossRef]
- VanDoorn, T.L.; Vasquez, J.C.; De Kooning, J.; Guerrero, J.M.; Vandevelde, L. Microgrids: Hierarchical Control and an Overview of the Control and Reserve Management Strategies. IEEE Ind. Electron. Mag. 2013, 7, 42–55. [Google Scholar] [CrossRef]
- Ghanbari, N.; Bhattacharya, S. SoC balancing of different energy storage systems in DC microgrids using modified droop control. In Proceedings of the 2018 IEEE Industrial Electronics Conference (IECON), Washington, DC, USA, 21–23 October 2018; pp. 1–6. [Google Scholar]
- Gkavanoudis, S.I.; Oureilidis, K.O.; Demoulias, C.S. An adaptive droop control method for balancing the SoC of distributed batteries in AC microgrids. In Proceedings of the 2016 IEEE 17th Workshop on Control and Modeling for Power Electronics (COMPEL), Trondheim, Norway, 27–30 June 2016; pp. 1–6. [Google Scholar]
- Li, C.; Chaudhary, S.K.; Savaghebi, M.; Vasquez, J.C.; Guerrero, J.M. Power Flow Analysis for Low-Voltage AC and DC Microgrids Considering Droop Control and Virtual Impedance. IEEE Trans. Smart Grid 2017, 8, 2754–2764. [Google Scholar] [CrossRef]
- Spanish Ministry of Economy. Royal Decree 1955/2000 of 1 December, which Regulates the Activities of Transport, Distribution, Marketing, Supply and Installations of Electricity Authorization Procedures. Available online: http://www.omie.es/files/tr_rd_1955-2000_de_1_diciembre.pdf (accessed on 17 December 2019).
- Zmood, D.N.; Holmes, D.G. Stationary frame current regulation of PWM inverters with zero steady-state error. IEEE Trans. Power Electron. 2003, 18, 814–822. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Teodorescu, R.; Liserre, M.; Timbus, A. Overview of Control and Grid Synchronization for Distributed Power Generation Systems. IEEE Trans. Ind. Electron. 2006, 53, 1398–1409. [Google Scholar] [CrossRef]
- Teodorescu, R.; Blaabjerg, F.; Liserre, M.; Loh, P. Proportional-resonant controllers and filters for grid-connected voltage-source converters. IEE Proc. Electr. Power Appl. 2006, 153, 750. [Google Scholar] [CrossRef]
- Husev, O.; Roncero-Clemente, C.; Makovenko, E.; Pimentel, S.P.; Vinnikov, D.; Martins, J. Optimization and Implementation of the Proportional-Resonant Controller for Grid-Connected Inverter With Significant Computation Delay. IEEE Trans. Ind. Electron. 2020, 67, 1201–1211. [Google Scholar] [CrossRef]
- Milanes-Montero, M.I.; Barrero-González, F.; Pando-Acedo, J.; Gonzalez-Romera, E.; Romero-Cadaval, E.; Moreno-Muñoz, A. Smart Community Electric Energy Micro-Storage Systems With Active Functions. IEEE Trans. Ind. Appl. 2018, 54, 1975–1982. [Google Scholar] [CrossRef]
| Season | α | β | kpf | kqf |
|---|---|---|---|---|
| Summer | 1.2 | 2.7 | 0.7 | −2.3 |
| Winter | 1.7 | 2.6 | 1.0 | −1.7 |
| Parameter | Value |
|---|---|
| Rbat | 0.3 Ω |
| Lbat | 8 mH |
| C0 | 1.1 mF |
| L1 | 3.6 mH |
| L2 | 4.2 mH |
| C | 2 µF |
| Rated UDC | 400 V |
| Rated AC voltage | 230 V |
| Rated ubat | 48 V |
| Rated frequency | 50 Hz |
| mp1 = kq1/5 | 3.3 × 10−4 Hz/W or Hz/VAr |
| mq1 = kp1 | 1.1 × 10−3 V/VAr or V/W |
| mp2 = kq2/5 | 3.1 × 10−3 Hz/W or Hz/VAr |
| mq2 = kp2 | 2.5 × 10−3 V/Var or V/W |
| Prosumer 1 | Initial Value | Updated Value | Prosumer 2 | Initial Value | Updated Value |
|---|---|---|---|---|---|
| PD-SEC1 | 445.15 W | 545.15 W | PD-SEC2 | 571.00 W | 571.00 W |
| QD-SEC1 | 146.31 VAr | 146.31 VAr | QD-SEC2 | 187.68 VAr | 217.68 VAr |
| PG-SEC1 | 341.54 W | 413.46 W | PG-SEC2 | 674.62 W | 702.71 W |
| QG-SEC1 | 146.31 VAr | 146.31 VAr | QG-SEC2 | 187.68 VAr | 217.68 VAr |
| USEC1 | 229.99 V | 229.99 V | USEC2 | 230.02 V | 230.03 V |
| δSEC1 | 0 | 0 | δSEC2 | 0 | 0 |
| PG-PRIM1 | 341.54 W | 413.46 W | PG-PRIM2 | 674.62 W | 702.71 W |
| QG-PRIM1 | 149.59 VAr | 150.88 VAr | QG-PRIM2 | 199.32 VAr | 230.53 VAr |
| Uc-PRIM1 | 230.79 V | 230.80 V | Uc-PRIM2 | 231.08 V | 231.25 V |
| δc-PRIM1 | 9.8 × 10−3 rad | 8.1 × 10−3 rad | δc-PRIM2 | 1.6 × 10−2 rad | 1.7 × 10−2 rad |
| Time | Event |
|---|---|
| 0 s | Battery setpoint to control UDC is generated |
| 0.02 s | PWM of battery DC/DC converter is activated |
| 0.5 s | SPWM of inverter is activated |
| 0.6 s | Current and voltage control of inverter are activated Power-reference for battery is generated |
| 0.65 s | Droop control is activated |
| 0.9 s | PV generation is connected |
| 1.2 s | Unexpected change in loads occurs |
| 1.6 s | Secondary control setpoints are updated |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
González-Romera, E.; Romero-Cadaval, E.; Roncero-Clemente, C.; Ruiz-Cortés, M.; Barrero-González, F.; Milanés Montero, M.-I.; Moreno-Muñoz, A. Secondary Control for Storage Power Converters in Isolated Nanogrids to Allow Peer-to-Peer Power Sharing. Electronics 2020, 9, 140. https://doi.org/10.3390/electronics9010140
González-Romera E, Romero-Cadaval E, Roncero-Clemente C, Ruiz-Cortés M, Barrero-González F, Milanés Montero M-I, Moreno-Muñoz A. Secondary Control for Storage Power Converters in Isolated Nanogrids to Allow Peer-to-Peer Power Sharing. Electronics. 2020; 9(1):140. https://doi.org/10.3390/electronics9010140
Chicago/Turabian StyleGonzález-Romera, Eva, Enrique Romero-Cadaval, Carlos Roncero-Clemente, Mercedes Ruiz-Cortés, Fermín Barrero-González, María-Isabel Milanés Montero, and Antonio Moreno-Muñoz. 2020. "Secondary Control for Storage Power Converters in Isolated Nanogrids to Allow Peer-to-Peer Power Sharing" Electronics 9, no. 1: 140. https://doi.org/10.3390/electronics9010140
APA StyleGonzález-Romera, E., Romero-Cadaval, E., Roncero-Clemente, C., Ruiz-Cortés, M., Barrero-González, F., Milanés Montero, M.-I., & Moreno-Muñoz, A. (2020). Secondary Control for Storage Power Converters in Isolated Nanogrids to Allow Peer-to-Peer Power Sharing. Electronics, 9(1), 140. https://doi.org/10.3390/electronics9010140







