Modeling of High-Resolution Data Converter: Two-Step Pipelined-SAR ADC based on ISDM
Abstract
:1. Introduction
2. ADC Architecture and Analysis
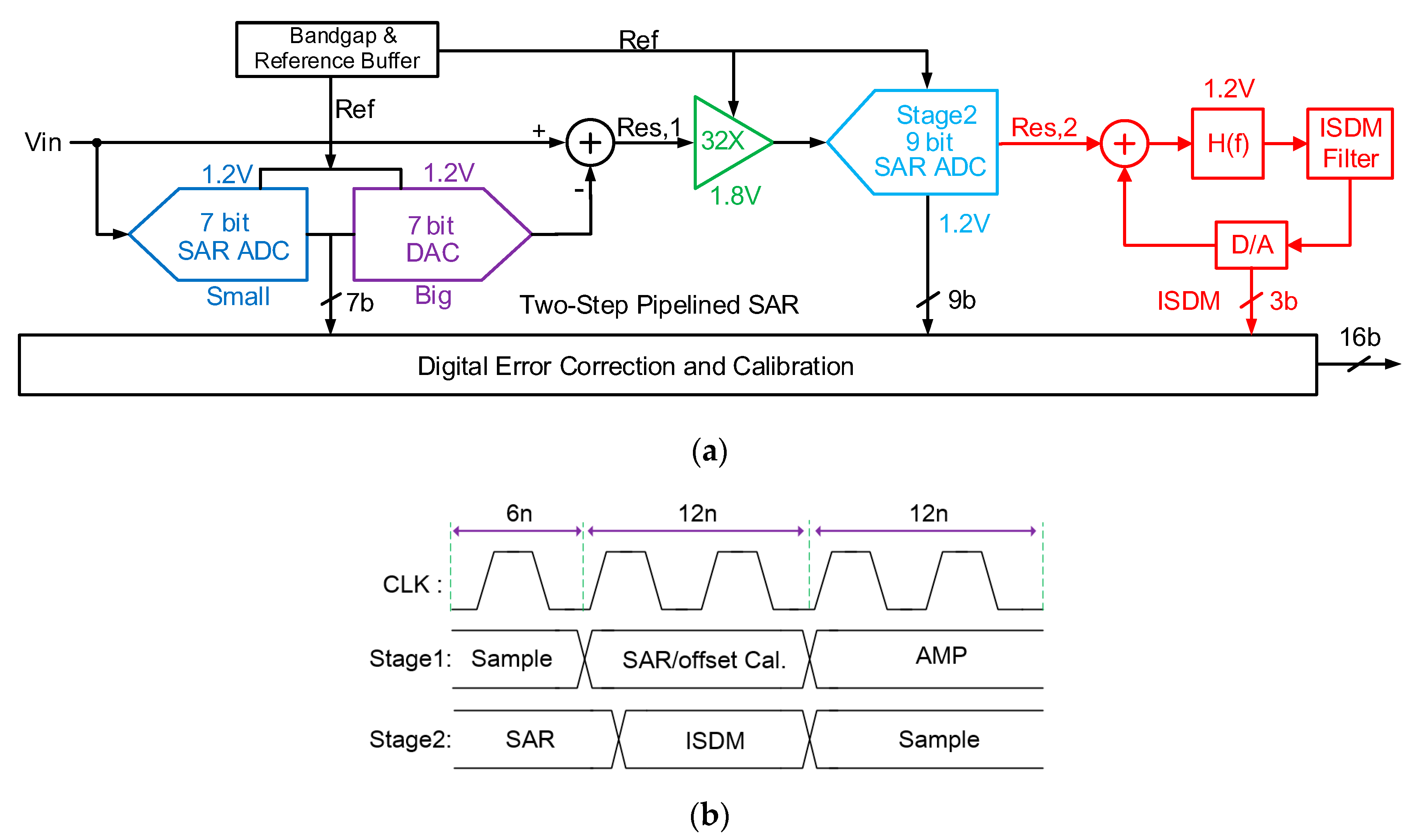
2.1. The Proposed Architecture Modeling of ADC
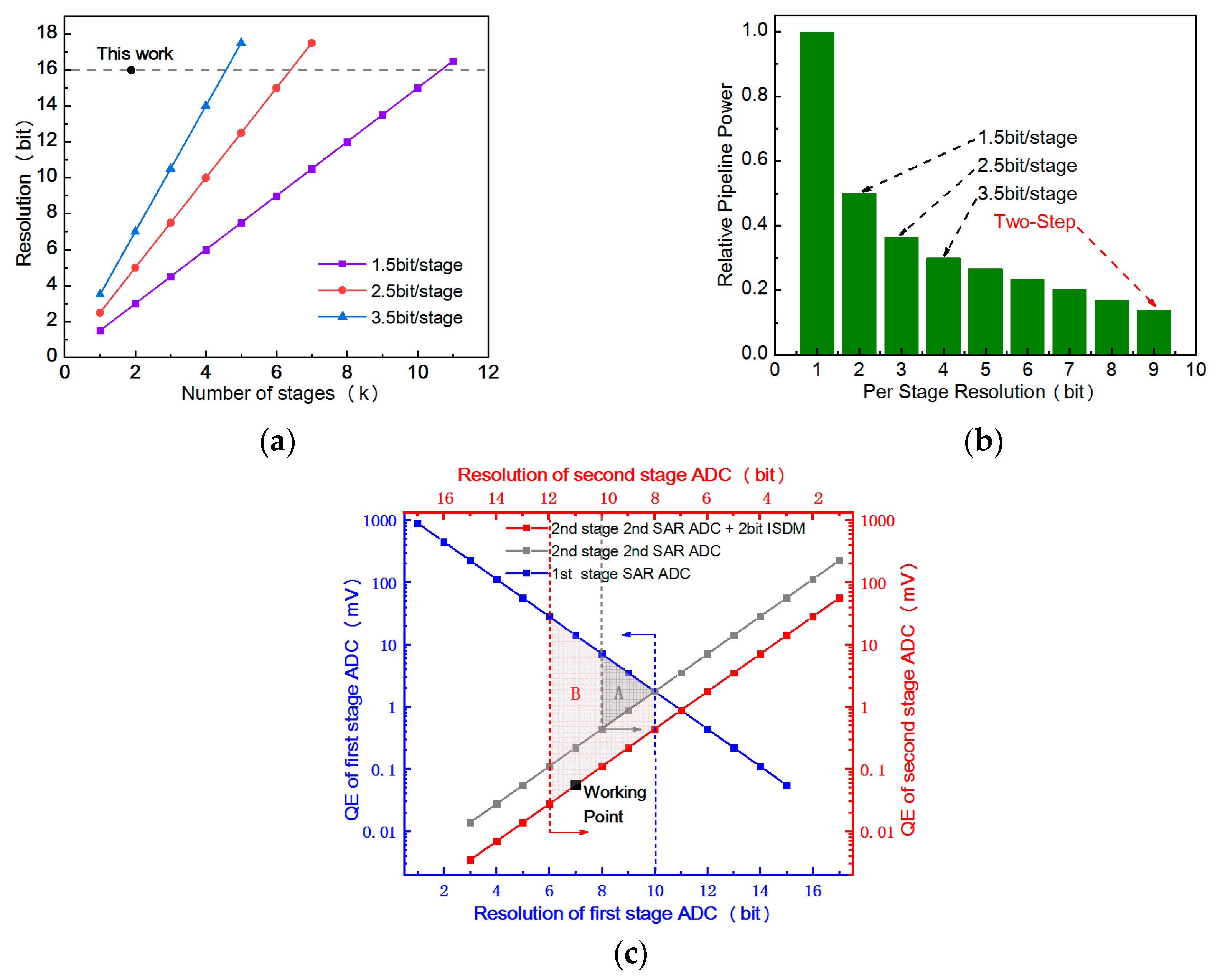
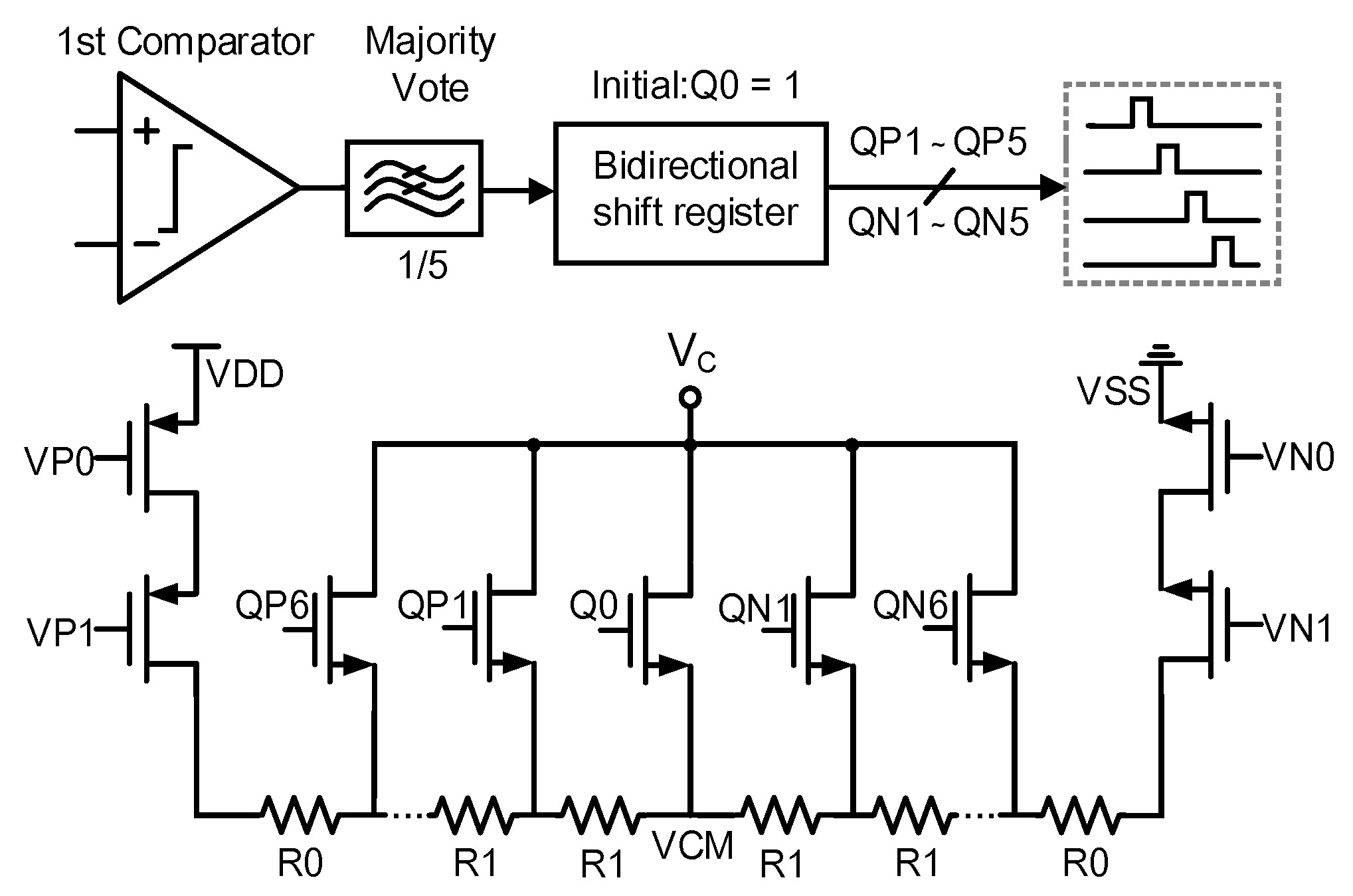
2.2. SNR Enhancement Technology
3. Circuit-Level Implementation
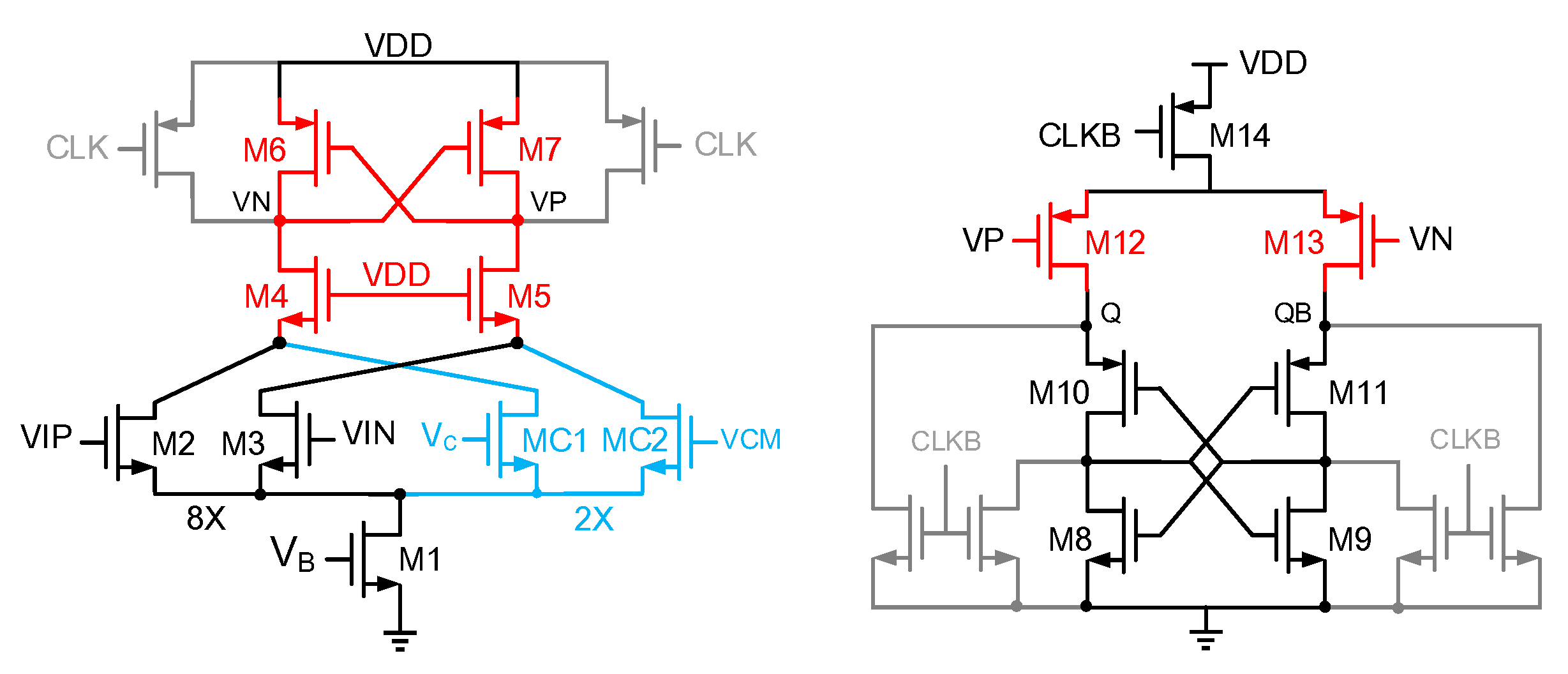
3.1. Inter-Stage Amplifier
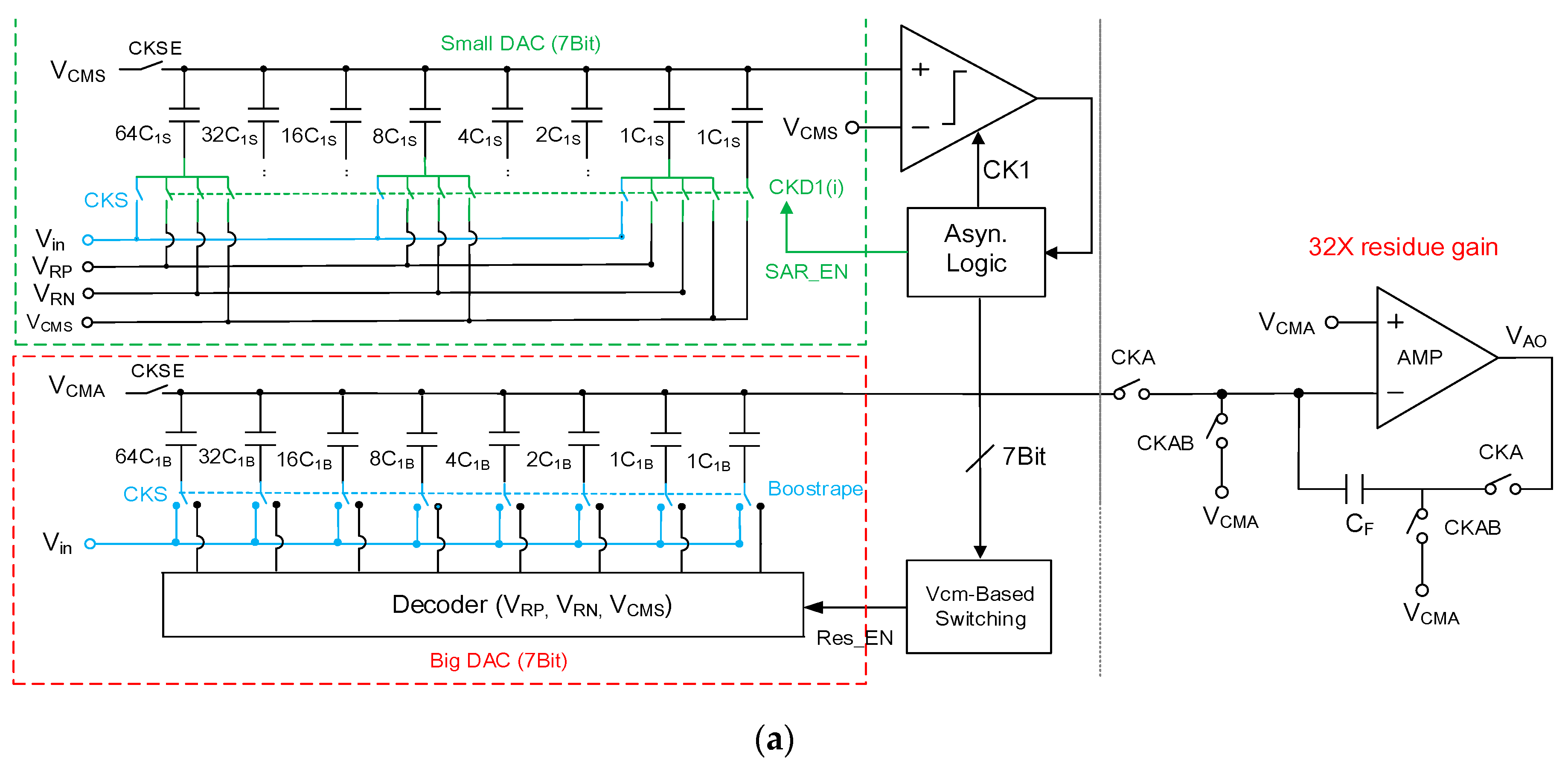
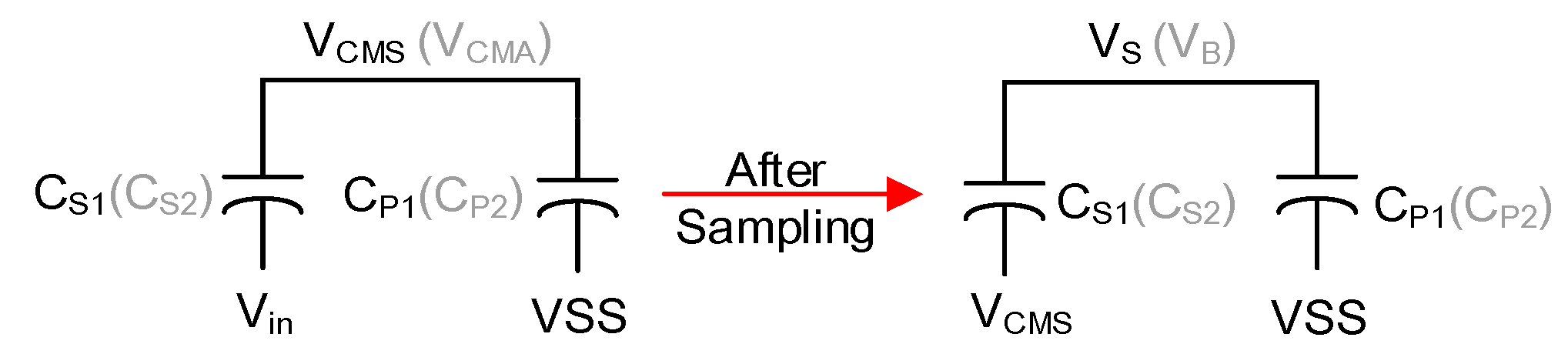
3.2. First Stage SAR ADC
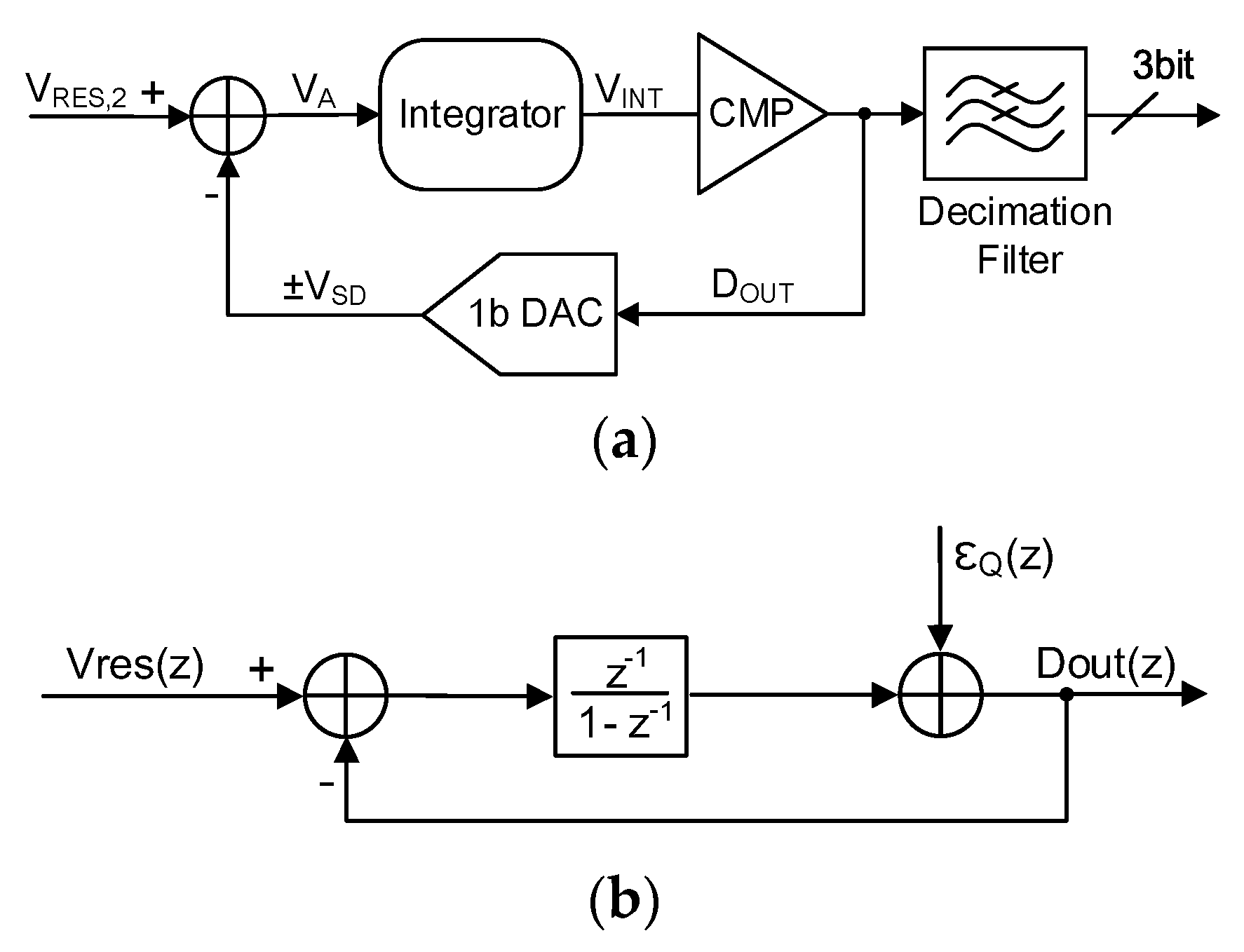
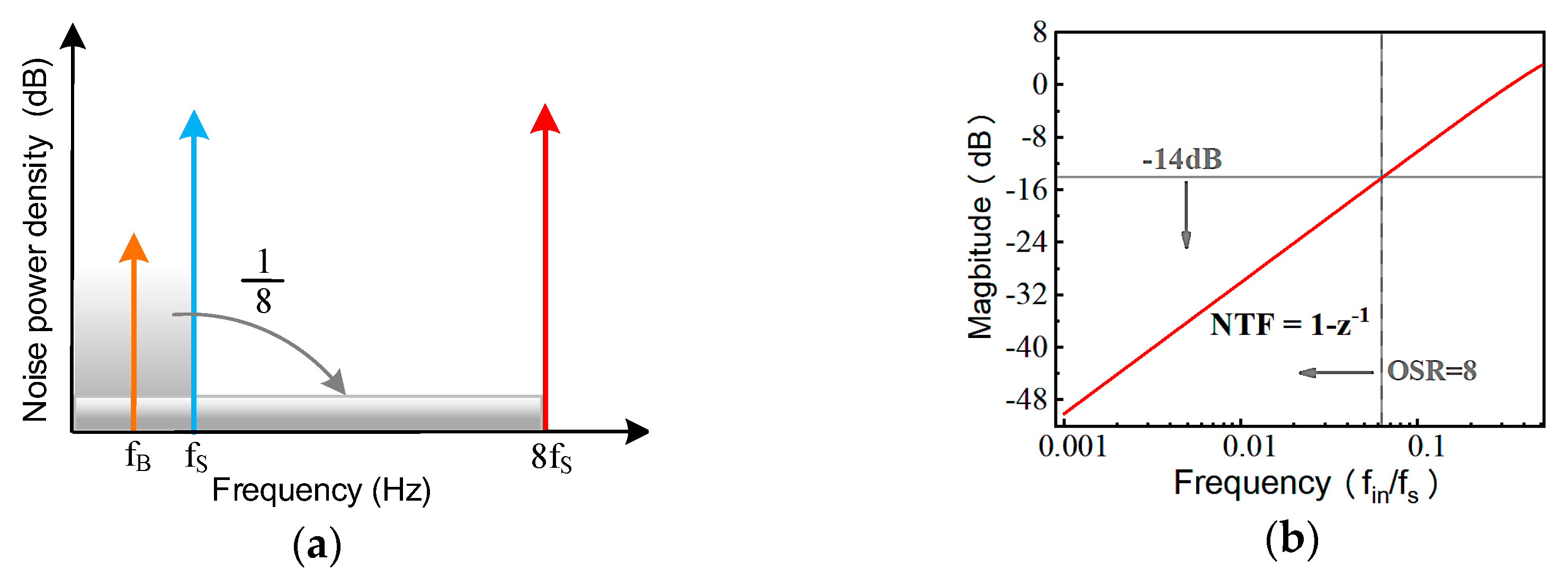
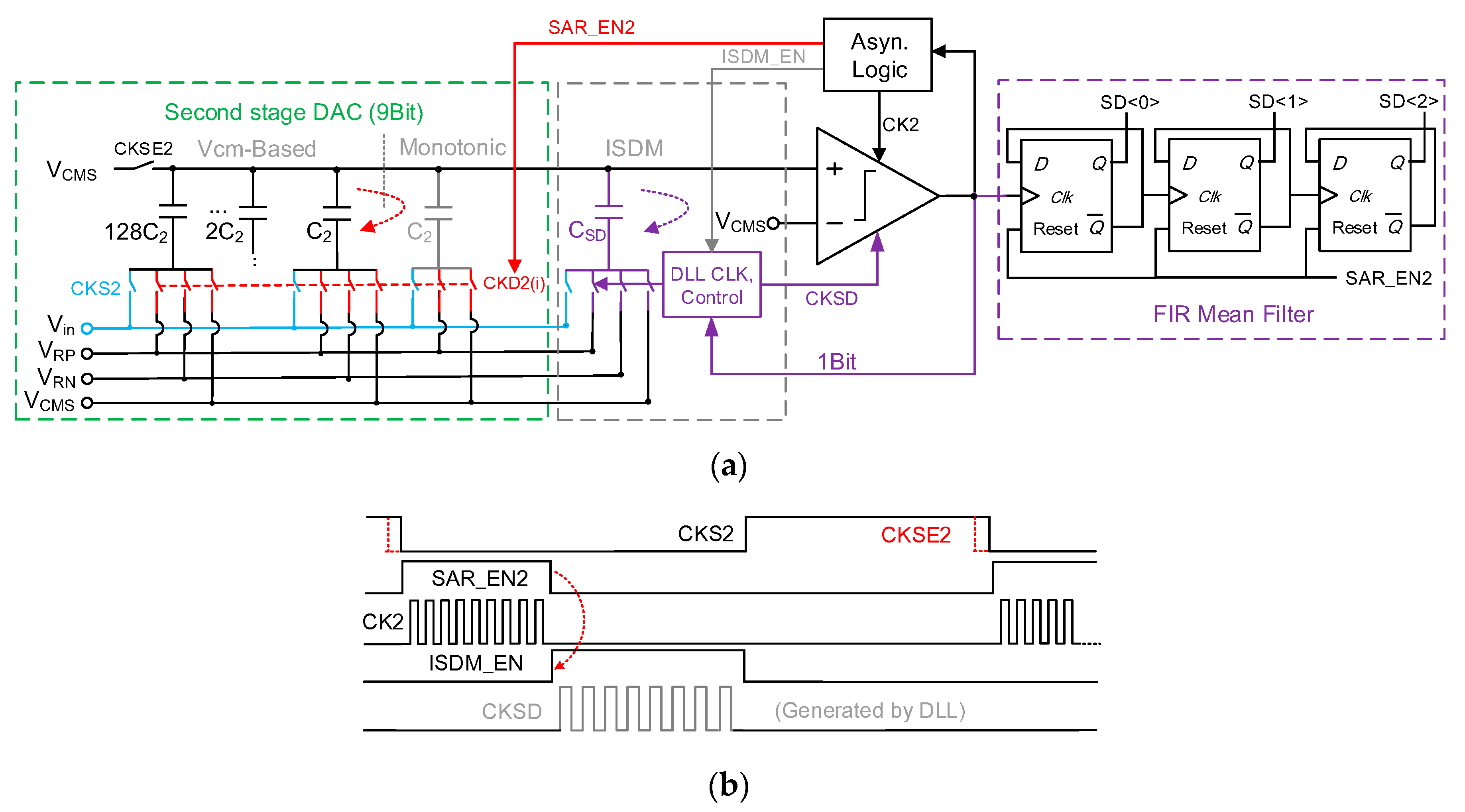
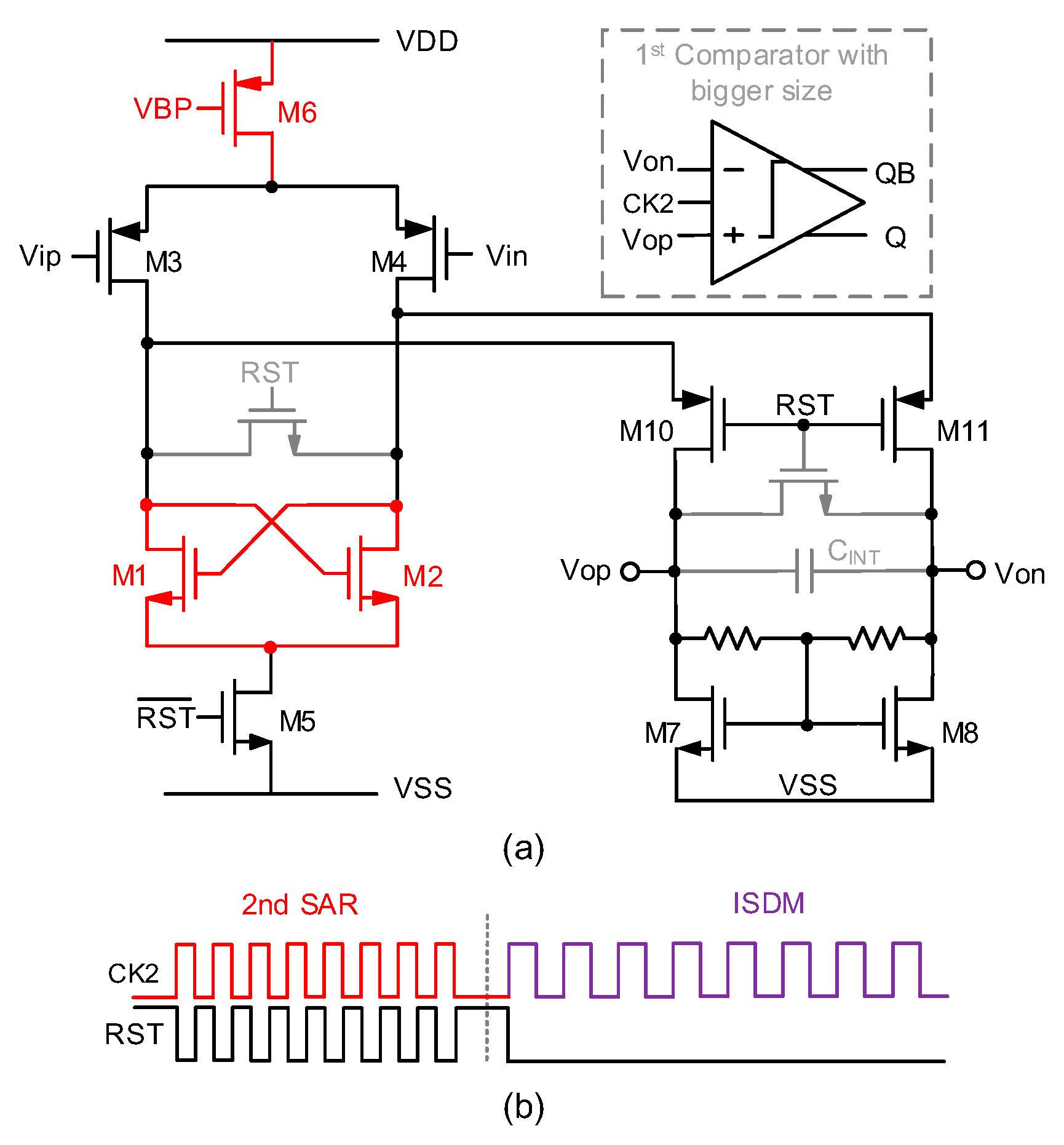
3.3. Second Stage ISDM SAR ADC
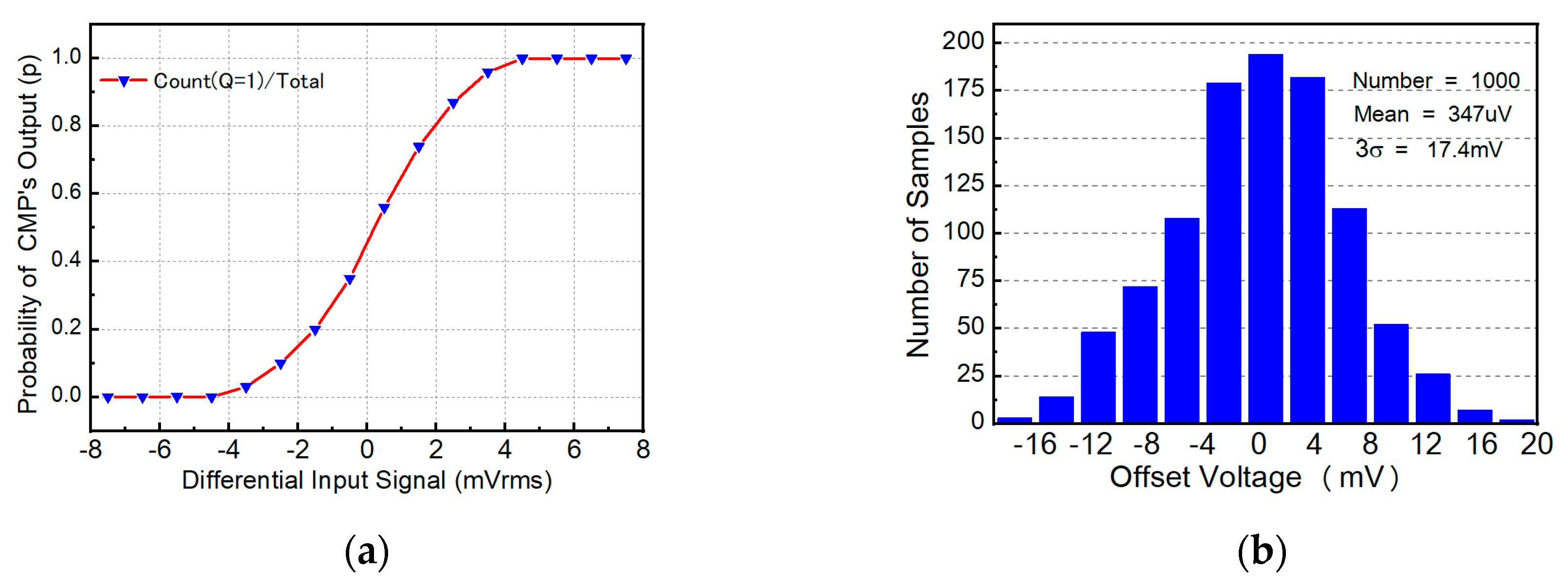
3.4. Comparator and Integrator
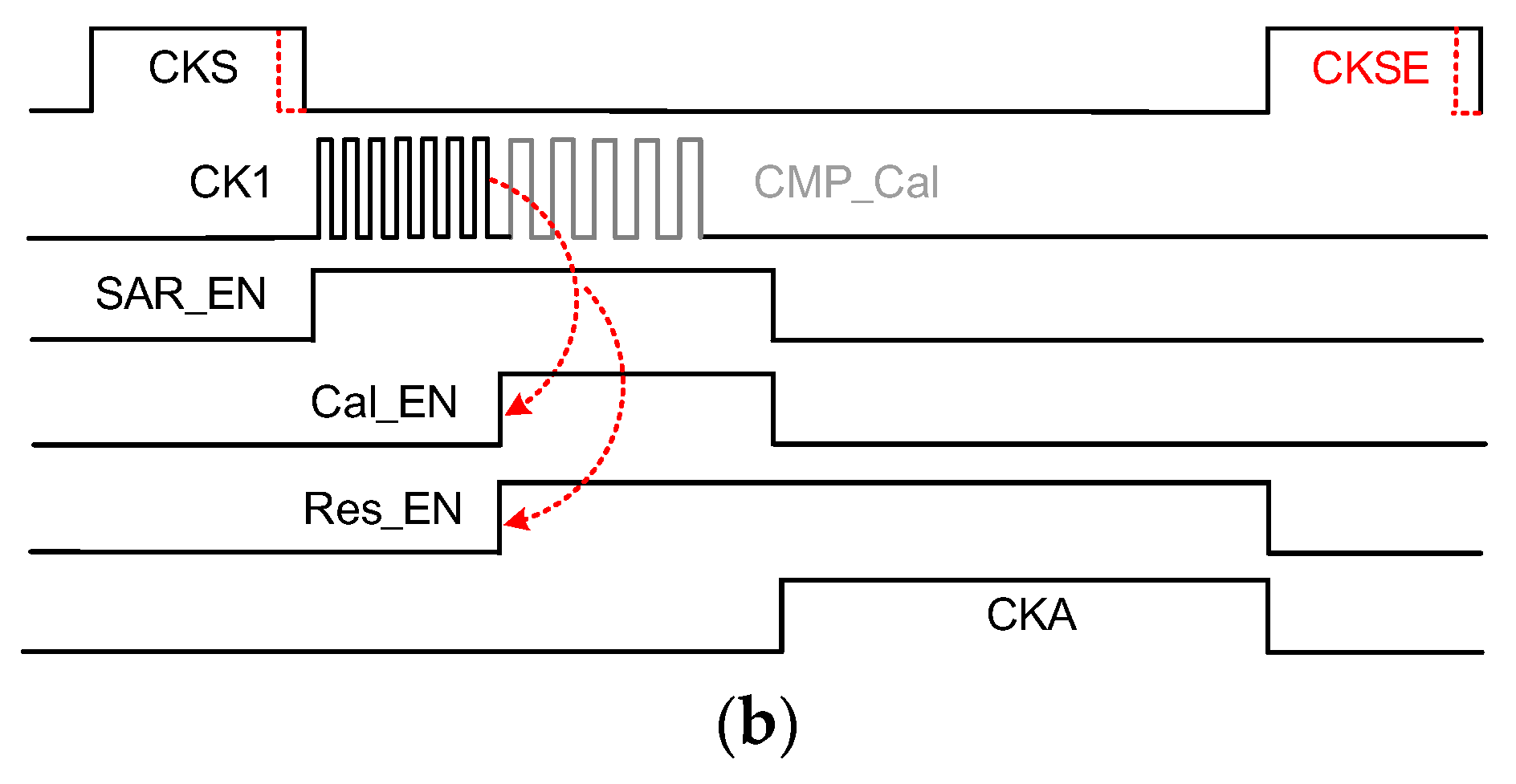
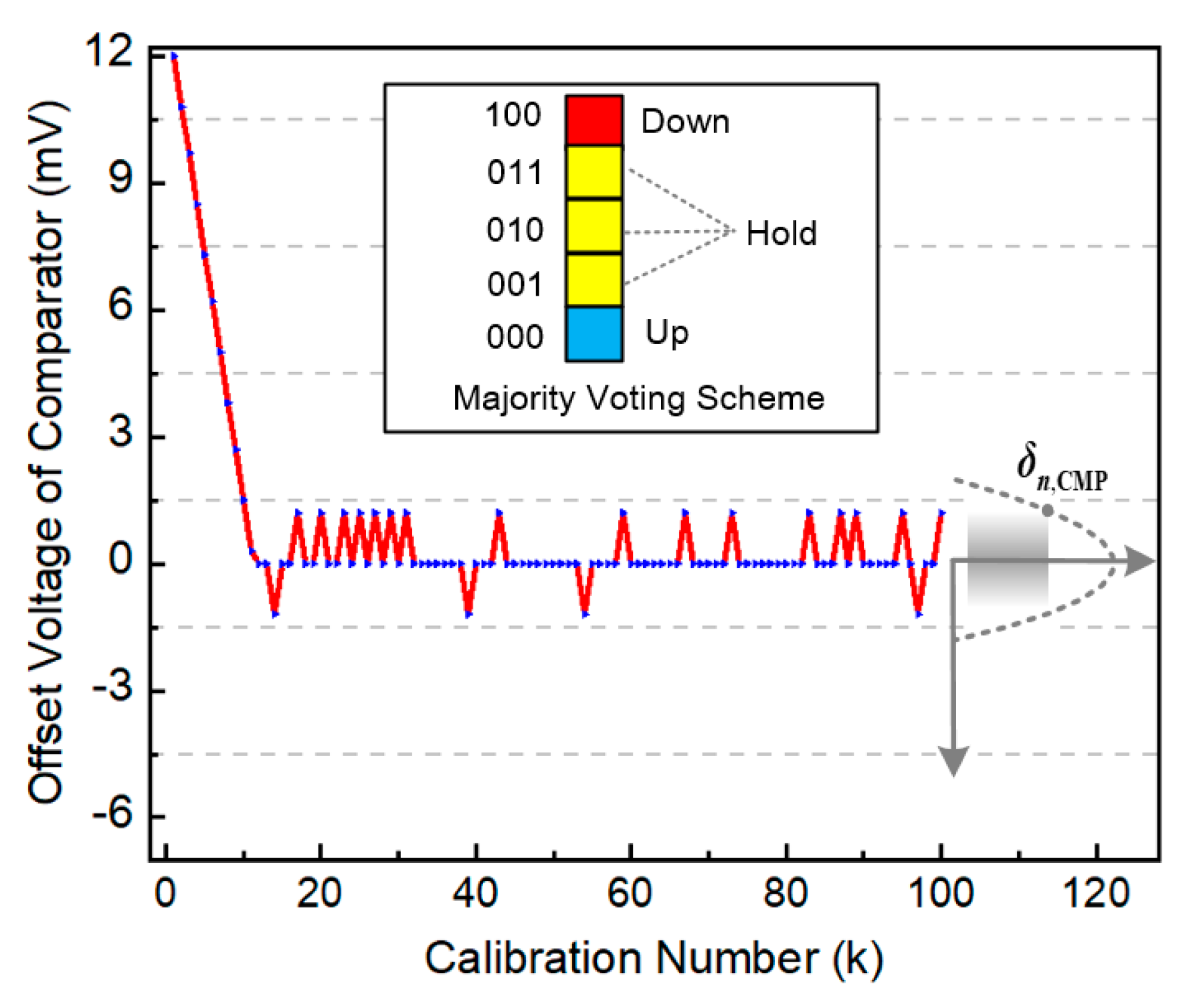
3.5. System Stabilization and Calibration
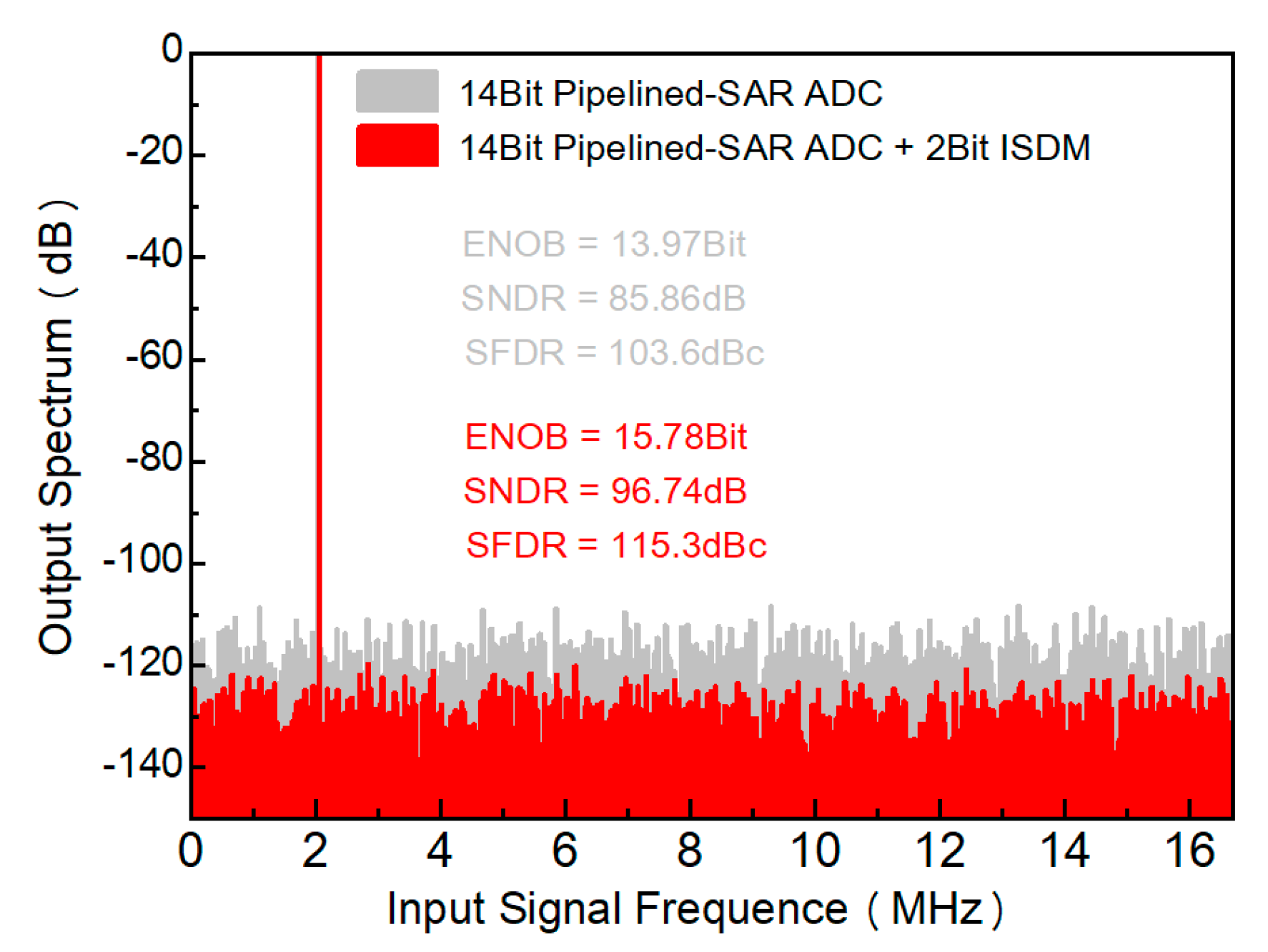
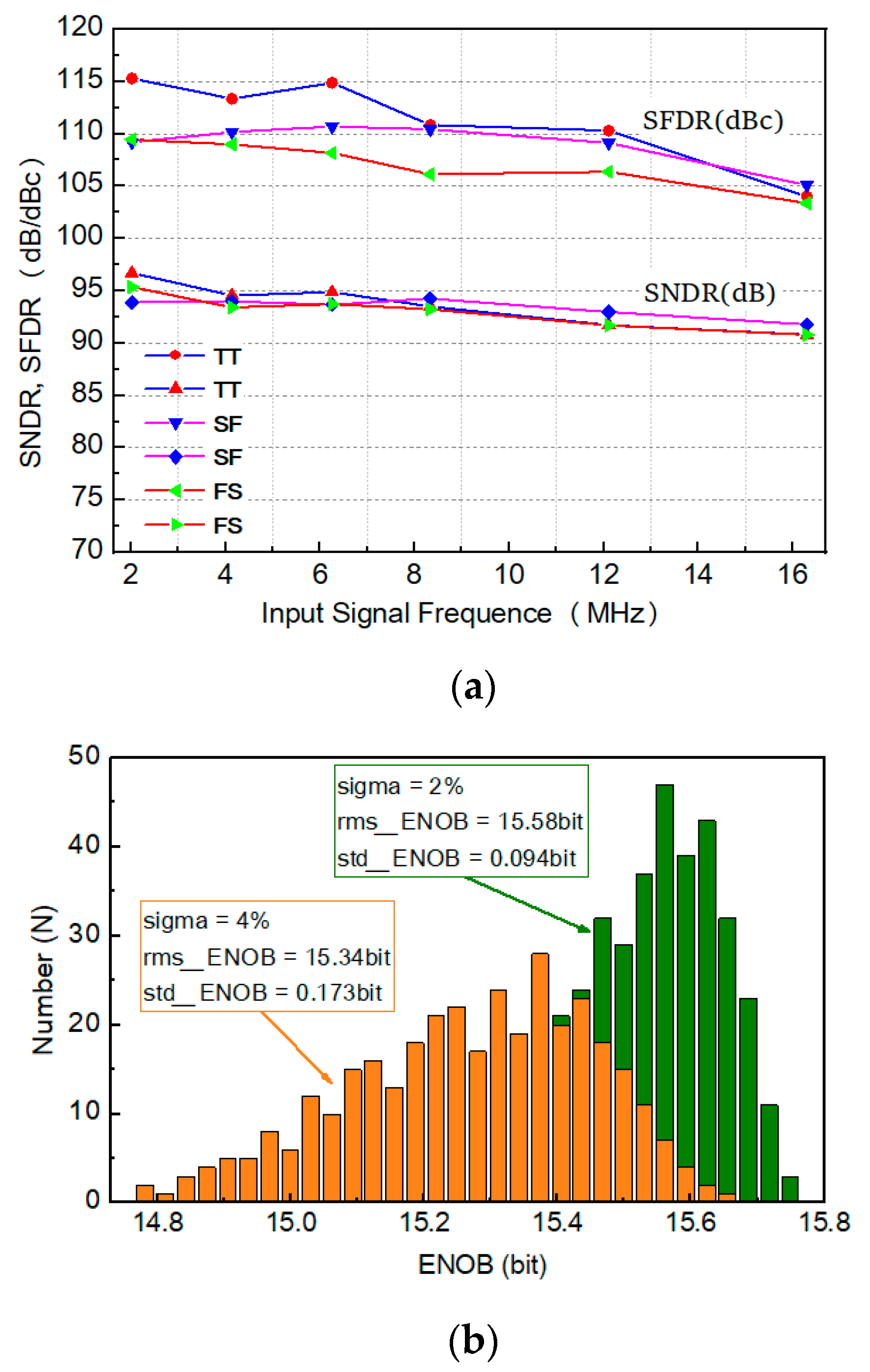
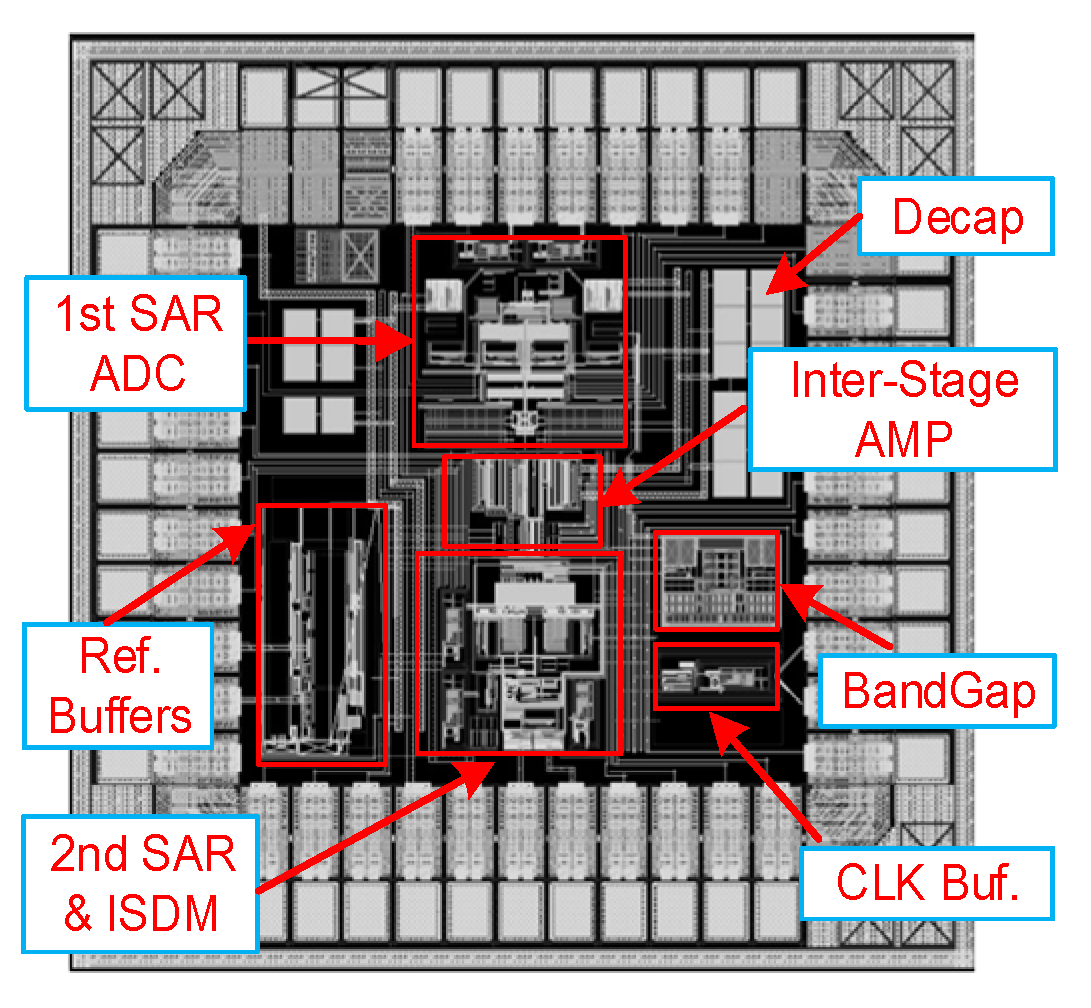
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Laporte-Fauret, B.; Ferré, G.; Dallet, D.; Minger, B.; Fuché, L. ADC Resolution for Simultaneous Reception of Two Signals with High Dynamic Range. In Proceedings of the IEEE International Conference on Electronics, Circuits and Systems (ICECS), Bordeaux, France, 9–12 December 2018; pp. 729–732. [Google Scholar]
- Zhang, F.; Guo, Q.; Wang, Z.; Zhou, P.; Zhang, G.; Sun, J.; Pan, S. Photonics-based broadband radar for high-resolution and real-time inverse synthetic aperture imaging. Opt. Express 2017, 25, 16274–16281. [Google Scholar] [CrossRef] [PubMed]
- Mohamed, N.S.; Wright, N.G.; Horsfall, A.B. High linearity silicon carbide detectors for medical applications. In Proceedings of the IEEE Nuclear Science Symposium, Medical Imaging Conference and Room-Temperature Semiconductor Detector Workshop, Strasbourg, France, 29 October–6 November 2016; pp. 1–5. [Google Scholar]
- Liu, M.; Van Roermund, A.; Harpe, P. A 10b 20MS/s SAR ADC with a low-power and area-efficient DAC-compensated reference. In Proceedings of the IEEE European Solid State Circuits Conference (ESSCIRC), Leuven, Belgium, 11–14 September 2017; pp. 231–234. [Google Scholar]
- Miki, T.; Morie, T.; Matsukawa, K.; Bando, Y.; Okumoto, T.; Obata, K.; Dosho, S. A 4.2 mW 50 MS/s 13 bit CMOS SAR ADC with SNR and SFDR Enhancement Techniques. IEEE J. Solid-State Circuits 2015, 50, 1372–1381. [Google Scholar] [CrossRef]
- Razavi, B. A tale of two ADCs: Pipelined versus SA. IEEE Solid-State Circuits Mag. 2015, 7, 38–46. [Google Scholar] [CrossRef]
- Brunsilius, J.; Siragusa, E.; Kosic, S.; Murden, F.; Yetis, E.; Luu, B.; Barlow, A. A 16b 80Ms/s 100mW 77.6 dB SNR CMOS Pipeline ADC. In Proceedings of the IEEE International Solid-State Circuits Conference, San Francisco, CA, USA, 20–24 February 2011; pp. 186–188. [Google Scholar]
- Cline, D.W.; Gray, P.R. A power optimized 13-b 5 Msamples/s pipelined analog-to-digital converter in 1.2μm CMOS. IEEE J. Solid-State Circuits 1996, 31, 294–303. [Google Scholar] [CrossRef]
- Steiner, M.; Greer, N. A 22.3 b 1kHz 12.7 mW switched-capacitor ΔΣ modulator with stacked split-steering amplifiers. In Proceedings of the IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 31 January–4 February 2016; pp. 284–286. [Google Scholar]
- Márkus, J.; Silva, J.; Temes, G.C. Theory and applications of incremental ∆ Σ converters. IEEE Trans. Circuits Syst. I Regul. Pap. 2004, 51, 678–690. [Google Scholar] [CrossRef]
- Hurrell, C.P.; Lyden, C.; Laing, D.; Hummerston, D.; Vickery, M. An 18 b 12.5 MS/s ADC with 93 dB SNR. IEEE J. Solid-State Circuits 2010, 45, 2647–2654. [Google Scholar] [CrossRef]
- Lee, C.C.; Flynn, M.P. A 12b 50MS/s 3.5 mW SAR assisted 2-stage pipeline ADC. In Proceedings of the Symposium on VLSI Circuits, Honolulu, HI, USA, 16–18 June 2010; pp. 239–240. [Google Scholar]
- Lim, Y.; Flynn, M.P. A calibration-free 2.3 mW 73.2 dB SNDR 15b 100 MS/s four-stage fully differential ring amplifier based SAR-assisted pipeline ADC. In Proceedings of the Symposium on VLSI Circuits, Kyoto, Japan, 5–8 June 2017; pp. 98–99. [Google Scholar]
- Tripathi, V.; Murmann, B. A 160 MS/s, 11.1 mW, single-channel pipelined SAR ADC with 68.3 dB SNDR. In Proceedings of the IEEE Custom Integrated Circuits Conference, San Jose, CA, USA, 15–17 September 2014; pp. 1–4. [Google Scholar]
- Ramkaj, A.T.; Strackx, M.; Steyaert, M.S.; Tavernier, F. A 1.25-GS/s 7-b SAR ADC with 36.4-dB SNDR at 5 GHz Using Switch-Bootstrapping, USPC DAC and Triple-Tail Comparator in 28-nm CMOS. IEEE J. Solid-State Circuits 2018, 53, 1889–1901. [Google Scholar] [CrossRef]
- Venca, A.; Ghittori, N.; Bosi, A.; Nani, C. A 0.076 mm2 12 b 26.5 mW 600 MS/s 4-Way Interleaved Sub-ranging SAR-∆ Σ ADC with On-Chip Buffer in 28 nm CMOS. IEEE J. Solid-State Circuits 2016, 51, 2951–2962. [Google Scholar] [CrossRef]
- Chopra, A.; Chatterjee, S. A 24 mW, 80 dB SNR, 50 MHz multi-bit continuous time ΣΔ ADC in 28 nm FD-SOI. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS), Montreal, QC, Canada, 22–25 May 2016; pp. 65–68. [Google Scholar]
- Hsieh, S.E.; Hsieh, C.C. A 0.4-V 13-bit 270-kS/s SAR-ISDM ADC with Opamp-Less Time-Domain Integrator. IEEE J. Solid-State Circuits 2019, 54, 1648–1656. [Google Scholar] [CrossRef]
- Lyu, Y.; Ramkaj, A.; Tavernier, F. High-gain and power-efficient dynamic amplifier for pipelined SAR ADCs. Electron. Lett. 2017, 53, 1510–1512. [Google Scholar] [CrossRef]
- Yang, Y.; Binkley, D.M.; Li, C. Modeling and optimization of fast-settling time gain-boosted cascode CMOS amplifiers. In Proceedings of the IEEE SoutheastCon, Concord, NC, USA, 18–21 March 2010; pp. 33–36. [Google Scholar]
- Wu, J.; Chen, C.Y.; Li, T.; He, L.; Liu, W.; Shih, W.T.; Hung, H.T. A 240-mW 2.1-GS/s 52-dB SNDR Pipeline ADC Using MDAC Equalization. IEEE J. Solid-State Circuits 2013, 48, 1818–1828. [Google Scholar]
- Wang, L.; Yin, Y.S.; Guan, X.Z. Design of a gain-boosted telescopic fully differential amplifier with CMFB circuit. In Proceedings of the 2nd International Conference on Consumer Electronics, Communications and Networks (CECNet), Yichang, China, 21–23 April 2012; pp. 252–255. [Google Scholar]
- Zhu, Y.; Chan, C.H.; Chio, U.F.; Sin, S.W.; Seng-Pan, U.; Martins, R.P.; Maloberti, F. A 10-bit 100-MS/s reference-free SAR ADC in 90 nm CMOS. IEEE J. Solid-State Circuits 2010, 45, 1111–1121. [Google Scholar] [CrossRef]
- Liu, C.C.; Chang, S.J.; Huang, G.Y.; Lin, Y.Z. A 10-bit 50-MS/s SAR ADC with a monotonic capacitor switching procedure. IEEE J. Solid-State Circuits 2010, 45, 731–740. [Google Scholar] [CrossRef]
- Tsai, J.H.; Wang, H.H.; Yen, Y.C.; Lai, C.M.; Chen, Y.J.; Huang, P.C.; Lee, C.C. A 0.003 mm2 10 b 240 MS/s 0.7 mW SAR ADC in 28 nm CMOS with Digital Error Correction and Correlated-Reversed Switching. IEEE J. Solid-State Circuits 2015, 50, 1382–1398. [Google Scholar] [CrossRef]
- Kull, L.; Toifl, T.; Schmatz, M.; Francese, P.A.; Menolfi, C.; Braendli, M.; Leblebici, Y. A 3.1 mW 8b 1.2 GS/s single-channel asynchronous SAR ADC with alternate comparators for enhanced speed in 32 nm digital SOI CMOS. IEEE J. Solid-State Circuits 2013, 48, 3049–3058. [Google Scholar] [CrossRef]
- Nuzzo, P.; De Bernardinis, F.; Terreni, P.; Van der Plas, G. Noise analysis of regenerative comparators for reconfigurable ADC architectures. IEEE Trans. Circuits Syst. I Regul. Pap. 2008, 55, 1441–1454. [Google Scholar] [CrossRef]
- Ragab, K.; Sun, N. A 1.4 mW 8b 350MS/s loop-unrolled SAR ADC with background offset calibration in 40nm CMOS. In Proceedings of the European Solid-State Circuits Conference (ESSCIRC), Lausanne, Switzerland, 12–15 September 2016; pp. 417–420. [Google Scholar]
- Ahmadi, M.; Namgoong, W. A 3.3 fJ/conversion-step 250kS/s 10b SAR ADC using optimized vote allocation. In Proceedings of the IEEE Custom Integrated Circuits Conference, San Jose, CA, USA, 22–25 September 2013; pp. 1–4. [Google Scholar]
- Hung, T.C.; Kuo, T.H. A 75.3-dB SNDR 24-MS/s Ring Amplifier-Based Pipelined ADC Using Averaging Correlated Level Shifting and Reference Swapping for Reducing Errors from Finite Opamp Gain and Capacitor Mismatch. IEEE J. Solid-State Circuits 2019, 54, 1425–1435. [Google Scholar] [CrossRef]
- Shen, J.; Shikata, A.; Fernando, L.D.; Guthrie, N.; Chen, B.; Maddox, M.; Coln, M.C. A 16-bit 16-MS/s SAR ADC with on-chip calibration in 55-nm CMOS. IEEE J. Solid-State Circuits 2018, 53, 1149–1160. [Google Scholar] [CrossRef]
- Chang, D.Y.; Munoz, C.; Daly, D.; Shin, S.K.; Guay, K.; Thurston, T.; Straayer, M. A 21mW 15b 48MS/s zero-crossing pipeline ADC in 0.13 μm CMOS with 74dB SNDR. In Proceedings of the IEEE International Solid-State Circuits Conference Digest of Technical Papers (ISSCC), San Francisco, CA, USA, 22–26 February 2015; pp. 204–205. [Google Scholar]


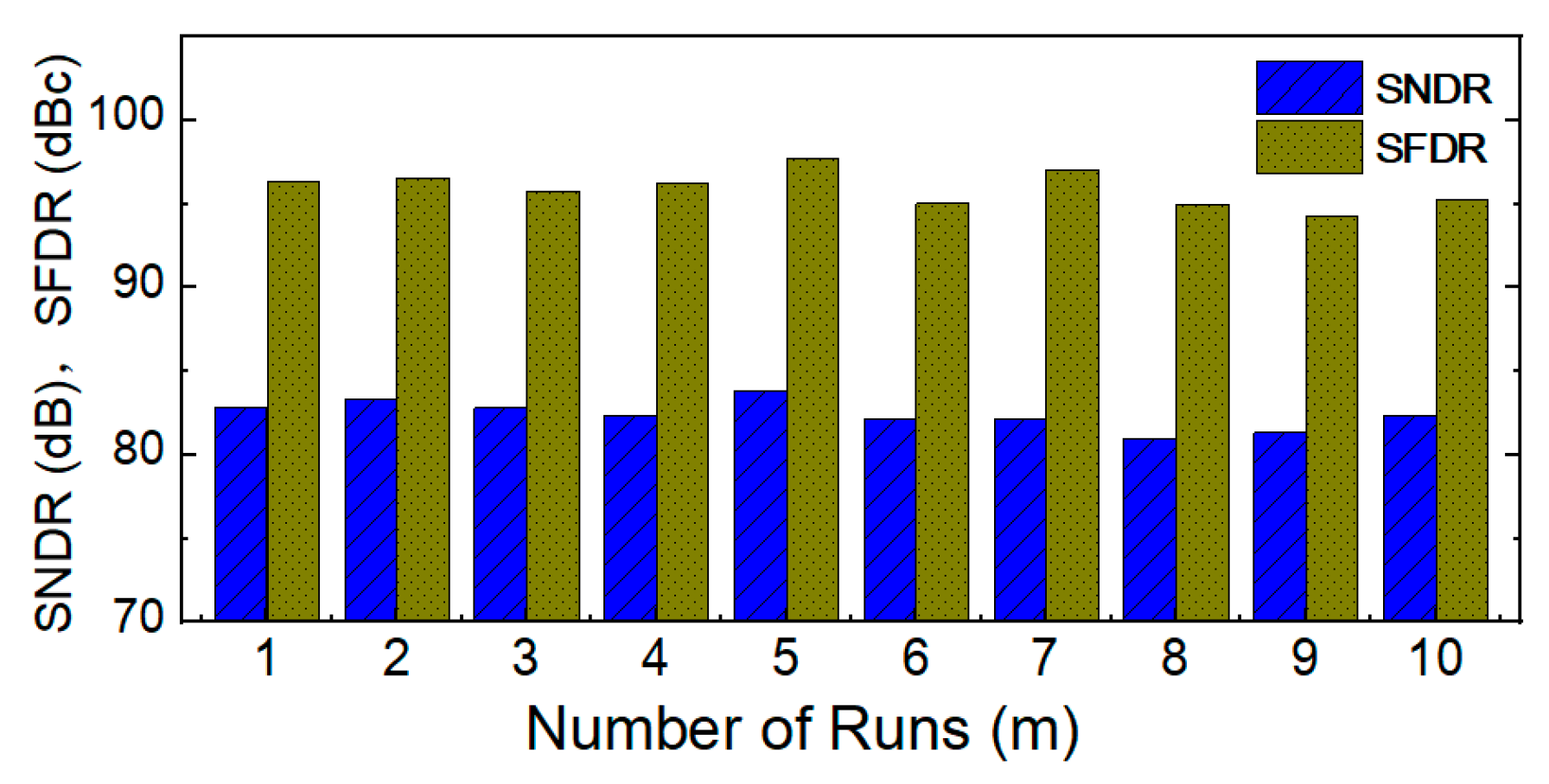
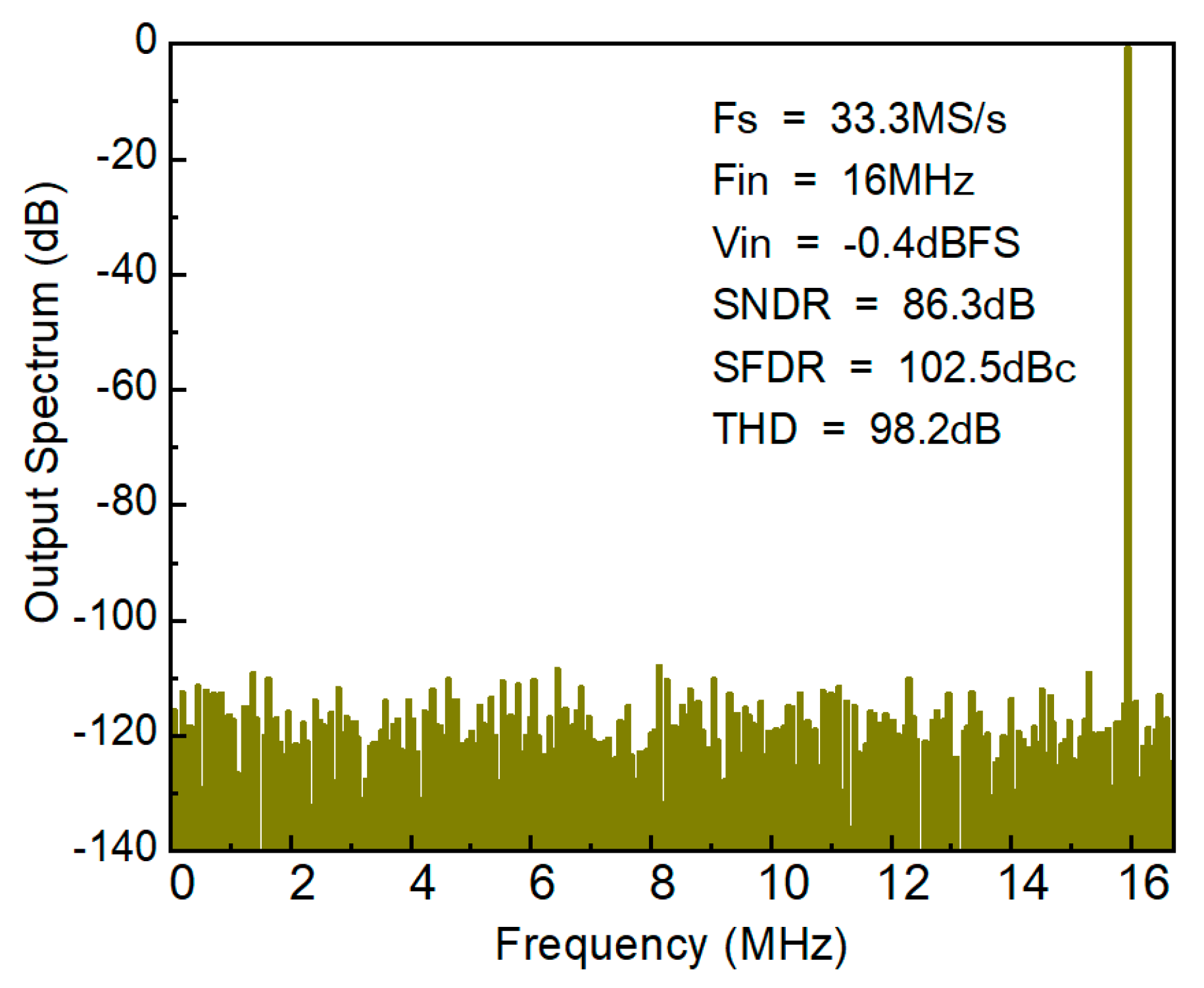
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Loop Gain (dB) | 79.3 | Phase Margin () | 73.5 |
| GBW (MHz) | 328.3 | A0 (dB) | 104 |
| 32.15 | P2 (GHz) | 1.87 | |
| PAU_P (MHz) | 704 | PAU_N (MHz) | 755 |
| CS (pF) | 4.096 | CL (pF) | 2.05 |
| C (fF) | 126 | R () | 1.2 |
| Slew Rate (V/μs) | 560 | Vn,OTA (nVrms) | 27 |
| SNDR (dB) | 75 | SFDR (dBc) | 84 |
| Parameter | This Work 1 | [7] | [30] | [31] | [32] |
|---|---|---|---|---|---|
| Architecture | Pipe-SAR+ ISDM | Pipe | Pipe | SAR | Pipe |
| Amplifier | GainBoost | GainBoost | Ring-AMP | N.G. | ZCBC |
| Resolution (Bit) | 16 | 16 | 16 | 16 | 15 |
| Process (nm) | 40 | 180 | 90 | 55 | 130 |
| Area (mm2) | 0.202 | 9.9 | 0.368 | 0.55 | 0.96 |
| Supply (V) | 1.8/1.2 | 1.8 | 1.1 | 3.3/1.2 | 1.8/1.2 |
| Input Range (V) | 1.8 | N.G. | 1.1 | 6.6 | 2 |
| Power (mW) | 19.2 | 100 | 5.1 | 16.3 | 21.6 |
| Fs (MS/s) | 33.3 | 80 | 24 | 16 | 48 |
| Fin (MHz) | 16 | 9.7 | 10 | 0.1 | 5 |
| SFDR (dBc) | 102.5 | 95 | 89.4 | 98 | 95 |
| SNDR (dB) | 86.3 | 77.6 | 75.4 | 78 | 74.5 |
| FoMs (dB) | 175.5 | 163.6 | 169 | 165 | 165.1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, B.; Li, X.; Sun, J.; Wu, J. Modeling of High-Resolution Data Converter: Two-Step Pipelined-SAR ADC based on ISDM. Electronics 2020, 9, 137. https://doi.org/10.3390/electronics9010137
Gao B, Li X, Sun J, Wu J. Modeling of High-Resolution Data Converter: Two-Step Pipelined-SAR ADC based on ISDM. Electronics. 2020; 9(1):137. https://doi.org/10.3390/electronics9010137
Chicago/Turabian StyleGao, Bo, Xin Li, Jie Sun, and Jianhui Wu. 2020. "Modeling of High-Resolution Data Converter: Two-Step Pipelined-SAR ADC based on ISDM" Electronics 9, no. 1: 137. https://doi.org/10.3390/electronics9010137
APA StyleGao, B., Li, X., Sun, J., & Wu, J. (2020). Modeling of High-Resolution Data Converter: Two-Step Pipelined-SAR ADC based on ISDM. Electronics, 9(1), 137. https://doi.org/10.3390/electronics9010137





