Low-Complexity Failed Element Diagnosis for Radar-Communication mmWave Antenna Array with Low SNR
Abstract
:1. Introduction
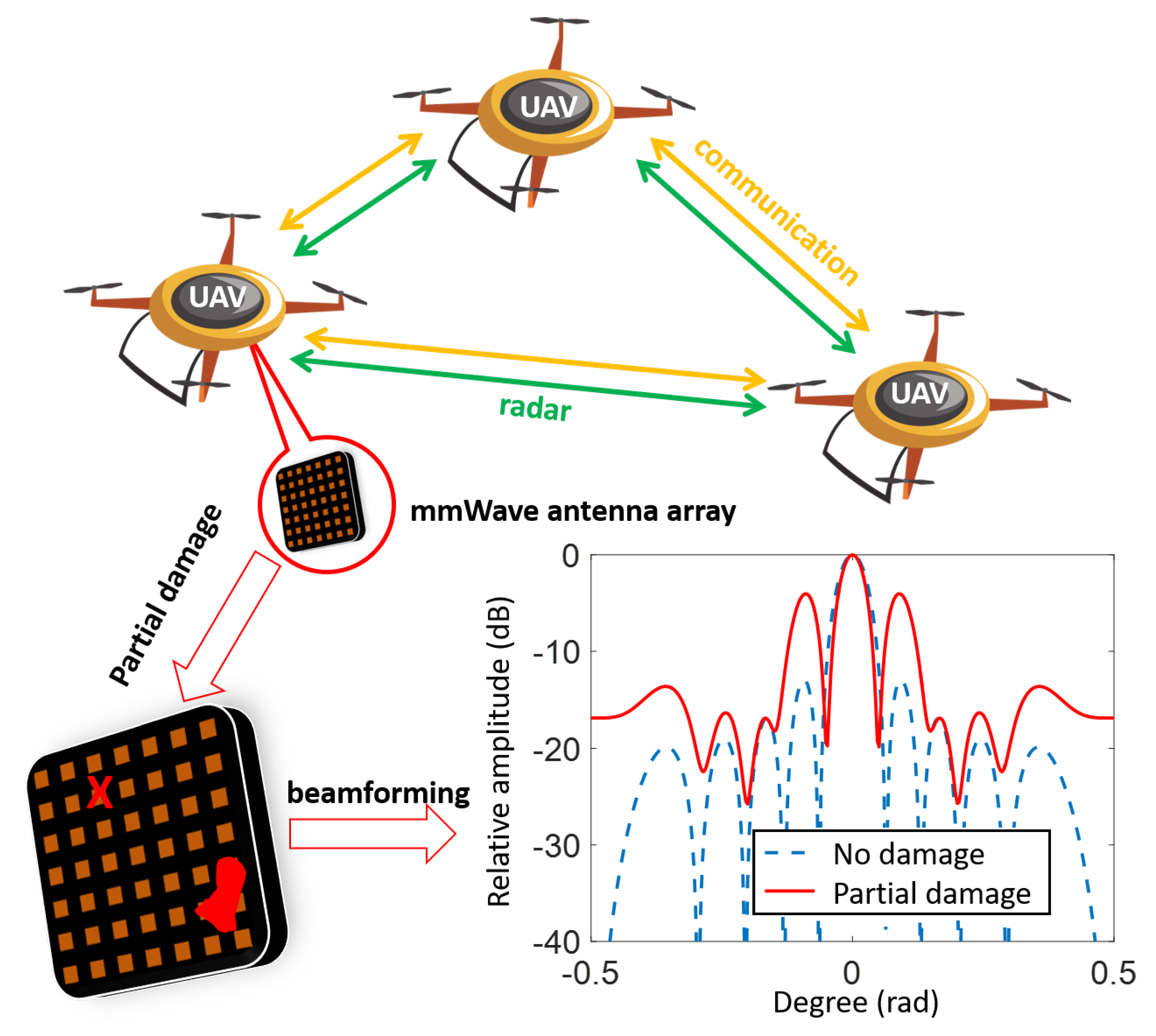
2. System Model
2.1. Joint Diagnosis Based on Radar-Communication System
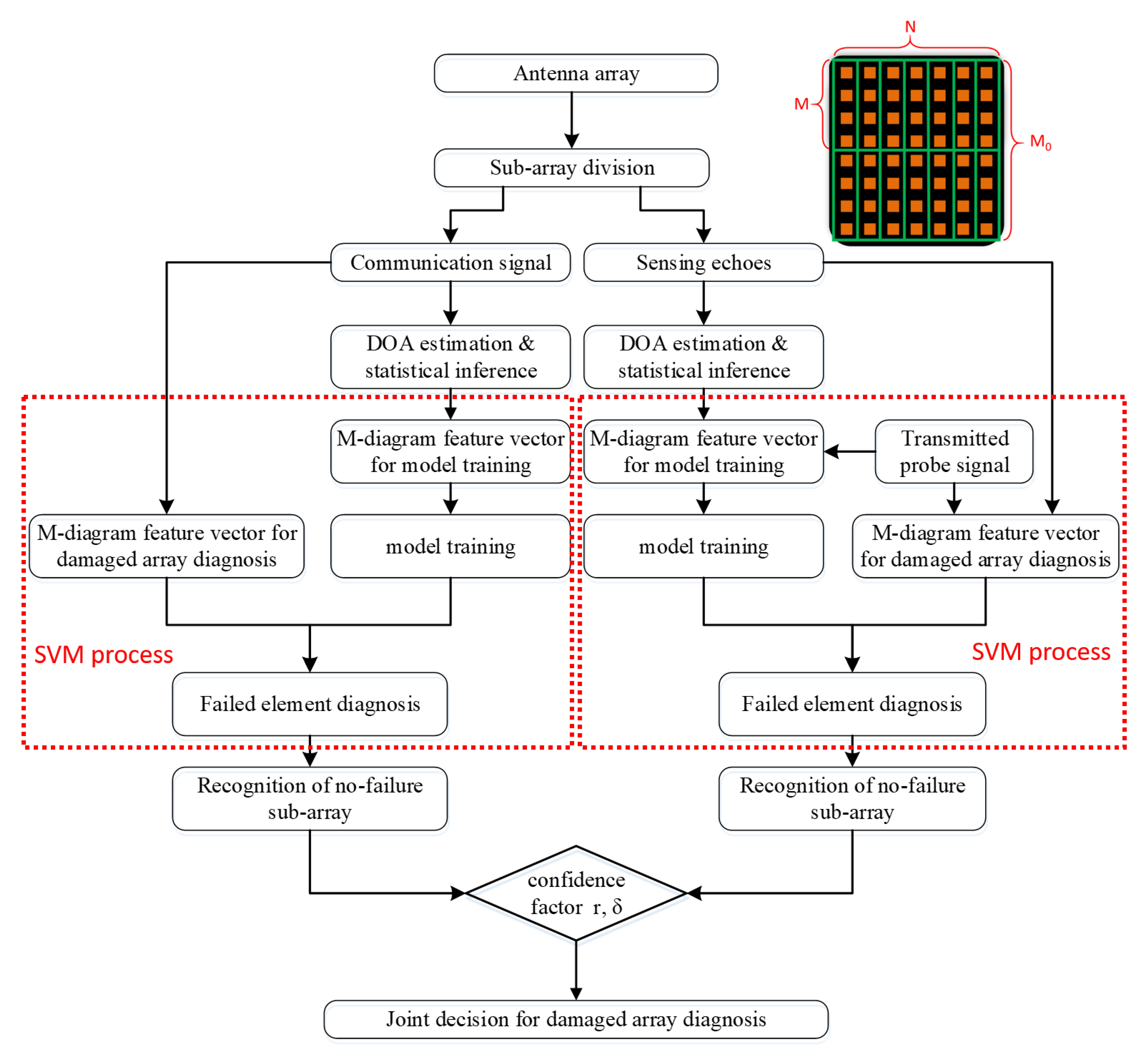
2.2. M-Dimensional Classification Vector for SVM
| Algorithm 1: M-diagram feature vector. |
 |
2.3. Accurate Estimation of DOA Based on Statistical Analysis
| Algorithm 2: DOA estimation and statistical inference. |
 |
2.4. Recognition of No-Failure Subarray
| Algorithm 3: No-failure sub-array recognition. |
 |
3. Results and Discussion
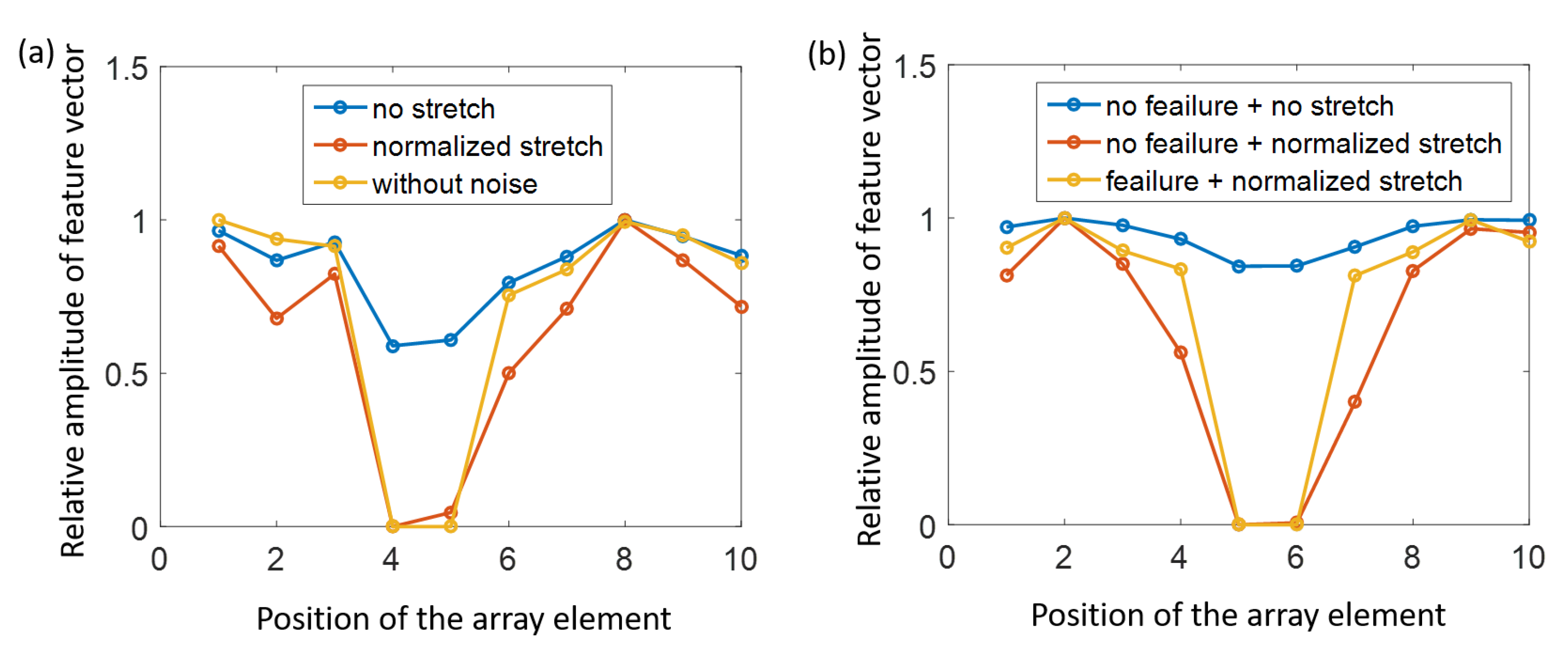
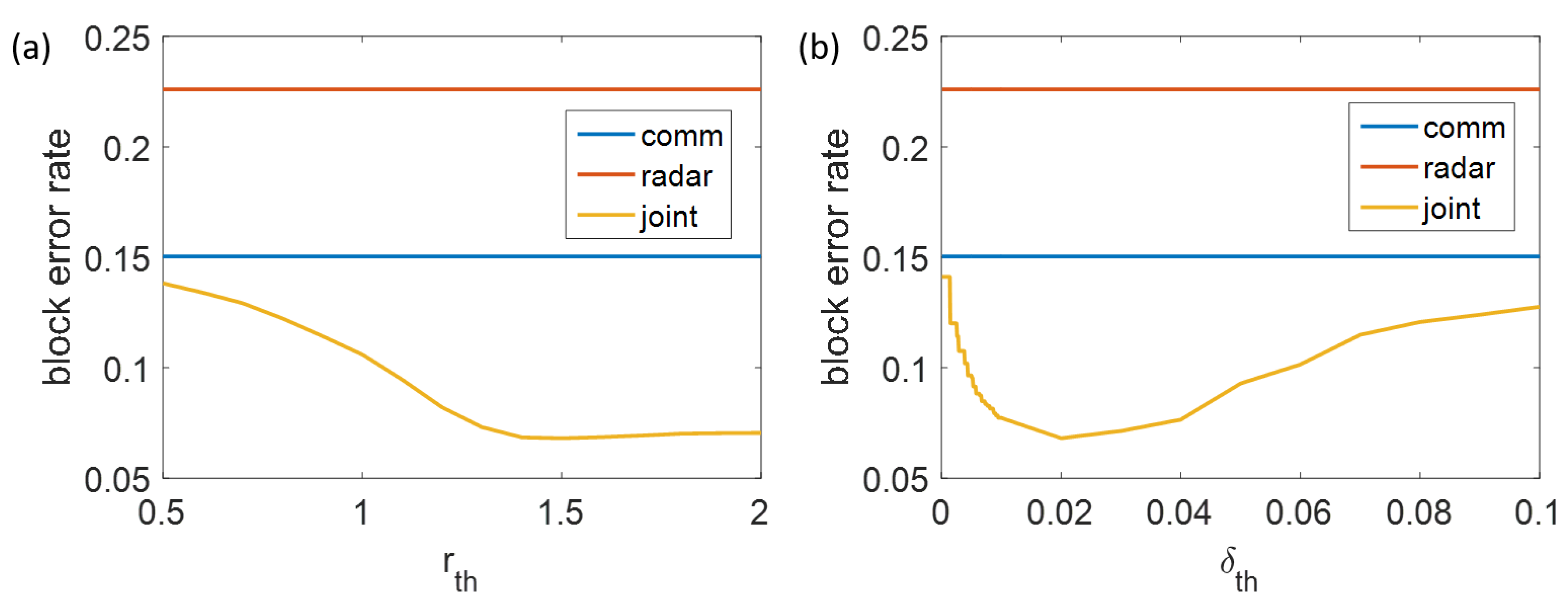
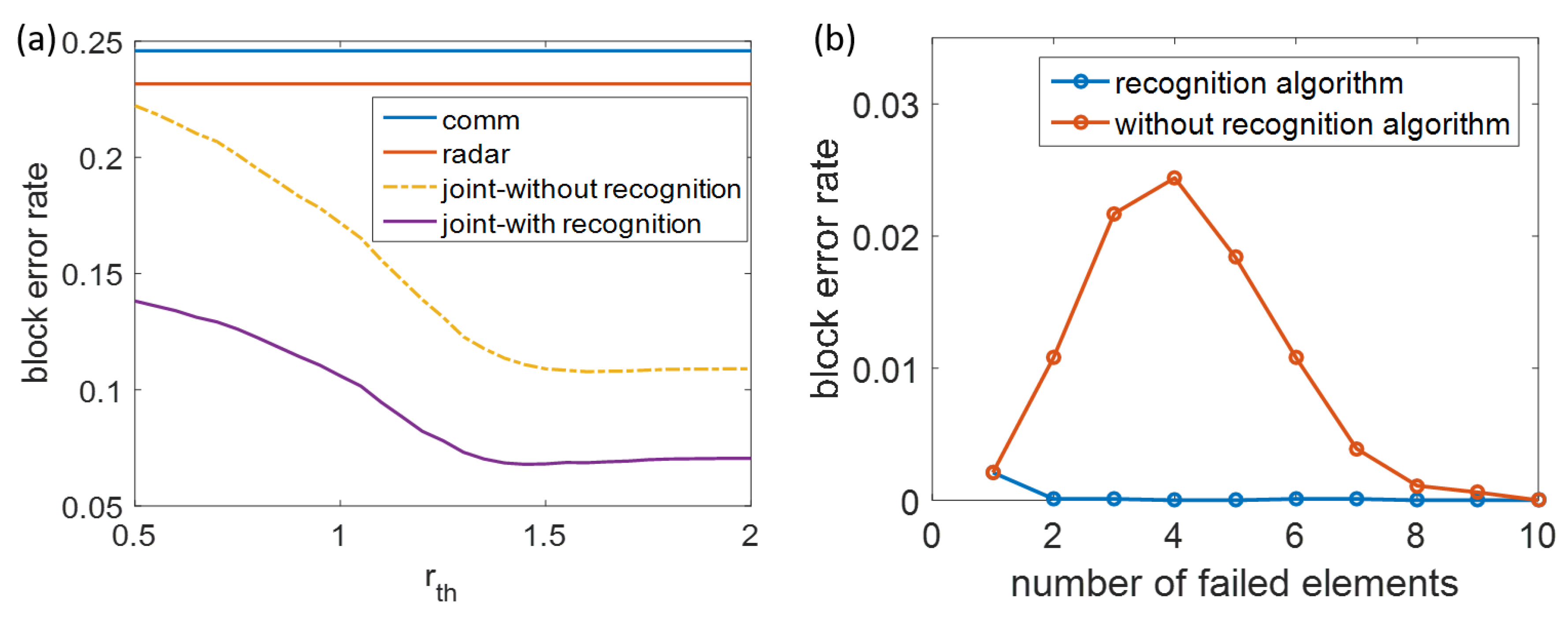
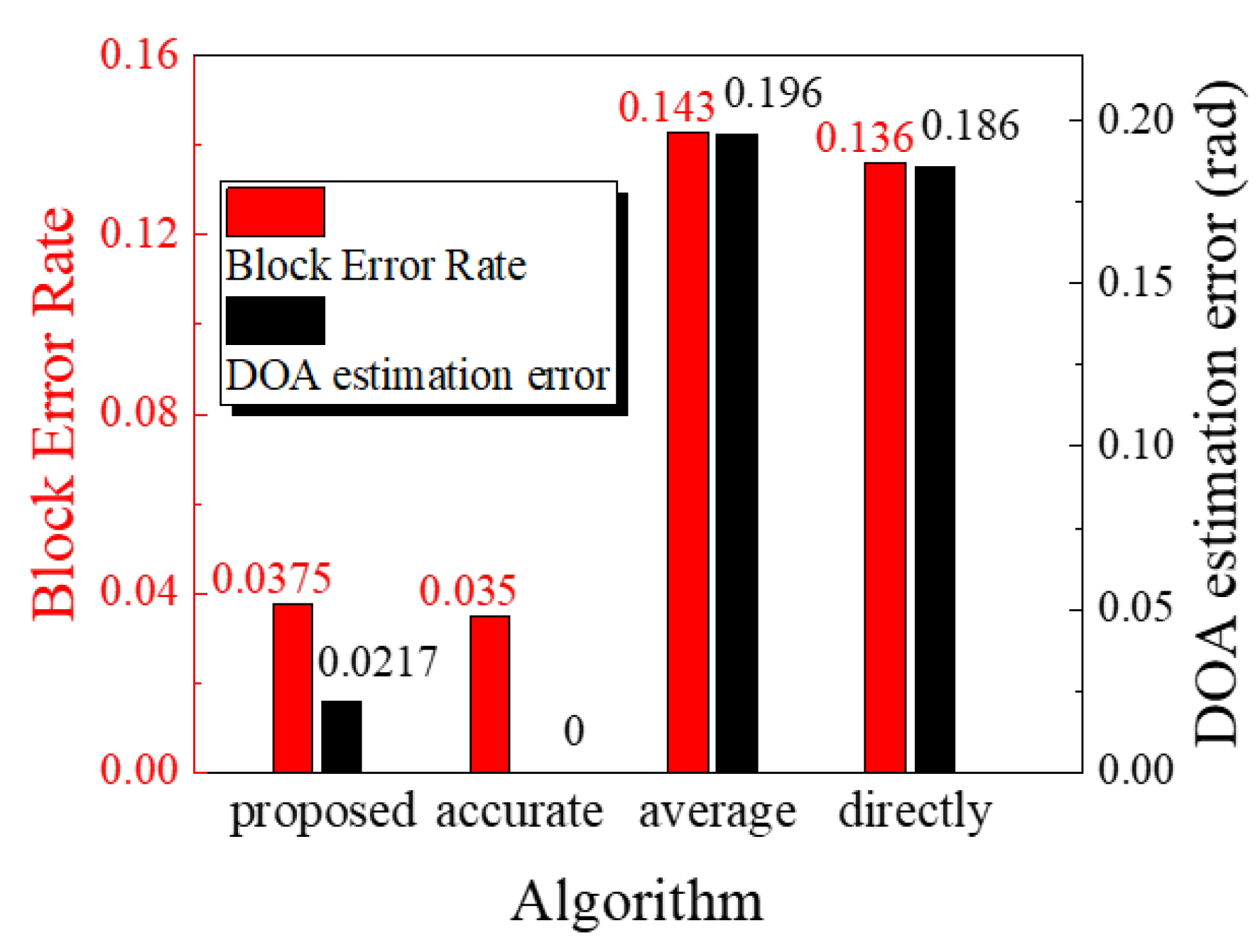
3.1. Accuracy of the Diagnosis
3.2. Algorithm Complexity Analysis
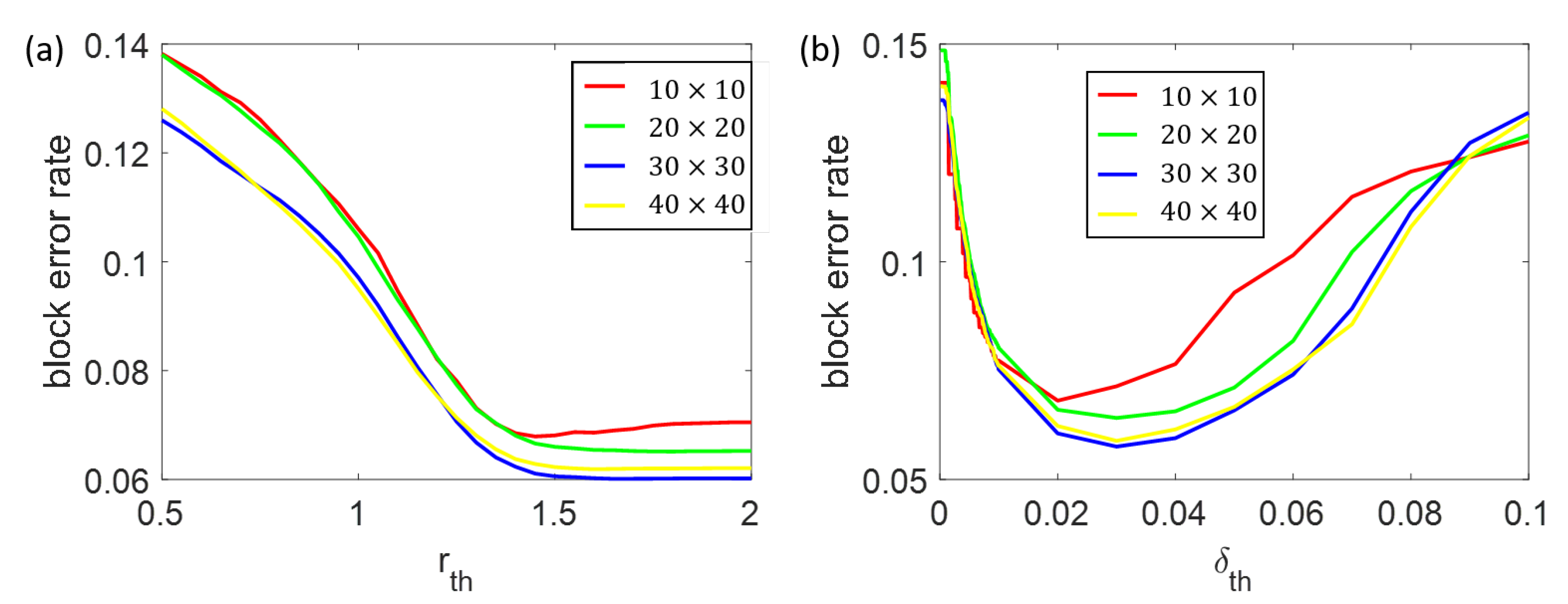
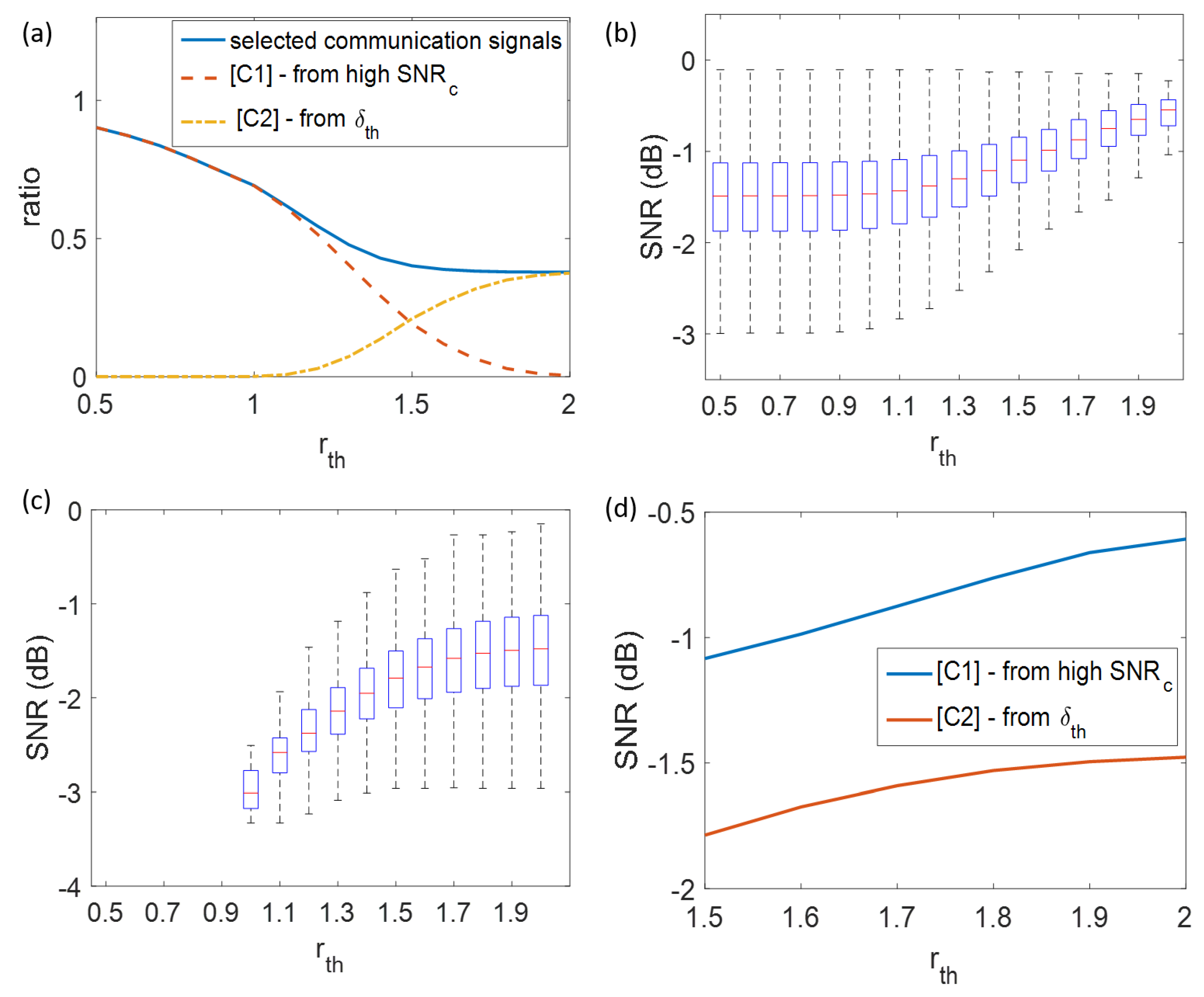
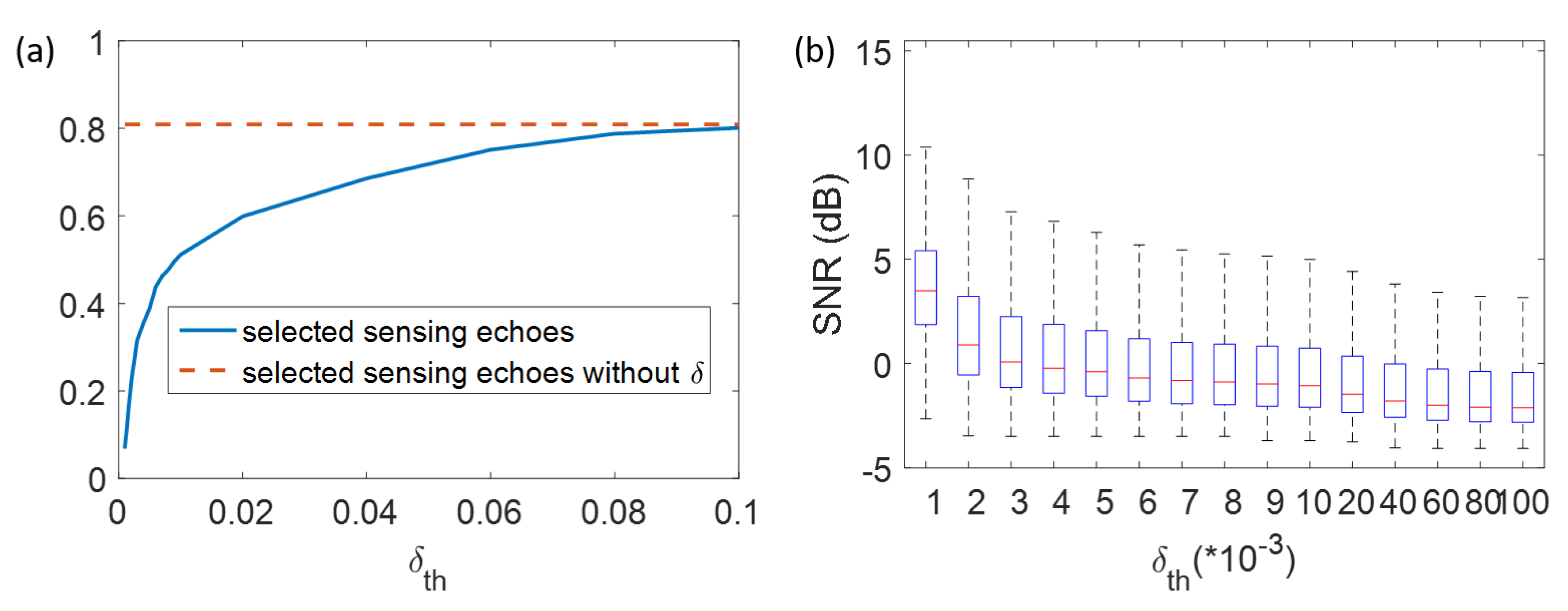
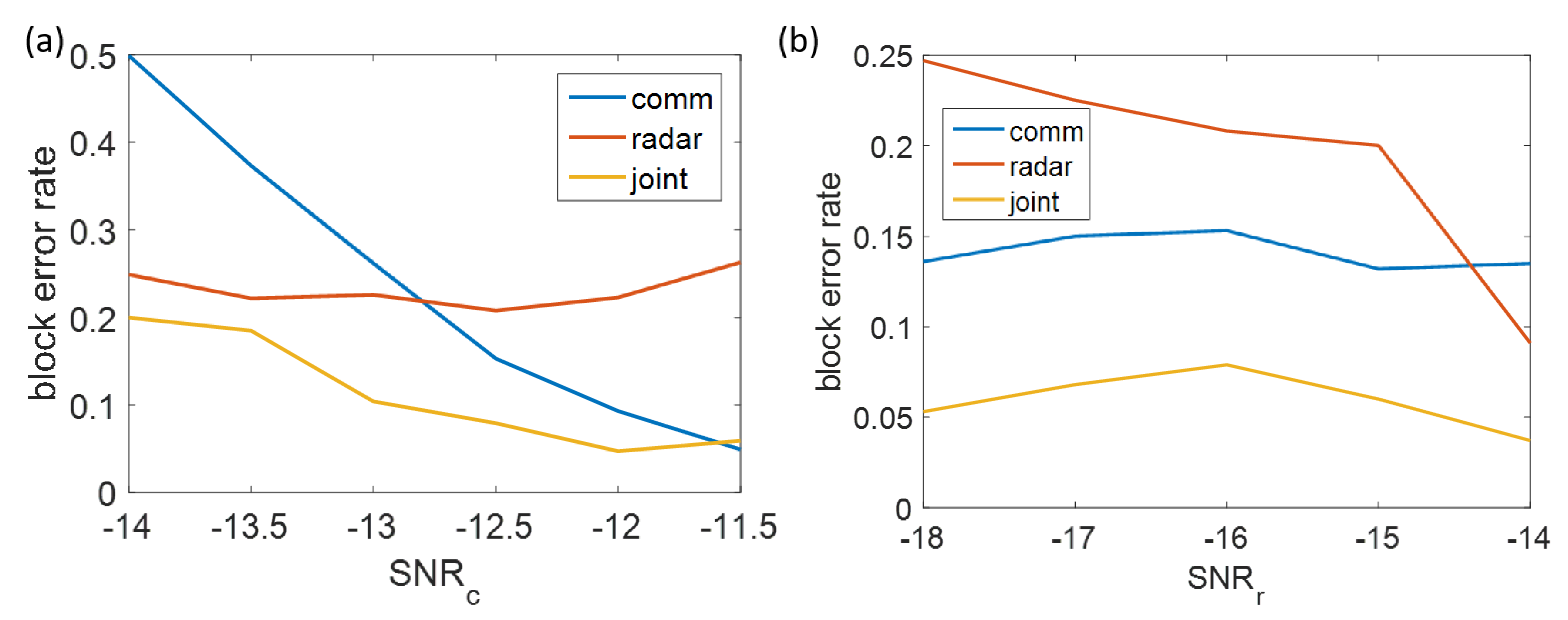
3.3. Robustness of Environmental Parameters
3.4. Discussion of Performance
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| WSN | wireless sensors networks |
| UAV | unmanned aerial vehicle |
| SVM | support vector machine |
| DOA | degree of arrival |
References
- Niu, Y.; Li, Y.; Jin, D.; Su, L.; Vasilakos, A.V. A survey of millimeter wave communications (mmWave) for 5G: opportunities and challenges. Wirel. Netw. 2015, 21, 2657–2676. [Google Scholar] [CrossRef]
- Patole, S.M.; Torlak, M.; Wang, D.; Ali, M. Automotive radars: A review of signal processing techniques. IEEE Signal Process. Mag. 2017, 34, 22–35. [Google Scholar] [CrossRef]
- Hao, G.; Matters-Kammerer, M.; Milosevic, D.; Baltus, P.G.M. System Analysis of mm-Wave Wireless Sensor Networks; Springer International Publishing: Cham, Switzerland, 2018; pp. 13–19. [Google Scholar]
- Qi, N.; Dai, K.; Yi, F.; Wang, X.; You, Z.; Zhao, J. An Adaptive Energy Management Strategy to Extend Battery Lifetime of Solar Powered Wireless Sensor Nodes. IEEE Access 2019, 7, 88289–88300. [Google Scholar] [CrossRef]
- Li, Y.; Jin, D.; Su, L.; Zeng, L.; Rashvand, H.F. Performance evaluation of routing schemes for energy-constrained delay/fault-tolerant mobile sensor network. IET wirel. sens. syst. 2012, 2, 262–271. [Google Scholar] [CrossRef]
- Zhang, W.; Dong, Y.; Tan, Y.; Zhang, M.; Qian, X.; Wang, X. Electric power self-supply module for WSN sensor node based on MEMS vibration energy harvester. Micromachines 2018, 9, 161. [Google Scholar] [CrossRef] [PubMed]
- Sheng, G.; Min, M.; Xiao, L.; Liu, S. Reinforcement Learning-Based Control for Unmanned Aerial Vehicles. J. Commun. Inf. Netw. 2018, 3, 39–48. [Google Scholar] [CrossRef]
- Xiao, Z.; Xia, P.; Xia, X. Enabling UAV cellular with millimeter-wave communication: potentials and approaches. IEEE Commun. Mag. 2016, 54, 66–73. [Google Scholar] [CrossRef]
- Xu, N.; Christodoulou, C.; Barbin, S.; Martinez-Ramon, M. Detecting failure of antenna array elements using machine learning optimization. In Proceedings of the IEEE Antennas and Propagation Society International Symposium Conference, Honolulu, HI, USA, 9–15 June 2007; pp. 5753–5756. [Google Scholar]
- Suthaharan, S. Support vector machine. In Machine Learning Models and Algorithms for Big Data Classification; Springer: Boston, MA, USA, 2016; pp. 207–235. [Google Scholar]
- Yeo, B.K.; Lu, Y. Expeditious diagnosis of linear array failure using support vector machine with low-degree polynomial kernel. IET Microw. Antennas Propag. 2012, 6, 1473–1480. [Google Scholar]
- Zhu, C.; Wang, W.Q.; Chen, H.; So, H.C. Impaired sensor diagnosis, beamforming, and doa estimation with difference co-array processing. IEEE Sens. J. 2015, 15, 3773–3780. [Google Scholar] [CrossRef]
- Nowak, M.; Wicks, M.; Zhang, Z.; Wu, Z. Co-Designed Radar-Communication Using Linear Frequency Modulation Waveform. IEEE Aerosp. Electron. Syst. Mag. 2016, 31, 28–35. [Google Scholar] [CrossRef]
- Hassanien, A.; Amin, M.G.; Zhang, Y.D.; Ahmad, F. Dual-Function Radar-Communications: Information Embedding Using Sidelobe Control and Waveform Diversity. IEEE Trans. Signal Process. 2016, 64, 2168–2181. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Q.; Huang, L.; Dai, K.; Song, J. Optimal Design of Cascade LDPC-CPM System Based on Bionic Swarm Optimization Algorithm. IEEE Trans. Broadcast. 2018, 64, 762–770. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, Y.; Dai, K.; Huang, L.; Pan, C.; Song, J. An Adaptive Diagnose Scheme for Integrated Radar-Communication Antenna Array with Huge Noise. IEEE Access 2018, 6, 25785–25796. [Google Scholar] [CrossRef]
- Li, Q.; Dai, K.; Zhang, Y.; Zhang, H. Integrated Waveform for a Joint Radar-Communication System with High-Speed Transmission. IEEE Wirel. Commun. Lett. 2019. [Google Scholar] [CrossRef]
- Zhang, P.; Wang, X.; Chen, J.; You, W.; Zhang, W. Spectral and Temporal Feature Learning with Two-Stream Neural Networks for Mental Workload Assessment. IEEE Trans. Neural Syst. Rehabil. Eng. 2019, 27, 1149–1159. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Wang, X.; Zhang, W.; Chen, J. Learning Spatial–Spectral–Temporal EEG Features With Recurrent 3D Convolutional Neural Networks for Cross-Task Mental Workload Assessment. IEEE Trans. Neural Syst. Rehabil. Eng. 2018, 27, 31–42. [Google Scholar] [CrossRef] [PubMed]
- Belouchrani, A.; Amin, M.G. Time-Frequency MUSIC. IEEE Signal Process. Lett. 1999, 6, 109–110. [Google Scholar] [CrossRef]
- Kundu, D. Modified MUSIC Algorithm for Estimating DOA of Signals. Signal Proces. 1996, 48, 85–90. [Google Scholar] [CrossRef]
- Burges, C.J. A tutorial on support vector machines for pattern recognition. Data Min. Knowl. Discov. 1998, 2, 121–167. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Dai, K.; Wang, X.; Zhang, Y.; Zhang, H.; Jiang, D. Low-Complexity Failed Element Diagnosis for Radar-Communication mmWave Antenna Array with Low SNR. Electronics 2019, 8, 904. https://doi.org/10.3390/electronics8080904
Li Q, Dai K, Wang X, Zhang Y, Zhang H, Jiang D. Low-Complexity Failed Element Diagnosis for Radar-Communication mmWave Antenna Array with Low SNR. Electronics. 2019; 8(8):904. https://doi.org/10.3390/electronics8080904
Chicago/Turabian StyleLi, Qingyu, Keren Dai, Xiaofeng Wang, Yu Zhang, He Zhang, and Defu Jiang. 2019. "Low-Complexity Failed Element Diagnosis for Radar-Communication mmWave Antenna Array with Low SNR" Electronics 8, no. 8: 904. https://doi.org/10.3390/electronics8080904
APA StyleLi, Q., Dai, K., Wang, X., Zhang, Y., Zhang, H., & Jiang, D. (2019). Low-Complexity Failed Element Diagnosis for Radar-Communication mmWave Antenna Array with Low SNR. Electronics, 8(8), 904. https://doi.org/10.3390/electronics8080904





