On Performance Analysis of Underlay Cognitive Radio-Aware Hybrid OMA/NOMA Networks with Imperfect CSI
Abstract
1. Introduction
- A CR network is recommended to permit a secondary network containing the secondary users (SU) that intend to access the 5G spectrum in two situations including the absence and presence of the primary user (PU). In particular, SU is able to choose the hybrid OMA/NOMA scheme to communicate with two destinations and this scheme can improve the spectrum utilization greatly compared with the normal NOMA or normal OMA scheme.
- Impacts of imperfect CSI on system evaluation have not been well studied in [25,26,27,28,29,30]. We first propose a policy to achieve improved performance of the far user by assigning the close user as relay. Such advantage of a hybrid scheme of OMA/NOMA can be obtained as performing simulations to compare two models. Moreover, we investigate the imperfect CSI to achieve realistic evaluations on the CR network in practical applications. To the authors’ best knowledge, this is the first work that considers hybrid OMA/NOMA selection and imperfect CSI in terms of CR downlink transmission.
- We derive the closed-form expressions of the outage probability. Under the high complexity in computation, it is necessary to explore asymptotic outage performance of each user to provide an insight for such CR network. In addition, we develop an approach to achieve optimal outage performance evaluations in NOMA mode as considering varying values of power allocation factors assigned to two users.
- Due to the difficulty of exhibiting outage performance for two users through these closed-form expressions, asymptotic expressions are introduced to verify this outage event in the simple manner. It is expected that approximate outage performance matches with corresponding analytical results at a certain considered range.
- Simulation results show the performance comparison in various scenarios of the proposed scheme in terms of the outage probability and throughput, which show significant differences as a comparison of several values of levels of CSI imperfections.
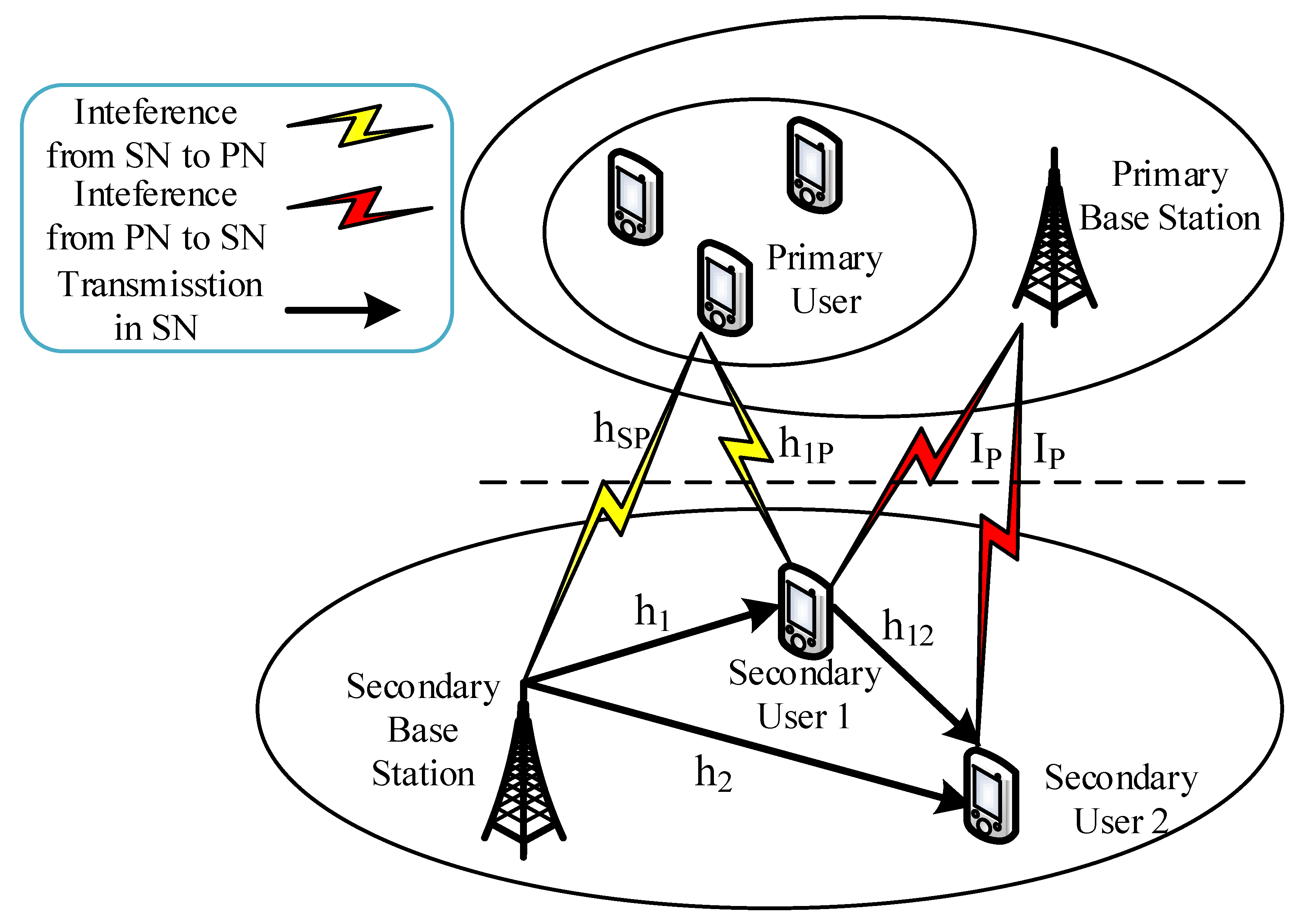
2. System Model
2.1. Calculation of SNR
2.2. OMA/NOMA Selection Mode
2.3. OMA Mode
3. Outage Performance Analysis
3.1. Outage Probability of the
3.2. Outage Probability of the
4. Asymptotic and Throughput Analysis
4.1. Asymptotic Analysis
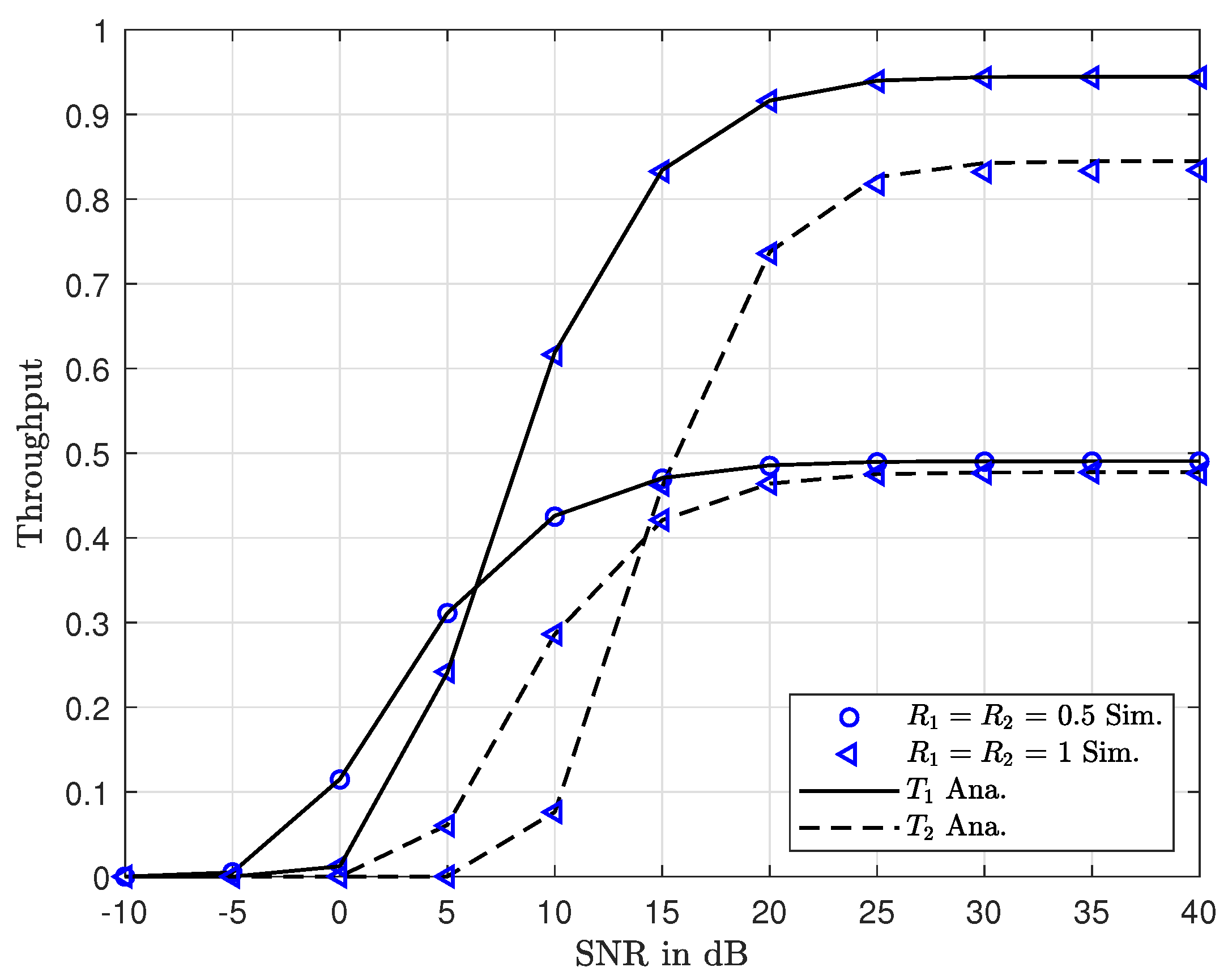
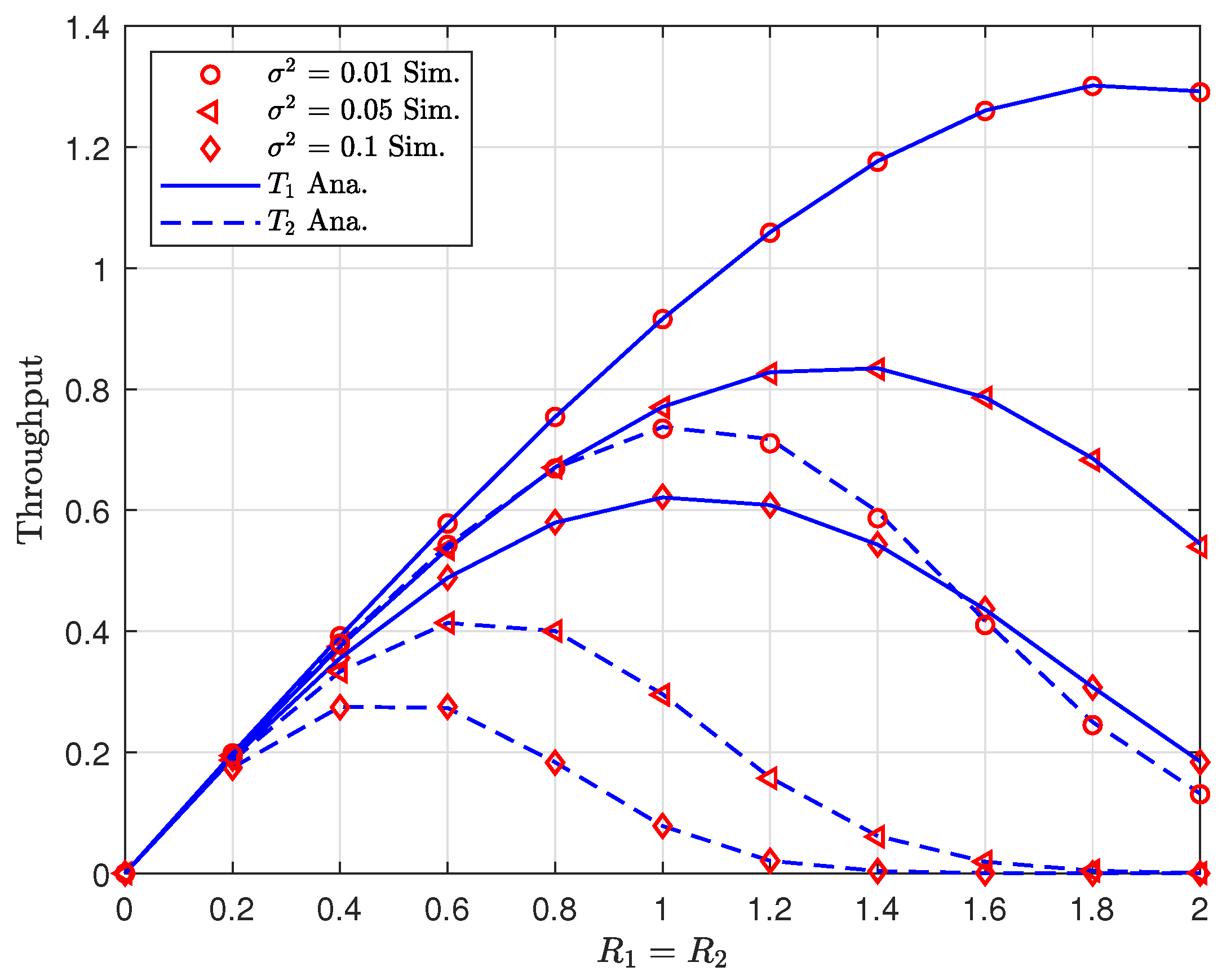
4.2. Throughput
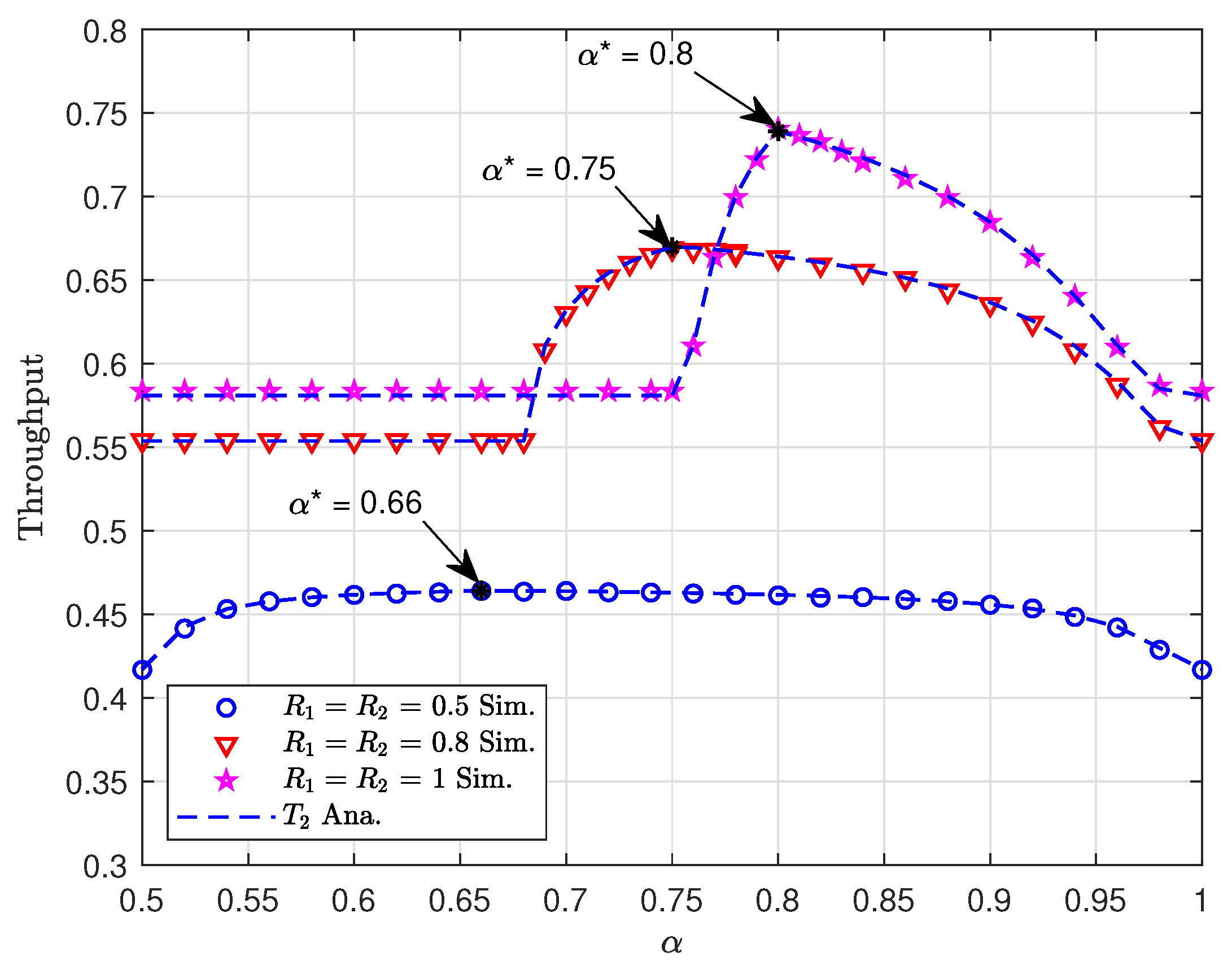
4.3. Optimal Selection of in NOMA Mode
5. Extended Scheme of Multiple Antenna at the BS
5.1. Outage Probability of U2
5.2. Outage Probability of U1
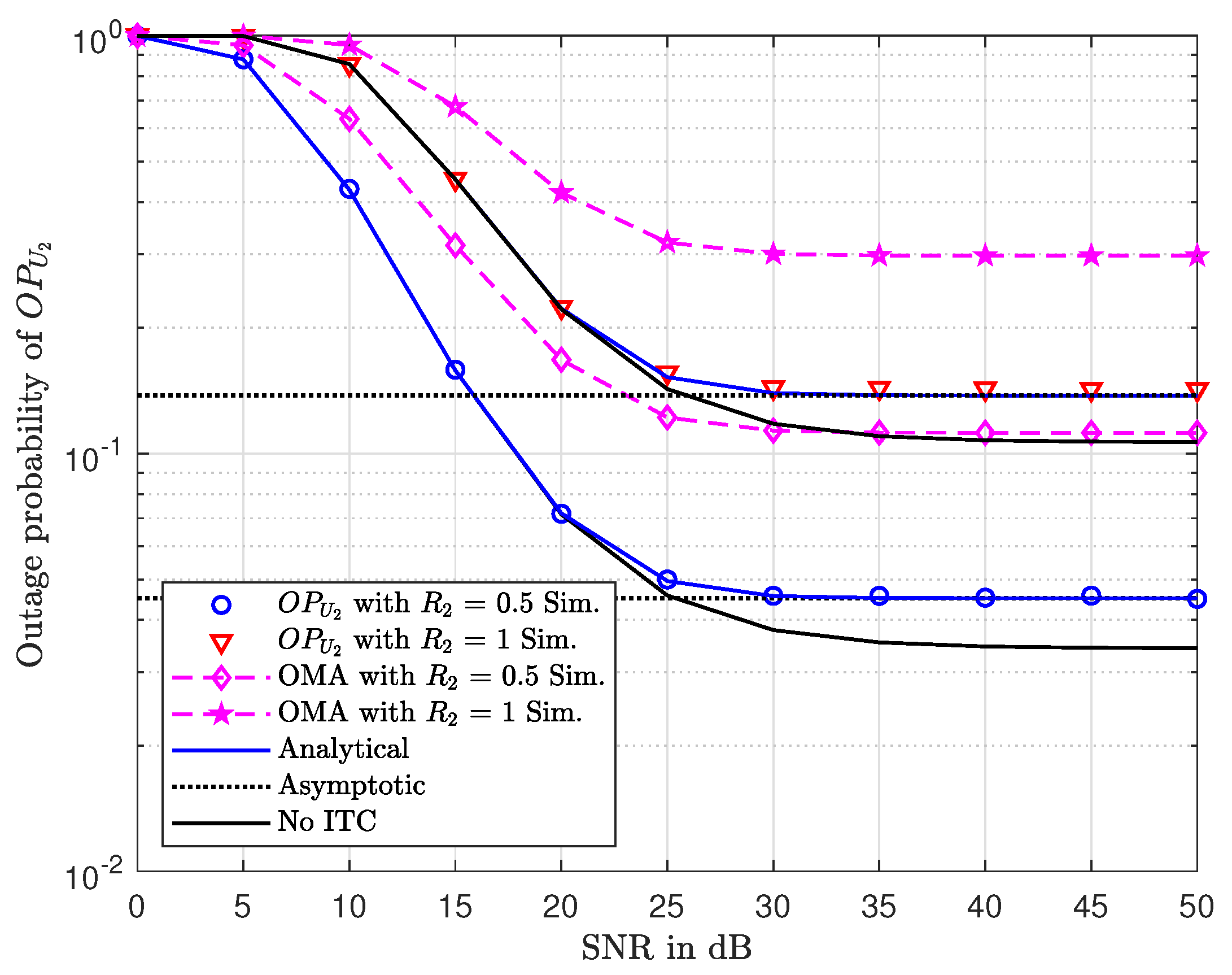
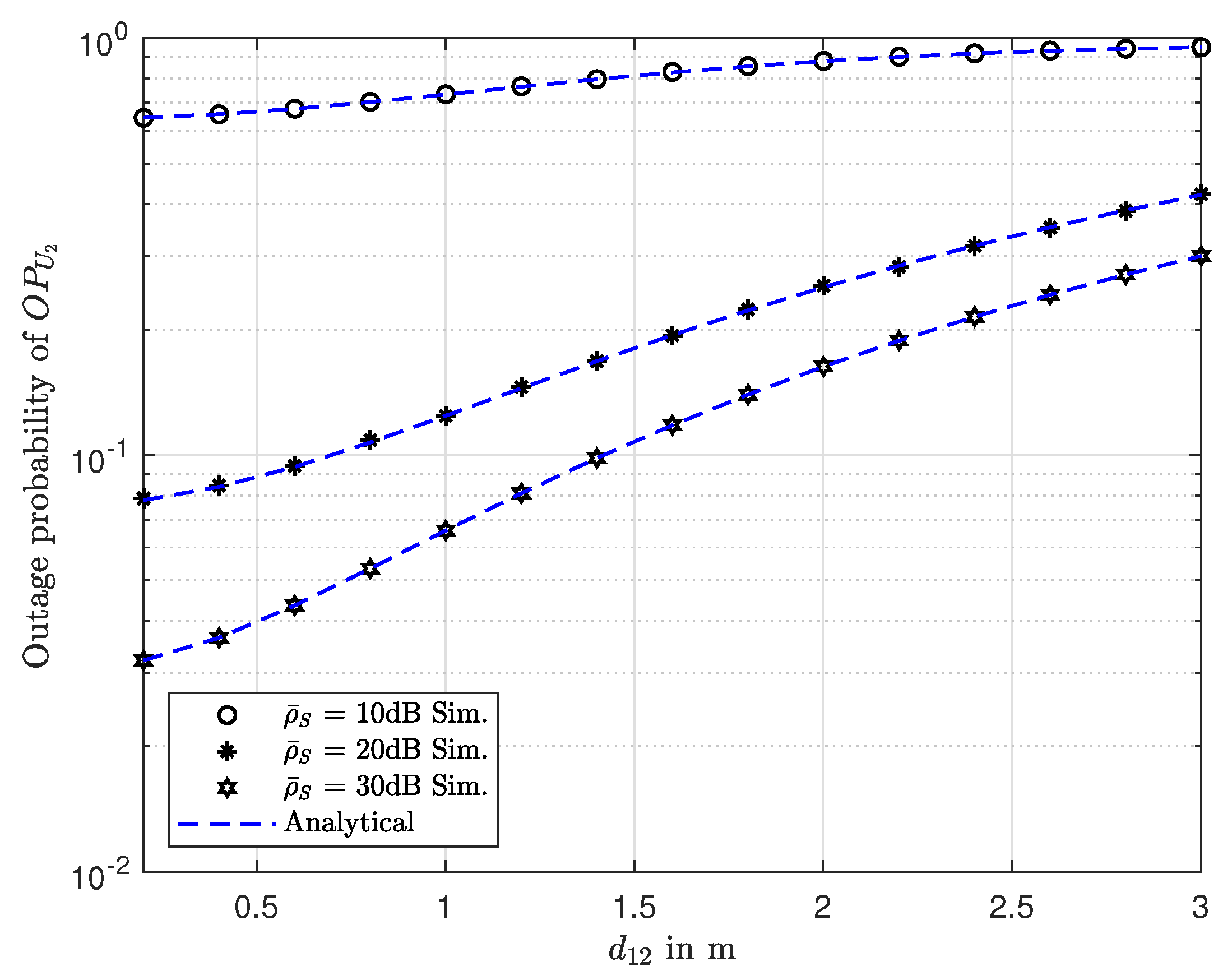
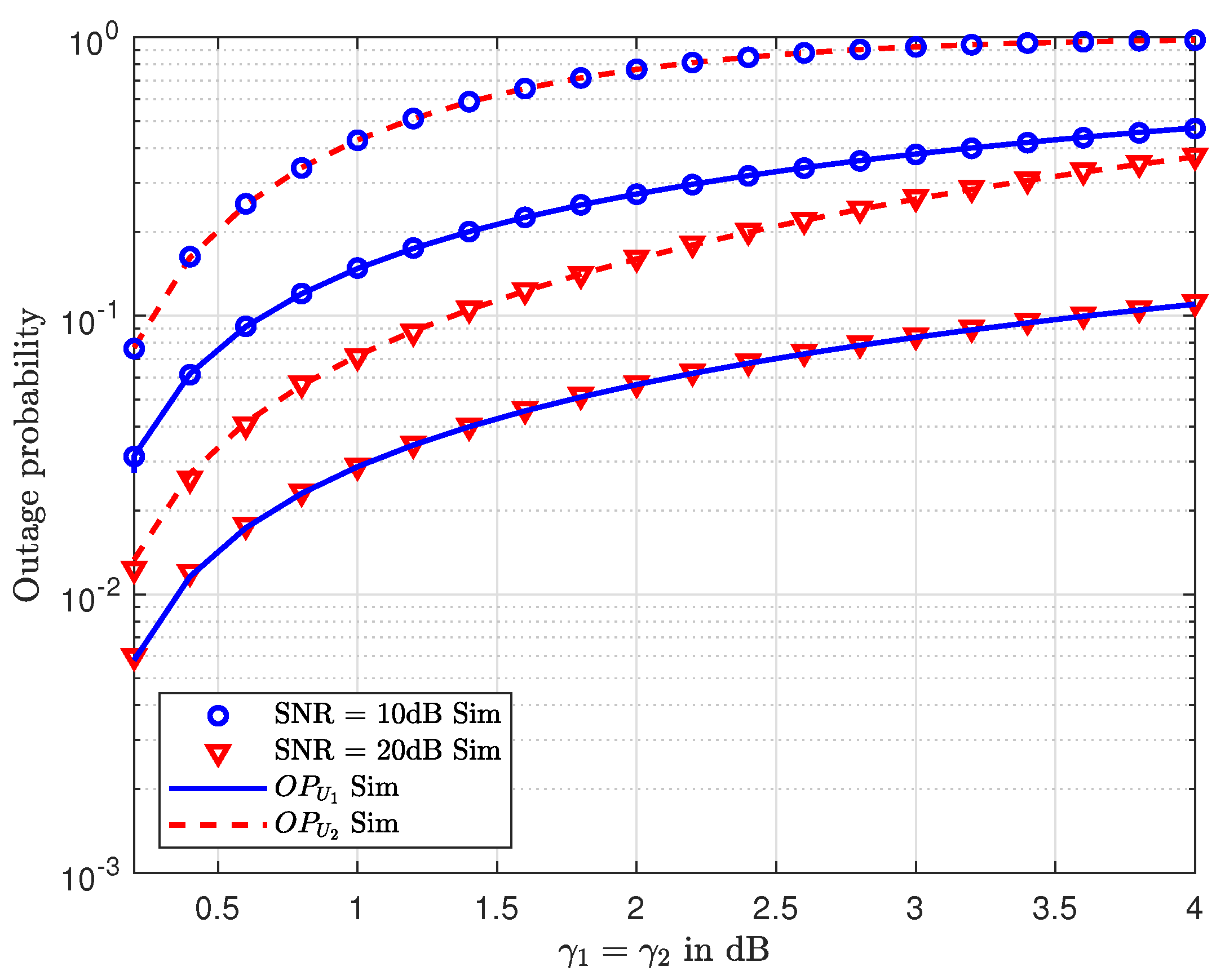
6. Numerical and Simulation Results
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
References
- Islam, S.R.; Avazov, N.; Dobre, O.A.; Kwak, K.S. Power-domain non-orthogonal multiple access (NOMA) in 5G systems: Potentials and challenges. IEEE Commun. Surv. Tutor. 2015, 2, 721–742. [Google Scholar] [CrossRef]
- Ding, Z.; Lei, X.; Karagiannidis, G.K.; Schober, R.; Yuan, J.; Bhargava, V.K. A survey on non-orthogonal multiple access for 5G networks: Research challenges and future trends. IEEE J. Sel. Areas Commun. 2017, 10, 2181–2195. [Google Scholar] [CrossRef]
- Nguyen, T.L.; Do, D.T. Exploiting Impacts of Intercell Interference on SWIPT-assisted Non-orthogonal Multiple Access. Wirel. Commun. Mob. Comput. 2018, 2018, 2525492. [Google Scholar] [CrossRef]
- Nguyen, X.X.; Do, D.T. Maximum Harvested Energy Policy in Full-Duplex Relaying Networks with SWIPT. Int. J. Commun. Syst. 2017, 30, e3359. [Google Scholar] [CrossRef]
- Do, D.T.; Nguyen, H.S.; Vozňák, M.; Nguyen, T.S. Wireless powered relaying networks under imperfect channel state information: System performance and optimal policy for instantaneous rate. Radioengineering 2017, 26, 869–877. [Google Scholar] [CrossRef]
- Nguyen, X.X.; Do, D.T. Optimal Power Allocation and Throughput Performance of Full-Duplex DF Relaying Networks with Wireless Power Transfer-Aware Channel. EURASIP J. Wirel. Commun. Netw. 2017, 2017, 152. [Google Scholar] [CrossRef]
- Nguyen, H.S.; Do, D.T.; Nguyen, T.S.; Voznak, M. Exploiting hybrid time switching-based and power splitting-based relaying protocol in wireless powered communication networks with outdated channel state information. Automatika 2017, 58, 111–118. [Google Scholar] [CrossRef]
- Nguyen, T.N.; Tran, M.; Tran, P.T.; Tin, P.T.; Nguyen, T.L.; Ha, D.H.; Voznak, M. On the Performance of Power Splitting Energy Harvested Wireless Full-Duplex Relaying Network with Imperfect CSI over Dissimilar Channels. Secur. Commun. Netw. 2018, 2018, 6036087. [Google Scholar] [CrossRef]
- Nguyen, T.; Tran Tin, P.; Ha, D.; Voznak, M.; Tran, P.; Tran, M.; Nguyen, T.L. Hybrid TSR–PSR Alternate Energy Harvesting Relay Network over Rician Fading Channels: Outage Probability and SER Analysis. Sensors 2018, 18, 3839. [Google Scholar] [CrossRef]
- Nguyen, T.N.; Tran, P.T.; Vozňák, M. Power-splitting-based energy harvesting protocol for wireless powered communication networks with a bidirectional relay. Int. J. Commun. Syst. 2018, 31, e3721. [Google Scholar] [CrossRef]
- Do, D.T.; Le, C.B. Application of NOMA in Wireless System with Wireless Power Transfer Scheme: Outage and Ergodic Capacity Performance Analysis. Sensors 2018, 18, 3501. [Google Scholar] [CrossRef] [PubMed]
- Tsinos, C.G.; Berberidis, K. Decentralized Adaptive Eigenvalue-Based Spectrum Sensing for Multiantenna Cognitive Radio Systems. IEEE Trans. Wirel. Commun. 2015, 14, 1703–1715. [Google Scholar] [CrossRef]
- Gao, F.; Zhang, R.; Liang, Y.C.; Wang, X. Design of Learning-Based MIMO Cognitive Radio Systems. IEEE Trans. Veh. Technol. 2010, 59, 1707–1720. [Google Scholar]
- Zhang, H.; Jiang, C.; Mao, X.; Chen, H.H. Interference-limited resource optimization in cognitive femtocells with fairness and imperfect spectrum sensing. IEEE Trans. Veh. Technol. 2016, 65, 1761–1771. [Google Scholar] [CrossRef]
- Zhang, H.; Nie, Y.; Cheng, J.; Leung, V.C.; Nallanathan, A. Sensing time optimization and power control for energy efficient cognitive small cell with imperfect hybrid spectrum sensing. IEEE Trans. Wirel. Commun. 2017, 16, 730–743. [Google Scholar] [CrossRef]
- Nam, P.M.; Do, D.T.; Tung, N.T.; Tin, P.T. Energy harvesting assisted cognitive radio: Random location-based transceivers scheme and performance analysis. Telecommun. Syst. 2018, 67, 123–132. [Google Scholar] [CrossRef]
- Kumar, B.; Prakriya, S. Performance of adaptive link selection with buffer-aided relays in underlay cognitive networks. IEEE Trans. Veh. Technol. 2018, 67, 1492–1509. [Google Scholar] [CrossRef]
- Tsinos, C.G.; Berberidis, K. Blind Opportunistic Interference Alignment in MIMO Cognitive Radio Systems. IEEE J. Emerg. Sel. Top. Circuits Syst. 2013, 3, 626–639. [Google Scholar] [CrossRef]
- Zhang, R. On peak versus average interference power constraints for protecting primary users in cognitive radio networks. IEEE Trans. Wirel. Commun. 2009, 8, 2112–2120. [Google Scholar] [CrossRef]
- Liu, Y.; Ding, Z.; Elkashlan, M.; Yuan, J. Non-orthogonal multiple access in large-scale underlay cognitive radio networks. IEEE Trans. Veh. Technol. 2016, 65, 10152–10157. [Google Scholar] [CrossRef]
- Lv, L.; Chen, J.; Ni, Q.; Ding, Z. Design of cooperative nonorthogonal multicast cogntive radio multiple access for 5G systems: User scheduling and performance analysis. IEEE Trans. Commun. 2017, 65, 2641–2656. [Google Scholar] [CrossRef]
- Lv, L.; Ni, Q.; Ding, Z.; Chen, J. Application of non-orthogonal multiple access in cooperative spectrum-sharing networks over Nakagami-m fading channels. IEEE Trans. Veh. Technol. 2017, 66, 5506–5511. [Google Scholar] [CrossRef]
- Do, D.T.; Vaezi, M.; Nguyen, T.L. Wireless Powered Cooperative Relaying Using NOMA with Imperfect CSI. In Proceedings of the 2018 IEEE Globecom Workshops (GC Wkshps), Abu Dhabi, UAE, 9–13 December 2018; pp. 1–6. [Google Scholar]
- Cui, J.; Ding, Z.; Fan, P. Outage Probability Constrained MIMO-NOMA Designs Under Imperfect CSI. IEEE Trans. Wirel. Commun. 2018, 17, 8239–8255. [Google Scholar] [CrossRef]
- Fang, F.; Zhang, H.; Cheng, J.; Roy, S.; Leung, V.C. Joint User Scheduling and Power Allocation Optimization for Energy-Efficient NOMA Systems With Imperfect CSI. IEEE J. Sel. Areas Commun. 2017, 35, 2874–2885. [Google Scholar] [CrossRef]
- Arzykulov, S.; Tsiftsis, T.A.; Nauryzbayev, G.; Abdallah, M. Outage Performance of Cooperative Underlay CR-NOMA With Imperfect CSI. IEEE Commun. Lett. 2019, 23, 176–179. [Google Scholar] [CrossRef]
- Zamani, M.R.; Eslami, M.; Khorramizadeh, M.; Ding, Z. Energy-Efficient Power Allocation for NOMA with Imperfect CSI. IEEE Trans. Veh. Technol. 2019, 68, 1009–1013. [Google Scholar] [CrossRef]
- Song, X.; Dong, L.; Wang, J.; Qin, L.; Han, X. Energy Efficient Power Allocation for Downlink NOMA Heterogeneous Networks with Imperfect CSI. IEEE Access 2019, 7, 39329–39340. [Google Scholar] [CrossRef]
- Janghel, K.; Prakriya, S. Performance of Adaptive OMA/Cooperative-NOMA Scheme with User Selection. IEEE Commun. Lett. 2018, 22, 2092–2095. [Google Scholar] [CrossRef]
- Nauryzbayev, G.; Arzykulov, S.; Tsiftsis, T.A.; Abdallah, M. Performance of Cooperative Underlay CR-NOMA Networks over Nakagami-m Channels. In Proceedings of the 2018 IEEE International Conference on Communications Workshops (ICC Workshops), Kansas City, MO, USA, 20–24 May 2018; pp. 1–6. [Google Scholar]
- Xinh, N.X.; Do, D.T. An adaptive-harvest-then-transmit protocol for wireless powered communications: Multiple antennae system and performance analysis. KSII Trans. Internet Inf. Syst. 2017, 11, 1889–1910. [Google Scholar]
- Zwillinger, D. Table of Integrals, Series, and Products, 7th ed.; Academic Press: Cambridge, MA, USA, 2007. [Google Scholar]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Do, D.-T.; Le, A.-T.; Lee, B.M. On Performance Analysis of Underlay Cognitive Radio-Aware Hybrid OMA/NOMA Networks with Imperfect CSI. Electronics 2019, 8, 819. https://doi.org/10.3390/electronics8070819
Do D-T, Le A-T, Lee BM. On Performance Analysis of Underlay Cognitive Radio-Aware Hybrid OMA/NOMA Networks with Imperfect CSI. Electronics. 2019; 8(7):819. https://doi.org/10.3390/electronics8070819
Chicago/Turabian StyleDo, Dinh-Thuan, Anh-Tu Le, and Byung Moo Lee. 2019. "On Performance Analysis of Underlay Cognitive Radio-Aware Hybrid OMA/NOMA Networks with Imperfect CSI" Electronics 8, no. 7: 819. https://doi.org/10.3390/electronics8070819
APA StyleDo, D.-T., Le, A.-T., & Lee, B. M. (2019). On Performance Analysis of Underlay Cognitive Radio-Aware Hybrid OMA/NOMA Networks with Imperfect CSI. Electronics, 8(7), 819. https://doi.org/10.3390/electronics8070819





