1. Introduction
Cross-eye jamming is an electronic countermeasure (ECM) technique which deceives the monopulse radar with a significant angular error. Inspired by the radar glint phenomenon, cross-eye jamming was proposed in the 1950s and also called artificial glint jamming [
1,
2,
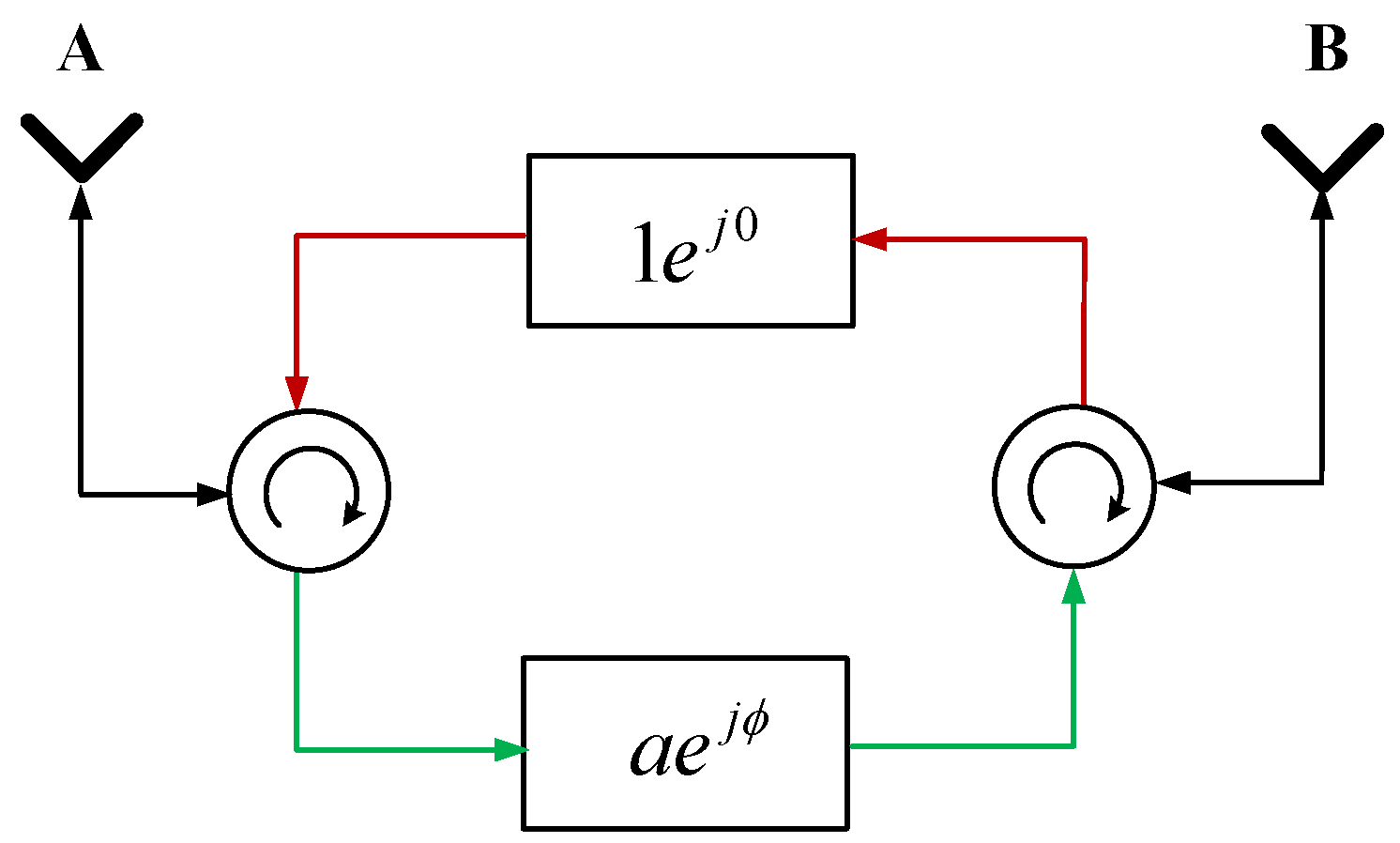
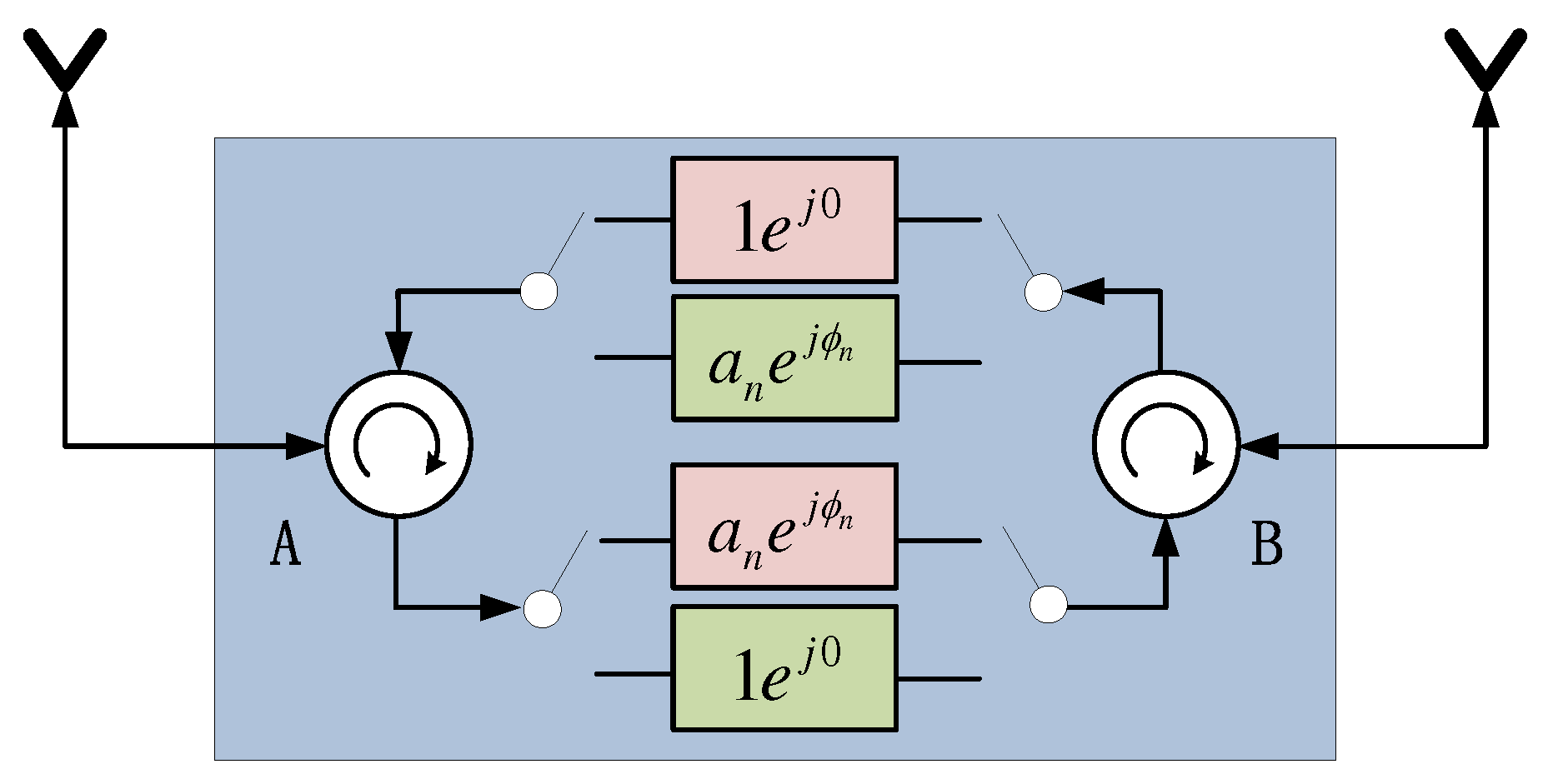
3]. As an effective jamming technique against monopulse radar, cross-eye jamming has remained of interest to researchers in the field of electronic warfare. In the past ten years, the analyses of the cross-eye jamming with retrodirective implementation, as shown in
Figure 1, were presented in [
4,
5,
6]. It is widely believed that the retrodirective implementation is the right way to build a practical cross-eye jamming system. The requirements of the tolerance and the jammer-to-signal ratio (JSR) for a retrodirective cross-eye jammer were discussed in [
7,
8,
9]. The performance of a retrodirective cross-eye jamming system can induce an angular error into monopulse radar that even breaks the radar’s lock.
However, the high JSR and strict tolerance requirements limit the realization of a two-element retrodirective cross-eye jamming (TRCJ) system [
7,
8,
9,
10]. One feasible way to help overcome the above limitations is providing more degrees of freedom in a jammer which can control the desired field pattern better [
11]. Herein, multiple amplitude gains and phase shifts as additional degrees of freedom were used, and multiple-element cross-eye jamming (MRCJ) was proposed in [
12]. However, the analysis associated with MCJ did not take the retrodirective implementation into account and, thus, had limited practicality [
4,
5]. Considering the retrodirective implementation, multiple-element retrodirective cross-eye jamming (MRCJ) was researched [
13,
14,
15,
16,
17,
18,
19]. Previous studies in [
13,
14] indicated that MRCJ employing a linear retrodirective array, notation L-MRCJ for convenience, has a superior performance due to additional degrees of freedom, and showed that L-MRCJ can reduce both the JSR requirements and the tolerance sensitivity.
Unfortunately, L-MRCJ will be ineffective when the threat radar appears in the end-fire direction of the jammer antenna array. It is because the angular separation of the jammer antenna array approaches zero. Although the wide-beamwidth antenna elements are used to construct L-MRCJ system for covering a wide angle range, there are still angular areas where the jammer is ineffective. To offer protection for the ineffective area, a cross-eye jammer mounted on a fighter is often used in combination with a towed decoy [
20]. Thus, L-MRCJ cannot always induce continuous angular error in the threat radar.
To provide effective protection in whichever direction the potential threat signal transmits, the idea of using multiple independent jammer loops to cover a
angular region was mentioned naturally by Neri in [
21], where a different single jammer loop is chosen to confront the threat from different directions. However, this “switch” approach providing continuous jamming with a single jammer loop gives up the superiority of additional degrees of freedom and still suffers from the limitations associated with a two-element cross-eye jammer.
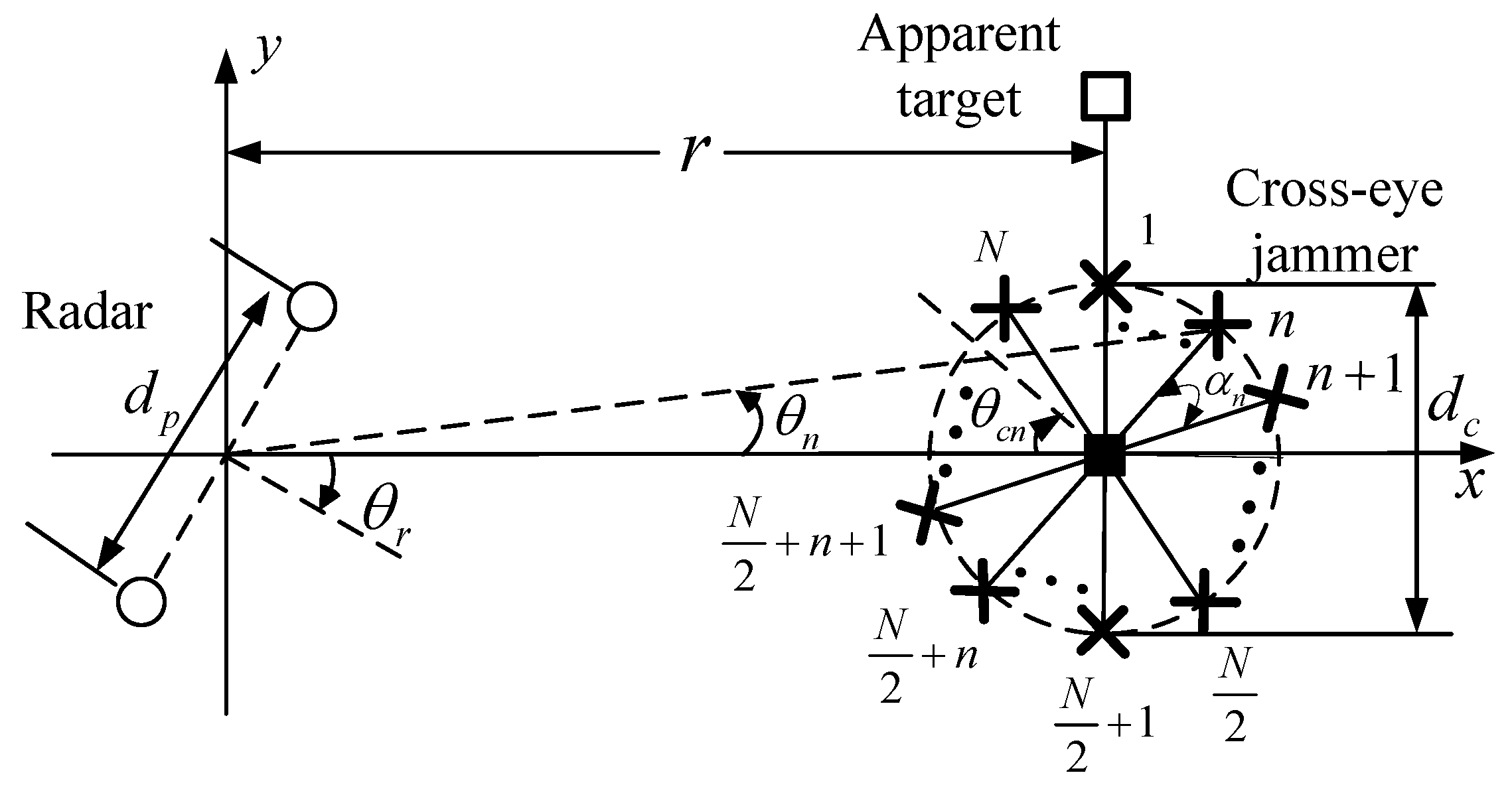
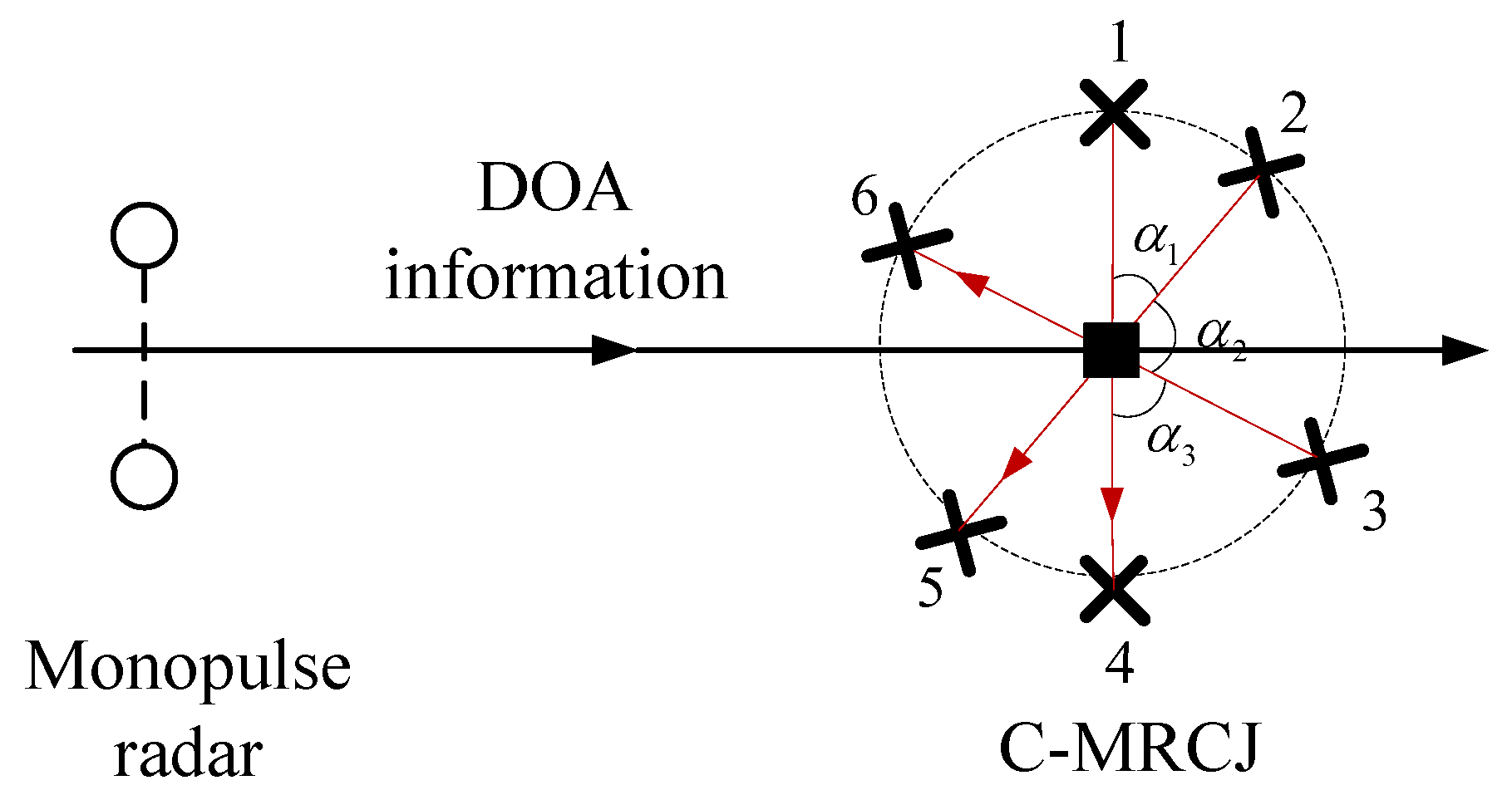
MRCJ employing a circular retrodirective array, notation C-MRCJ, will be investigated in this paper. Unlike the “switch” approach, C-MRCJ uses multiple jammer loops together against the threat radar in one direction. The C-MRCJ has the advantage over L-MRCJ by employing multiple rotational angles from its jammer configuration, which makes C-MRCJ have the potential to deal with the threat from various incident angles. However, C-MRCJ can also be ineffective since the angular error induced by C-MRCJ can still be zero in certain directions. To provide continuous cross-eye jamming, we further propose a modified C-MRCJ based on
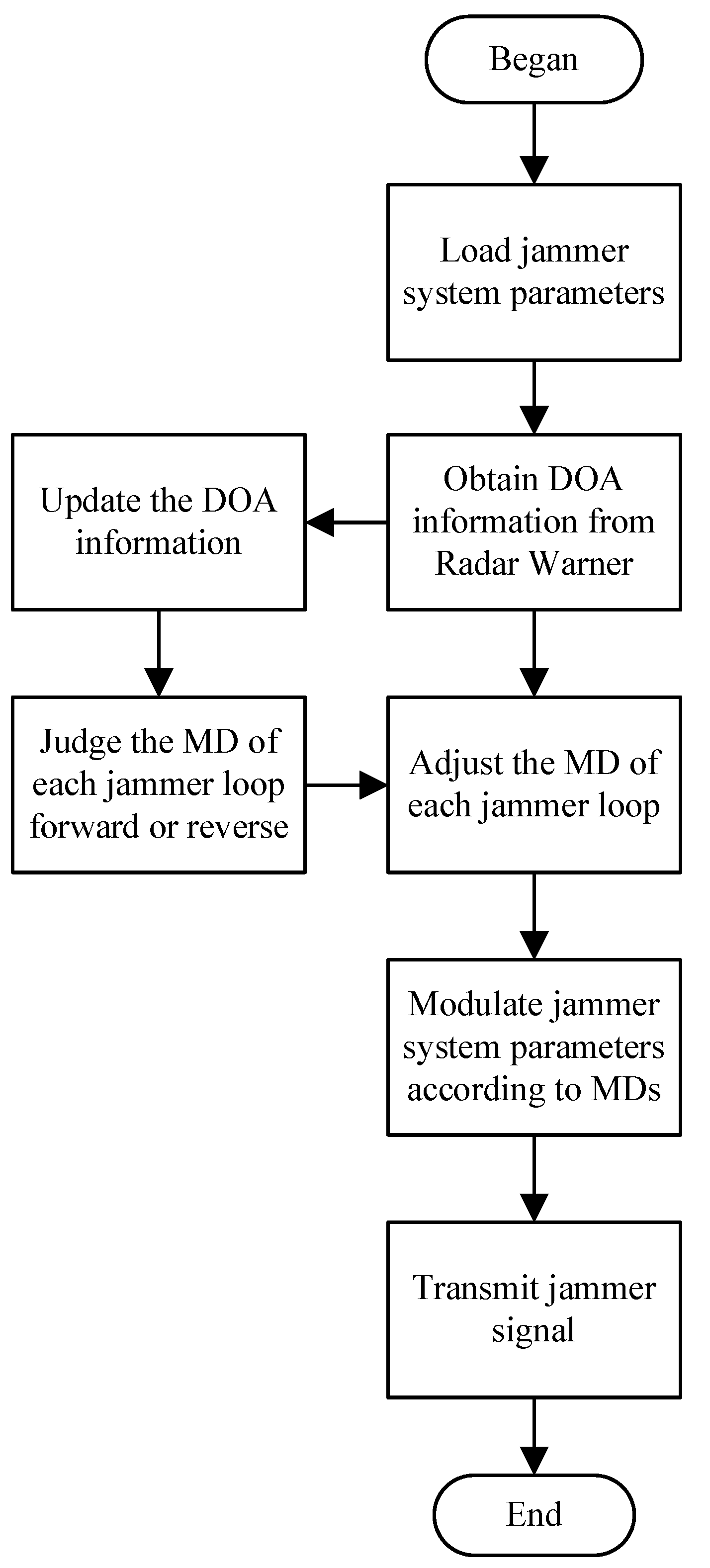
a priori information of Direction Of Arrival (DOA) of radar waves by defining the modulation direction (MD) of jammer loops. Modified C-MRCJ changes the MDs of jammer loops according to the DOA information provided by a missile approach warner (MAW) or other radar signal detectors [
22,
23,
24], in order to make multiple jammer loops superimpose their contributions to the monopulse ratio. Thus, the angular error induced by modified C-MRCJ will never be zero within the coverage of
. Synchronously, modified C-MRCJ has the potential to achieve stable jamming performance with special configuration. Continuous and stable jamming performance can produce a fixed and stable apparent target away from the platform, which is desirable for a jammer mounted on a moving and rotating platform in practical operations.
As far as we known, the literature [
25] had proposed a similar jamming configuration consisting of two jammer loops to address the problem brought by the rotating platform. Its contributions is that it gave a basis analysis of MRCJ employing a rectangular array. Actually, the rotating cross-eye jammer consisting of two jammer loops is a special and the simplest scenario of C-MRCJ, considering the fact that a rectangular array can always be simplified by a circular array. On the basis of the analysis in [
25], this paper further extends the rectangular array to the circular array and proposes C-MRCJ. The results will indicate that a rectangular array employed by the MRCJ system is not the best array configuration when considering jamming performance.
Overcoming the limitations of existing literature, this paper gives the major contributions to the area of cross-eye jamming as follows:
MRCJ with a circular antenna array is proposed which has the potential to deal with the radar threat in any likely direction.
The modulation direction of the jammer loop is defined which makes the jammer have the ability to provide continuous jamming performance.
The array configuration with uniform-spacing angular separation is proved to be the optimal configuration for modified C-MRCJ to achieve stable jamming performance.
Six antenna elements are advised for modified C-MRCJ in consideration of considerable jamming performance and moderate hardware cost.
The mathematical expression of the monopulse-indicated angle under the action of C-MRCJ is derived in
Section 2. Defining the MD of the jammer loop, the modified C-MRCJ providing continuous jamming performance is proposed in
Section 2. The jamming performance of C-MRCJ compared to TRCJ and L-MRCJ is discussed in
Section 3. Furthermore, the ability of modified C-MRCJ in achieving continuous and stable jamming performance and the choice of the number of jammer loops are demonstrated in
Section 3. In
Section 4, brief conclusions and future research directions are presented.
For readers’ convenience, the notations used in the rest of the paper are listed partly here. r is the range between the radar and the jammer, is the distance between the two antennas of monopulse radar, is the rotational angle to the platform measured from the radar’s boresight, is the baseline length of the jammer loop or the diameter of the circular array, is the rotational angle of the nth jammer loop, is the half angular separation of the nth jammer loop, is the angular separation measured from the nth jammer loop to the th jammer loop, and are respectively the total sum-channel and difference-channel returns received by the radar, is the monopulse ratio which is used to compute the monopulse-indicated angel , is the cross-eye gain of cross-eye jamming. The other notations will be given in appropriate locations in the paper.
3. Results and Discussion
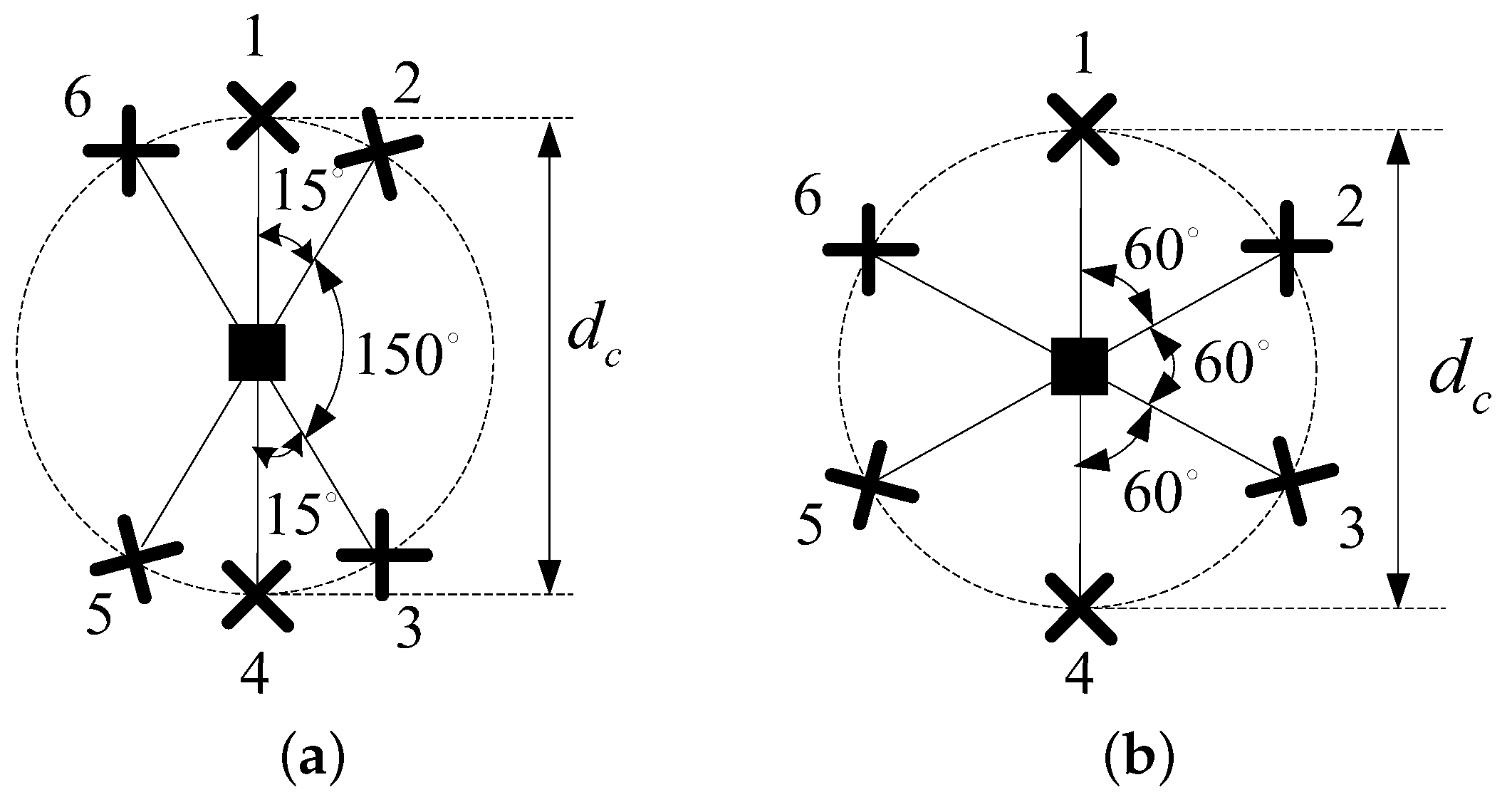
Considering the large number of system parameters of C-MRCJ with
N antenna elements, two circular array configurations with different angular separations between the jammer loops are employed by C-MRCJ system as shown in
Figure 6. The angular separations between jammer loops are shown in the figure. The base-lengths of the jammer loops of these two configurations are
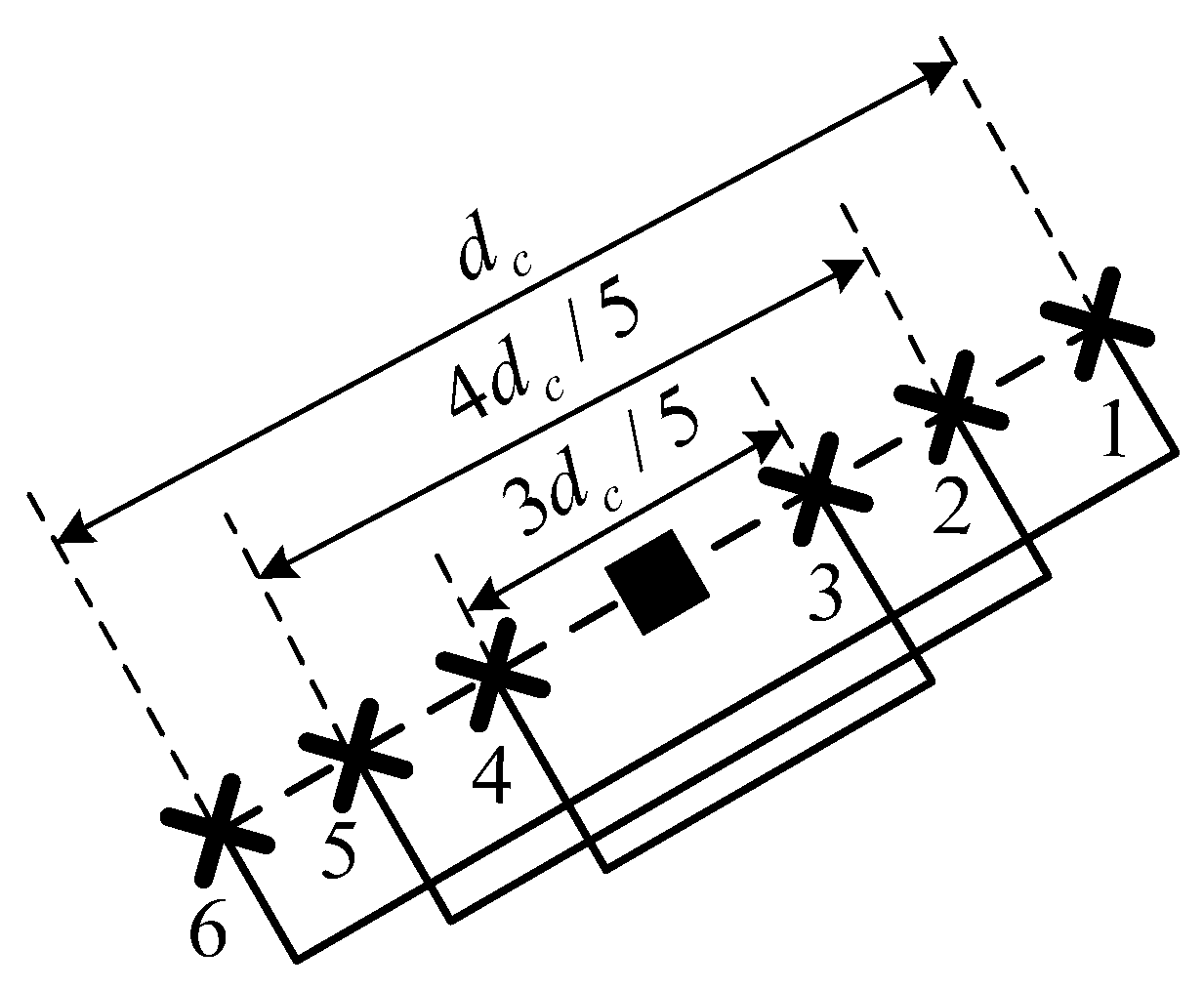
. For comparison, we consider a L-MRCJ system with six antenna elements as shown in
Figure 7. We denote the jammer loop of L-MRCJ constituted by antennas
n and
as jammer loop
n. For example, antennas 1 and 6 comprise the jammer loop 1 of L-MRCJ as shown in
Figure 7.
The values of the scenario parameters for simulation are given as follows:
the radar carrier frequency is 9 GHz,
the radar antenna aperture is ,
the jammer range is 1 km,
the jammer base-length is 10 m.
We assume that the path-length differences have been well compensated for and assume that .
3.1. Angular Error Induced by C-MRCJ
Assume the rotational angle of jammer loop 1 is for both L-MRCJ and C-MRCJ. The rotational angles of jammer loop 2 and 3 of configuration 1 of C-MRCJ (C-MRCJ 1) are and respectively, and those of configuration 2 of C-MRCJ (C-MRCJ 2) are and respectively.
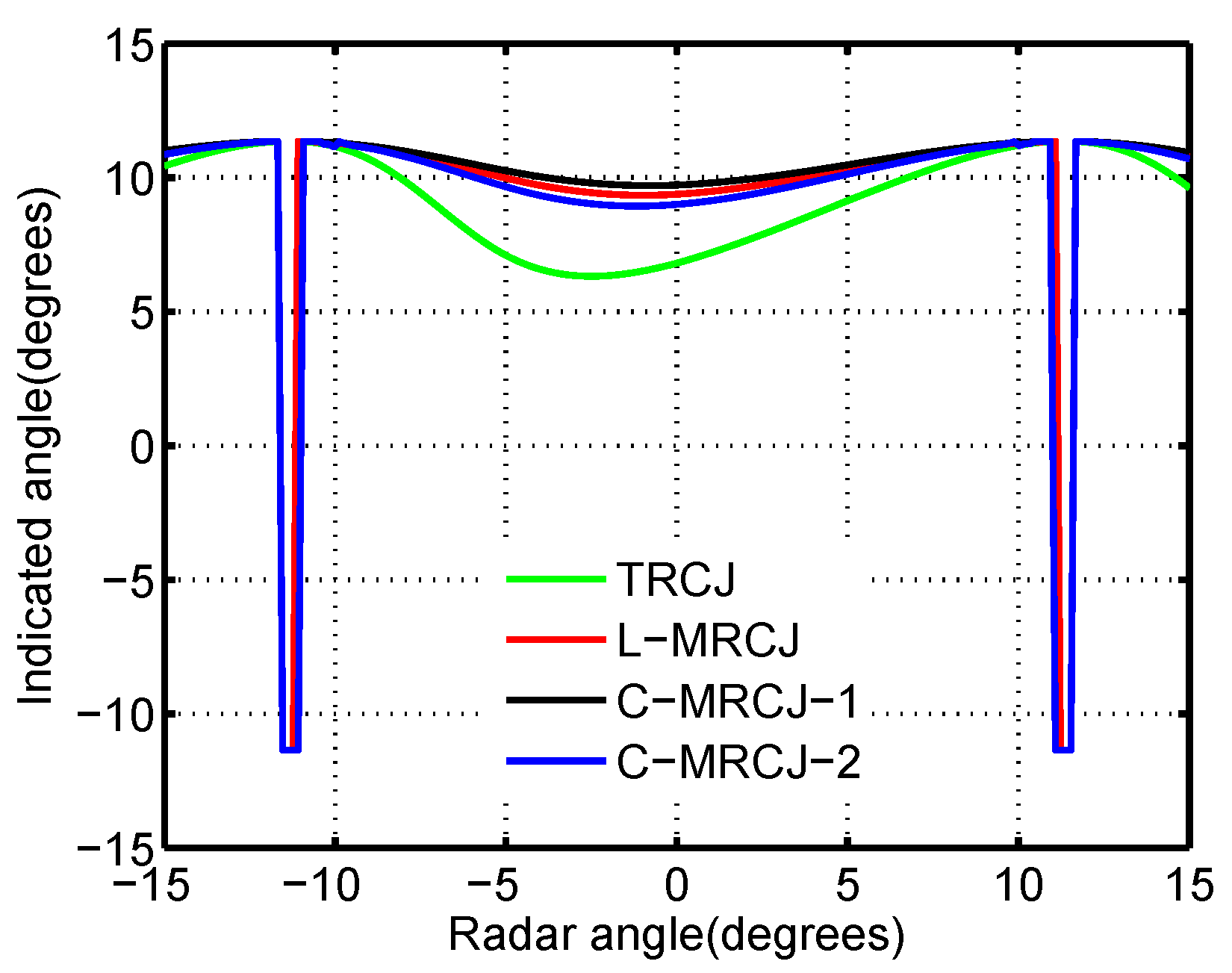
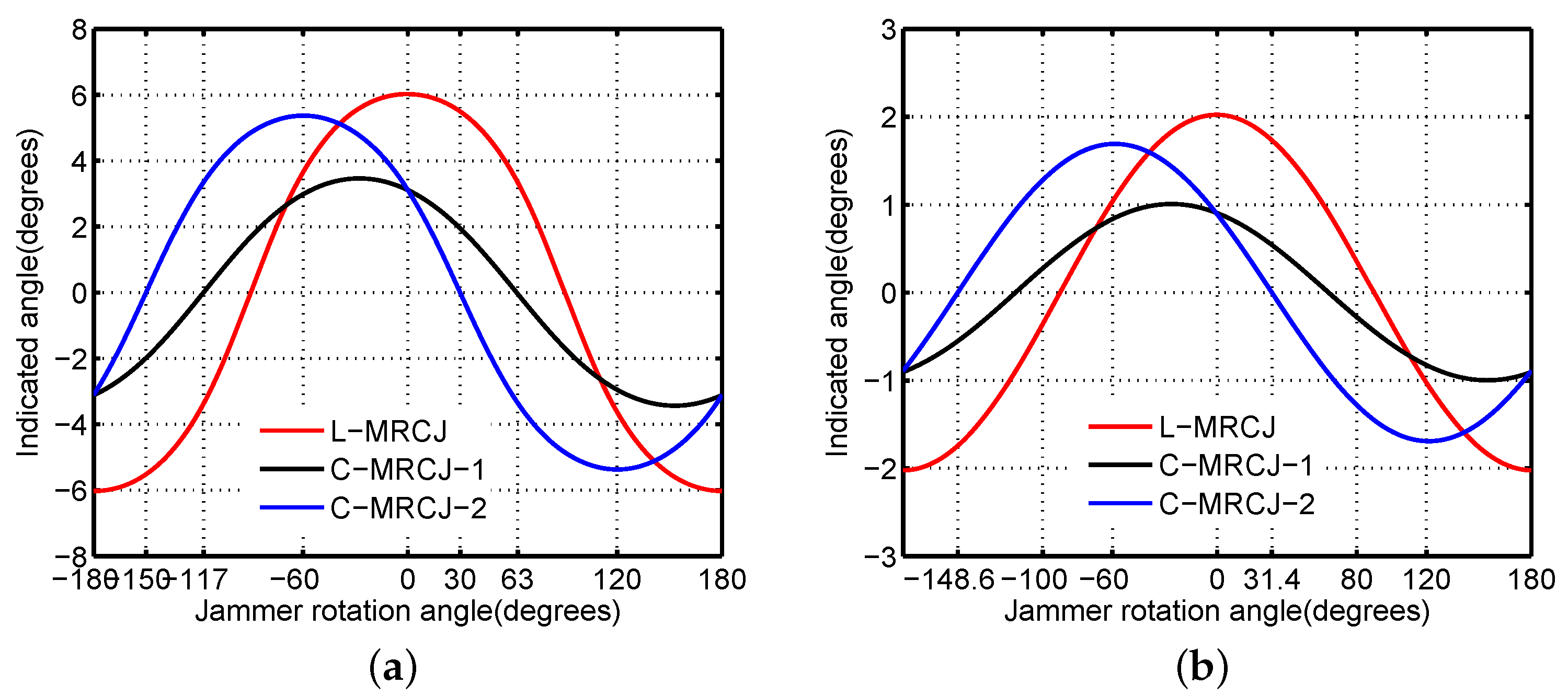
Monopulse-indicated angles of different jammer array configurations are plotted in
Figure 8 when the system parameters
are described in the figure caption.
An obvious conclusion which arises from
Figure 8 is that the curves of the monopulse-indicated angle for the four configurations considered have no zeros in the radar 3 dB beamwidth. It means that the monopulse radar cannot lock its target under the action of either TRCJ or MRCJ. In other words, C-MRCJ has the same potential as TRCJ and L-MRCJ to break the lock of a monopulse radar.
The monopulse-indicated angle can be regarded as the angular error when the radar angle is zero.
Figure 8 demonstrates that either C-MRCJ or L-MRCJ can induces much larger angular error into the monopulse radar than TRCJ for the specified system parameters. The superiority of MRCJ to obtain the larger angular errors benefits form the more degrees of freedom which allows the system parameters to be endowed with appropriate values to obtain larger cross-eye gain.
Comparing the curves of C-MRCJ with the curve of L-MRCJ in
Figure 8 gives the conclusion that there is no superiority for C-MRCJ in the aspect of inducing angular error compared to L-MRCJ. C-MRCJ can obtain either a larger or smaller angular error compared to L-MRCJ which is determined by the sum of the base-lengths of the inner jammer loops (except the jammer loop 1) against the radar’s boresight when the system parameters are the same. For example, the base-length sum of inner jammer loops of C-MRCJ 1 against the radar’s boresight is
which is larger than L-MRCJ, and the base-length sum of C-MRCJ 2 is
which is smaller than L-MRCJ. Actually, the difference between C-MRCJ and L-MRCJ is that the factor affecting the value of cross-eye gain is not the same, which is the ratio of base-lengths of jammer loops for L-MRCJ and is the angular separations between the jammer loops for C-MRCJ.
3.2. Continuous Jamming Provided by Modified C-MRCJ
We firstly investigate the variation of the angular error induced by C-MRCJ without the use of MD modification. We assume that the radar angle is zero, i.e.,
. Thus, the monopulse-indicated angle will indicate the value of angular error when
. The rotational angle of jammer loop 1 is limited in
. The monopulse-indicated angles of L-MRCJ and C-MRCJ for different system parameters
are plotted in
Figure 9.
It can be observed from
Figure 9 that the monopulse-indicated angle of L-MRCJ will be zero when the rotational angle of jammer loop 1 is
. This means that L-MRCJ will be ineffective when the radar being jammed appears in the end-fire direction of jammer antenna array.
However, C-MRCJ can also induce a monopulse-indicated angle of zero in specified angles as shown in
Figure 9. Taking C-MRCJ 2 as an example, the monopulse-indicated angle will be zero when the rotational angle of jammer loop 1 is
or
as shown in
Figure 9a. Comparisons between the results in
Figure 9a,b demonstrate that the changes of system parameters and angular separations between the jammer loops only change the value of the angular error and the specified angles making C-MRCJ ineffective.
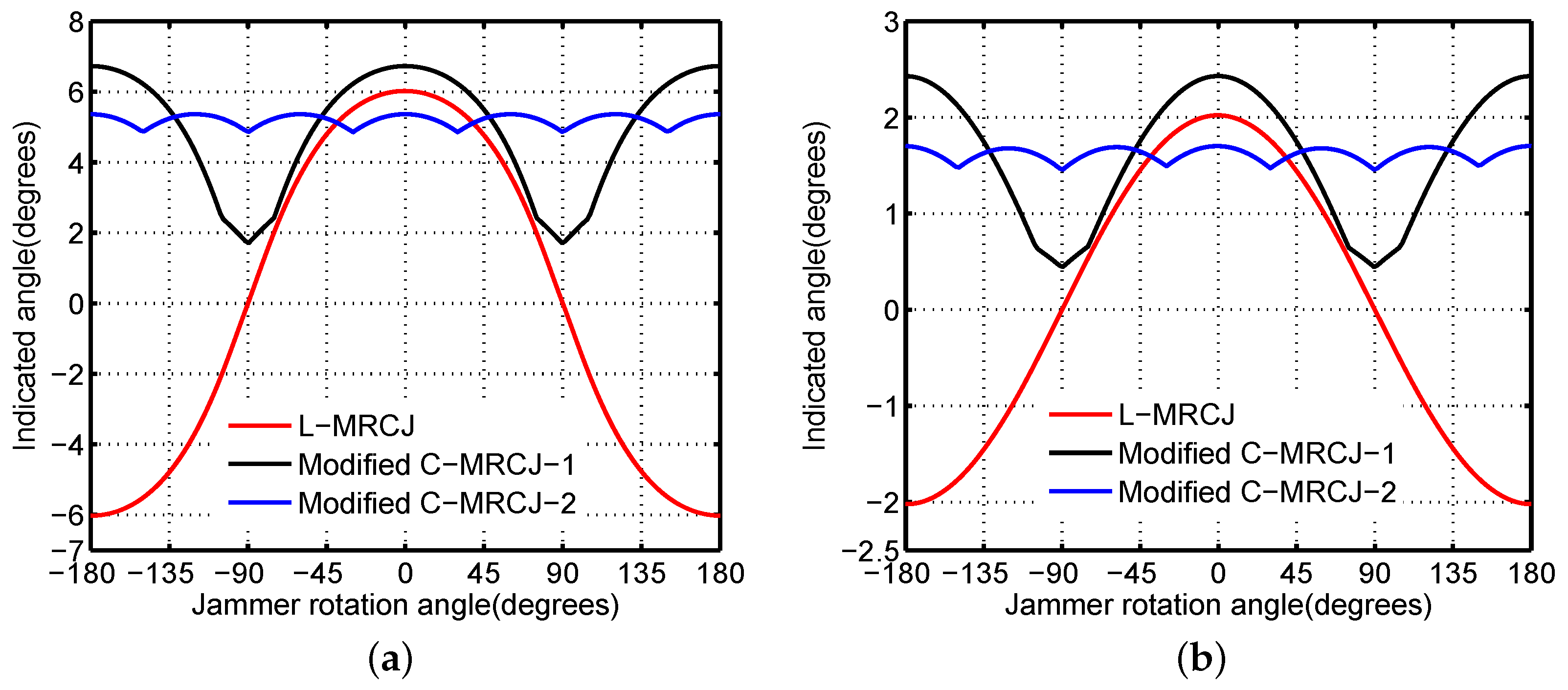
We secondly investigate the continuous jamming performance achieved by the modified C-MRCJ with modified MD. To produce a continuous apparent target above the rotating platform, the modification details of MDs according to DOA information for modified C-MRCJ are given in
Table 1. Substituting the modified MDs into (
28)–(
30) gives the monopulse-indicated angle of modified C-MRCJ, which is plotted in
Figure 10 for different system parameters
.
An important conclusion from
Figure 10 is that the monopulse-indicated angle of modified C-MRCJ never becomes zero wherever the radar was being jammed, while L-MRCJ cannot. This means that modified C-MRCJ can provide continuous angular error within the coverage of
. The continuous jamming performance is important for a cross-eye jammer mounted on a rotating platform, which makes the jammer avoid becoming a beacon. Furthermore, modified C-MRCJ has the ability to fix the apparent target despite the direction the radar appears. The modification details given in
Table 1 limit the apparent target locating above the platform.
Another conclusion from comparisons between
Figure 10a,b is that the system parameters
do not affect the shape of the monopulse-indicated angle curves, but affect the value of the monopulse-indicated angle. This conclusion is useful for building a practical C-MRCJ system, the system parameters and the MD, respectively, take charge of the value of the induced angular error and the ability of continuous jamming.
3.3. Stable Jamming Provided by Modified C-MRCJ
Besides providing continuous jamming performance, modified C-MRCJ has the potential to achieve stable jamming performance. The ability to produce a stable apparent target is desirable for a cross-eye jammer mounted on a rotating platform.
Figure 10 illustrates that the variation of the monopulse-indicated angle of C-MRCJ 2 is much smaller than C-MRCJ 1. Hence, C-MRCJ 2 with uniform-spacing angular separation is a better option than C-MRCJ 1 because it allows the jammer to provide a stable angular error over the coverage of
.
However, only two configurations of C-MRCJ are considered in
Figure 10. To explore the optimal configuration of modified C-MRCJ pursuing the stablest jamming performance, we consider the following two cases of values which include all configurations with one angular separation is
:
Symmetrical case: , , and vary from to with the step of ;
Asymmetrical case: , , , varies from to with the step of .
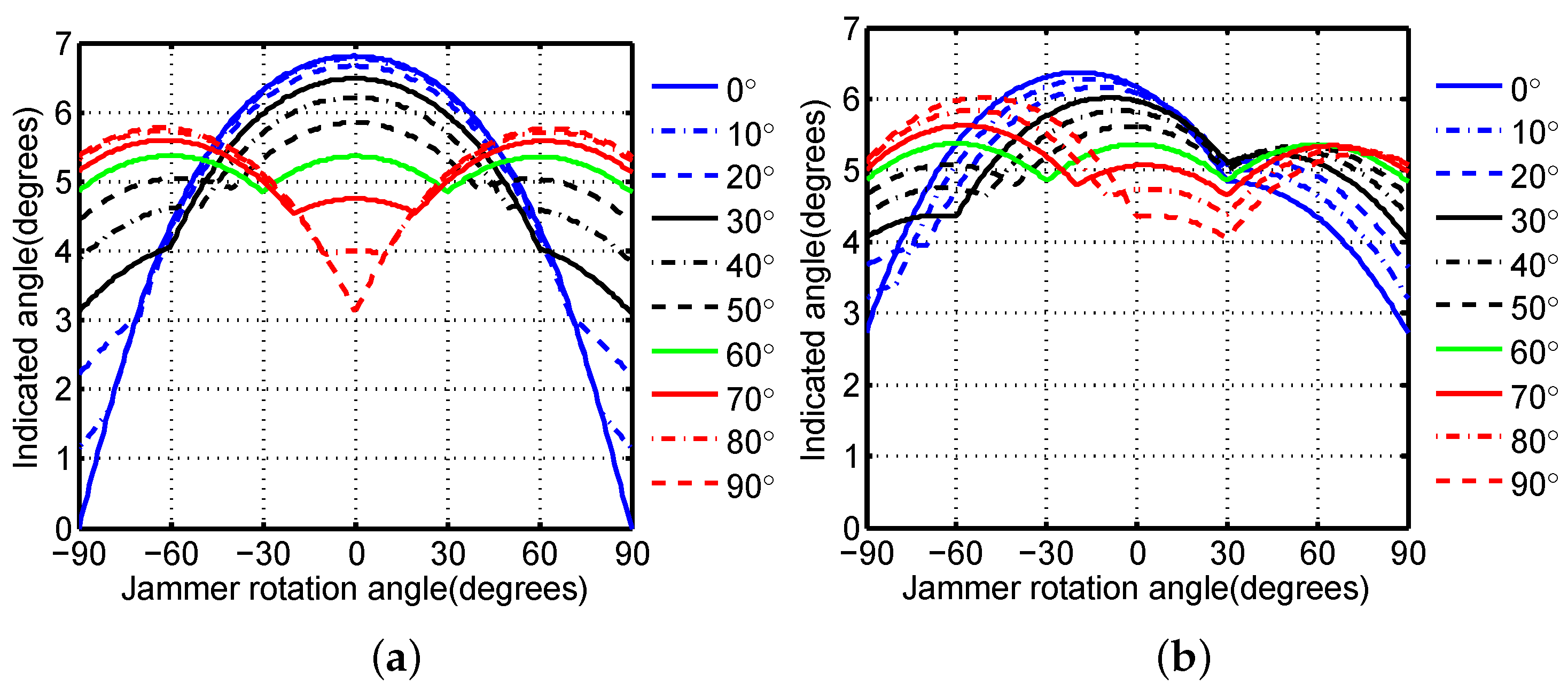
The monopulse-indicated angles for the above two cases are plotted in
Figure 11. It can be observed that the configuration
induces the stablest angular error which is limited in the range of
, for both the symmetrical and the asymmetrical cases.
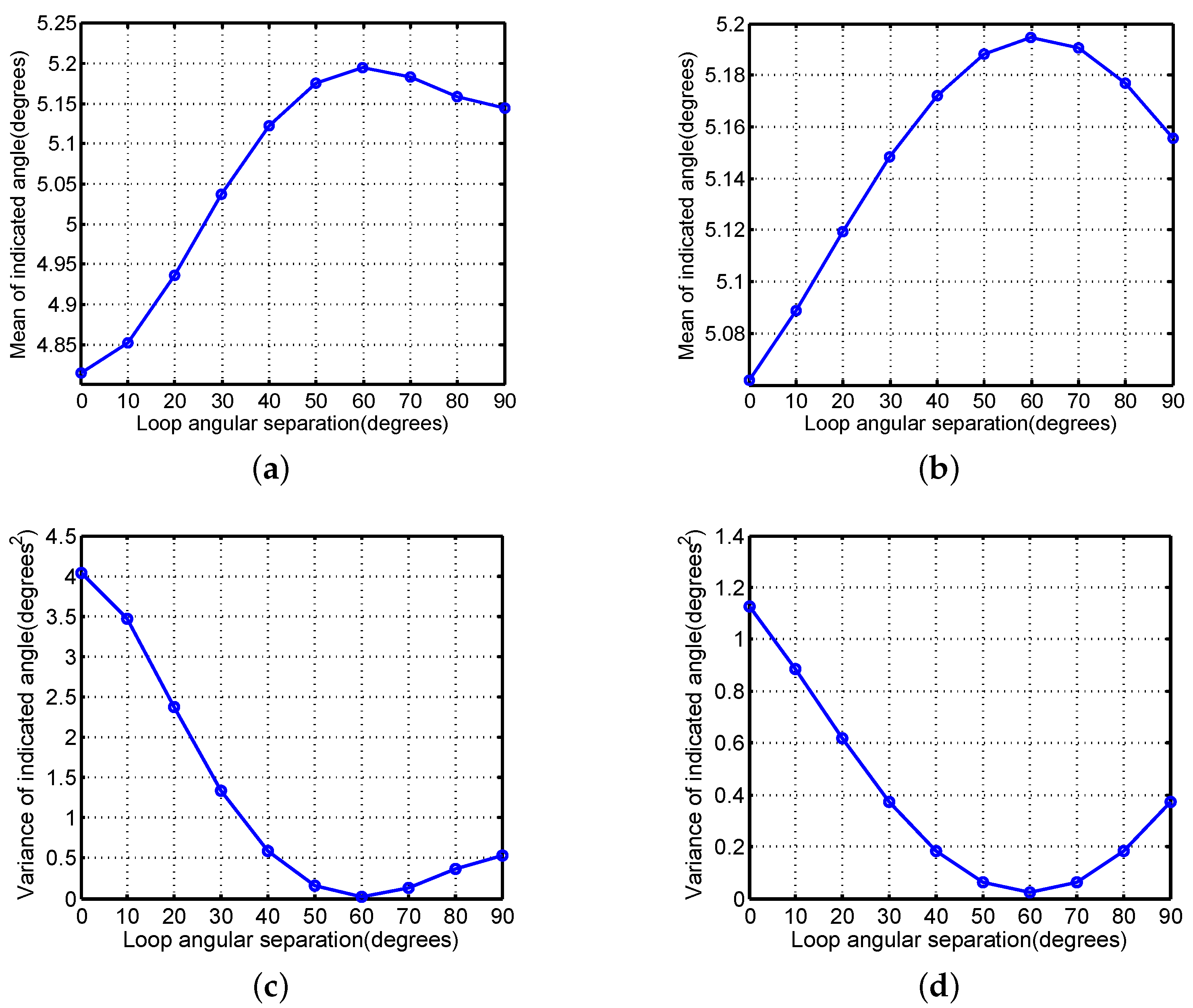
We use the arithmetic mean and variance of the monopulse-indicated angle to quantify the stable jamming performance. The arithmetic mean and variance of the monopulse-indicated angle for the cases considered in
Figure 11 are plotted in
Figure 12.
Figure 12 shows that the configuration
has the largest arithmetic mean and the smallest variance of the monopulse-indicated angle compared to the other configurations considered. Hence, the configuration with uniform-spacing angular separation is the optimal configuration for modified C-MRCJ to achieve stable jamming performance.
3.4. Choice of the Number of Antenna Elements
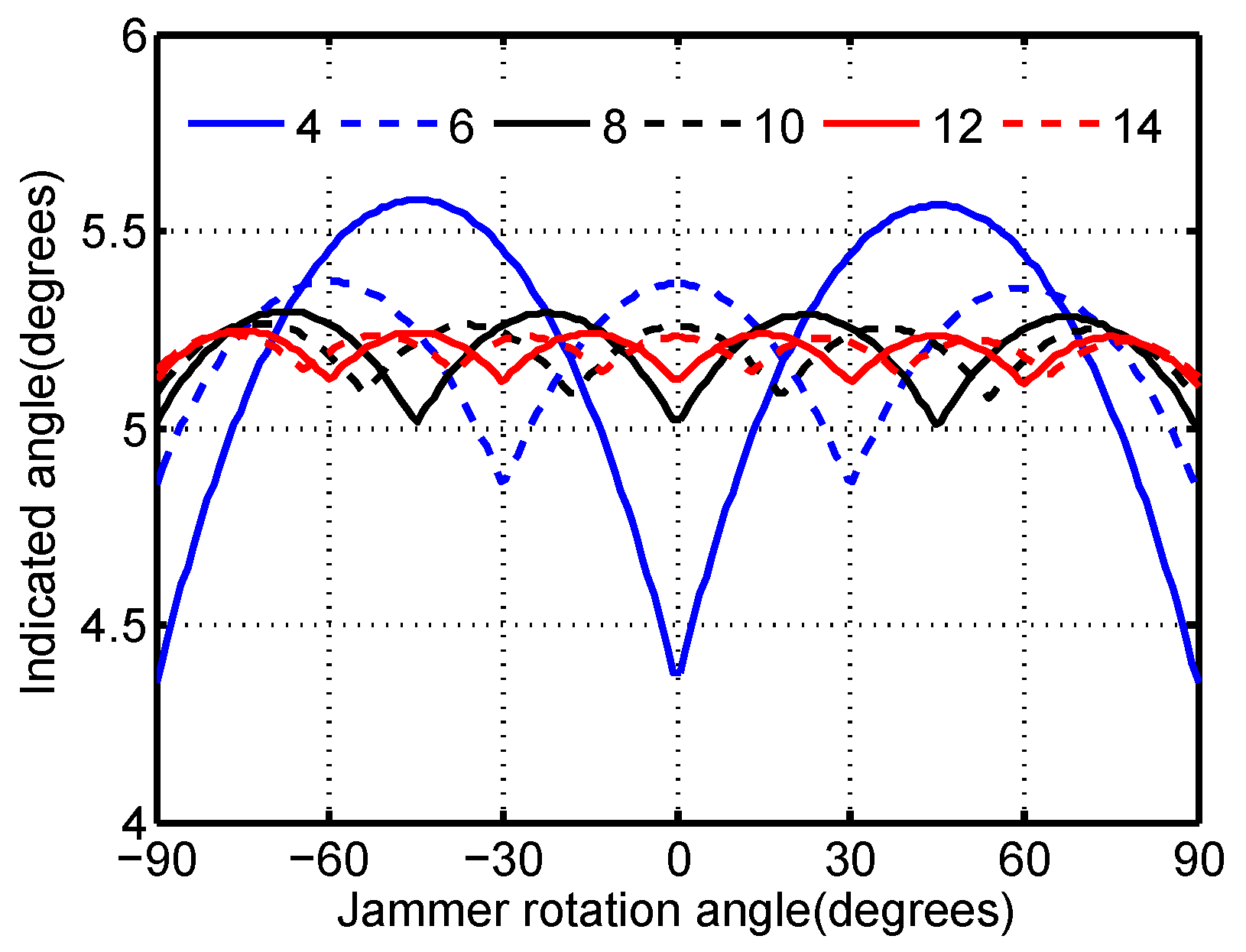
The choice of the number of antenna elements is discussed, giving consideration to the hardware cost and the jamming performance. The monopulse-indicated angles of modified C-MRCJ with the optimal configuration for a range of antenna numbers are plotted in
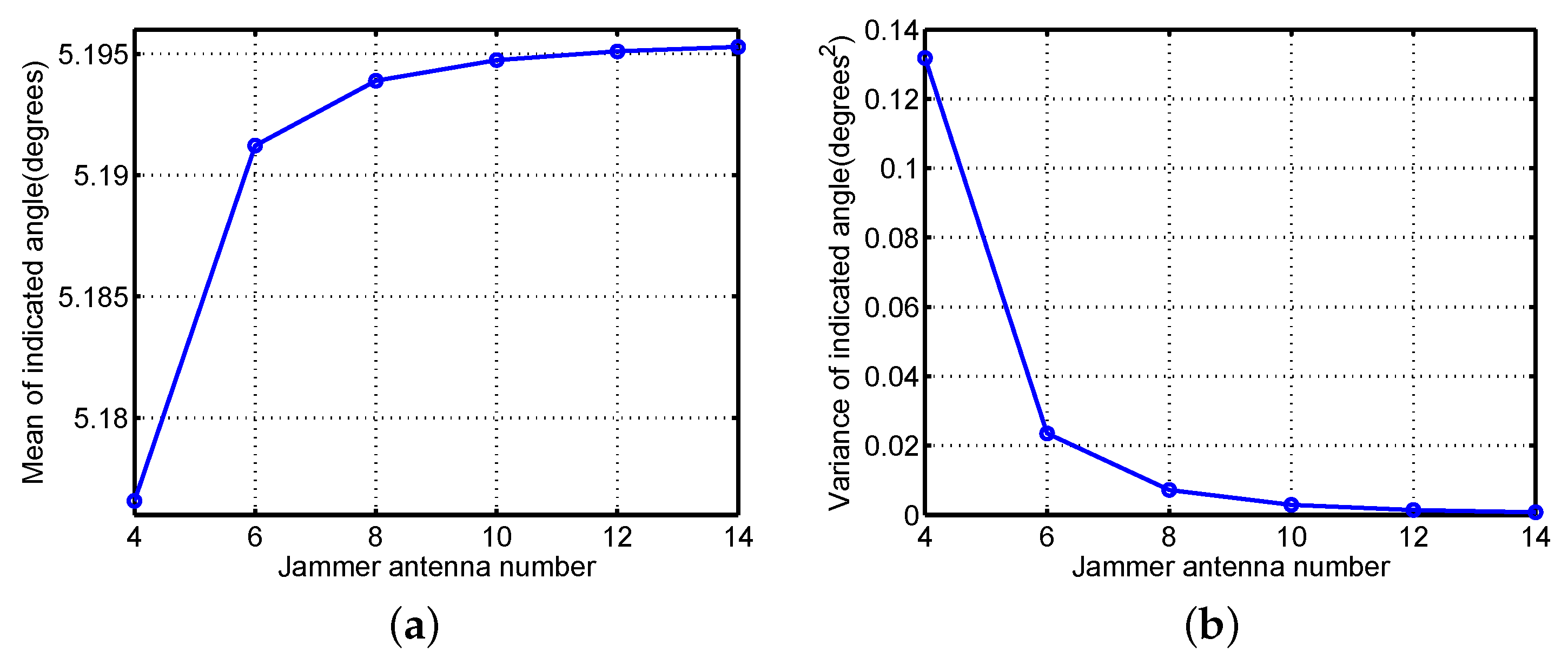
Figure 13, and their arithmetic mean and variance are plotted in
Figure 14.
Figure 13 shows that the stability of the induced angular error is improved by increasing antenna elements, although the improvement of the stability is not significant. This conclusion can also be obtained by
Figure 14. The arithmetic mean and the variance of the indicated angle increases and decreases, respectively, as the number of the jammer antenna elements increases. Moreover, the enhancement of the stability is obvious when increasing antenna elements from 4 to 6. Hence, considering the stable jamming performance, the antenna array analyzed in [
25] is not the best configuration.
However, the slightly enhanced performance of modified C-MRCJ by increasing antenna numbers is not tempting enough, because a large number of antenna elements will make the jammer system more complicated. Given that four antenna elements lead to poor jamming performance and eight or more antenna elements raise the hardware cost, six antenna elements are recommended for modified C-MRCJ.
4. Conclusions
MRCJ employing a circular retrodirective array was proposed in this paper. After defining the modulation direction of the jammer loop, the modified C-MRCJ was further presented to pursue continuous and stable jamming performance wherever the radar being jammed appears.
There is no superiority for C-MRCJ to induce large angular error compared to L-MRCJ. The difference between C-MRCJ and L-MRCJ is that the factor affecting the value of cross-eye gain is different. Simulation results demonstrated that modified C-MRCJ can achieve continuous jamming performance by modifying the MDs of jammer loops according to the DOA information. Meanwhile, The optimal configuration of modified C-MRCJ with uniform-spacing angular separation between jammer loops can provide the stablest jamming performance. Six antenna elements are recomended for modified C-MRCJ which has considerable jamming performance and moderate hardware cost.
Actually, for the practical platform protected by a cross-eye jammer, such as a ship or aircraft, the antenna configuration proposed is too idealistic. The MRCJ with distributed jammer loops appropriate for the practical platform geometry will be worth researching.