Measuring the Power Law Phase Noise of an RF Oscillator with a Novel Indirect Quantitative Scheme
Abstract
1. Introduction
2. System Model
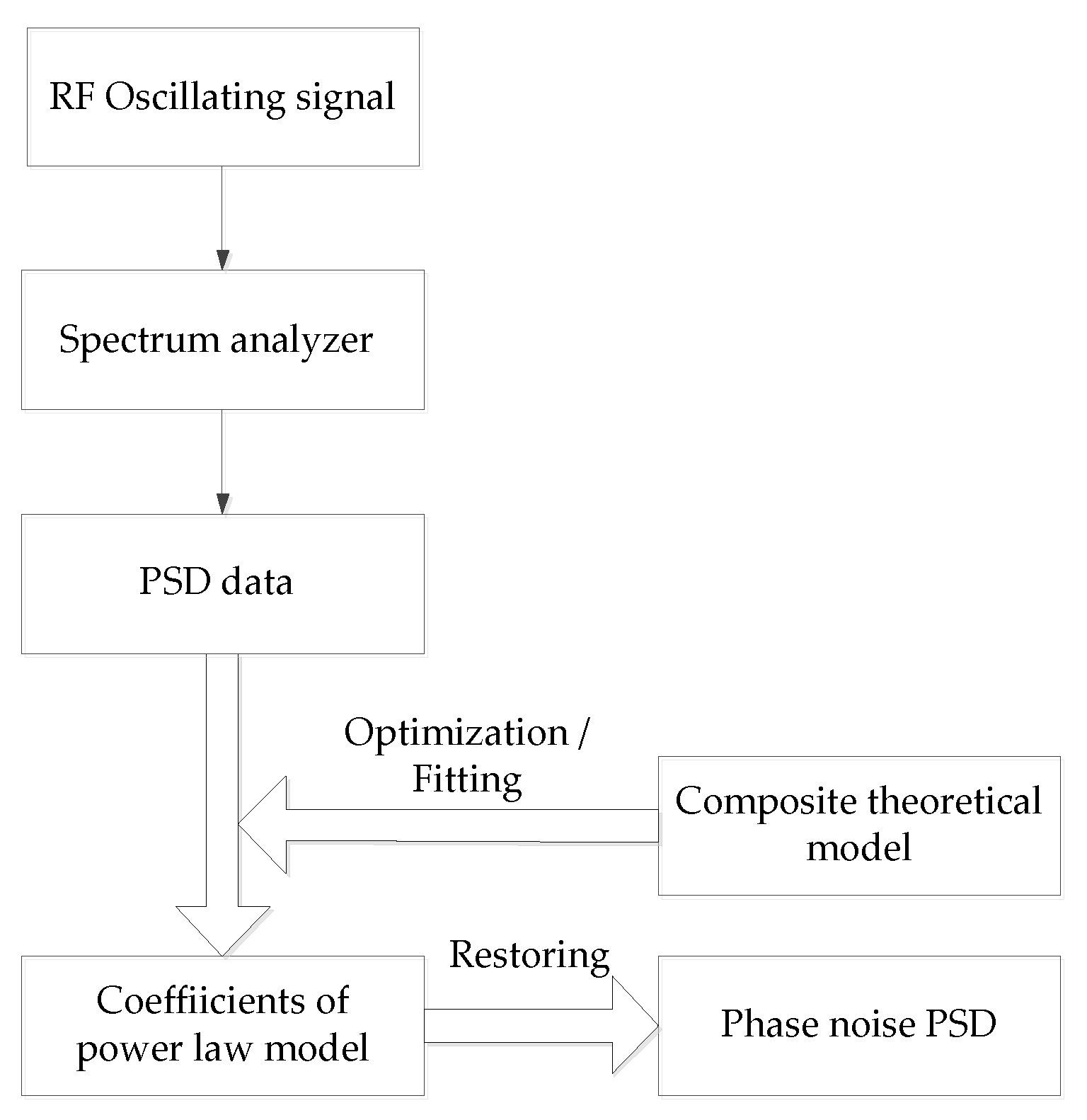
2.1. Testing Modality
2.2. Phase Noise Model
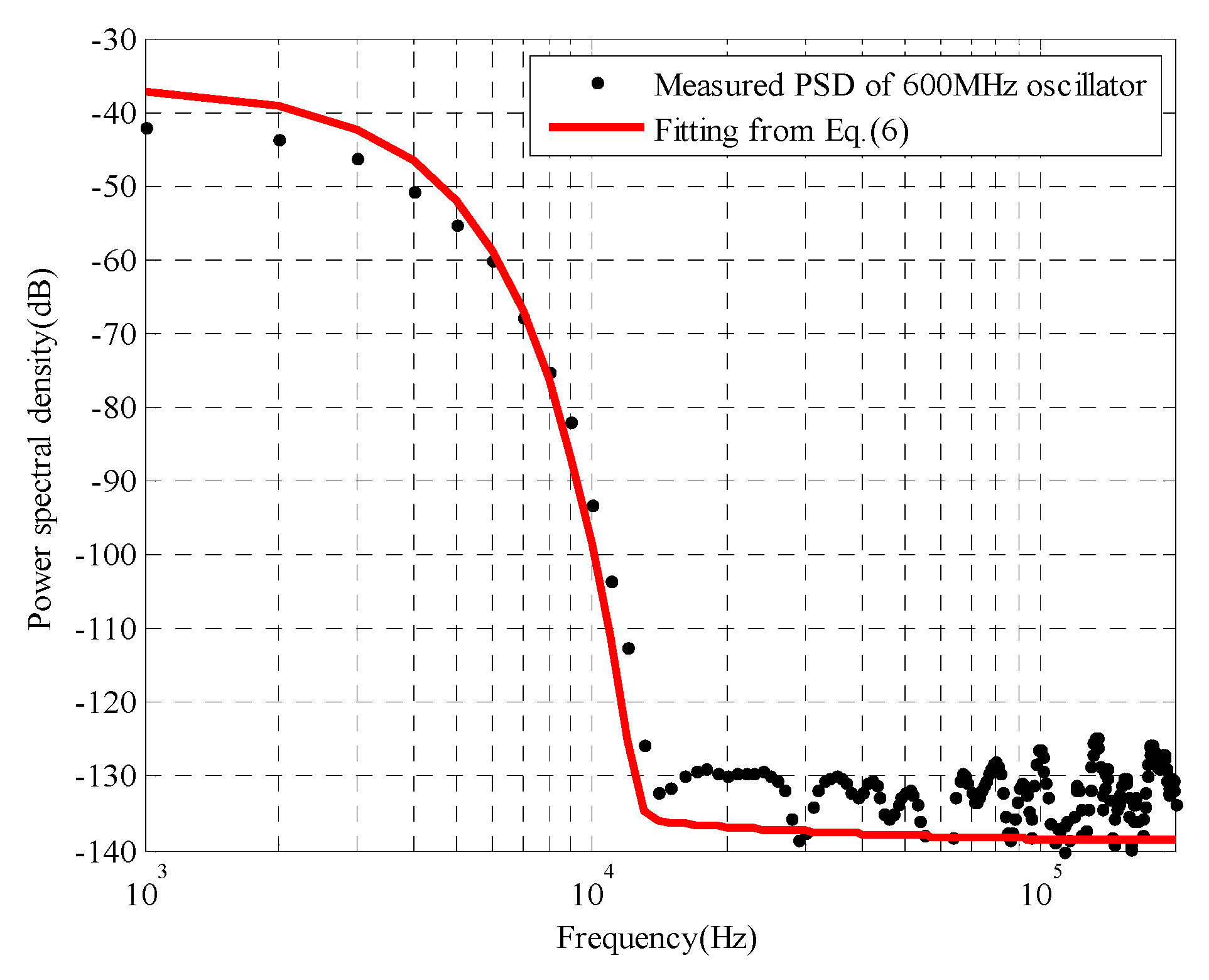
2.3. Factor Approximation
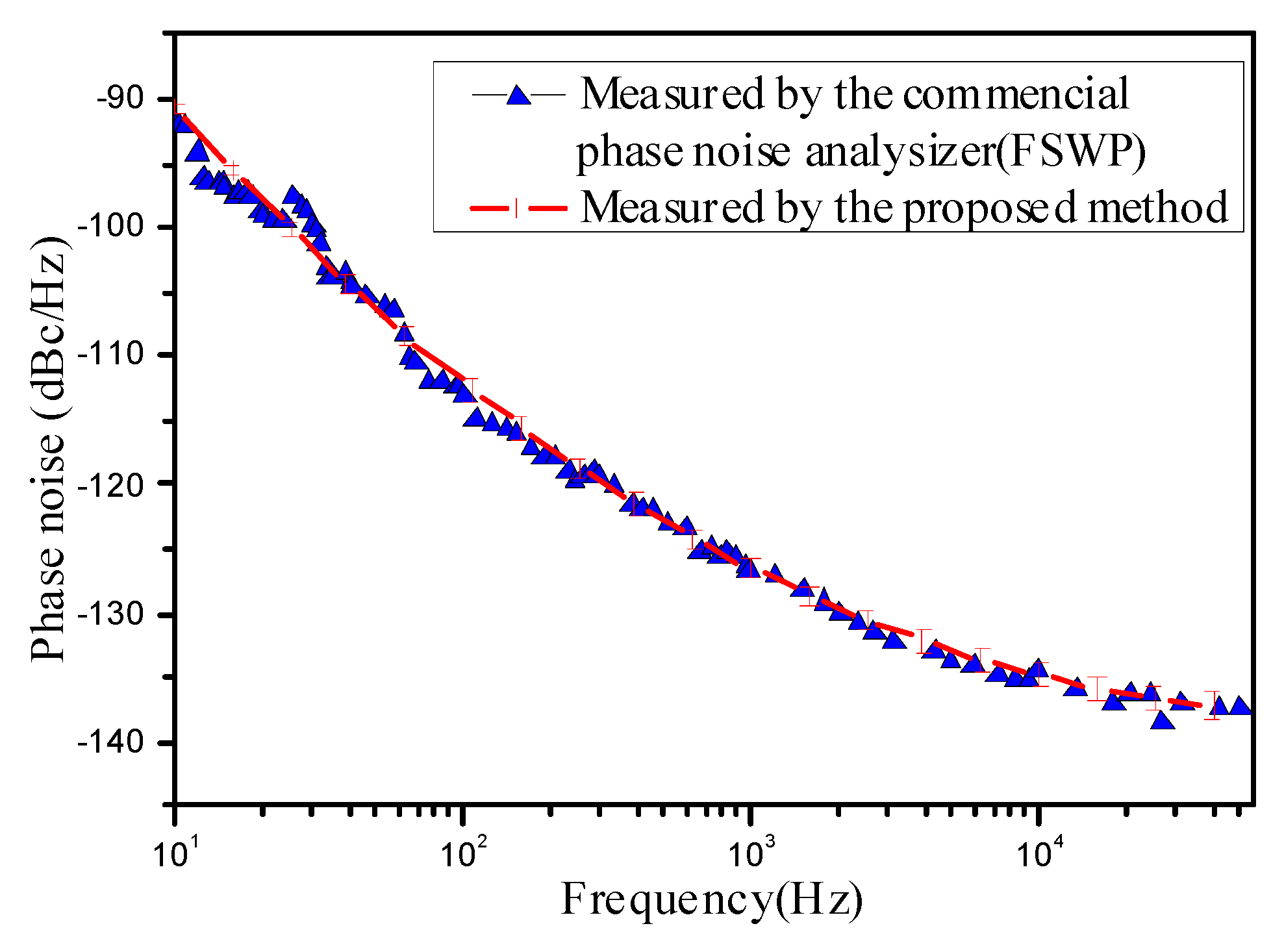
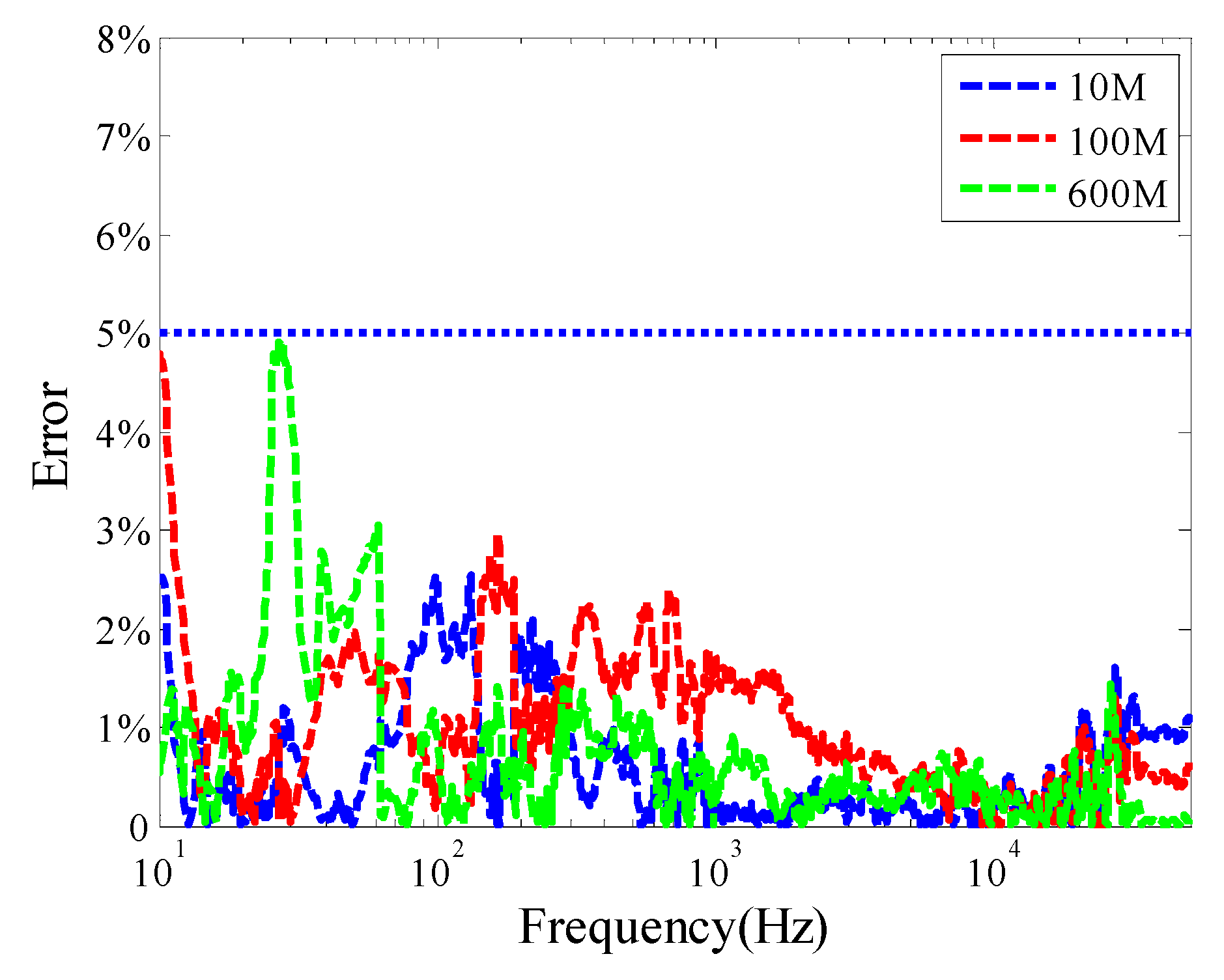
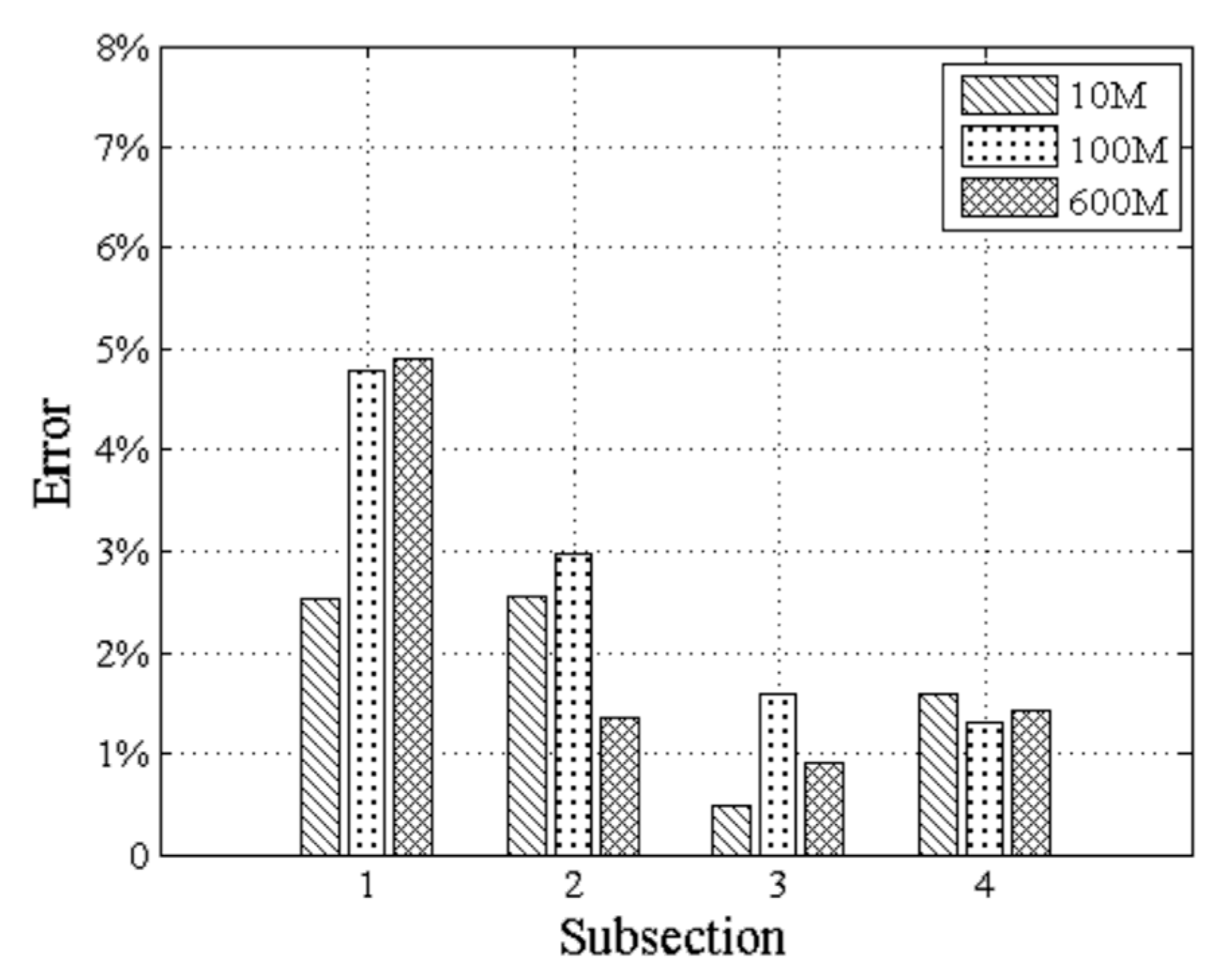
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jurgo, M.; Navickas, R. Structure of All-Digital Frequency Synthesiser for IoT and IoV Applications. Electronics 2019, 8, 29. [Google Scholar] [CrossRef]
- Khanzadi, M.R.; Krishnan, R.; Kuylenstierna, D.; Eriksson, T. Oscillator phase noise and small-scale channel fading in higher frequency bands. In Proceedings of the 2014 IEEE Globecom Workshops (GC Wkshps), Austin, TX, USA, 8–12 December 2014; pp. 410–415. [Google Scholar] [CrossRef]
- Meng, Z.; Hu, Y.M.; Xiong, S.D.; Stewart, G.; Whitenett, G.; Culshaw, B. Phase noise characteristics of a diode-pumped Nd:YAG laser in an unbalanced fiber-optic interferometer. Appl. Opt. 2012, 44, 3425–3428. [Google Scholar] [CrossRef] [PubMed]
- Barton, D.K. Radar system analysis and modeling. IEEE Aerosp. Electron. Syst. Mag. 2005, 20, 23–25. [Google Scholar] [CrossRef]
- Chan, E.H.W. Suppression of phase-induced intensity noise in fibre optic delay line signal processors using an optical phase modulation technique. Opt. Express 2010, 18, 21573–21584. [Google Scholar] [CrossRef] [PubMed]
- Leeson, D.B. Oscillator phase noise: A 50-year review. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2016, 63, 1208–1225. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Jonsson, F.; Zheng, L.R. A fast and accurate phase noise measurement of free running oscillators using a single spectrum analyzer. In Proceedings of the IEEE Norchip Conference, Tampere, Finland, 15–16 November 2010; pp. 1–4. [Google Scholar]
- Angrisani, L.; Baccigalupi, A.; D’Arco, M. A new method for phase noise measurement. In Proceedings of the IEEE Instrumentation & Measurement Technology Conference, Anchorage, AK, USA, 21–23 May 2002; pp. 663–668. [Google Scholar]
- Rohde, U.L.; Poddar, A.K.; Apte, A.M. Getting its measure. IEEE Microw. Mag. 2013, 14, 73–86. [Google Scholar] [CrossRef]
- Gheidi, H.; Banai, A. Phase-noise measurement of microwave oscillators using phase-shifterless delay-line discriminator. IEEE Trans. Microw. Theory Tech. 2010, 58, 468–477. [Google Scholar] [CrossRef]
- Chen, X.L.; Zhang, X.F.; Wang, J.L. A new algorithm for eliminating the frequency difference in phase noise measurement of the microwave signal. Prog. Electromagn. Res. M 2012, 23, 13–28. [Google Scholar] [CrossRef]
- Agrawal, D.K.; Bizzarri, F.; Brambilla, A.; Seshia, A. Numerical verification of an analytical model for phase noise in MEMS oscillators. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2016, 63, 1204–1207. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Demir, A.; Mehrotra, A.; Roychowdhury, J. Phase noise in oscillators: A unifying theory and numerical methods for characterization. IEEE Trans. Circuits Syst. I-Fundam. Theory Appl. 2000, 47, 655–674. [Google Scholar] [CrossRef]
- D’Arco, M.; De Vito, L. A novel method for phase noise measurement based on cyclic complementary autocorrelation. IEEE Trans. Instrum. Meas. 2016, 65, 2685–2692. [Google Scholar] [CrossRef]
- Kasdin, N.J. Discrete simulation of colored noise and stochastic processes and 1/fα power law noise generation. Proc. IEEE 1995, 83, 802–827. [Google Scholar] [CrossRef]
- Leeson, D.B. A simple model of feedback oscillator noise spectrum. Proc. IEEE 1966, 4682, 329–330. [Google Scholar] [CrossRef]
- Vernotte, F. Estimation of the power spectral density of phase: comparison of three methods. In Proceedings of the 1999 Joint Meeting of the European Frequency and Time Forum and the IEEE International Frequency Control Symposium, Besancon, France, 13–16 April 1999; pp. 1109–1112. [Google Scholar]
- Yousefi, S.; Eriksson, T.; Kuylenstierna, D. A novel model for simulation of RF oscillator phase noise. In Proceedings of the 2010 IEEE Radio and Wireless Symposium (RWS), New Orleans, LA, USA, 10–14 January 2010; pp. 428–431. [Google Scholar]
- Chorti, M.B. A spectral model for RF oscillators with power-law phase noise. IEEE Trans. Circuits Syst. 2006, 53, 1989–1999. [Google Scholar] [CrossRef]
- IEEE. IEEE Standard Definitions of Physical Quantities for Fundamental Frequency and Time Metrology—Random Instabilities; IEEE Standards 1139-1999; IEEE: Piscatway, NJ, USA, 2009. [Google Scholar]
- Klimovitch, G. A nonlinear theory of near-carrier phase noise in free running oscillators. In Proceedings of the 2000 Third IEEE International Caracas Conference on Devices, Circuits and Systems, Cancun, Mexico, 17 March 2000; pp. 1–6. [Google Scholar]
- Greenhall, C.A. An approach to power-law phase-noise models through generalized funcitons. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2015, 62, 116–128. [Google Scholar]
- Ashbby, N. Probability distributions and confidence intervals for simulated power law noise. Metrologia 2010, 47, 605–615. [Google Scholar] [CrossRef] [PubMed]
- Moré, J.J. The Levenberg-Marquardt algorithm: implementation and theory. In Numerical Analysis; Watson, G.A., Ed.; Springer: Berlin/Heidelberg, Germany, 1978; Volume 630, pp. 105–116. [Google Scholar]
- Marquardt, D.W. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–440. [Google Scholar] [CrossRef]
- R&S®SMW200A Vector Signal Generator. The Fine Art of Signal Generation. 2016. Available online: https://www.rohde-schwarz.com/ae/product/smw200a-productstartpage_63493-38656.html (accessed on 20 June 2019).
| Noise Type | α | Sφ(f) | SV(f) | Comments |
|---|---|---|---|---|
| White phase noise | 0 | B is the bandwidth of the testing instruments. SV(f) and Sφ(f) become constants only if B ≫ f | ||
| Flicker phase noise | −1 | 0 < ν1 ≪ 1 | ||
| White FM noise | −2 | SV(f) and Sφ(f) become identical if | ||
| Flicker FM phase noise | −3 | q is a function of ν3 as (0 < ν3 ≪ 1): | ||
| Random walk FM phase noise | −4 | is the starting offset frequency for f −4 noise, p is a constant and H(*) denotes the Heaviside step function. |
| Controlled Variable | Value (10 MHz) | Value (100 MHz) | Value (600 MHz) |
|---|---|---|---|
| q | 0.240 | 0.500 | 0.500 |
| ν3 | 9.00 × 10−4 | 2.00 × 10−4 | 2.0 × 10−4 |
| p | 3.95 × 10−15 | 7.54 × 10−19 | 4.55 × 10−16 |
| h0 | 1.69 × 10−14 | 1.55 × 10−14 | 1.28 × 10−14 |
| h−1 | 1.36 × 10−10 | 1.51 × 10−10 | 1.58 × 10−10 |
| h−2 | 1.36 × 10−8 | 2.33 × 10−8 | 3.79 × 10−8 |
| h−3 | 4.91 × 10−7 | 4.31 × 10−7 | 3.22 × 10−7 |
| h−4 | 8.81 × 10−10 | 1.81 × 10−13 | 8.13 × 10−11 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Peng, C.; Huan, H.; Nian, F.; Yang, B. Measuring the Power Law Phase Noise of an RF Oscillator with a Novel Indirect Quantitative Scheme. Electronics 2019, 8, 767. https://doi.org/10.3390/electronics8070767
Chen X, Peng C, Huan H, Nian F, Yang B. Measuring the Power Law Phase Noise of an RF Oscillator with a Novel Indirect Quantitative Scheme. Electronics. 2019; 8(7):767. https://doi.org/10.3390/electronics8070767
Chicago/Turabian StyleChen, Xiaolong, Cuiling Peng, Huiting Huan, Fushun Nian, and Baoguo Yang. 2019. "Measuring the Power Law Phase Noise of an RF Oscillator with a Novel Indirect Quantitative Scheme" Electronics 8, no. 7: 767. https://doi.org/10.3390/electronics8070767
APA StyleChen, X., Peng, C., Huan, H., Nian, F., & Yang, B. (2019). Measuring the Power Law Phase Noise of an RF Oscillator with a Novel Indirect Quantitative Scheme. Electronics, 8(7), 767. https://doi.org/10.3390/electronics8070767





