Dual-Hop Cooperative Relaying with Beamforming Under Adaptive Transmission in κ–μ Shadowed Fading Environments
Abstract
1. Introduction
1.1. Related Works
1.2. Contributions
- We obtain new and exact results in an analytic form for the OP and average capacity using adaptive transmission techniques, such as optimal power and rate adaptation (OPRA), optimal rate adaptation with a constant transmit power (ORA), truncated channel inversion with a fixed rate (TIFR), and channel inversion with a fixed rate (CIFR).
- Using the obtained analytical results, we analyzed the system performance for various combinations of source and destination antennas and for different shadowing and fading parameters.
- It should be noted that all the obtained analytical expressions are general for shadowed fading scenario, and we can therefore easily transform these expressions into some special cases, namely, Nakagami-/Nakagami-, /, Rayleigh/Rayleigh, Rician-shadowed/Rician-shadowed, Rician/Rician, and mixed Rayleigh, , Rician-shadowed, Nakagami-, and Rician fading links. These fading arrangements can occur in various applications including satellite, micro-/macro-cellular, and/or hybrid satellite/terrestrial communication systems.
- Our results can efficiently be used to investigate the behavior of various channels like the ones in land mobile satellite systems, underwater acoustic communications, body centric communications, and other different wireless communication applications.
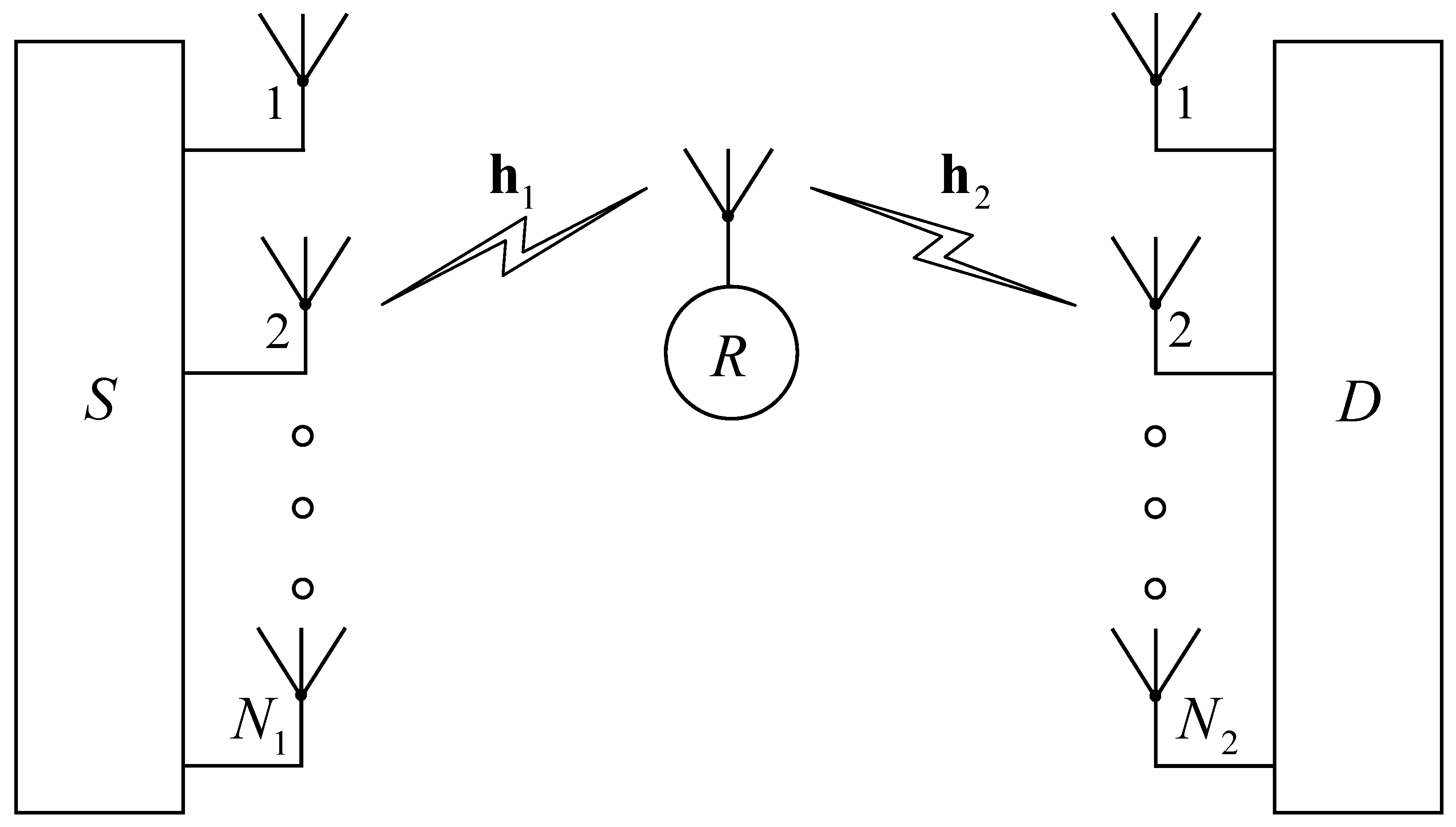
2. System and Channel Models
2.1. System Model
2.2. Shadowed Fading Model
3. Performance Analysis
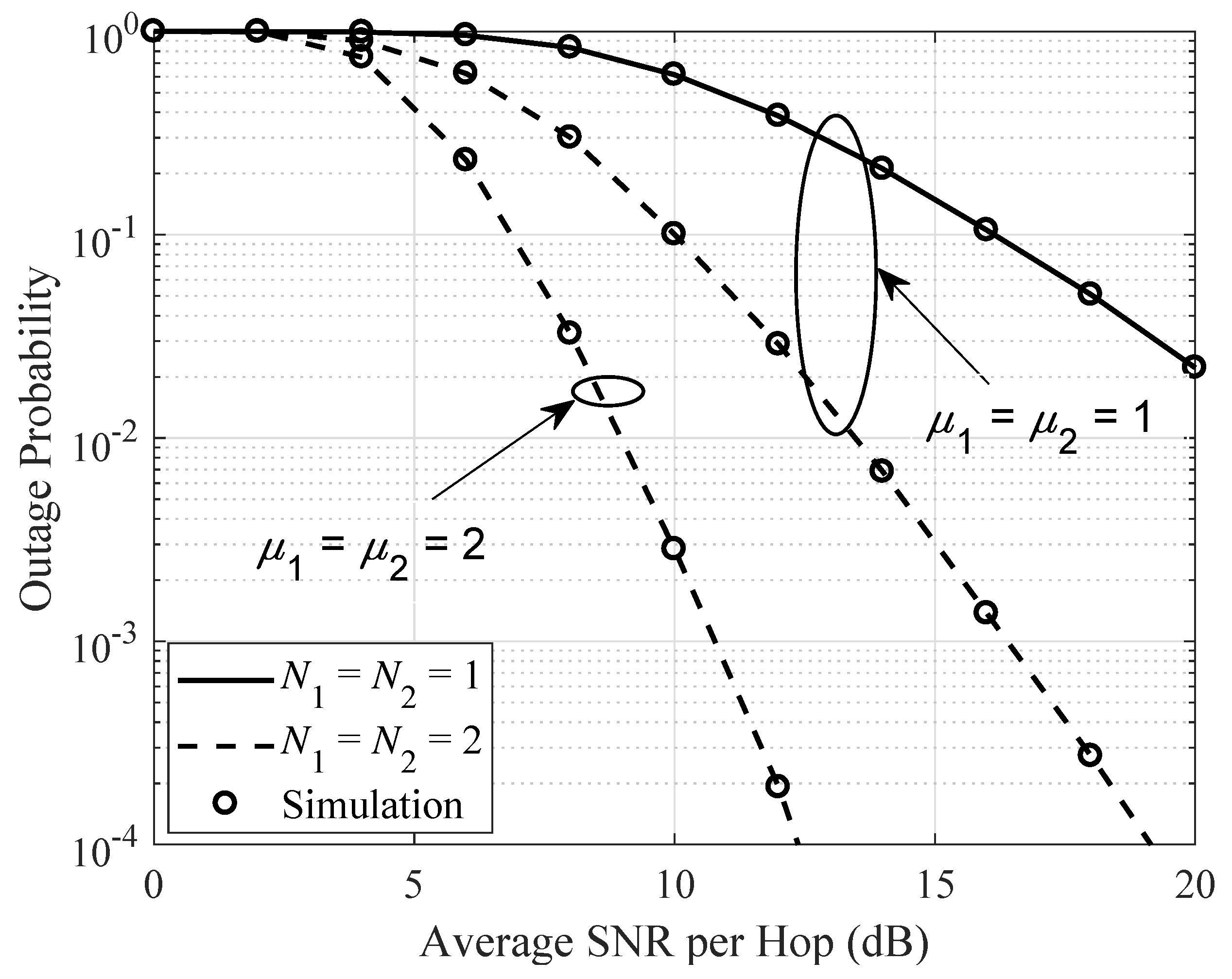
3.1. Outage Probability Analysis
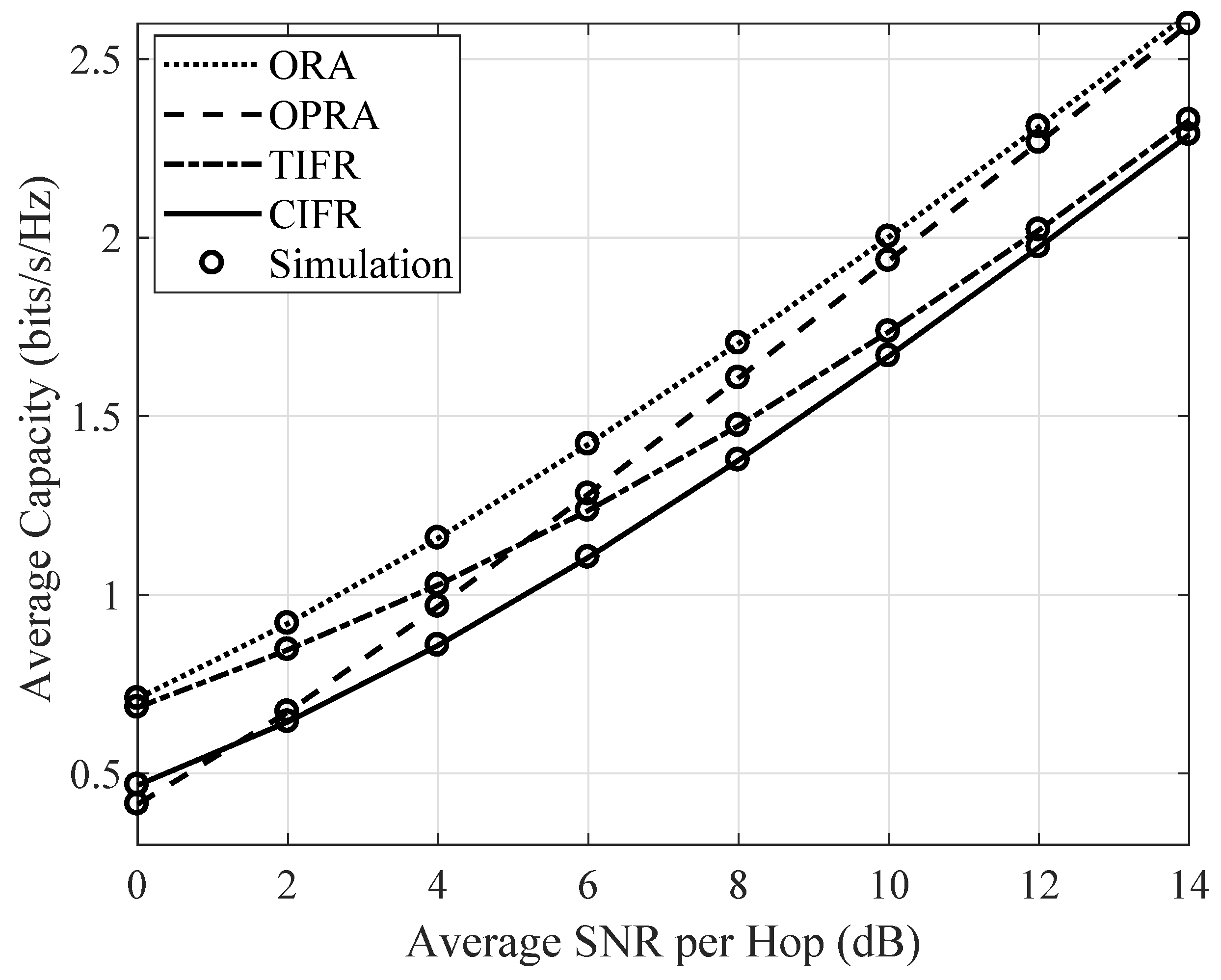
3.2. Capacity Analysis with Adaptive Transmission
3.2.1. Optimal Power and Rate Adaptation (OPRA)
3.2.2. Optimal Rate Adaptation with Constant Transmit Power (ORA)
3.2.3. Channel Inversion with Fixed Rate (CIFR)
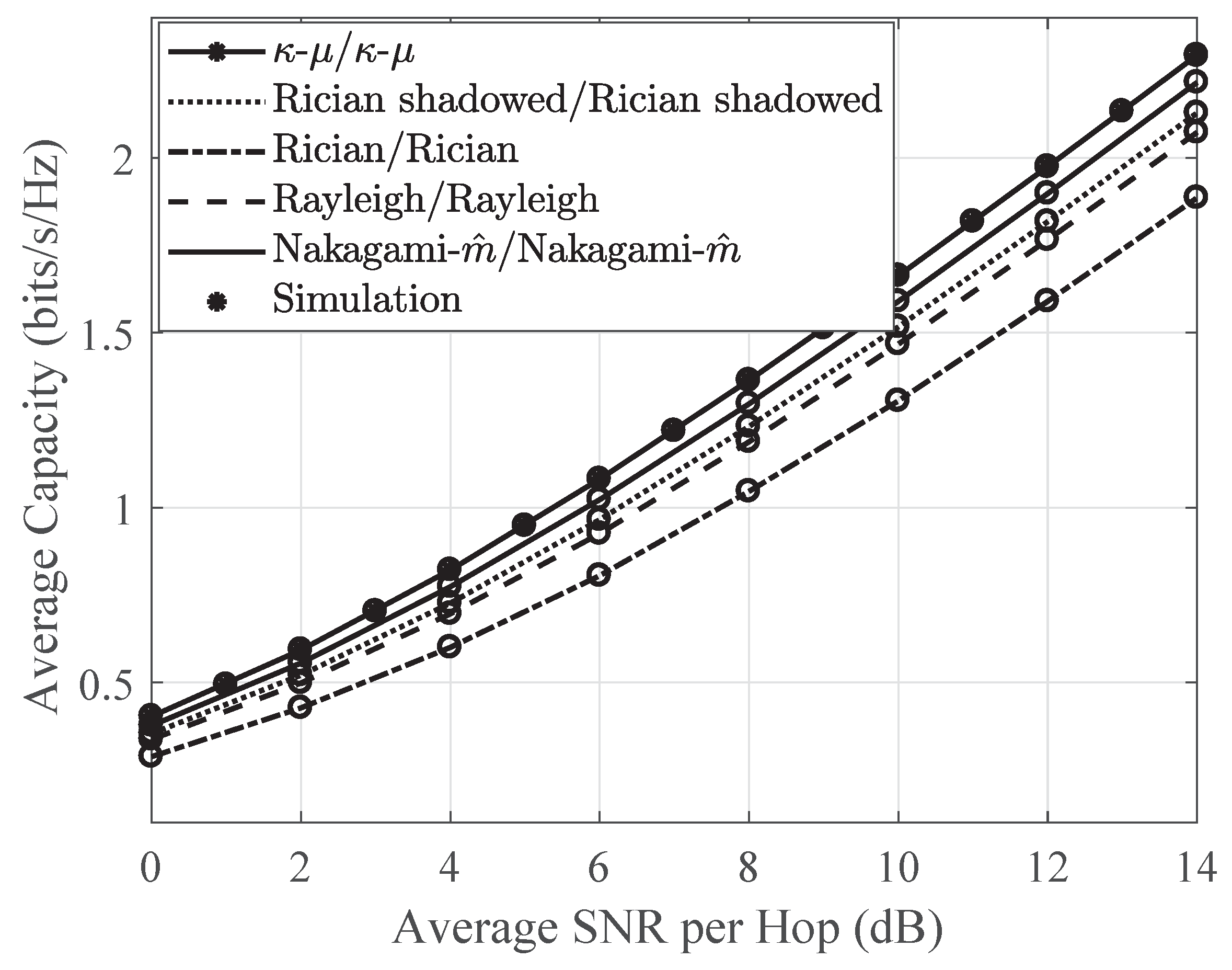
4. Special Cases
4.1. Special Cases for Outage Probability Analysis
4.2. Special Cases for Average Capacity Analysis
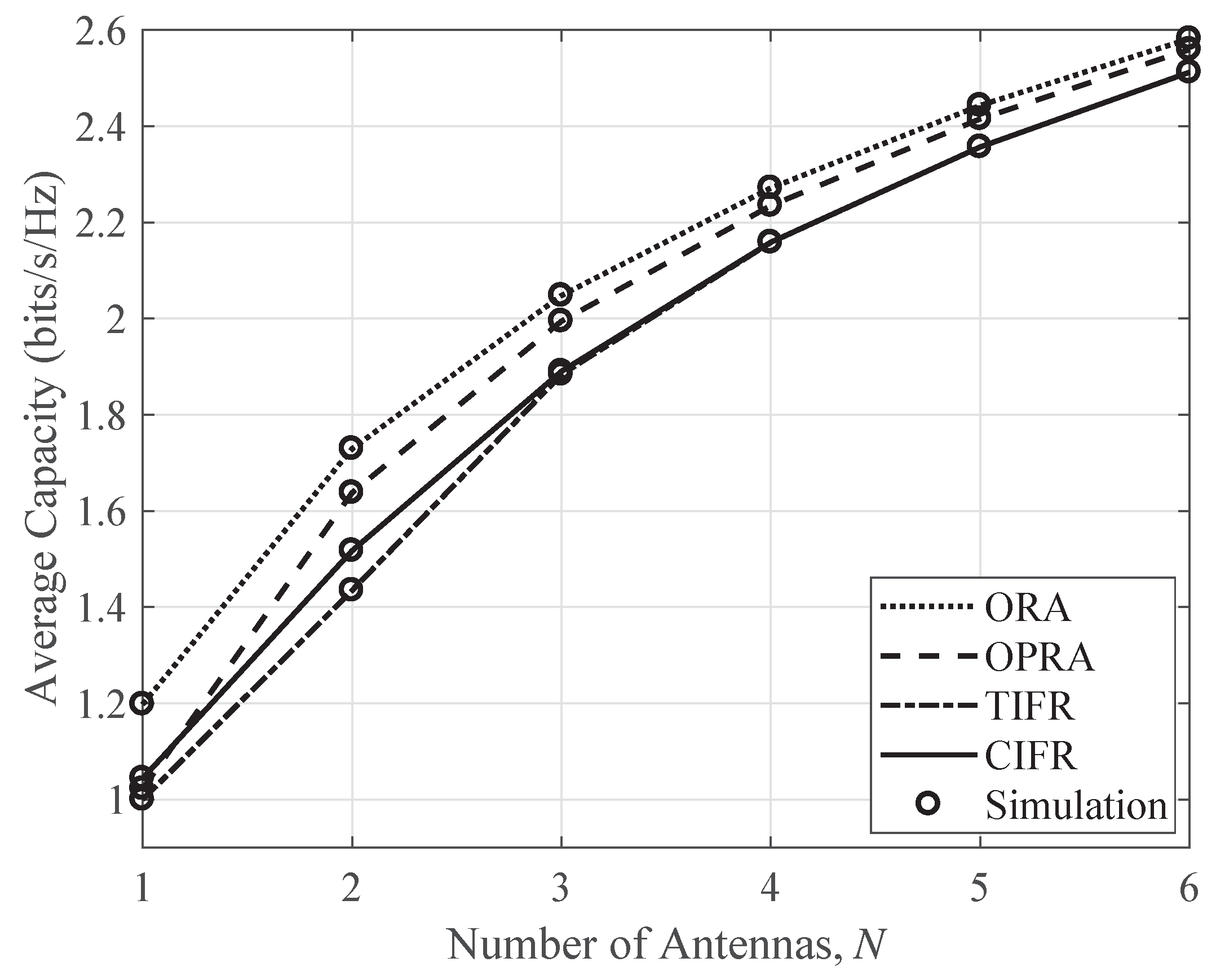
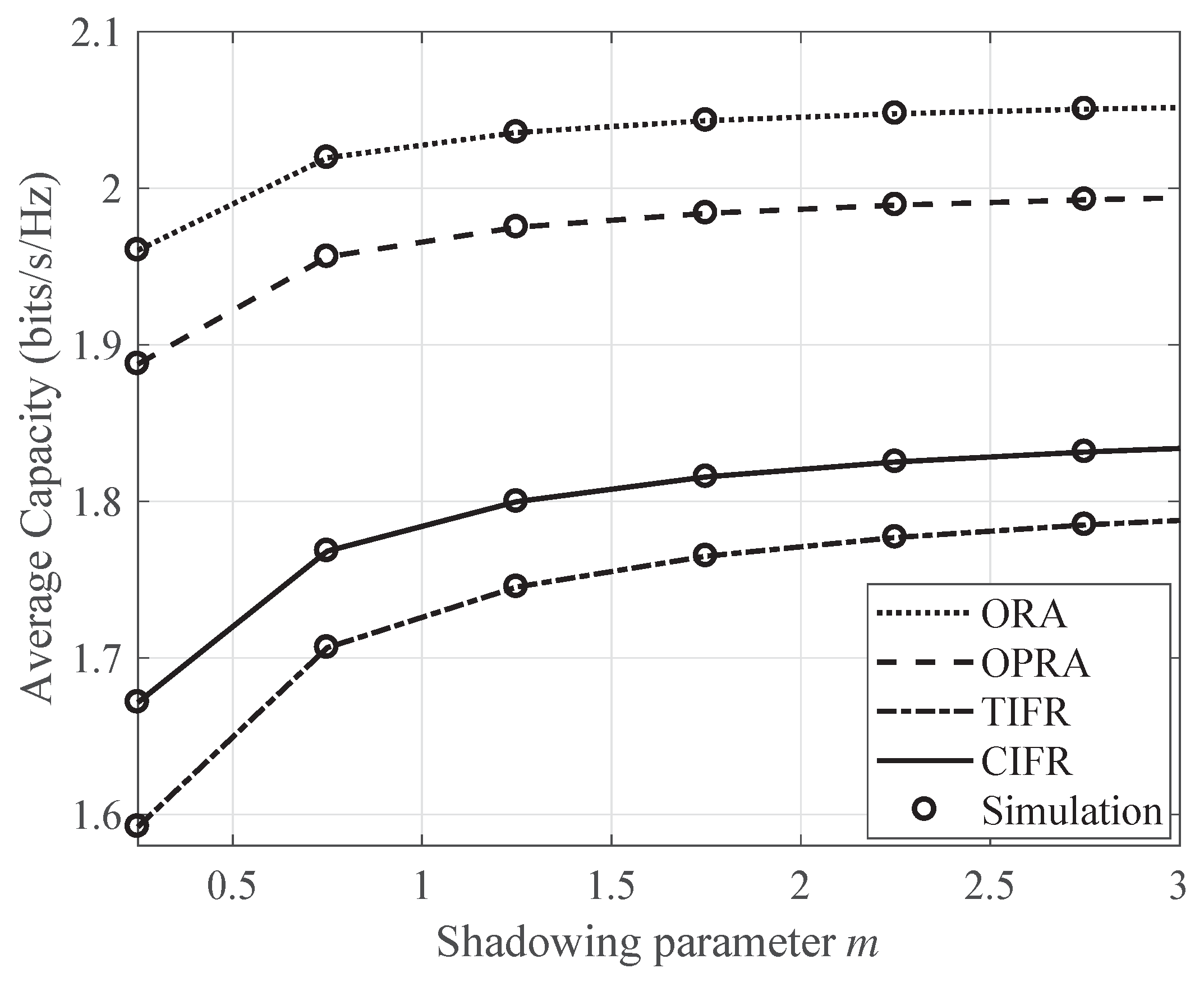
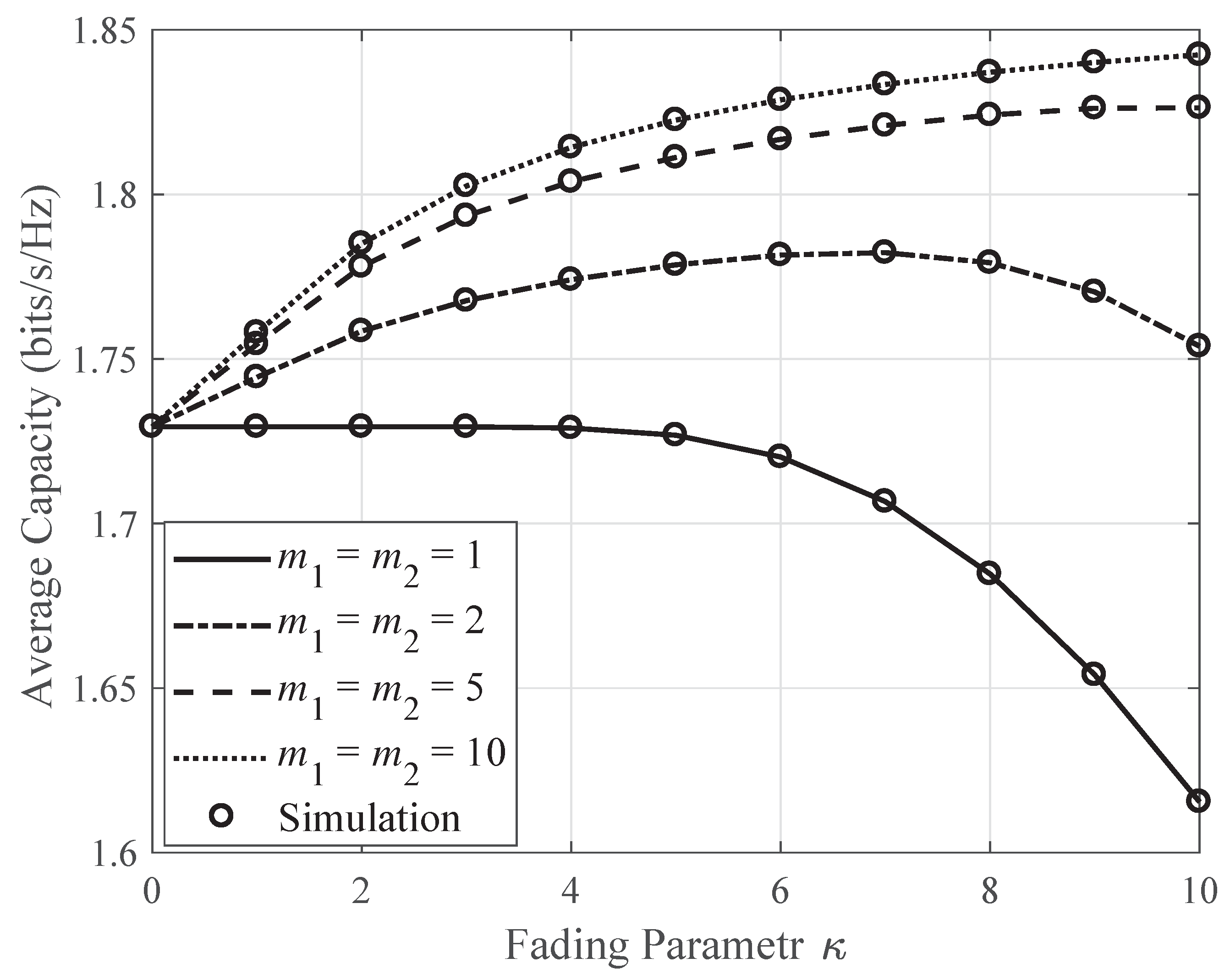
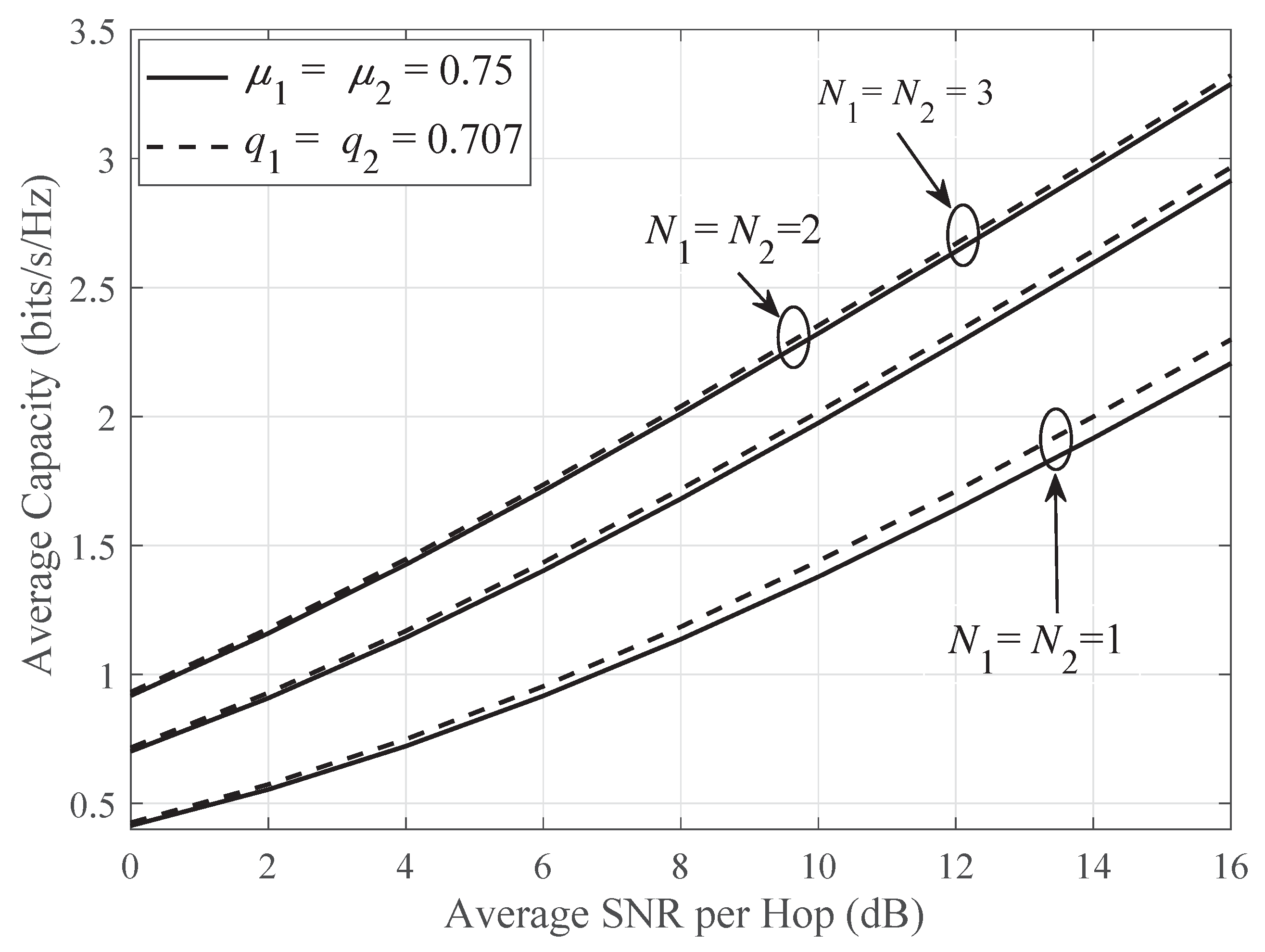
5. Numerical Results and Discussions
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Baki, A.K.M.; Absar, M.W.; Rehman, T.; Ahamed, K.M.A. Investigation of Rayleigh and Rician Fading Channels for State of the Art (SOA) LTE-OFDM Communication System. In Proceedings of the 4th International Conference on Advances in Electrical Engineering (ICAEE), Dhaka, Bangladesh, 28–30 September 2017. [Google Scholar]
- Kumar, R.; Aziz, A.; Joe, I. Opportunistic Relaying Analysis using Antenna Selection under Adaptive Transmission. IEICE Trans. Commun. 2016, E99-B, 2435–2441. [Google Scholar] [CrossRef]
- Hussain, A.; Kim, S.H.; Chang, S.H. On the Performance of Dual-Hop Variable-Gain AF Relaying with Beamforming over η-μ Fading Channels. IEICE Trans. Commun. 2017, E100-B, 619–626. [Google Scholar] [CrossRef]
- Hussain, A.; Kim, S.H.; Chang, S.H. Dual-hop Variable-Gain AF Relaying with Beamforming over κ–μ Shadowed Fading Channels. In Proceedings of the 2016 IEEE Global Communications Conference (GLOBECOM), Washington, DC, USA, 4–8 December 2016. [Google Scholar]
- Hussain, A.; Lee, K.; Kim, S.H.; Chang, S.H.; Kim, D.I. Performance Analysis of Dual-hop Variable-Gain Relaying with Beamforming over κ–μ Fading Channels. IET Commun. 2017, 11, 1587–1593. [Google Scholar] [CrossRef]
- Tran, T.; Voznak, M. Multi-Points Cooperative Relay in NOMA System with N-1 DF Relaying Nodes in HD/FD Mode for N User Equipments with Energy Harvesting. Electronics 2019, 8, 167. [Google Scholar] [CrossRef]
- Ai, Y.; Cheffena, M. On Multi-Hop Decode-and-Forward Cooperative Relaying for Industrial Wireless Sensor Networks. Sensors 2017, 17, 695. [Google Scholar] [CrossRef] [PubMed]
- Nyarko, J.K.N.; Mbom, C.A. A Performance Study of Massive MIMO Heterogeneous Networks with Ricean/Rayleigh Fading. Electronics 2018, 7, 79. [Google Scholar] [CrossRef]
- Nechiporenko, T.; Phan, K.T.; Tellambura, C.; Nguyen, H.H. On the Capacity of Rayleigh Fading Cooperative Systems under Adaptive Transmission. IEEE Trans. Wirel. Commun. 2009, 8, 1626–1631. [Google Scholar] [CrossRef]
- Nguyen, B.Q.; Doung, T.Q.; Tran, N.N. Ergodic Capacity of Cooperative Networks using Adaptive Transmission and Selection Combining. In Proceedings of the 3rd International Conference on Signal Processing and Communication Systems (ICSPCS), Omaha, NE, USA, 28–30 September 2009. [Google Scholar]
- Ikki, S.S.; Ahmed, M.H. On the Capacity of Relay-Selection Cooperative-Diversity Networks under Adaptive Transmission. In Proceedings of the 72nd IEEE Vehicular Technology Conference (VTC), Ottawa, ON, Canada, 6–9 September 2010. [Google Scholar]
- Torabi, M.; Haccoun, D.; Frigon, J.F. On the Performance of AF Opportunistic Relaying with Adaptive Transmission over Rayleigh Fading Channels. In Proceedings of the 2011 IEEE Pacific Rim Conference on Communications, Computers and Signal Processing, Victoria, BC, Canada, 22–24 August 2011. [Google Scholar]
- Kong, H.Y.; Bao, V.N. Capacity Analysis of Opportunistic Cooperative Networks under Adaptive Transmission over Rayleigh Fading Channels. Wirel. Pers. Commun. 2006, 62, 411–430. [Google Scholar] [CrossRef]
- Torabi, M.; Haccoun, D. Capacity of Amplify-and-Forward Selective Relying with Adaptive Transmission under Outdated Channel Information. IEEE Trans. Veh. Technol. 2011, 60, 2416–2422. [Google Scholar] [CrossRef]
- Torabi, M.; Haccoun, D.; Frigon, J.F. Impact of Outdated Relay Selection on the Capacity of AF Opportunistic Relaying Systems with Adaptive Transmission over Non-Identically Distributed Links. IEEE Trans. Wirel. Commun. 2011, 10, 3626–3631. [Google Scholar] [CrossRef]
- Kim, S.; Lee, S.; Lee, H.; Hong, D. Capacity Analysis of Outdated Relay Selection in Opportunistic Relaying System using an Adaptive Transmission Technique. In Proceedings of the 2014 IEEE Wireless Communications and Networking Conference (WCNC), Istanbul, Turkey, 3–6 April 2014. [Google Scholar]
- Zhong, B.; Zhang, X.; Li, Y.; Zhang, Z.; Long, K. Impact of Partial Relay Selection on the Capacity of Communications Systems with Outdated CSI and Adaptive Transmission Techniques. In Proceedings of the 2013 IEEE Wireless Communications and Networking Conference (WCNC), Shanghai, China, 7–10 April 2013. [Google Scholar]
- Bhatnagar, M.R. On the Capacity of Decode-and-Forward Relaying over Rician Fading Channels. IEEE Commun. Lett. 2013, 17, 1100–1103. [Google Scholar] [CrossRef]
- Modi, B.; Olabiyi, O.; Annamalai, A.; Vaman, D. On Ergodic Capacity of Cooperative Non-regenerative Relay Networks in Rice Fading Environments. In Proceedings of the IEEE Global Communications Conference, Houston, TX, USA, 5–9 December 2011. [Google Scholar]
- Modi, B.; Annamalai, A.; Olabiyi, O.; Palat, R.C. Ergodic Capacity Analysis of Cooperative Amplify-and-Forward Relay Networks over Rice and Nakagami Fading Channels. Int. J. Wirel. Mob. Netw. 2012, 14, 97–116. [Google Scholar] [CrossRef]
- Modi, B.; Annamalai, A.; Olabiyi, O.; Palat, R.C. Ergodic Capacity Analysis of Cooperative Amplify-and-Forward Relay Networks over Generalized Fading Channels. Wirel. Commun. Mob. Comput. 2015, 15, 1259–1273. [Google Scholar] [CrossRef]
- Phan, H.; Duong, T.Q.; Zepernick, H.J.; Shu, L. Adaptive Transmission in MIMO AF Relay Networks with Orthogonal Space-Time Block Codes over Nakagami-m Fading. EURASIP J. Wirel. Commun. Netw. 2011, 2012, 1–13. [Google Scholar] [CrossRef]
- Torabi, M.; Frigon, J.F.; Haccoun, D. Adaptive Transmission in Amplify-and-Forward Cooperative Communications using Orthogonal Space-Time Block Codes under Spatially Correlated Antennas. IET Commun. 2015, 9, 1683–1690. [Google Scholar] [CrossRef]
- Thanh, T.L.; Bao, V.N.Q.; Duy, T.T. Capacity Analysis of Multi-Hop Decode-and-Forward over Rician Fading Channels. In Proceedings of the 2014 International Conference on Computing, Management and Telecommunications (ICCMT), Da Nang, Vietnam, 27–29 April 2014. [Google Scholar]
- Farhadi, G.; Beaulieu, N.C. Capacity of Amplify-and-Forward Multi-Hop Relaying Systems under Adaptive Transmission. IEEE Trans. Commun. 2010, 58, 758–763. [Google Scholar] [CrossRef]
- Pairs, J.F. Statistical Characterization of κ–μ Shadowed Fading. IEEE Trans. Veh. Technol. 2014, 63, 518–526. [Google Scholar] [CrossRef]
- Corrales, C.G.; Canete, F.J.; Paris, J.F. Capacity of κ–μ Shadowed Fading Channels. Int. J. Antennas Propag. 2014, 2014, 1–8. [Google Scholar] [CrossRef]
- Martinez, F.J.; Paris, J.F.; Jerez, J.M. The κ–μ Shadowed Fading Model with Integer Fading Parameters. IEEE Trans. Veh. Technol. 2017, 66, 7653–7662. [Google Scholar] [CrossRef]
- Kumar, S. Approximate Outage Probability and Capacity for κ–μ Shadowed Fading. IEEE Wirel. Commun. Lett. 2015, 4, 301–304. [Google Scholar] [CrossRef]
- Aloqlah, M.S.; Atawi, M.S.; Mistarihi, M.F. On the Performance of Fixed Gain Amplify-and-Forward Dual-hop Relay Systems with Beamforming under κ–μ Shadowed Fading. In Proceedings of the IEEE Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), Hongkong, China, 30 August–2 September 2015. [Google Scholar]
- Arti, M.K. Beamforming and Combining Based Scheme over κ–μ Shadowed Fading Satellite Channels. IET Commun. 2016, 10, 1–9. [Google Scholar]
- Zhang, J.; Li, X.; Ansari, I.S.; Liu, Y.; Qaraqe, K.A. Performance Analysis of Dual-Hop DF Satellite Relaying over κ–μ Shadowed Fading. In Proceedings of the 2017 IEEE Wireless Communications and Networking Conference (WCNC), San Francisco, CA, USA, 19–22 March 2017. [Google Scholar]
- Hussain, A.; Kim, S.H.; Chang, S.H. Nonlinear Energy-Harvesting Relaying with Beamforming and Hardware Impairments in κ–μ Shadowed Fading Environment. Trans. Emerg. Telecommun. Technol. 2018, 29, e3303. [Google Scholar] [CrossRef]
- Ferdinand, N.S.; Rajatheva, N. Unified Performance Analysis of Two-Hop Amplify-and-Forward Relay Systems with Antenna Correlation. IEEE Trans. Wirel. Commun. 2011, 10, 3002–3011. [Google Scholar] [CrossRef]
- Costa, D.B.; Aissa, S. Beamforming in Dual-Hop Fixed Fain Relaying Systems. In Proceedings of the 2009 IEEE International Conference on Communications (ICC), Dresden, Germany, 14–18 June 2009. [Google Scholar]
- Costa, D.B.; Aissa, S. Cooperative Dual-Hop Relaying Systems with Beamforming over Nakagami-m Fading channels. IEEE Trans. Wirel. Commun. 2009, 8, 3950–3954. [Google Scholar] [CrossRef]
- Yang, N.; Elkashlan, M.; Yuan, J.; Shen, T. On the SER of Fixed Gain Amplify-and-Forward Relaying with Beamforming in Nakagami-m Fading. IEEE Commun. Lett. 2010, 14, 942–944. [Google Scholar] [CrossRef]
- Lin, M.; An, K.; Ouyang, J.; Huang, Y.; Li, M. Effect of Beamforming on Multi-Antenna Two hop Asymmetric Fading Channels with Fixed Gain Relays. Prog. Electron. Res. 2013, 133, 367–390. [Google Scholar] [CrossRef]
- Badarneh, O.S.; Mesleh, R. Cooperative Dual-Hop Wireless Communication Systems with Beamforming over η-μ Fading Channels. IEEE Trans. Veh. Technol. 2016, 65, 37–46. [Google Scholar] [CrossRef]
- Louie, R.H.Y.; Li, Y.; Vucetic, B. Performance Analysis of Beamforming in Two-Hop Amplify-and-Forward Relay Networks. In Proceedings of the 2008 IEEE International Conference on Communications (ICC), Beijing, China, 19–23 May 2008. [Google Scholar]
- Louie, R.H.Y.; Li, Y.; Vucetic, B. Performance Analysis of Beamforming in Two-Hop Amplify-and-Forward Relay Networks with Antenna Correlation. IEEE Trans. Wirel. Commun. 2009, 8, 3132–3141. [Google Scholar] [CrossRef]
- Duong, T.Q.; Zepernick, H.J.; Bao, V.N.Q. Symbol Error Probability of Hop-by-Hop Beamforming in Nakagami-m Fading. Electron. Lett. 2009, 45, 1042–1044. [Google Scholar] [CrossRef]
- Chen, S.; Liu, F.; Zhang, X.; Han, Y.; Yang, D. On the Performance of Two-Hop Amplify-and-Forward Relay Networks with Beamforming over Rayleigh-Rician Fading Channels. In Proceedings of the 72nd IEEE Vehicular Technology Conference (VTC), Ottawa, ON, Canada, 6–9 September 2010. [Google Scholar]
- Miridakis, N.I.; Vergados, D.D.; Michalas, A. Dual-Hop Communication over a Satellite Relay and Shadowed Rician Channels. IEEE Trans. Veh. Technol. 2015, 64, 4031–4040. [Google Scholar] [CrossRef]
- Kumar, R.; Aziz, A.; Joe, I. Cooperative Dual-Hop Decode-and-Forward Relaying with Beamforming over κ–μ Fading Channels. J. Next Gen. Technol. 2016, 7, 38–49. [Google Scholar]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products, 7th ed.; Academic Press: San Diego, CA, USA, 2007. [Google Scholar]
- Vagenas, E.D.; Karadimas, P.; Kotsopoulos, S.A. Ergodic Capacity for the SIMO Nakagami-m Channel. EURASIP J. Wirel. Commun. Netw. 2009, 2009, 1–9. [Google Scholar] [CrossRef]
- Simon, M.K.; Alouini, M.-S. Digital Communication over Fading Channels, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2000. [Google Scholar]
| Fading Distribution | m | ||
|---|---|---|---|
| Rician shadowed | |||
| Nakagami- | |||
| Rician | |||
| Rayleigh | |||
| One-sided Gaussian |
| First Hop/Second Hop | ||||||
|---|---|---|---|---|---|---|
| shadowed/ | ∞ | |||||
| shadowed/Rician-shadowed | 1 | |||||
| shadowed/Rician | 1 | ∞ | ||||
| shadowed/Nakagami- | 0 | ∞ | ||||
| shadowed/Rayleigh | 0 | 1 | ∞ | |||
| / | ∞ | ∞ | ||||
| / shadowed | ∞ | |||||
| /Rician-shadowed | 1 | ∞ | ||||
| /Rician | 1 | ∞ | ∞ | |||
| /Nakagami- | 0 | ∞ | ∞ | |||
| /Rayleigh | 0 | 1 | ∞ | ∞ | ||
| Rician-shadowed/Rician-shadowed | 1 | 1 | ||||
| Rician-shadowed/ shadowed | 1 | |||||
| Rician-shadowed/ | 1 | ∞ | ||||
| Rician-shadowed/Rician | 1 | 1 | ∞ | |||
| Rician-shadowed/Nakagami- | 1 | 0 | ∞ | |||
| Rician-shadowed/Rayleigh | 1 | 0 | 1 | ∞ | ||
| Rician/Rician | 1 | 1 | ∞ | ∞ | ||
| Rician/ shadowed | 1 | ∞ | ||||
| Rician/ | 1 | ∞ | ∞ | |||
| Rician/Rician-shadowed | 1 | 1 | ∞ | |||
| Rician/Nakagami- | 1 | 0 | ∞ | ∞ | ||
| Rician/Rayleigh | 1 | 0 | 1 | ∞ | ∞ | |
| Nakagami-/Nakagami- | 0 | 0 | ∞ | ∞ | ||
| Nakagami-/ shadowed | 0 | ∞ | ||||
| Nakagami-/ | 0 | ∞ | ∞ | |||
| Nakagami-/Rician-shadowed | 0 | 1 | ∞ | |||
| Nakagami-/Rician | 0 | 1 | ∞ | ∞ | ||
| Nakagami-/Rayleigh | 0 | 0 | 1 | ∞ | ∞ | |
| Rayleigh/Rayleigh | 0 | 1 | 0 | 1 | ∞ | ∞ |
| Rayleigh/ shadowed | 0 | 1 | ∞ | |||
| Rayleigh/ | 0 | 1 | ∞ | ∞ | ||
| Rayleigh/Rician-shadowed | 0 | 1 | 1 | ∞ | ||
| Rayleigh/Rician | 0 | 1 | 1 | ∞ | ∞ | |
| Rayleigh/Nakagami- | 0 | 1 | 0 | ∞ | ∞ |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhutto, Z.; Yoon, W. Dual-Hop Cooperative Relaying with Beamforming Under Adaptive Transmission in κ–μ Shadowed Fading Environments. Electronics 2019, 8, 658. https://doi.org/10.3390/electronics8060658
Bhutto Z, Yoon W. Dual-Hop Cooperative Relaying with Beamforming Under Adaptive Transmission in κ–μ Shadowed Fading Environments. Electronics. 2019; 8(6):658. https://doi.org/10.3390/electronics8060658
Chicago/Turabian StyleBhutto, Zuhaibuddin, and Wonyong Yoon. 2019. "Dual-Hop Cooperative Relaying with Beamforming Under Adaptive Transmission in κ–μ Shadowed Fading Environments" Electronics 8, no. 6: 658. https://doi.org/10.3390/electronics8060658
APA StyleBhutto, Z., & Yoon, W. (2019). Dual-Hop Cooperative Relaying with Beamforming Under Adaptive Transmission in κ–μ Shadowed Fading Environments. Electronics, 8(6), 658. https://doi.org/10.3390/electronics8060658





