Abstract
During the non-contact geomagnetic detection of pipeline defects, measured signals generally contain noise, which reduces detection efficiency. Complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN) has recently emerged as a signal filtering method, but its filtering performance is influenced by two parameters: the amplitude of added noise and the number of ensemble trials. To solve this issue and improve detection accuracy and distinguishability, a detection method based on improved CEEMDAN (ICEEDMAN) and the Teager energy operator (TEO) is proposed. The magnetic detection signal was first decomposed into a series of intrinsic mode functions (IMFs) by CEEMDAN with initial parameters. Signal IMFs were then distinguished using the Hurst exponent to reconstruct the preliminary filtered signal, and its maximum value (except the zero point) of the normalized autocorrelation function was defined as salp swarm algorithm (SSA) fitness. The optimal parameters that maximize fitness were found by SSA iterations, and their corresponding filtered signal was obtained. Finally, the gradient calculation and TEO were carried out to complete non-contact geomagnetic detection. The results of the simulated signal based on magnetic dipole under a noisy environment and field testing prove that ICEEMDAN denoising has better filtering performance than conventional CEEMDAN denoising methods, and ICEEMDAN-TEO has obvious advantages compared to other detection methods in the aspects of location error, peak side-lobe ratio, and integrated side-lobe ratio.
1. Introduction
Buried steel pipelines are used for oil and gas transportation across the world and thus directly influence national economies and public security. However, pipelines are invariably attacked by surrounding factors such as corrosion, natural disasters, and stress and must be regularly inspected to reduce the risk of failure. A well-proven technique for the pipelines inspection uses in-line inspection (ILI) tools or inspection robotics [1,2] which utilize magnetic flux leakage (MFL) [3,4], pulsed eddy current (PEC) [5,6], ultrasonic technology (UT) [7], electromagnetic acoustic transducer (EMAT) [8], and radiographic technology [9]. Nevertheless, their practicality is restricted by the limitations of inspection robotics. External inspection techniques represented by the transient electromagnetic method (TEM) [10] and Nopig [11] can be applied for the inspection of buried steel pipelines where the use of ILI is challenging. However, these techniques have low detection efficiencies and are influenced by the excitation source.
Non-contact geomagnetic detection, a passive non-destructive testing technology, has been successfully implemented to evaluate the integrity of buried steel pipelines under trenchless conditions [12,13]. This technology identifies pipeline defects by measuring ground leakage magnetic fields. The measured signals typically contain substantial random noise, including environmental disturbances and instrument noise, which dramatically affect the detection consequences of pipeline defects. To improve the non-contact geomagnetic detection efficiency, it is essential to implement a useful method to suppress noise.
Thus far, there are many filtering methods available for noisy signals. Traditional filters, such as the moving average filter [14] and Winner filter [15], are only suitable for stationary and linear signals. Wavelet threshold denoising [16] is a common non-linear method used to reduce noise, but its wavelet base and decomposition layer need to be predefined. The empirical mode decomposition (EMD) method was proposed by Huang [17], which was demonstrated to be a powerful tool that deals with non-stationary and non-linear signals [18,19,20]. The multicomponent signal can be adaptively decomposed into a succession of oscillatory functions, which are called the intrinsic mode functions (IMFs). The EMD has excellent filtering performance for noisy signals [21,22,23]. However, the mixing of modes heavily impacts the EMD effect. To alleviate this drawback, Wu developed ensemble empirical mode decomposition (EEMD) [24], which is viewed as multiple EMDs with added white Gaussian noise. However, the EEMD produces residual noise and generates different modes using different iterations [25]. The complementary EEMD (CEEMD) was proven to overcome the reconstruction problem by adding paired positive and negative white Gaussian noise, but the redundant modes problem still exists [26]. Therefore, the complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN) was presented to achieve accurate reconstruction and solve the redundant modes [27,28,29].
Although CEEMDAN denoising has a stronger filtering ability than EMD, EEMD, and CEEMD denoising [30,31,32], it is also necessary to study how the selection of two parameters (the amplitude of added noise and the number of ensemble trials) must be performed, as they directly influence decomposition and filtering performance. If the added amplitude of noise is too small, the different time-scale signals cannot be automatically distributed to a suitable reference scale. Therefore, the mode mixing problem cannot be efficiently solved. On the contrary, an excessively large amplitude of added noise will generate redundant IMF components. An unlimited number of ensemble trials is needed to offset the influence of white noise. However, this is unrealistic for the real-world signals. In the current research on CEEMDAN denoising, these parameters are defined as constant values [33,34], which result in great blindness for different kinds of signals. To achieve accurate non-contact geomagnetic detection, the filtering performance of CEEMDAN denoising for noisy signals needs to be further enhanced.
Gradient calculation is a common method to amplify magnetic signals of pipeline defects, but its effect is not apparent as encountering strong noise [35,36]. The Teager energy operator (TEO) is a non-linear difference operator [37]. TEO estimates the total energy required for the source to produce a dynamic signal which can calculate instantaneous amplitude and instantaneous frequency and extract instantaneous energy. This method has been successfully applied in speech recognition [38], bearing fault detection [39], and power system oscillation diagnosis [40]. However, the research about TEO that applies to magnetic signals is almost blank.
In this paper, a non-contact geomagnetic detection methodology based on improved CEEMDAN (ICEEMDAN) and TEO is proposed. First, the magnetic detection signal was decomposed into a series of IMFs via CEEMDAN with an initial amplitude of added noise and a number of ensemble trials. Second, signal IMFs were distinguished via computing the Hurst exponent to reconstruct the preliminary filtered signal. Third, the maximum value (except for the zero point) of the normalized autocorrelation function of the preliminary filtered signal was then calculated as fitness. Fourth, the optimal parameters that maximize fitness were sought via salp swarm algorithm (SSA) iterations, and the final filtered signal was obtained. Finally, the gradient calculation and TEO were used to identify the locations of pipeline defects.
2. Relevant Principles
2.1. EMD
The EMD can self-adaptively decompose a signal into a series of IMFs and a residue. The IMF must meet two conditions: (a) the difference between the number of extremum points and zero-crossing is equal to zero or one and (b) the mean value of the upper envelope and the lower envelope is zero. The flowchart of EMD is shown in Figure 1. The EMD steps can be defined as follows [41,42]:
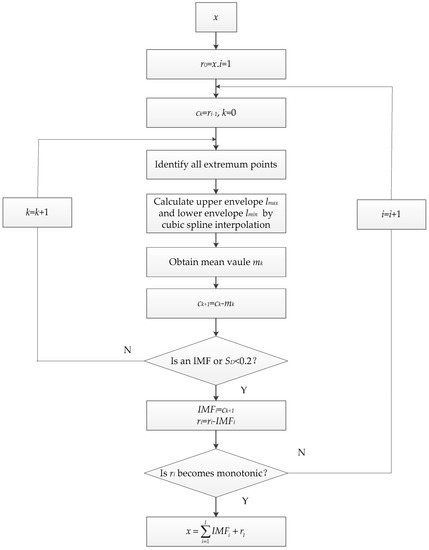
Figure 1.
A flowchart of the empirical mode decomposition (EMD).
- (1)
- Identify all extremum points and define an upper and lower envelope, and , respectively, using a cubic spline interpolation.
- (2)
- Compute the mean envelope.
- (3)
- Calculate the first IMF candidate as follows:
- (4)
- If satisfies IMF conditions, define . Otherwise, treat as the new signal and repeat the above sifting procedure times until an is IMF, as follows:However, continuous sifting to calculate IMF is not possible in reality. The stopping criterion is defined to finish the iteration.If the ( is set to 0.2 in this study), the iteration will be stopped.
- (5)
- Let replace and repeat Steps (1) to (4) to obtain the next IMF. The EMD process will be terminated when the residue is a monotonic function. Finally, the signal can be defined as:
However, EMD has a serious mode mixing problem, which is defined as oscillations of different scales coexisting in a mode or oscillations of similar scales existing in different modes. Therefore, this problem not only decreases the decomposition efficiency but also degrades the filtering performance.
2.2. CEEMDAN
To alleviate the mode mixing problem and improve the decomposition precision, CEEMDAN was proposed by Torres. The flowchart of CEEMDAN is shown in Figure 2. The CEEMDAN process can be defined as follows [43,44]:
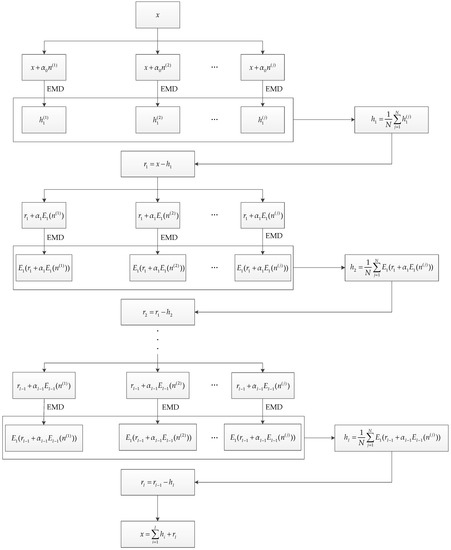
Figure 2.
A flowchart of the complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN).
- (1)
- Decompose to obtain the first IMF using EMD.where is the amplitude of the added white noise, is the white noise under the circumstances of the jth ensemble trials, and N is a total number of ensemble trials.
- (2)
- Calculate the first residue.
- (3)
- Decompose to acquire the first mode and compute the second IMF.
- (4)
- For , compute the ith residue.
- (5)
- Decompose to acquire the first mode and calculate the (i + 1)th IMF as:where represents the ith IMF by EMD.
- (6)
- Repeat Steps (4) to (5) until the residue no longer be decomposed. The signal can be represented as:
2.3. IMF Selection Method Based on the Hurst Exponent
The Hurst exponent is an effective index to examine randomness for a time series [45,46], and this was utilized to distinguish signal IMFs and noise IMFs in this study. The aggregated variance method can calculate the Hurst exponent of a signal. The steps for this can be defined as follows:
- (1)
- For times series , set the window size to .
- (2)
- Compute the standard deviation of and record the point .
- (3)
- Find the average data of the adjacent points and overwrite the original data.
- (4)
- Rescale appropriately as .
- (5)
- When , repeat Steps (2) to (4).
- (6)
- Plot the log–log graph and calculate its slope as Hurst exponent h.
In this paper, IMFs with were defined as signal IMFs decomposed by CEEMDAN [47,48].
2.4. Salp Swarm Algorithm
SSA is a novel heuristic swarm intelligence algorithm inspired by the swarming behavior of salp: salp chain, which has been applied for cantilever beam design, welded beam design, and two-dimensional airfoil design [49]. SSA defines the salp population as two classes: leader and followers. The first salp in the chain is a leader, and the rest of salps are followers. The locations of salps are defined in n-dimensional space, where n represents the number of optimized parameters. The locations of all salps exist in the matrix . The food source is a target for the salp swarm.
The location of the leader in the jth dimension is updated using the following formula.
where is the location of the leader salp, is the location of the food source, is the upper boundary, is the lower boundary, and , , and represent random numbers.
is the most significant coefficient because it controls leader exploration and exploitation, which can be expressed as:
where is the current iteration, and is the maximum number of iterations. The coefficients and are random numbers in the interval of [0,1]. The locations of followers in the jth dimension is updated using following the formula.
where , is the location of ith follower, is time, is the initial velocity, and where . As the difference between iterations is equal to one and , Equation (15) can be revised to become:
The SSA begins with initializing random locations for salps. The fitness of each salp is then calculated to seek the best fitness, and its location is defined as the food source (). During this period, the coefficient is updated utilizing Equation (14), and the location of leader salp is updated utilizing Equation (13). In addition, the locations of follower salps are updated utilizing Equation (16). If the location of any salp is beyond the search region, it will be got back on the upper or lower boundary. The above steps, except for initialization, are required to be reiteratively executed until the final result satisfies predefined criteria.
2.5. Teager Energy Operator
The Teager energy operator (TEO) is a nonlinear operator, which was used to improve defect identification ability [50]. For signal , TEO is defined as:
where is the first derivative of signal with respect to time t, and is the second derivative.
A linear undamped vibration system was composed of an object with mass and a spring with stiffness , and its motion equation is:
where is the displacement of the object relative to the equilibrium position, is the vibration amplitude, is inherent frequency, and is initial phase. The instantaneous total energy of the system is:
By substituting from Equation (18) into Equation (17), the following equation is derived.
By comparing Equation (19) and Equation (20), it can be seen that there is a constant difference between the output of the energy operator and the instantaneous total energy of the undamped vibration system, Thus, the TEO can accurately reflect the total energy required to generate an undamped vibration.
For a discrete time signal (), the difference is used instead of differentiation. Thus, TEO can be rewritten as:
For a discrete time signal, TEO only needs three sample data in order to calculate the signal energy at n. Therefore, TEO has a good time resolution for the instantaneous changes of the signal and can detect the transient components in the signal.
3. Geomagnetic Detection for Pipeline Defects Using ICEEMDAN and TEO
The normalized autocorrelation function is a measurement method in the time domain and reflects the similarity signal itself at a different time, which can be defined as:
where represents the normalized autocorrelation function, and represents the mean value. The normalized autocorrelation function of noise has a maximum value at the zero point and immediately goes to zero at the rest of the point. The normalized autocorrelation function of the actual signal has a maximum value at the zero point and slowly descends to zero at the rest of the points. According to the above properties, we propose a geomagnetic detection method based on ICEEMDAN and TEO, which is represented by the flowchart shown in Figure 3. The steps are as follows:
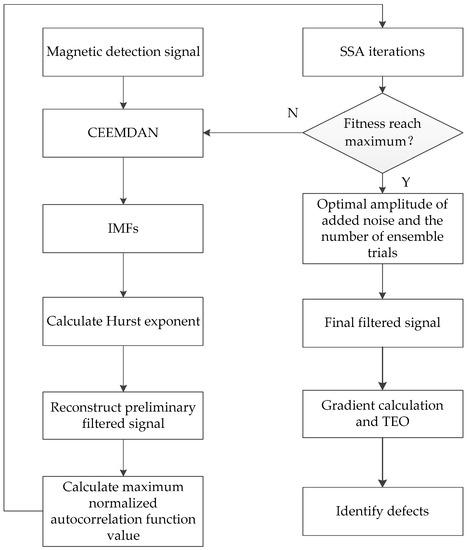
Figure 3.
A flowchart of the proposed method.
- (1)
- Decompose the magnetic detection signal by CEEMDAN, with an initial noise amplitude and ensemble trial number, into a series of IMFs. Signal IMFs are then extracted using the Hurst exponent to reconstruct the preliminary filtered signal.
- (2)
- Calculate the maximum value (except for the zero point) of the normalized autocorrelation function of the preliminary filtered signal as the SSA fitness and update the values of two parameters using SSA iterations.
- (3)
- Repeat Steps (1) to (2) until the optimal amplitude of added noise and the number of ensemble trials to maximize fitness is found and their corresponding filtered signal is a final clean magnetic signal.
- (4)
- Use gradient calculation and TEO to amplify the amplitude of defect signal and then identify pipeline defects.
4. Numerical Simulation
Generally, a pipeline defect can be considered as a magnetic dipole because the distance between the defect and the detection point is 2.5 times greater than the maximum dimension of the defect [51]. If the dipole moment and the displacement vector from the source to the measurement point , the magnetic field vector is:
The magnetic moment can be defined as:
where is the damage volume, is the magnetic susceptibility, and is the geomagnetic field intensity.
Three components of geomagnetic field intensity can be expressed as:
where is a magnetic inclination, and is a magnetic declination.
Figure 4 illustrates a defect on the pipeline upper surface locating the coordinate original, with length a of 0.1 m, width b of 0.3 m, depth c of 0.003 m. The magnetic susceptibility . The measurement length is 2L = 20 m, and the sampling interval is o = 0.1 m. The distance between the sensor to ground is h1 = 0.5 m, the distance between ground to pipeline upper surface is h2 = 1 m. The geomagnetic field intensity is H = 43.56 A/m, the magnetic declination is , and the magnetic inclination is .
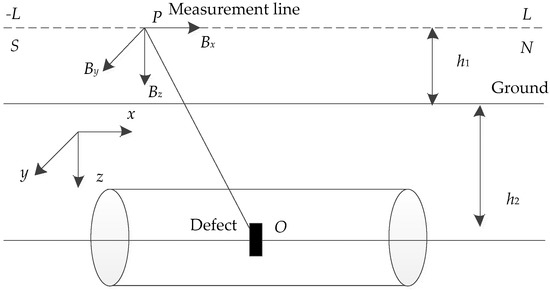
Figure 4.
The pipeline defect model.
The axial component of the defect magnetic signal generated by the Figure 4 model was considered as an input signal to evaluate the proposed methods availability. White Gaussian noise was added to original signal with an input signal-to-noise ratio at 5 dB. In order to clearly verify the ICEEMDAN denoising effectiveness, conventional CEEMDAN denoising 1 (i.e., the amplitude of added noise is 0.1 and the number of ensemble trials is 300 as described in Reference [33]), conventional CEEMDAN denoising 2 (i.e., the amplitude of added noise is 0.2 and the number of ensemble trials is 500 as described in Reference [34]), and ICEEMDAN denoising were utilized to filter noisy signals. For SSA, the range of the added noise amplitude was 0.01–0.5, the range of ensemble trials number was 1–500, the number of search agents was 20, and the maximum number of iterations was 100. To clearly compare different methods, signal-to-noise ratio (SNR) and root mean square error (RMSE) were used to evaluate filtering performance.
where is the original signal, is the denoised signal, and is the sampling point.
The optimal the amplitude of added noise and the number of ensemble trials were equal to 0.196 and 58, respectively. Figure 5 shows the noisy signal and filtered signal based on conventional CEEMDAN denoising 1, conventional CEEMDAN denoising 2, and ICEEMDAN denoising. It is evident that the three denoising methods have the ability to remove noise. Table 1 presents the SNR and RMSE of three denoising methods. As seen in Table 1, the ICEEMDAN denoising had a maximum SNR and minimum RMSE. As expected, ICEEMDAN denoising had better filtering performance than conventional CEEMDAN denoising.
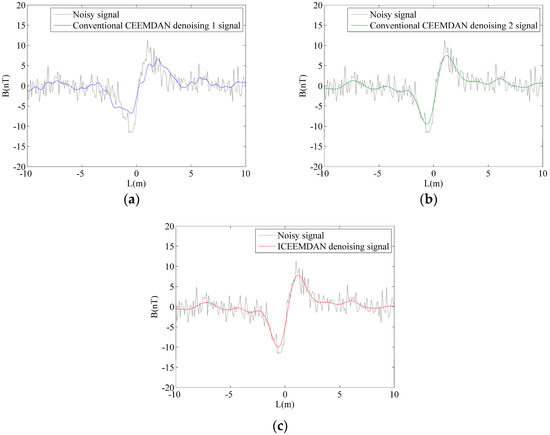
Figure 5.
The noisy signal and three denoised signals. (a) Conventional CEEMDAN denoising 1. (b) Conventional CEEMDAN denoising 2. (c) ICEEMDAN denoising.

Table 1.
Signal-to-noise ratio (SNR) and root mean square error (RMSE) of the three denoising methods.
Location error, peak side-lobe ratio (PSLR), and integrated side-lobe ratio (ISLR) were used to evaluate detection accuracy and distinguishability. Location error was defined as the absolute value of the difference between signal peak location () and actual defect location ().
PSLR [52] and ISLR [53] are determined as:
where represents the value of the highest side lobe (second highest peak), represents the value of main lobe (highest peak), represents all side lobe energy, and represents for main lobe energy. Smaller PSLR and ISLR values mean better detection consequences.
Figure 6 presents the detection results of conventional CEEMDAN denoising 1-TEO, conventional CEEMDAN denoising 2-TEO, ICEEMDAN-gradient, and the proposed method. As shown in Figure 6, the proposed method had the clearest detection effect. The location error, PSLR, and ISLR based on four methods are presented in Table 2. The error of the proposed method was smaller than in other detection methods. In addition, the PSLR of the proposed method was higher than that of conventional CEEMDAN denoising 1-TEO by approximately 6.00 dB, conventional CEEMDAN denoising 2-TEO by approximately 6.03 dB, and ICEEMDAN-gradient by approximately 3.84 dB. For the ISLR index, the ISLR of the proposed method was higher than that of conventional CEEMDAN denoising 1-TEO by approximately 12.60 dB, conventional CEEMDAN denoising 2-TEO by approximately 11.49 dB, and ICEEMDAN-gradient by approximately 8.03 dB. Therefore, the proposed method has a better detection accuracy and defect identification ability than other conventional detection methods.
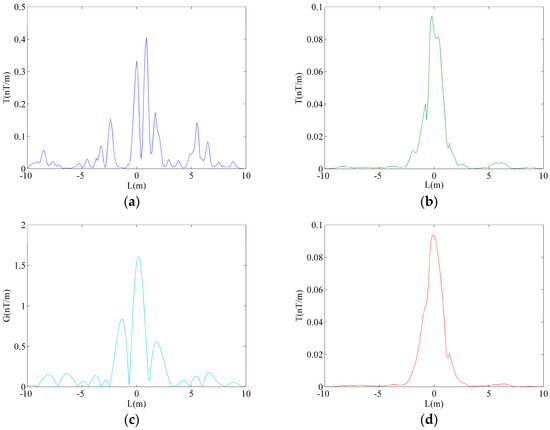
Figure 6.
The four detection results for the simulation signal. (a) Conventional CEEMDAN denoising 1-TEO. (b) Conventional CEEMDAN denoising 2-TEO. (c) ICEEMDAN-gradient. (d) Proposed method.

Table 2.
The evaluation indexes of the detection results based on different methods.
5. Experiment Verification
Figure 7 shows a field-testing process for the buried pipeline. The measurement system contained high-precision magnetic TMR2309 sensors (with a measurement range of ±10 Oe and a sensitivity of 100 mV/V/Oe), an ADLINK USB-1901 data acquisition card (with a resolution of 16-Bits and a sampling rate of 250 kS/s), an industrial personal computer, and GPS. The segment pipeline was made from Q235 steel with a diameter of 323 mm, a wall thickness of 5 mm, a buried depth of 1 m, and an operating pressure of 2.5 Mpa. It was put into production in Hebei Province, China.

Figure 7.
Field testing for the buried pipeline.
Figure 8 shows the magnetic detection signal and gradient signal in field testing. Due to the original signal containing a lot of random noise, it was difficult to locate defects from the gradient signal. The optimal amplitude of added noise was 0.480, and the number of ensemble trials was 126 by SSA. Their corresponding decomposition results are shown in Figure 9. It is evident that the magnetic detection signal was decomposed into 10 IMFs and a residue. The noise was concentrated in the first few IMFs and decreased as the IMF number increased. The calculation results of the Hurst exponent for each IMF are shown in Table 3. According to the selection rule, the IMF6-10 and residue were selected to reconstruct the filtered signal.
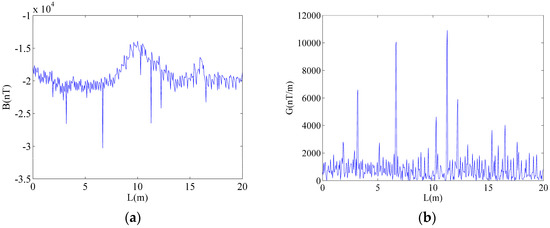
Figure 8.
The magnetic detection signal. (a) Original signal. (b) Gradient signal.
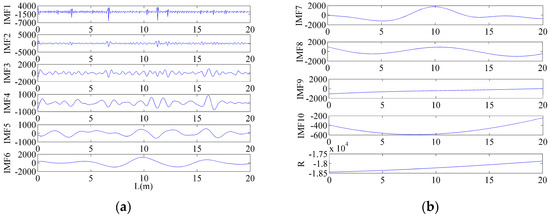
Figure 9.
Decomposition results of the magnetic detection signal via optimal CEEMDAN. (a) IMF1–IMF6 results. (b) IMF7–IM10 and residue results.

Table 3.
Calculation results of the Hurst exponent.
Figure 10 shows the magnetic detection signal and filtered signal using conventional CEEMDAN denoising 1, conventional CEEMDAN denoising 2, and ICEEMDAN denoising. It shows that three methods are able to extract signal fluctuation characteristics. After examining it carefully, the filtered signal based on the ICEEMDAN denoising was found to be smoother than in other methods.
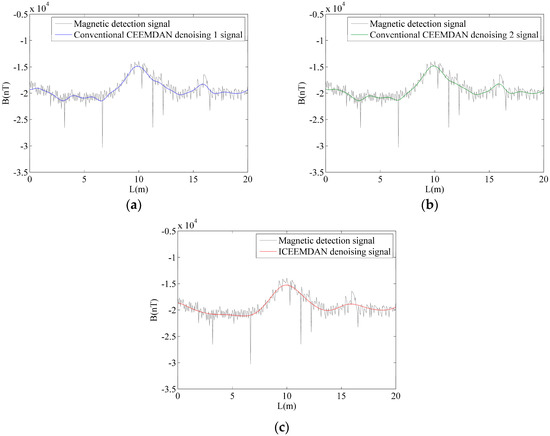
Figure 10.
Figure10. The filtering results of three denoising methods. (a) Conventional CEEMDAN denoising 1. (b) Conventional CEEMDAN denoising 2. (c) ICEEMDAN denoising.
Detrended fluctuation analysis (DFA) is a useful method for researching the fluctuation of time series, which can remove the different orders of foreign trends and show the statistical behavior characteristics accurately [54]. The scaling index represents the roughness of the times series. A larger means a smoother time series. DFA has been successfully used to evaluate filtering performance for impact signals [55] and pipeline leakage signals [56]. The of each denoising method is shown in Figure 11. It is evident that the of the ICEEMDAN denoising is larger than that of the other denoising methods. The results prove that ICEEMDAN denoising can adaptively select parameters to achieve the most effective filtering for the noisy magnetic detection signal.
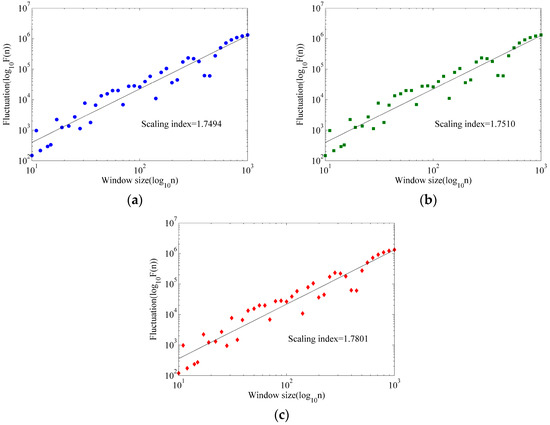
Figure 11.
The scaling index of four denoising methods. (a) Conventional CEEMDAN denoising 1. (b) Conventional CEEMDAN denoising 2. (c) ICEEMDAN denoising.
Figure 12 and Table 4 show the detection results and evaluation indexes of conventional CEEMDAN denoising 1-TEO, conventional CEEMDAN denoising 2-TEO, ICEEMDAN-gradient, and the proposed method. After pavement opening, a scratch defect (with a length of 10 mm, width of 5 mm, and depth of 1.5 mm) was found on the pipeline at 9 m. From Table 4, it is evident that the proposed method had a minimum location error in the four methods. For the PSLR index, the PSLR of the proposed method was higher than that of conventional CEEMDAN denoising 1-TEO by approximately 6.42 dB, conventional CEEMDAN denoising 2-TEO by approximately 4.21 dB, and ICEEMDAN-gradient by approximately 5.41 dB. The ISLR of the proposed method was higher than that of conventional CEEMDAN denoising 1-TEO by approximately 11.57 dB, conventional CEEMDAN denoising 2-TEO by approximately 6.95 dB, and ICEEMDAN-gradient by approximately 6.35 dB. In conclusion, the proposed method can detect buried pipeline defects precisely and efficiently.
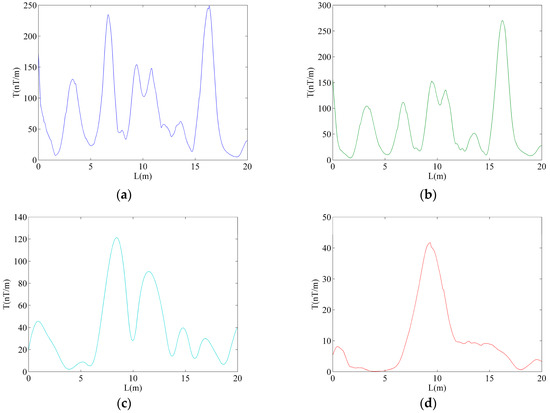
Figure 12.
The four detection results of field testing. (a) Conventional CEEMDAN denoising 1-TEO. (b) Conventional CEEMDAN denoising 2-TEO. (c) ICEEMDAN-gradient. (d) Proposed method.

Table 4.
The evaluation indexes of the four detection results.
6. Conclusions
In this paper, a non-contact geomagnetic detection method using ICEEMDAN and TEO is proposed. According to the difference of normalized autocorrelation function values between signal and noise, ICEEMDAN uses SSA to adaptively find the optimal amplitude of added noise and the number of ensemble trials. This improves CEEMDAN filtering performance. In addition, TEO is used to further enhance the amplitude of defect magnetic signals and improve detection distinguishability. The simulation results of the defect magnetic signal based on magnetic dipole in a noisy environment certified that ICEEMDAN denoising has a higher SNR and smaller RMSE than conventional CEEMDAN denoising methods, and ICEEMDAN-TEO is superior to other detection methods in terms of location error, PSLR, and ISLR. In this study, the practical magnetic detection signal of field testing was used to validate that ICEEMDAN denoising performs more effective filtering and produces a smoother signal compared to the other denoising methods as evaluated by DFA, and ICEEMDAN-TEO has a higher detection accuracy and distinguishability than other detection methods. In the future, the proposed method will require further verification via more non-contact geomagnetic detection applications.
Author Contributions
Data curation, Y.Z.; Formal analysis, T.Z.; Funding acquisition, X.W.; Methodology, T.Z.; Software, Z.U.; Supervision, Y.C.; Validation, H.J.; Writing—original draft, T.Z.; Writing—review & editing, X.W.
Funding
This research was funded by the National Key Research and Development Program of China (grant number 2017YFC0805005), the Joint Program of Beijing Municipal Natural Science Foundation Commission and Beijing Municipal Education Commission (grant number 18JH0005), and Rixin Scientist of Beijing University of Technology.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Miro, J.V.; Ulapane, N.; Shi, L.; Hunt, D.; Behrens, M. Robotic pipeline wall thickness evaluation for dense nondestructive testing inspection. J. Field Robot. 2018, 35, 1293–1310. [Google Scholar] [CrossRef]
- Mirats-Tur, J.M.; Garthwaite, W. Robotic devices for water main in-pipe inspection: A survey. J. Field Robot. 2010, 27, 491–508. [Google Scholar] [CrossRef]
- Hari, K.C.; Nabi, M.; Kulkarni, S.V. Improved FEM model for defect-shape construction from MFL signal by using genetic algorithm. Iet Sci. Meas. Technol. 2007, 1, 196–200. [Google Scholar] [CrossRef]
- Afzal, M.; Udpa, S. Advanced signal processing of magnetic flux leakage data obtained from seamless gas pipeline. NDT&E Int. 2002, 35, 449–457. [Google Scholar] [CrossRef]
- Ulapane, N.; Alempijevic, A.; Calleja, T.V.; Miro, J.V. Pulsed eddy current sensing for critical pipe condition assessment. Sensors 2017, 17, 2208. [Google Scholar] [CrossRef] [PubMed]
- Miro, J.V.; Hunt, D.; Ulapane, N.; Behrens, M. Towards automatic robotic NDT dense mapping for pipeline integrity inspection. In Proceedings of the Robotics Field and Service, ETH Zurich, Switzerland, 12–15 September 2017. [Google Scholar] [CrossRef]
- Skjelvareid, M.H.; Birkelund, Y.; Larsen, Y. Internal pipeline inspection using virtual source synthetic aperture ultrasound imaging. NDT&E Int. 2013, 54, 151–158. [Google Scholar] [CrossRef]
- Yeomans, M.; Ashworth, B.; Strohmeier, U. Development of 36” EmatScan® crack detection (CD) tool. In Proceedings of the 4th International Pipeline Conference, Calgary, AB, Canada, 29 September–3 October 2002. [Google Scholar] [CrossRef]
- Liu, Z.; Kleiner, Y. State of the art review of inspection technologies for condition assessment of water pipes. Measurement 2013, 46, 1–15. [Google Scholar] [CrossRef]
- Dang, B.; Yang, L.; Liu, C.; Zheng, Y.; Li, H.; Dang, R.; Sun, B. A uniform linear multi-coil array-based borehole transient electromagnetic system for non-destructive evaluations of downhole casings. Sensors 2018, 18, 2707. [Google Scholar] [CrossRef] [PubMed]
- Caleyo, F.; Valor, A.; Alfonso, L.; Vidal, J.; Perez-Baruchd, E.; Hallena, J.M. Bayesian analysis of external corrosion data of non-piggable underground pipelines. Corros. Sci. 2015, 90, 33–45. [Google Scholar] [CrossRef]
- Li, C.C.; Chen, K.; Liao, A. Quantitative study of signal characteristics of non-contact pipeline magnetic testing. Insight 2015, 57, 324–330. [Google Scholar] [CrossRef]
- Li, Z.; Jarvis, R.; Nagy, P.B.; Dixon, S.; Cawley, P. Experimental and simulation methods to study the magnetic tomography method (Mtm) for pipe defect detection. NDT&E Int. 2017, 92, 59–66. [Google Scholar] [CrossRef]
- Dougherty, E.R.; Kraus, E.J. Shape analysis and reduction of the morphological basis for digital moving-average filters. SIAM J. Appl. Math. 1991, 51, 1764–1781. [Google Scholar] [CrossRef]
- Goldstein, J.S.; Reed, I.S.; Scharf, L.L. A multistage representation of the wiener filter based on orthogonal projections. IEEE Trans. Inf. Theory 1998, 44, 2943–2959. [Google Scholar] [CrossRef]
- Poornachandra, S. Wavelet-based denoising using subband dependent threshold for ECG signals. Digit. Signal. Process. 2008, 18, 49–55. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.A.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis. Proc. R. Soc. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Khaldi, K.; Boudraa, A.O.; Komaty, A. Speech enhancement using empirical mode decomposition and the Teager-Kaiser energy operator. J. Acoust. Soc. Am. 2014, 135, 451–459. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.Y.; Kim, Y. A comparison of sea level projections based on the observed and reconstructed sea level data around the Korean Peninsula. Clim. Chang. 2017, 142, 23–36. [Google Scholar] [CrossRef]
- Wang, X.; Chen, Z.; Luo, J. ECG compression based on combining of EMD and wavelet transform. Electron. Lett. 2016, 52, 23–36. [Google Scholar] [CrossRef]
- Yang, G.; Liu, Y.; Wang, Y.; Zhu, Z. EMD interval thresholding denoising based on similarity measure to select relevant modes. Signal Process. 2015, 109, 95–109. [Google Scholar] [CrossRef]
- Liu, P.; Huang, W.; Zhang, W.; Li, F. An EMD-SG algorithm for spectral noise reduction of FBG-FP static strain sensor. IEEE Photonics Technol. Lett. 2017, 29, 814–817. [Google Scholar] [CrossRef]
- Flandrin, P.; Rilling, G.; Goncalves, P. Empirical mode decomposition as a filter bank. IEEE Signal Proc. Lett. 2004, 11, 112–114. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Wang, J.; He, X.; Ferreira, V.G. Ocean wave separation using CEEMD-Wavelet in GPS wave measurement. Sensors 2015, 15, 19416–19428. [Google Scholar] [CrossRef] [PubMed]
- Yeh, J.R.; Shieh, J.S.; Huang, N.E. Complementary ensemble empirical mode decomposition: A novel noise enhanced data analysis method. Adv. Adapt. Data Anal. 2010, 2, 135–156. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Process, Prague, Czech Republic, 22–27 May 2011. [Google Scholar] [CrossRef]
- Kuai, M.; Cheng, G.; Pang, Y.; Li, Y. Research of planetary gear fault diagnosis based on permutation entropy of CEEMDAN and ANFIS. Sensors 2018, 18, 782. [Google Scholar] [CrossRef] [PubMed]
- Olvera-Guerrero, O.A.; Prieto-Guerrero, A.; Espinosa-Paredes, G. Decay ratio estimation in BWRs based on the improved complete ensemble empirical mode decomposition with adaptive noise. Ann. Nucl. Energy 2017, 102, 280–296. [Google Scholar] [CrossRef]
- Dang, S.W.; Han, H.W.; Wang, K.L.; Cheng, P.Z. Application of different emd-based denosing methods for fiber optic gyro. In Proceedings of the International Conference on Communication and Information Processing, Singapore, 26–29 November 2016. [Google Scholar] [CrossRef]
- Li, Y.X.; Li, Y.A.; Chen, X.; Yu, J.; Yang, H.; Wang, L. A new underwater acoustic signal denoising technique based on CEEMDAN, Mutual Information, Permutation Entropy, and Wavelet Threshold Denoising. Entropy 2018, 20, 563. [Google Scholar] [CrossRef]
- Bai, L.L.; Han, Z.N.; Li, Y.F.; Ning, S.H. A hybrid de-noising algorithm for the gear transmission system based on CEEMDAN-PE-TFPF. Entropy 2018, 20, 361. [Google Scholar] [CrossRef]
- Li, C.; Zhan, L.; Shen, L. Friction signal denoising using complete ensemble EMD with adaptive noise and mutual information. Entropy 2015, 17, 5965–5979. [Google Scholar] [CrossRef]
- Huang, W.; Cai, N.; Xie, W.; Ye, Q.; Yang, Z.J. ECG baseline wander correction based on ensemble empirical mode decomposition with complementary adaptive noise. J. Med. Imaging Health Inf. 2015, 5, 1796–1799. [Google Scholar] [CrossRef]
- Kaiser, J.F. On a simple algorithm to calculate the ‘Energy’ of a signal. In Proceedings of the International Conference on Acoustics, Speech, and Signal Processing, Albuquerque, NM, USA, 3–6 April 1990. [Google Scholar] [CrossRef]
- Dubov, A.A.; Dubov, A.A.; Kolokolnikov, S.M. Non-contact magnetometric diagnostics of potentially hazardous sections of buried and insulated pipelines susceptible to failure. Weld. World 2017, 61, 107–115. [Google Scholar] [CrossRef]
- Kolokolnikov, S.M.; Dubov, A.A.; Dubov, A.A. Non-contact magnetometric diagnostics of welded joints of main gas pipelines susceptible to sudden failures. In Proceedings of the 19th World Conference on Non-Destructive Testing, Munich, Germany, 13–17 June 2016. [Google Scholar]
- Asadi, R.; Fell, H. Improving the accuracy of speech emotion recognition using acoustic landmarks and Teager energy operator features. J. Acoust. Soc. Am. 2015, 137, 2303. [Google Scholar] [CrossRef]
- Rodríguez, P.H.; Alonso, J.B.; Ferrer, M.A.; Travieso, C.M. Application of the Teager-Kaiser energy operator in bearing fault diagnosis. ISA Trans. 2013, 52, 278–284. [Google Scholar] [CrossRef] [PubMed]
- Kamwa, I.; Pradhan, A.K.; Joos, G. Robust detection and analysis of power system oscillations using the Teager-Kaiser energy operator. IEEE Trans. Power Syst. 2011, 26, 323–333. [Google Scholar] [CrossRef]
- Nguyen, H.P.; Kim, J. Adaptive ECG denoising using genetic algorithm-based thresholding and ensemble empirical mode decomposition. Inf. Sci. 2016, 373, 499–511. [Google Scholar] [CrossRef]
- Yan, J.; Lu, L. Improved Hilbert—Huang transform based weak signal detection methodology and its application on incipient fault diagnosis and ECG signal analysis. Signal Process. 2014, 9, 74–87. [Google Scholar] [CrossRef]
- Yang, X.; Luo, M.Z.; Li, T.; Song, J.B. ECG signal de-noising and baseline wander correction based on CEEMDAN and wavelet threshold. Sensors 2017, 17, 2754. [Google Scholar] [CrossRef]
- Dai, S.Y.; Niu, D.X.; Li, Y. Daily peak load forecasting based on complete ensemble empirical mode decomposition with adaptive noise and support vector machine optimized by modified grey wolf optimization algorithm. Energies 2018, 11, 163. [Google Scholar] [CrossRef]
- Zhang, C.; Li, Y.; Lin, H.; Yang, B. Signal preserving and seismic random noise attenuation by Hurst exponent based time–frequency peak filtering. Geophys. J. Int. 2015, 203, 901–909. [Google Scholar] [CrossRef]
- Mielniczuk, J.; Wojdy, O.P. Estimation of Hurst exponent revisited. Comput. Stat. Data Anal. 2007, 51, 4510–4525. [Google Scholar] [CrossRef]
- Mandelbrod, B.B.; Van Ness, J.W. Fractional Brownian motions, fractional noises and applications. SIAM Rev. 1968, 10, 422–437. [Google Scholar] [CrossRef]
- Li, M.; Li, J.; Jiang, G.; Zhang, J. Rolling bearing fault diagnosis based on EEMD and sparse decomposition. In Proceedings of the Prognostics & System Health Management Conference, Harbin, China, 9–12 July 2017. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z. Salp swarm algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Bahoura, M.; Rouat, J. Wavelet speech enhancement based on the Teager energy operator. IEEE Signal Proc. Lett. 2001, 8, 10–12. [Google Scholar] [CrossRef]
- Song, Q.; Ding, W.; Peng, H.; Gu, J.; Shuai, J. Pipe defect detection with remote magnetic inspection and wavelet analysis. Wirel. Pers. Commun. 2017, 95, 1–15. [Google Scholar] [CrossRef]
- Lefebvre, D.; Arsenault, H.H.; Garcia-Martinez, P.; Ferreira, C. Recognition of unsegmented targets invariant under transformations of intensity. Appl. Opt. 2002, 41, 6135–6142. [Google Scholar] [CrossRef] [PubMed]
- Yigit, E.; Demirci, S.; Ozdemir, C.; Tekbas, M. Short-range ground-based synthetic aperture radar imaging: Performance comparison between frequency-wavenumber migration and back-projection algorithms. J. Appl. Remote. Sems. 2013, 7, 073483. [Google Scholar] [CrossRef]
- Leistedt, S.; Dumont, M.; Lanquart, J.P.; Jurysta, F.; Linkowski, P. Characterization of the sleep EEG in acutely depressed men using detrended fluctuation analysis. Clin. Neurophysiol. 2007, 118, 940–950. [Google Scholar] [CrossRef] [PubMed]
- Zhan, L.; Li, C. A comparative study of empirical mode decomposition-based filtering for impact signal. Entropy 2016, 19, 13. [Google Scholar] [CrossRef]
- Ma, W.; Yin, S.; Jiang, C.; Zhang, Y.S. Variational mode decomposition denoising combined with the Hausdorff distance. Rev. Sci. Instrum. 2017, 88, 035109. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).