Data-Driven Control Techniques for Renewable Energy Conversion Systems: Wind Turbine and Hydroelectric Plants
Abstract
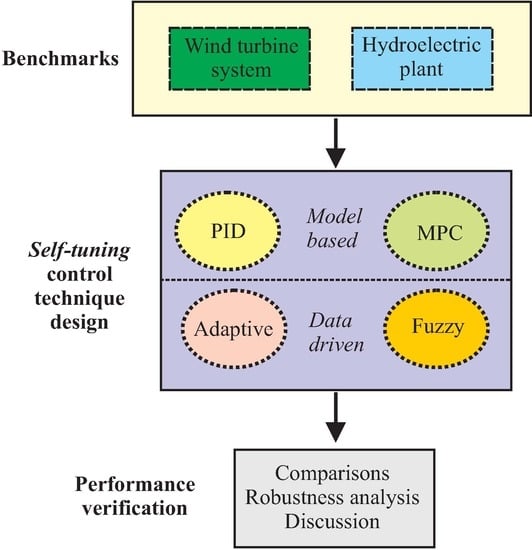
1. Introduction
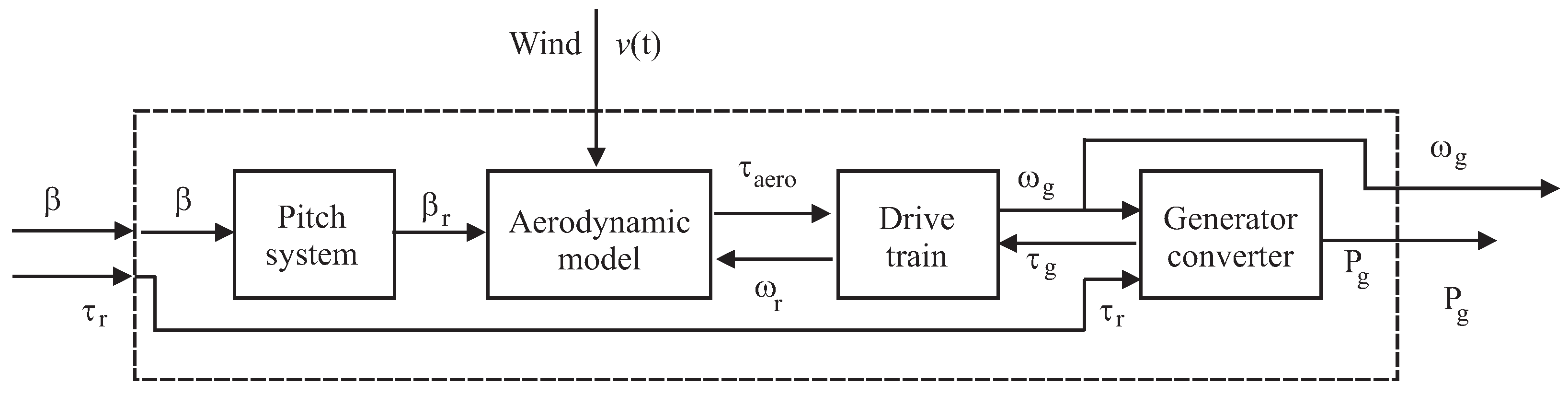
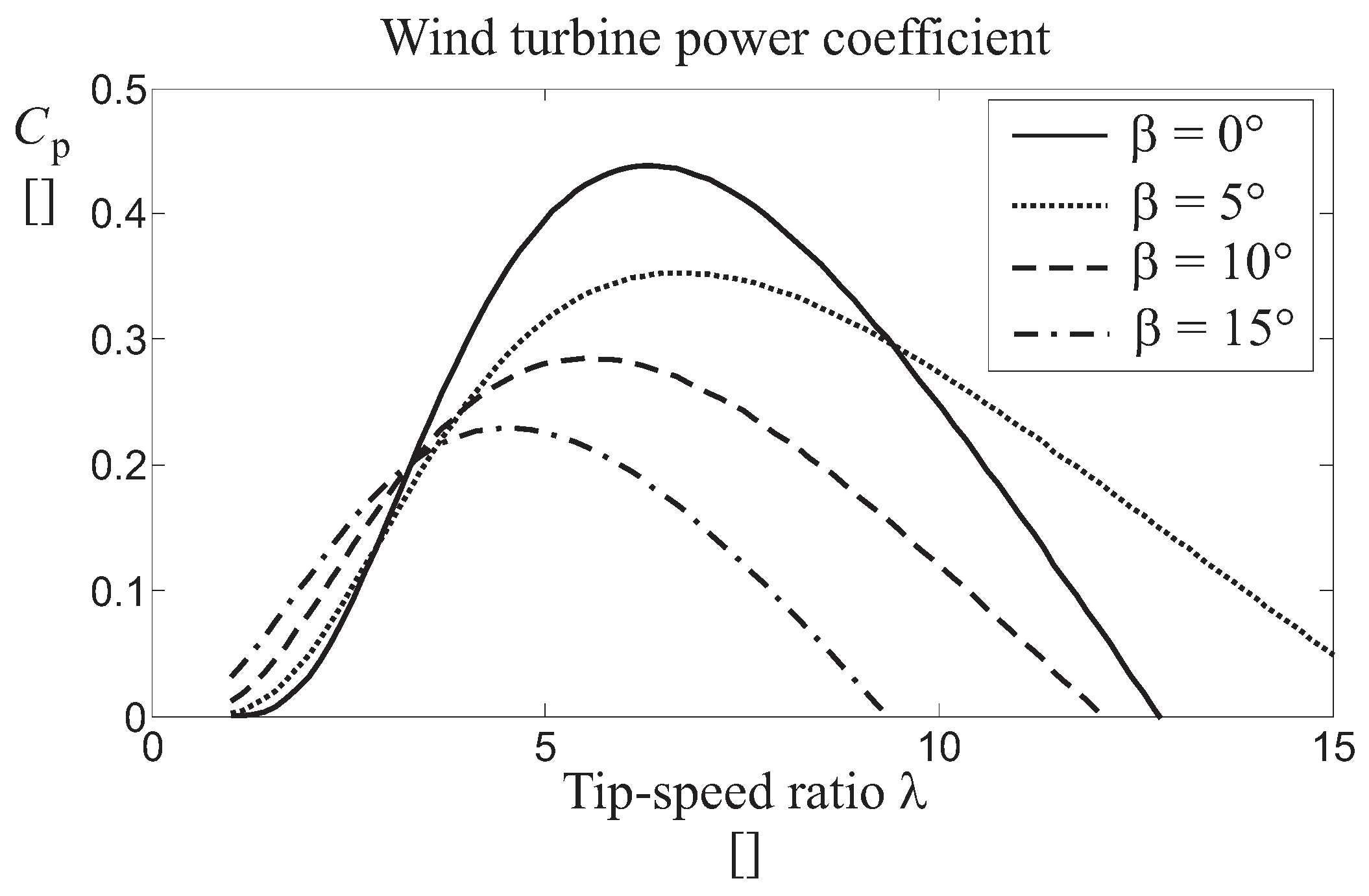
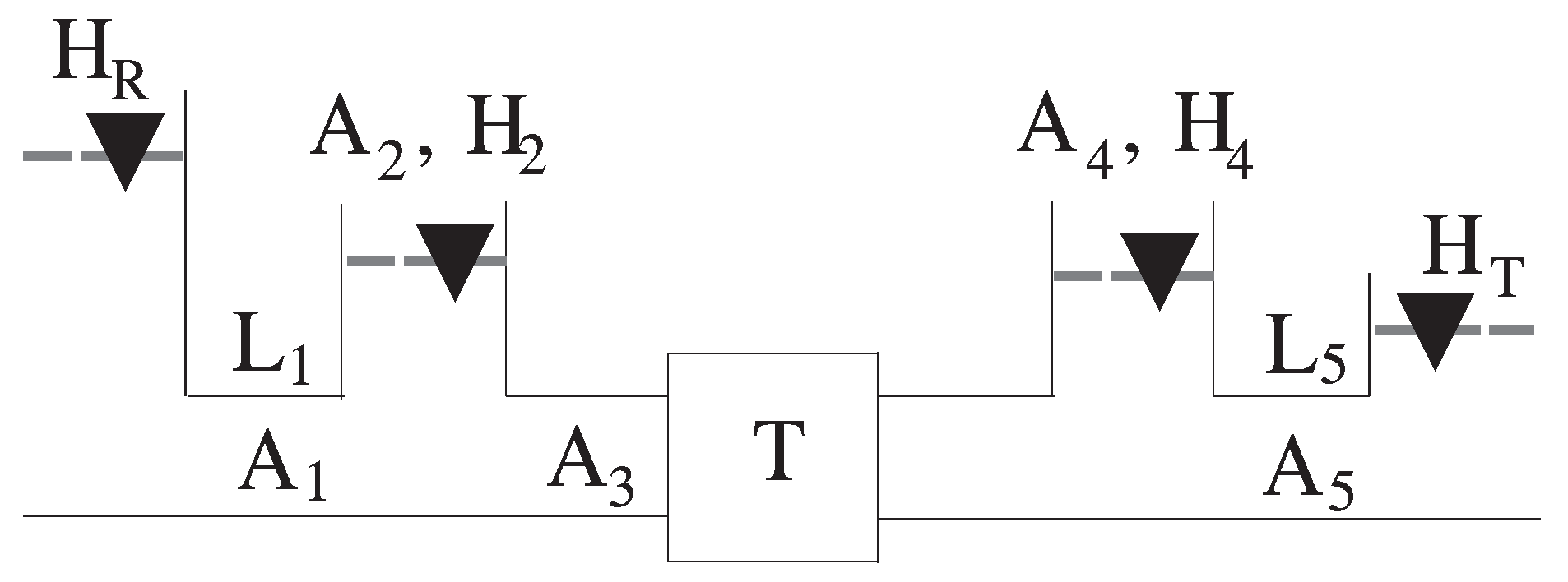
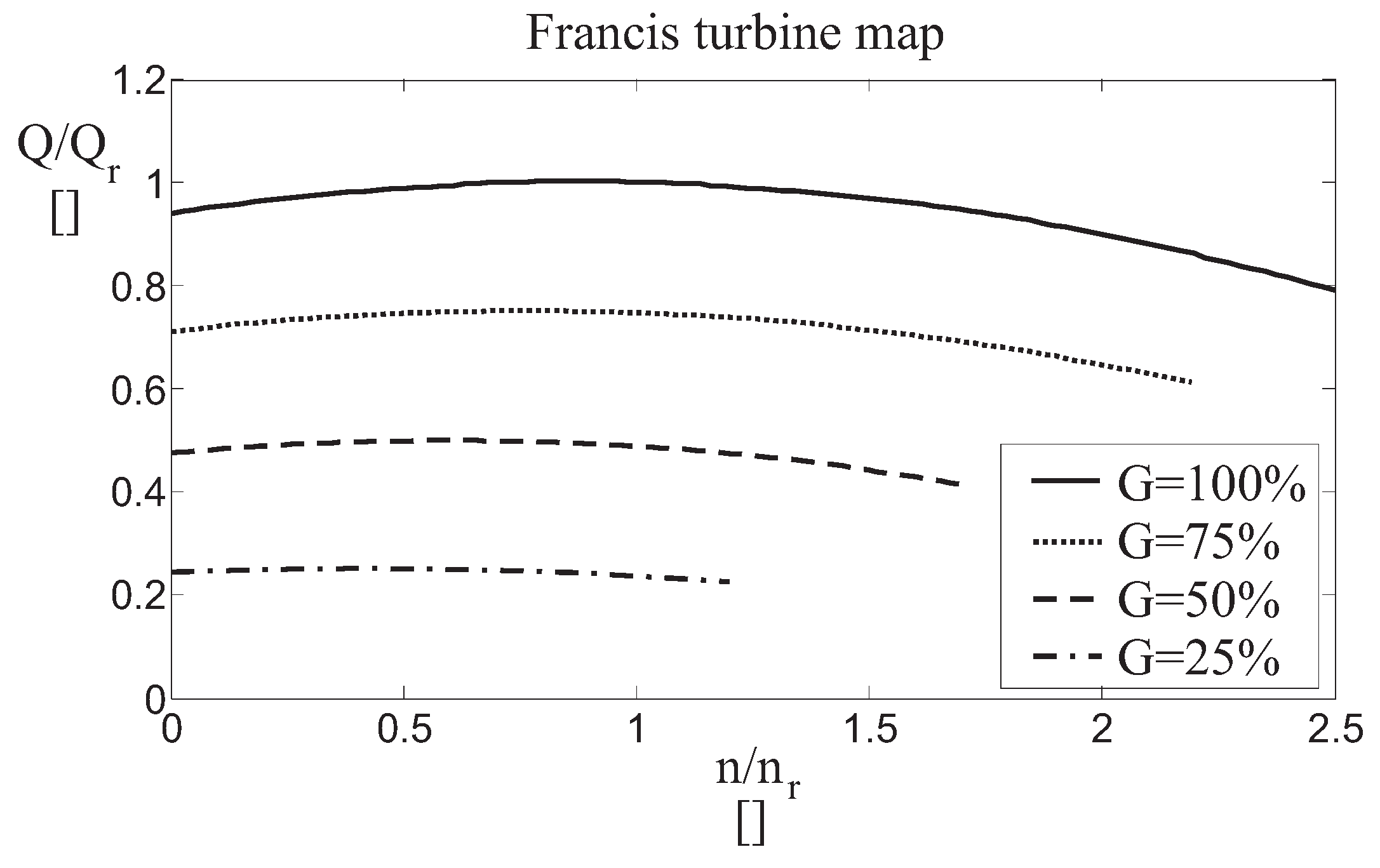
2. Simulator Models and Reference Governors
3. Control Techniques for Energy Conversion Systems
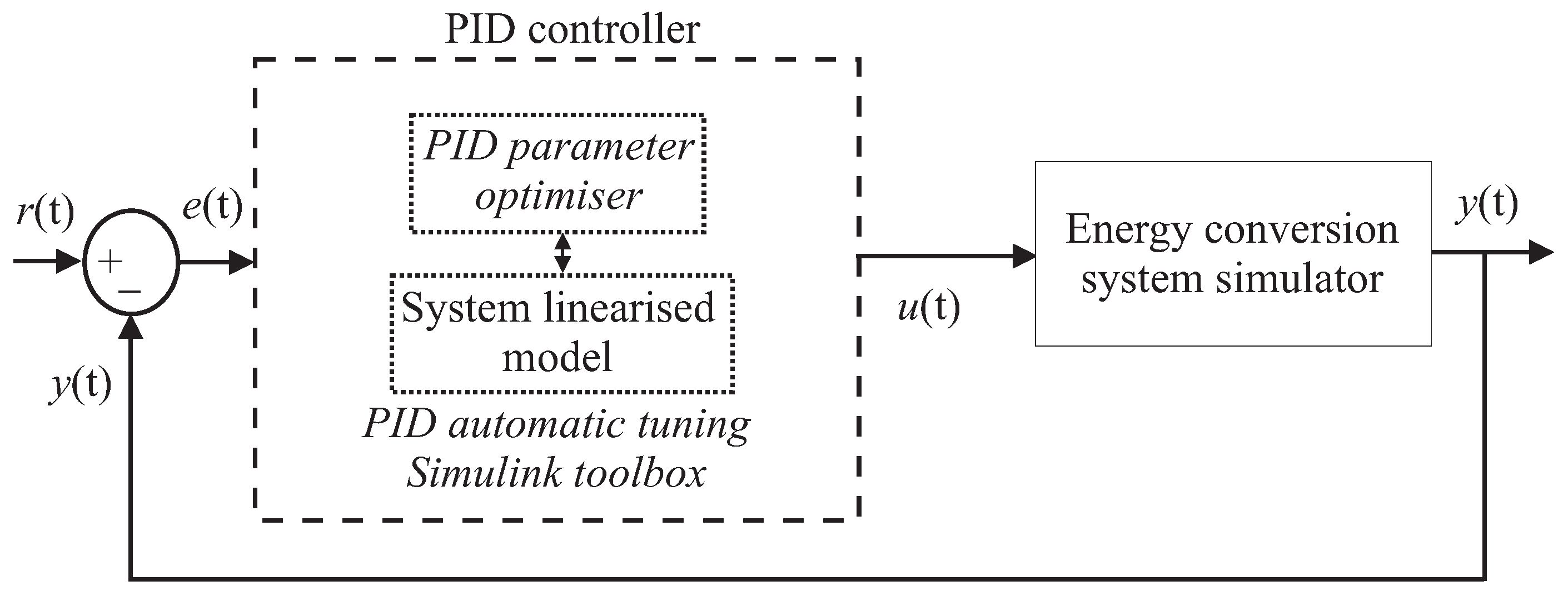
3.1. Self-Tuning PID Control
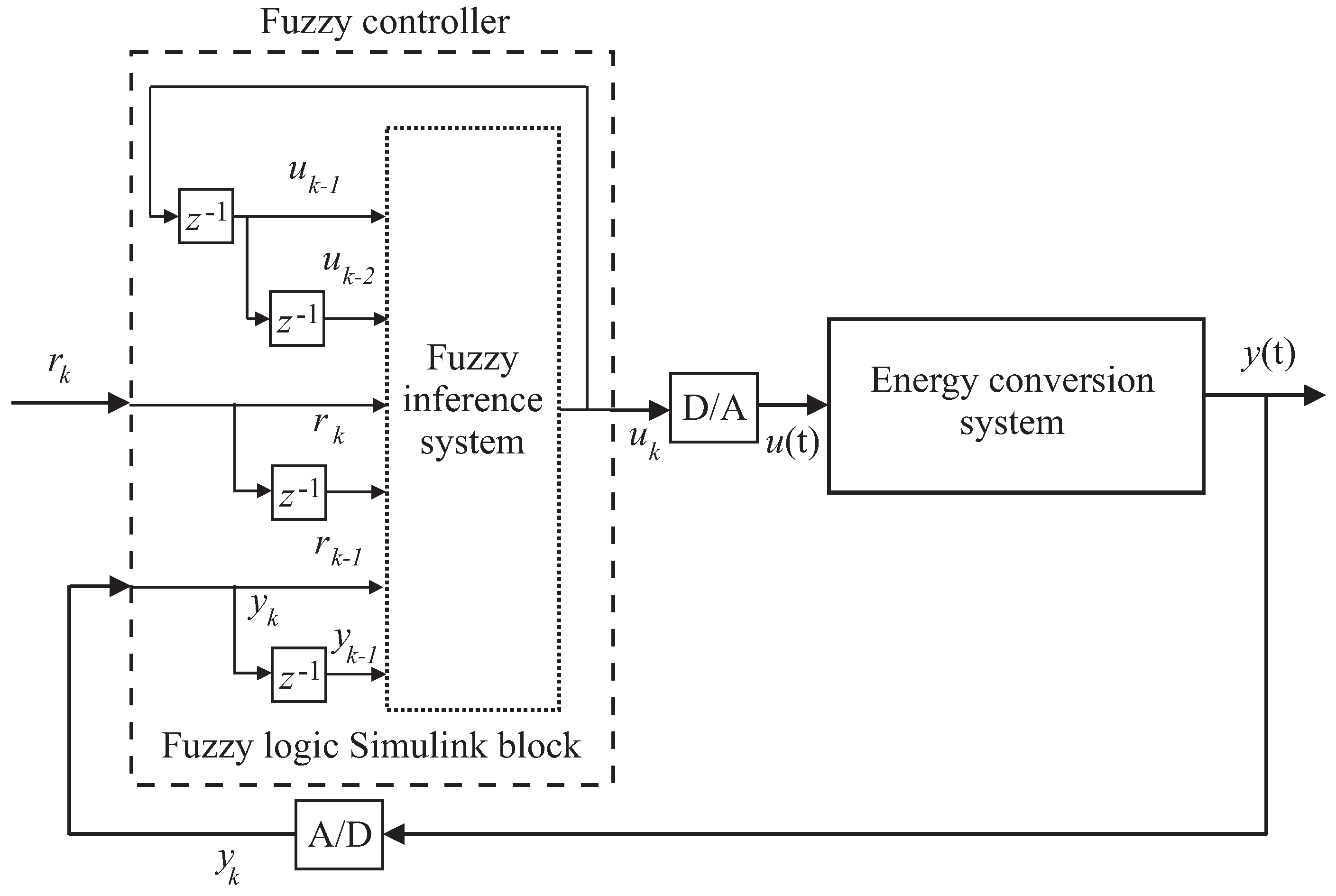
3.2. Data-Driven Fuzzy Control
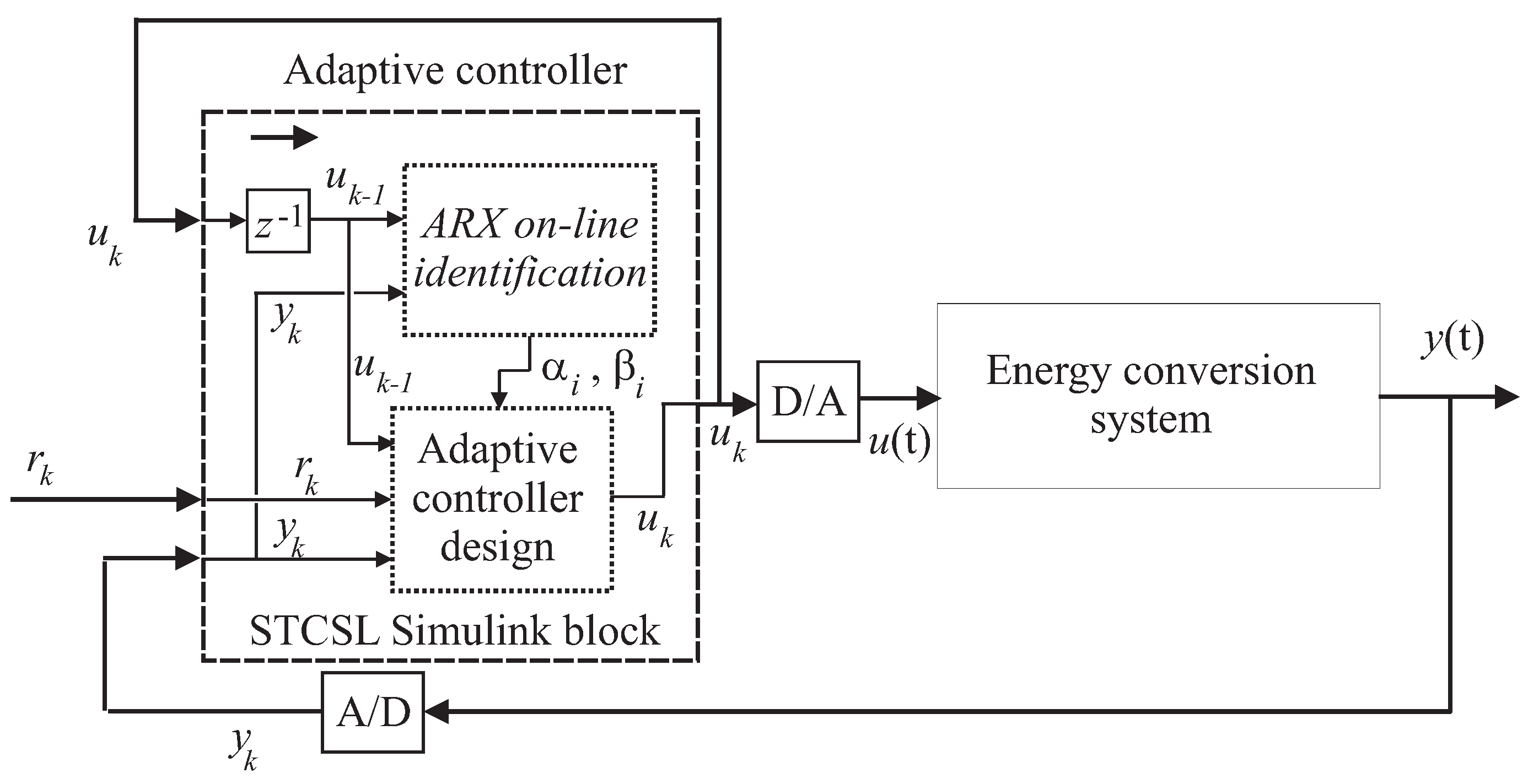
3.3. Data-Driven Adaptive Control
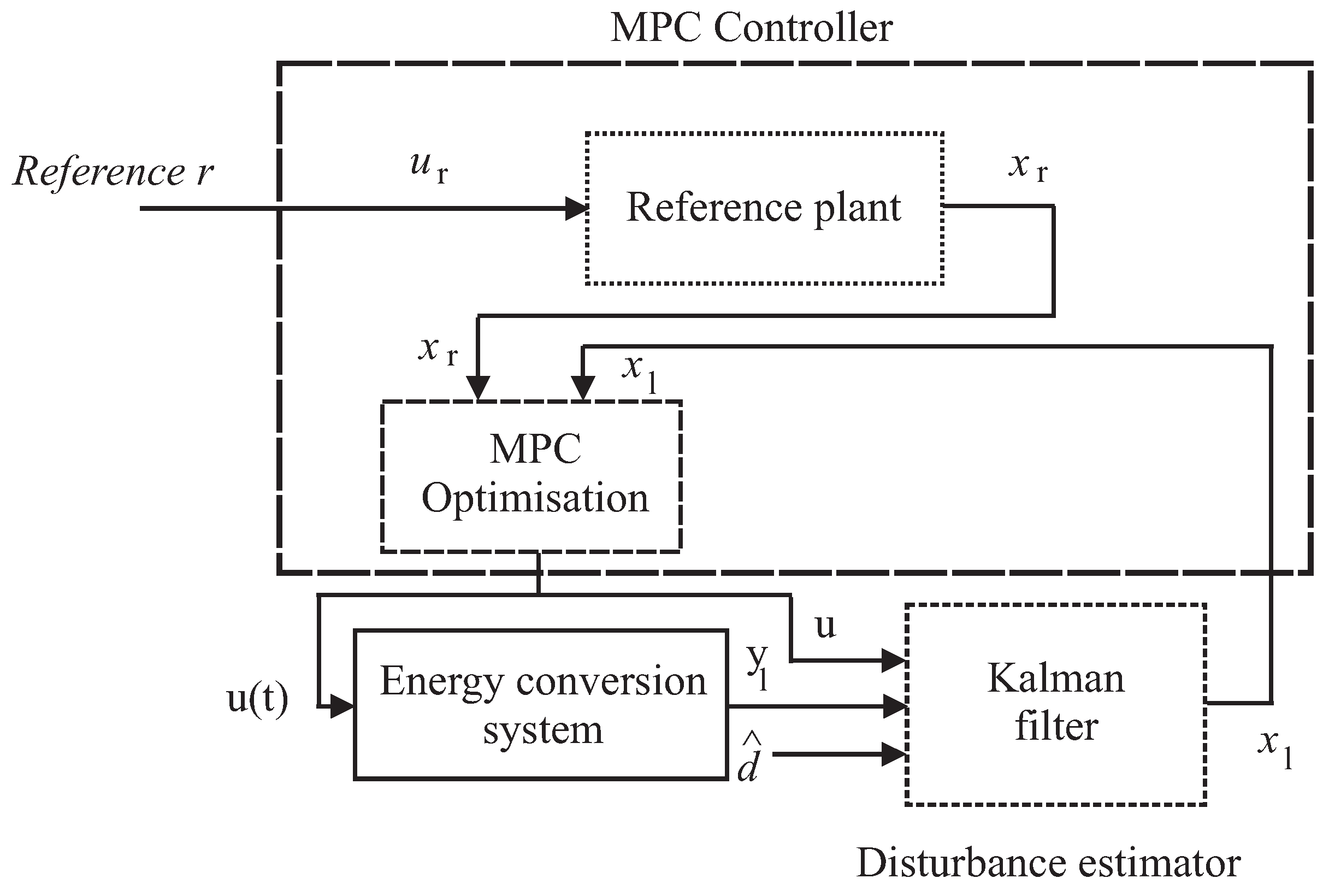
3.4. Model Predictive Control with Disturbance Decoupling
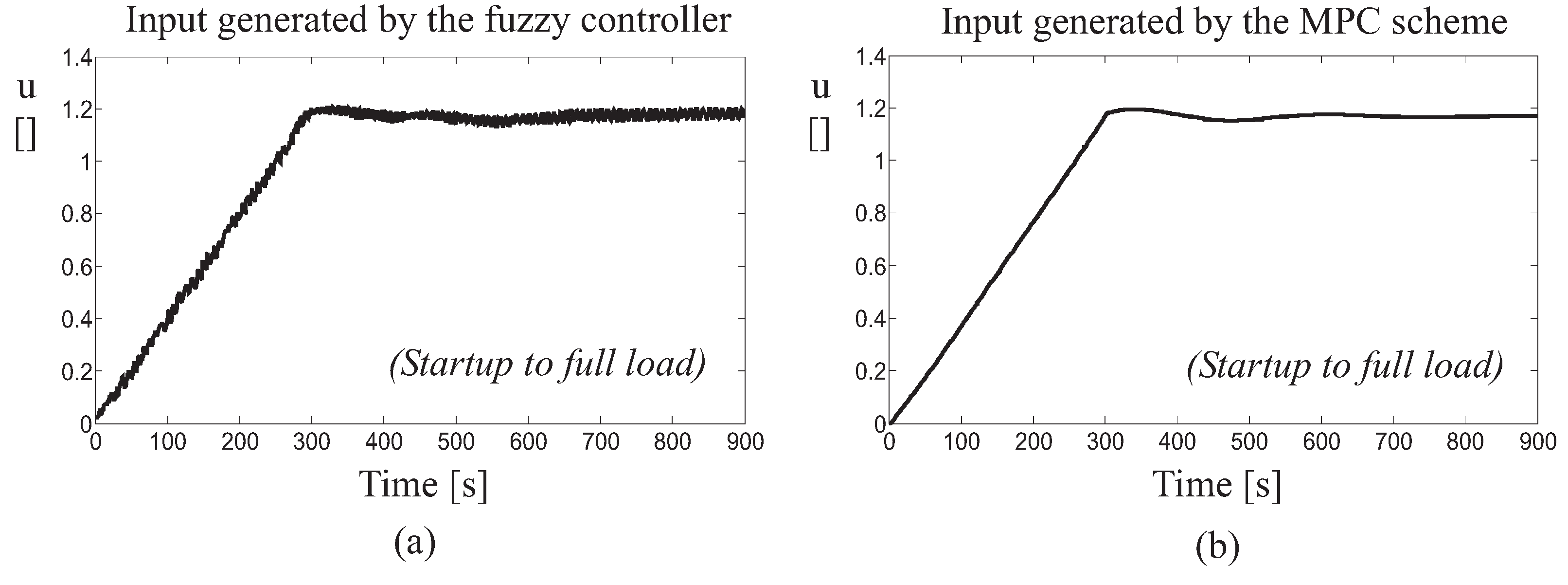
4. Simulation Results
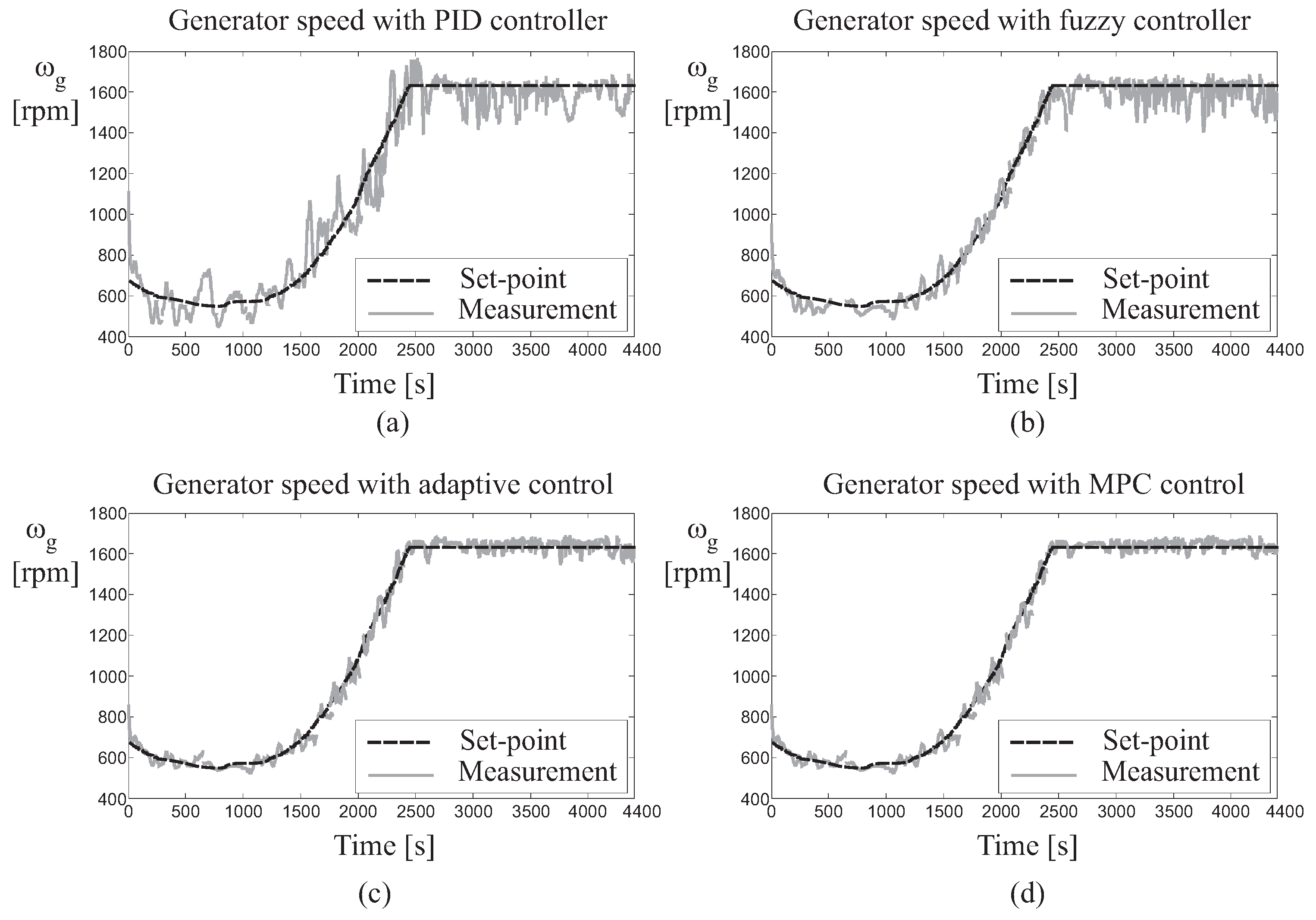
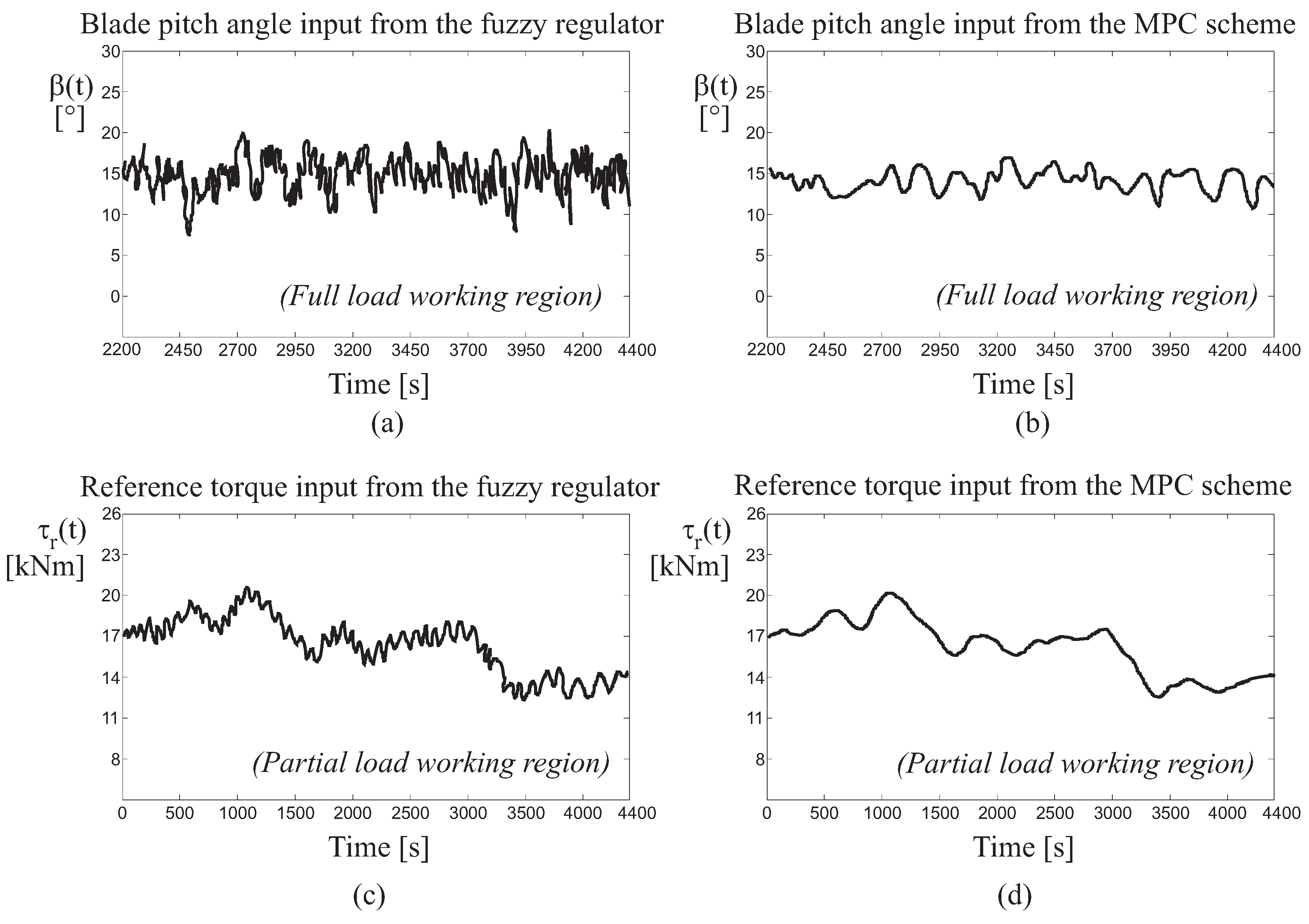
4.1. Control Technique Performances and Comparisons
4.2. Sensitivity Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tetu, A.; Ferri, F.; Kramer, M.B.; Todalshaug, J.H. Physical and Mathematical Modeling of a Wave Energy Converter Equipped with a Negative Spring Mechanism for Phase Control. Energies 2018, 11, 2362. [Google Scholar] [CrossRef]
- Hassan, M.; Balbaa, A.; Issa, H.H.; El-Amary, N.H. Asymptotic Output Tracked Artificial Immunity Controller for Eco-Maximum Power Point Tracking of Wind Turbine Driven by Doubly Fed Induction Generator. Energies 2018, 11, 2632. [Google Scholar] [CrossRef]
- Fernendez-Guillamon, A.; Villena-Lapaz, J.; Vigueras-Rodriguez, A.; Garcia-Sanchez, T.; Molina-Garcia, A. An Adaptive Frequency Strategy for Variable Speed Wind Turbines: Application to High Wind Integration into Power Systems. Energies 2018, 11, 1436. [Google Scholar] [CrossRef]
- Blanco-M., A.; Gibert, K.; Marti-Puig, P.; Cusido, J.; Sole-Casals, J. Identifying Health Status of Wind Turbines by using Self Organizing Maps and Interpretation-Oriented Post-Processing Tools. Energies 2018, 11, 723. [Google Scholar] [CrossRef]
- World Energy Council (Ed.) Cost of Energy Technologies; World Energy Perspective, World Energy Council: London, UK, 2018; ISBN 9780946121304. Available online: www.worldenergy.org (accessed on 23 January 2019).
- Odgaard, P.F.; Stoustrup, J.; Kinnaert, M. Fault-Tolerant Control of Wind Turbines: A Benchmark Model. IEEE Trans. Control Syst. Technol. 2013, 21, 1168–1182. [Google Scholar] [CrossRef]
- Simani, S.; Alvisi, S.; Venturini, M. Fault Tolerant Control of a Simulated Hydroelectric System. Control Eng. Pract. 2016, 51, 13–25. [Google Scholar] [CrossRef]
- Odgaard, P.F.; Stoustrup, J. A Benchmark Evaluation of Fault Tolerant Wind Turbine Control Concepts. IEEE Trans. Control Syst. Technol. 2015, 23, 1221–1228. [Google Scholar] [CrossRef]
- Honrubia-Escribano, A.; Gomez-Lazaro, E.; Fortmann, J.; Sorensen, P.; Martin-Martinez, S. Generic dynamic wind turbine models for power system stability analysis: A comprehensive review. Renew. Sustain. Energy Rev. 2018, 81, 1939–1952. [Google Scholar] [CrossRef]
- Singh, V.K.; Singal, S.K. Operation of hydro power plants—A review. Renew. Sustain. Energy Rev. 2017, 69, 610–619. [Google Scholar] [CrossRef]
- Bianchi, F.D.; Battista, H.D.; Mantz, R.J. Wind Turbine Control Systems: Principles, Modelling and Gain Scheduling Design, 1st ed.; Springer: London, UK, 2007; ISBN 1-84628-492-9. [Google Scholar]
- Kishor, N.; Saini, R.; Singh, S. A review on hydropower plant models and control. Renew. Sustain. Energy Rev. 2007, 11, 776–796. [Google Scholar] [CrossRef]
- Hanmandlu, M.; Goyal, H. Proposing a new advanced control technique for micro hydro power plants. Int. J. Electr. Power Energy Syst. 2008, 30, 272–282. [Google Scholar] [CrossRef]
- Kishor, N.; Singh, S.; Raghuvanshi, A. Dynamic simulations of hydro turbine and its state estimation based LQ control. Energy Convers. Manag. 2006, 47, 3119–3137. [Google Scholar] [CrossRef]
- Mahmoud, M.; Dutton, K.; Denman, M. Design and simulation of a nonlinear fuzzy controller for a hydropower plant. Electr. Power Syst. Res. 2005, 73, 87–99. [Google Scholar] [CrossRef]
- Sarasua, J.I.; Martinez-Lucas, G.; Platero, C.A.; Sanchez-Fernandez, J.A. Dual Frequency Regulation in Pumping Mode in a Wind-Hydro Isolated System. Energies 2018, 11, 2865. [Google Scholar] [CrossRef]
- Martinez-Lucas, G.; Sarasua, J.I.; Sanchez-Fernandez, J.A. Eigen analysis of wind-hydro joint frequency regulation in an isolated power system. Int. J. Electr. Power Energy Syst. 2018, 103, 511–524. [Google Scholar] [CrossRef]
- Popescu, M.; Arsenie, D.; Vlase, P. Applied Hydraulic Transients: For Hydropower Plants and Pumping Stations; CRC Press: Lisse, The Netherlands, 2003. [Google Scholar]
- Fang, H.; Chen, L.; Dlakavu, N.; Shen, Z. Basic Modeling and Simulation Tool for Analysis of Hydraulic Transients in Hydroelectric Power Plants. IEEE Trans. Energy Convers. 2008, 23, 424–434. [Google Scholar]
- Åström, K.J.; Hägglund, T. Advanced PID Control; ISA—The Instrumentation, Systems, and Automation Society: Research Triangle Park, NC, USA, 2006; ISBN 978-1-55617-942-6. [Google Scholar]
- Jang, J.S.R.; Sun, C.T. Neuro-Fuzzy and Soft Computing: A Computational Approach to Learning and Machine Intelligence, 1st ed.; Prentice Hall: London, UK, 1997; ISBN 9780132610667. [Google Scholar]
- Babuška, R. Fuzzy Modeling for Control; Kluwer Academic Publishers: Boston, MA, USA, 1998. [Google Scholar]
- Bobál, V.; Böhm, J.; Fessl, J.; Machácek, J. Digital Self-Tuning Controllers: Algorithms, Implementation and Applications, 1st ed.; Springer: London, UK, 2005. [Google Scholar]
Sample Availability: The software codes for the proposed control strategies, the simulated benchmarks and the generated data are available from the authors on demand in the Maltab and Simulink environments. |
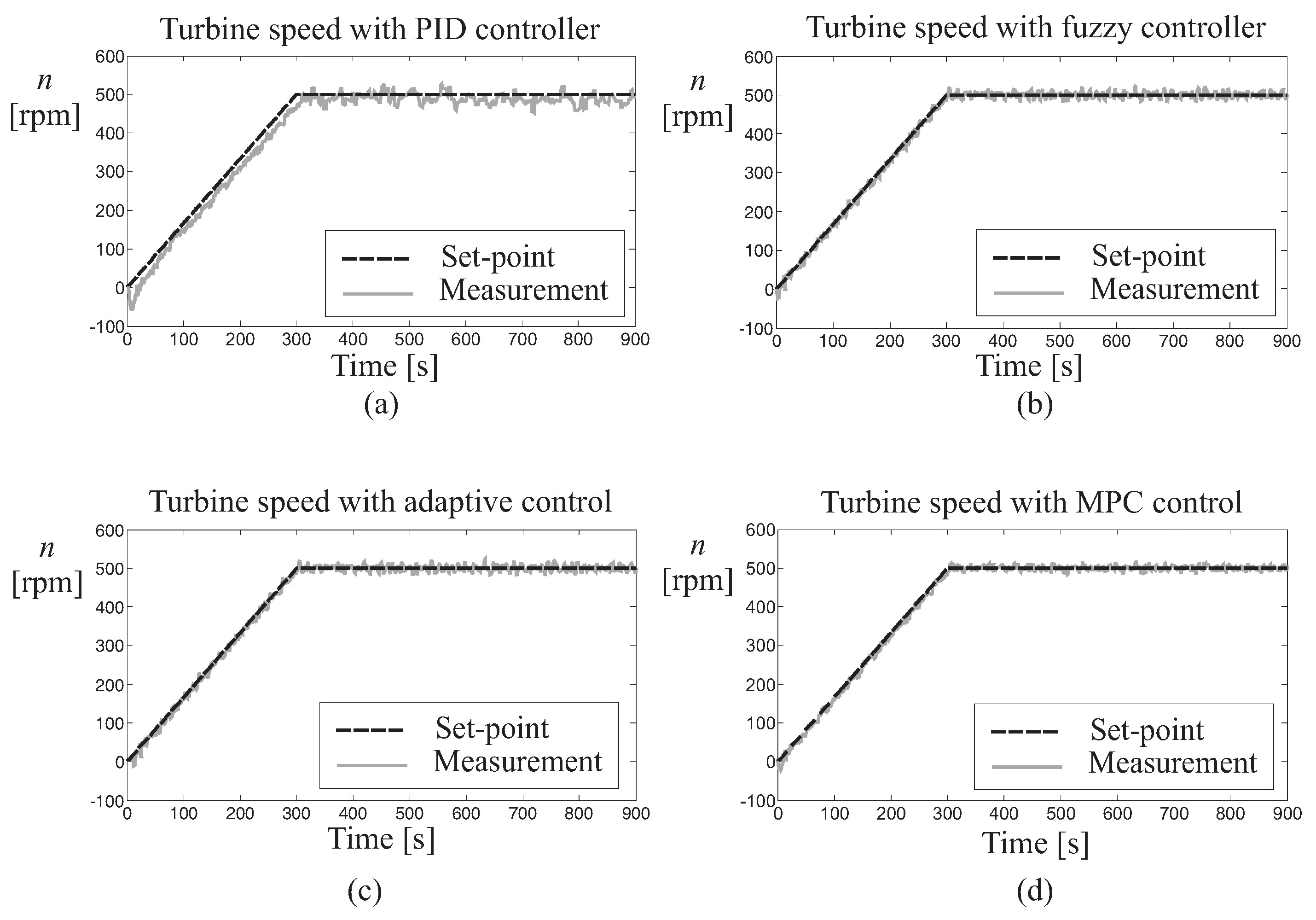
| Simulated System | Working Condition | Standard PID | Self-Tuning PID | Fuzzy PID | Adaptive PID | MPC Scheme |
|---|---|---|---|---|---|---|
| Wind turbine | From partial to full load |
| Simulated System | Working Condition | Standard PID | Self-Tuning PID | Fuzzy PID | Adaptive PID | MPC Scheme |
|---|---|---|---|---|---|---|
| Hydro plant | From start-up to full load |
| Variable | R | ||||
| Nominal value | m | rpm | N m s rad | N m s rad | |
| Variable | |||||
| Nominal value | N m s rad | N m rad | 390 kg m | kg m |
| Variable | a | b | c | ||||
| Nominal value | −0.08 | 0.14 | 0.94 | 0.0481 m | 0.0481 m | 0.0047 m | 5.9 s |
| Variable | |||||||
| Nominal value | 20 s | 476.05 s | 5000 s | 3.22 s | 0.83 s | 0.1 s |
| Standard PID | Self-Tuning PID | Fuzzy PID | Adaptive PID | MPC Scheme |
|---|---|---|---|---|
| Standard PID | Self-Tuning PID | Fuzzy PID | Adaptive PID | MPC Scheme |
|---|---|---|---|---|
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Simani, S.; Alvisi, S.; Venturini, M. Data-Driven Control Techniques for Renewable Energy Conversion Systems: Wind Turbine and Hydroelectric Plants. Electronics 2019, 8, 237. https://doi.org/10.3390/electronics8020237
Simani S, Alvisi S, Venturini M. Data-Driven Control Techniques for Renewable Energy Conversion Systems: Wind Turbine and Hydroelectric Plants. Electronics. 2019; 8(2):237. https://doi.org/10.3390/electronics8020237
Chicago/Turabian StyleSimani, Silvio, Stefano Alvisi, and Mauro Venturini. 2019. "Data-Driven Control Techniques for Renewable Energy Conversion Systems: Wind Turbine and Hydroelectric Plants" Electronics 8, no. 2: 237. https://doi.org/10.3390/electronics8020237
APA StyleSimani, S., Alvisi, S., & Venturini, M. (2019). Data-Driven Control Techniques for Renewable Energy Conversion Systems: Wind Turbine and Hydroelectric Plants. Electronics, 8(2), 237. https://doi.org/10.3390/electronics8020237