Role of the Product λ′(0)ρ′(1) in Determining LDPC Code Performance
Abstract
1. Introduction
2. Graphical Representation of LDPC Codes
3. Gaussian Approximation
4. Mathematical Method of [16]
5. Upper Bounds on LDPC Codes Decoding Thresholds
5.1. Upper Bound on LDPC Codes Decoding Thresholds Holding for
5.2. Further Upper Bounds on LDPC Codes Decoding Thresholds Holding for
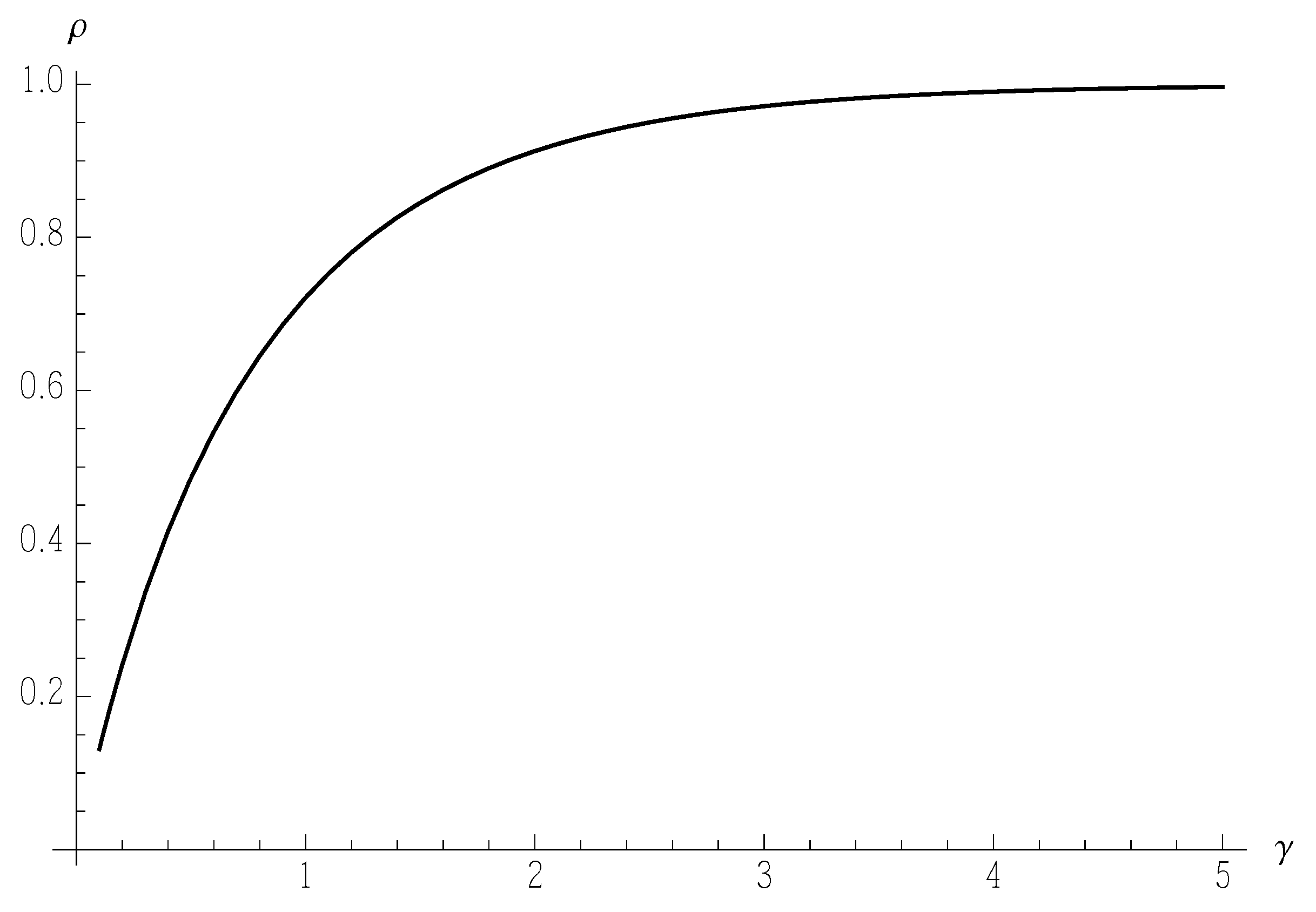
6. Role of the Product in Determining the Weight Distribution of LDPC Codes
7. Role of the Product in Determining the Decoding Threshold of LDPC Codes
8. Numeric Results
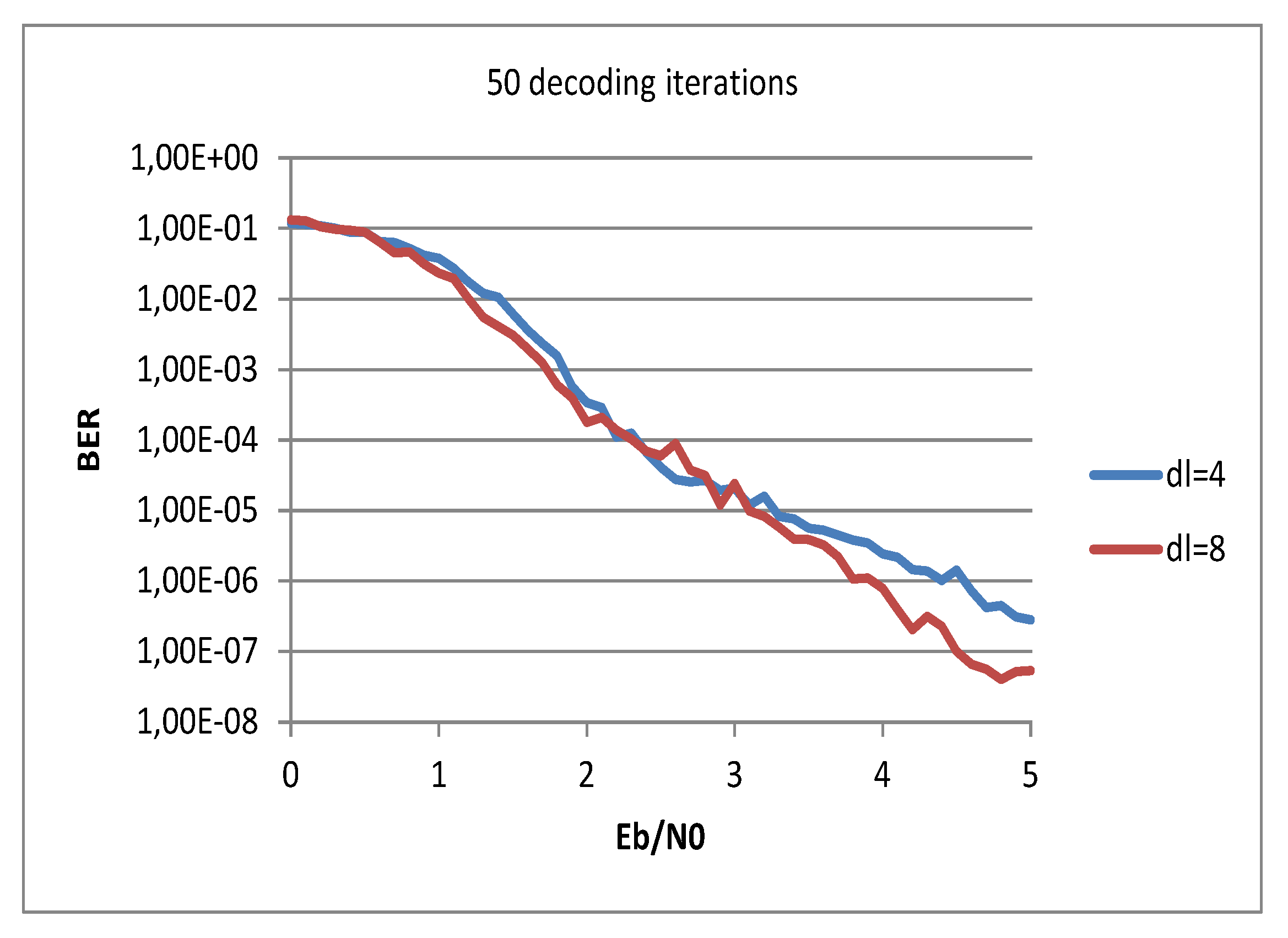
9. Discussion and Simulation Results
- and
- .
9.1. Case 1:
9.2. Case 2:
10. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Approximation of the Functions and
- s[y_] = Interpolation[v, y];
References
- Gallager, R.G. Low-Density Parity-Check Codes; MIT Press: Cambridge, UK, 1963. [Google Scholar]
- Tanner, R.M. A recursive approach to low complexity codes. IEEE Trans. Inf. Theory 1981, 5, 533–547. [Google Scholar] [CrossRef]
- Mackay, D.J.C. Good error correcting codes based on very sparse matrices. IEEE Trans. Inf. Theory 1999, 2, 399–431. [Google Scholar] [CrossRef]
- Luby, M.G.; Mitzenmacher, M.; Shokrollahi, M.A.; Spielman, D.A. Improved low-density parity-check codes using irregular graphs. IEEE Trans. Inf. Theory 2001, 2, 585–598. [Google Scholar] [CrossRef]
- Babich, F.; Vatta, F. Turbo Codes Construction for Robust Hybrid Multitransmission Schemes. J. Commun. Softw. Syst. (JCOMSS) 2011, 4, 128–135. [Google Scholar] [CrossRef]
- Vatta, F.; Soranzo, A.; Comisso, M.; Buttazzoni, G.; Babich, F. Performance Study of a Class of Irregular LDPC Codes through Low Complexity Bounds on Their Belief-Propagation Decoding Thresholds. In Proceedings of the 2019 AEIT International Annual Conference, AEIT’19, Florence, Italy, 18–20 September 2019. [Google Scholar]
- Babich, F.; Comisso, M. Multi-Packet Communication in Heterogeneous Wireless Networks Adopting Spatial Reuse: Capture Analysis. IEEE Trans. Wirel. Commun. 2013, 10, 5346–5359. [Google Scholar] [CrossRef]
- Babich, F.; D’Orlando, M.; Vatta, F. Distortion Estimation Algorithms for Real-Time Video Streaming: An Application Scenario. In Proceedings of the 2011 International Conference on Software, Telecommunications and Computer Networks, SoftCOM’11, Split, Croatia, 15–17 September 2011. [Google Scholar]
- Di, C.; Richardson, T.J.; Urbanke, R. Weight distribution of low-density parity-check codes. IEEE Trans. Inf. Theory 2006, 11, 4839–4855. [Google Scholar] [CrossRef]
- Vatta, F.; Soranzo, A.; Babich, F. Low-Complexity bound on irregular LDPC belief-propagation decoding thresholds using a Gaussian approximation. Electron. Lett. 2018, 17, 1038–1040. [Google Scholar] [CrossRef]
- Chung, S.-Y.; Richardson, T.J.; Urbanke, R. Analysis of sum-product decoding of low-density parity-check codes using a Gaussian approximation. IEEE Trans. Inf. Theory 2001, 2, 657–670. [Google Scholar] [CrossRef]
- Babich, F.; Noschese, M.; Soranzo, A.; Vatta, F. Low complexity rate compatible puncturing patterns design for LDPC codes. In Proceedings of the 2017 International Conference on Software, Telecommunications and Computer Networks, SoftCOM’17, Split, Croatia, 21–23 September 2017. [Google Scholar]
- Babich, F.; Noschese, M.; Vatta, F. Analysis and design of rate compatible LDPC codes. In Proceedings of the 27th IEEE International Symposium on Personal, Indoor and Mobile Radio Communications, PIMRC ’16, Valencia, Spain, 4–8 September 2016. [Google Scholar]
- Tan, B.S.; Li, K.H.; Teh, K.C. Bit-error rate analysis of low-density parity-check codes with generalised selection combining over a Rayleigh-fading channel using Gaussian approximation. IET Commun. 2012, 1, 90–96. [Google Scholar] [CrossRef]
- Chen, X.; Lau, F.C.M. Optimization of LDPC codes with deterministic UEP properties. IET Commun. 2011, 11, 1560–1565. [Google Scholar] [CrossRef]
- Babich, F.; Soranzo, A.; Vatta, F. Useful mathematical tools for capacity approaching codes design. IEEE Commun. Lett. 2017, 9, 1949–1952. [Google Scholar] [CrossRef]
- Vatta, F.; Babich, F.; Ellero, F.; Noschese, M.; Buttazzoni, G.; Comisso, M. Performance study of a class of irregular LDPC codes based on their weight distribution analysis. In Proceedings of the 2019 International Conference on Software, Telecommunications and Computer Networks, SoftCOM’19, Split, Croatia, 19–21 September 2019. [Google Scholar]
- Richardson, T.J.; Shokrollahi, A.; Urbanke, R. Design of capacity- approaching irregular low-density parity-check codes. IEEE Trans. Inf. Theory 2001, 2, 619–637. [Google Scholar] [CrossRef]
- Vatta, F.; Soranzo, A.; Comisso, M.; Buttazzoni, G.; Babich, F. New explicitly invertible approximation of the function involved in LDPC codes density evolution analysis using a Gaussian approximation. Electron. Lett. 2019, 22, 1183–1186. [Google Scholar] [CrossRef]
- Vatta, F.; Soranzo, A.; Babich, F. More accurate analysis of sum-product decoding of LDPC codes using a Gaussian approximation. IEEE Commun. Lett. 2019, 2, 230–233. [Google Scholar] [CrossRef]
- Chung, S.-Y. On the Construction of Some Capacity-Approaching Coding Schemes. Ph.D. Thesis, MIT, Cambridge, MA, USA, 2000. Available online: http://dspace.mit.edu/handle/1721.1/8981 (accessed on 9 December 2019).
- Boscolo, A.; Vatta, F.; Armani, F.; Viviani, E.; Salvalaggio, D. Physical AWGN channel emulator for Bit Error Rate test of digital baseband communication. Appl. Mech. Mater. 2013, 241–244, 2491–2495. [Google Scholar] [CrossRef]



| 4 | 6 | 7 | 8 | |
|---|---|---|---|---|
| 0.38354 | 0.33241 | 0.31570 | 0.30013 | |
| 0.04237 | 0.24632 | 0.41672 | 0.28395 | |
| 0.57409 | 0.11014 | |||
| 0.31112 | ||||
| 0.43810 | ||||
| 0.41592 | ||||
| 0.24123 | ||||
| 0.75877 | 0.76611 | 0.43810 | 0.22919 | |
| 0.23389 | 0.56190 | 0.77081 | ||
| 0.38354 | 0.33241 | 0.31570 | 0.30013 | |
| 4.75877 | 5.23389 | 5.56190 | 5.77081 | |
| 1.82518 | 1.73980 | 1.75589 | 1.73199 | |
| 0.34942 | 0.32770 | 0.35934 | 0.29671 | |
| 0.54883 | 0.50719 | 0.43927 | 0.50577 | |
| 0.9114 | 0.9304 | 0.9424 | 0.9497 | |
| 0.91160 | 0.95021 | 0.94241 | 0.95409 | |
| 0.60903 | 0.24872 | 0.32032 | 0.21333 | |
| 0.61687 | 0.25656 | 0.32815 | 0.22117 |
| 9 | 10 | 11 | 12 | |
|---|---|---|---|---|
| 0.27684 | 0.25105 | 0.23882 | 0.24426 | |
| 0.28342 | 0.30938 | 0.29515 | 0.25907 | |
| 0.00104 | 0.03261 | 0.01054 | ||
| 0.05510 | ||||
| 0.01455 | ||||
| 0.43974 | ||||
| 0.43853 | 0.01275 | |||
| 0.43342 | ||||
| 0.40373 | ||||
| 0.01568 | ||||
| 0.85244 | 0.63676 | 0.43011 | 0.25475 | |
| 0.13188 | 0.36324 | 0.56989 | 0.73438 | |
| 0.01087 | ||||
| 0.27684 | 0.25105 | 0.23882 | 0.24426 | |
| 6.11620 | 6.36324 | 6.56989 | 6.75612 | |
| 1.69321 | 1.59749 | 1.56902 | 1.65025 | |
| 0.28175 | 0.27276 | 0.26535 | 0.25888 | |
| 0.49128 | 0.46020 | 0.45001 | 0.47176 | |
| 0.9540 | 0.9558 | 0.9572 | 0.9580 | |
| 0.97439 | 1.03314 | 1.05356 | 0.99908 | |
| 0.03046 | 0.47807 | 0.64807 | 0.18689 | |
| 0.03830 | 0.47023 | 0.64023 | 0.17905 |
| 15 | 20 | 30 | 50 | |
|---|---|---|---|---|
| 0.23802 | 0.21991 | 0.19606 | 0.17120 | |
| 0.20997 | 0.23328 | 0.24039 | 0.21053 | |
| 0.03492 | 0.02058 | 0.00273 | ||
| 0.12015 | ||||
| 0.08543 | 0.00228 | |||
| 0.01587 | 0.06540 | 0.05516 | 0.00009 | |
| 0.04767 | 0.16602 | 0.15269 | ||
| 0.01912 | 0.04088 | 0.09227 | ||
| 0.01064 | 0.02802 | |||
| 0.00480 | ||||
| 0.37627 | 0.01206 | |||
| 0.08064 | ||||
| 0.22798 | ||||
| 0.00221 | ||||
| 0.28636 | 0.07212 | |||
| 0.25830 | ||||
| 0.98013 | 0.64854 | 0.00749 | ||
| 0.01987 | 0.34747 | 0.99101 | 0.33620 | |
| 0.00399 | 0.00150 | 0.08883 | ||
| 0.57497 | ||||
| 0.23802 | 0.21991 | 0.19606 | 0.17120 | |
| 7.01987 | 7.35545 | 7.99401 | 9.23877 | |
| 1.67087 | 1.61754 | 1.56731 | 1.58168 | |
| 0.24945 | 0.24017 | 0.22240 | 0.19699 | |
| 0.47708 | 0.45783 | 0.44078 | 0.43454 | |
| 0.9622 | 0.9649 | 0.9690 | 0.9718 | |
| 0.98692 | 1.01966 | 1.05485 | 1.04429 | |
| 0.08052 | 0.36399 | 0.65870 | 0.57131 | |
| 0.07268 | 0.35615 | 0.65086 | 0.56347 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vatta, F.; Babich, F.; Ellero, F.; Noschese, M.; Buttazzoni, G.; Comisso, M. Role of the Product λ′(0)ρ′(1) in Determining LDPC Code Performance. Electronics 2019, 8, 1515. https://doi.org/10.3390/electronics8121515
Vatta F, Babich F, Ellero F, Noschese M, Buttazzoni G, Comisso M. Role of the Product λ′(0)ρ′(1) in Determining LDPC Code Performance. Electronics. 2019; 8(12):1515. https://doi.org/10.3390/electronics8121515
Chicago/Turabian StyleVatta, Francesca, Fulvio Babich, Flavio Ellero, Matteo Noschese, Giulia Buttazzoni, and Massimiliano Comisso. 2019. "Role of the Product λ′(0)ρ′(1) in Determining LDPC Code Performance" Electronics 8, no. 12: 1515. https://doi.org/10.3390/electronics8121515
APA StyleVatta, F., Babich, F., Ellero, F., Noschese, M., Buttazzoni, G., & Comisso, M. (2019). Role of the Product λ′(0)ρ′(1) in Determining LDPC Code Performance. Electronics, 8(12), 1515. https://doi.org/10.3390/electronics8121515






