A Deep Learning Based Transmission Algorithm for Mobile Device-to-Device Networks
Abstract
:1. Introduction
2. Related Work
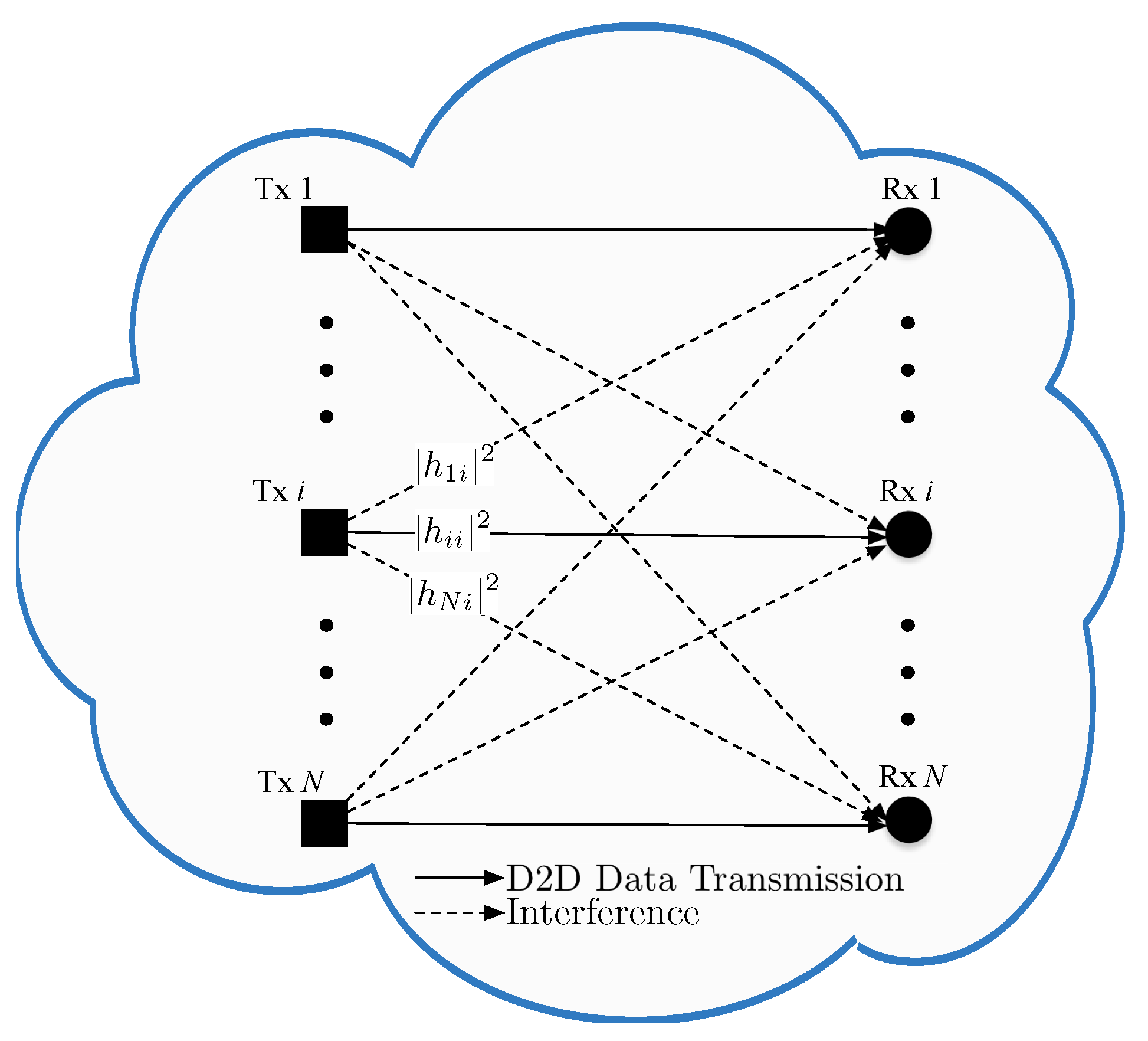
3. Network Model
4. Proposed Deep Learning Based Scheme
4.1. A Sub-Optimal Scheme to Obtain Data Samples for Training
| Algorithm 1 A sub-optimal algorithm to obtain training samples. |
| Sort in descending order Initialize: and for to N do for to k do Calculate the SINR for the pair, end for if then else break end if end for |
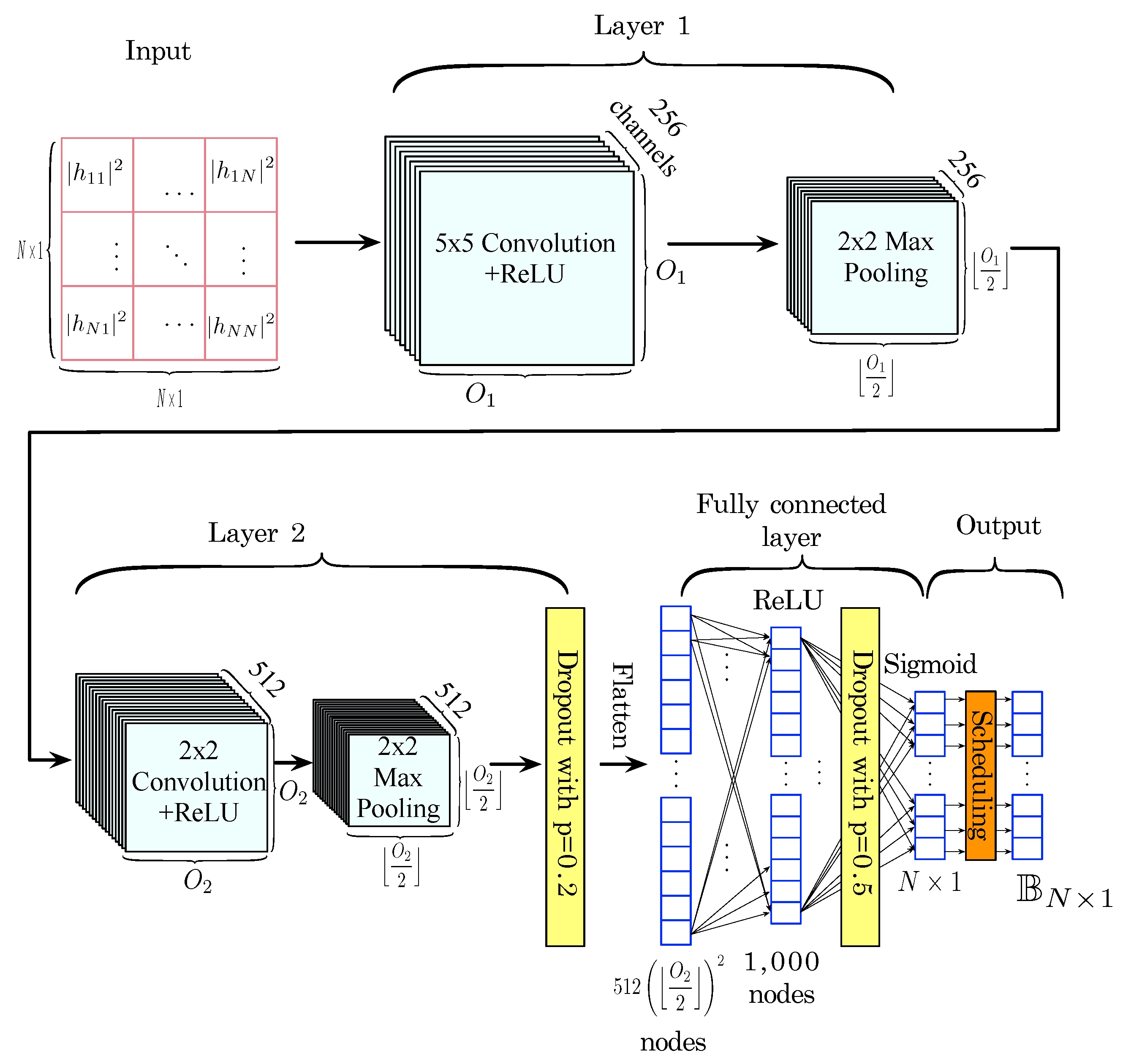
4.2. A Proposed Scheme Based on Convolutional Neural Networks
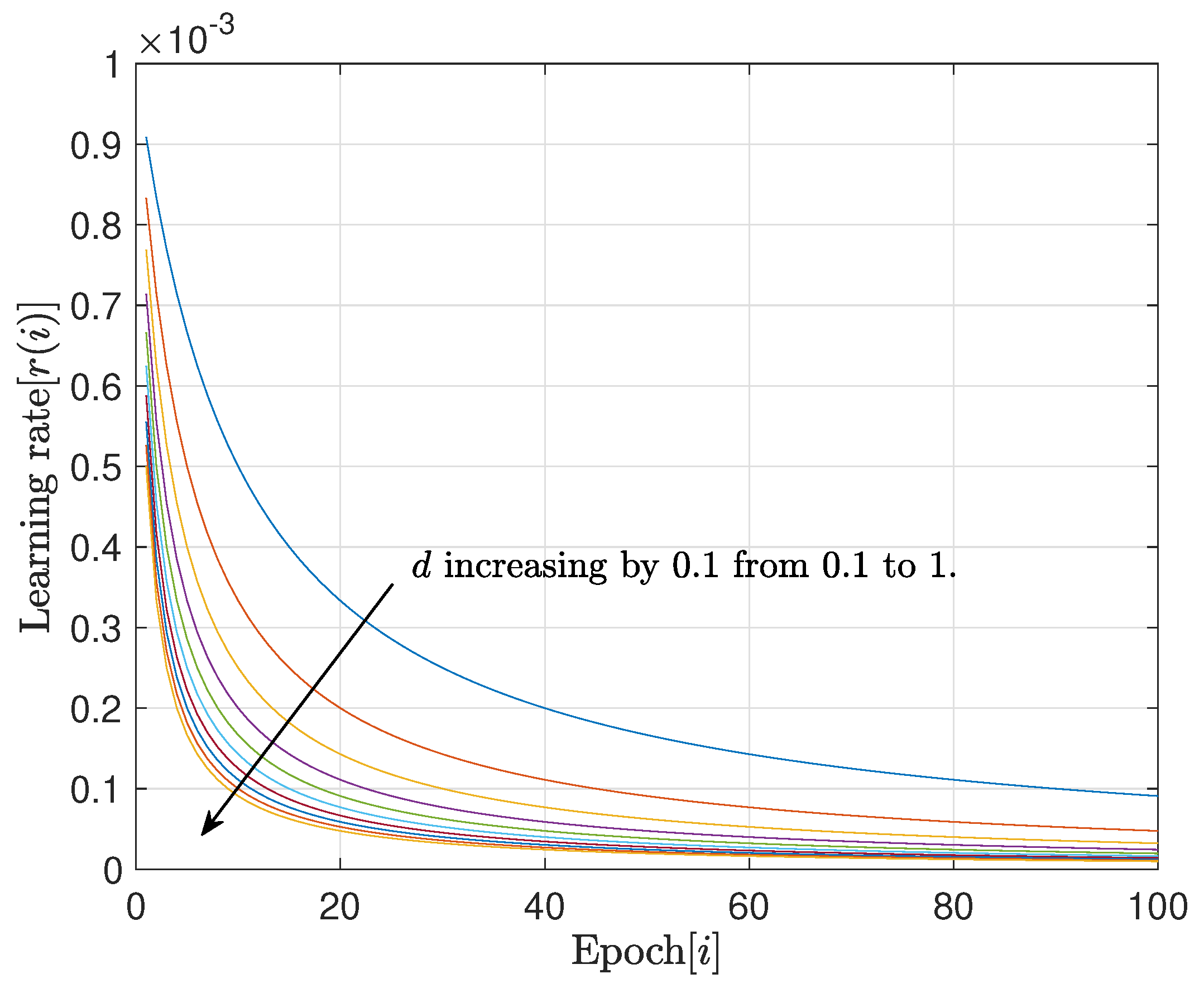
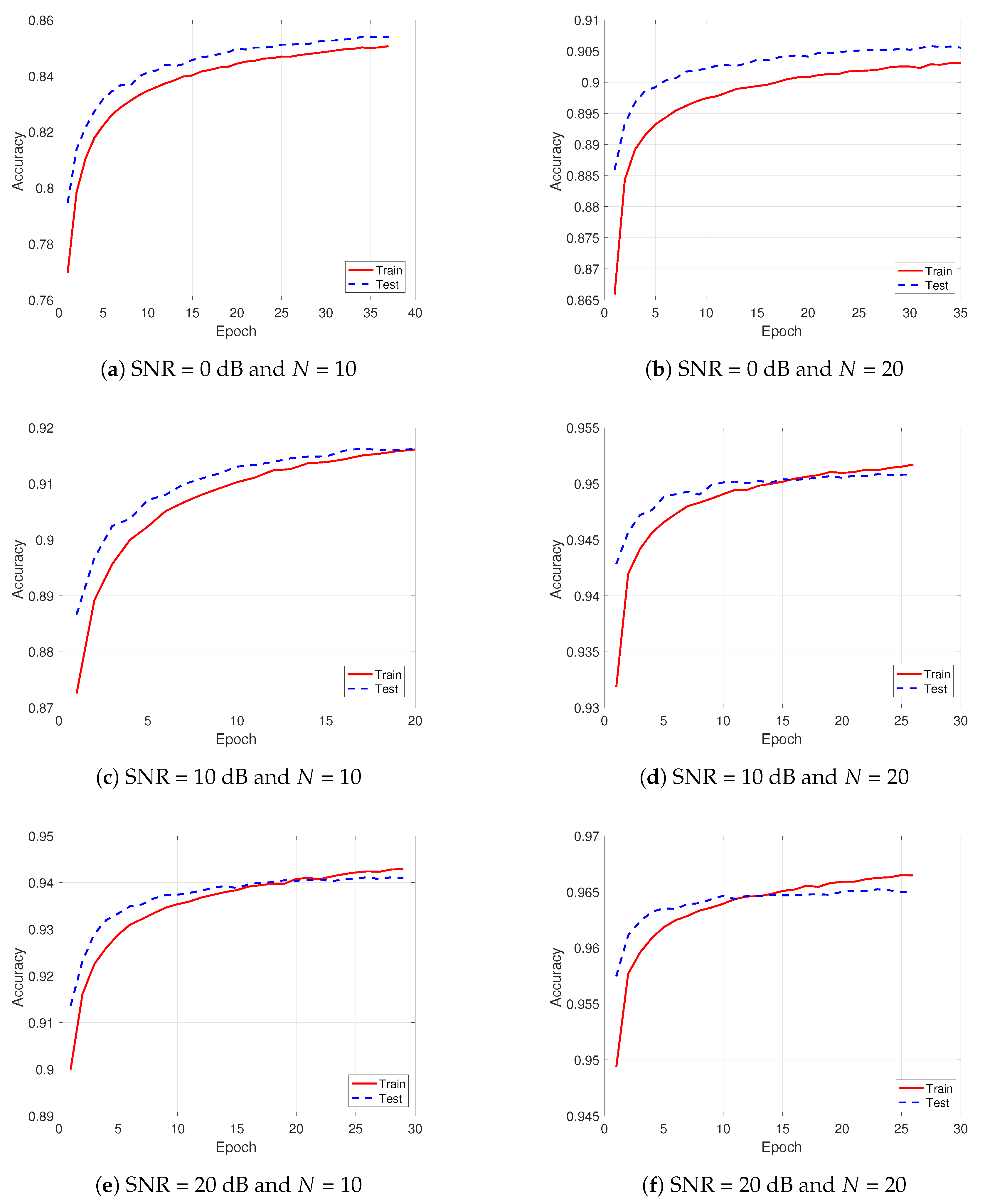
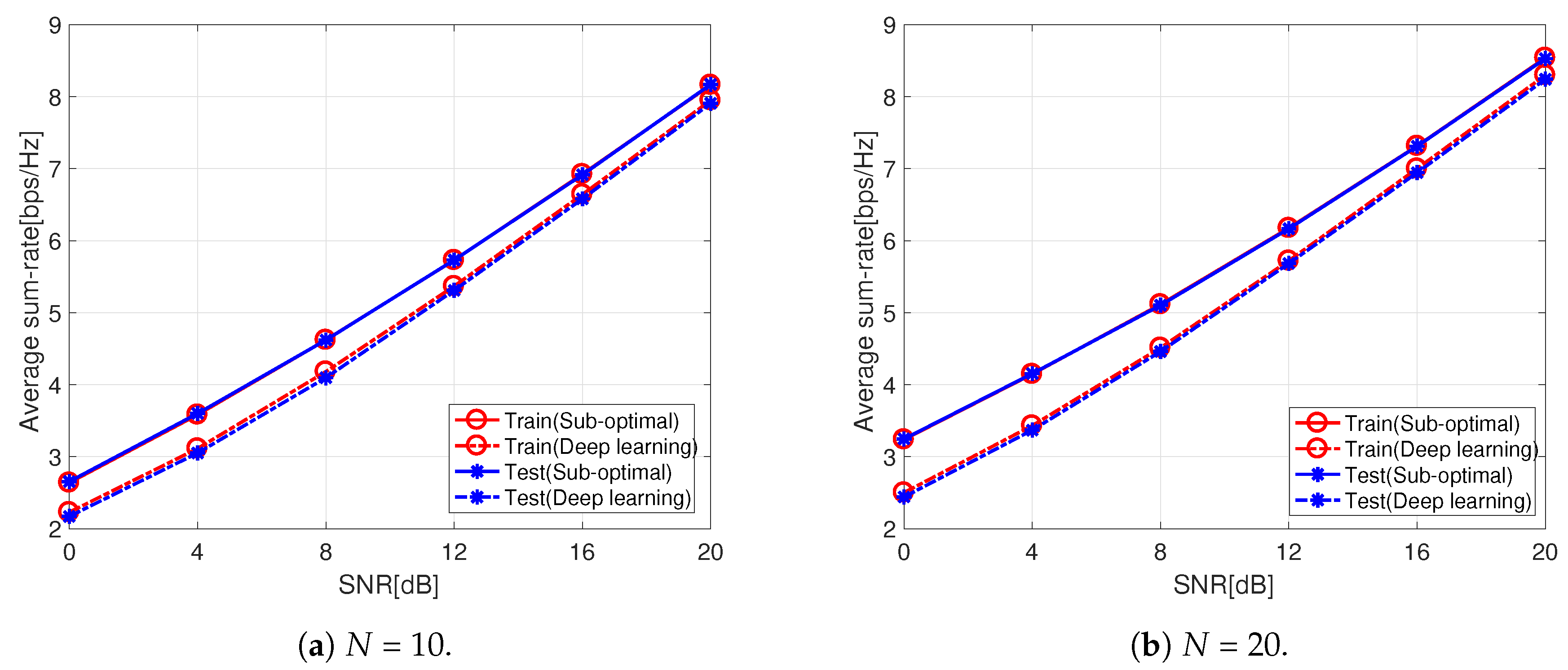
5. Numerical Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cisco, Visual Networking Index: Global Mobile Data Traffic Forecast Update, 2017–2022, Whitepaper. 2018. Available online: https://www.cisco.com/c/en/us/solutions/collateral/service-provider/visual-networking-index-vni/white-paper-c11-741490.html (accessed on 30 October 2019).
- Yang, P.; Zhang, N.; Zhang, S.; Yu, L.; Zhang, J.; Shen, X. Content Popularity Prediction Towards Location-Aware Mobile Edge Caching. IEEE Trans. Multimed. 2019, 21, 915–929. [Google Scholar] [CrossRef]
- Kang, H.J.; Kang, C.G. Mobile Device-to-Device (D2D) Content Delivery Networking: A design and Optimization Framework. IEEE J. Commun. Netw. 2014, 16, 568–577. [Google Scholar] [CrossRef]
- Malak, D.; Al-Shalash, M.; Andrews, J.G. Optimizing Content Caching to Maximize the Density of Successful Receptions in Device-to-Device Networking. IEEE Trans. Commun. 2016, 64, 4365–4380. [Google Scholar] [CrossRef]
- Golrezaei, N.; Mansourifard, P.; Molisch, A.F.; Dimakis, A.G. Base-Station Assisted Device-to-Device Communications for High-Throughput Wireless Video Networks. IEEE Trans. Wirel. Commun. 2014, 13, 3665–3676. [Google Scholar] [CrossRef]
- Golrezaei, N.; Dimakis, A.G.; Molisch, A.F. Scaling Behavior for Device-to-Deivce Communications with Distributed Caching. IEEE Trans. Inf. Theory 2014, 60, 286–4298. [Google Scholar] [CrossRef]
- Zhang, L.; Xiao, M.; Wu, G.; Li, S. Efficient Scheduling and Power Allocation for D2D-Assisted Wireless Caching Networks. IEEE Trans. Commun. 2016, 64, 2438–2452. [Google Scholar] [CrossRef]
- Doppler, K.; Yu, C.; Ribeiro, C.B.; Jänis, P. Mode selection for Device-to-Device Communication underlaying an LTE-Advanced Network. In Proceedings of the 2010 IEEE Wireless Communication and Networking Conference, Sydney, Australia, 18–21 April 2010. [Google Scholar]
- Hakola, S.; Chen, T.; Lehtomäki, J.; Koskela, T. Device-to-Device (D2D) Communication in Cellular Network—Performance Analysis of Optimum and Practical Communication Mode Selection. In Proceedings of the 2010 IEEE Wireless Communication and Networking Conference, Sydney, Australia, 18–21 April 2010. [Google Scholar]
- Zhu, K.; Hossain, E. Joint Mode Selection and Spectrum Partitioning for Device-to-Device Communication: A Dynamic Stackelberg Game. IEEE Trans. Wirel. Commun. 2015, 14, 1406–1420. [Google Scholar] [CrossRef]
- Peng, T.; Lu, Q.; Wang, H.; Xu, S.; Wang, W. Interference avoidance mechanisms in the hybrid cellular and device-to-device systems. In Proceedings of the 2009 IEEE 20th International Symposum on Personal, Indoor and Mobile Radio Communications, Tokyo, Japan, 13–16 September 2009. [Google Scholar]
- Kim, J.; Karim, N.A.; Cho, S. An Ineterference Mitigation Scheme of Device-to-Device Communications for Sensor Networks Underlying LTE-A. Sensors 2017, 17, 1088. [Google Scholar]
- Katsinis, G.; Tsiropoulou, E.E.; Papavassiliou, S. Multicell Interference Management in Device-to-Device Underlay Cellular Networks. Future Ineternet 2017, 9, 44. [Google Scholar] [CrossRef]
- Wu, X.; Tavildar, S.; Shakkottai, S.; Richardson, T.; Li, J.; Laroia, R.; Jovicic, A. FlashLinQ: A Synchronous Distributed Scheduler for Peer-to-Peer Ad Hoc Networks. IEEE/ACM Trans. Netw. 2013, 21, 1215–1228. [Google Scholar] [CrossRef]
- Janis, P.; Koivunen, V.; Ribeiro, C.; Korhonen, J.; Doppler, K.; Hugl, K. Interference-aware resource allocation for device-to-device radio underlaying cellular networks. In Proceedings of the IEEE 69th Vehicular Technology Conference, Barcelona, Spain, 26–29 April 2009. [Google Scholar]
- Zulhasnine, M.; Huang, C.; Srinivasan, A. Efficient resource allocation for device-to-device communication underlaying LTE network. In Proceedings of the 2010 IEEE 6th International Conference on Wireless and Mobile Computing, Networking and Communications, Niagara Falls, ON, Canada, 11–13 October 2010; pp. 368–375. [Google Scholar]
- Zhang, R.; Cheng, X.; Yang, L.; Jiao, B. Interference Graph-Based Resource Allocation (InGRA) for D2D Communications Underlaying Cellular Networks. IEEE Trans. Veh. Technol. 2015, 64, 3844–3850. [Google Scholar] [CrossRef]
- Zhang, J.; Wu, G.; Xiong, W.; Chen, Z.; Li, S. Utility-Maximization Resource Allocation for Device-to-Device Communication Underlaying Cellular Networks. In Proceedings of the 2013 IEEE Globecom Workshop, Atlanta, GA, USA, 9–13 December 2013; pp. 623–628. [Google Scholar]
- Wang, L.; Tang, H.; Wu, H.; Stüber, G.L. Resource Allocation for D2D Communications Underlay in Rayleigh Fading channels. IEEE Trans. Veh. Technol. 2017, 66, 1159–1170. [Google Scholar] [CrossRef]
- Ban, T.-W.; Jung, B.C. On the Link Scheduling for Cellular-Aided Device-to-Device Networks. IEEE Trans. Veh. Technol. 2016, 65, 9404–9409. [Google Scholar] [CrossRef]
- Esmat, H.H.; Elmesalawy, M.M.; Ibrahim, I.I. Adaptive Resource Sharing Algorithm for Device-to-Device Communications Underlaying Cellular Networks. IEEE Commun. Lett. 2016, 20, 530–533. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, S.; Liu, W.; Guo, W.; Chu, X. Iunius: A Cross-Layer Peer-to-Peer System with Device-to-Device Communications. IEEE Trans. Wirel. Commun. 2016, 15, 7005–7017. [Google Scholar] [CrossRef]
- Fadlullah, Z.M.; Tang, F.; Mao, B.; Kato, N.; Akashi, O.; Inoue, T.; Mizutani, K. State-of-the-Art Deep Learning: Evolving Machine Intelligence toward Tomorrow’s Intelligent Network Traffic Control Systems. IEEE Commun. Surv. Tutor. 2017, 19, 2432–2455. [Google Scholar] [CrossRef]
- Ye, H.; Li, G.Y.; Juang, B. Power of Deep Learning for Channel Estimation and Signal Detection in OFDM Systems. IEEE Wirel. Commun. Lett. 2018, 7, 114–117. [Google Scholar] [CrossRef]
- Huang, H.; Song, Y.; Yang, J.; Gui, G.; Adachi, F. Deep-Learning-Based Millimeter-Wave Massive MIMO for Hybrid Precoding. IEEE Trans. Veh. Technol. 2019, 68, 3027–3032. [Google Scholar] [CrossRef]
- Ferreira, P.V.R.; Paffenroth, R.; Wyglinski, A.M.; Hackett, T.M.; Bilén, S.G.; Reinhart, R.C.; Mortensen, D.J. Multiobjective Reinforcement Learning for Cognitive Satellite Communications Using Deep Neural Network Ensembles. IEEE J. Sel. Areas Commun. 2018, 36, 1030–1041. [Google Scholar]
- Liu, C.H.; Chen, Z.; Tang, J.; Xu, J.; Piao, C. Energy-Efficient UAV Control for Effective and Fair Communication Coverage: A Deep Reinforcement Learning Approach. IEEE J. Sel. Areas Commun. 2018, 36, 2059–2070. [Google Scholar] [CrossRef]
- Arulkumaran, K.; Deisenroth, M.P.; Brundage, M.; Bharath, A.A. Deep Reinforcement Learning: A Brief Survey. IEEE Signal Process. Mag. 2017, 34, 26–38. [Google Scholar] [CrossRef]
- Hanin, B.; Rolnick, D. How to Start Training: The Effect of Initialization and Architecture. In Proceedings of the 32nd Conference on Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018. [Google Scholar]
- Graham, R.L.; Knuth, D.E.; Patashnik, O. Concrete Mathematics: A Foundation for Computer Science. Comput. Phys. 1989, 3, 106–107. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ban, T.-W.; Lee, W. A Deep Learning Based Transmission Algorithm for Mobile Device-to-Device Networks. Electronics 2019, 8, 1361. https://doi.org/10.3390/electronics8111361
Ban T-W, Lee W. A Deep Learning Based Transmission Algorithm for Mobile Device-to-Device Networks. Electronics. 2019; 8(11):1361. https://doi.org/10.3390/electronics8111361
Chicago/Turabian StyleBan, Tae-Won, and Woongsup Lee. 2019. "A Deep Learning Based Transmission Algorithm for Mobile Device-to-Device Networks" Electronics 8, no. 11: 1361. https://doi.org/10.3390/electronics8111361
APA StyleBan, T.-W., & Lee, W. (2019). A Deep Learning Based Transmission Algorithm for Mobile Device-to-Device Networks. Electronics, 8(11), 1361. https://doi.org/10.3390/electronics8111361




