1. Introduction
Along with the booming of mobile applications and the Internet of Things (IoT), a momentously increasing number of mobile devices and applications are widely used at the network edge. Based on a report from Cisco [
1], it is predicted that around 850 ZB data will be generated at the network edge by 2021, which significantly exceeds the traffic in global data centers. Besides handling tremendous data, popular mobile applications and services, e.g., video surveillance, interactive gaming, and voice assistants, require intensive computational resources. In particular, with the proliferation of artificial intelligence (AI) supported smart applications, mobile and IoT devices face big challenges due to their limited computational capacities, as well as constrained power.
One of the conventional ways to deal with this issue is to offload the computation-intensive work and service data from mobile devices to remote cloud data centers. However, moving from the network edge to remote cloud data centers via wide area networks (WAN) results in prohibitively high transmission latency and monetary cost, which is nontrivial especially for latency-sensitive applications. Another major concern of processing data on remote clouds is the privacy leakage issue.
To fulfill the requirements of latency-sensitive and resource-intensive applications, the novel paradigm Multi-access Edge Computing (MEC) is proposed and promptly ascends to the spotlight [
2,
3]. By pushing computation tasks and data to small-sized cloudlets near mobile users, MEC reduces the transmission delay, alleviates the congestion in the network core, and saves the communication cost compared with remote cloud data centers [
4,
5]. As an essential component in the MEC paradigm, a cloudlet [
6], which consists of trusted computers with rich resources, serves the last mile of the Internet [
7] as a complement to centralized remote clouds.
Despite the benefits of sinking the data and computation to the network edge, new concerns on the placement and capacity planning of cloudlets have risen. It is not a trivial problem to balance the service performance and the infrastructure providers’ (ISP) costs while additionally considering user mobility, cloudlets’ coverage, and the large scale of Wireless Metropolitan Area Network (WMAN). Specifically, deploying more cloudlets closer to mobile users could reduce transmission delay and communication costs. However, this will definitely add more costs of purchasing and operating physical servers. Furthermore, to cope with user mobility, service migration has to be performed when a mobile user moves from the service region of one cloudlet to another. Service migration ensures that users could seamlessly access network services, yet it poses additional migration costs and may suffer from handover failure. Therefore, to deploy latency-sensitive and resource-intensive mobile services at network edge, one of the vital yet essential issues is to plan the cloudlets, including where to permanently place the cloudlets, what is the service region of each cloudlet, and how many physical resources should be assigned to each cloudlet considering the ISPs’ cost and performance requirements by mobile users.
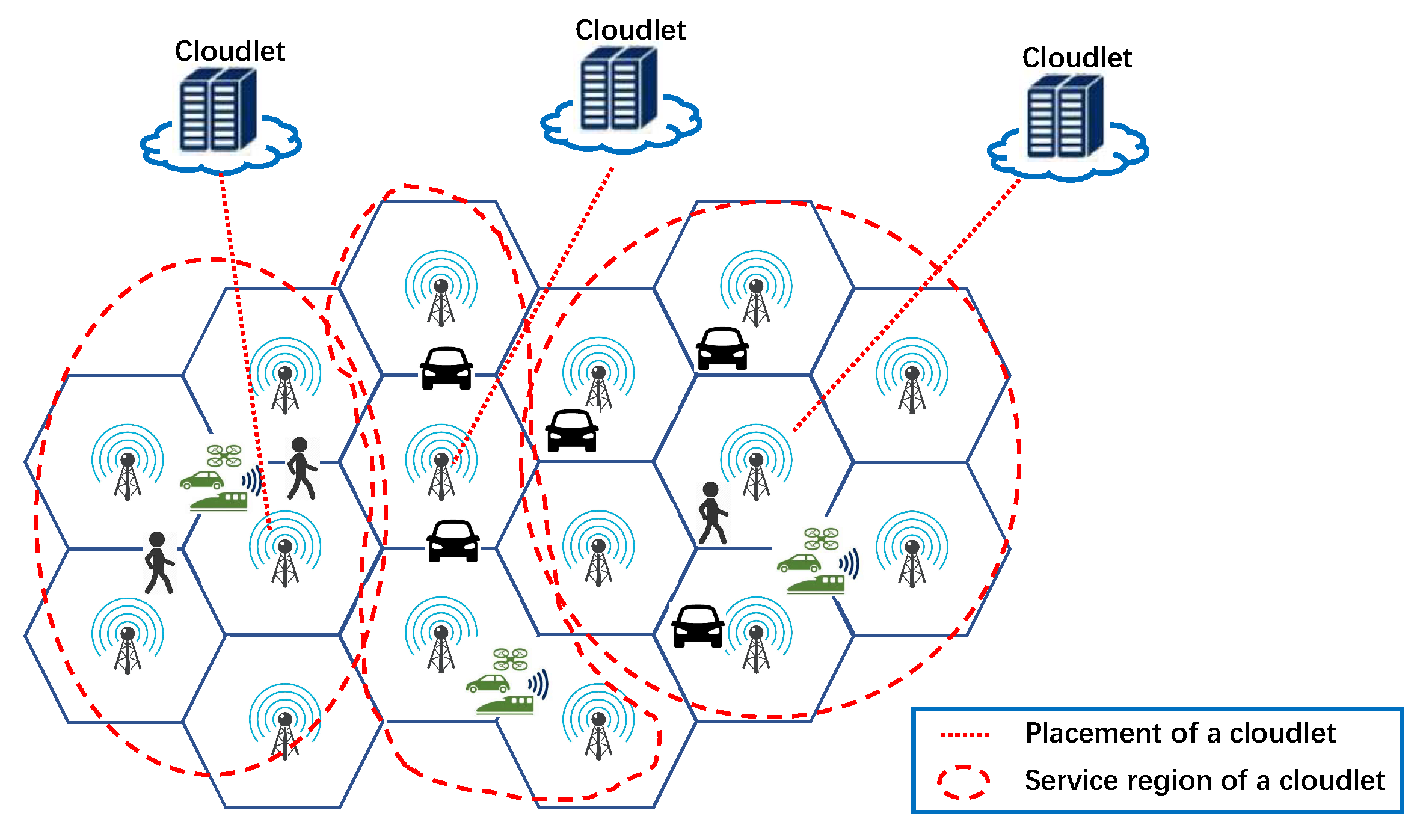
Figure 1 demonstrates an example of a cloudlet planning in a WMAN with multiple access point (AP) cells. As shown in
Figure 1, each AP is covered by exactly one cloudlet and each cloudlet is co-existed with one AP in its service region.
However, most existing studies are limited to improving the Quality of Service (QoS) of mobile applications or services by properly offloading tasks to physically deployed cloudlets, e.g., [
4,
8,
9,
10]. These studies focus on how the tasks or virtual services should be embedded in cloudlets that are equipped with virtualization techniques. Obviously, the computational resources that could be assigned to each task or virtual service are bounded by the maximum available physical resources in each cloudlet. In contrast, the planning of each cloudlet’s physical location, capacity, and service region coverage has been ignored.
In our previous work [
11], we noticed the impact of the cloudlet planning and started with an initial step of carefully partitioning the entire WMAN into disjoint service regions. However, in [
11] only the minimization of service handover costs is discussed, while the cloudlet construction costs and operation costs are ignored. Therefore, in the proposed solution, we only suggested the way to determine the service regions without the planning of cloudlets’ physical placement and capacities.
In contrast to existing work, in this paper, we aim to optimize the long-term total cost of mobile services through cloudlet planning in WMAN. We jointly consider the cloudlet placement, capacity and service region towards the minimization of the long-term total cost, including cloudlet construction cost, server operation cost, and service migration cost under the guarantee on the transmission delay. Please note that in the real world, moving a cloudlet between different sites is expensive and may cause service interruption. We assume that the cloudlets are static once they are deployed, and focus on the long-term optimization goal. This optimization problem is formulated and its hardness is proved. In contrast to most previous work, the capacities of cloudlets are not given but computed based on the expected workload from active mobile users associated with the access points in the service region of each cloudlet. This is rational as in planning traditional remote data centers, their capacities are decided based on the expected workload [
12]. Nevertheless, to avoid an unacceptably large network delay, we set a constraint on the distance between a mobile user and its corresponding cloudlet. To solve the long-term cost-oriented cloudlets planning problem efficiently, we decompose the original problem into two sub-problems, the service region planning problem and the capacity decision problem, respectively. We then develop a two-stage randomized algorithm for the cloudlet service region planning problem and the cloudlet capacities decision based on the historical workload of mobile users associated with each access point. Extensive evaluations based on the real and simulated traces demonstrate the performance of the proposed solution. The contribution of this paper could be summarized as follows:
We identify and formulate the long-term cost-oriented cloudlet planning problem aiming to minimize the long-term overhead under the constraint on the transmission delay.
We decompose the optimization problem into sub-problems, and design algorithms to solve them respectively. Specifically, we develop a randomized service region planning algorithm that carefully divides a WMAN into disjoint service regions so that the cloudlet placement cost and service migration cost are minimized. Based on the determined service regions and cloudlet locations, we plan the cloudlet capacity to optimize long-term cloudlet operation costs.
We evaluate the proposed solution with randomly generated traces as well as real traces. Evaluation results show the effectiveness of the proposed solution on saving the long-term cost of cloudlets in WMAN.
The remainder of the paper is organized as follows. We discuss the background and related work in
Section 2. The long-term cost-oriented cloudlet planning problem is formulated and analyzed in
Section 3, while the proposed solution is presented in
Section 4. The performance evaluations are shown in
Section 5, and the concluding remarks are provided in
Section 6.
2. Related Work
MEC paradigm enables the computation-intensive tasks to be pushed to the cloudlet located at the network edge, through which the transmission delay would be reduced and the congestion in network core would be alleviated. Due to its benefits, MEC attracts much attention in recent years. In particular, in MEC scenarios, the user-to-cloudlet association problem and virtual service placement problem are recognized as a key issue. In MEC user-to-cloudlet association problem, e.g., [
8,
9], algorithms were proposed to guide the mapping from a mobile user’s request to a proper cloudlet considering various optimization goals, such as improving the performance of the services, or the resource usage efficiency. Jia et al. [
4] studied the workload balancing among multiple cloudlets. In [
4], the average service response time was minimized through efficiently redirecting users’ requests to the appropriate cloudlets. Yang et al. [
10] considered the mobility and changes of mobile applications, and designed a dynamic virtual service placement method. In [
13], spot pricing mechanism was adopted to provide virtual machines through markets. The above-mentioned works tried to place virtual services or applications on physically deployed cloudlets towards various targets for better using physical resources in the cloudlets.
Besides the virtual service placement, a few researchers started to realize the importance of the cloudlet facility placement problem. In [
5], to save the average users’ waiting time including network delay and queuing delay, Jia et al. jointly considered the placement of multiple cloudlets and the assignments between mobile users to the cloudlets. Ceselli et al. [
14] modeled this problem as a linear programming problem to reduce the cloudlet installation cost, then solved it using a heuristic algorithm. For more general cases, [
15,
16] studied the placement of heterogeneous cloudlets with different amounts of computation resources. Mondal et al. [
17] aimed to minimize the cloudlet installation cost by carefully planning cloudlet placement. However, the network is assumed to be static without considering users’ movement. The placement and user-to-cloudlet association could also be determined by the geographic area partition scheme as proposed in [
18]. In [
18], Bouet et al. observed that the high communication cost is induced by the traffic between mobile users belong to different service regions. To reduce the communication cost, the entire network is partitioned into disjoint clusters, and all the mobile users in a cluster would be offloaded and served by the cloudlet in this cluster under the capacity limitation of this cloudlet. Here, [
18] did not assume any candidate location for cloudlets as most previous works did, which made this work more practical.
In general, major existing works are based on the assumption that the computational capacity of each cloudlet is fixed and constrained, e.g., [
5,
14,
16]. Some studies, such as [
18], set a bound on the number of communications. This is because these methods are designed for allocating virtual services or applications on deployed cloudlets. In this paper, we aim to optimize the application performance at the cloudlet planning phase. We consider the capacity of cloudlets as a part that could be determined in the cloudlet planning phase, rather than a constraint, which is different from existing work. Once the placement and the service region of each cloudlet have been determined, the cloudlet capacity could be carefully and efficiently computed based on the expected workload of mobile users. The prediction of mobile users’ workload was extensively studied at different levels [
19,
20].
At the same time, virtualization of physical machines and network functions offer more flexible for the deployment of mobile services. To deal with the mobility of mobile users and provide seamless services to resource-intensive and latency-sensitive applications, the replicas of virtual services are enabled to be migrated between different cloudlets. To avoid service interruption and service delay, service migrations could be performed before the users moving to a new service region, based on the prediction of their movements. However, the overhead induced by service migration, e.g., the bandwidth for moving service replicas and intermediate service data, cannot be eliminated. Nevertheless, this overhead is overlooked in most previous work, such as [
5,
15,
16,
18]. In our work, we take the service migration overhead as an important part of the long-term total cost, then formulate the cloudlet planning optimization problem considering the cloudlet construction cost, long-term operation cost, and service migration cost.
3. Problem Formulation
We model the long-term cost-oriented (LTCO) cloudlet planning problem as an optimization problem aiming to minimize the long-term cost for offering edge service to mobile users. Specifically, the total cost consists of the cloudlet construction cost, server operation cost, and service migration cost. To balance various facts impacting the total cost and to be more practical, we consider monetary cost when modeling the long-term cost. The main constraints of the cloudlet planning problem include transmission delay limitation, integrity requirements, and binary limitations.
3.1. Notations
In this section, we model the LTCO cloudlet planning problem with practical assumptions and migration awareness. Notations used in this paper are listed in
Table 1.
Assume that a WMAN
is equipped with a group of
A access points (AP) (For convenience, we use AP to generalize the equipments, e.g., wireless access points, or base stations, that assist mobile users to connect to the Internet.), and a set of physical links
L that connect APs. For simplicity, we further assume that each AP
covers a disjoint region
, and serves all the mobile users in the region
. Based on the historical mobile users’ traces and existing traffic estimation schemes, e.g., [
19,
20], the AP that serves mobile user
at time
t is represented as
. When
, it is known that a mobile user travels crossing the boundary between two regions. Boundary crossing may cause handoff in cellular network as widely discussed in existing studies, e.g., [
21,
22]. In this study, we focus on the service migration between cloudlets without involving too much in AP handoff. Assume that each time slot
t is short enough that any user cannot travel more than one region at a single time slot. Then, by aggregating the traces of all mobile users, we obtain the number of boundary crossing
between any two regions
and
as defined in Equation (
1).
Here, the function ↑ compares two APs as defined in Equation (
2).
Through APs, mobile users could access the wireless network, and their requests would be transmitted to cloudlets. We denote the minimal desired resources of mobile users in AP at time t as (Here, we consider a general computational resources. In real applications, it could be CPU capacity or available storage size.). By scaling up or down, a cloudlet could satisfy the requests from its associated APs. For simplicity of our discussion, we only consider homogeneous servers when planning cloudlets capacities, and we assume that the maximum available resource on a single server is .
Thus, the objective of the long-term cost-oriented cloudlet planning could be defined as follows:
3.2. Cloudlet Construction Cost
We model the one time cloudlet construction cost as the summation of the cost for site construction and servers:
Here, a binary variable
is used to indicate whether or not a cloudlet would be constructed and co-located with AP
as shown in Equation (
5), while an integer variable
is used to represent the number of servers that is deployed at AP
. Obviously,
.
The basic site construction cost may vary based on the geographic condition of each site , and the unit cost for purchasing and placing a server is .
3.3. Cloudlet Operation Cost
Once the cloudlets have been constructed, they could be used for responding to mobile users’ service requests. The daily operation of cloudlets consumes energy for computing, communication, and other aspects. Here, we focus on the operation cost of servers and the communication cost between mobile users to their corresponding cloudlets.
Various techniques were developed and used to save energy consumption by servers, e.g., DVFS [
23], virtualization [
24]. Those techniques were widely studied and deployed in cloud data centers. Here, we employ the assumptions on energy consumption of data centers in existing studies, e.g., [
25,
26], while modeling the operation cost for a single server as:
Assume the workload of a single server at time
t is
, we have the operation cost
of this server at time
t as:
is the maximum operation cost when the server is fully used, and
k is the ratio that the cost of an idle server to a fully used one. To balance the workload of servers in each cloudlet, we assume that the received requests from mobile users are evenly distributed among all the servers in the cloudlet. In other words, the workload of a server in cloudlet co-located with AP
is:
In Equation (
8),
is the total workload for mobile users in AP
at time
t. Variable
indicates whether or not the requests from mobile users in AP
would be processed at the cloudlet at AP
as defined in Equation (
9).
Besides the operation cost of servers, the communication cost would be taken into consideration. We model it as:
Here, indicates the amount of communication flow for mobile users served by AP i at time t. Please note that we focus on latency-intensive applications offloaded to cloudlets rather than remote data centers, thus the communication cost mainly comes from the traffic between mobile users and the cloudlets. In the future, we would consider more general scenarios that remote data centers and cloudlets cooperate to serve applications with various priorities and demands. In that case, the long-term cost model would be extended to include communication cost between remote data centers and cloudlets.
From the definitions in Equation (
6)–(
10), we can derive the total operation cost for all the cloudlets as:
3.4. Service Migration Cost
To provide seamless, low-latency services to mobile users, some status and data should be duplicated from the origin cloudlet to the new cloudlet before the user moving to a new service region. However, service migration introduces additional overheads. We model the service migration cost as below:
Here, we formulate the service migration cost as the summation of duplicating the status and data for every movement between any two cloudlets.
is the coefficient of migration cost. Assuming that the data transmission cost is proportional to the migration distance,
, the distance between APs
and
, indicates the unit data transmission cost between the cloudlets co-located with APs
and
respectively. Binary variable
indicates if the requests from users in AP
are processed at the cloudlet co-located with AP
. In Equation (
12), for each boundary crossing between any two APs
and
, if the two APs are served by cloudlets co-located with AP
i and AP
j, respectively, a data transmission cost
is accumulated to the total service migration cost.
3.5. Constraints
The optimization goal in Equation (
3) is subjected to a set of constraints as listed below.
Constraint (
13) ensures that for each mobile user, the transmission delay would exceed a predetermined bound
D. Constraint (
14) guarantees that the distributed workload on each server in any cloudlet would not exceed the maximum available resource on the server. Constraint (
15) makes sure that the requests received via each AP
would be handled by exactly one cloudlet. Constraints (
16) and (
17) are introduced to set the relationship between variables. Intuitively, constraint (
16) indicates that if there is a cloudlet co-located with AP
, there must be at least one server at AP
. Constraint (
17) implies that if requests via AP
are handled at AP
, there must be a cloudlet co-located with AP
.
3.6. Hardness of the Problem
Through solving the optimization problem in Equation (
3) under a set of constraints (
13)–(
17), we could obtain the optimal solution of the LTCO cloudlet planning. However, it could be proved that the graph partition with size limitation [
27], a known NP-complete problem, could be reduced to a special case of the LTCO cloudlet planning problem. Here, we re-state the LTCO cloudlet planning problem as well as the graph partition problem, and prove the NP-completeness of the proposed LTCO cloudlet planning problem.
LTCO cloudlet planning problem: Given a set of n APs each of which serves a set of mobile users in a disjoint region, and assume that the traces and workload of mobile users could be estimated, the problem is to determine if there is any planning X, with which the weighted long-term total cost of this cloudlet planning is smaller than a constant value E, and the transmission delay between any mobile user to its corresponding cloudlet is less than a given threshold D.
Graph partition with size limitation: Given a graph , the weight of each edge , and a size constraint k, the problem is if the vertices could be partitioned into clusters with bounded size k that the sum of the cut between clusters is smaller than a constant F.
Theorem 1. The proposed LTCO cloudlet planning problem is NP-complete.
It is easy to prove that the LTCO cloudlet planning problem belongs to NP. Given any placement and capacity planning, it could be checked whether it is a feasible solution that the weighted long-term total cost is smaller than E or and if it satisfies the transmission delay constraints in polynomial time.
Then we consider a special case of the LTCO cloudlet planning problem. Here, we have the maximum allowed transmission delay as D and the transmission delay between any neighbor cells is 1 unit. Thus, any cluster with at most vertices would not break this constraint. Furthermore, the , , P, and are all set of 0. Then we have a reduced and simpler problem. By letting the number of boundary-crossing between two cells corresponds to weight of each edge , and letting the bounded size , the graph partition with size limitation is reduced to the proposed LTCO cloudlet planning problem. When the solution of the graph partition with size limitation is obtained, the corresponding clustering is a solution to the LTCO cloudlet planning problem. Therefore, the LTCO cloudlet planning problem is NP-complete.
Considering the hardness of this problem, we come up with a randomized two-step algorithm to determine the optimal placement, service region and capacity of each cloudlet in the WMAN.
4. Algorithm
To deal with the formulated LTCO cloudlet planning problem, we develop a two-step algorithm. In the first step, we focus on the service migration cost and aim to partition the entire WMAN into disjoint service regions. Then, aiming to reduce the cloudlet construction cost and operation cost, a header AP is selected to place a cloudlet to serve all the APs in the same service region. In the second step, the number of servers in each cloudlet would be determined based on the historical workload.
4.1. Randomized Migration Aware Service Region Planning
By carefully partition the entire WMAN into disjoint service regions, the number of service region boundary crossing could be reduced, so that the service migration cost is minimized. To achieve this goal, the migration aware service region planning algorithm (SRP) is proposed to explore the optimal way of partitioning the service region. It iteratively combines AP cells that have the most frequently boundary-crossing while respecting transmission delay constraints. After that, to improve the quality of the solution, randomness is imported into the SRP. Some randomly selected service regions may be dismissed and their member cells could be re-grouped with adjacent cells. The detailed description of the SRP is presented in Algorithm 1.
| Algorithm 1 Service Region Planning Algorithm (SRP) |
Input: set of cells C, set of number of boundary crossing between adjacent cells W, maximum allowed transmission delay D, threshold , lower bound b
Output: Service region planning decision X- 1:
Compute an initial planning for service regions by calling the Service Region Initialization Algorithm (SRI) - 2:
For each pair of adjacent regions, set a counter with an initial value 0 and put the pairs in set E - 3:
while set E is not empty do - 4:
Randomly select a pair of regions i and j from set E and dismiss the two regions i and j - 5:
Create a sub-group that consists of cells in the dismissed regions i and j, and all their neighbor regions - 6:
Call the Service Region Re-group Algorithm (SRR) on the sub-group - 7:
if there is no better planning then - 8:
Increase the counter for the pair of regions i and j and the region pair would be removed from set E if the counter is larger than - 9:
else - 10:
Reset counters for the regions in the sub-group and update the intermediate planning with the improved planning for the sub-group - 11:
end if - 12:
end while - 13:
for each region i in the planning do - 14:
Set , if and - 15:
end for
|
As presented in Algorithm 1, the SRP firstly calculates an initial solution for partition the entire MWAN into disjoint regions by calling Service Region Initialization Algorithm (SRI) (Step 1). The initial solution obtained by the SRI may trap into the local optimum. However, it could be a good start to approach the optimal solution. Randomized algorithms are widely employed to solve NP-complete problems in an efficient way. It could prevent the algorithms from trapping into a local optimum. Thus, we adopt randomness in the SRP by iteratively selecting a random part of the intermediate solution (Step 4). Then, the Service Region Re-group Algorithm (SRR) (Algorithm 2) is executed on the randomly selected part of the solution (Step 6) to explore the possibility of finding a better solution. Steps 4–11 are repeatedly performed until that the solution could not be improved (Step 8).
| Algorithm 2 Service Region Re-group Algorithm (SRR) |
Input: sub-group , maximum allowed transmission delay D, lower bound b
Output: an updated planning of service region - 1:
Compute the profit function of combining two regions u and v as , where r is a random number uniformed selected from , and keep a record of the profit for each pair of regions in set - 2:
while set is not empty do - 3:
Sort region pairs in based on the profit function - 4:
ifthen - 5:
Contract the pairs of region i and region j with the largest profit, and remove the region pair from set - 6:
Update the size of combined region, generate random number r, profit function and number of boundary crossing for all related region pairs - 7:
else - 8:
Remove the region pair i and j from set - 9:
end if - 10:
end while - 11:
Return the contracted regions that consist of cells
|
The SRI (Algorithm 3) returns a feasible solution for the service region planning problem. This solution is treated as a start point in the SRP (Algorithm 1). Algorithm 3 may consolidate two cells or two regions into a new service region based on the potential profit of consolidating them. Intuitively, the cells or regions with relatively small size but a large number of boundary-crossing are expected to be combined as a new service region. More specifically, the profit function of combining regions i and j is proportional to the number of boundary-crossing between the two regions, but inversely proportional to the sum of the size of regions i and j (Step 2). Once the profit of combining each pair of regions has been calculated, we repeatedly merge regions with the largest profit until that the largest transmission delay in the combined region exceeds the maximum allowed transmission delay (Step 6). After that, the profits of combining the new region and its neighbors are updated (Step 7).
| Algorithm 3 Service Region Initialization Algorithm (SRI) |
Input: set of cells C, set of number of boundary crossing between adjacent cells W, maximum allowed transmission delay D
Output: an initial planning of service region - 1:
Initially set each cell as a single service region - 2:
Compute the profit function of combining two regions u and v as , and keep a record of the profit for each pair of regions in set - 3:
while set is not empty do - 4:
Sort region pairs in based on the profit function - 5:
ifthen - 6:
Contract the pairs of region i and region j with the largest profit, and remove the region pair from set - 7:
Update the size of combined region, profit function and number of boundary crossing for all related region pairs - 8:
else - 9:
Remove the region pair i and j from set - 10:
end if - 11:
end while - 12:
Return the contracted regions that consist of cells
|
Once obtained the initial solution from calling Algorithm 3, it would be repeatedly improved by randomly dismissing and re-union. Specifically, a pair of adjacent regions are randomly picked. Then, both of them are dismissed into a set of AP cells. These AP cells, as well as their adjacent regions, constitute a sub-group . Later, a randomized algorithm, Service Region Re-group Algorithm (SRR) (Algorithm 2) is executed to explore possible better service region planning on the sub-group .
As demonstrated in Algorithm 2, SRR repeatedly calculates the profit of combining two adjacent regions, until there is no more feasible combination under the constraints on the maximum transmission delay. The computation of profit in the SRR (Step 1) is similar to that in the SRI. The difference between the profit computation is that the randomness factor r is imported in Algorithm 2. r is randomly picked in the range of following the uniform distribution. We will generate a new r once there is an improvement in the intermediate solution (Step 6 in Algorithm 2).
For better illustration, a demo example is presented in
Figure 2.
Figure 2a draws the traces of mobile users including pedestrians and vehicles. Based on the traces, the number of boundary-crossing between each pair of neighbor cells could be counted as shown in
Figure 2b. These numbers would be used as a part of inputs of Algorithms 1 and 3. Then, Algorithm 3 is executed. Cells are combined based on the number of boundary-crossing between them and the size of the combined regions as shown in
Figure 2c–f. To further improve the solution, two regions would be randomly selected. In the demo example, the regions
and
are selected. After that, the selected regions would be dismissed and formed a new sub-graph with their neighbors as depicted in
Figure 2g. Finally, Step 6 would check if the solution could be improved by exploring the updated graph.
4.2. Cloudlet Capacity Decision Algorithm
Once the origin WMAN has been partitioned into disjoint service regions, one AP in each service region would be selected to build the cloudlet with a certain amount of resources. We develop a deterministic algorithm named Cloudlet Capacity Decision (CCD) algorithm to determine the location of AP in each service region, and the amount of capacity it should have to satisfy mobile users’ requirements. Considering the number of APs is limited in each partitioned region, it is possible to explore the entire solution space for the optimal weighted center of APs in the region so that the communication cost for mobile users in this region is minimized. Later, based on the capacity of a single server and the aggregated requests from mobile users, the number of servers in each cloudlet would be determined. The Cloudlet Capacity Decision (CCD) algorithm is presented in Algorithm 4.
As demonstrated in Algorithm 4, the CCD would be distributedly run for each determined service region. For each AP , we generate a tree using the Breadth-First Search (BFS) method and compute the total communication cost if the cloudlet would be co-located with (Step 3). Finally, the number of servers is calculated based on the expected total workload and the capacity of a single server (Step 19).
| Algorithm 4 Cloudlet Capacity Decision Algorithm (CCD) |
Input: Set of APs A, array of communication flows F, array of workloads C, matrix of the distance D, maximum available resource on a single server
Output: Selected location for the cloudlet, number of servers placed in the cloudlet n- 1:
Initialize the current minimum communication as infinite, and the optimal weighted center as - 2:
Initialize the peak computation workload - 3:
for each in A do - 4:
Run BFS to generate a tree rooted at - 5:
Compute the communication cost - 6:
ifthen - 7:
Update the optimal weighted center as and current minimum communication cost - 8:
end if - 9:
end for - 10:
fort in T do - 11:
Initialize the computation workload - 12:
for in A do - 13:
Accumulate the computation workload - 14:
end for - 15:
ifthen - 16:
The current peak computation workload - 17:
end if - 18:
end for - 19:
Compute
|
4.3. Analysis
As presented above, SRP partitions the WMAN into disjoint service regions; based on which, CCD selects a proper AP cell to place a cloudlet and computes the capacity of the cloudlet. To ensure the proposed algorithm feasible, we prove that they could always obtain a feasible solution in a finite number of steps.
Theorem 2. The algorithm SRP and CCD determine the service regions, placement and capacities of cloudlets for a WMAN correctly and then terminates.
Firstly, SRP calls SRI while in SRI, each cell itself either forms a single region, or it is grouped with others to form a service region. The initial regions computed by SRI may be dismissed in SRP. However, it would either be re-grouped with neighbor regions in SRR, or it becomes a single-cell region. Therefore, each cell must belong to exactly one region (Constraint (
15) in
Section 3).
Secondly, in CCD, for a single-cell group, a cloudlet would be built and co-located with the cell. Otherwise, one of the cells
would be selected to place a cloudlet. According to CCD, the number of servers in each cloudlet is computed based on the peak value of the total workload in the service region and the capacity of a single server. Thus, it is guaranteed that each region is served by exactly one cloudlet and the capacity of the cloudlet is enough to serve all mobile users in the region at any time (Constraint (
14) and (
15)) in
Section 3).
In addition, in SRI and SRR, each time before combining two regions, the transmission delay between any two cells in the combined region would not exceed the maximum allowed transmission delay
D. As a result, no matter which cell in a region is selected to place a cloudlet, the constraint of transmission delay would not be violated (Constraint (
13) in
Section 3).
Finally, SRI and SRR go through each pair of regions for only once. The two regions may be combined as a new region. The size of decreases eventually since (1) regions combine; (2) two regions are impossible to be combined. SRP may go through a pair of regions at most times. However, the size of E in SRP keeps in reduced as (1) regions combine, or (2) the counter for a pair of regions reaches . Therefore, SRI and SRR, or SRP terminate, when every member in set or E is removed, respectively.
The time complexity of the CCD is , assuming that is the number of APs in a single region, is the number of links connecting APs, and the number of time slot in a cycle is . Since the BFS rooted at could be computed in , the communication cost of this tree could be calculated in , and the peak computation workload during time T could be obtained in and all other tasks can be performed in time .
5. Performance Evaluations
We evaluate the performance of the proposed algorithms using both simulated mobility traces and real mobility traces. Since this is the first work to study the LTCO cloudlet planning problem, there is no existing algorithm to directly solve this problem. Thus, we adapt four existing algorithms for performance comparison with the proposed solution. The four comparison algorithms are an approximation algorithm for capacitated minimum forest (AACMF) ([
28]), a graph-based greedy algorithm (Greedy) ([
18]), a heuristic algorithm designed for container placement and task assignment in fog computing which using the same traces ([
29]), and an even-division algorithm (Even). These algorithms are originally designed for optimally partitioning the MWAN towards different goals, e.g., minimizing the communication cost, balancing the workload. In our performance comparison, the CCD algorithm is applied to all comparison algorithms when service regions are decided. We implement the proposed algorithms and comparison algorithms using Python 3.6. A python package NetworkX [
30] is employed to generate the underlay complex network. All the algorithms run on a cluster computing machine built on Lenovo System X Flex Compute Nodes. The descriptions of the four algorithms are summarized below.
AACMF: computes an MST of all the cells, then performs a preorder tree walk to generate a TSP tour
L. Finally partitions
L into segments each containing
c cells without breaking the constraint (
13). It was proposed to find a minimum cost forest rooted from the given gateways.
Greedy: regions with the most frequent service migrations are continuously combined until the maximum allowed cluster size is reached. It was originally designed for reducing communication costs over different regions. We modify it to be applicable to the LTCO problem by using the number of service migrations between regions instead of the number of communications.
Adapt: the cell with the heaviest load would be selected to deploy a cloudlet. The neighbor of the selected cell with the most frequent boundary-crossing would be combined if it would not violate the transmission delay constraints. Keep in combining cells until no more cell could be added into the region. Then in the remaining un-grouped cells, pick the one with the heaviest load and repeat these steps.
Even: evenly partitions the MWAN area into regions with the same size and same shape under the latency constraint. It is the simplest way to obtain a feasible solution.
We investigate the impact of the maximum allowed transmission delay D and the threshold in the LTCO cloudlet planning problem on the quality of solutions. The basic settings about the traces are summarized as below.
Randomly generated mobility traces: simulate the movements of 100 independent vehicles running in a 30km * 30km WMAN covered by small regions with a size of 1km * 1km. We use a random walk model to update the location of each vehicle every 30 seconds, and the speed of the vehicles is set from 0 to 120 km/h.
Figure 3 draws the aggregation of randomly generated vehicle locations at each time slot. The
x and
y axes in
Figure 3 represent the coordinates of each vehicle.
Real mobility traces: contain the traces of 320 taxi cabs in Rome, Italy from February 1st, 2014 to March 2nd, 2014 [
31]. During this period, each taxi reported its GPS coordinates every 7 s.
Figure 4 [
11] draws the taxi traces. The
x and
y axes in
Figure 4 represent the latitude and longitude respectively. The entire area is divided into small grid cells, each of which is with the size 1km * 1km. Each time, when a taxi crosses the cells’ boundary, it may lead to a service handover and increase the service migration cost.
We examine the impact of various scenarios on the proposed solution. Specifically, we inspect the changes in the total cost, construction cost, operation cost, and migration cost while varying the maximum allowed transmission delay
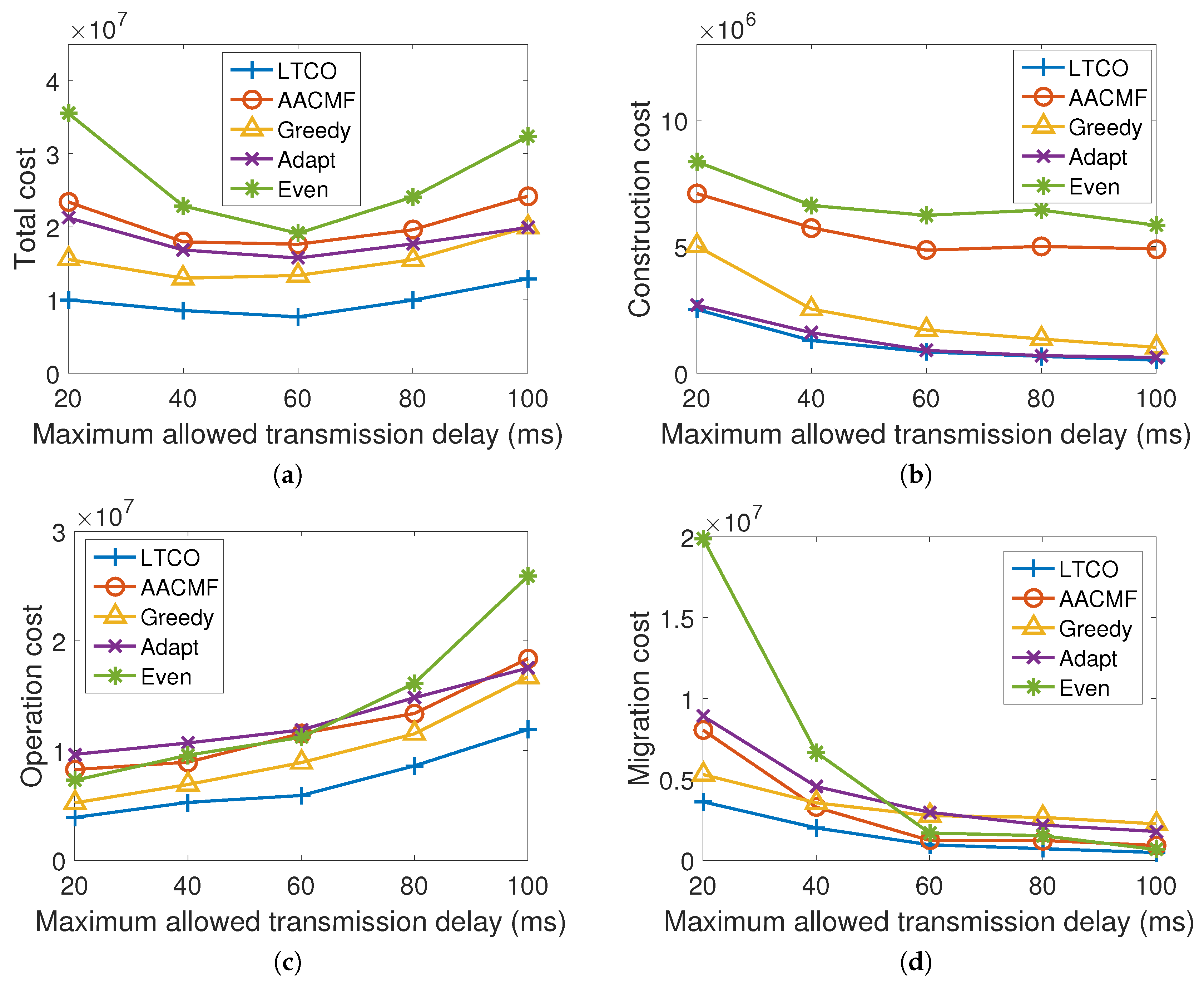
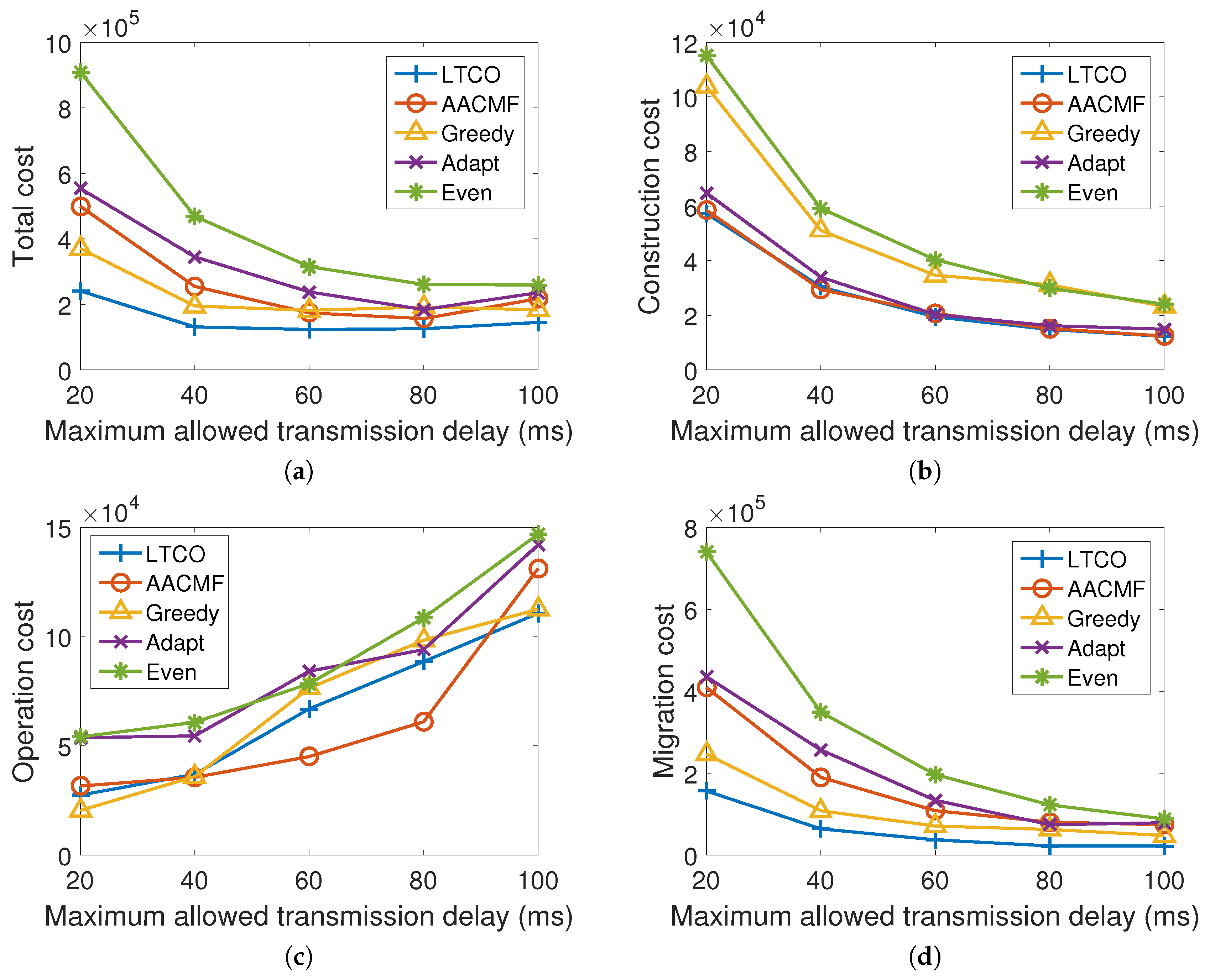
D that is used to ensure the delay experienced by each mobile user would not be too large. The results of the proposed solution (LTCO) and four comparison algorithms for the randomly generated traces, and the real mobility traces are presented in
Figure 5 and in
Figure 6, respectively. Here, we vary the maximum allowed delay from 20 ms to 100 ms, and fix the amount of communication flow
as 10 unit per time slot. The basic site construction cost
is randomly picked in the range (1–10) following a uniform distribution.
, the unit cost for purchasing and placing a single server, is set to 1. The desired resource of mobile users in AP
at time
t is randomly picked in the range
.
k the cost ratio of an idle server to a fully used one as 0.3.
the maximum operation cost for a single server at its peak workload as 10.
the coefficient of migration cost as 1. We further set the threshold
as 6, and lower bound
b as 0.6 in LTCO solution. For simplicity, we test with two sets of parameters; however, the LTCO solution could be applied to general scenarios.
In
Figure 5 and
Figure 6, it can be observed that the proposed LTCO solution always outperforms the AACMF, Greedy, Adapt and Even algorithms in reducing the total cost. Specifically, the saved total cost could be as high as 72% for randomly generated mobility traces and 74% for real mobile traces. In addition, as shown in
Figure 5b,d and
Figure 6b,d, the LTCO has the smallest construction cost and the smallest migration cost among the five algorithms, which are only 11% (48%) and 18% (18%) for the construction cost and the migration cost using random generated traces (real traces), respectively, compared to the cloudlet planning computed by the EVEN. While the maximum allowed delay is less than 40 ms (in the range of (40, 60) ms), the Greedy algorithm (the AACMF) has the lowest operation cost using the real mobility traces. However, the proposed LTCO solution could find a better trade-off between construction cost, migration cost and the operation cost, which leads to a lower total cost compared with the other four algorithms.
In addition, all of the five algorithms have the same trend that as the maximum allowed delay increases to 60 ms, the total cost decreases, after that the total cost increases. This is because that when the maximum allowed delay raises, it is possible that more cells would be combined into one service region. In that case, the number of service migration would be reduced, and fewer cloudlets would be built, which leads to a smaller migration cost and construction cost as shown in
Figure 5b,d and
Figure 6b,d. On the other hand, an increased number of cells in a single region means a wider service region and may result in a longer transmission distance between mobile users and the cloudlet in the region. It would bring in higher communication delay and finally increase the operation cost as depicted in
Figure 5c and
Figure 6c.
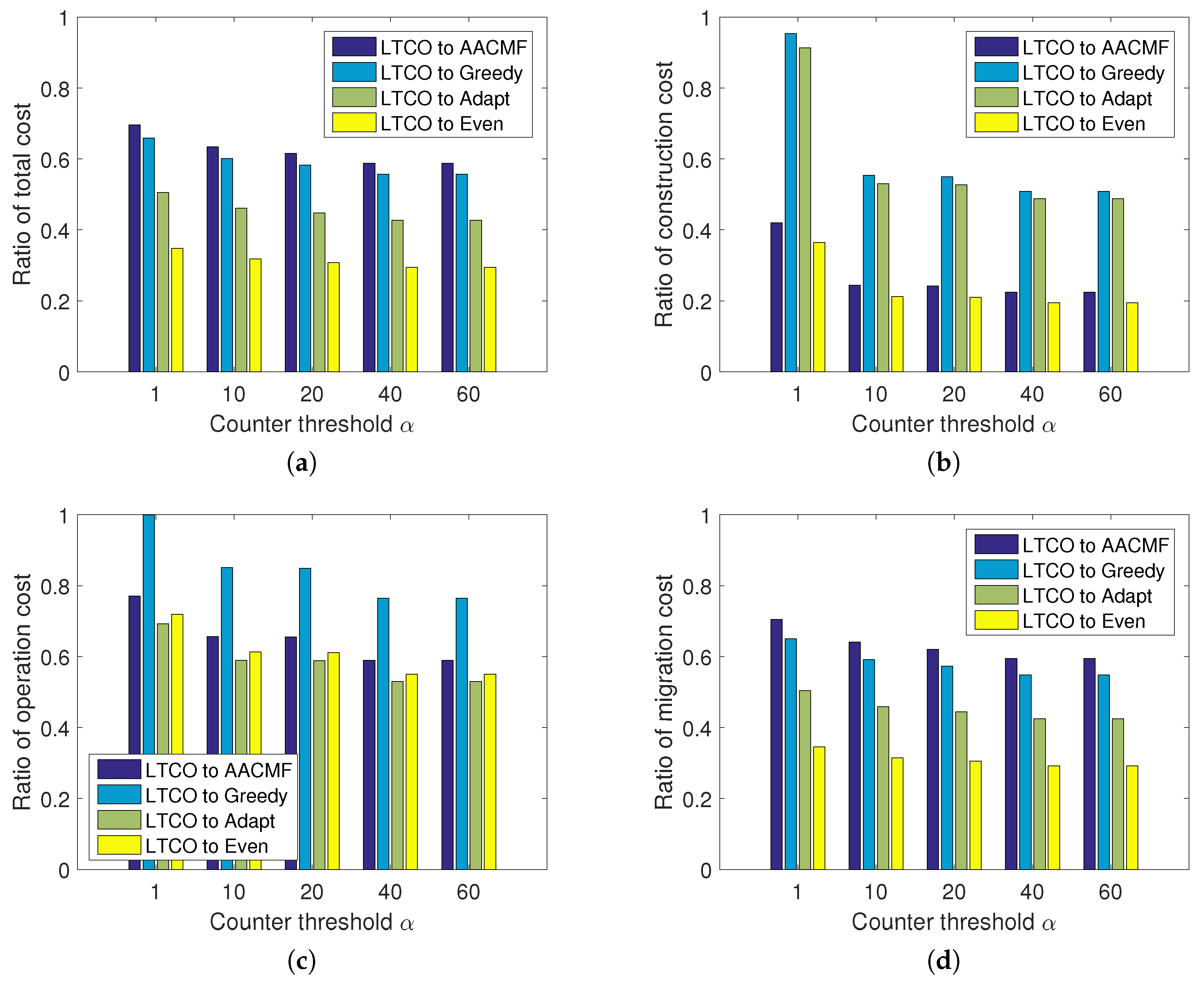
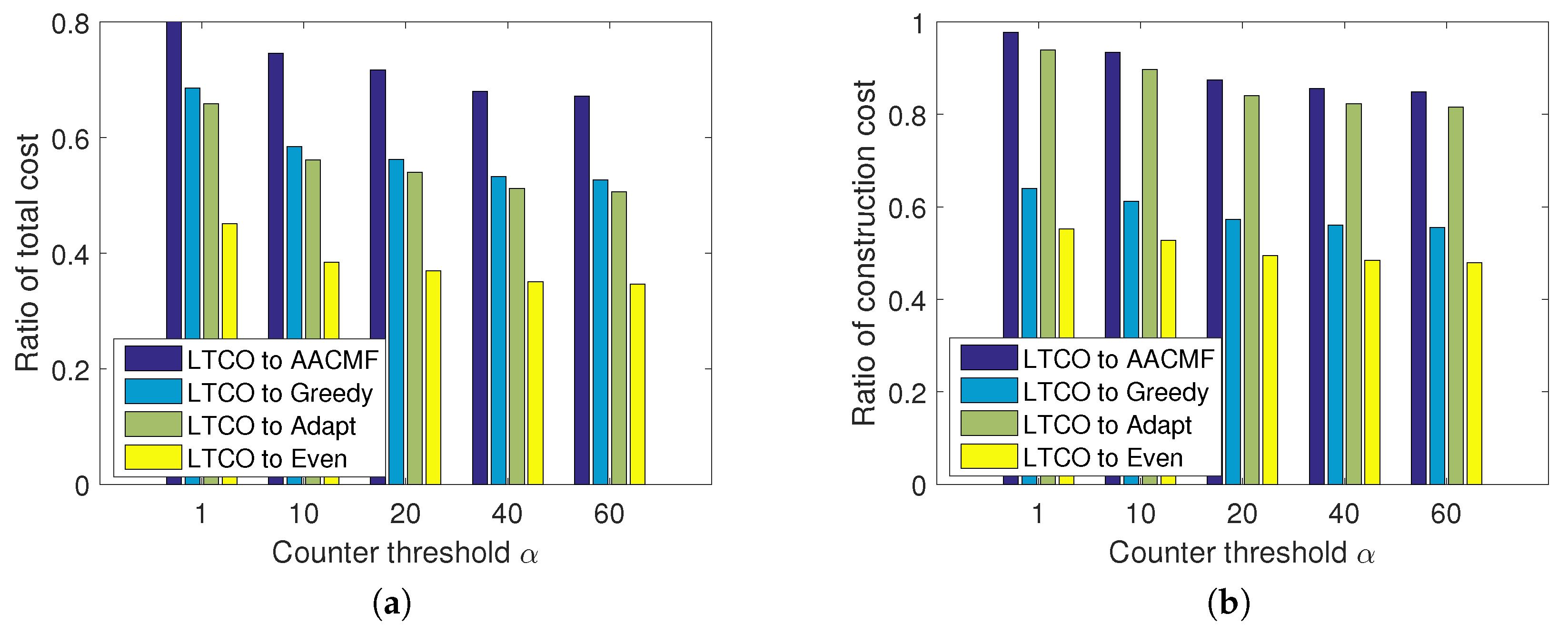
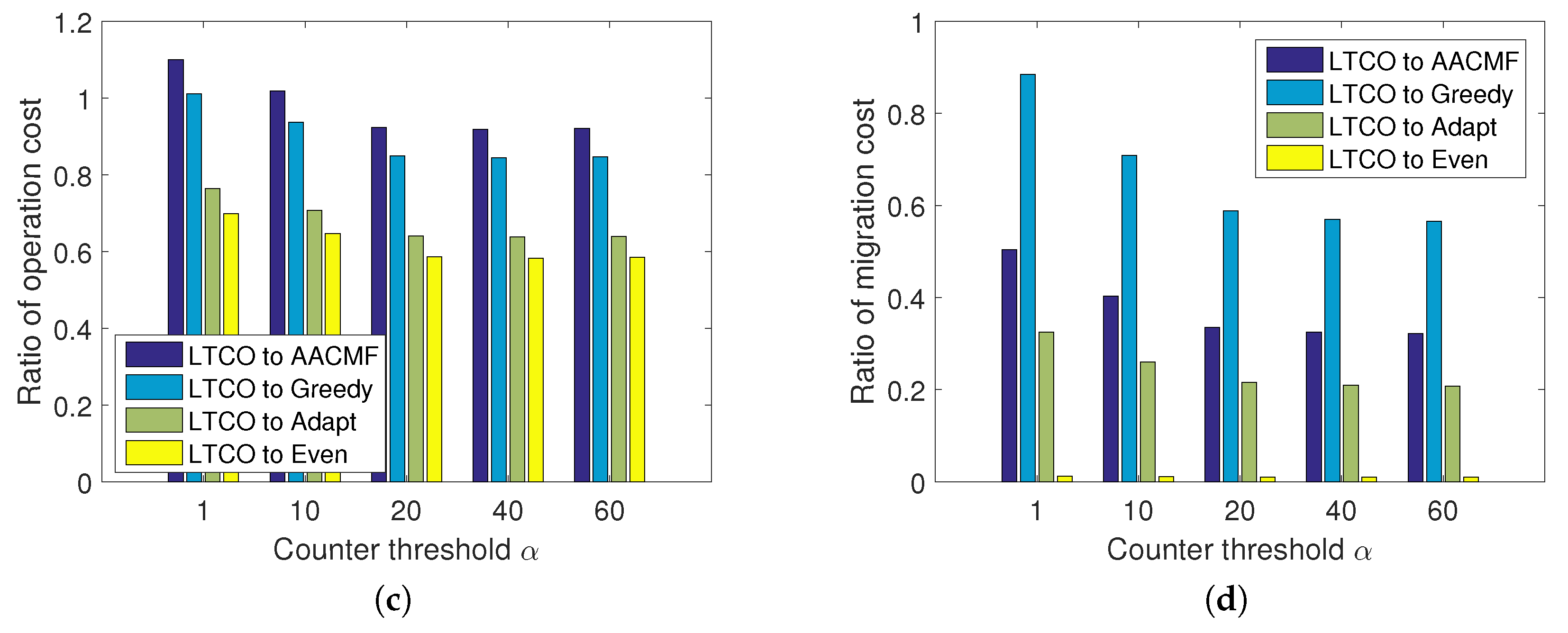
We also inspect the influence of counter threshold
on the costs, while the maximum allowed delay is kept as 40 ms. For better illustration of the performance comparison, we use the ratio of each cost of LTCO solution to the cost of that of the AACMF, Greedy, Adapt and Even algorithms, respectively. When the ratio is smaller than 1, it means that the proposed LTCO solution achieves better results compared with the other four algorithms. As presented in
Figure 7a–d and
Figure 8a–d, the ratio of cost is almost always smaller than 1, which indicates that the LTCO outperforms the other algorithms even if
is 1. Besides, as the counter threshold
grows, the ratio drops. For instance, the ratio of total cost between the LTCO and the AACMF decreases from 69% to 58% for the randomly generated traces and from 87% to 67% for the real traces, respectively. Since when that SRP (Algorithm 1) executes more times, more opportunities would be offered to find a better solution. However, this also means a longer searching time.