Predicting the Influence of Rain on LIDAR in ADAS
Abstract
1. Introduction
2. Materials and Methods
2.1. Lidar Theory
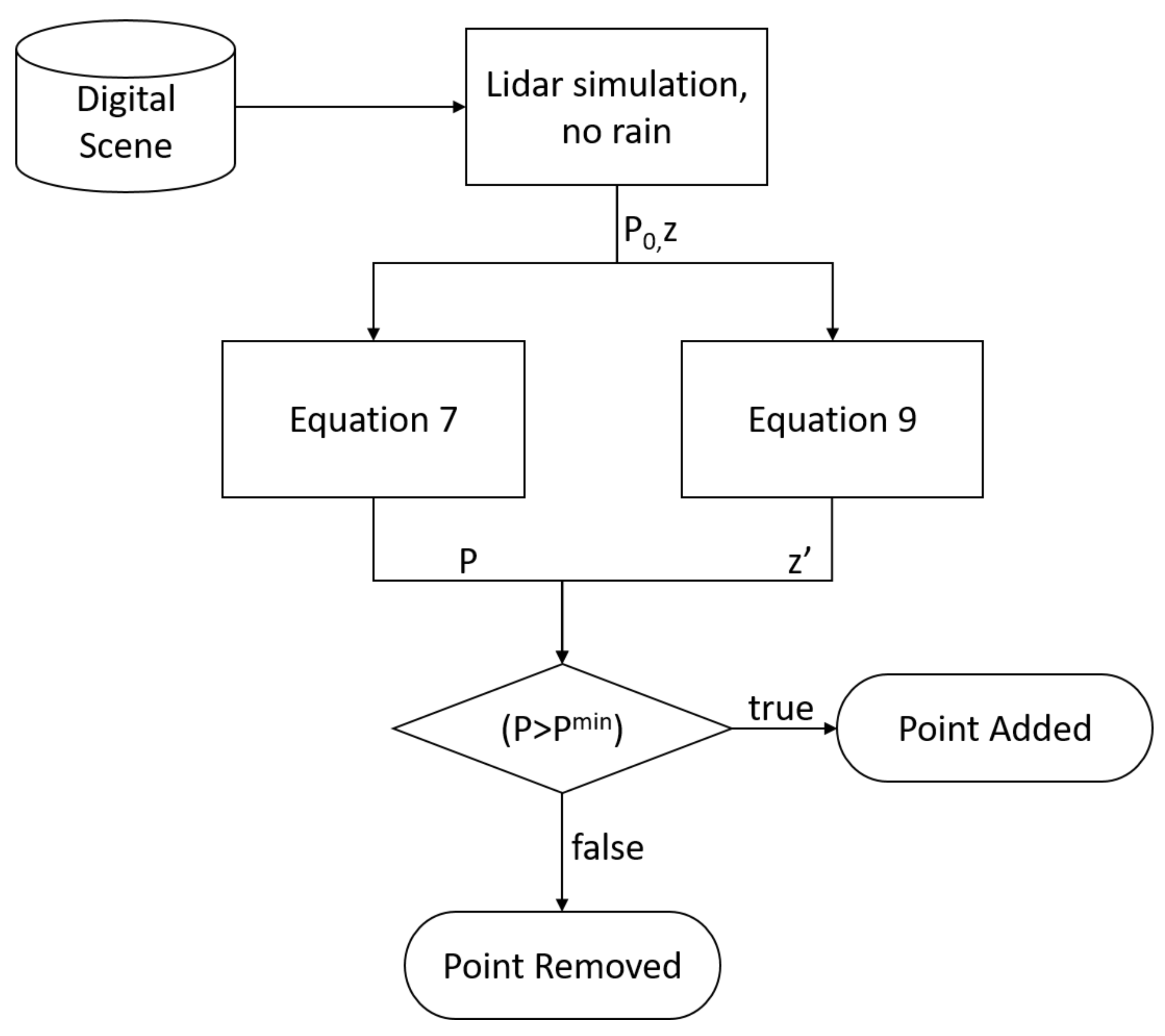
2.2. Integration into a 3D Simulator
- The MAVS LIDAR simulation is used to calculate the returned range and intensity in the absence of rain.
- Equation (9) is used to calculate the new range rain-induced with error.
- Equation (7) is used to calculate the reduced intensity value.
- If the reduced intensity falls below the threshold value defined by Equation (4), the point is removed from the point cloud.
2.3. Maximum Range Experiments
2.4. Obstacle Detection in a Realistic Scenario
3. Results
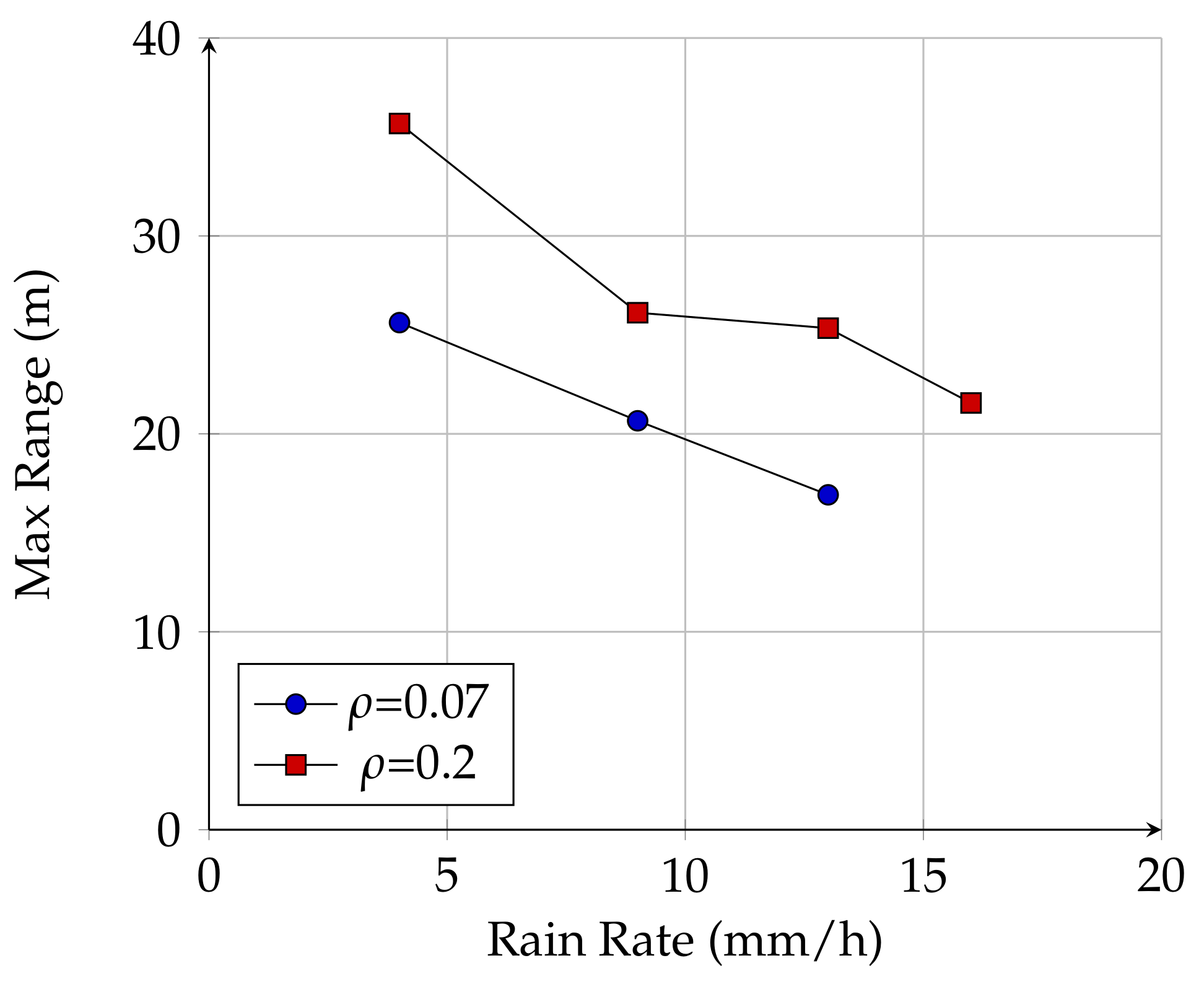
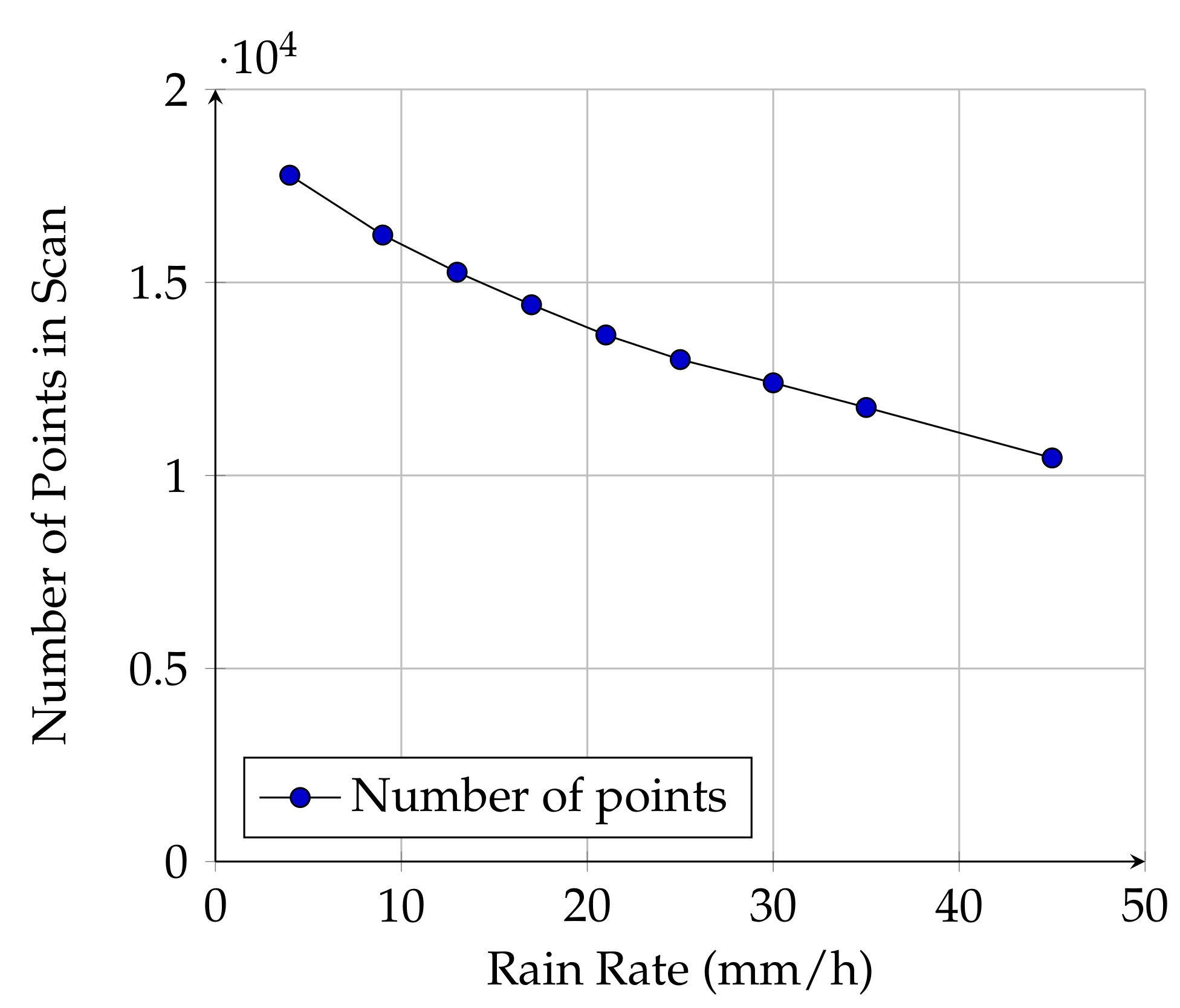
3.1. Maximum Range Experiments
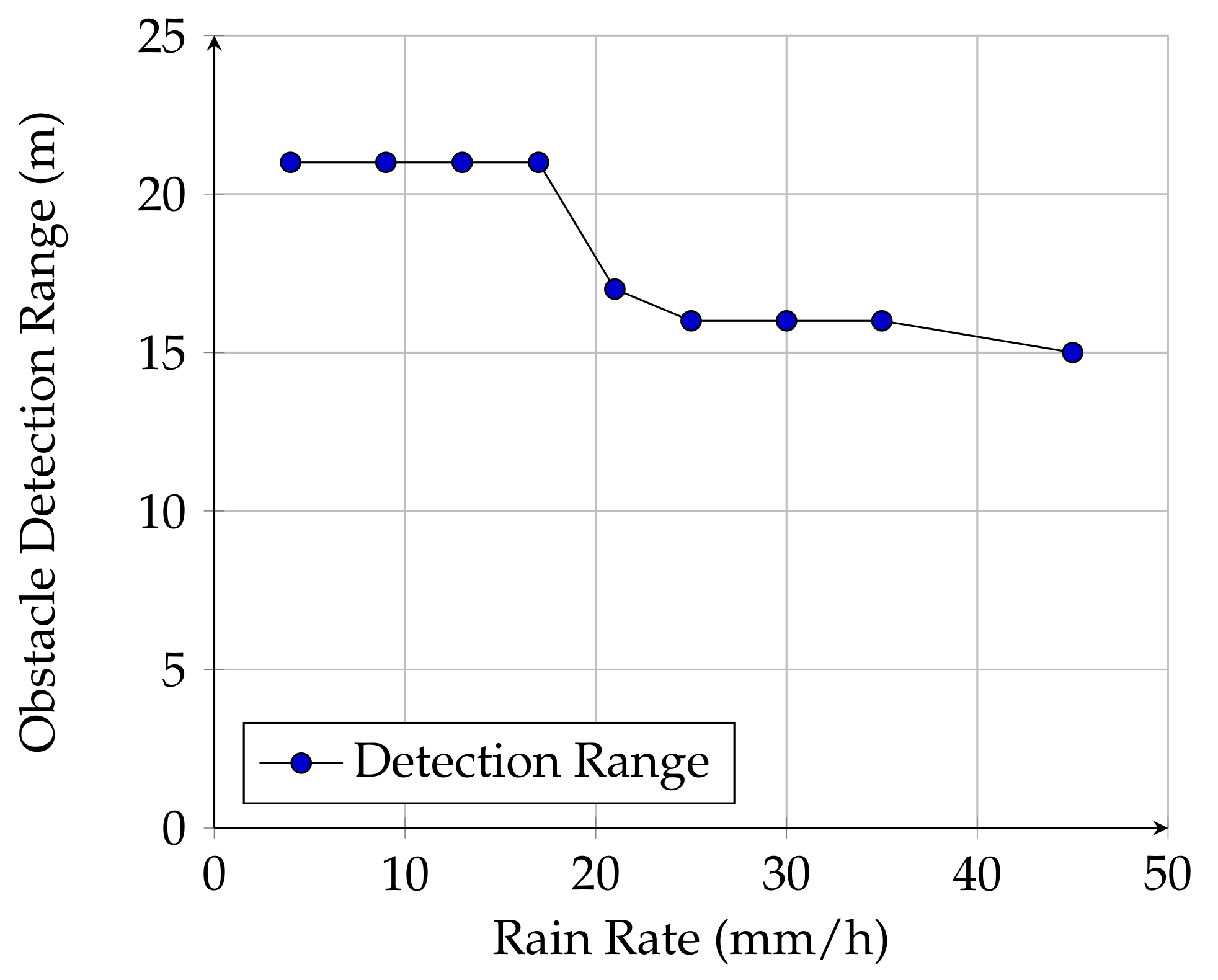
3.2. Obstacle Detection in a Realistic Scenario
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Stock, K. Self-Driving Cars Can Handle Neither Rain nor Sleet nor Snow. Bloomberg Businessweek, 17 September 2018. [Google Scholar]
- Rasshofer, R.; Gresser, K. Automotive radar and lidar systems for next generation driver assistance functions. Adv. Radio Sci. 2005, 3, 205–209. [Google Scholar] [CrossRef]
- Hasirlioglu, S.; Doric, I.; Lauerer, C.; Brandmeier, T. Modeling and simulation of rain for the test of automotive sensor systems. In Proceedings of the 2016 IEEE Intelligent Vehicles Symposium (IV), Gothenburg, Sweden, 19–22 June 2016; pp. 286–291. [Google Scholar]
- Filgueira, A.; González-Jorge, H.; Lagüela, S.; Díaz-Vilariño, L.; Arias, P. Quantifying the influence of rain in LiDAR performance. Measurement 2017, 95, 143–148. [Google Scholar] [CrossRef]
- Rasshofer, R.H.; Spies, M.; Spies, H. Influences of weather phenomena on automotive laser radar systems. Adv. Radio Sci. 2011, 9, 49–60. [Google Scholar] [CrossRef]
- Fofi, D.; Sliwa, T.; Voisin, Y. A comparative survey on invisible structured light. In Proceedings of the Machine Vision Applications in Industrial Inspection XII; International Society for Optics and Photonics: Bellingham, WA, USA, 2004; Volume 5303, pp. 90–99. [Google Scholar]
- Okubo, Y.; Ye, C.; Borenstein, J. Characterization of the Hokuyo URG-04LX laser rangefinder for mobile robot obstacle negotiation. In Proceedings of the Unmanned Systems Technology XI; International Society for Optics and Photonics: Bellingham, WA, USA, 2009; Volume 7332, p. 733212. [Google Scholar]
- SICK AG. LMS200/211/221/291 Laser Measurement Systems, Technical Description; SICK AG: Reute, Germany, 2006. [Google Scholar]
- Fersch, T.; Buhmann, A.; Koelpin, A.; Weigel, R. The influence of rain on small aperture LiDAR sensors. In Proceedings of the 2016 German Microwave Conference (GeMiC), Bochum, Germany, 14–16 March 2016; pp. 84–87. [Google Scholar]
- Wang, B.; Lin, J.X. Monte Carlo simulation of laser beam scattering by water droplets. In Proceedings of the International Symposium on Photoelectronic Detection and Imaging 2013: Laser Sensing and Imaging and Applications; International Society for Optics and Photonics: Bellingham, WA, USA, 2013; Volume 8905, p. 89052. [Google Scholar]
- Dannheim, C.; Icking, C.; Mäder, M.; Sallis, P. Weather Detection in Vehicles by Means of Camera and LIDAR Systems. In Proceedings of the 2014 Sixth International Conference on Computational Intelligence, Communication Systems and Networks (CICSyN), Tetova, Macedonia, 27–29 May 2014; pp. 186–191. [Google Scholar]
- Lewandowski, P.A.; Eichinger, W.E.; Kruger, A.; Krajewski, W.F. Lidar-based estimation of small-scale rainfall: Empirical evidence. J. Atmos. Ocean. Technol. 2009, 26, 656–664. [Google Scholar] [CrossRef]
- Goodin, C.; Doude, M.; Hudson, C.; Carruth, D. Enabling Off-Road Autonomous Navigation-Simulation of LIDAR in Dense Vegetation. Electronics 2018, 7, 154. [Google Scholar] [CrossRef]
- Velodyne Acoustics, Inc. VLP-16 User’s Manual and Programming Guide; Velodyne Acoustics, Inc.: Morgan Hill, CA, USA, 2016. [Google Scholar]
- Schafer, H.; Hach, A.; Proetzsch, M.; Berns, K. 3D obstacle detection and avoidance in vegetated off-road terrain. In Proceedings of the 2008 IEEE International Conference on Robotics and Automation (ICRA 2008), Pasadena, CA, USA, 19–23 May 2008; pp. 923–928. [Google Scholar]
- Starik, S.; Werman, M. Simulation of rain in videos. In Proceedings of the 2003 Texture Workshop, Nice, France, 17 October 2003; Volume 2, pp. 406–409. [Google Scholar]
- Velodyne Acoustics, Inc. HDL-64E User’s Manual, Rev. D; Velodyne Acoustics, Inc.: Morgan Hill, CA, USA, 2008. [Google Scholar]
- Rusu, R.B. Semantic 3D object maps for everyday manipulation in human living environments. Künstliche Intelligenz 2010, 24, 345–348. [Google Scholar] [CrossRef]
- Rusu, R.B.; Cousins, S. 3D is here: Point cloud library (PCL). In Proceedings of the 2011 IEEE International Conference on Robotics and automation (ICRA), Shanghai, China, 9–13 May 2011; pp. 1–4. [Google Scholar]
- Queensland Government. Stopping Distances on Wet and Dry Roads; Queensland Government: Queensland, Australia, 2016.
- Jiménez, F.; Naranjo, J.E. Improving the obstacle detection and identification algorithms of a laserscanner- based collision avoidance system. Transport. Res. Part C Emerg. Technol. 2011, 19, 658–672. [Google Scholar] [CrossRef]
- Aarthi, R.; Harini, S. A Survey of Deep Convolutional Neural Network Applications in Image Processing. Int. J. Pure Appl. Math. 2018, 118, 185–190. [Google Scholar]
- Ferguson, D.; Darms, M.; Urmson, C.; Kolski, S. Detection, prediction, and avoidance of dynamic obstacles in urban environments. In Proceedings of the 2008 IEEE Intelligent Vehicles Symposium, Eindhoven, The Netherlands, 4–6 June 2008; pp. 1149–1154. [Google Scholar]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goodin, C.; Carruth, D.; Doude, M.; Hudson, C. Predicting the Influence of Rain on LIDAR in ADAS. Electronics 2019, 8, 89. https://doi.org/10.3390/electronics8010089
Goodin C, Carruth D, Doude M, Hudson C. Predicting the Influence of Rain on LIDAR in ADAS. Electronics. 2019; 8(1):89. https://doi.org/10.3390/electronics8010089
Chicago/Turabian StyleGoodin, Christopher, Daniel Carruth, Matthew Doude, and Christopher Hudson. 2019. "Predicting the Influence of Rain on LIDAR in ADAS" Electronics 8, no. 1: 89. https://doi.org/10.3390/electronics8010089
APA StyleGoodin, C., Carruth, D., Doude, M., & Hudson, C. (2019). Predicting the Influence of Rain on LIDAR in ADAS. Electronics, 8(1), 89. https://doi.org/10.3390/electronics8010089






