Design of Electroporation Process in Irregularly Shaped Multicellular Systems
Abstract
:1. Introduction
2. Mathematical Formulation
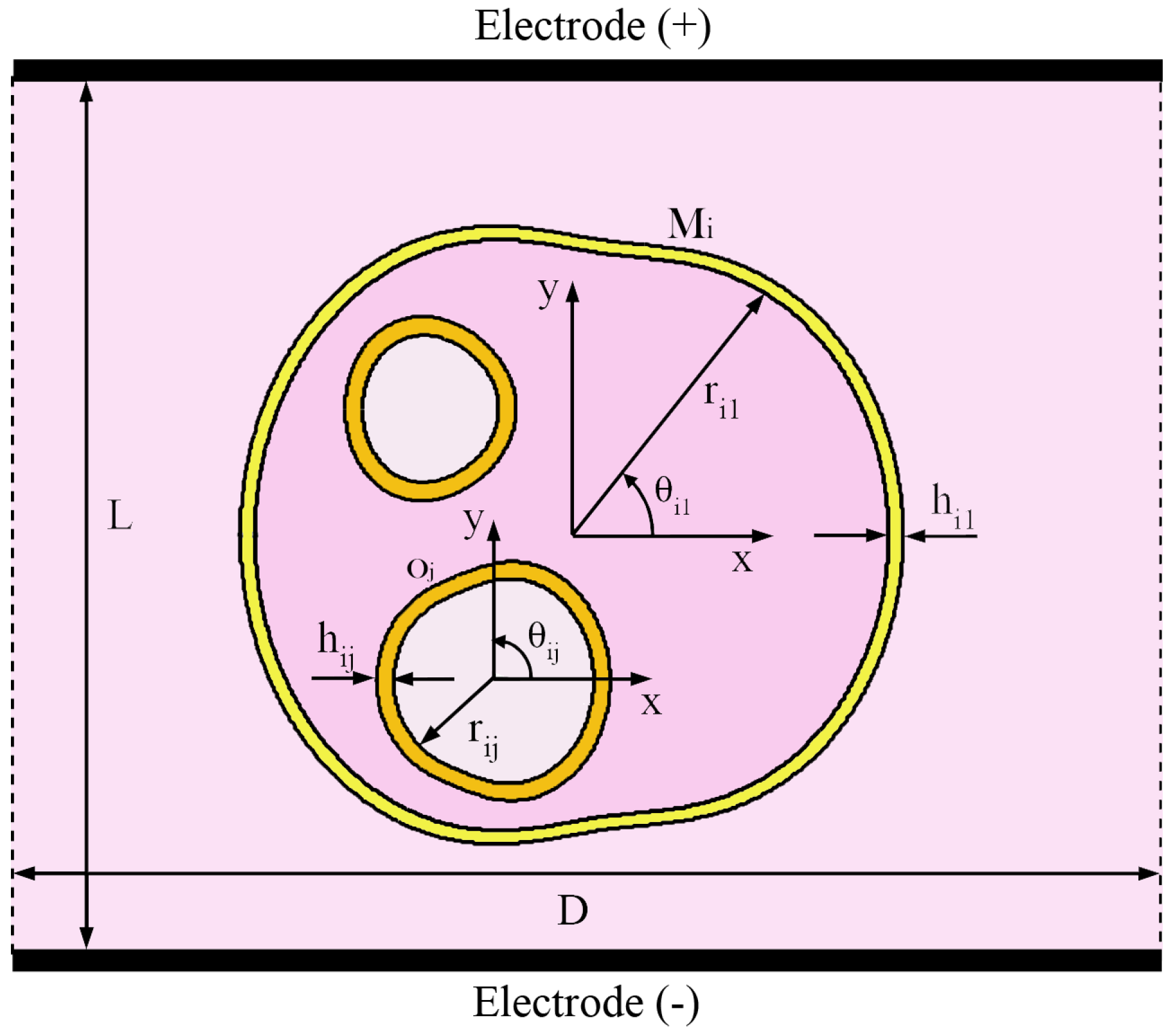
2.1. Cells Geometry Model
2.2. Complex Permittivity Model
2.3. Electromagnetic Model
2.4. Pore Model
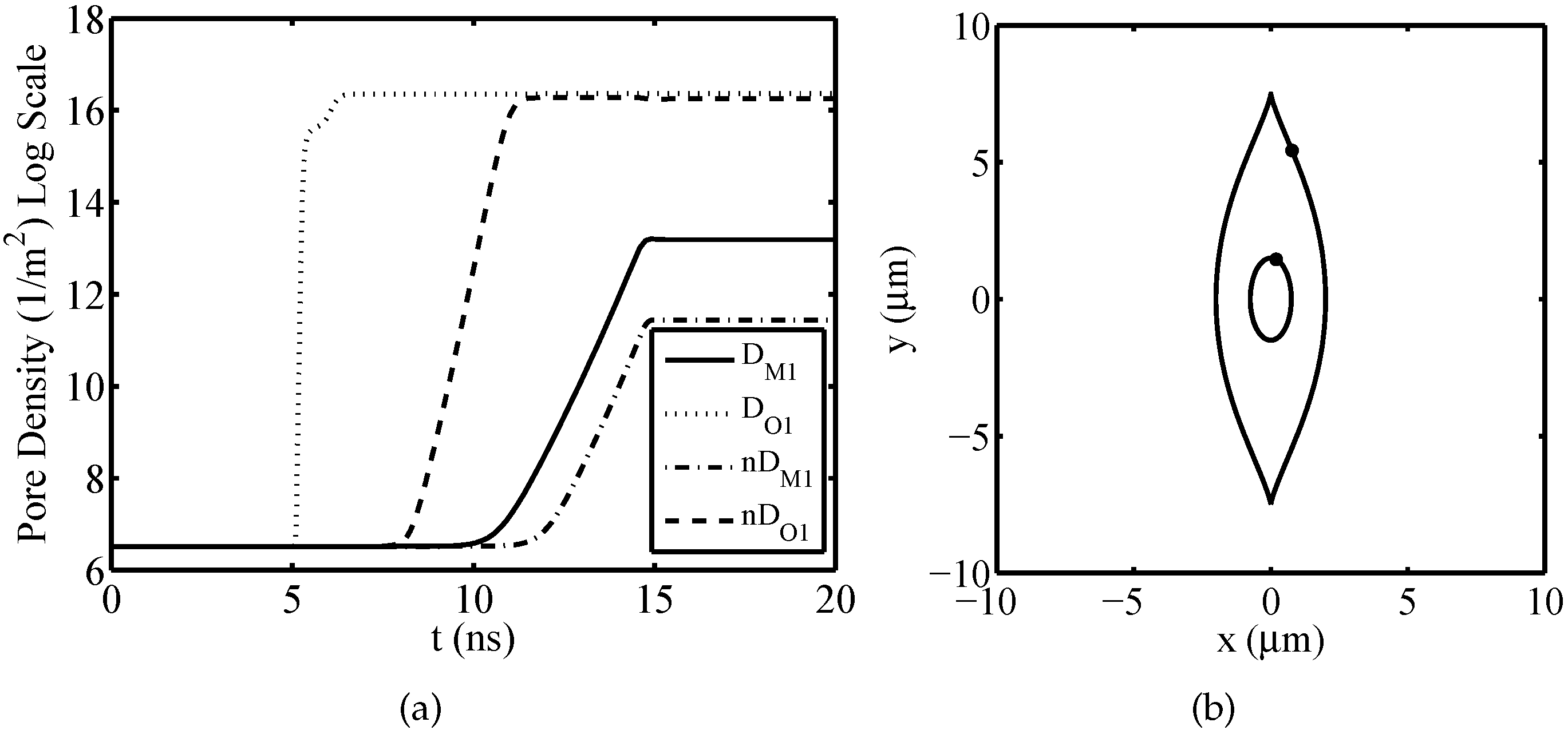
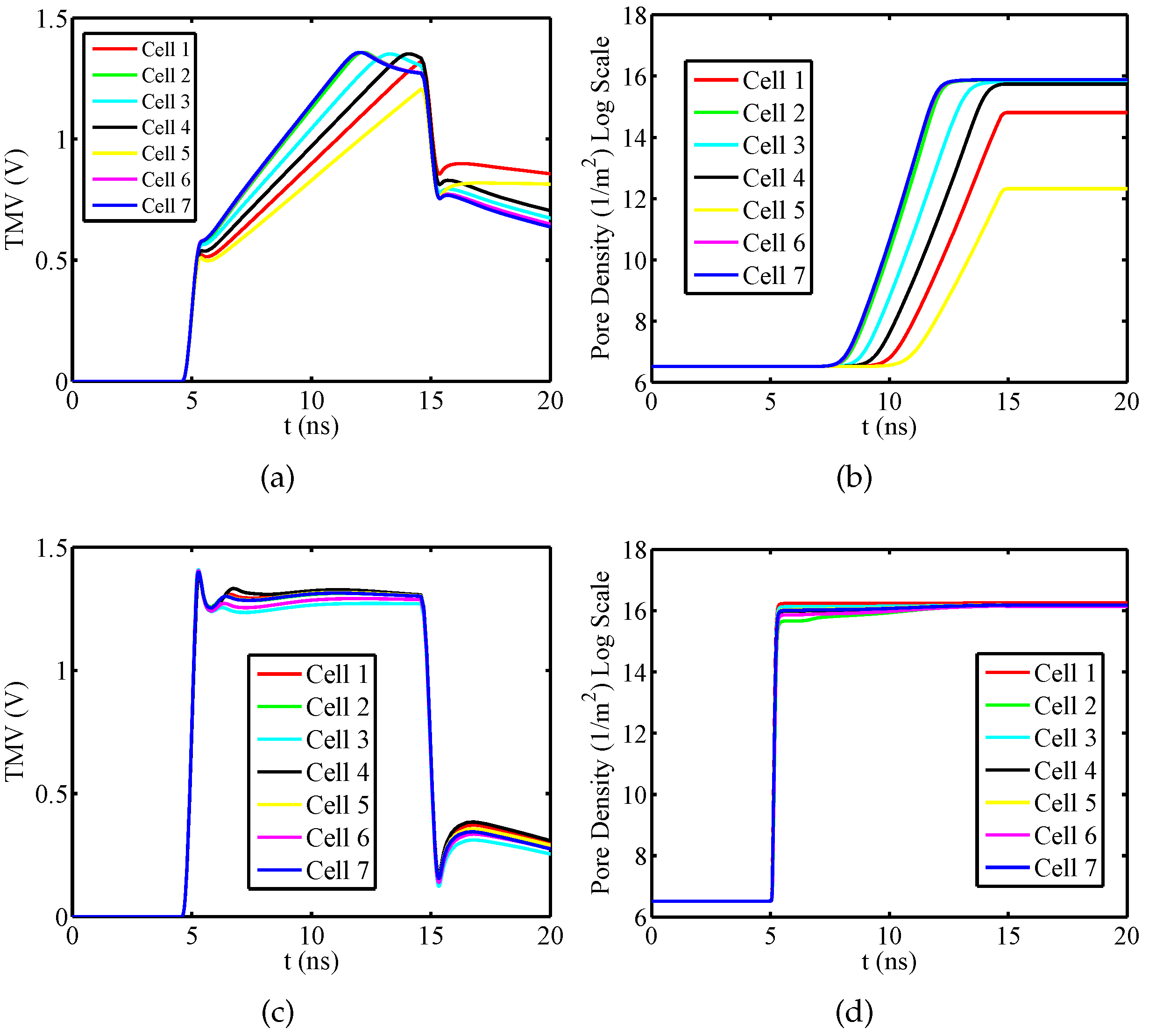
3. Results and Discussion
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| AC | Alternating Current |
| DC | Direct Current |
| DNA | DeoxyriboNucleic Acid |
| EP | Electroporation |
| EPRL | Electroporation Relative Length |
| PEF | Pulsed Electric Field |
| RNA | RiboNucleic Acid |
| TMV | Transmembrane Voltage |
References
- MacQueen, L.A.; Thibault, M.; Buschmann, M.D.; Wertheimer, M.R. Electro-manipulation of Biological Cells in Microdevices. IEEE Trans. Dielectr. Electr. Insul. 2012, 19, 1261–1268. [Google Scholar] [CrossRef]
- Chow, Y.T.; Chen, S.; Wang, R.; Liu, C.; Kong, C.; Li, R.A.; Cheng, S.H.; Sun, D. Single cell transfection through precise microinjection with quantitatively controlled injection volumes. Sci. Rep. 2016, 6, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Yarmush, M.L.; Golberg, A.; Sersa, G.; Kotnik, T.; Miklavcic, D. Electroporation-based technologies for medicine: Principles, applications and challenges. Annu. Rev. Biomed. Eng. 2014, 16, 295–320. [Google Scholar] [CrossRef] [PubMed]
- Santra, T.S.; Lee, C.W.; Kar, S.; Borana, J.; Wang, P.C.; Tseng, F.G. Nanolocalized single cell membrane nanoelectroporation: For higher efficiency with high cell viability. IEEE Nanotechnol. Mag. 2014, 8, 30–34. [Google Scholar] [CrossRef]
- Gehl, J. Electroporation: Theory and methods, perspectives for drug delivery, gene therapy and research. Acta Physiol. Scand. 2003, 177, 437–447. [Google Scholar] [CrossRef] [PubMed]
- Rao, M.; Baraban, J.; Rajaii, F.; Sockanathan, S. In vivo comparative study of rnai methodologies by in ovo electroporation in the chick embryo. Dev. Dyn. 2004, 231, 592–600. [Google Scholar] [CrossRef] [PubMed]
- Sustarsic, M.; Plochowietz, A.; Aigrain, L.; Yuzenkova, Y.; Zenkin, N.; Kapanidis, A. Optimized delivery of fluorescently labeled proteins in live bacteria using electroporation. Histochem. Cell Biol. 2014, 142, 113–124. [Google Scholar] [CrossRef] [Green Version]
- Yan, K.; Todo, H.; Sugibayashi, K. Transdermal drug delivery by in-skin electroporation using a microneedle array. Int. J. Pharm. 2010, 397, 77–83. [Google Scholar] [CrossRef] [Green Version]
- Baron, S.; Poast, J.; Rizzo, D.; McFarland, E.; Kieff, E. Electroporation of antibodies, DNA, and other macromolecules into cells: A highly efficient method. J. Immunol. Methods 2000, 242, 115–126. [Google Scholar] [CrossRef]
- Yumura, S. Rapid redistribution of myosin ii in living dictyostelium amoebae, as revealed by fluorescent probes introduced by electroporation. Protoplasma 1996, 192, 217–227. [Google Scholar] [CrossRef]
- Liu, C.; Xie, X.; Zhao, W.; Liu, N.; Maraccini, P.A.; Sassoubre, L.M.; Boehm, A.B.; Cui, Y. Conducting nanosponge electroporation for affordable and highefficiency disinfection of bacteria and viruses in water. Am. Chem. Soc. Nano Lett. 2013, 13, 4288–4293. [Google Scholar] [CrossRef] [PubMed]
- Lin, H.Y.; Lin, S.E.; Chien, S.F.; Chern, M.K. Electroporation for three commonly used yeast strains for two-hybrid screening experiments. Anal. Biochem. 2011, 416, 117–119. [Google Scholar] [CrossRef] [PubMed]
- Bates, G.W. Genetic transformation of plants by protoplast electroporation. Mol. Biotechnol. 1994, 2, 135–145. [Google Scholar] [CrossRef] [PubMed]
- Fujimoto, H.; Kato, K.; Iwata, H. Electroporation microarray for parallel transfer of small interfering RNA into mammalian cells. IEEE Trans. Dielectr. Electr. Insul. 2008, 392, 1309–1316. [Google Scholar] [CrossRef] [PubMed]
- Guo, F.; Yao, C.; Li, C.; Mi, Y.; Wen, Y.; Tang, J. Dependence on pulse duration and number of tumor cell apoptosis by nanosecond pulsed electric fields. IEEE Trans. Dielectr. Electr. Insul. 2013, 20, 1195–1200. [Google Scholar]
- Lamberti, P.; Tucci, V.; Romeo, S.; Sannino, A.; Scarfi, M.R.; Zeni, O. nsPEF-induced effects on cell membranes: Use of electrophysical model to optimize experimental design. IEEE Trans. Dielectr. Electr. Insul. 2013, 20, 1231–1238. [Google Scholar] [CrossRef]
- Beebe, S.J. Bioelectrics in basic science and medicine: Impact of electric fields on cellular structures and functions. J. Nanomed. Nanotechol. 2013, 4, 1–8. [Google Scholar] [CrossRef]
- Pakhomov, A.G.; Miklavcic, D.; Markov, M.S. Advanced Electroporation Techniques in Biology and Medicine; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Denzi, A.; Camera, F.; Merla, C.; Benassi, B.; Consales, C.; Paffi, A.; Apollonio, F.; Liberti, M. A microdosimetric study of electropulsation on multiple realistically shaped cells: Effect of neighbours. J. Membr. Biol. 2016, 249, 691–701. [Google Scholar] [CrossRef] [PubMed]
- Pucihar, G.; Krmelj, J.; Rebersek, M.; Napotnik, T.B.; Miklavicic, D. Equivalent pulse parameters for electroporation. IEEE Trans. Biomed. Eng. 2011, 58, 3279–3288. [Google Scholar] [CrossRef]
- Retelj, L.; Pucihar, G.; Miklavcic, D. Electroporation of intracellular liposomes using nanosecond electric pulses—A theoretical study. IEEE Trans. Biomed. Eng. 2013, 60, 2624–2635. [Google Scholar] [CrossRef]
- Salimi, E.; Thomson, D.J.; Bridges, G.E. Membrane dielectric dispersion in nanosecond pulsed electroporation of biological cells. IEEE Trans. Dielectr. Electr. Insul. 2013, 20, 1256–1265. [Google Scholar] [CrossRef]
- Murovec, T.; Sweeney, D.C.; Latouche, E.; Davalos, R.V.; Brosseau, C. Modeling of transmembrane potential in realistic multicellular structures before electroporation. Biophys. J. 2016, 111, 2286–2295. [Google Scholar] [CrossRef] [PubMed]
- Mescia, L.; Bia, P.; Chiapperino, M.A.; Caratelli, D. Fractional Calculus Based FDTD Modeling of Layered Biological Media Exposure to Wideband Electromagnetic Pulses. Electronics 2017, 6, 106. [Google Scholar] [CrossRef]
- Towhidi, L.; Kotnik, T.; Pucihar, G.; Firoozabadi, S.M.P.; Mozdaran, H.; Miklavcic, D. Variability of the minimal transmembrane voltage resulting in detectable membrane electroporation. Electromagn. Biol. Med. 2008, 27, 372–385. [Google Scholar] [CrossRef]
- Qiu, H.; Xiao, S.; Joshi, R.P. Simulations of voltage transients across intacellular mitochondrial membranes due to nanosecond electrical pulses. IEEE Trans. Dielectr. Electr. Insul. 2014, 42, 3113–3120. [Google Scholar]
- Mescia, L.; Chiapperino, M.A.; Bia, P.; Gielis, J.; Caratelli, D. Modeling of electroporation induced by pulsed electric fields in irregularly shaped cells. IEEE Trans. Biomed. Eng. 2018, 65, 414–423. [Google Scholar] [CrossRef]
- Gielis, J. A generic geometric transformation that unifies a wide range of natural and abstract shapes. Am. J. Bot. 2003, 90, 333–338. [Google Scholar] [CrossRef] [Green Version]
- Bia, P.; Caratelli, D.; Mescia, L.; Gielis, J. Analysis and synthesis of supershaped dielectric lens antennas. IET Microw. Antennas Propag. 2015, 9, 1497–1504. [Google Scholar] [CrossRef]
- Mescia, L.; Bia, P.; Caratelli, D.; Chiapperino, M.A.; Stukach, O.; Gielis, J. Electromagnetic mathematical modeling of 3D supershaped dielectric lens antennas. Math. Probl. Eng. 2016, 2016, 8130160. [Google Scholar] [CrossRef]
- Kotnik, T.; Miklavcic, D. Theoretical evaluation of the distributed power dissipation in biological cells exposed to electric fields. Bioelectromagnetics 2000, 21, 385–394. [Google Scholar] [CrossRef] [Green Version]
- Caratelli, D.; Mescia, L.; Bia, P.; Stukach, O.V. Fractional-calculus-based FDTD algorithm for ultrawideband electromagnetic characterization of arbitrary dispersive dielectric materials. IEEE Trans. Antennas Propag. 2016, 64, 3533–3544. [Google Scholar] [CrossRef]
- Martinsen, O.G.; Grimmes, S.; Schwan, H.P. Interface phenomena and dielectric properties of biological tissue. In Encyclopedia of Surface and Colloid Science; Taylor & Francis: New York, NY, USA, 2002; pp. 2643–2652. [Google Scholar]
- Krassowska, W.; Filev, F.D. Modeling electroporation in a single cell. Biophys. J. 2007, 92, 404–417. [Google Scholar] [CrossRef] [PubMed]
- Gielis, J. The Geometrical Beauty of Plants; Atlantis Press: Paris, France, 2017. [Google Scholar]
- Rems, L.; Uaj, M.; Kanduer, M.; Reberek, M.; Miklavcic, D.; Pucihar, G. Cell electrofusion using nanosecond electric pulses. Sci. Rep. 2013, 3, 3382. [Google Scholar] [CrossRef] [PubMed]
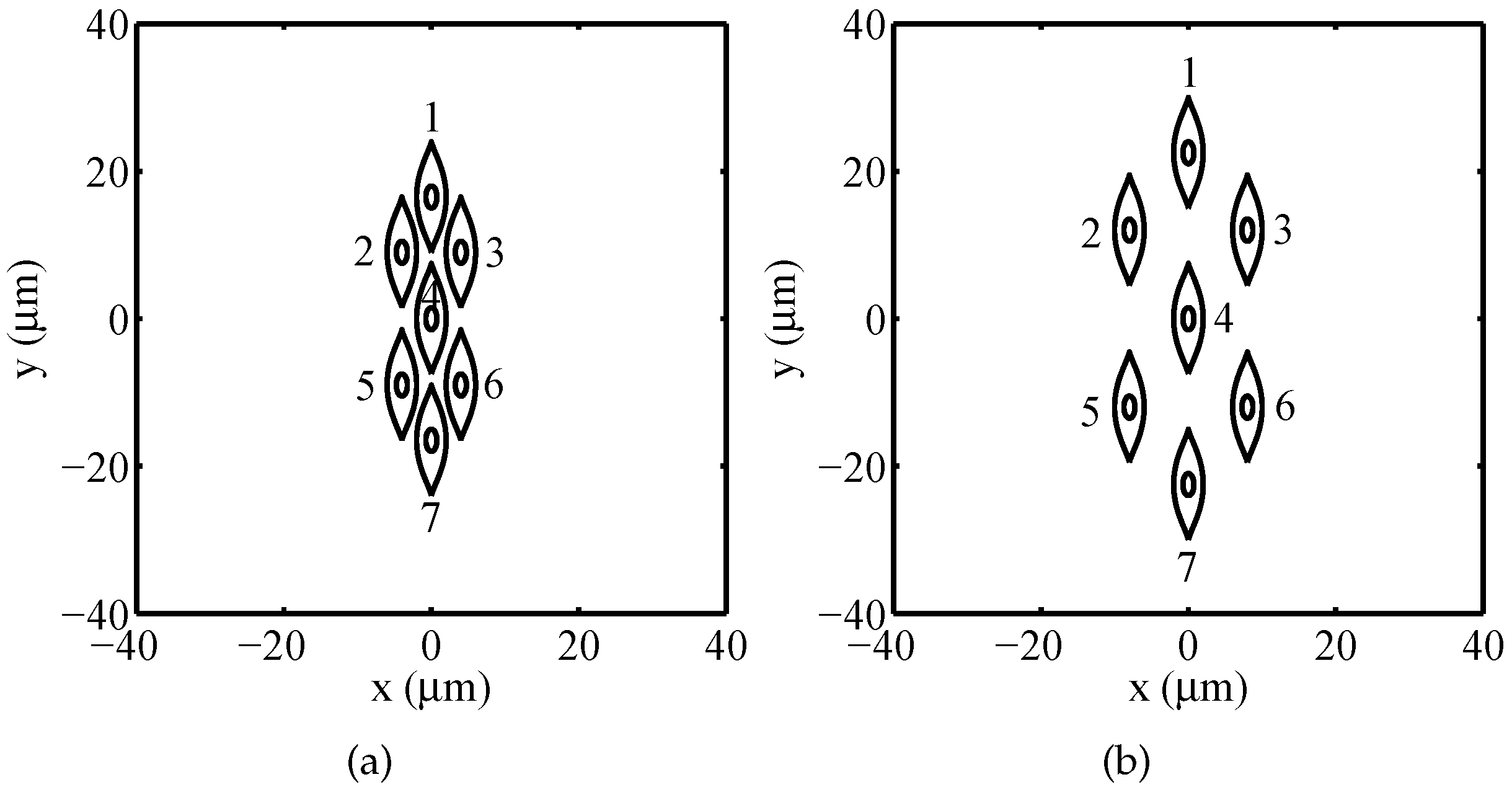
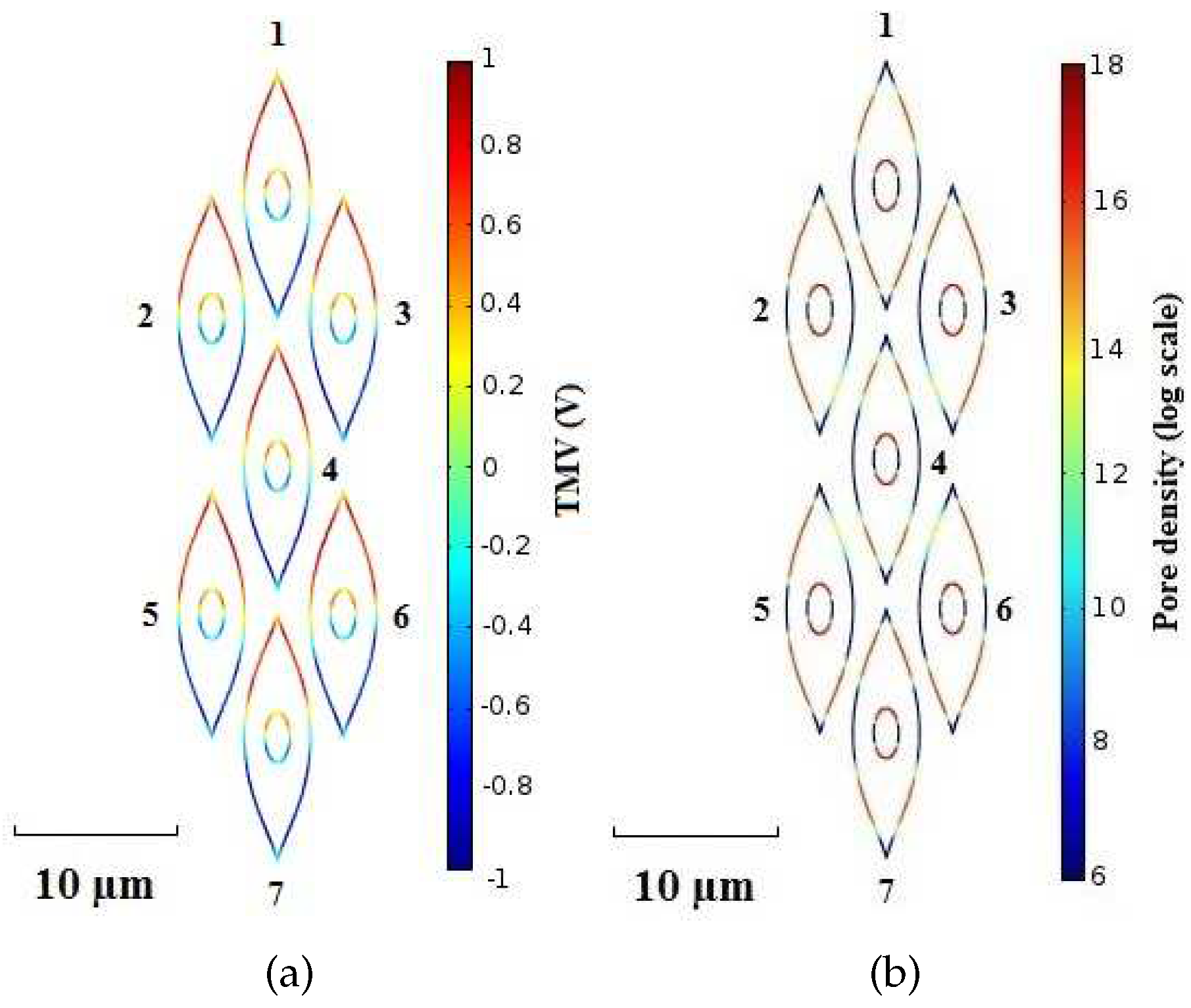

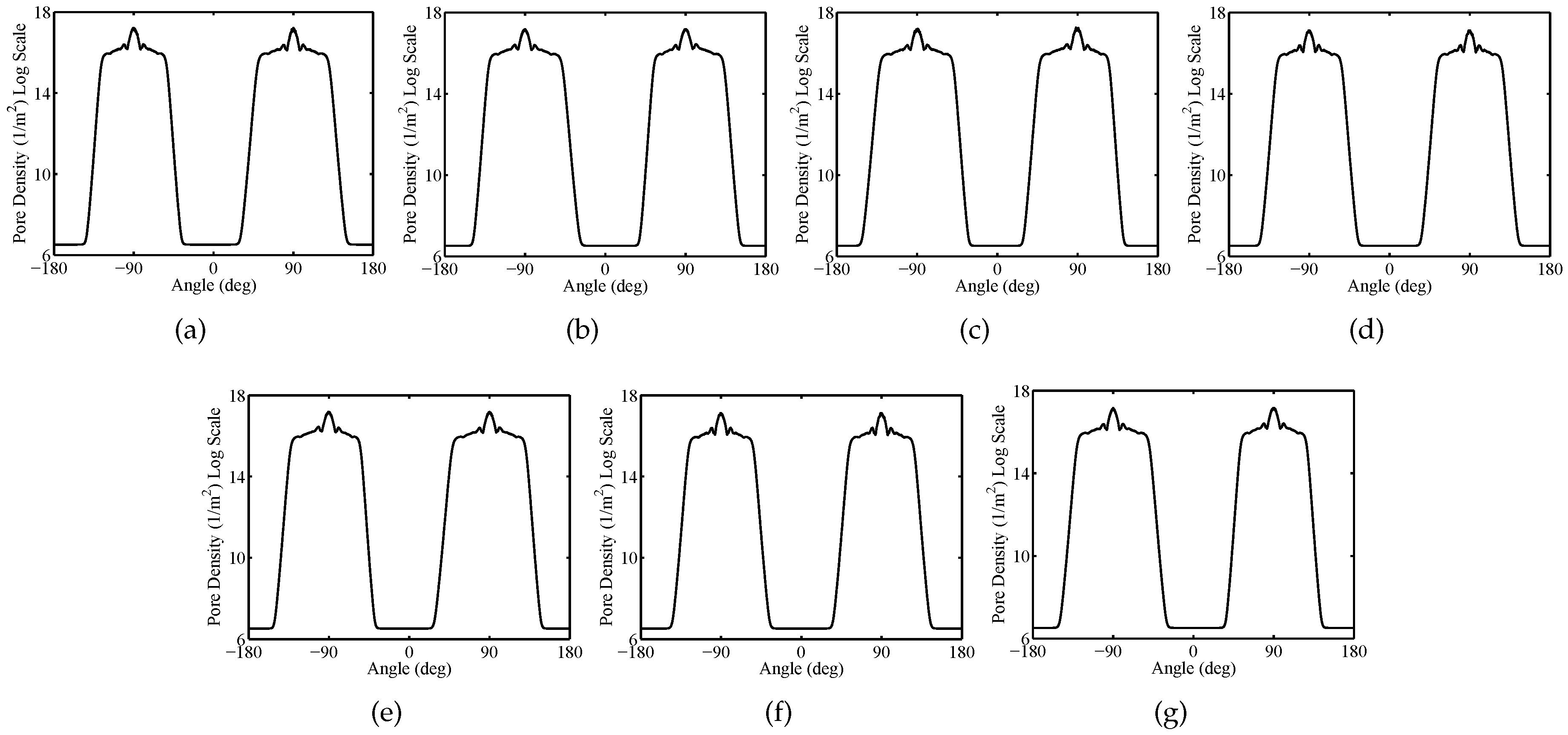

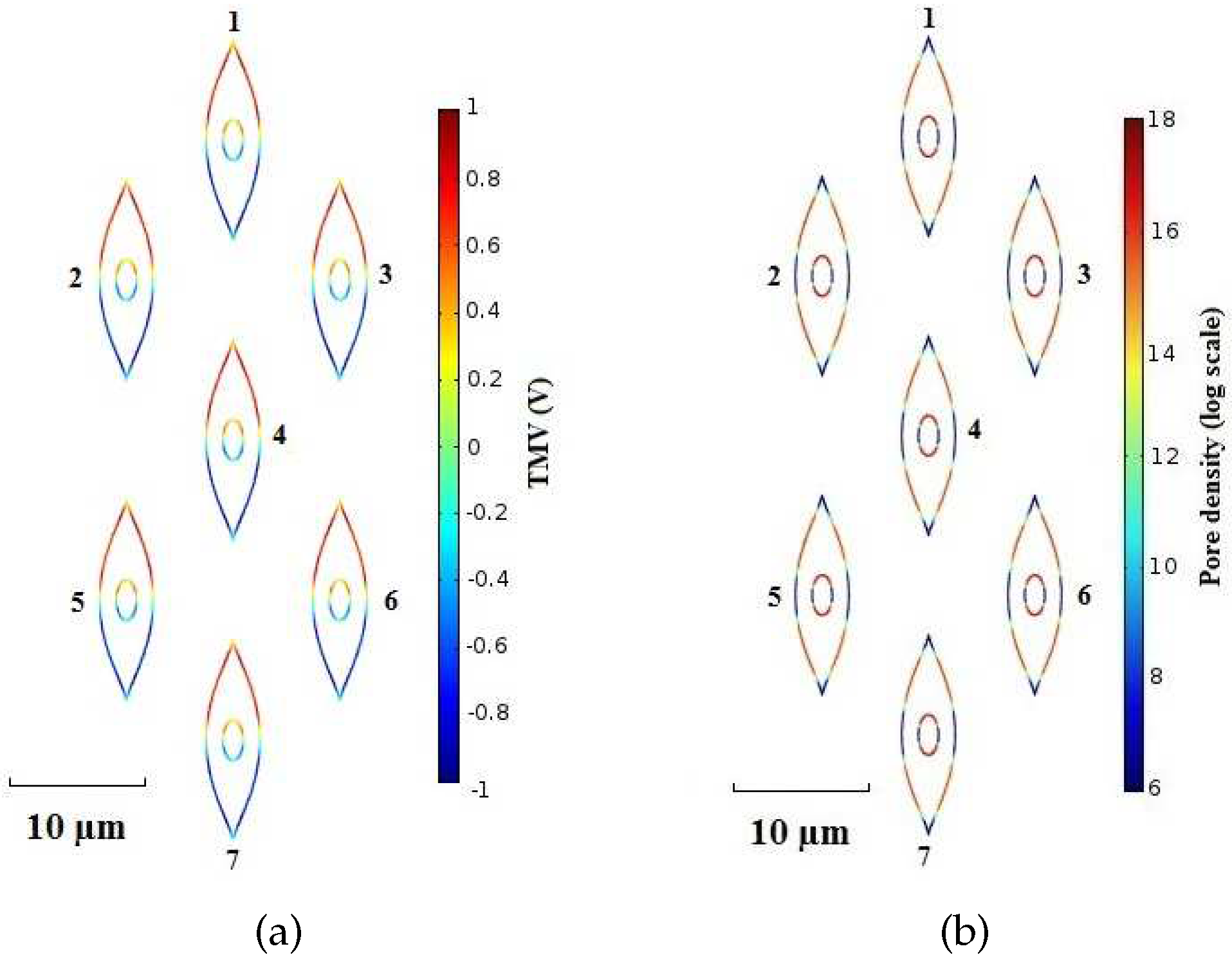
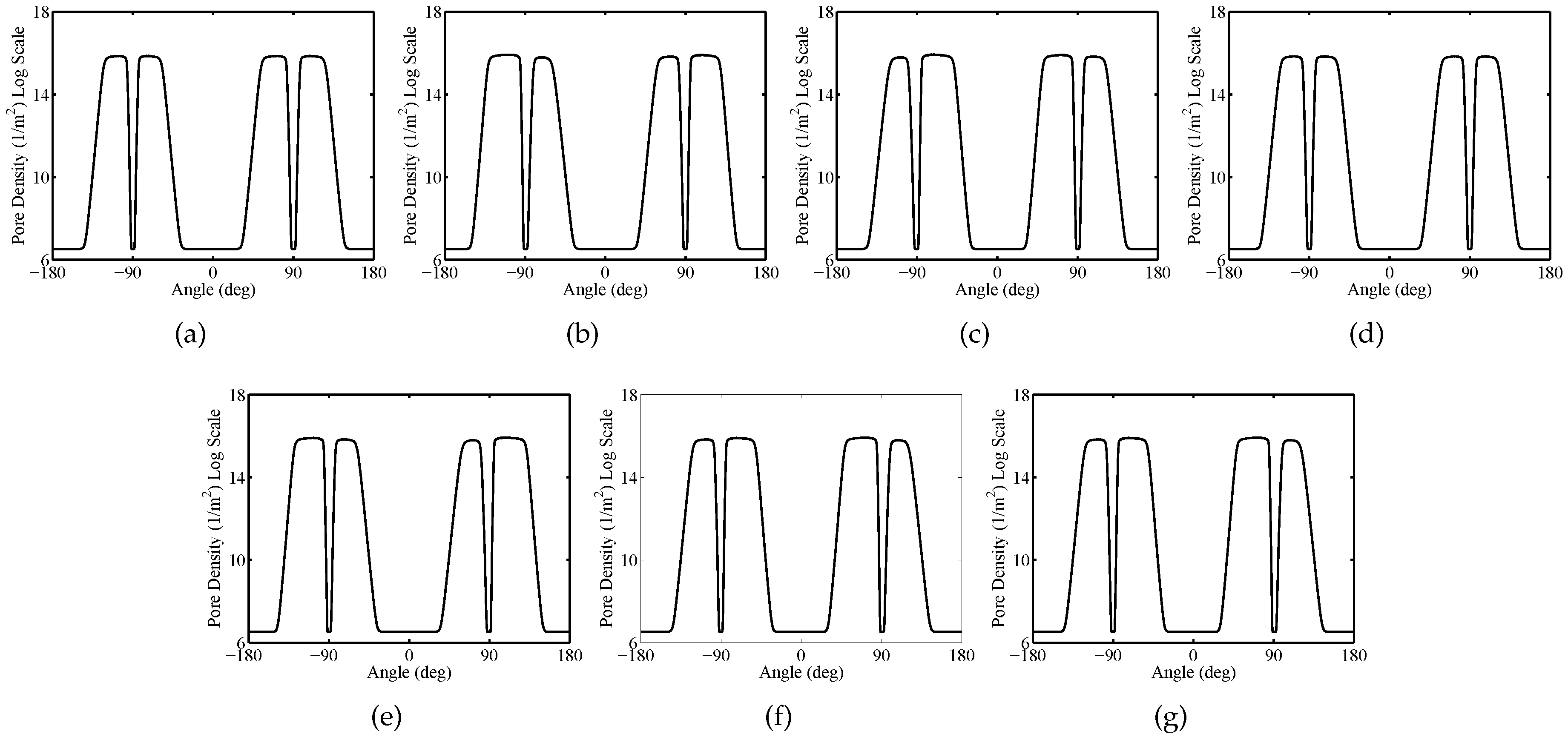

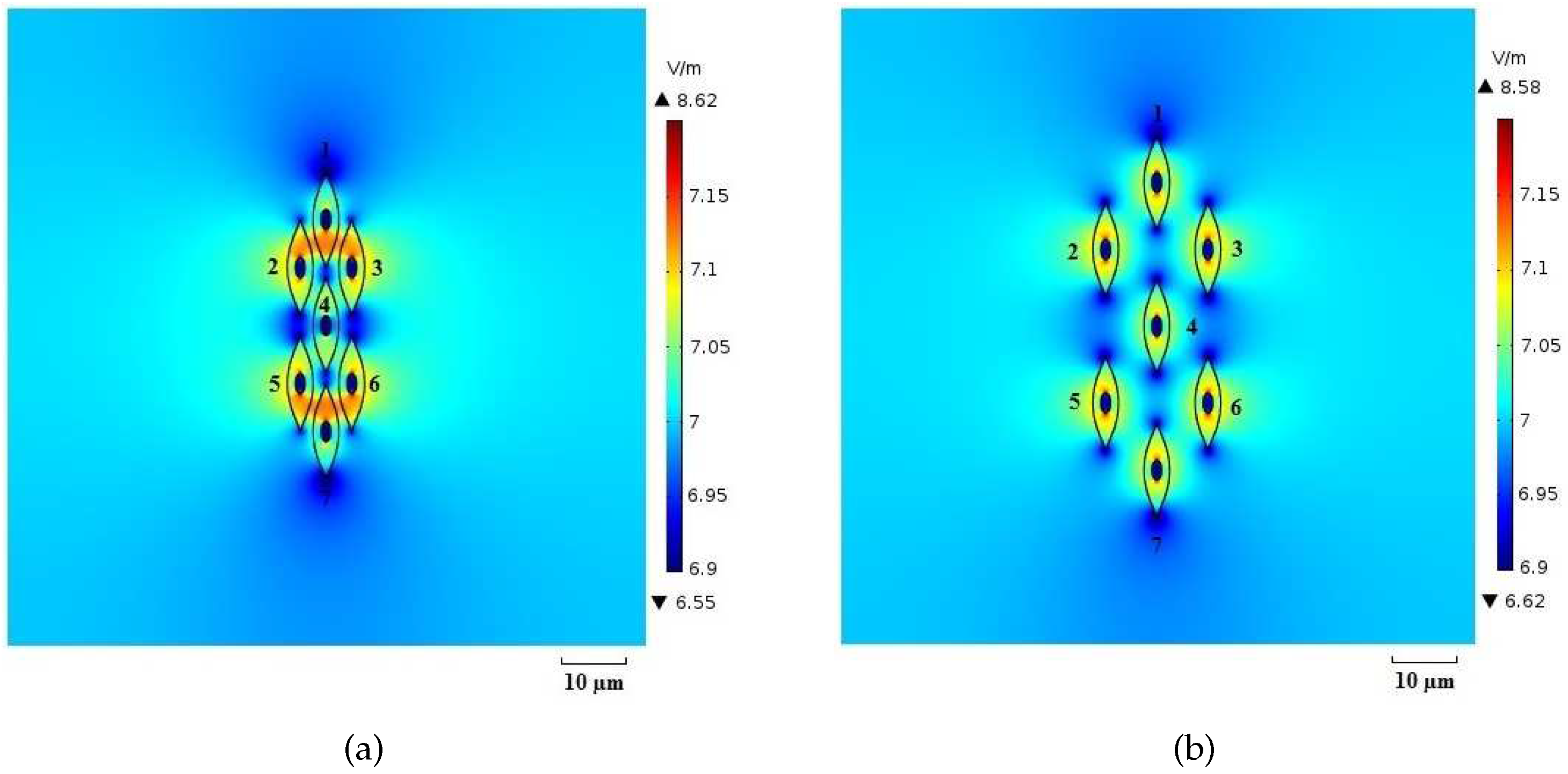

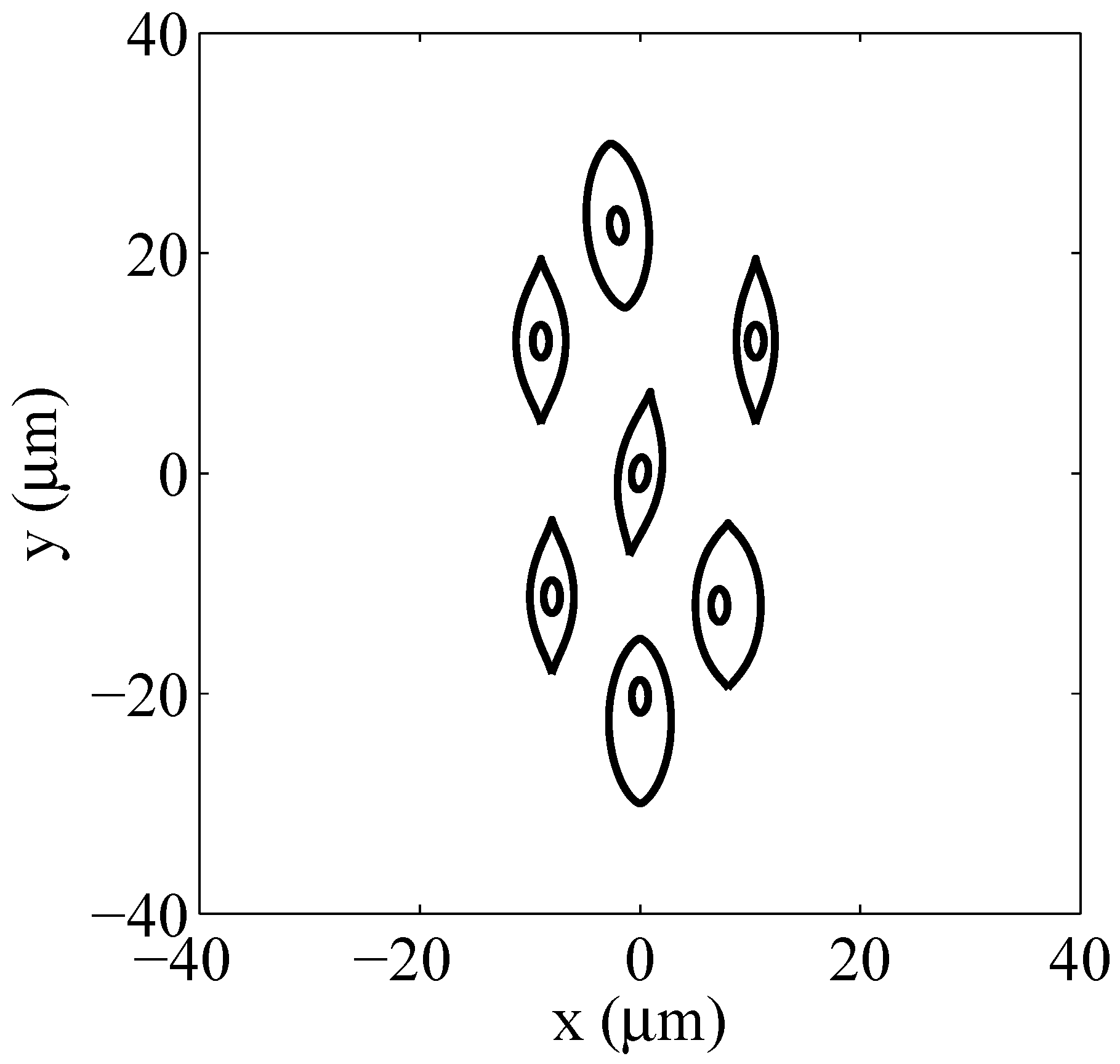
| Packed System | Sparse System | |||
|---|---|---|---|---|
| Cell | (μm) | (μm) | (μm) | (μm) |
| 1 | 0 | 16.5 | 0 | 22.5 |
| 2 | −4 | 9 | −8 | 12 |
| 3 | 4 | 9 | 8 | 12 |
| 4 | 0 | 0 | 0 | 0 |
| 5 | −4 | −9 | −8 | −12 |
| 6 | 4 | −9 | 8 | −12 |
| 7 | 0 | −16.5 | 0 | −22.5 |
| Symbol | Value | Description |
|---|---|---|
| First relaxation time of plasma and nuclear membrane [22] | ||
| Second relaxation time of plasma and nuclear membrane [22] | ||
| Relaxation time of extracellular medium [31] | ||
| Relaxation time of cytoplasm and nucleoplasm [31] | ||
| First relaxation amplitude of plasma and nuclear membrane [22] | ||
| Second relaxation amplitude of plasma and nuclear membrane [22] | ||
| Relaxation amplitude of extracellular medium [31] | ||
| Relaxation amplitude of cytoplasm and nucleoplasm [31] | ||
| High frequency permittivity [22] | ||
| Dielectric permittivity of vacuum | ||
| Conductivity of the extracellular medium [22] | ||
| Passive Conductivity of the plasma membrane [22] | ||
| Conductivity of cytoplasm [22] | ||
| Passive Conductivity of the nuclear membrane [36] | ||
| Conductivity of nucleoplasm [36] | ||
| Conductivity of solution inside the pore for plasma membrane [36] | ||
| Conductivity of solution inside the pore for nuclear membrane [36] | ||
| Pore radius [22] | ||
| Pore creation rate density [22] | ||
| 1 | Electroporation constant [22] | |
| Characteristic voltage of electroporation [22] | ||
| Equilibrium pore density [22] | ||
| 3.2 | Energy barrier inside the pore [22] | |
| 0.15 | Relative length of pore entrance area [22] | |
| Electron electric charge | ||
| k | Boltzmann constant | |
| T | Temperature | |
| Plasma membrane thickness [36] | ||
| Nuclear membrane thickness [36] |
| Cell | Plasma EPRL % | Nuclear EPRL % |
|---|---|---|
| 1 | 37.42 | 56.50 |
| 2 | 37.46 | 58.24 |
| 3 | 37.34 | 58.25 |
| 4 | 24.22 | 53.56 |
| 5 | 37.51 | 58.24 |
| 6 | 37.46 | 58.24 |
| 7 | 37.61 | 56.55 |
| Cell | Plasma EPRL % | Nuclear EPRL % |
|---|---|---|
| 1 | 47.22 | 58.14 |
| 2 | 48.72 | 58.82 |
| 3 | 48.67 | 58.81 |
| 4 | 47.78 | 57.57 |
| 5 | 48.73 | 58.82 |
| 6 | 48.72 | 58.82 |
| 7 | 47.40 | 58.14 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mescia, L.; Chiapperino, M.A.; Bia, P.; Lamacchia, C.M.; Gielis, J.; Caratelli, D. Design of Electroporation Process in Irregularly Shaped Multicellular Systems. Electronics 2019, 8, 37. https://doi.org/10.3390/electronics8010037
Mescia L, Chiapperino MA, Bia P, Lamacchia CM, Gielis J, Caratelli D. Design of Electroporation Process in Irregularly Shaped Multicellular Systems. Electronics. 2019; 8(1):37. https://doi.org/10.3390/electronics8010037
Chicago/Turabian StyleMescia, Luciano, Michele Alessandro Chiapperino, Pietro Bia, Claudio Maria Lamacchia, Johan Gielis, and Diego Caratelli. 2019. "Design of Electroporation Process in Irregularly Shaped Multicellular Systems" Electronics 8, no. 1: 37. https://doi.org/10.3390/electronics8010037
APA StyleMescia, L., Chiapperino, M. A., Bia, P., Lamacchia, C. M., Gielis, J., & Caratelli, D. (2019). Design of Electroporation Process in Irregularly Shaped Multicellular Systems. Electronics, 8(1), 37. https://doi.org/10.3390/electronics8010037








