An Improved Frequency Measurement Method from the Digital PLL Structure for Single-Phase Grid-Connected PV Applications
Abstract
:1. Introduction
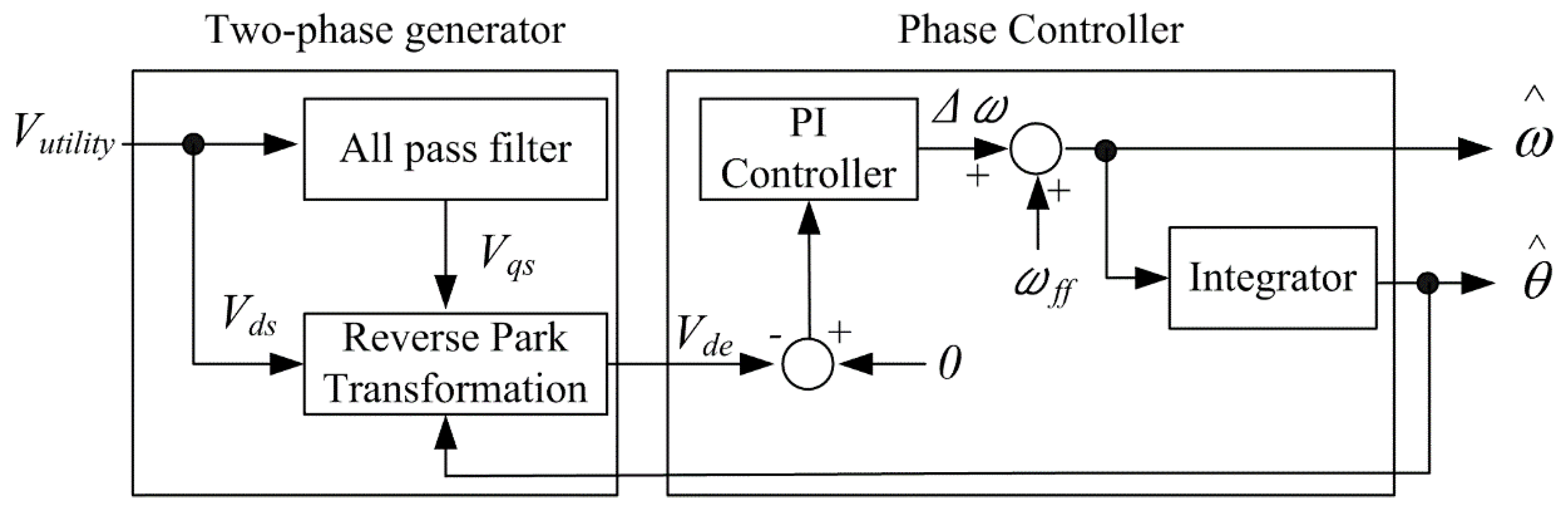
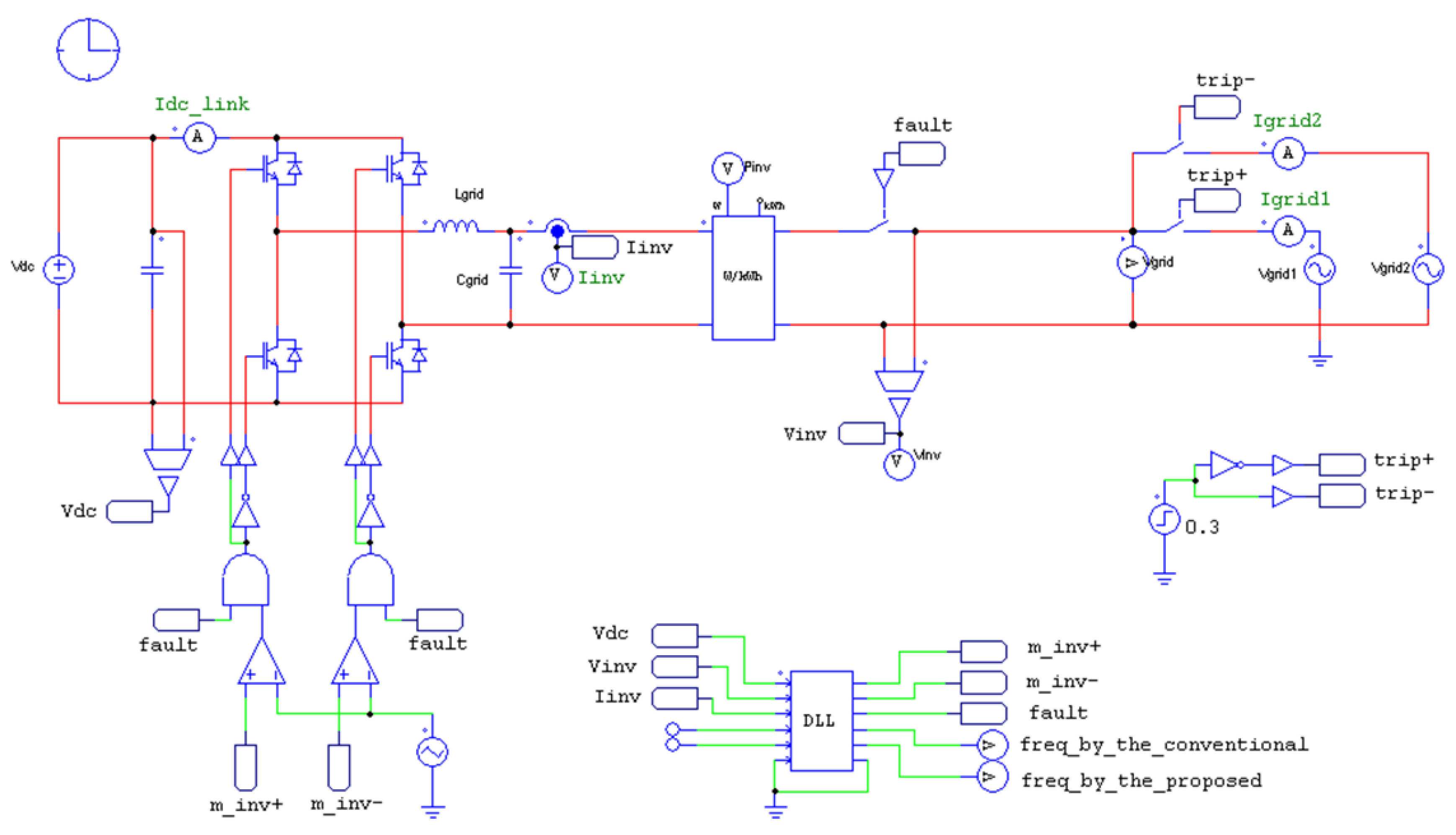
2. System Configuration
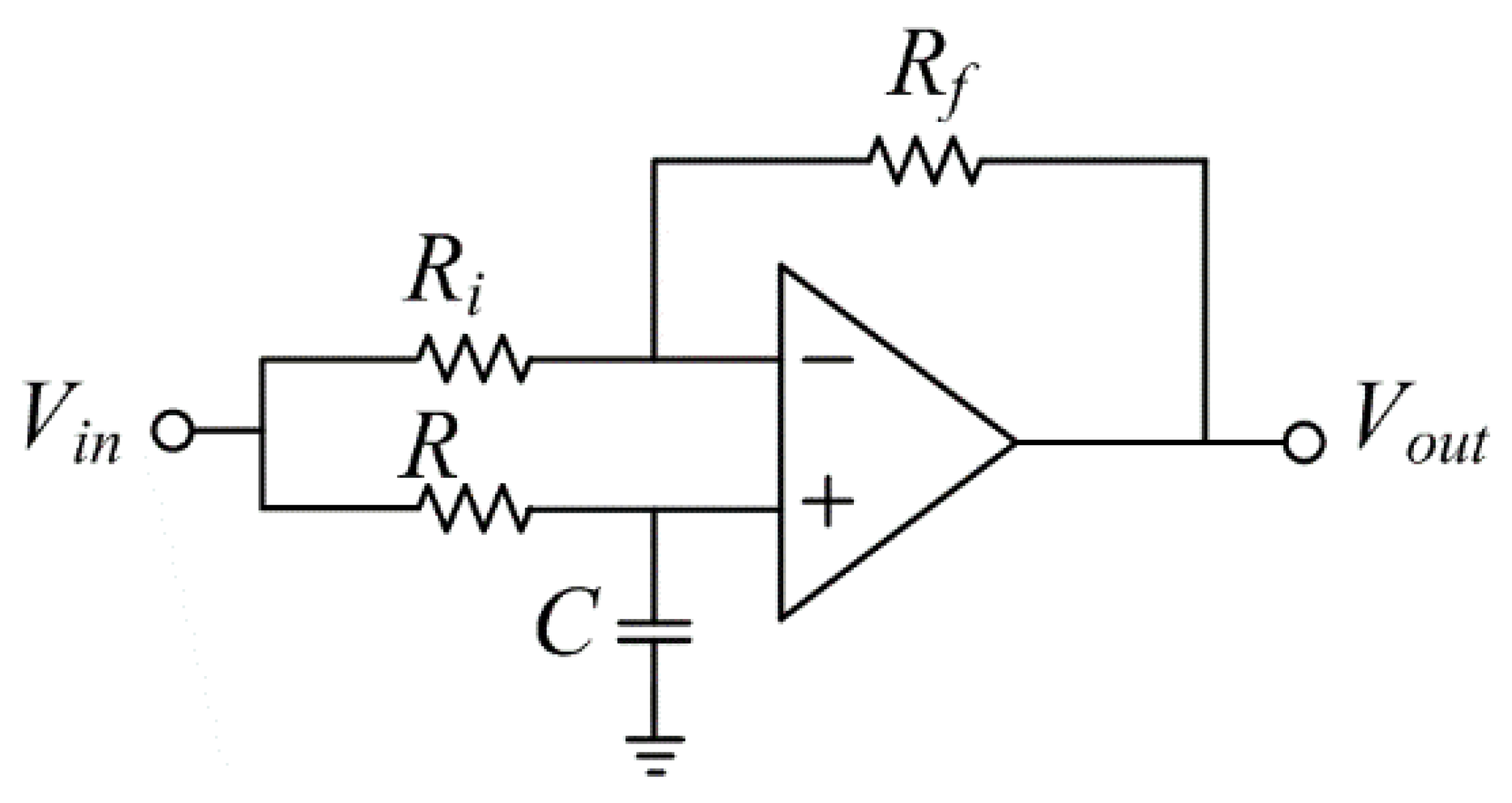
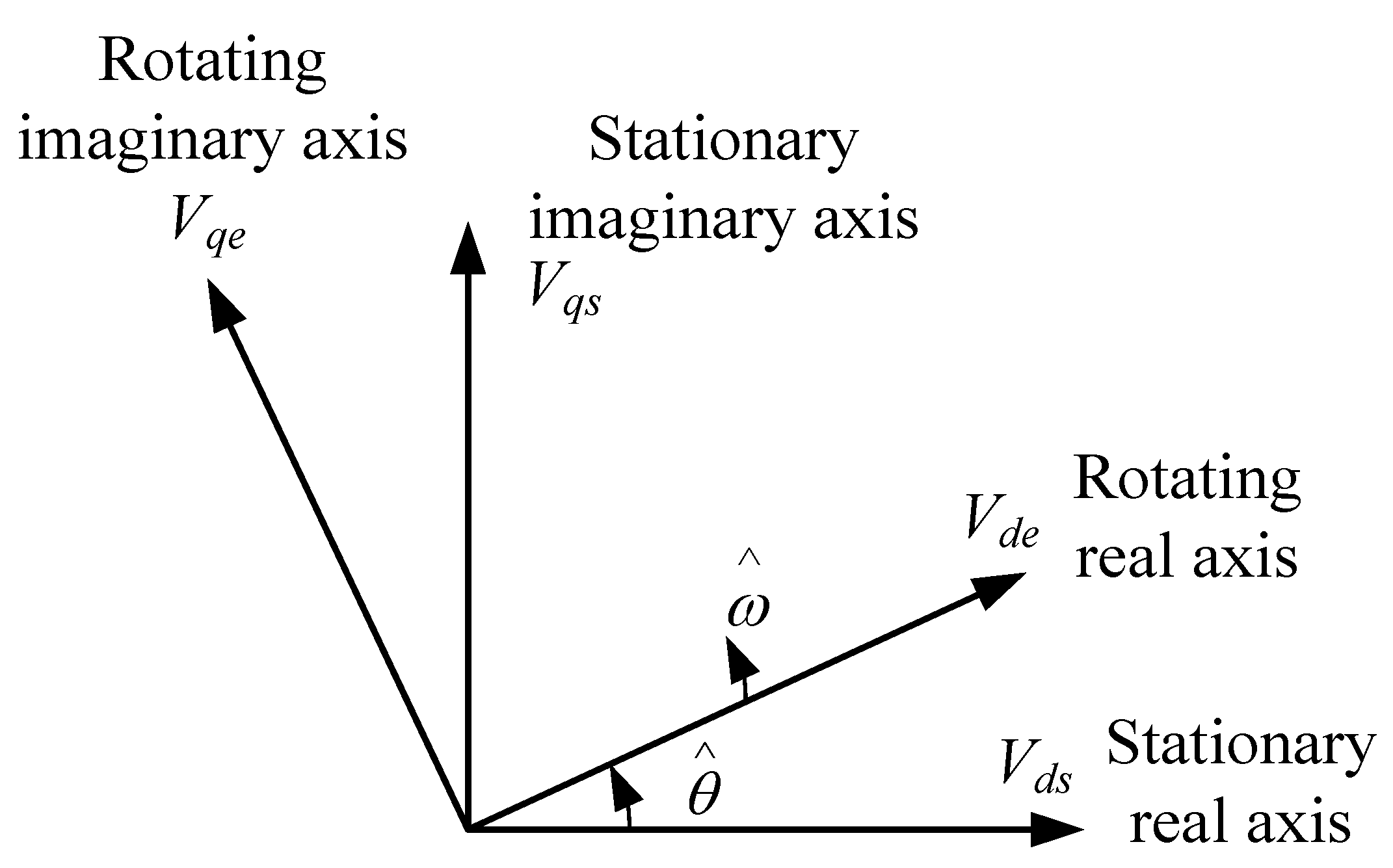
2.1. Two-Phase Generator
2.2. Phase Controller
3. The Line Frequency Measurement Techniques from the Digital PLL
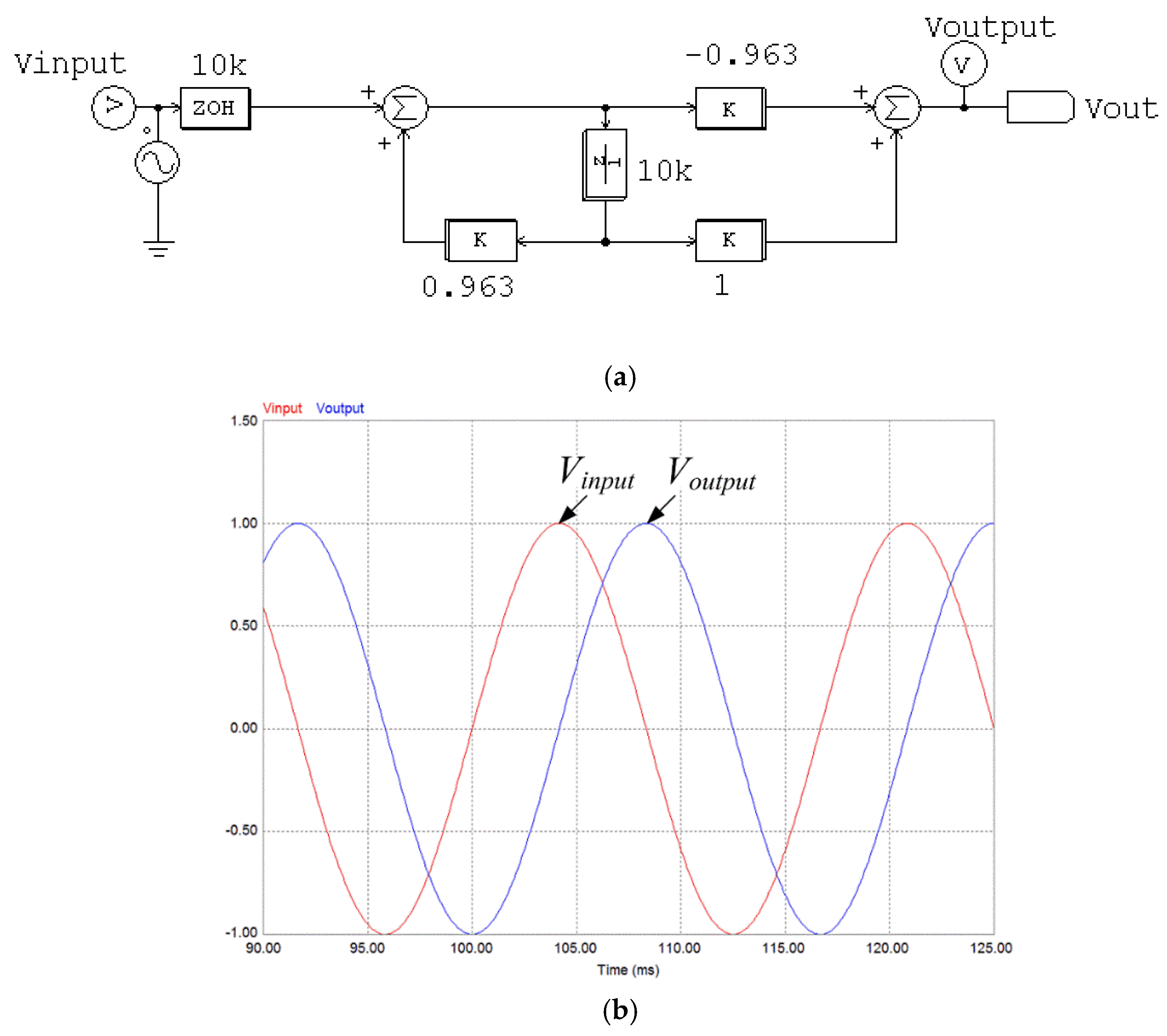
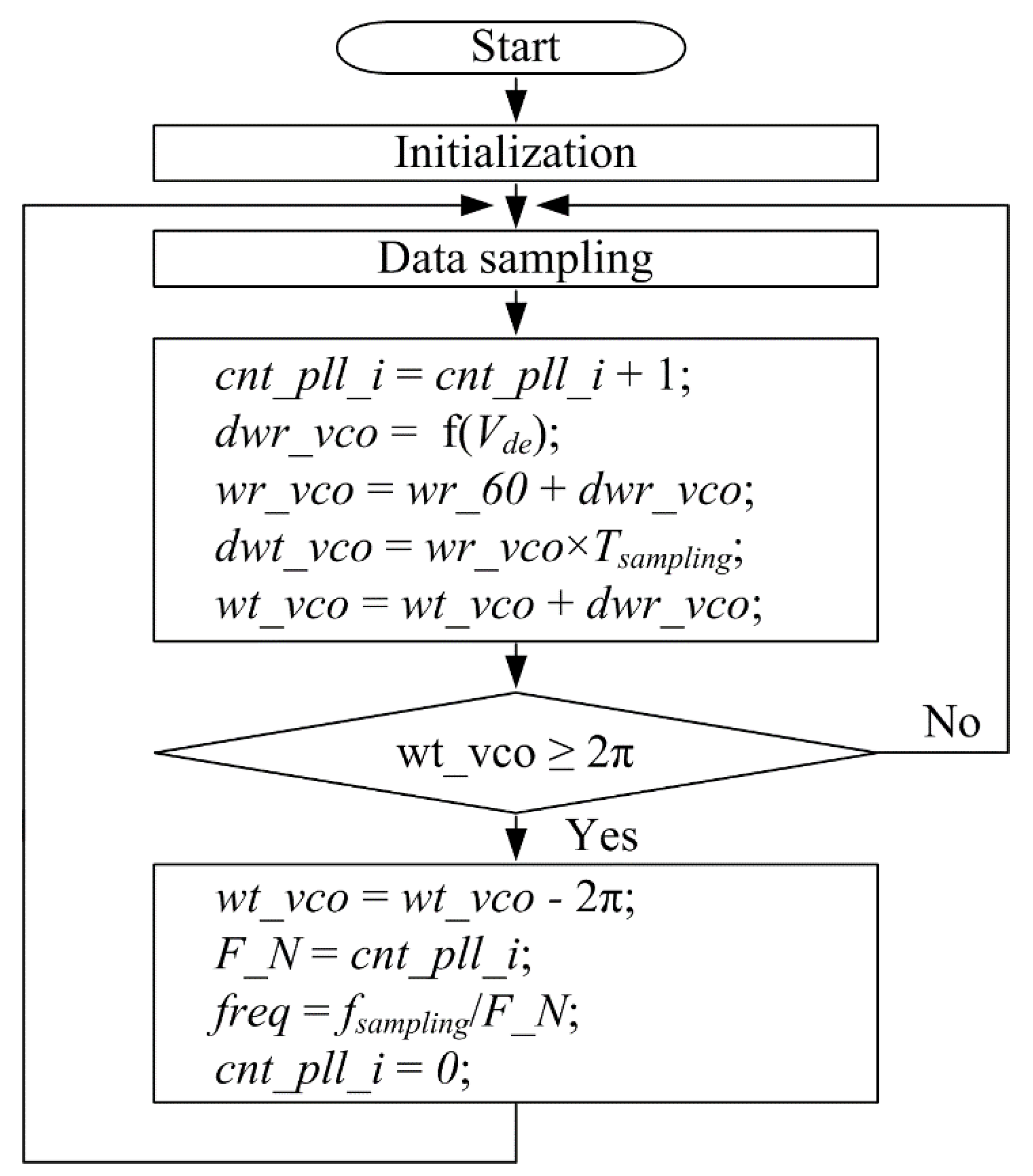
3.1. The Conventional Method
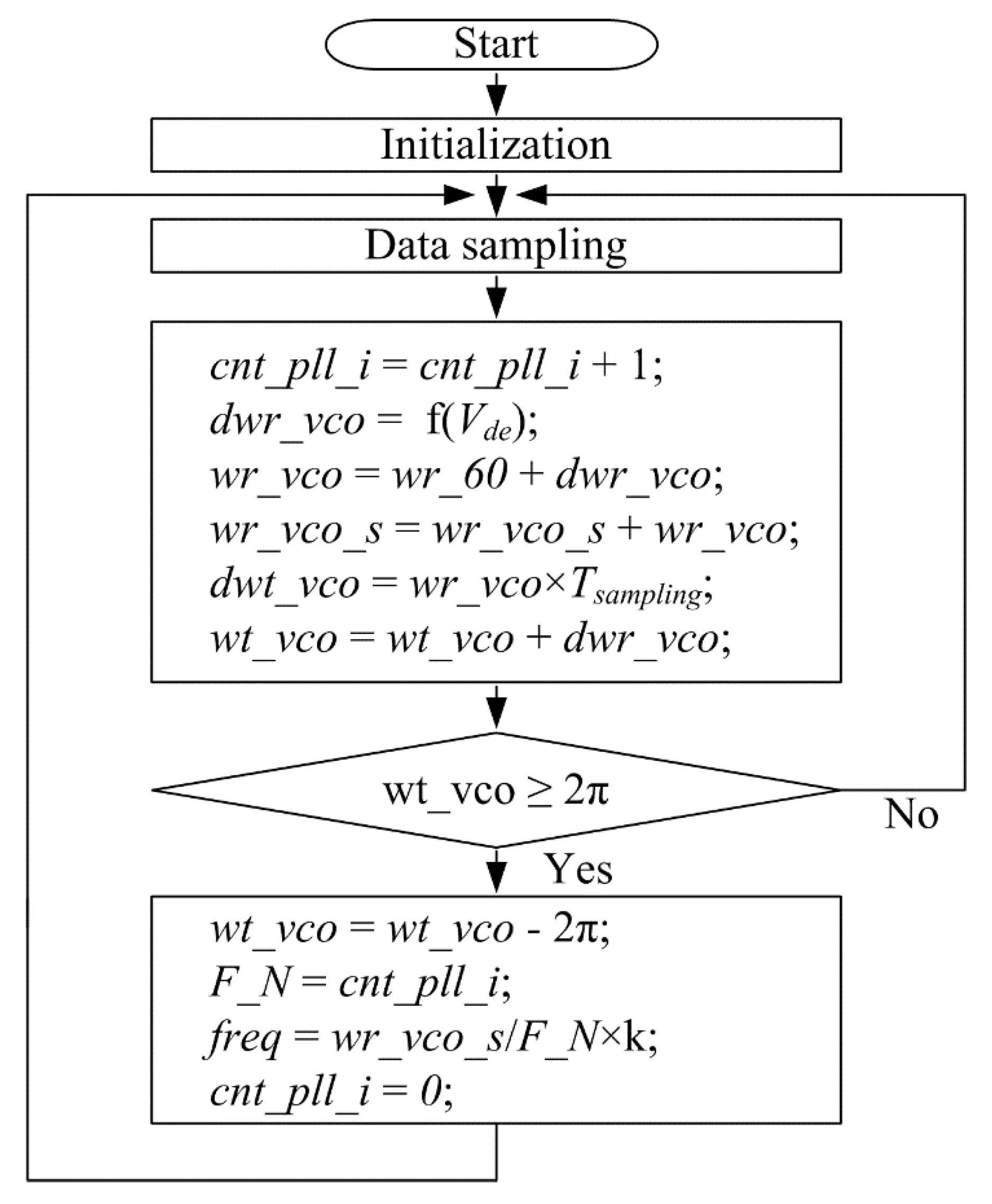
3.2. The Proposed Method
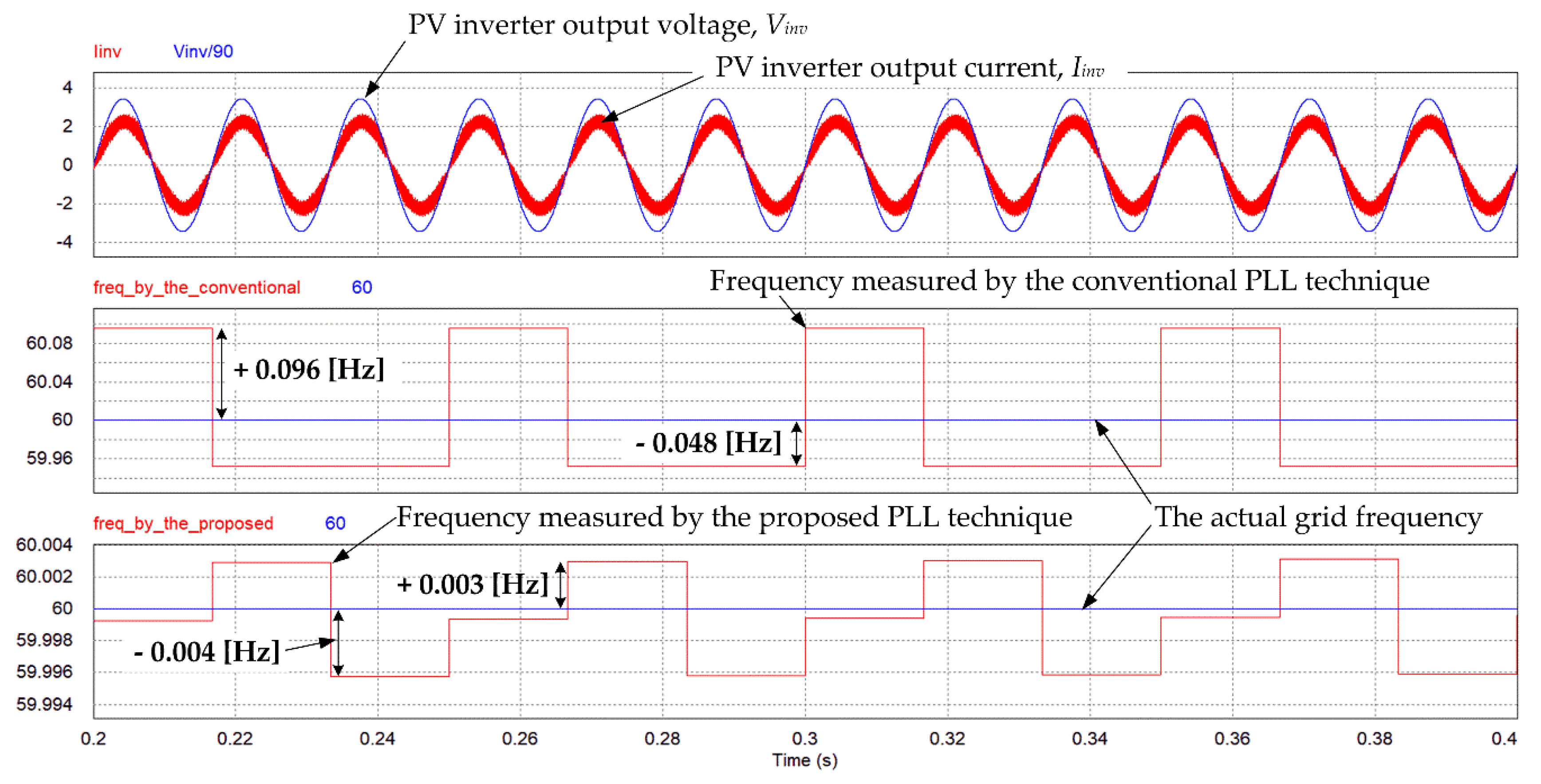
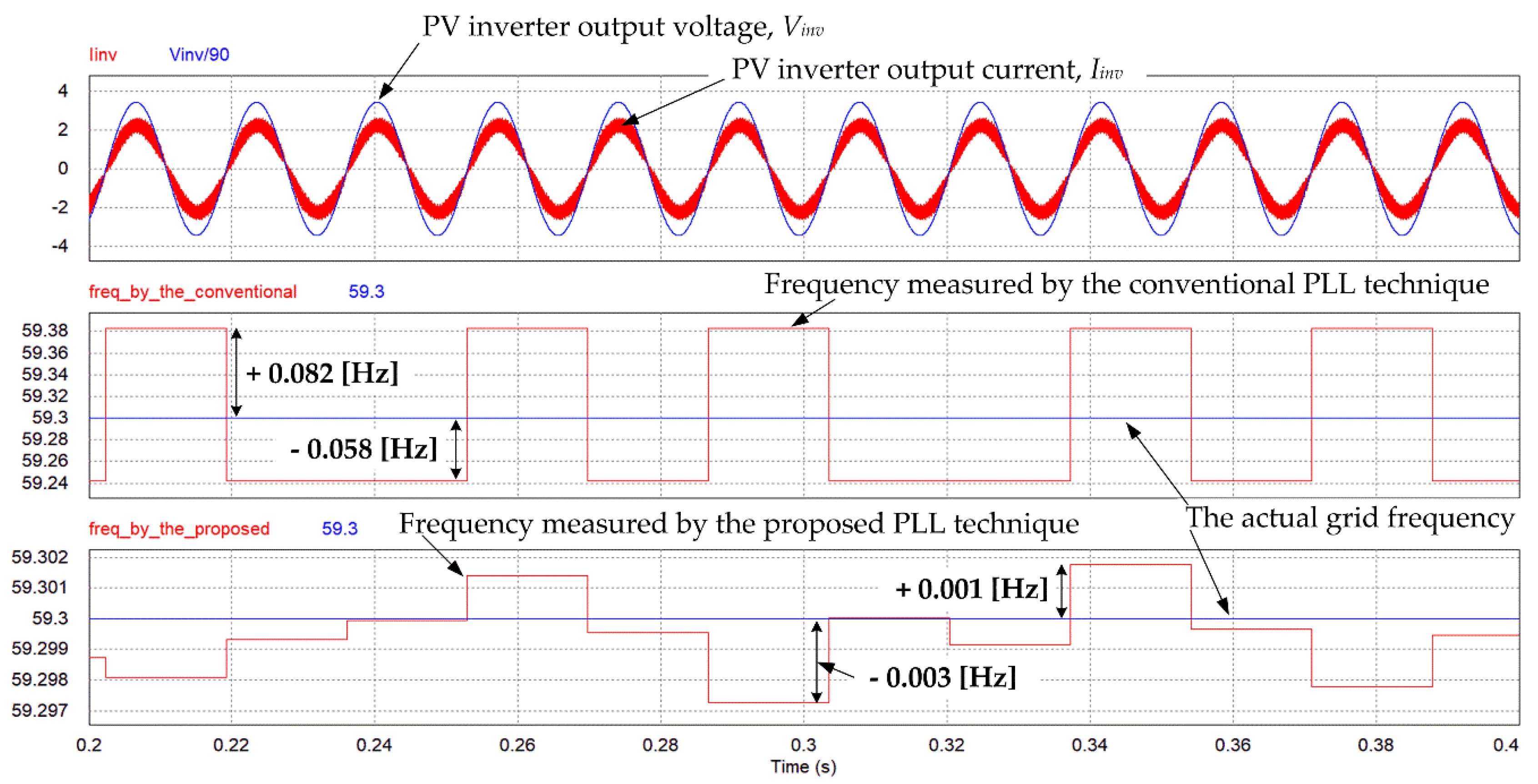
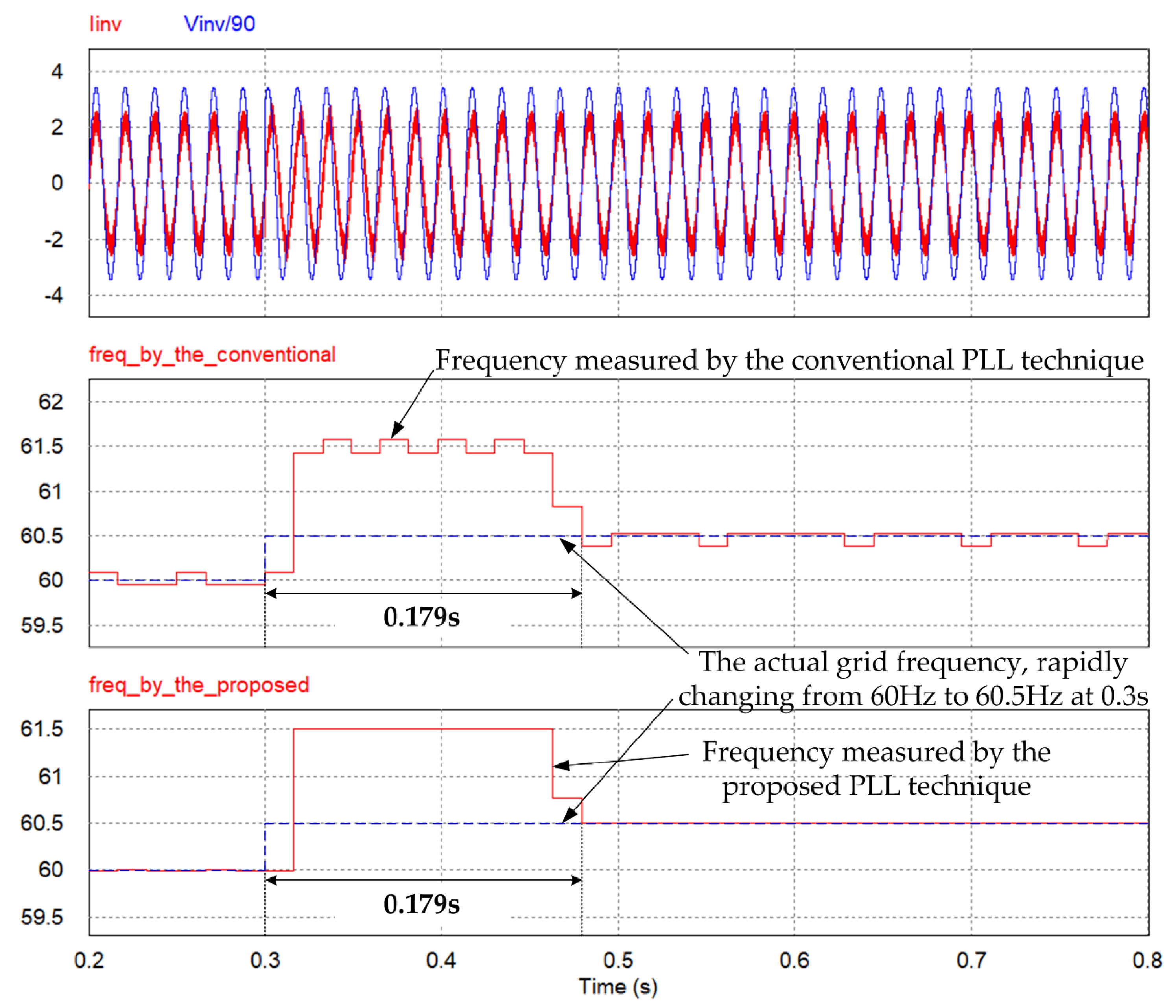
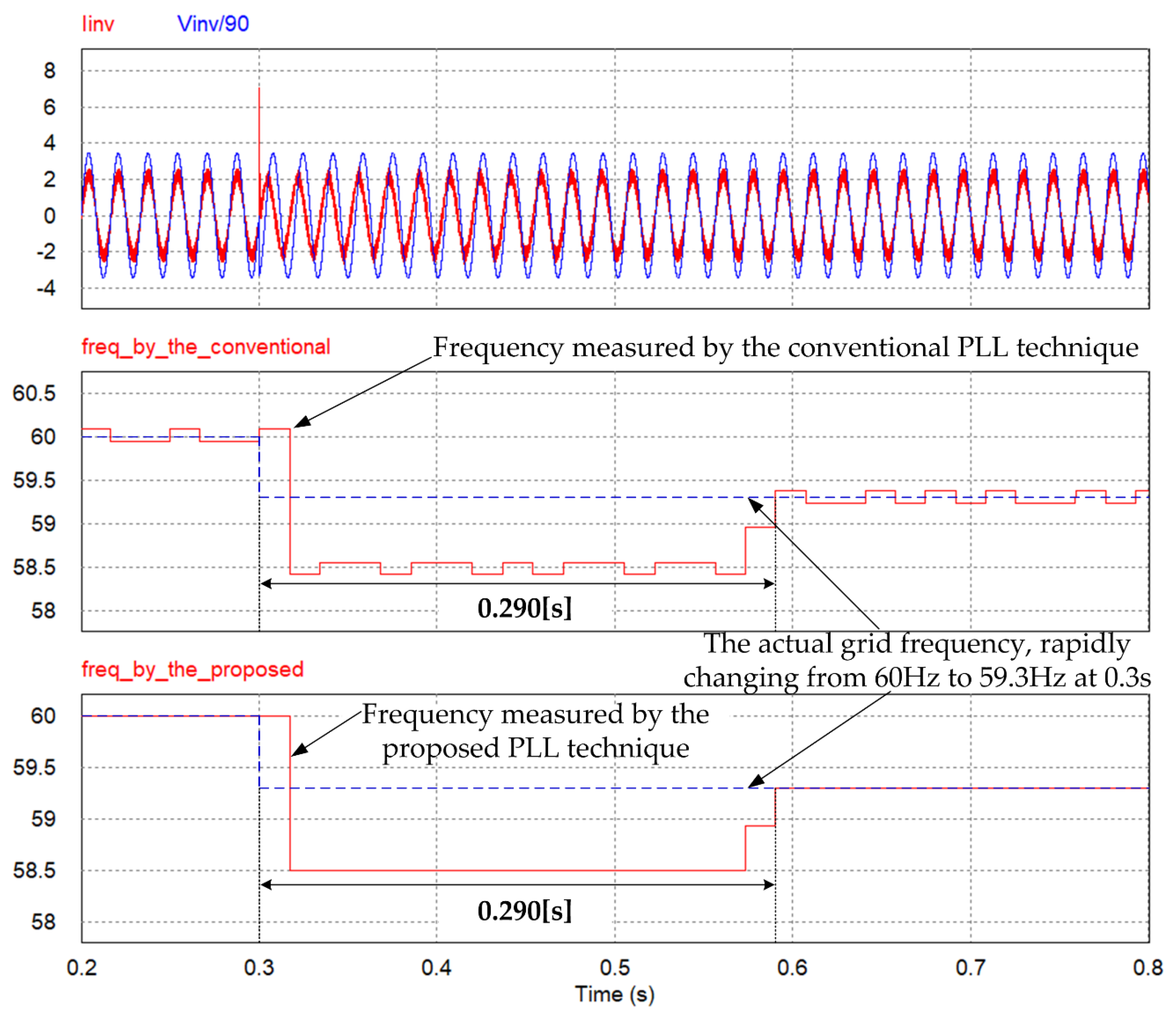
4. Simulation Results
5. Conclusions
Funding
Conflicts of Interest
References
- Kurtz, S.; Sample, T.; Wohlgemuth, J.; Zhou, W.; Bosco, N.; Althaus, J.; Philips, N.; Deceglie, M.; Flueckiger, C.; Hacke, P.; et al. Moving toward quantifying reliability—The next step in a rapidly maturing PV industry. In Proceedings of the 2015 IEEE 42nd Photovoltaic Specialist Conference, New Orleans, LA, USA, 14–19 June 2015; pp. 1–8. [Google Scholar]
- Jaber, A.; Abu, Q.; Jiang, Y. Distributed photovoltaic solar system architecture with single-power inductor single-power converter and single-sensor single maximum power point tracking controller. IET Power Electron. 2014, 7, 2600–2609. [Google Scholar]
- Blaabjerg, F.; Consoli, A.; Ferreira, J.A.; Wyk, J.D. The future of electronic power processing and conversion. IEEE Trans. Power Electron. 2005, 20, 715–720. [Google Scholar] [CrossRef]
- Chung, S.K. A phase tracking system for three phase utility interface inverters. IEEE Trans. Power Electron. 2000, 15, 431–438. [Google Scholar] [CrossRef]
- Hadjidemetriou, L.; Kyriakides, E.; Blaabjerg, F. A robust synchronization to enhance the power quality of renewable energy systems. IEEE Trans. Ind. Electron. 2015, 62, 4858–4868. [Google Scholar] [CrossRef]
- Golestan, S.; Guerrero, J.M.; Vasquez, J.C. Single-phase PLLs: A review of recent advances. IEEE Trans. Power Electron. 2017, 32, 9013–9030. [Google Scholar] [CrossRef]
- Xun, P.; Zhu, P.; Zhang, Z.; Cui, P.; Xiong, Y. Detectors on edge nodes against false data injection on transmission lines of smart grid. Electronics 2018, 7, 89. [Google Scholar] [CrossRef]
- Capizzi, G.; Tina, G. Long-term operation optimization of integrated generation systems by fuzzy logic-based management. Energy 2007, 32, 1047–1054. [Google Scholar] [CrossRef]
- Bonanno, F.; Gapizzi, G.; Sciuto, G.L. A neuro wavelet-based approach for short-term load forecasting in integrated generation systems. In Proceedings of the 2013 International Conference on Clean Electrical Power (ICCEP), Alghero, Italy, 11–13 June 2018; pp. 772–776. [Google Scholar]
- Ropp, M.E.; Begovic, M.; Rohatgi, A. Analysis and performance assessment of the active frequency drift method of islanding prevention. IEEE Trans. Energy Convers. 1999, 14, 810–816. [Google Scholar] [CrossRef]
- Hung, G.K.; Chang, C.C.; Chen, C.L. Automatic phase-shift method for islanding detection of grid-connected photovoltaic inverters. IEEE Trans. Energy Convers. 2003, 18, 169–173. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, Y.; Xue, M.; Lin, X.; Kang, Y. Investigation and evaluation of active frequency drifting methods in multiple grid-connected inverters. IET Power Electron. 2012, 5, 485–492. [Google Scholar] [CrossRef]
- Vieira, J.C.; Freitas, W.; Xu, W.; Morelato, A. Performance of frequency relays for distributed generation protection. IEEE Trans. Power Deliv. 2006, 21, 1120–1127. [Google Scholar] [CrossRef]
- Lopes, L.A.C.; Zhang, Y. Islanding detection assessment of multi-inverter systems with active frequency drifting methods. IEEE Trans. Power Deliv. 2008, 23, 480–486. [Google Scholar] [CrossRef]
- Velasco, D.; Trujillo, C.L.; Narvaez, E.A. Review of anti-islanding methods: Analysis by figures of merit tools for controllers reconfiguration in microgrids. IEEE Lat. Am. Trans. 2015, 13, 679–686. [Google Scholar] [CrossRef]
- Thacker, T.; Boroyevich, D.; Burgos, R.; Wang, F. Phase-locked loop noise reduction via phase detector implementation for single phase systems. IEEE Trans. Ind. Electron. 2011, 58, 2482–2490. [Google Scholar] [CrossRef]
- Golesatan, S.; Guerrero, J.M.; Vasquez, J.C. A PLL-based controller for three-phase grid-connected power converters. IEEE Trans. Power Electron. 2018, 33, 911–916. [Google Scholar] [CrossRef]
- Chung, S.K. Phase-locked loop for grid-connected three-phase power conversion systems. IEE Proc.—Electr. Power Appl. 2000, 147, 213–219. [Google Scholar] [CrossRef]
- Pahlevani, M.; Jain, P. A fast DC-bus voltage controller for bidirectional single-phase AC/DC converters. IEEE Trans. Power Electron. 2015, 30, 4536–4547. [Google Scholar] [CrossRef]
- Liu, Y.C.; Chen, M.C.; Yang, C.Y.; Kim, K.A.; Chiu, H.J. High-efficiency isolated photovoltaic microinverter using wide-band gap switches for standalone and grid-tied applications. Energies 2018, 11, 569. [Google Scholar] [CrossRef]
- Dong, D.; Wen, B.; Boroyevich, D.; Mattavelli, P.; Xue, Y. Analysis of phase-locked loop low-frequency stability in three-phase grid-connected power converters considering impedance interactions. IEEE Trans. Ind. Electron. 2015, 62, 310–321. [Google Scholar] [CrossRef]
- Golestan, S.; Guerrero, J.M.; Abusorrah, A.; Al-Hindawi, M.; Al-Turki, Y. An adaptive quadrature singal generation-based single-phase phase-locked loop for grid-connected applications. IEEE Trans. Ind. Electron. 2017, 64, 2848–2854. [Google Scholar] [CrossRef]
- Yu, B.; Matsui, M.; Yu, G. A correlation-based islanding-detection method using current-magnitude disturbance for PV system. IEEE Trans. Ind. Electron. 2011, 58, 2935–2943. [Google Scholar] [CrossRef]
- Zhang, Q.; Sung, X.D.; Zhong, Y.R.; Matsui, M.; Ren, B.Y. Analysis and design of a digital phase-locked loop for single-phase grid-connected power conversion systems. IEEE Trans. Ind. Electron. 2011, 58, 3581–3592. [Google Scholar] [CrossRef]
- Geng, H.; Xu, D.; Wu, B. A novel hardware-based all-digital phase-locked loop applied to grid-connected power converters. IEEE Trans. Ind. Electron. 2011, 58, 1737–1745. [Google Scholar] [CrossRef]
- Yu, B. An improved active frequency drift anti-islanding method for multiple PV micro-inverter systems. IEICE Electron. Express 2014, 11, 1–11. [Google Scholar] [CrossRef]
- Golestan, S.; Ramezani, M.; Guerrero, J.M.; Freijedo, F.D.; Monfared, M. Moving average filter based phase-locked loops: Performance analysis and design guidelines. IEEE Trans. Power Electron. 2014, 29, 2750–2763. [Google Scholar] [CrossRef]
- Lu, C.; Zhou, Z.; Jiang, A.; Luo, M.; Shen, P.; Han, Y. Comparative performance evaluation of phase locked loop (PLL) algorithms for single-phase grid-connected converters. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 22–25 May 2016; pp. 902–907. [Google Scholar]
- IEEE Standard Conformance Test Procedures for Equipment Interconnecting Distributed Resources with Electric Power Systems; IEEE Std.1547.1-2005; IEEE Standard Association: Piscataway, NJ, USA, 2005.
- Photovoltaic (PV) Systems—Characteristics of the Utility Interface; IEC Standard IEC 61727:2004; IEC Webstore; IEC: Geneva, Switzerland, 2004.
- Test Procedure of Islanding Prevention Measures for Utility-Interconnected Photovoltaic Inverters; IEC Standard IEC 62116: 2014; IEC Webstore; IEC: Geneva, Switzerland, 2014.

| Parameters | Value |
|---|---|
| PV inverter nominal power, Pinv | 350 [W] |
| Nominal grid voltage, Vgrid | 220 [V] |
| Nominal grid frequency, fgrid | 60 [Hz] |
| Number of phase | Single |
| Normal frequency range | 59.3 [Hz] ≤ f ≤ 60.5 [Hz] |
| The scaling factor, k | 0.1592 |
| The sampling frequency, fsampling | 25 [kHz] |
| No | Grid Frequency | PLL Technique | Positive Error (%) | Negative Error (%) |
|---|---|---|---|---|
| 1 | 60 Hz | Conventional | 0.096 Hz (0.160%) | 0.048 Hz (0.080%) |
| Proposed | 0.003 Hz (0.005%) | 0.004 Hz (0.007%) | ||
| 2 | 60.5 Hz | Conventional | 0.033 Hz (0.055%) | 0.114 Hz (0.190%) |
| Proposed | 0.002 Hz (0.003%) | 0.004 Hz (0.007%) | ||
| 3 | 59.3 Hz | Conventional | 0.082 Hz (0.137%) | 0.058 Hz (0.097%) |
| Proposed | 0.001 Hz (0.002%) | 0.003 Hz (0.005%) |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, B. An Improved Frequency Measurement Method from the Digital PLL Structure for Single-Phase Grid-Connected PV Applications. Electronics 2018, 7, 150. https://doi.org/10.3390/electronics7080150
Yu B. An Improved Frequency Measurement Method from the Digital PLL Structure for Single-Phase Grid-Connected PV Applications. Electronics. 2018; 7(8):150. https://doi.org/10.3390/electronics7080150
Chicago/Turabian StyleYu, Byunggyu. 2018. "An Improved Frequency Measurement Method from the Digital PLL Structure for Single-Phase Grid-Connected PV Applications" Electronics 7, no. 8: 150. https://doi.org/10.3390/electronics7080150
APA StyleYu, B. (2018). An Improved Frequency Measurement Method from the Digital PLL Structure for Single-Phase Grid-Connected PV Applications. Electronics, 7(8), 150. https://doi.org/10.3390/electronics7080150





