An Effective Switching Algorithm for Single Phase Matrix Converter in Induction Heating Applications
Abstract
1. Introduction
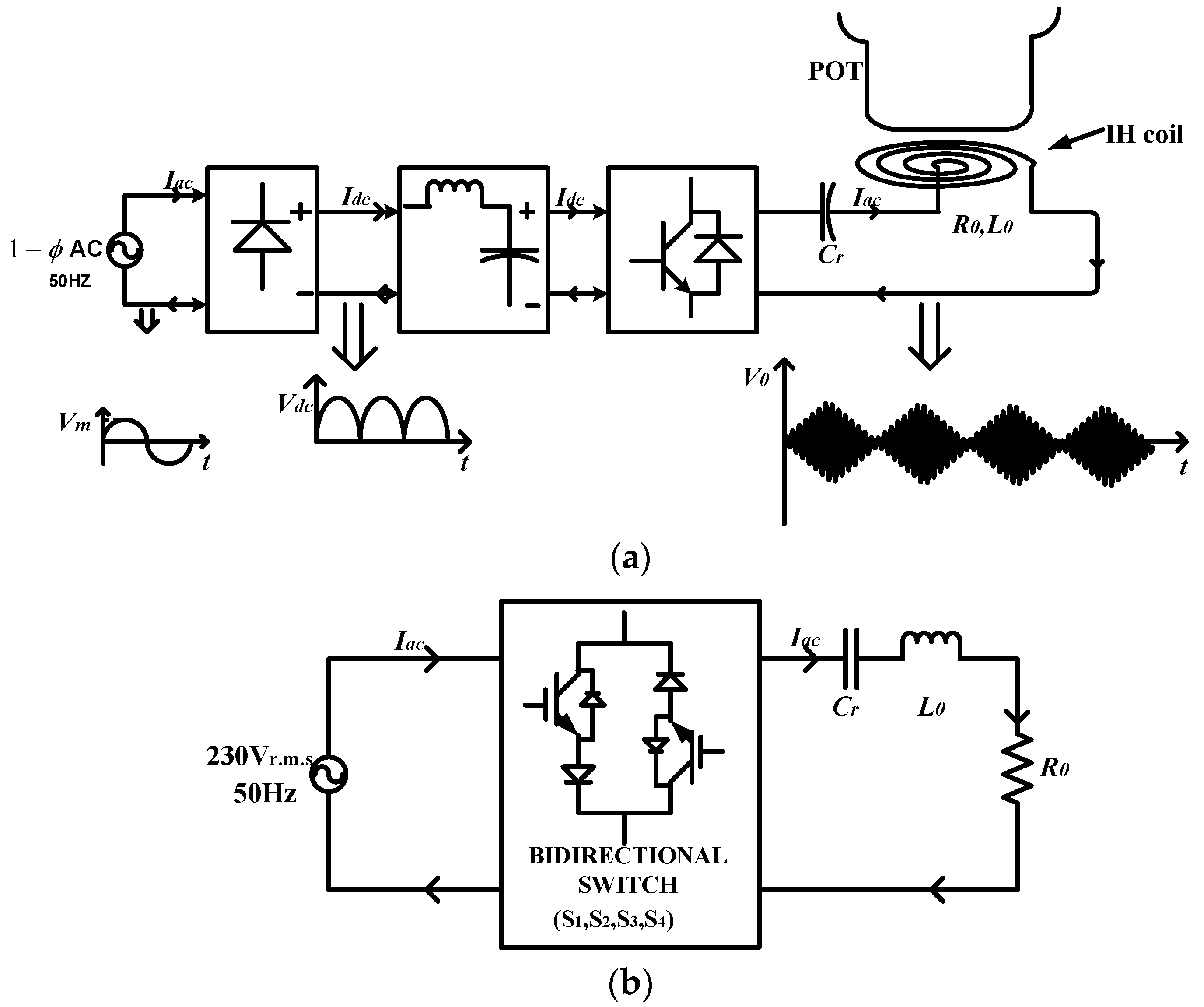
2. Single-Phase Matrix Converter and Its Modified Switching Technique for Induction Heating (IH) Applications
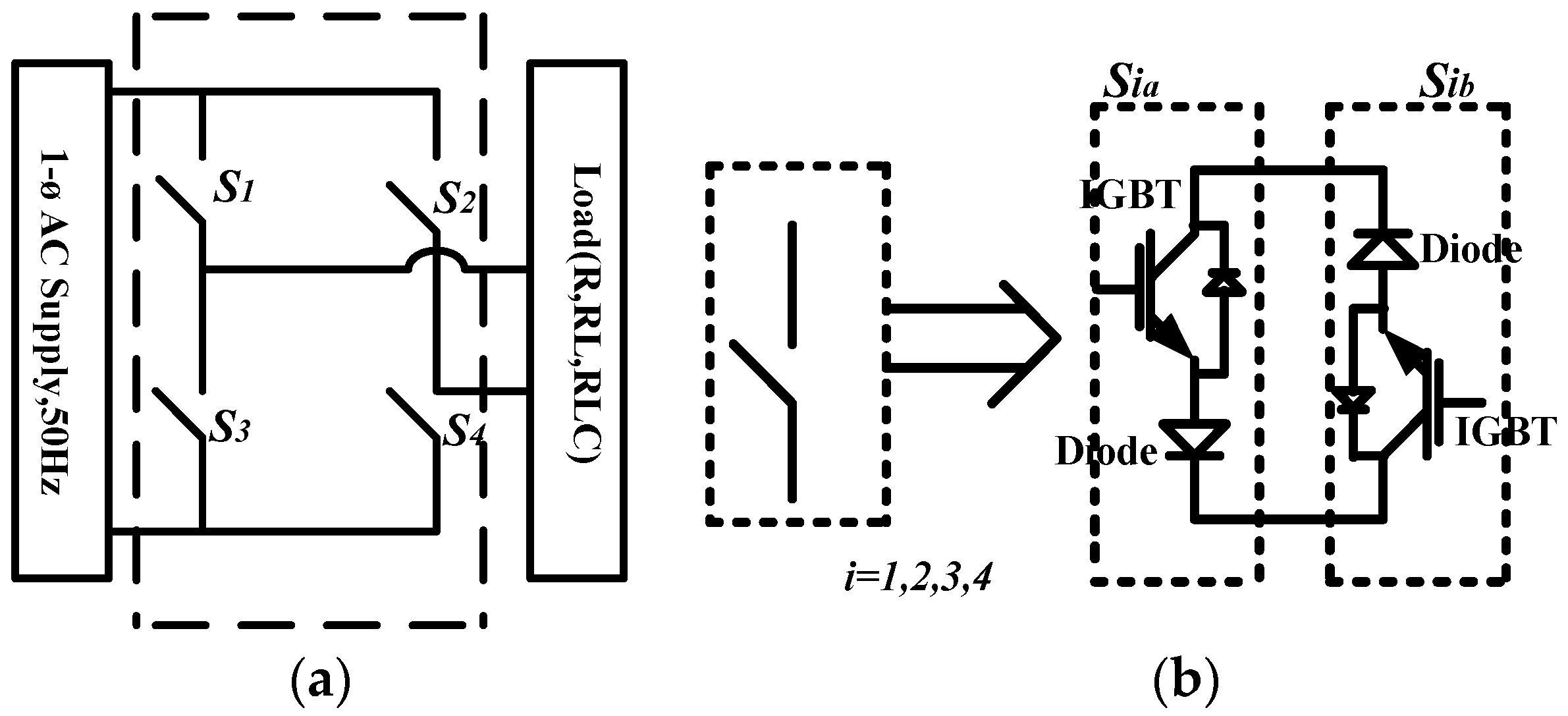
2.1. Single-Phase Matrix Converter (SPMC)
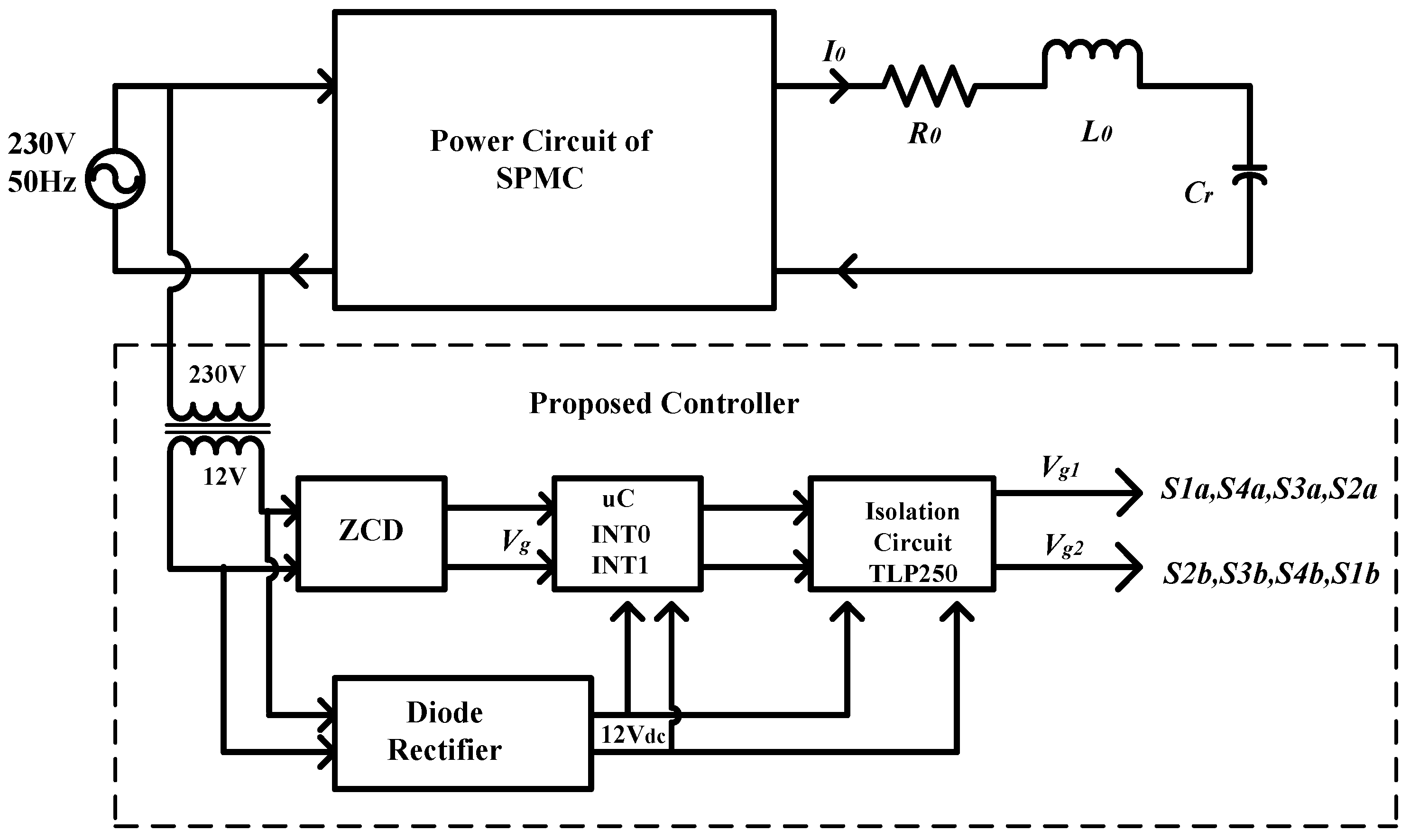
2.2. Proposed Switching Technique for SPMC in IH Applications
- Compared to a previous switching strategy, the modified switching strategy has a simple but unique generation capability of resonant frequency or switching frequency which is the basic need of SPMC as a resonant converter for IH application.
- Using this modified/proposed switching technique, SPMC can achieve a high frequency current very easily but using traditional/conventional switching technique, SPMC can generate only integral multiple of input supply frequency i.e., 50 Hz, 100 Hz, 150 Hz and so on. That is why previous switching topology cannot be applied in the field of IH applications.
- Also, the design of the controller for the proposed technique is quite simple because it needs to generate only two pulses as compared to previously developed switching techniques in which four pulses are needed for synthesization of frequency. Owing to this, the proposed technique reduces the design complexity of the controller.
- The proposed switching technique can be applied for both operation of SPMC i.e., as a frequency changer or as resonant converter.
2.2.1. Resonant Frequency
2.2.2. Characteristics Impedances
2.2.3. Load Quality Factor
2.2.4. Output Impedance of Equivalent Circuit (Figure 4a)
2.2.5. Fundamental Output Voltage
2.2.6. Ieq, That Is, Load Current Flowing Through Tank
2.2.7. The Output Power
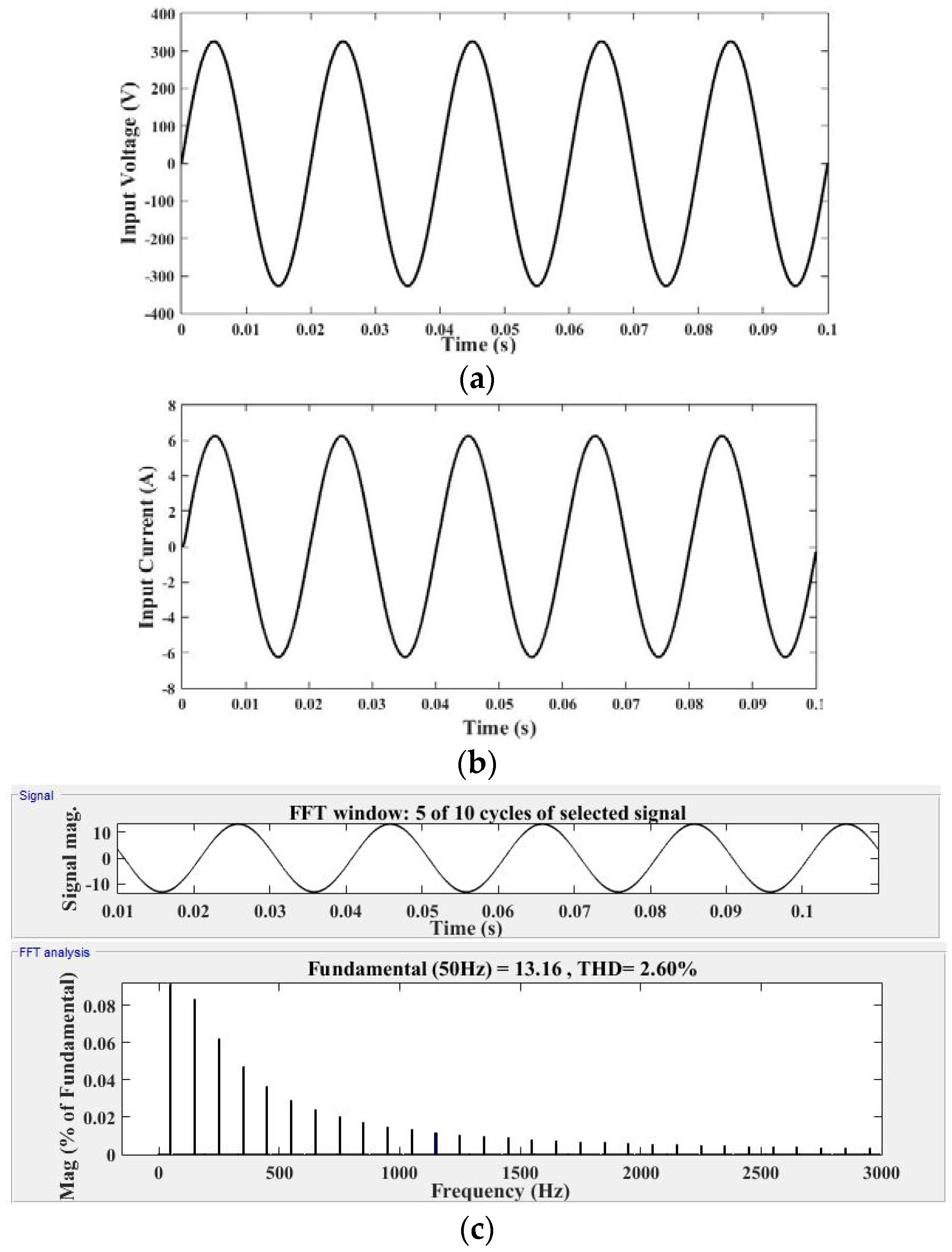
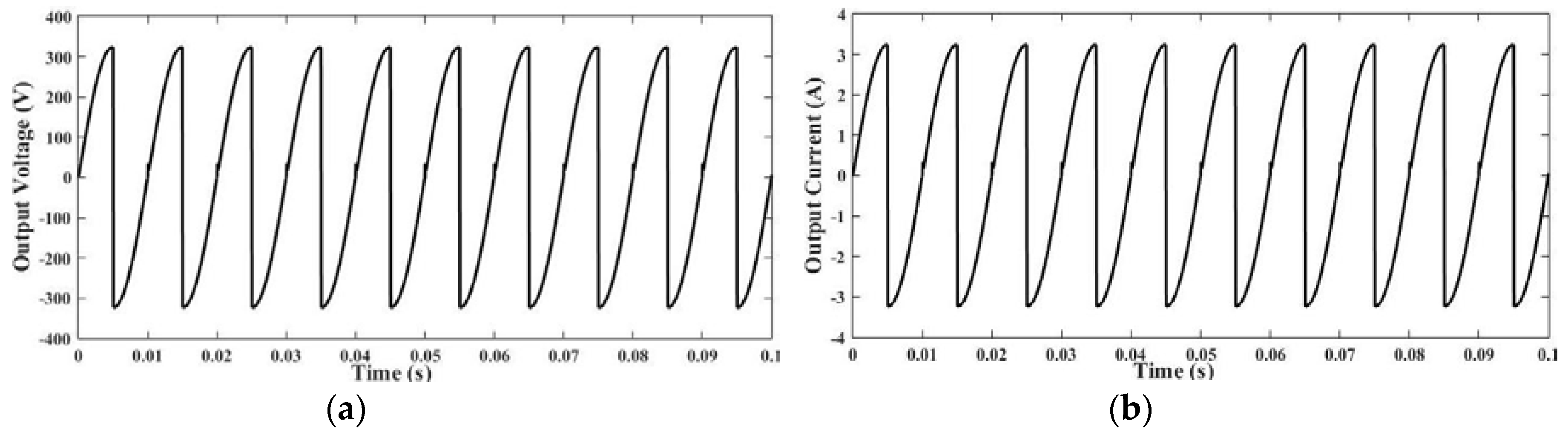
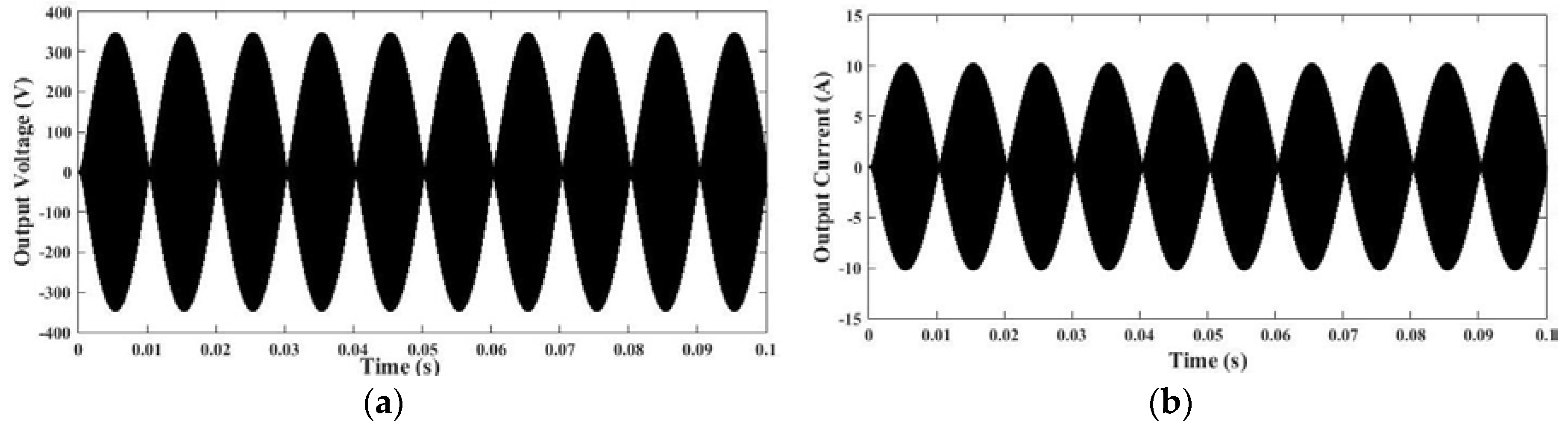
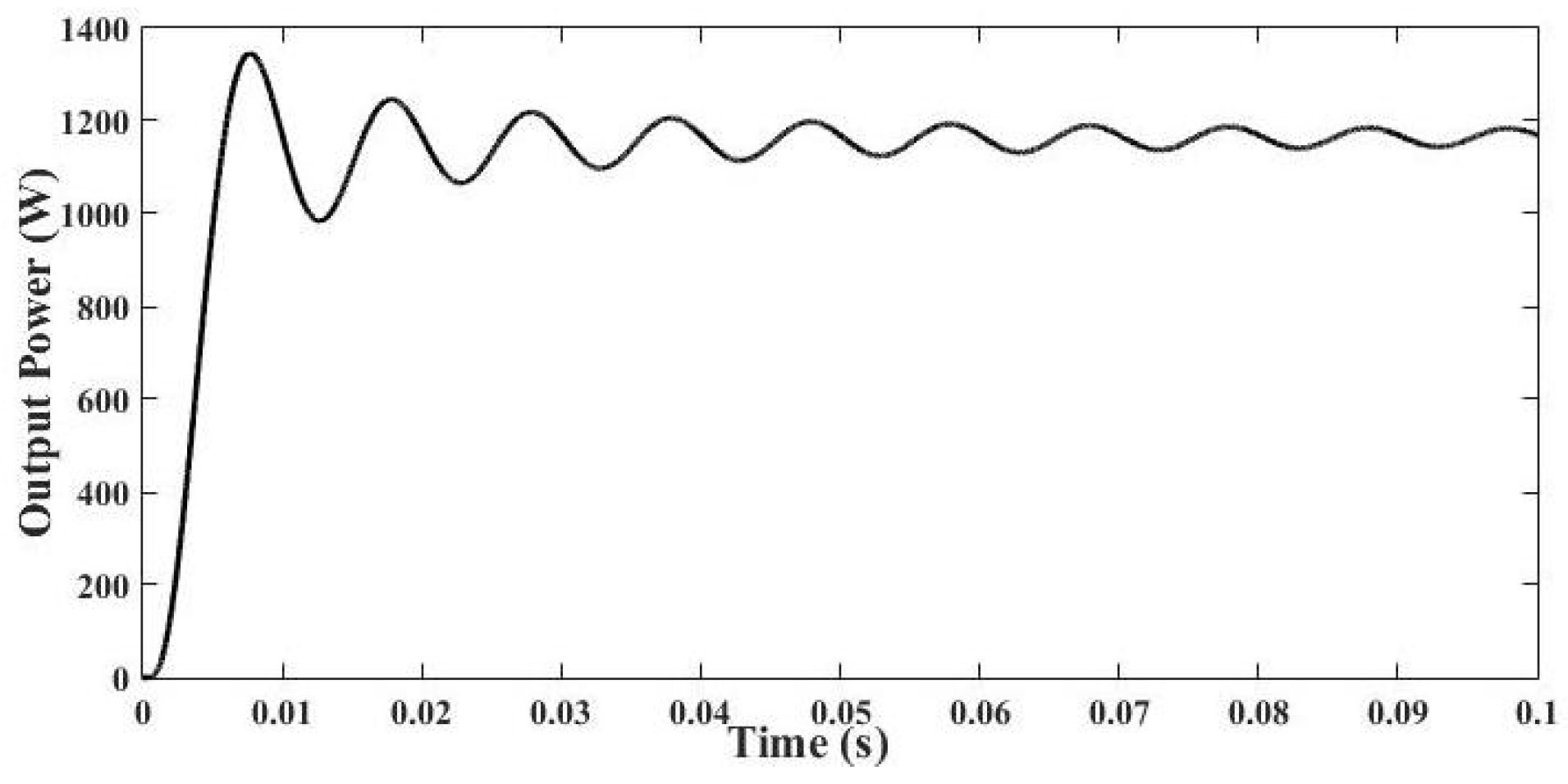
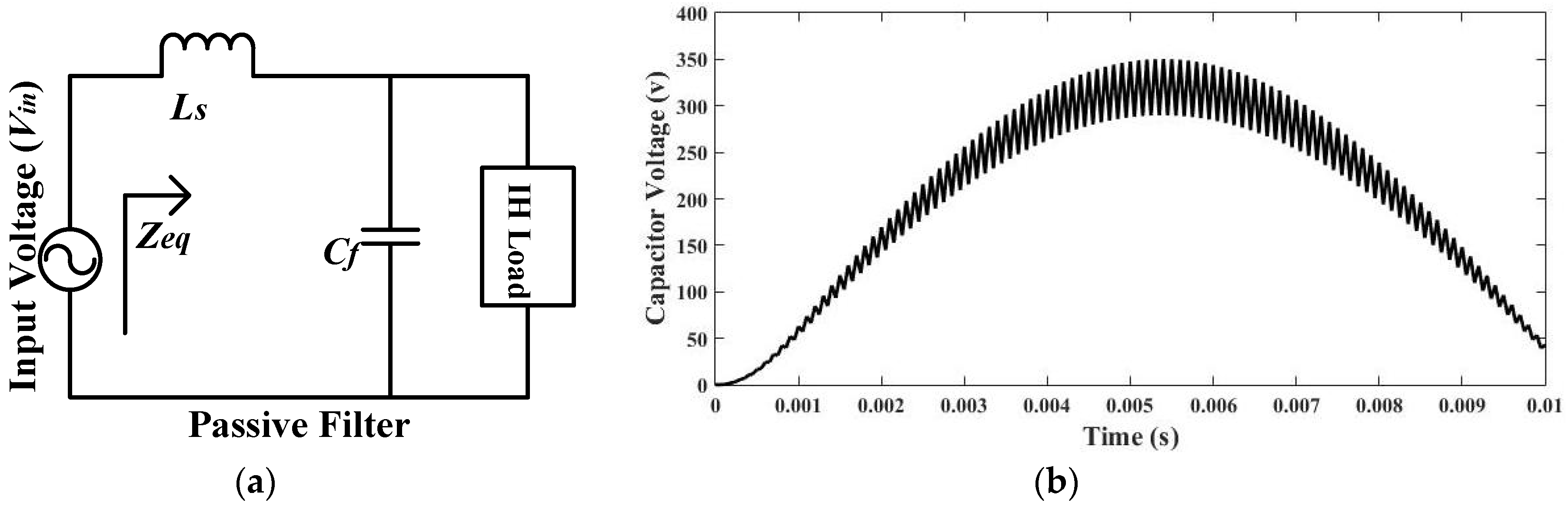
3. Simulation Results and Its Discussion
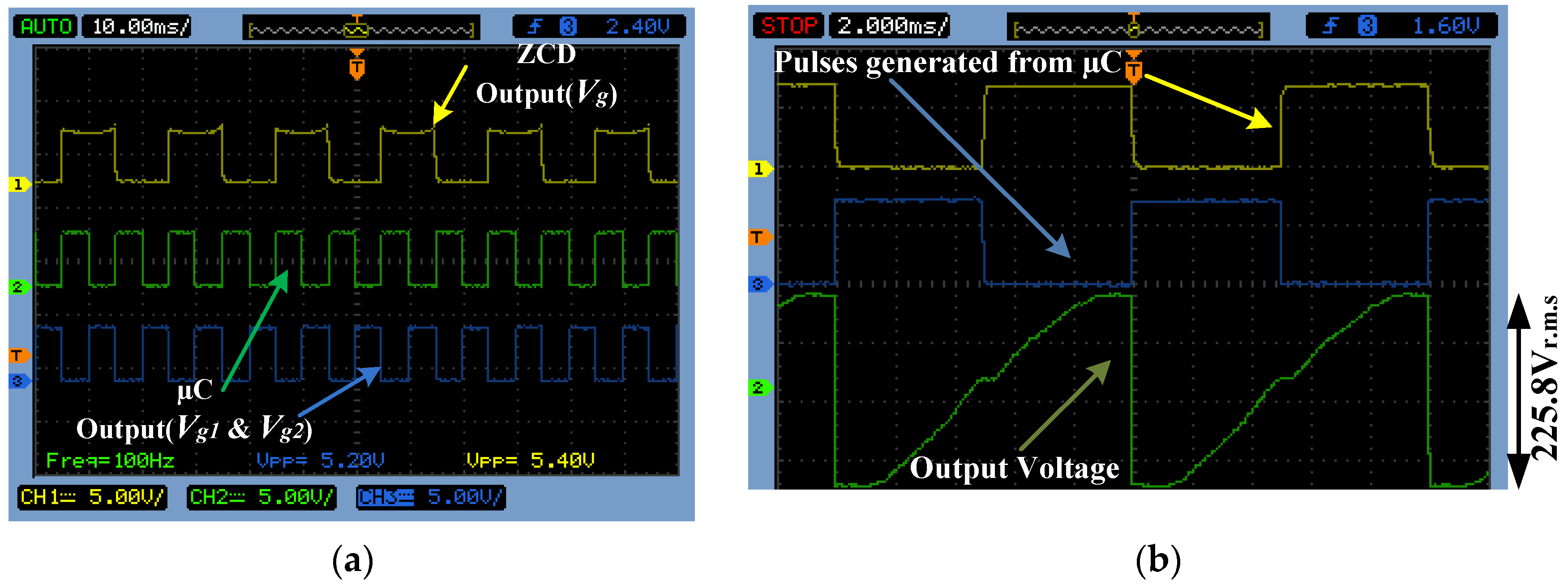
4. Prototype Implementation and Its Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Components | Specification/Ratings |
|---|---|
| GBT (IXRH40N120) diode (10A7) microcontroller op-amp diode (1N4007) centre taped transformer TLP250 IC Socket base heat sink resistance capacitor IH coil | (1200 V, 55 A) (700 V, 10 A) Atmega 2560 IC741 (1000 V, 1 A) (12–0–12) V, 2 A 25 kHz 8 pin DIP for IGBT 1 K, 12 K, 100 Ω, 44 K 470 μF Litz wire based |
References
- Acero, J.; Burdio, J.M.; Barragan, L.A.; Navarro, D.; Alonso, R.; Ramon, J.; Monterde, F.; Hernandez, P.; Llorente, S.; Garde, I. Domestic induction appliances. IEEE Ind. Appl. Mag. 2010, 16, 39–47. [Google Scholar] [CrossRef]
- Sarnago, H.; Lucia, O.; Mediano, A.; Burdio, J.M. Modulation scheme for improved operation of an RB-IGBT-based resonant inverter applied to domestic induction heating. IEEE Trans. Ind. Electron. 2013, 60, 2066–2073. [Google Scholar] [CrossRef]
- Sarnago, H.; Lucía, O.; Mediano, A.; Burdío, J.M. Class-D/DE dual-mode-operation resonant converter for improved-efficiency domestic induction heating system. IEEE Trans. Power Electron. 2013, 28, 1274–1285. [Google Scholar] [CrossRef]
- Lucia, O.; Burdio, J.M.; Millan, I.; Acero, J.; Puyal, D. Load-adaptive control algorithm of half-bridge series resonant inverter for domestic induction heating. IEEE Trans. Ind. Electron. 2009, 56, 3106–3116. [Google Scholar] [CrossRef]
- Lucía, O.; Maussion, P.; Dede, E.; Burdío, J.M. Induction heating technology and its applications: Past Developments, current Technology, and future challenges. IEEE Trans. Ind. Electron. 2011, 61, 2509–2520. [Google Scholar] [CrossRef]
- Mishima, T.; Takami, C.; Nakaoka, M. A new current phasor-controlled ZVS twin half-bridge high-frequency resonant inverter for induction heating. IEEE Trans. Ind. Electron. 2014, 61, 2531–2545. [Google Scholar] [CrossRef]
- Saha, B.; Kim, R.Y. High Power Density Series Resonant Inverter Using an Auxiliary Switched Capacitor Cell for Induction Heating Applications. IEEE Trans. Power Electron. 2014, 29, 1909–1918. [Google Scholar] [CrossRef]
- Lucía, O.; Burdío, J.M.; Millán, I.; Acero, J.; Barragán, L.A. Efficiency-oriented design of ZVS half-bridge series resonant inverter with variable frequency duty cycle control. IEEE Trans. Power Electron. 2010, 25, 1671–1674. [Google Scholar] [CrossRef]
- Sarnago, H.; Lucía, O.; Pérez-Tarragona, M.; Burdío, J.M. Dual-Output Boost Resonant Full-Bridge Topology and its Modulation Strategies for High-Performance Induction Heating Applications. IEEE Trans. Ind. Electron. 2016, 63, 3554–3561. [Google Scholar] [CrossRef]
- Singh, B.; Pandey, R. Improved Power Quality Buck-Boost Converter fed LLC Resonant Converter for Induction Heater. In Proceedings of the 2016 IEEE 6th International Conference on Power Systems (ICPS), New Delhi, India, 4–6 March 2016; pp. 1–6. [Google Scholar]
- Pham, H.; Fujita, H.; Ozaki, K.; Uchida, N. Dynamic analysis and control of a zone-control induction heating system. In Proceedings of the 2011 IEEE conference of Energy Conversion Congress and Exposition(ECCE), Phoenix, AZ, USA, 17–22 September 2011; pp. 4093–4100. [Google Scholar]
- Fujita, H.; Akagi, H. Pulse-Density-Modulated Power Control of a 4 kW, 450 kHz Voltage-Source Inverter for Induction Melting Applications. IEEE Trans. Ind. Appl. 1996, 32, 279–286. [Google Scholar] [CrossRef]
- Grajales, L.; Sabatk, J.A.; Wang, K.R.; Tabisz, W.A.; Lee, F.C. Design of a 10 kW, 500 kHz Phase-Shift Controlled Series-Resonant Inverter for Induction Heating. In Proceedings of the 1993 IEEE Industry Applications Conference Twenty-Eighth IAS Annual Meeting, Toronto, ON, Canada, 2–8 October 1993; pp. 843–849. [Google Scholar]
- Yilmaz, I.; Ermiş, M.; Çadirci, I. Medium-frequency induction melting furnace as a load on the power system. IEEE Trans. Ind. Appl. 2012, 48, 1203–1214. [Google Scholar] [CrossRef]
- Millan, I.; Burdio, J.M.; Acero, J.; Lucia, O.; Liorente, S. Series resonant inverter with selective harmonic operation applied to all-metal domestic induction heating. IET Power Electron. 2011, 4, 587–592. [Google Scholar] [CrossRef]
- Koertzen, H.W.; Van Wyk, J.D.; Ferreira, J.A. Design of the half-bridge series resonant converters for induction cooking. In Proceedings of the Power Electronics Specialist Conference (PESC), Atlanta, GA, USA, 18–22 June 1995; pp. 729–735. [Google Scholar]
- Dawson, F.P.; Jain, P. A Comparison of Load Commutated Inverter Systems for Induction Heating and Melting Applications. IEEE Trans. Power Electron. 1991, 6, 430–441. [Google Scholar] [CrossRef]
- Koertzen, H.W.; Ferreira, J.A.; Van Wyk, J.D. A comparative study of single switch induction heating converters using novel component effectivity concepts. In Proceedings of the 23rd Annual IEEE Power Electronics Specialists Conference (PESC), Toledo, Spain, 29 June–3 July 1992; pp. 298–305. [Google Scholar]
- Jimenez, O.; Lucia, O.; Urriza, I.; Barragan, L.A.; Mattavelli, P.; Boroyevich, D. An FPGA-based gain-scheduled controller for resonant converters applied to induction cooktops. IEEE Trans. Power Electron. 2014, 29, 2143–2152. [Google Scholar] [CrossRef]
- Nagarajan, B.; Sathi, R.R. Phase locked loop based pulse density modulation scheme for the power control of induction heating applications. J. Power Electron. 2015, 15, 65–77. [Google Scholar] [CrossRef]
- Idris, Z.; Hamzah, M.K.; Saidon, M.F. Implementation of single-phase matrix converter as a direct AC–AC converter with commutation strategies. In Proceedings of the 2006 37th IEEE Power Electronics Specialists Conference, Jeju, South Korea, 18–22 June 2006; pp. 1–7. [Google Scholar]
- Li, H.L.; Hu, A.P.; Covic, G.A. A direct AC–AC converter for inductive power-transfer systems. IEEE Trans. Power Electron. 2012, 27, 661–668. [Google Scholar] [CrossRef]
- Arevalo, S.L.; Zanchetta, P.; Wheeler, P.W.; Trentin, A.; Empringham, L. Control and implementation of a matrix-converter-based AC ground power-supply unit for aircraft servicing. IEEE Trans. Ind. Electron. 2010, 57, 2076–2084. [Google Scholar] [CrossRef]
- Kolar, J.W.; Schafmeister, F.; Round, S.D.; Ertl, H. Novel three-Phase AC–AC sparse matrix converters. IEEE Trans. Power Electron. 2007, 22, 1649–1661. [Google Scholar] [CrossRef]
- Trentin, A.; Zanchetta, P.; Clare, J.; Wheeler, P. Automated optimal design of input filters for direct ac/ac matrix converters. IEEE Trans. Ind. Electron. 2012, 59, 2811–2823. [Google Scholar] [CrossRef]
- Yamamoto, E.; Hara, H.; Uchino, T.; Kawaji, M.; Kume, T.J.; Kang, J.K.; Krug, H.P. Development of MCs and its applications in industry. IEEE Ind. Electron. Mag. 2011, 5, 4–12. [Google Scholar] [CrossRef]
- Hosseini, S.H.; Sharifian, M.B.; Sabahi, M.; Yazdanpanah, A.; Gharehpetian, G.H. Bi-directional power electronic transformer for induction heating systems. In Proceedings of the 2008 Canadian Conference on Electrical and Computer Engineering, Niagara Falls, ON, Canada, 4–7 May 2008; pp. 347–350. [Google Scholar]
- Kim, Y.; Okuma, S.; Iwata, K. Characteristics and Starting Method of a Cycloconverter With a Tank Circuit for Induction Heating. IEEE Trans. Power Electron. 1988, 3, 236–244. [Google Scholar] [CrossRef]
- Sugimura, H.; Mun, S.P.; Kwon, S.K.; Mishima, T.; Nakaoka, M. Direct AC–AC resonant converter using one-chip reverse blocking IGBT-Based bidirectional switches for HF induction heaters. In Proceedings of the 2008 IEEE International Symposium on Industrial Electronics, Cambridge, UK, 30 June–2 July 2008; pp. 406–412. [Google Scholar]
- Salehifar, M.; Moreno-eguilaz, M.; Sala, V.; Romeral, L. A Novel AC–AC Converter Based SiC for Domestic Induction Cooking Applications. In Proceedings of the 2013 28th Twenty-Eighth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 17–21 March 2013; pp. 3216–3223. [Google Scholar]
- Nguyen-Quang, N.; Stone, D.A.; Bingham, C.M.; Foster, M.P. Single phase matrix converter for radio frequency induction heating. In Proceedings of the International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Taormina, Italy, 23–26 May 2006; pp. 614–618. [Google Scholar]
- Mohite, S.B.; Gujarathi, P.K. A Design and Implementation of a Novel Multimode Single Phase Matrix Converter. In Proceedings of the 2010 IEEE Power Electronics Electrical Drives Automation and Motion SPEEDAM, Pisa, Italy, 14–16 June 2010; pp. 1227–1230. [Google Scholar]
- Nguyen-Quang, N.; Stone, D.A.; Bingham, C.M.; Foster, M.P. A three-phase to single-phase matrix converter for high-frequency induction heating. In Proceedings of the 2009 13th European Conference on Power Electronics and Applications, Barcelona, Spain, 8–10 September 2009; pp. 1–10. [Google Scholar]
- Nguyen-Quang, N.; Stone, D.A.; Bingham, C.M.; Foster, M.P. Comparison of single-phase matrix converter and H-bridge converter for radio frequency induction heating. In Proceedings of the 2007 European Conference on Power Electronics and Applications, Aalborg, Denmark, 2–5 September 2007; pp. 1–7. [Google Scholar]
- Jose, P.S.; Deepika, N.C.; Nisha, S.N. Applications of single phase matrix converter. In Proceedings of the 2011 International Conference on Emerging Trends in Electrical and Computer Technology, Nagercoil, India, 23–24 March 2011; pp. 386–391. [Google Scholar]
- Kumar, A.; Sadhu, M.; Das, N.; Sadhu, P.K.; Roy, D.; Ankur, G. A Survey on High-Frequency Inverter and Their Power Control Techniques for Induction Heating Applications. J. Power Technol. 2011, 97, 201–213. [Google Scholar]
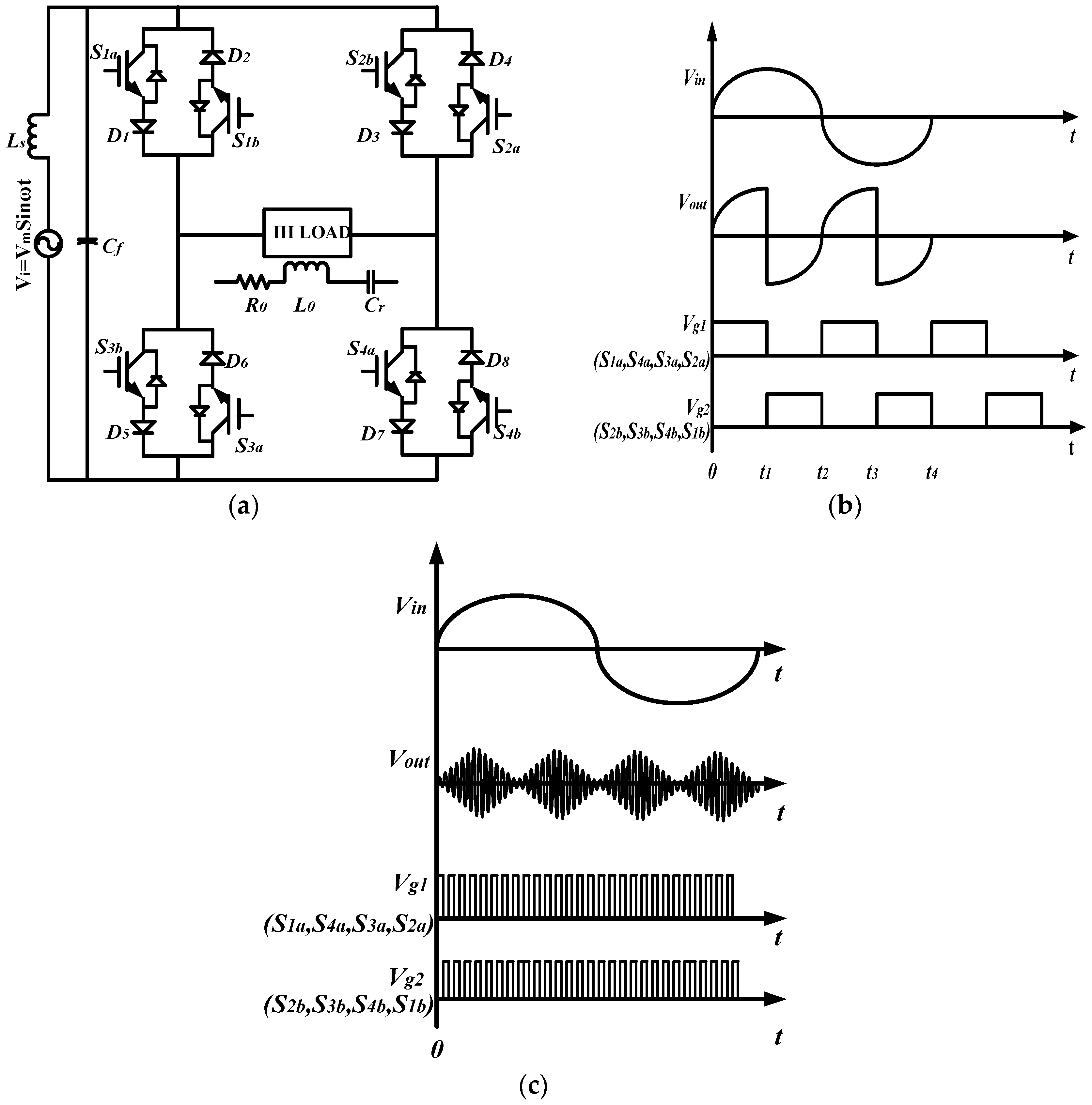
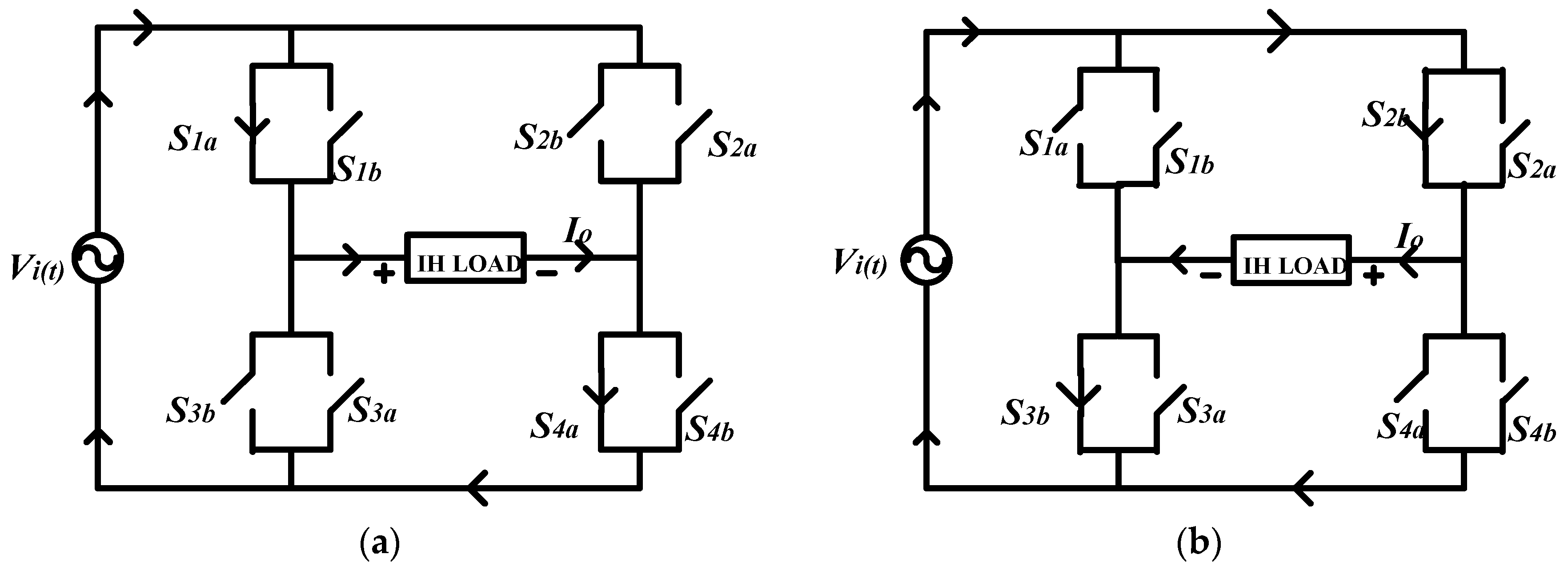
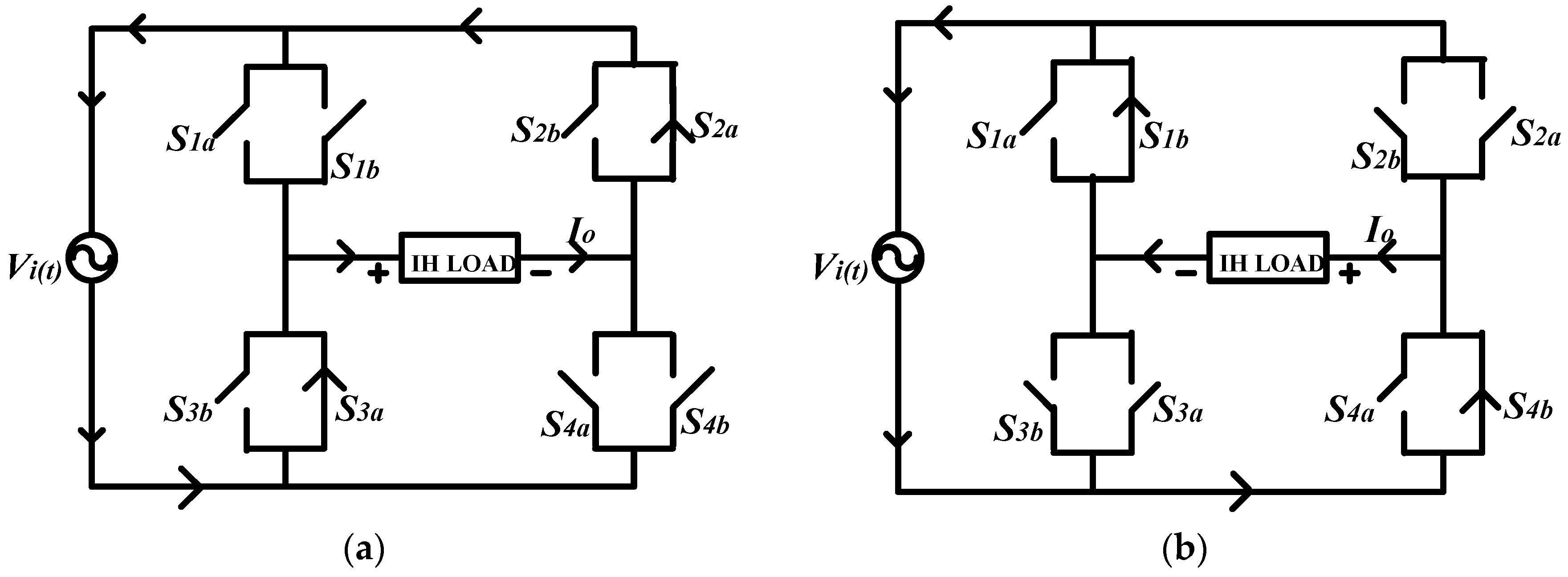



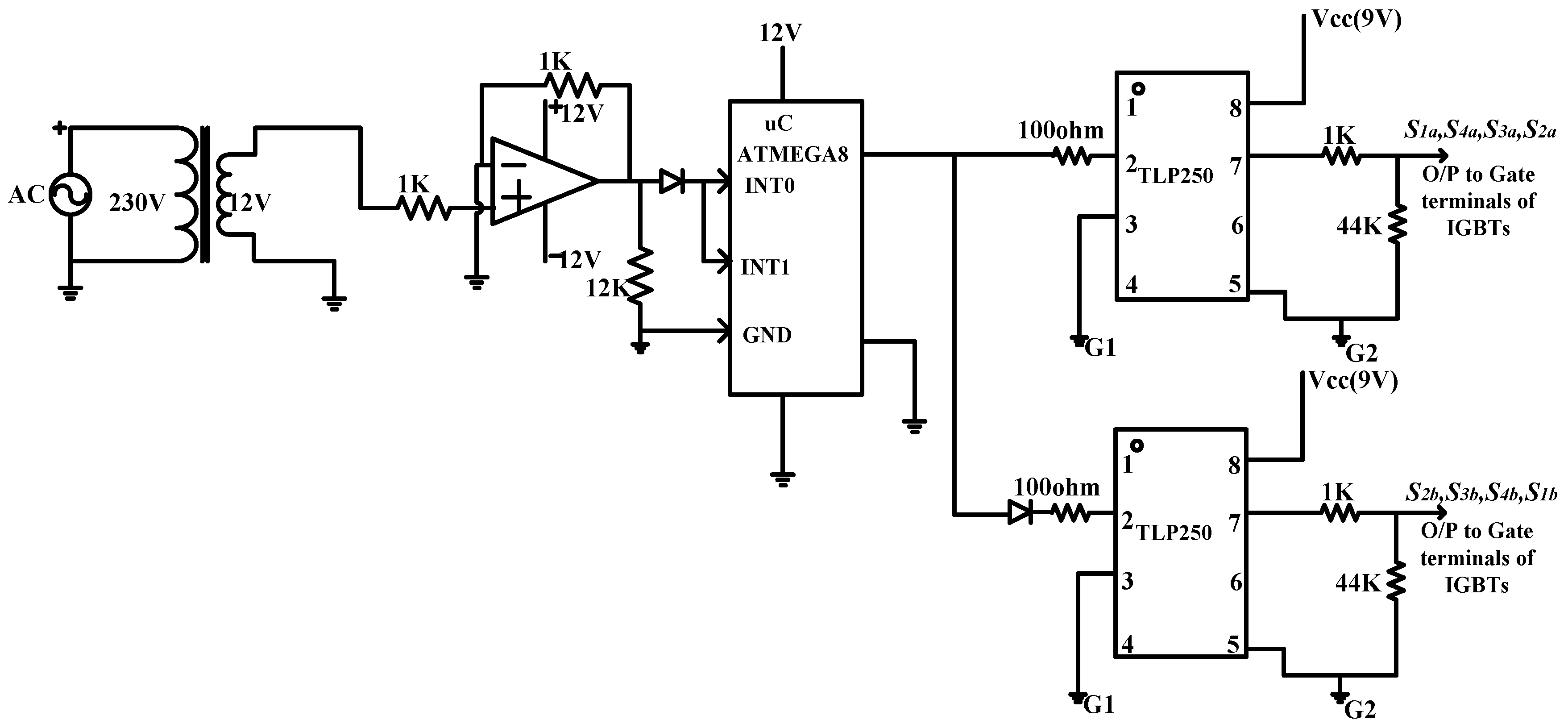
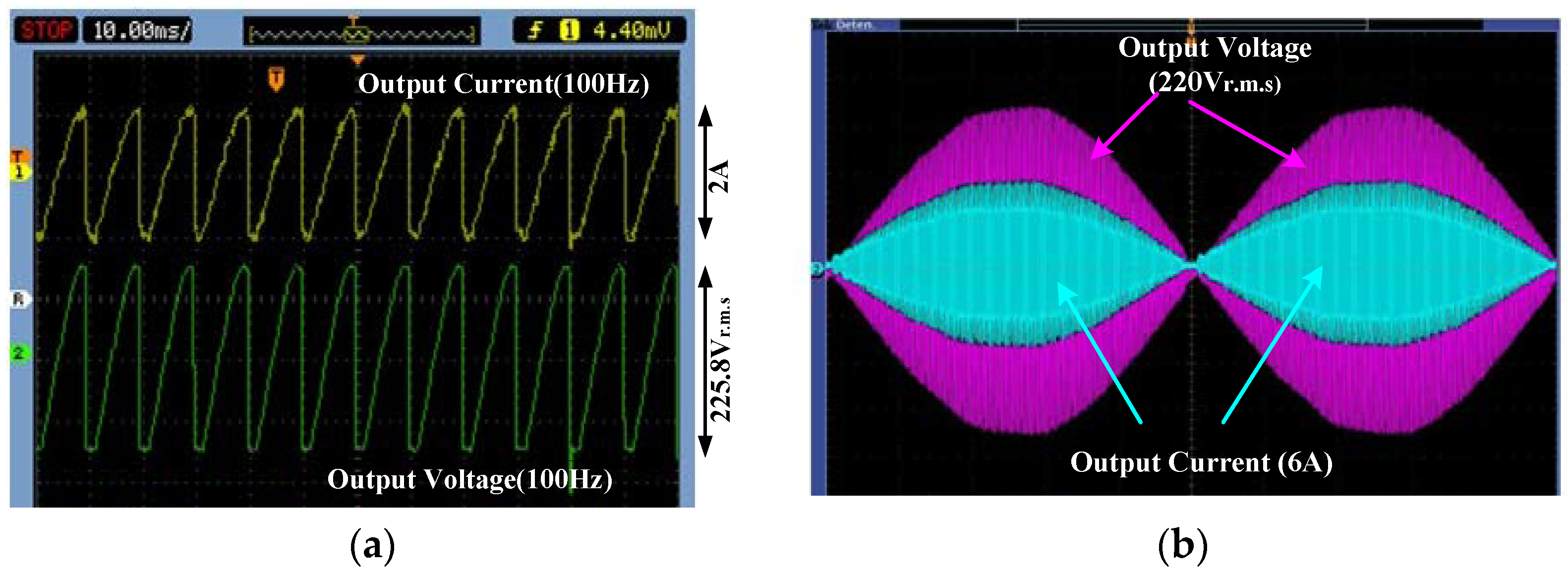
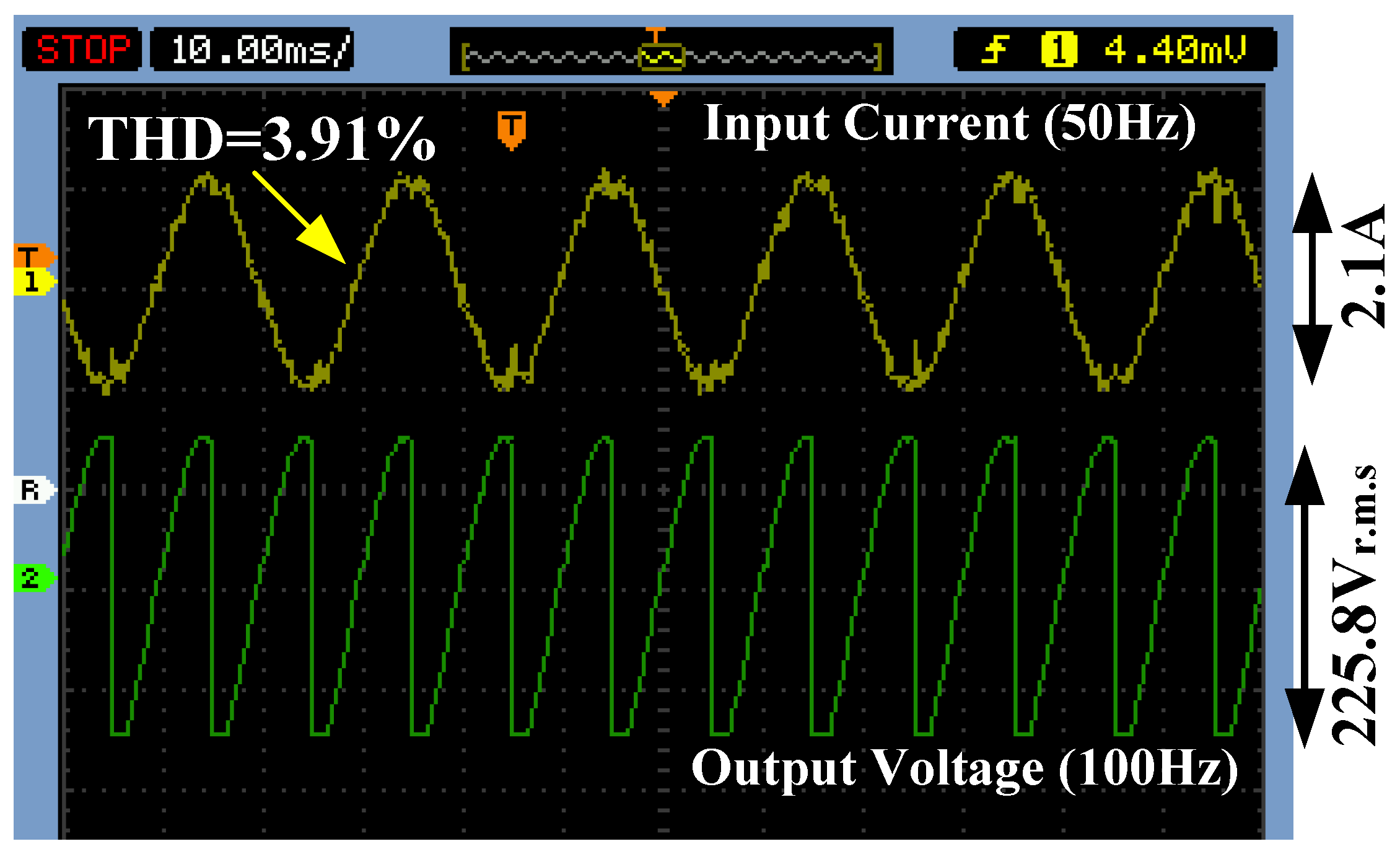
| Input Voltage (Vin) | Mode | Switches Status | Time Interval | Output Voltage (Vout) |
|---|---|---|---|---|
| Vin > 0 | Mode 1 | (S1a/S4a) ON (S2b/S3b) OFF | 0 to t1 | Vout > 0 |
| Mode 2 | (S1a/S4a) OFF (S2b/S3b) ON | t1 to t2 | Vout < 0 | |
| Vin < 0 | Mode 3 | (S3a/S2a) ON (S4b/S1b) OFF | t2 to t3 | Vout > 0 |
| Mode 4 | (S3a/S2a) OFF (S4b/S1b) ON | t3 to t4 | Vout < 0 |
| Symbol | Parameters | Value |
|---|---|---|
| Vin | Input Voltage | 230 Vr.m.s |
| Ls | Filter inductance | 20 mH |
| Cf | Filter Capacitance | 3 uF |
| f | Fundamental Frequency | 50 Hz |
| Cr | Resonant Capacitor | 0.8 uF |
| L0 | Coil Inductance | 52.7 uH |
| R0 | Coil Equivalent Resistance | 5 Ω |
| P0 | Output Power for heating | 1100 W |
| fs | Resonance Frequency (Switching Frequency) | 25 kHz |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, A.; Kumar Sadhu, P.; Kumar Mohanta, D.; Bharata Reddy, M.J. An Effective Switching Algorithm for Single Phase Matrix Converter in Induction Heating Applications. Electronics 2018, 7, 149. https://doi.org/10.3390/electronics7080149
Kumar A, Kumar Sadhu P, Kumar Mohanta D, Bharata Reddy MJ. An Effective Switching Algorithm for Single Phase Matrix Converter in Induction Heating Applications. Electronics. 2018; 7(8):149. https://doi.org/10.3390/electronics7080149
Chicago/Turabian StyleKumar, Anand, Pradip Kumar Sadhu, Dusmanta Kumar Mohanta, and Maddikara Jaya Bharata Reddy. 2018. "An Effective Switching Algorithm for Single Phase Matrix Converter in Induction Heating Applications" Electronics 7, no. 8: 149. https://doi.org/10.3390/electronics7080149
APA StyleKumar, A., Kumar Sadhu, P., Kumar Mohanta, D., & Bharata Reddy, M. J. (2018). An Effective Switching Algorithm for Single Phase Matrix Converter in Induction Heating Applications. Electronics, 7(8), 149. https://doi.org/10.3390/electronics7080149





