FPGA Implementation of a Functional Neuro-Fuzzy Network for Nonlinear System Control
Abstract
:1. Introduction
2. Related Work
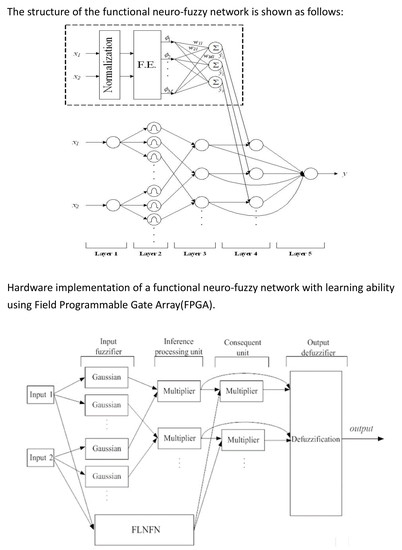
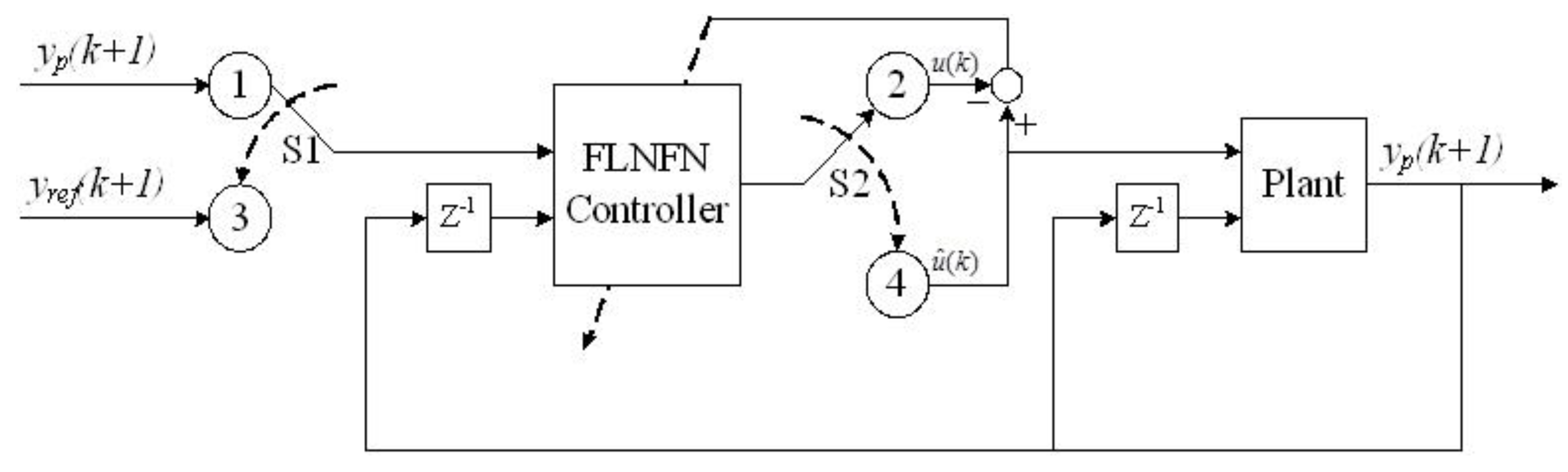
3. Architecture of Functional Neuro-Fuzzy Networks (FNFN)
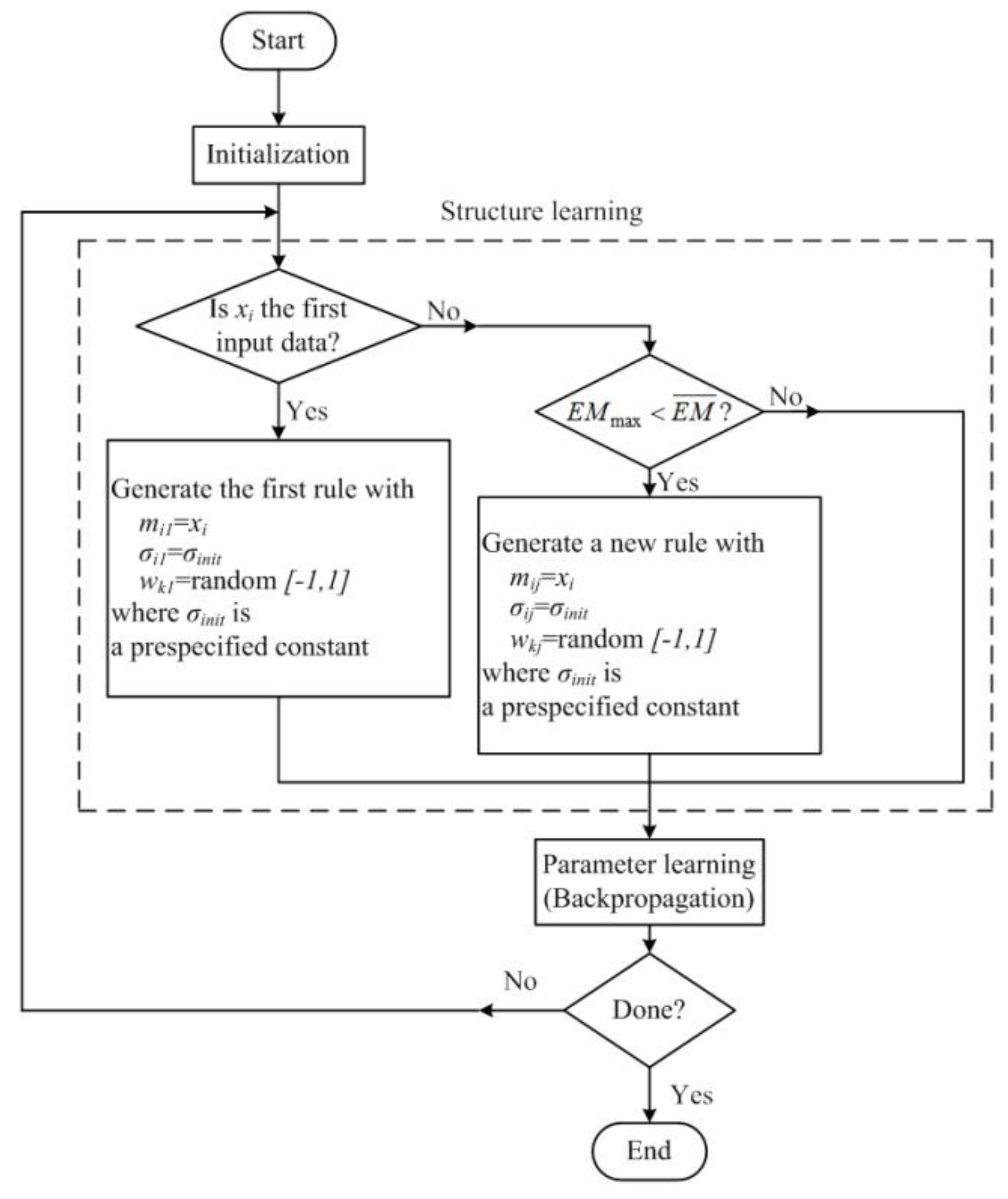
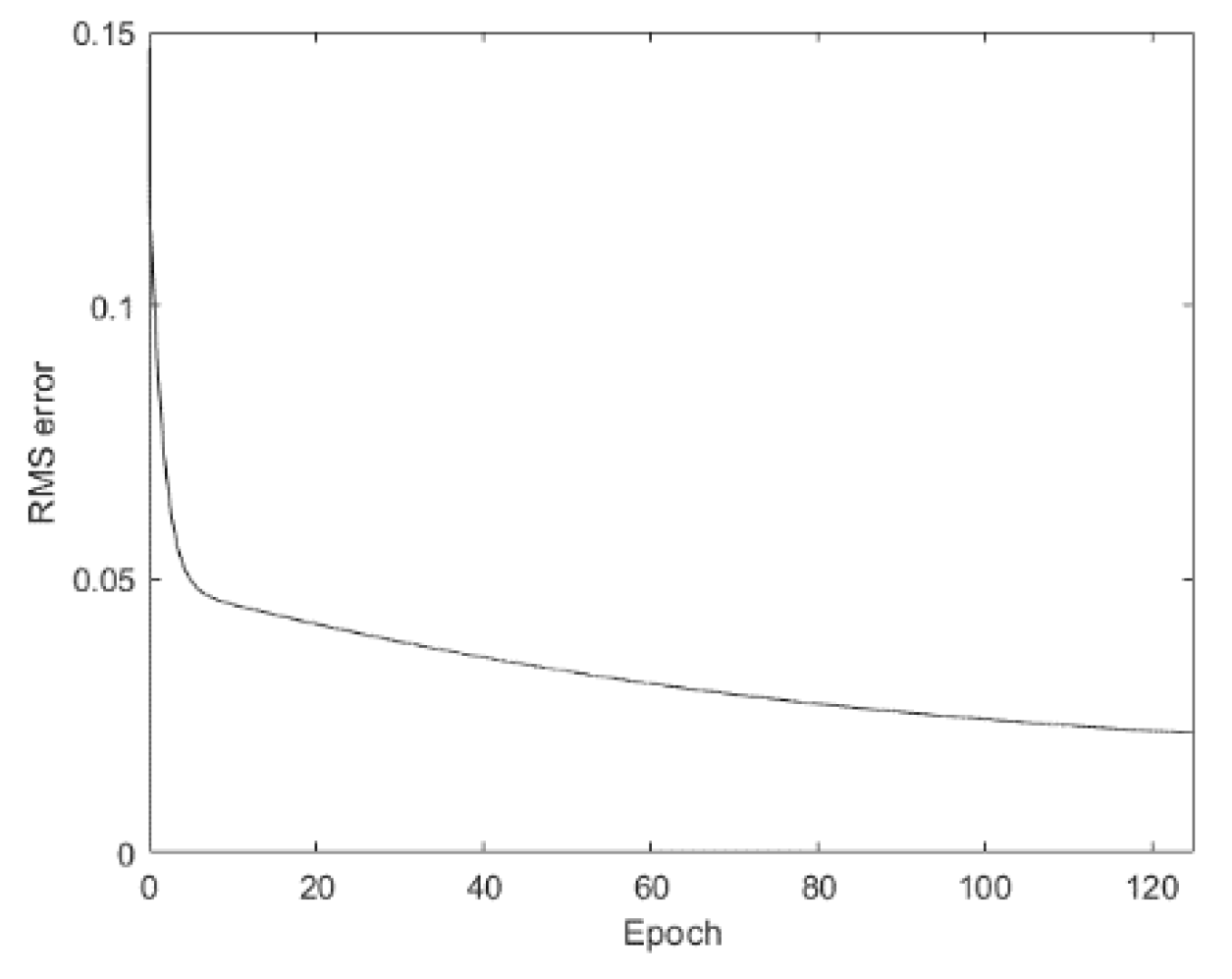
4. Proposed Learning Algorithm
4.1. Structure Learning
4.2. Parameter Learning
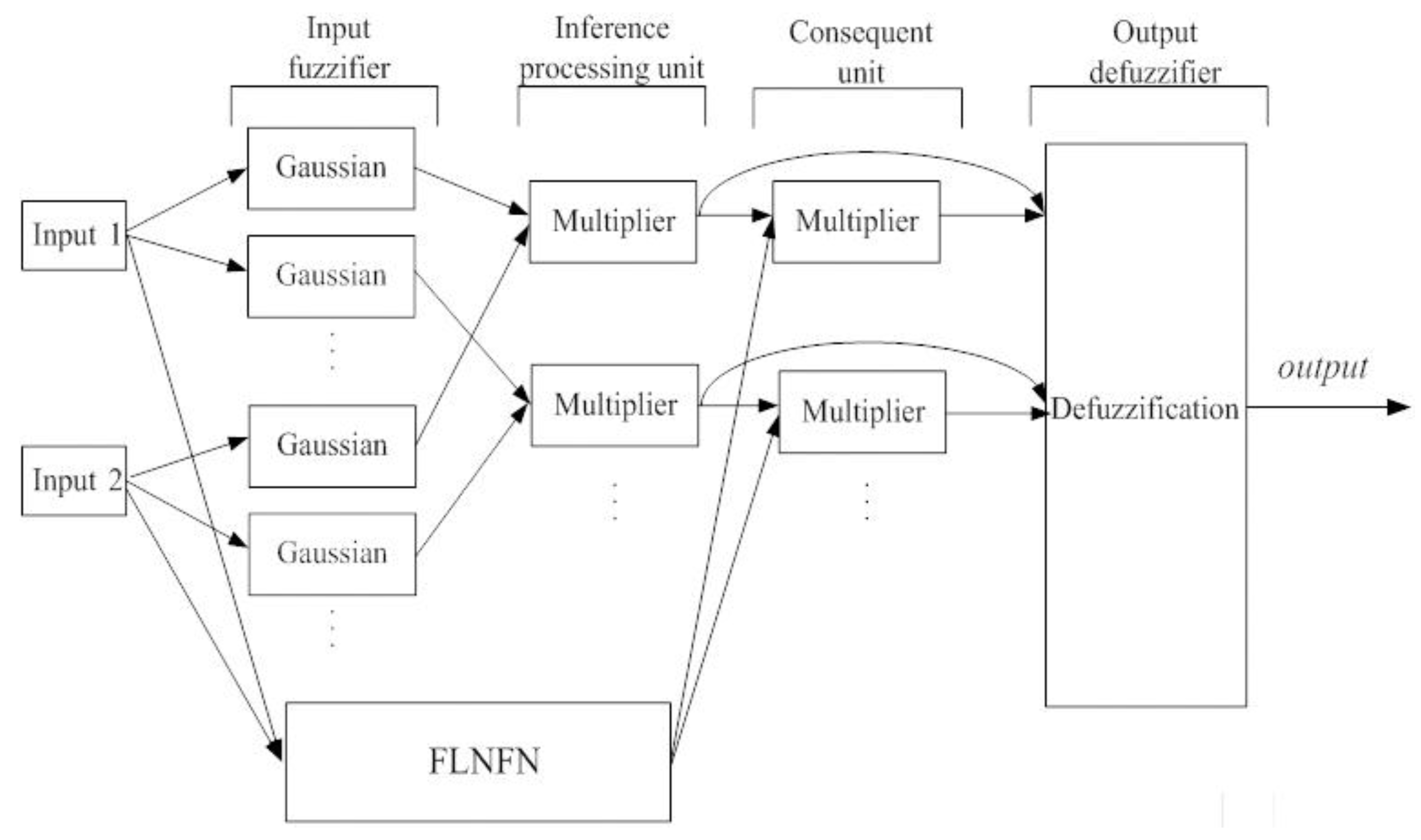
5. FPGA Implementation of the FNFN Controller
5.1. The Represented Data Format
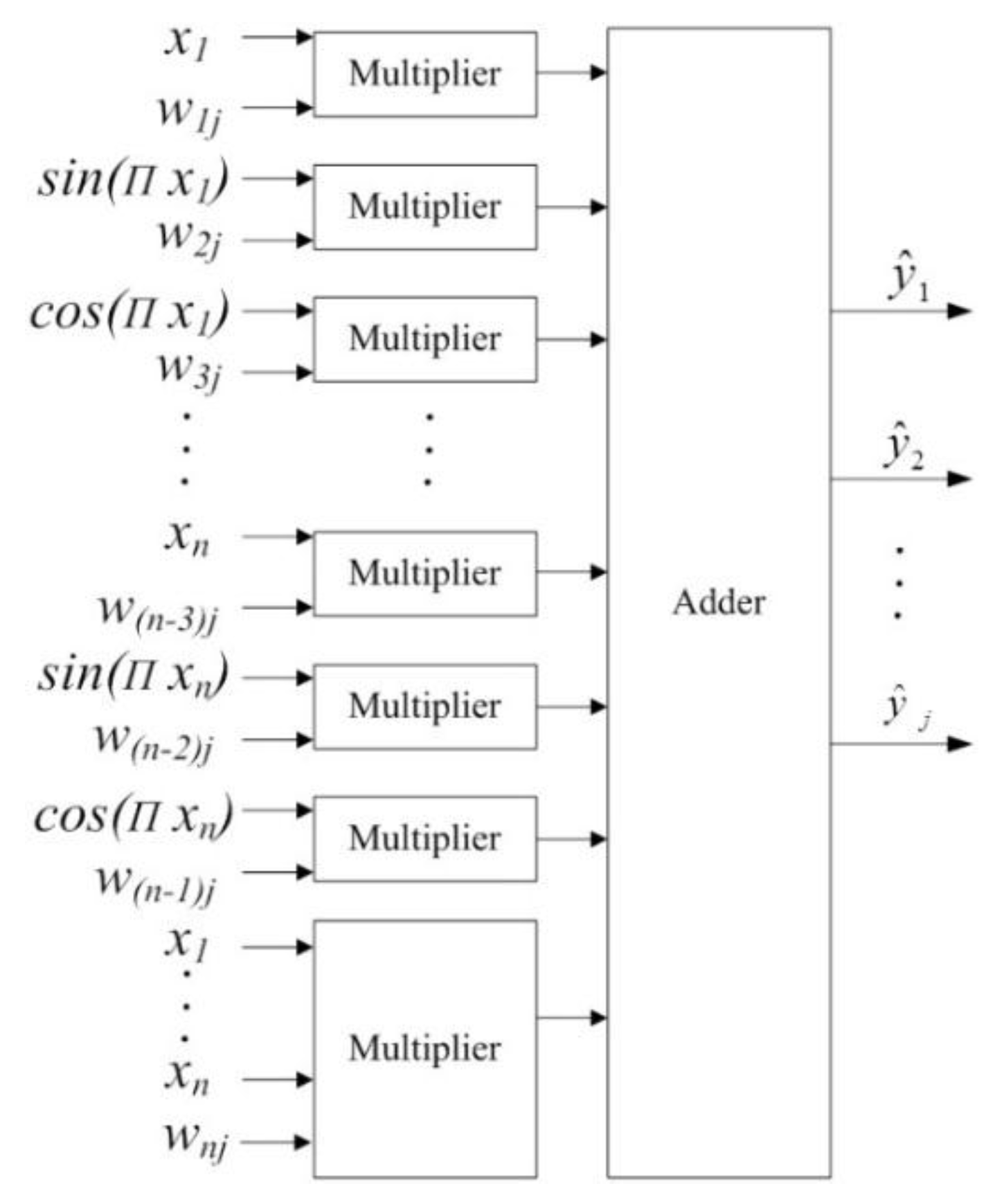
5.2. Design and Implementation of Function Unit
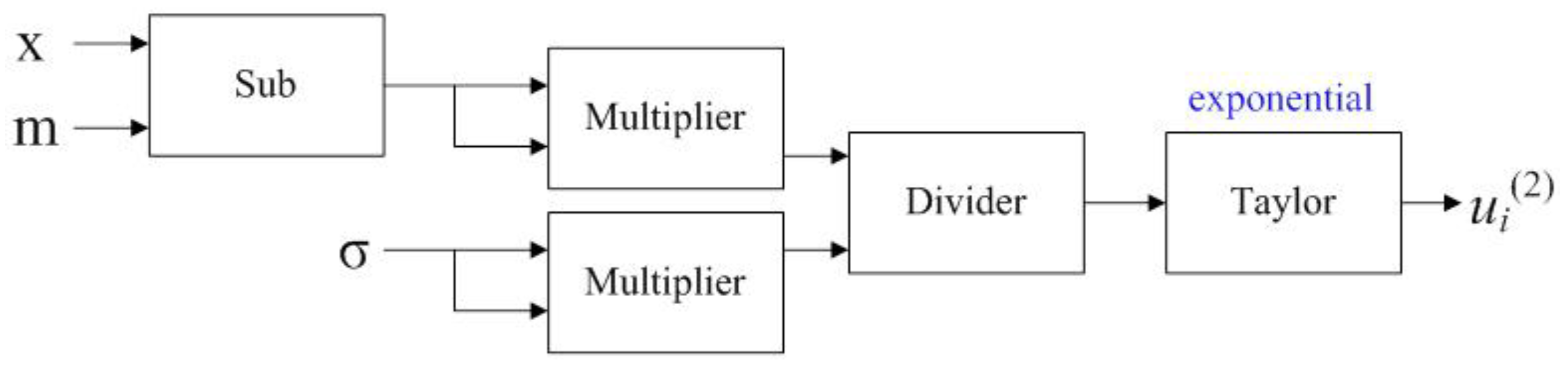
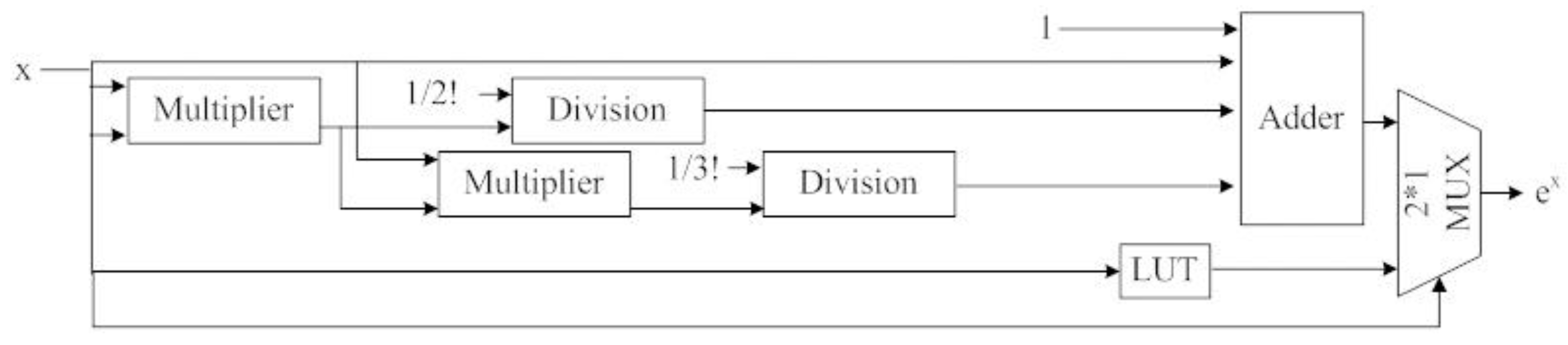
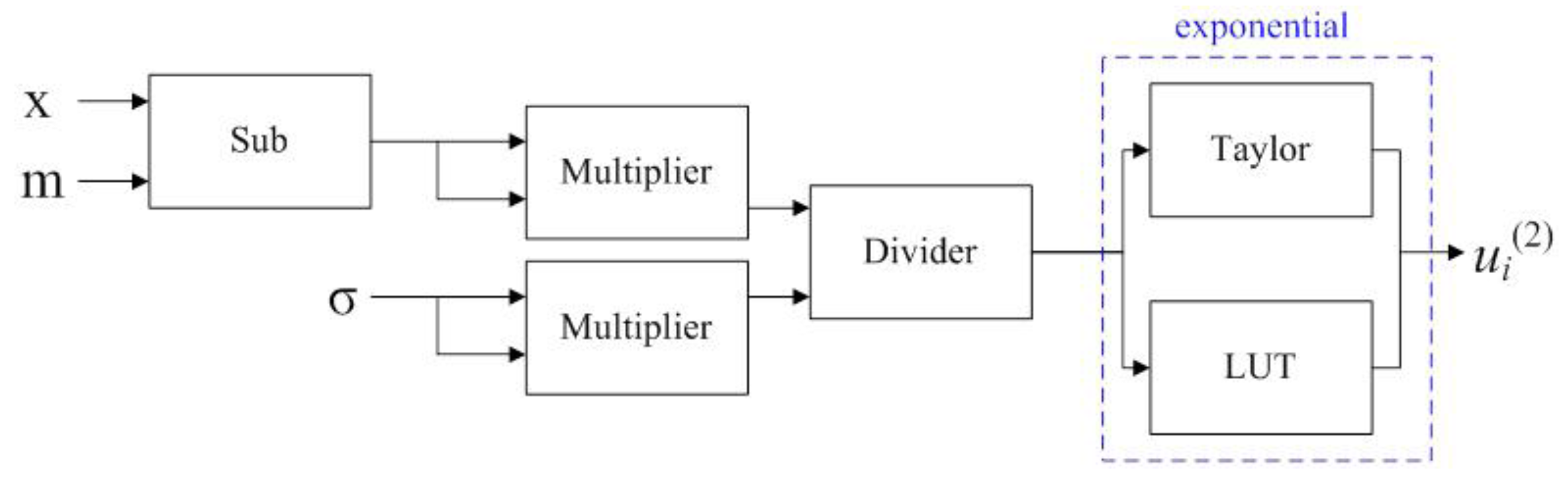
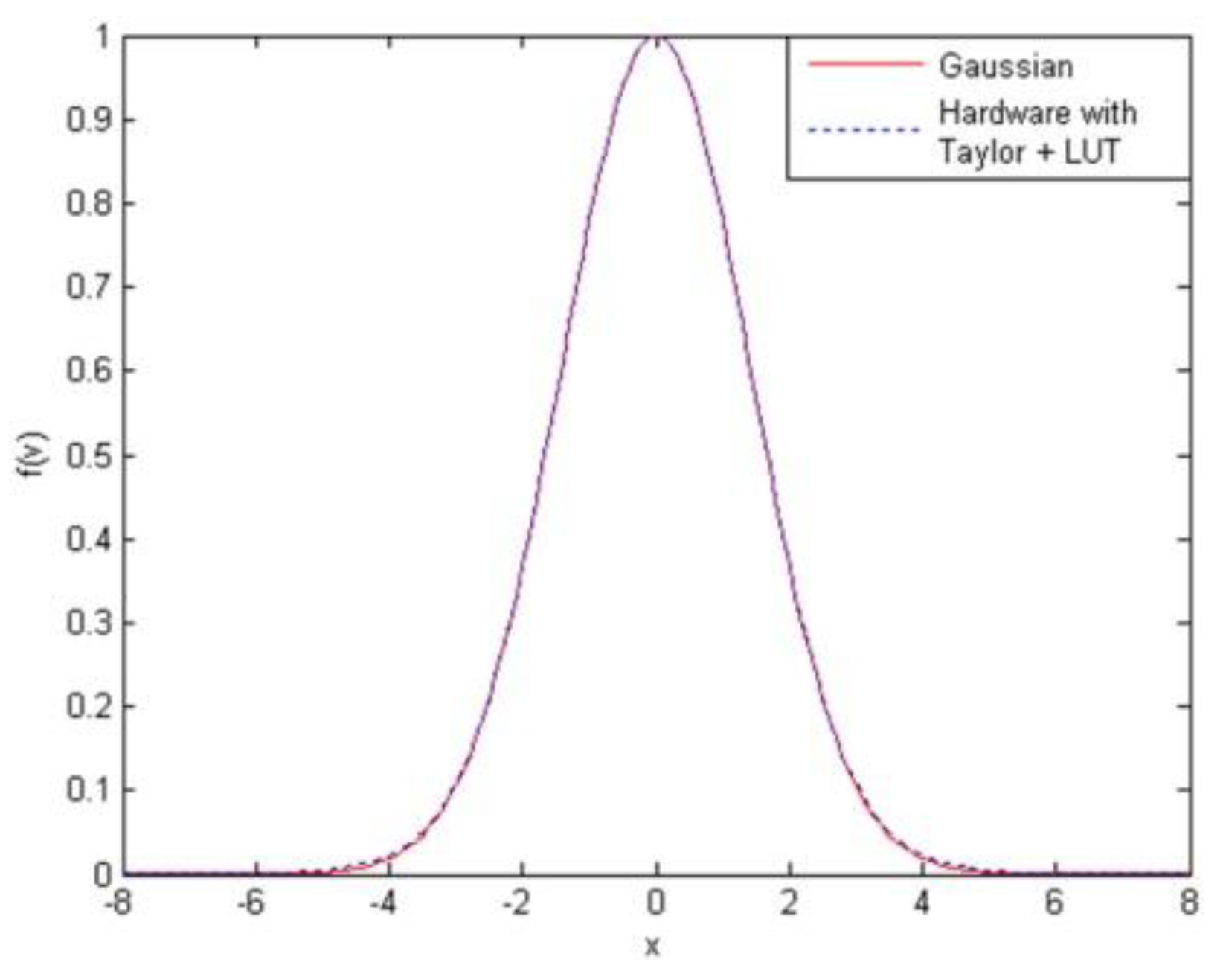
5.2.1. Gaussian Function Implementation
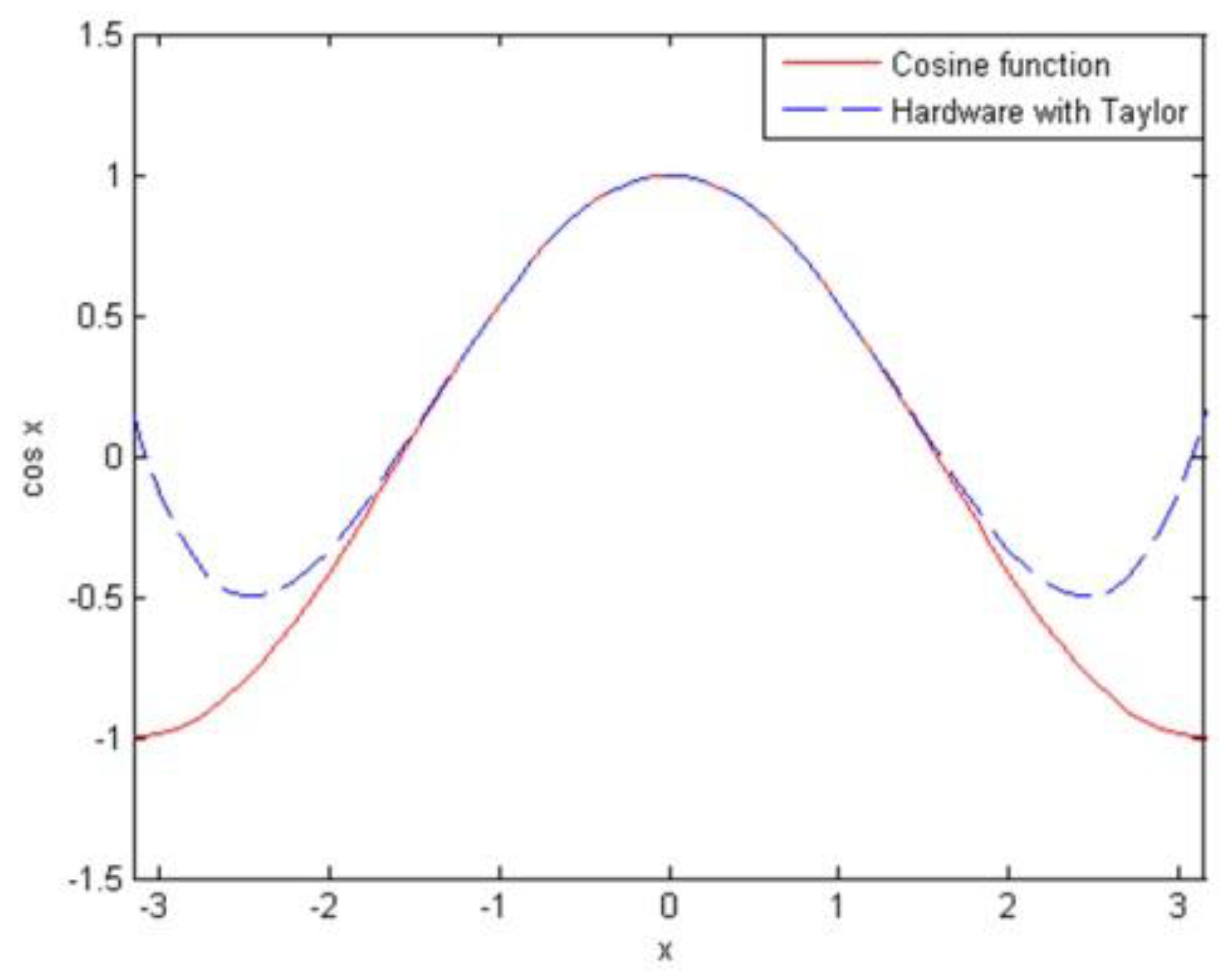
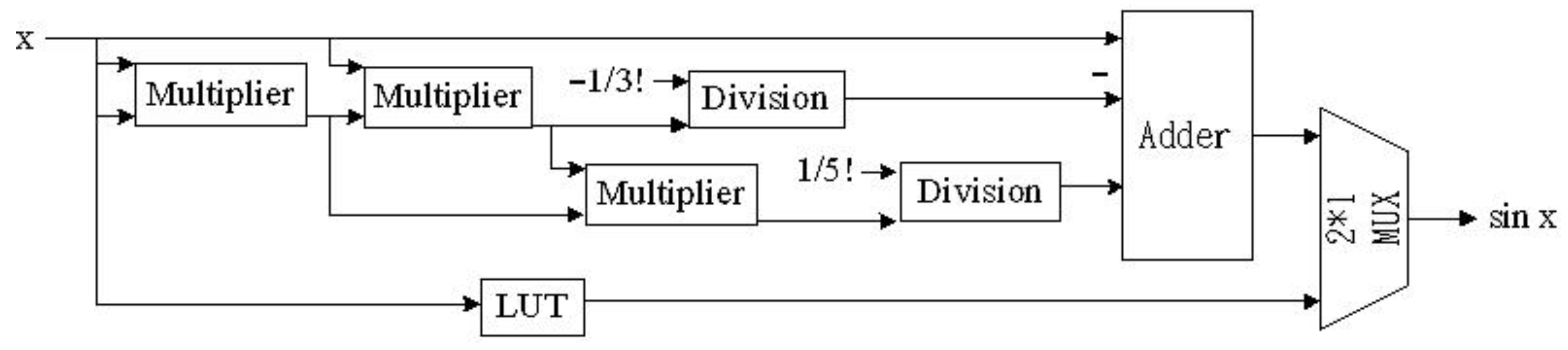
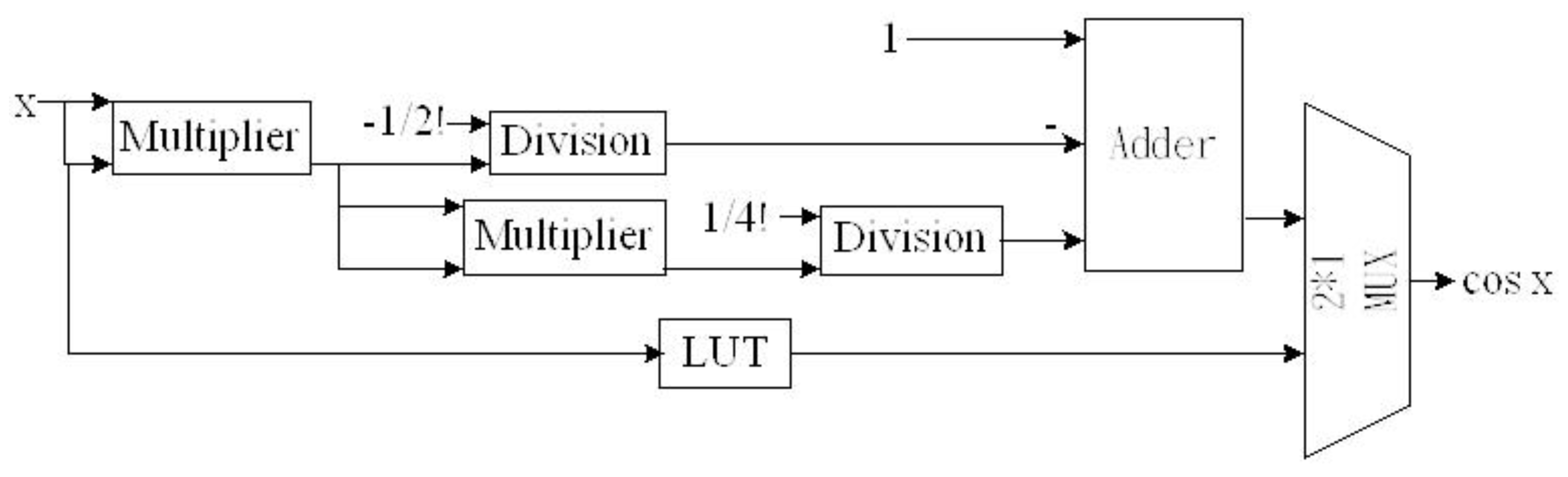
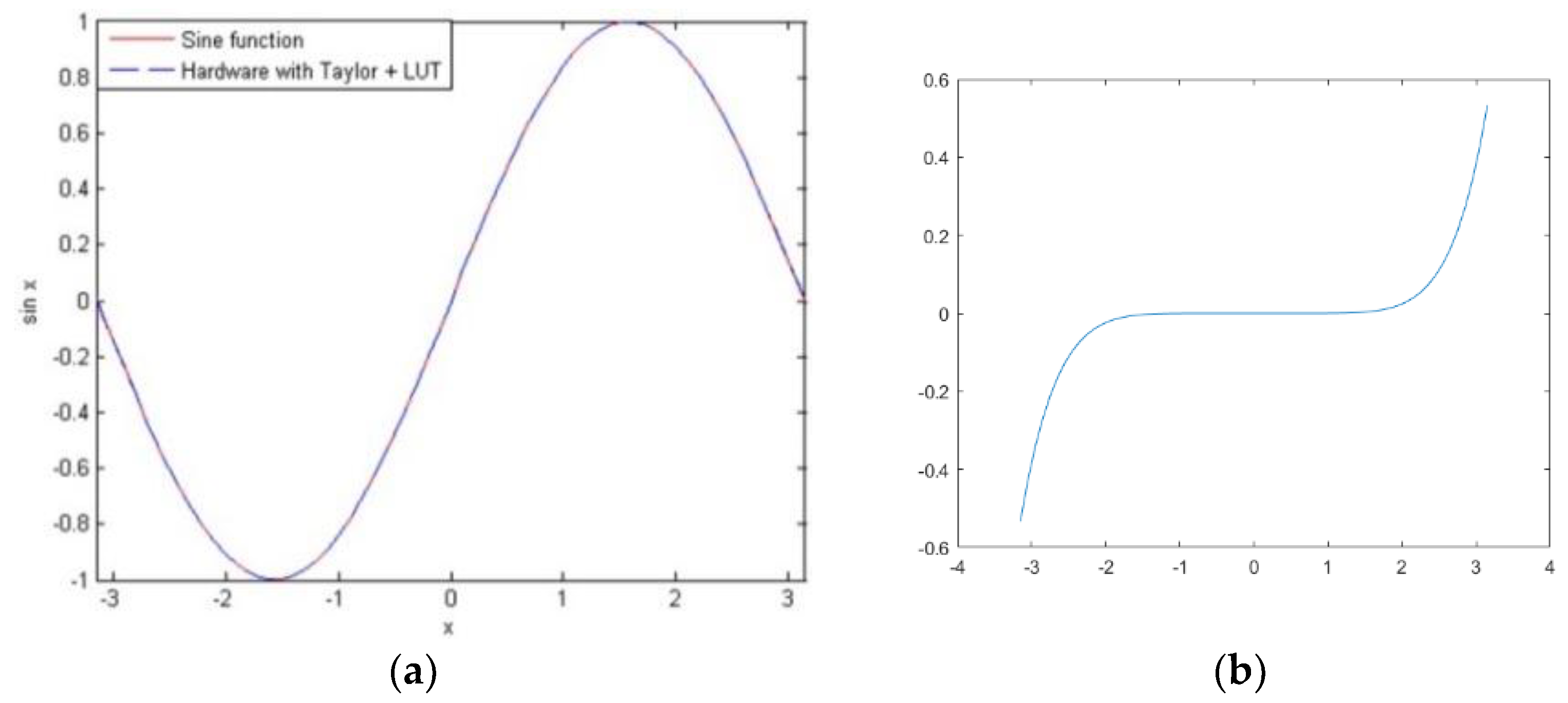
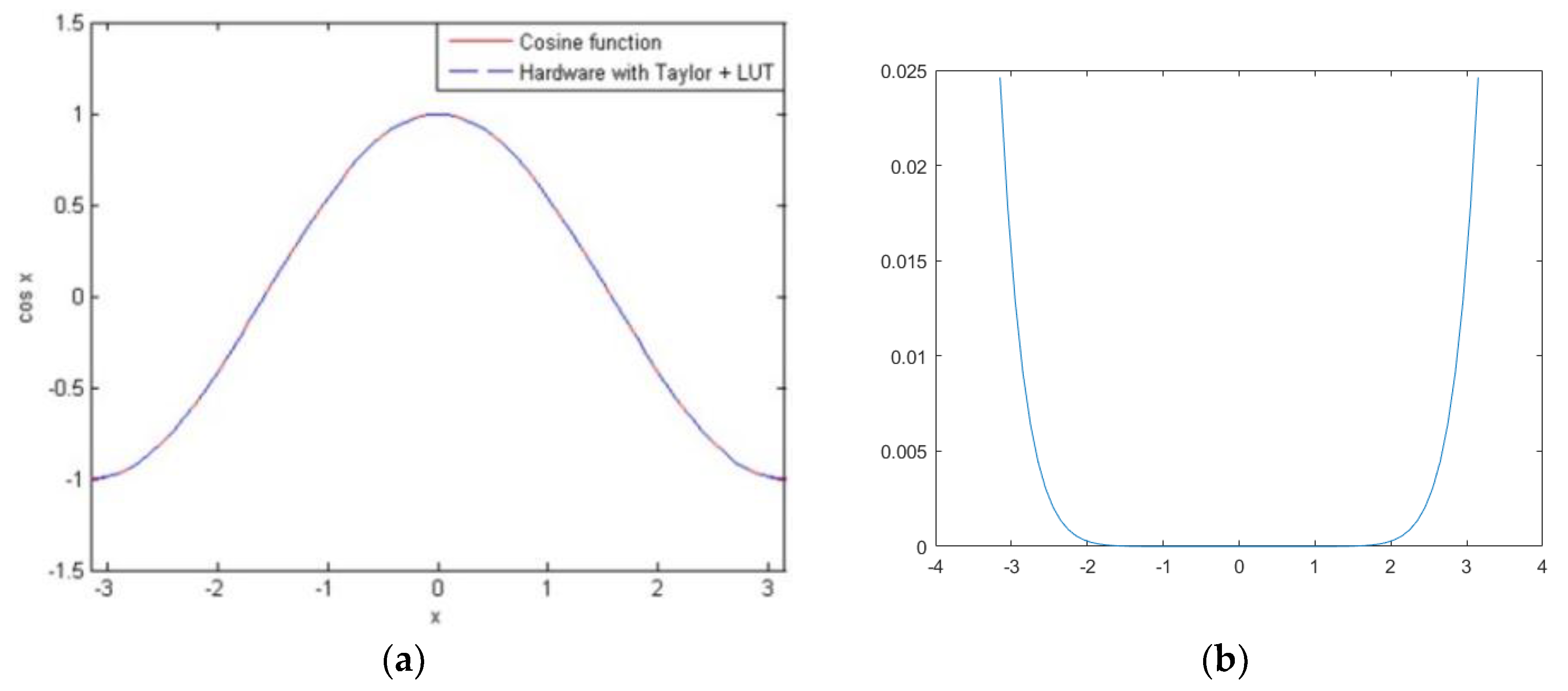
5.2.2. Sine Function and Cosine Function Implementation
5.3. Hardware Implementation of FNFN Controller
5.3.1. Input Fuzzifier
5.3.2. Inference Processing Unit
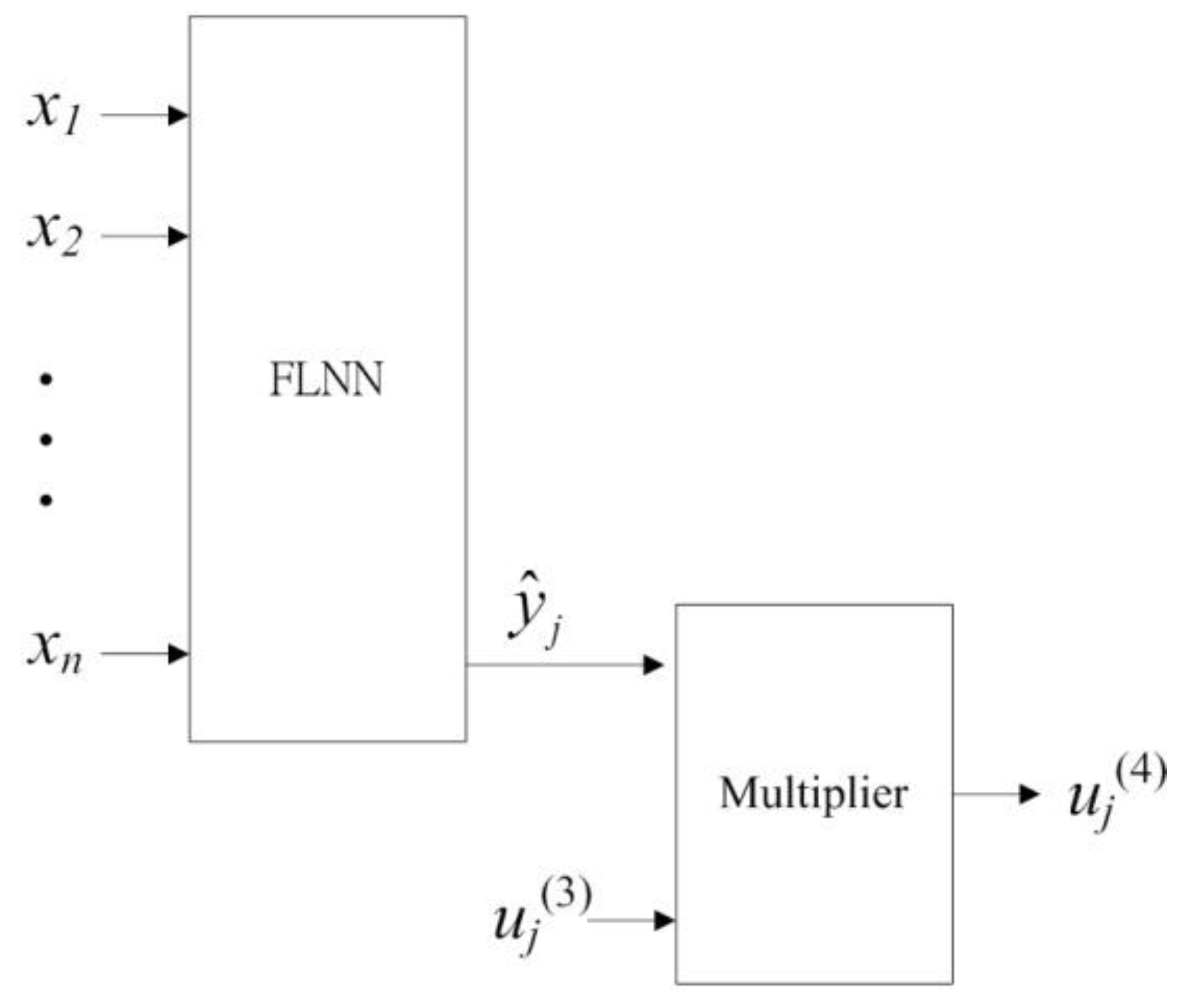
5.3.3. Consequence Unit
5.3.4. Output Defuzzifier
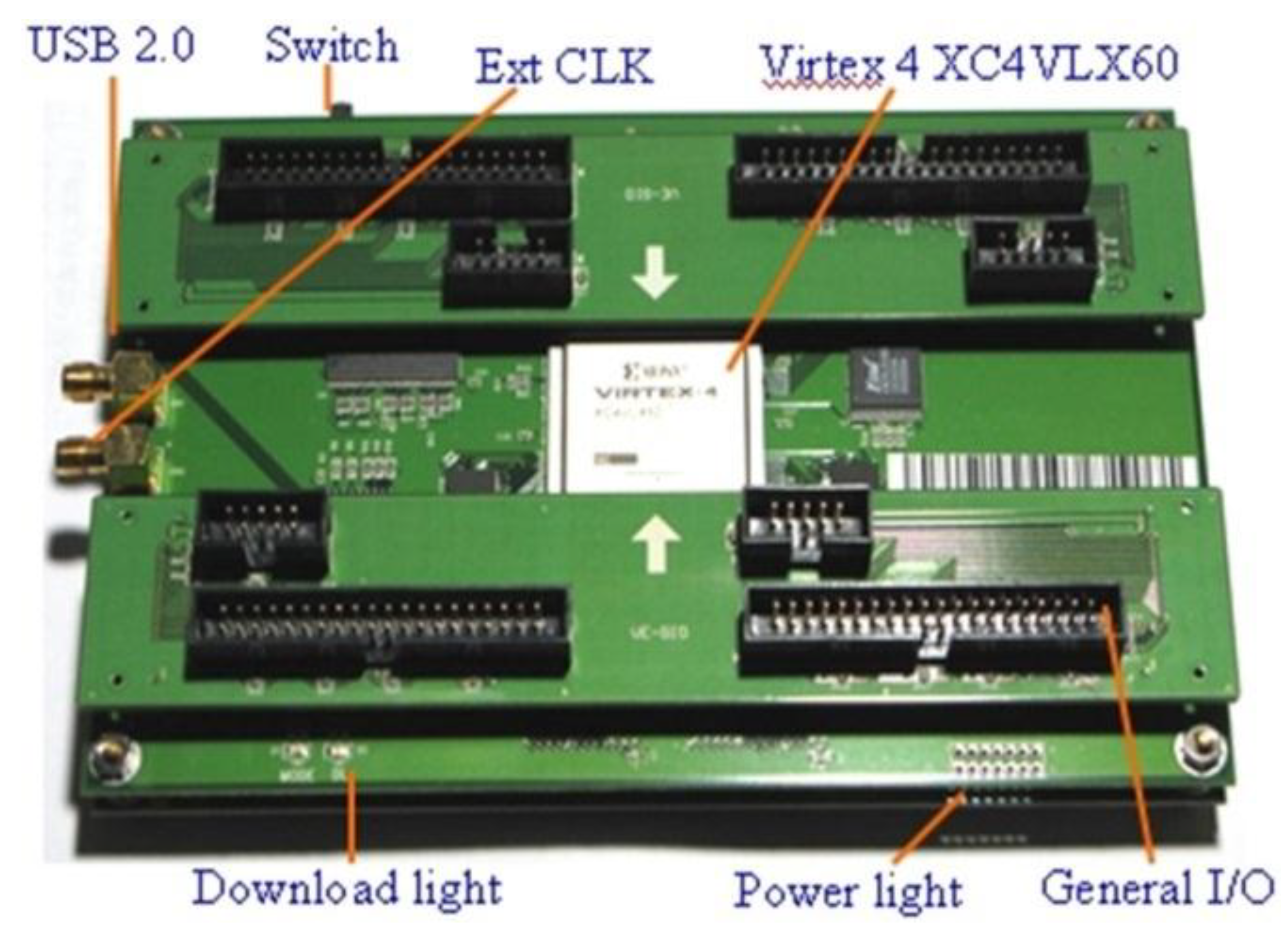
5.4. FPGA Development Platform
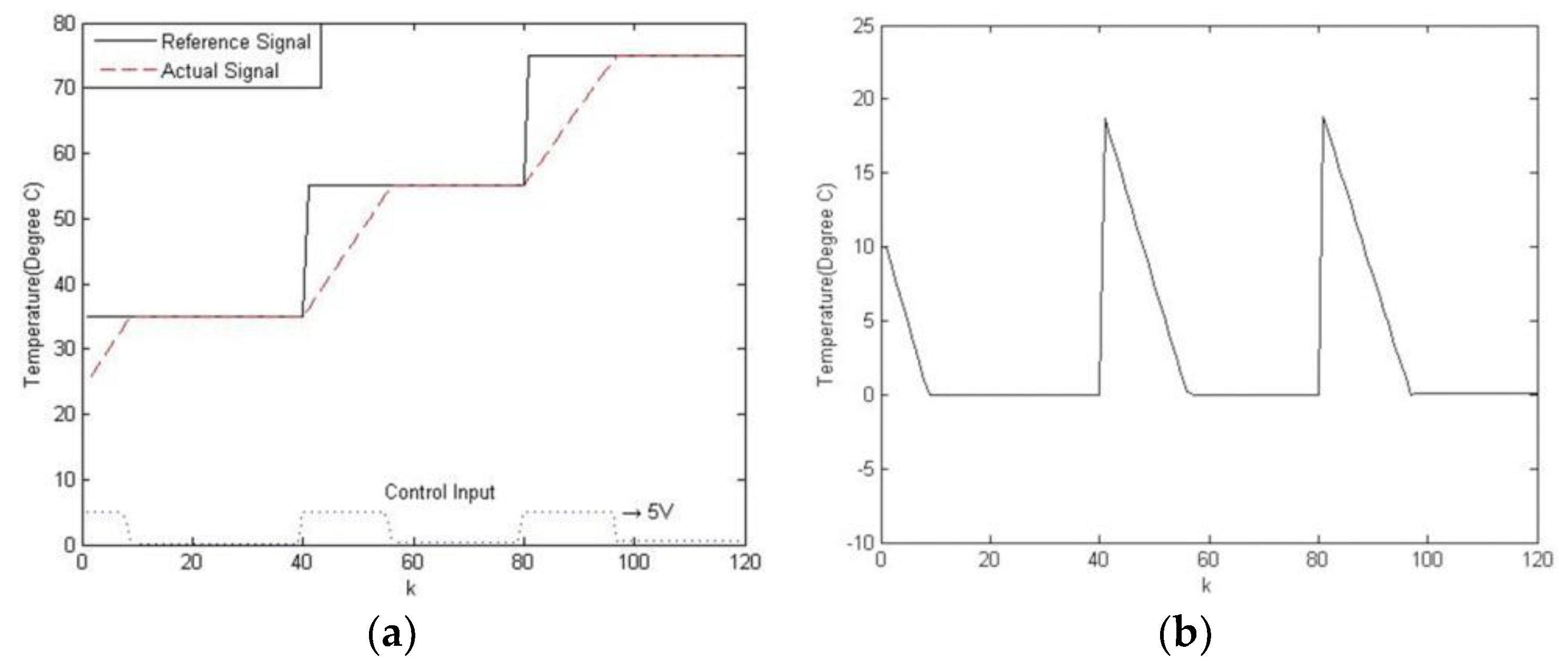
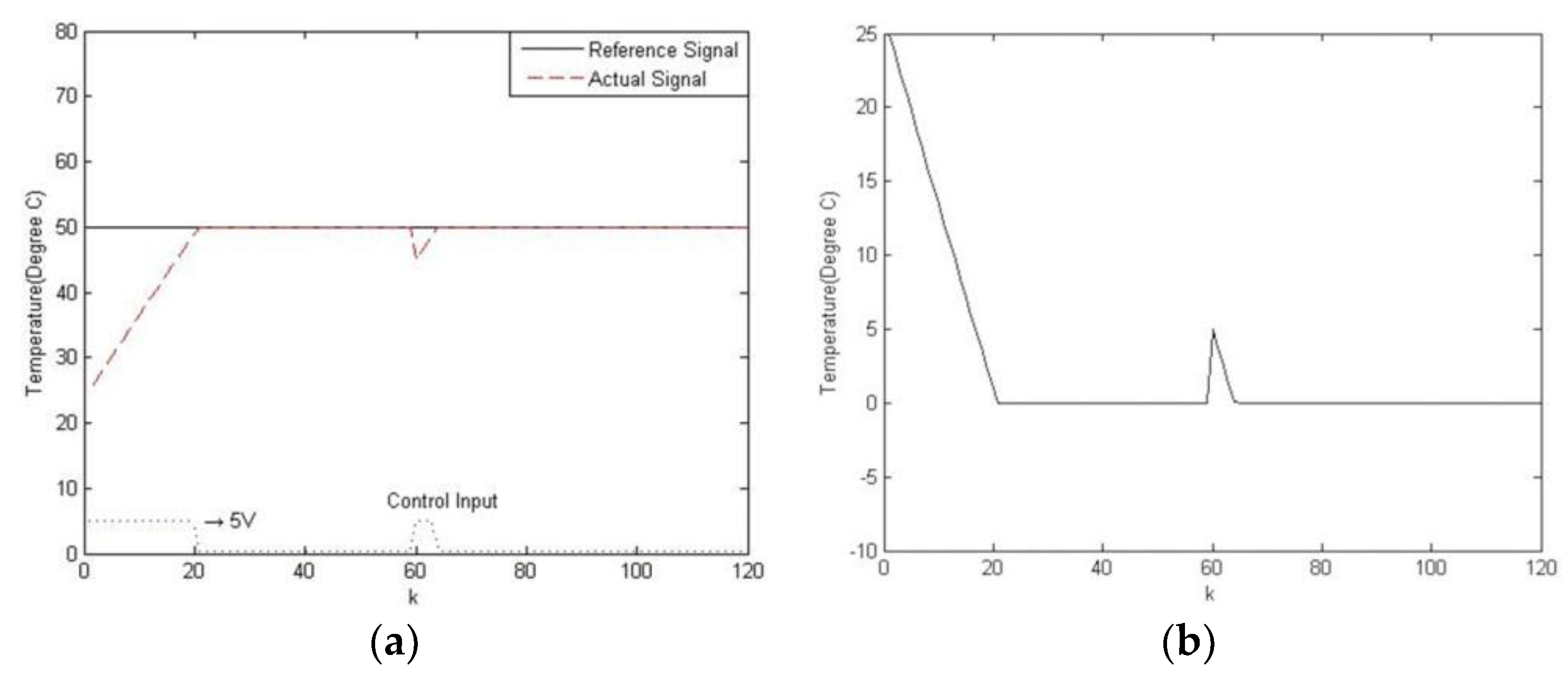
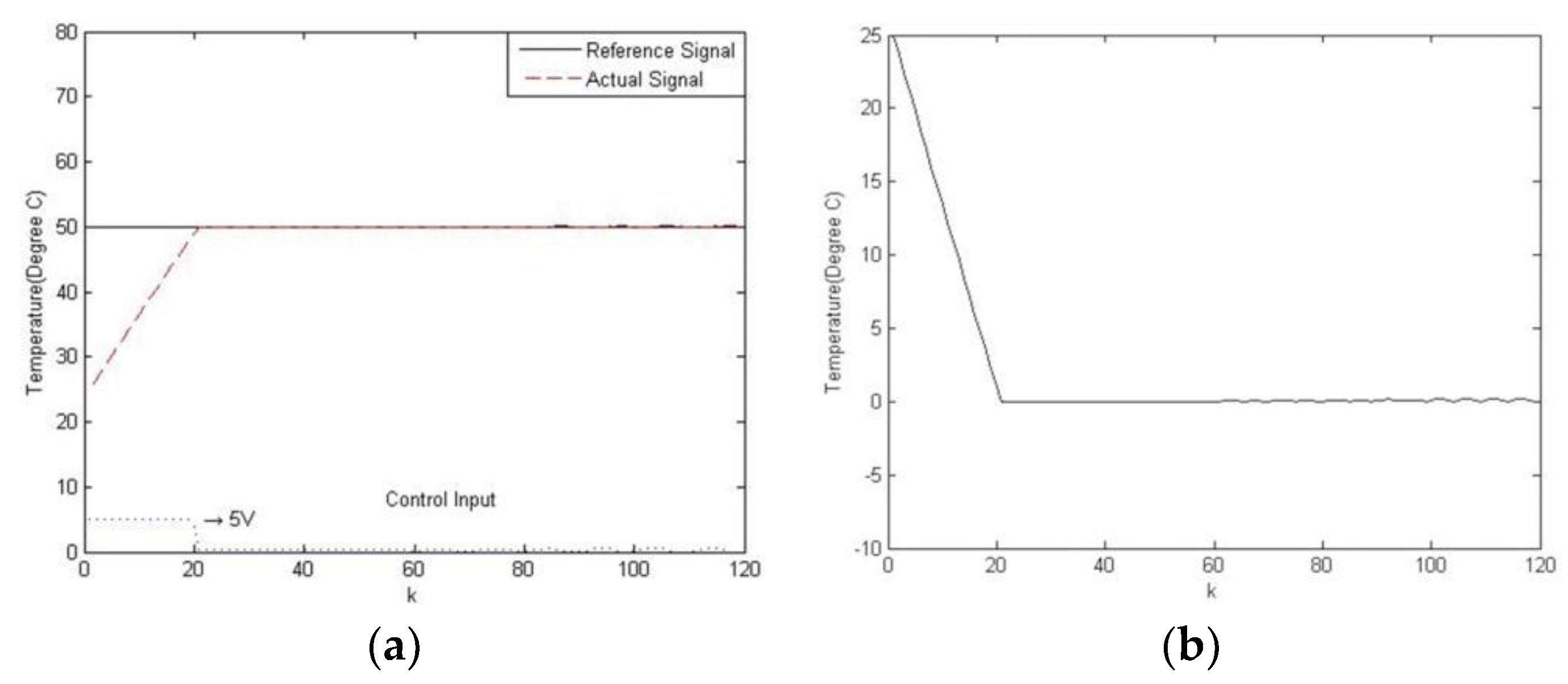
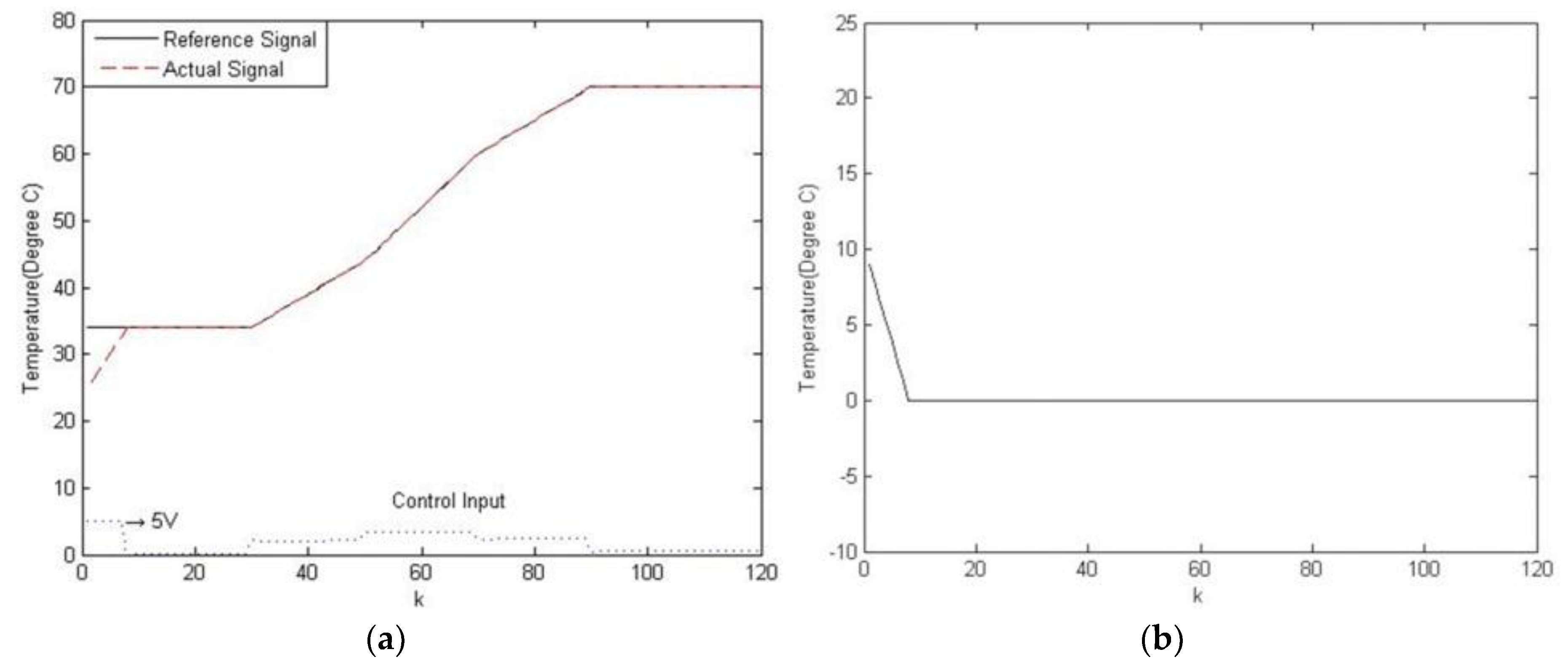
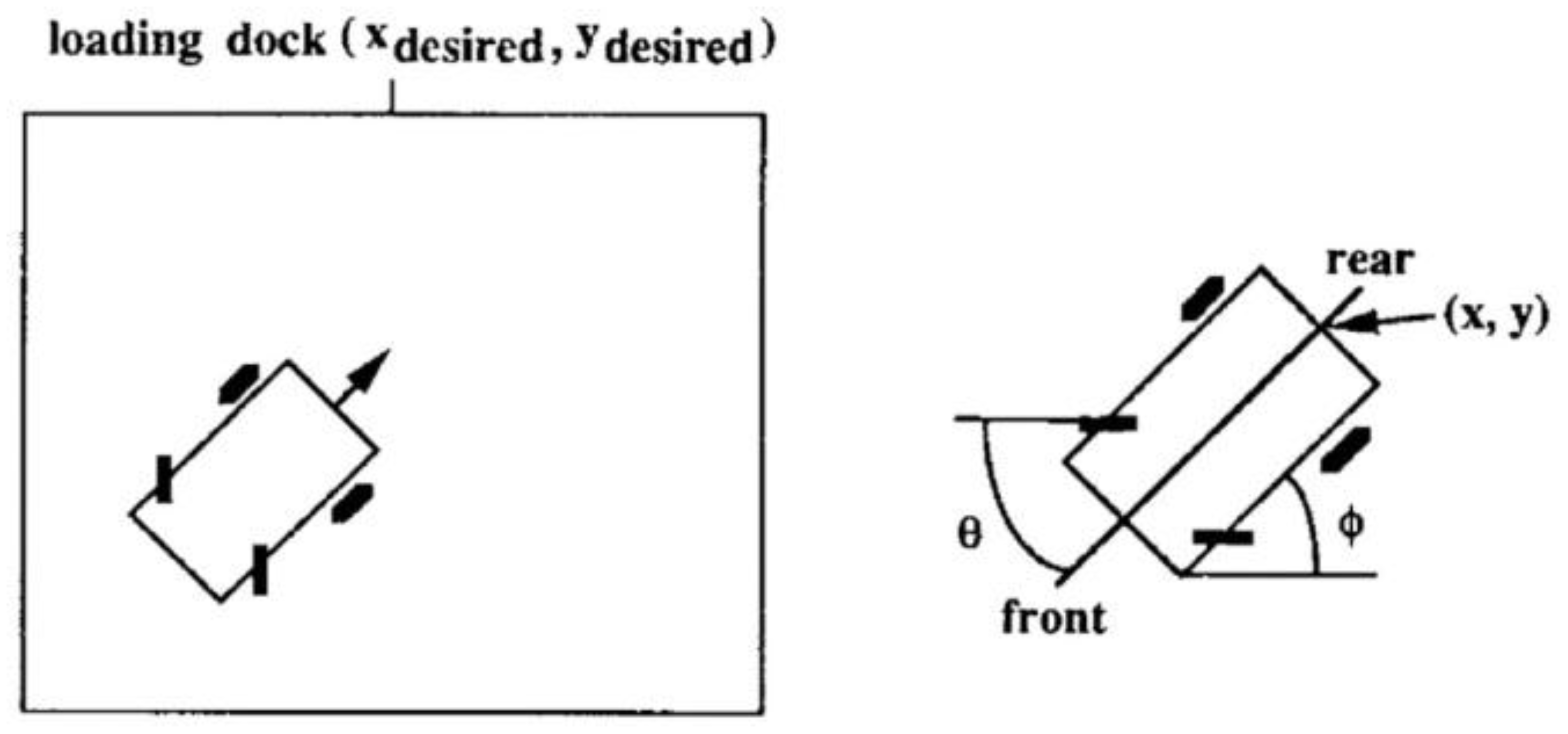
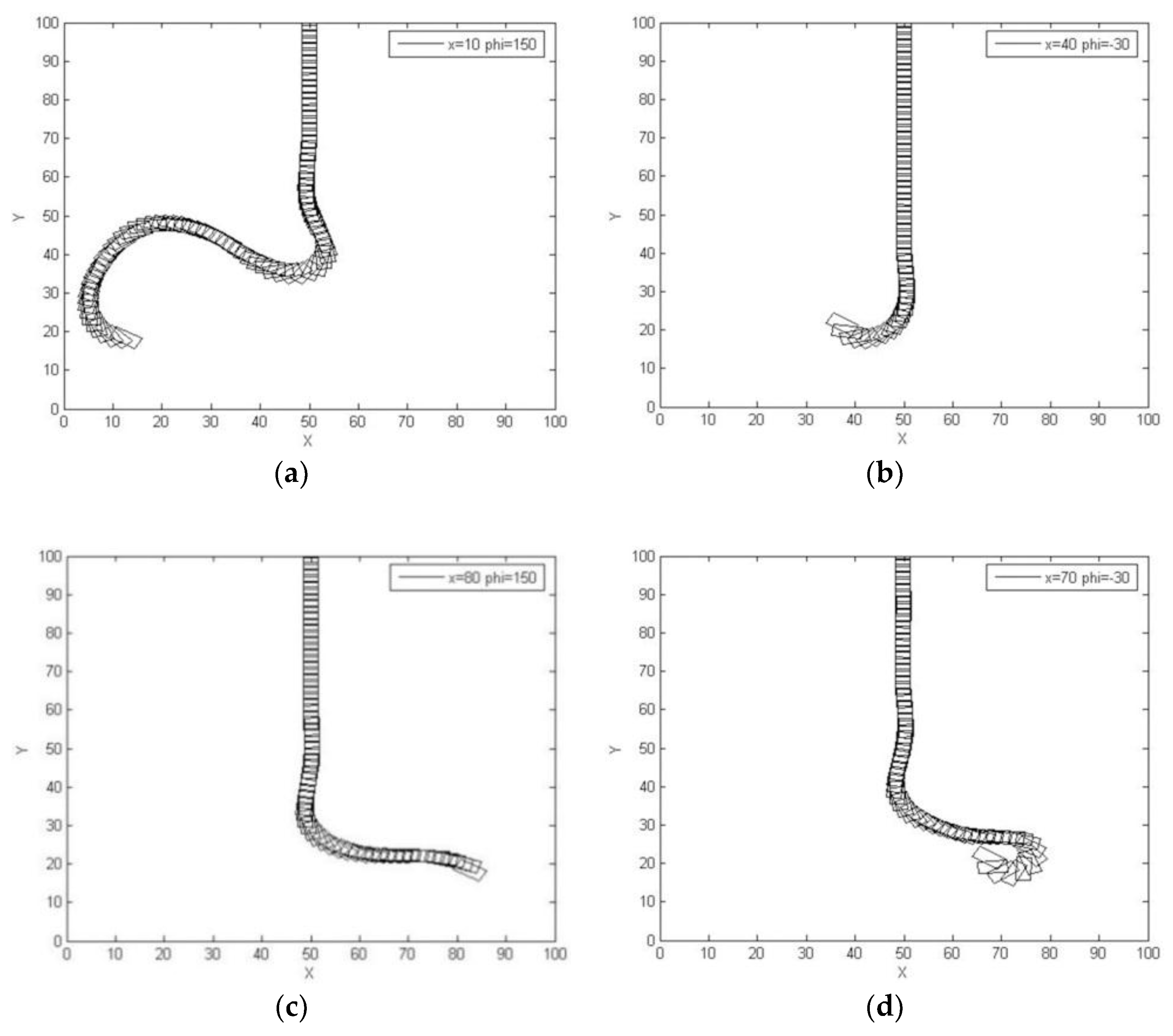
6. Experimental Results
6.1. Temperature Control of a Water Bath
6.2. Backing Control of a Car
7. Conclusions and Future Works
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, J.G.; Tai, S.C.; Lin, C.J. The application of an interactively recurrent self-evolving fuzzy CMAC classifier on face detection in color images. Neural Comput. Appl. 2018, 29, 201–213. [Google Scholar] [CrossRef]
- Jang, J.-S.R. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Wu, M.F.; Huang, W.C.; Juang, C.F.; Chang, K.M.; Wen, C.Y.; Chen, Y.H.; Lin, C.Y.; Chen, Y.C.; Lin, C.C. A new method for self-estimation of the severity of obstructive sleep apnea using easily available measurements and neural fuzzy evaluation system. IEEE J. Biomed. Health Inf. 2017, 21, 1524–1532. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.J.; Chen, C.H. Identification and prediction using recurrent compensatory neuro-fuzzy systems. Fuzzy Sets Syst. 2004, 150, 307–330. [Google Scholar] [CrossRef]
- Khayat, O. Structural parameter tuning of the first-order derivative of an adaptive neuro-fuzzy system for chaotic function modeling. J. Int. Fuzzy Syst. 2014, 27, 235–245. [Google Scholar]
- Ali, C.; Ambrish, C. Adaptive neuro-fuzzy based solar cell model. IET Renew. Power Gener. 2014, 8, 679–686. [Google Scholar]
- George, S.A.; Eftychios, E.P.; Kimon, P.V. Stock trend forecasting in turbulent market periods using neuro-fuzzy systems. Oper. Res. 2016, 16, 245–269. [Google Scholar]
- Fatemeh, Z.; Zahra, Z. A review of neuro-fuzzy systems based on intelligent control. arXiv, 2018; arXiv:1805.03138. [Google Scholar]
- Patra, J.C.; Pal, R.N.; Chatterji, B.N.; Panda, G. Identification of nonlinear dynamic systems using functional link artificial neural networks. IEEE Trans. Syst. Man Cybern. Part B Cybern. 1999, 29, 254–262. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Choi, K.; Lee, Y. Artificial Neural Network Implementation in FPGA: A Case Study. In Proceedings of the 2016 International Conference on SoC Design (ISOCC), Jeju, Korea, 23–26 October 2016; pp. 297–298. [Google Scholar]
- Page, A.; Mohsenin, T. FPGA-Based Reduction Techniques for Efficient Deep Neural Network Deployment. In Proceedings of the 2016 IEEE 24th Annual International Symposium on Field-Programmable Custom Computing Machines (FCCM), Washington, DC, USA, 1–3 May 2016; p. 200. [Google Scholar]
- Zhang, C.; Li, P.; Sun, G.; Guan, Y.; Xiao, B.; Cong, J. Optimizing FPGA-Based Accelerator Design for Deep Convolutional Neural Networks. In Proceedings of the 2015 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Monterey, CA, USA, 22–24 February 2015; pp. 161–170. [Google Scholar]
- Bettoni, M.; Urgese, G.; Kobayashi, Y.; Macii, E.; Acquaviva, A. A convolutional neural network fully implemented on FPGA for embedded platforms. In Proceedings of the 2017 New Generation of CAS, Genova, Genoa, 6–9 September 2017; pp. 49–52. [Google Scholar]
- Lu, S.M.; Li, D.J. Adaptive neural network control for nonlinear hydraulic servo-system with time-varying state constraints. Complexity 2017, 2017. [Google Scholar] [CrossRef]
- Lin, C.J.; Cheng, C.H. A recurrent neural fuzzy controller based on self-organizing improved particle swarm optimization for a magnetic levitation system. Int. J. Adapt. Control Signal Process. 2015, 29, 563–580. [Google Scholar] [CrossRef]
- Li, S.P. Adaptive control with optimal tracking performance. Int. J. Syst. Sci. 2018, 49, 496–510. [Google Scholar] [CrossRef]
- Gatti, C. The truck backer-upper problem. In Design of Experiments for Reinforcement Learning; Springer: Cham, Switzerland, 2015; pp. 111–127. [Google Scholar]
- Ontiveros-Robles, E.; Vázquez, J.G.; Castro, J.R.; Castillo, O. A FPGA-Based Hardware Architecture Approach for Real-Time Fuzzy Edge Detection. In Nature-Inspired Design of Hybrid Intelligent Systems; Springer: Cham, Switzerland, 2016; pp. 519–540. [Google Scholar]
- Aldair, A.A.; Obed, A.A.; Halihal, A.F. Design and Implementation of Neuro-Fuzzy Controller Using FPGA for Sun Tracking System. Iraqi J. Electr. Electron. Eng. 2016, 12, 123–136. [Google Scholar]
- Kaiser, M.S.; Chowdhury, Z.I.; Al Mamun, S.; Hussain, A.; Mahmud, M. A Neuro-Fuzzy Control System Based on Feature Extraction of Surface Electromyogram Signal for Solar-Powered Wheelchair. Cogn. Comput. 2016, 8, 946–954. [Google Scholar] [CrossRef]
- CastroCaicedo, Y.E.; Moreno, E.D.; Coelho, L.D.S.; Llanos, C.H. NeuroFuzzy Controller Design and FPGA-Based Embedded System for ACROBOT Model. Int. J. Comput. Digit. Syst. 2018, 6, 97–108. [Google Scholar] [CrossRef]
- Lin, C.J.; Wu, C.F.; Lin, H.Y.; Yu, C.Y. An interactively recurrent functional neural fuzzy network with fuzzy differential evolution and its applications. Sains Malaysiana 2015, 44, 1721–1728. [Google Scholar]
- Inacio, C.; Ombres, D. The DSP decision: fixed point or floating? IEEE Spectr. 1996, 33, 72–74. [Google Scholar] [CrossRef]
- Ewe, C.T.; Cheung, P.Y.K.; Constantinides, G.A. Dual fixed-point: An efficient alternative to floating-point computation. Lect. Notes Comput. Sci. 2004, 3203, 200–208. [Google Scholar]









| Method | Exponential Function (x = 0.8) | Taylor Approximation | Error Value | |
|---|---|---|---|---|
| Order | ||||
| 3 | 2.225541 | 2.205330 | 0.020208 | |
| 4 | 2.222400 | 0.003141 | ||
| 5 | 2.225131 | 0.000410 | ||
| E | FNFN Controller | TSK-Type NFN Controller [2] | FLNN Controller [4] | PID Controller [23] | Fuzzy Controller [24] | |
|---|---|---|---|---|---|---|
| Software | Hardware | |||||
| Regulation | 353.13 | 354.49 | 361.96 | 379.22 | 418.5 | 401.5 |
| Noise Influence | 270.72 | 271.59 | 274.75 | 324.51 | 311.5 | 275.8 |
| Plant Dynamics Altered | 263.68 | 264.57 | 265.48 | 311.54 | 322.2 | 273.5 |
| Tracking | 44.53 | 46.48 | 54.28 | 98.43 | 100.6 | 88.1 |
| Device Selected | XC4VLX60 | ||
|---|---|---|---|
| Logic Gate Utilization | Available | Used | Utilization |
| Slices | 26,624 | 26,352 | 98% |
| 4 input LUTs | 53,248 | 50,117 | 94% |
| Slice Flip Flops | 53,248 | 50,607 | 9% |
| GCLKs | 32 | 1 | 3% |
| Bonded IOBs | 640 | 61 | 9% |
| Gate counts | 6,000,000 | 507,064 | 8.5% |
| Position | E |
|---|---|
| (a) | 0.2691 |
| (b) | 0.1519 |
| (c) | 0.1955 |
| (d) | 0.2454 |
| Device Selected | XC4VLX60 | ||
|---|---|---|---|
| Logic Gate Utilization | Available | Used | Utilization |
| Slices | 26,624 | 26,352 | 98% |
| 4 input LUTs | 53,248 | 50,117 | 94% |
| Slice Flip Flops | 53,248 | 50,607 | 9% |
| GCLKs | 32 | 1 | 3% |
| Bonded IOBs | 640 | 61 | 9% |
| Gate counts | 6,000,000 | 507,064 | 8.5% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jhang, J.-Y.; Tang, K.-H.; Huang, C.-K.; Lin, C.-J.; Young, K.-Y. FPGA Implementation of a Functional Neuro-Fuzzy Network for Nonlinear System Control. Electronics 2018, 7, 145. https://doi.org/10.3390/electronics7080145
Jhang J-Y, Tang K-H, Huang C-K, Lin C-J, Young K-Y. FPGA Implementation of a Functional Neuro-Fuzzy Network for Nonlinear System Control. Electronics. 2018; 7(8):145. https://doi.org/10.3390/electronics7080145
Chicago/Turabian StyleJhang, Jyun-Yu, Kuang-Hui Tang, Chuan-Kuei Huang, Cheng-Jian Lin, and Kuu-Young Young. 2018. "FPGA Implementation of a Functional Neuro-Fuzzy Network for Nonlinear System Control" Electronics 7, no. 8: 145. https://doi.org/10.3390/electronics7080145
APA StyleJhang, J.-Y., Tang, K.-H., Huang, C.-K., Lin, C.-J., & Young, K.-Y. (2018). FPGA Implementation of a Functional Neuro-Fuzzy Network for Nonlinear System Control. Electronics, 7(8), 145. https://doi.org/10.3390/electronics7080145