High Frequency Transformer’s Parasitic Capacitance Minimization for Photovoltaic (PV) High-Frequency Link-Based Medium Voltage (MV) Inverter
Abstract
1. Introduction
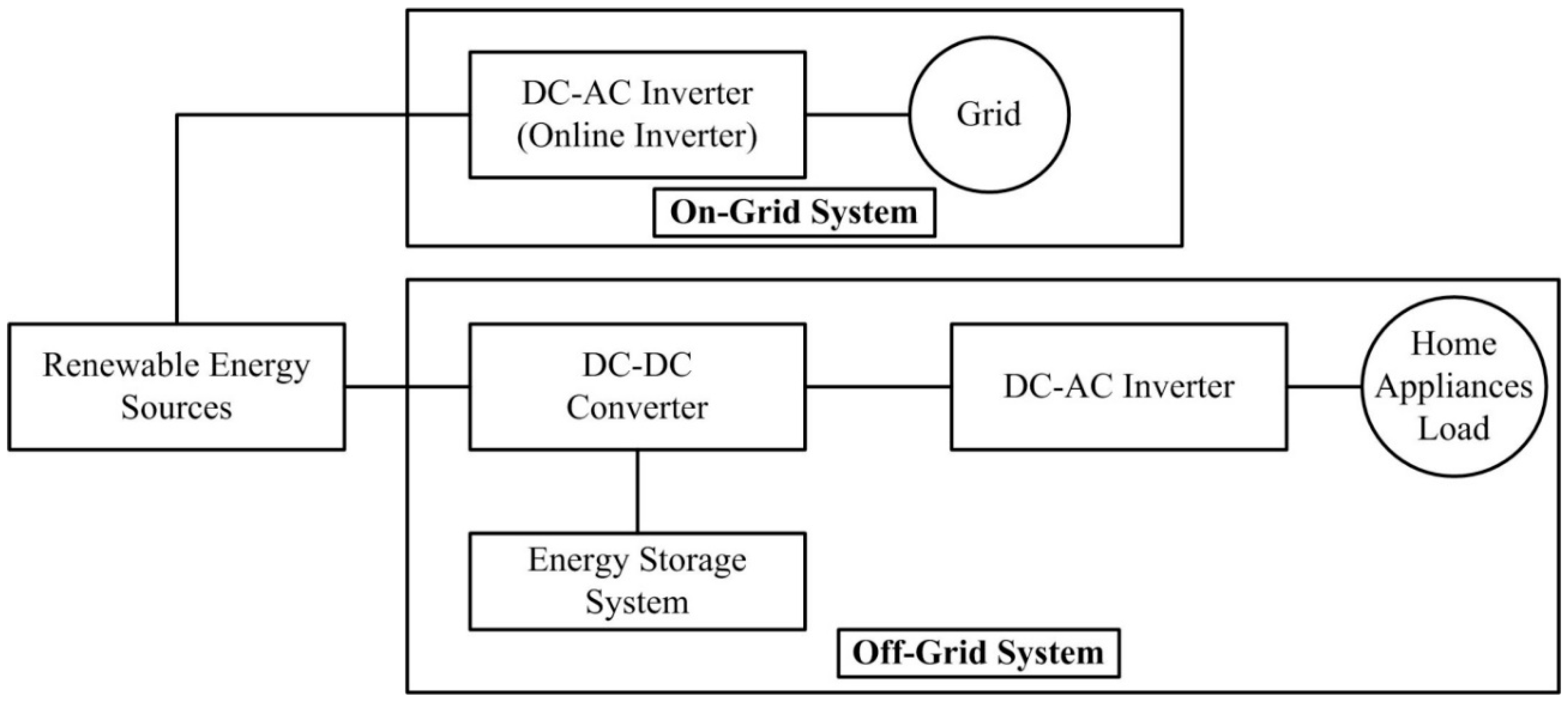
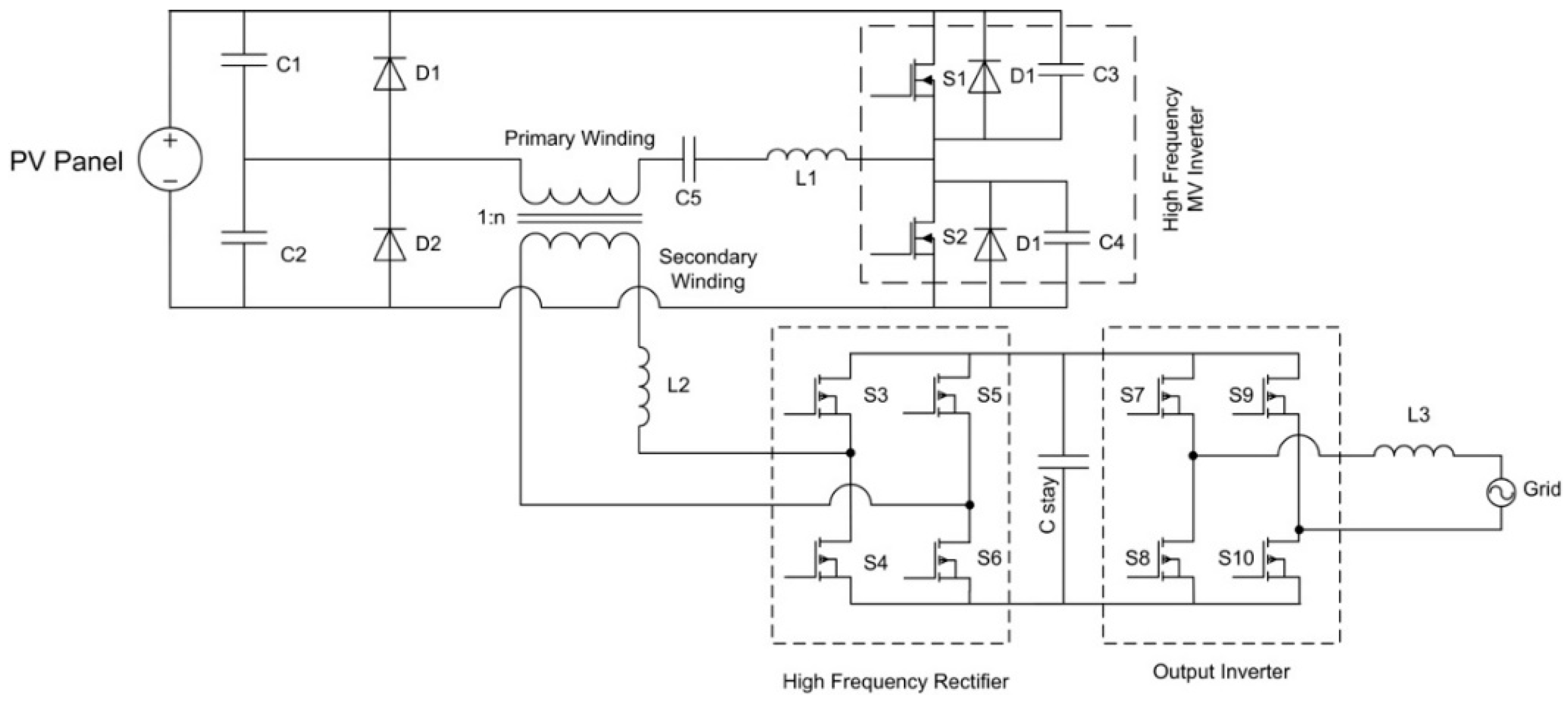
2. High-Frequency Link Based MV Inverter Design Consideration
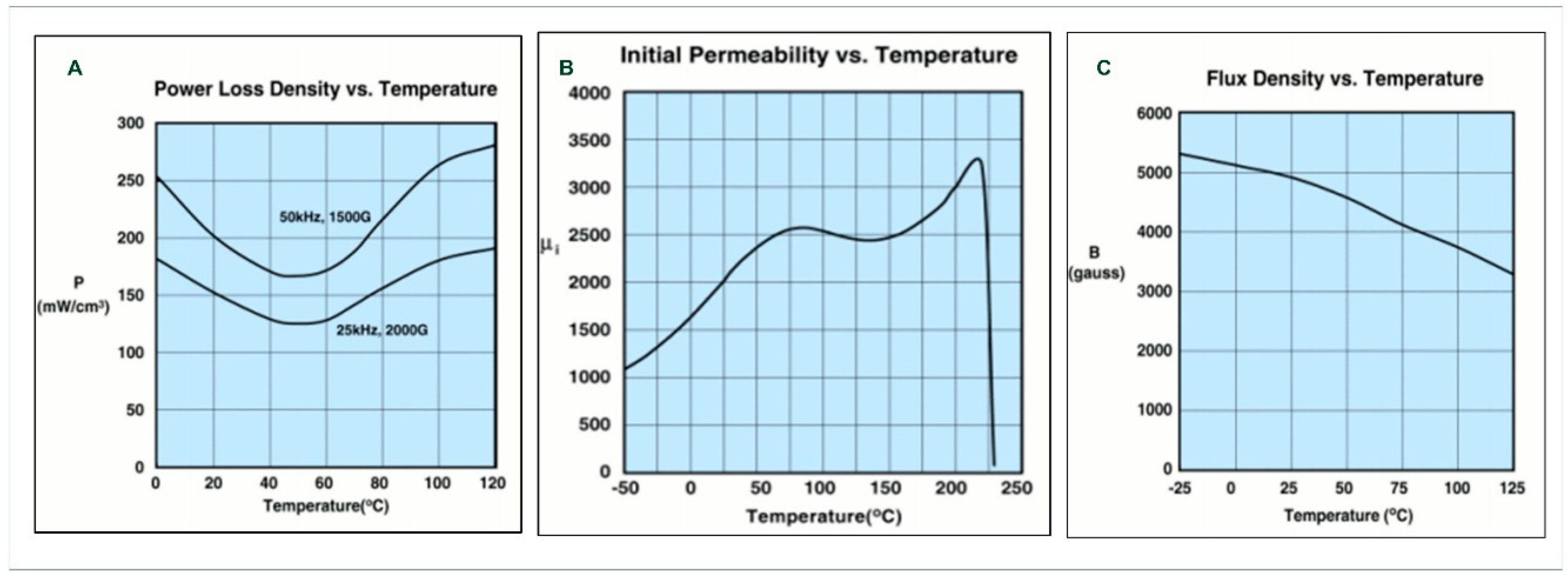
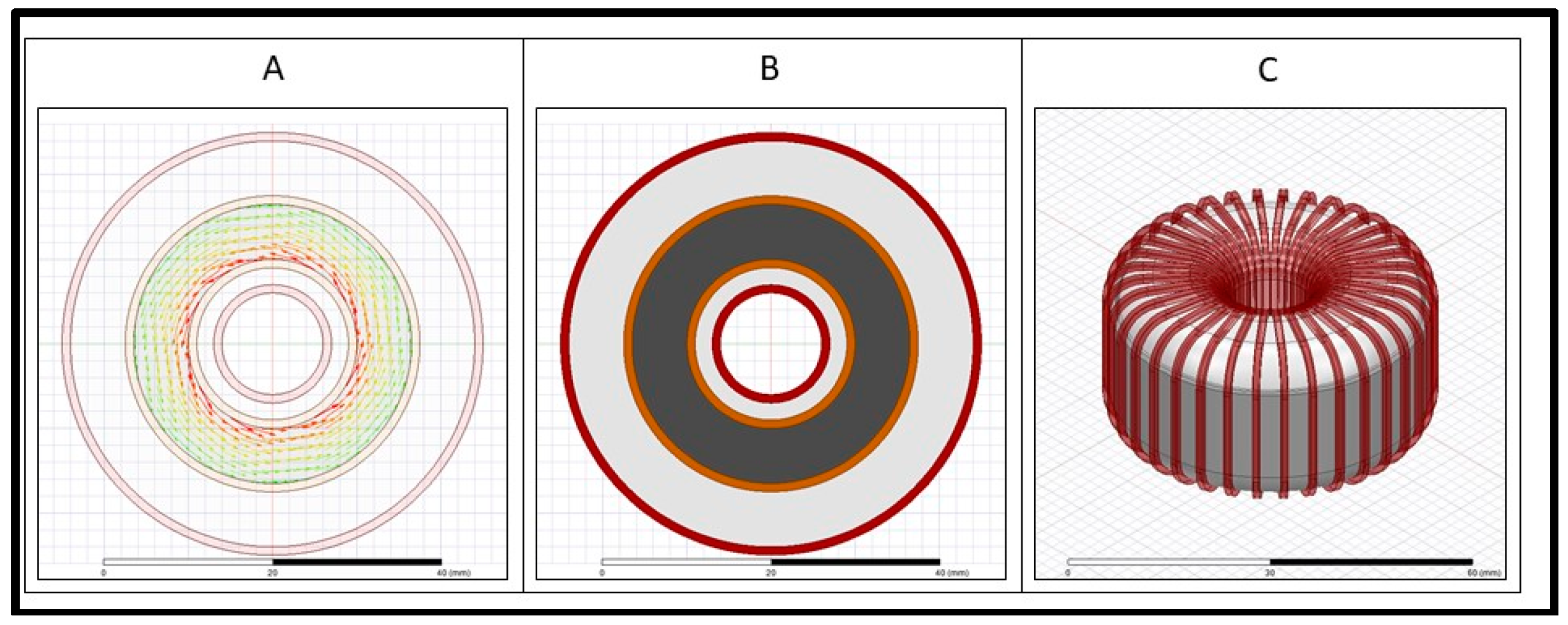
2.1. Toroid Ferrite Core
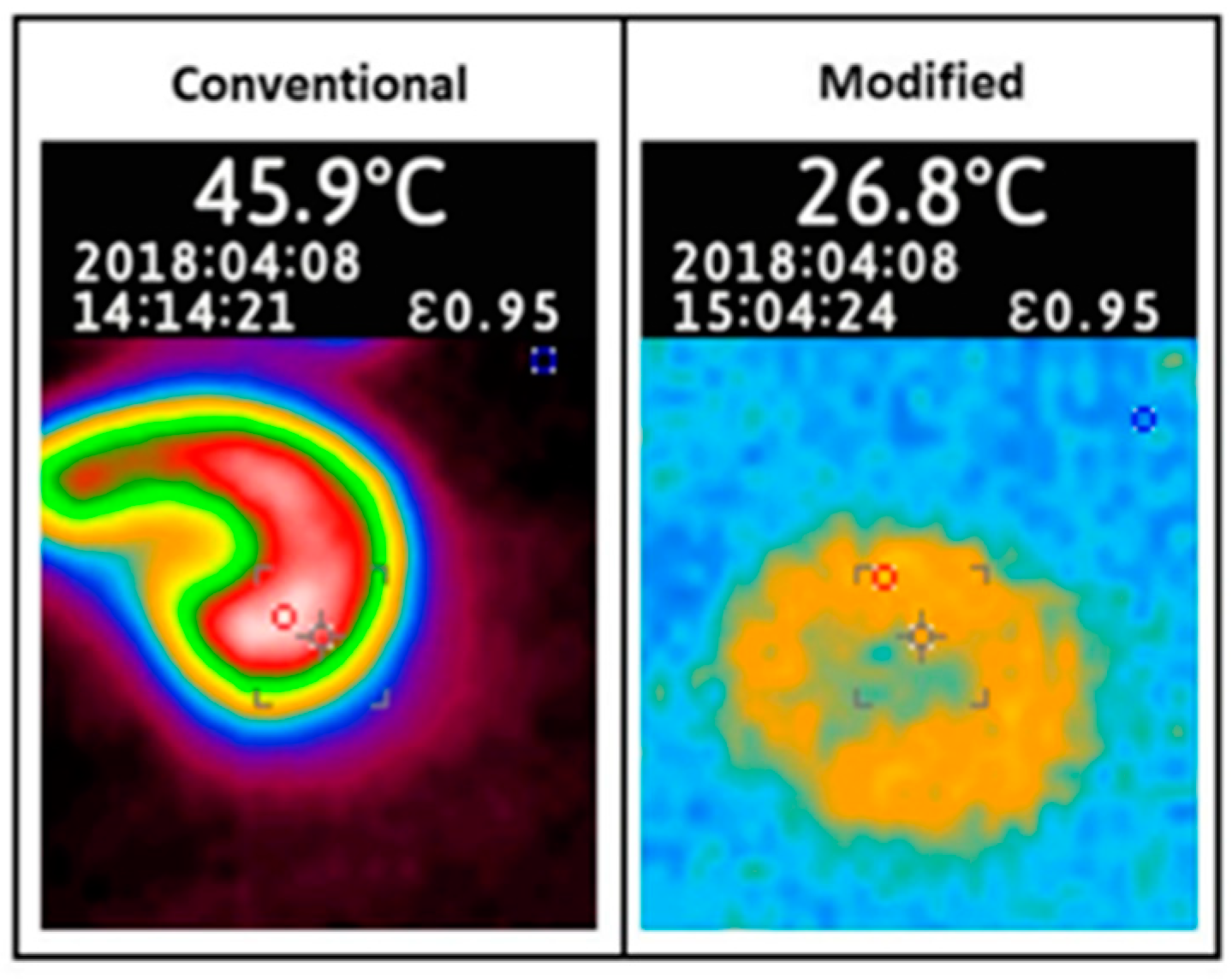
2.2. Harmonic Current Contribution on Transformer Losses and Temperature Rise
2.3. Circuit Operation
3. Fabrication
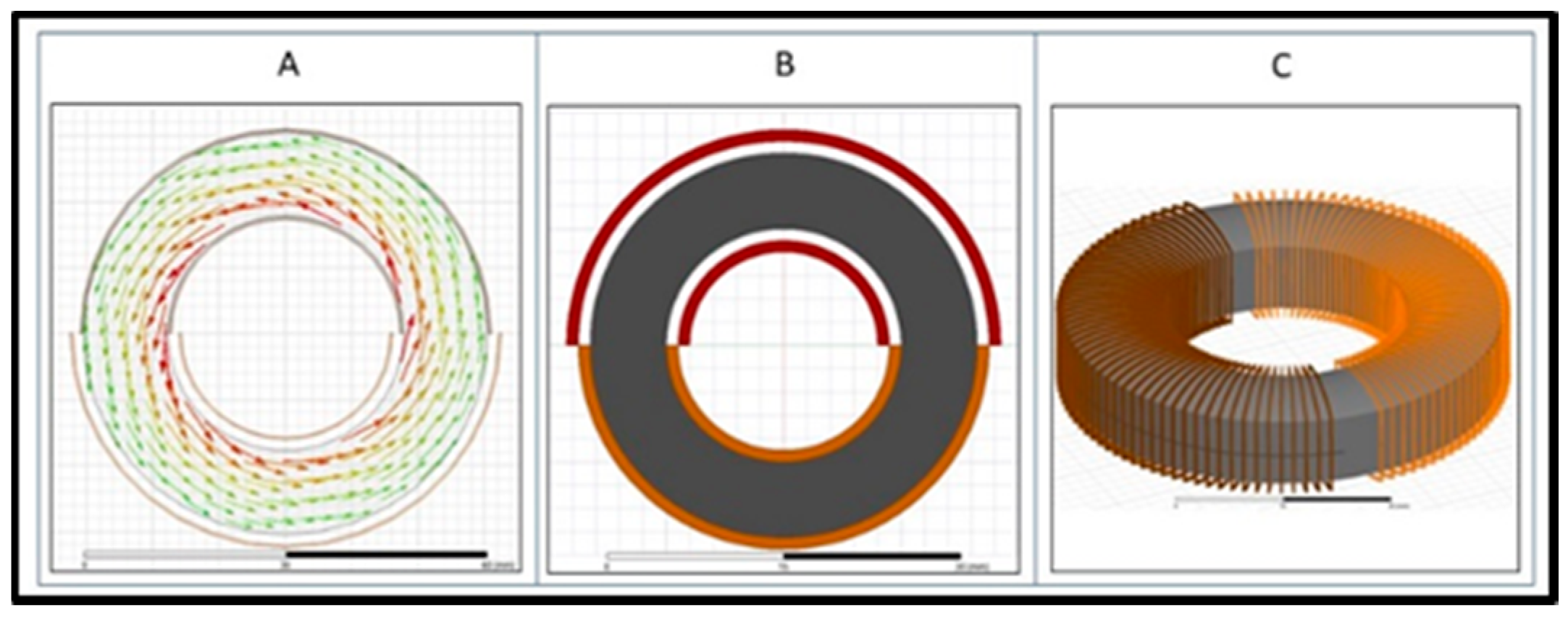
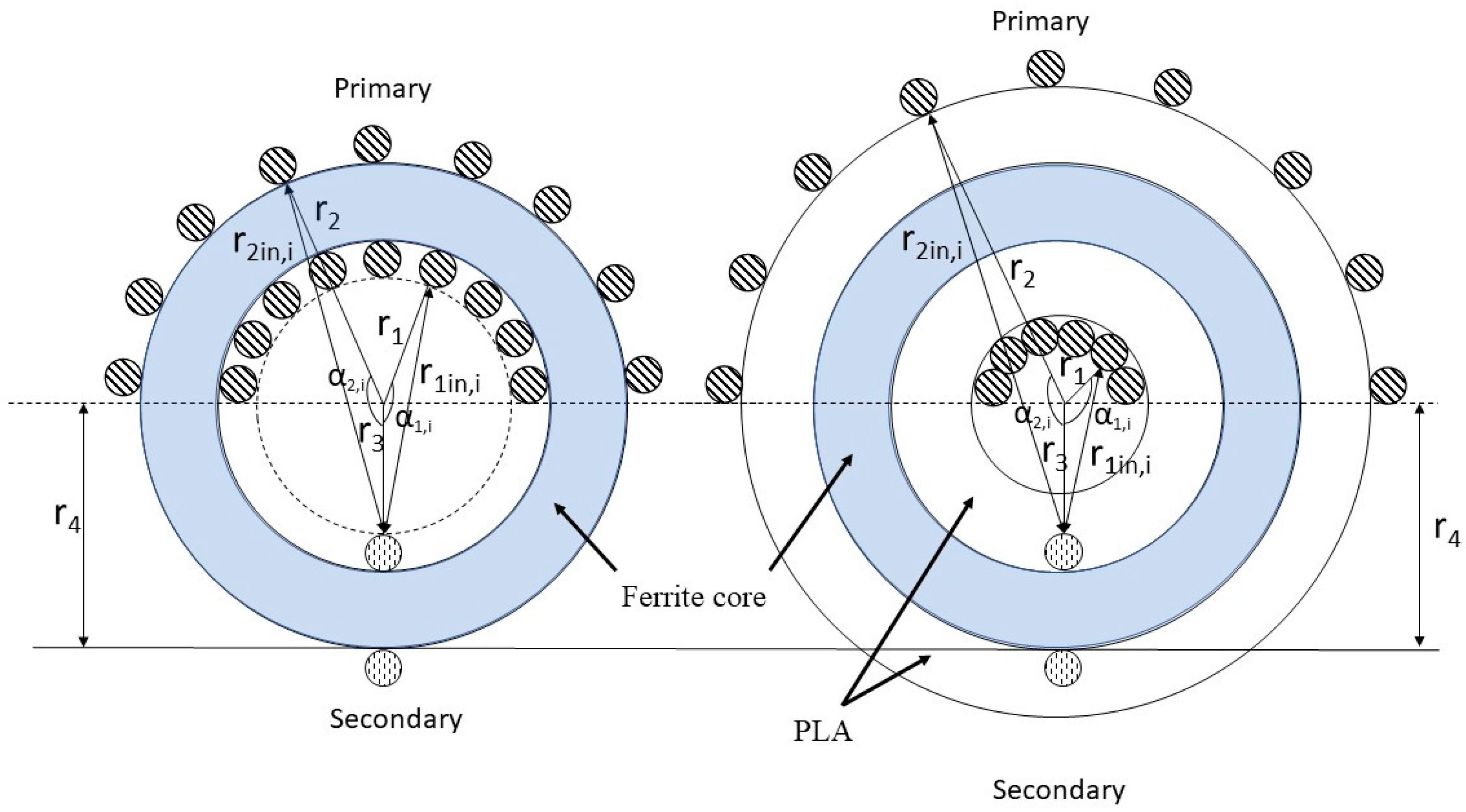
3.1. Case 1: Conventional Toroid Core Transformer with 180° Sector Windings
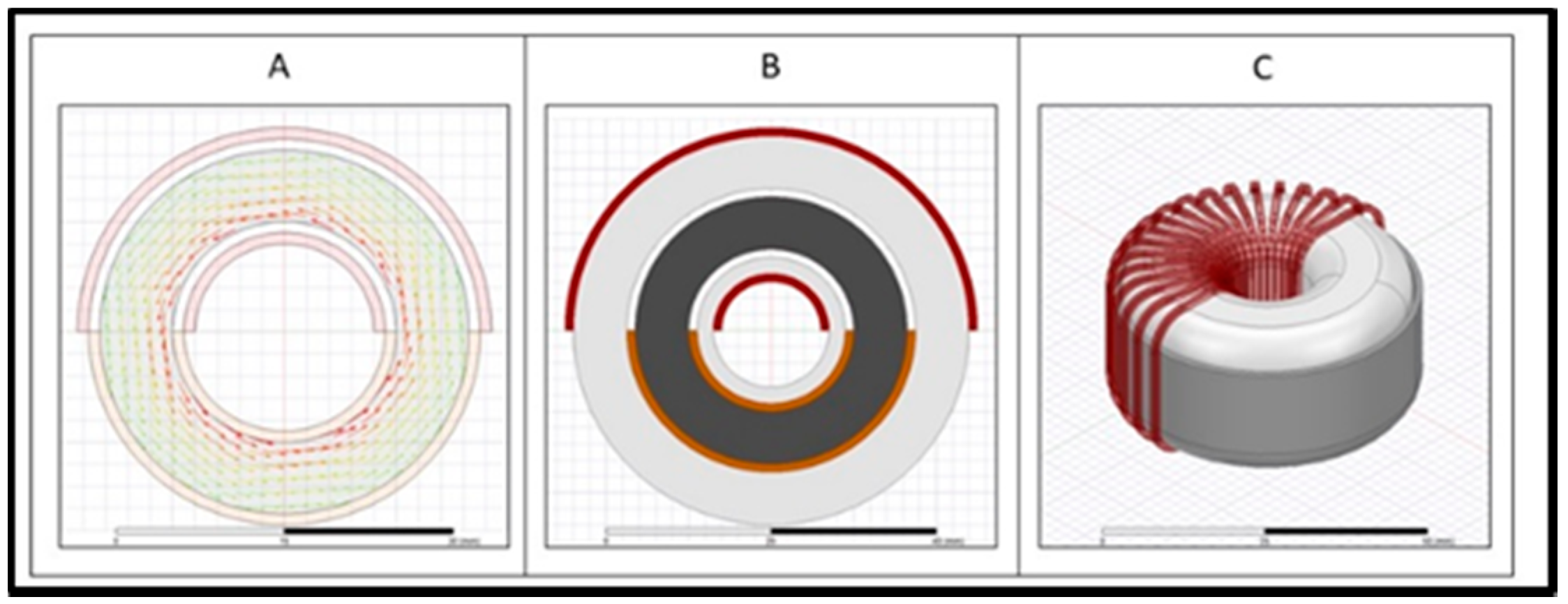
3.2. Case 2: Modified Toroid Core Transformer with 180° Sector Windings
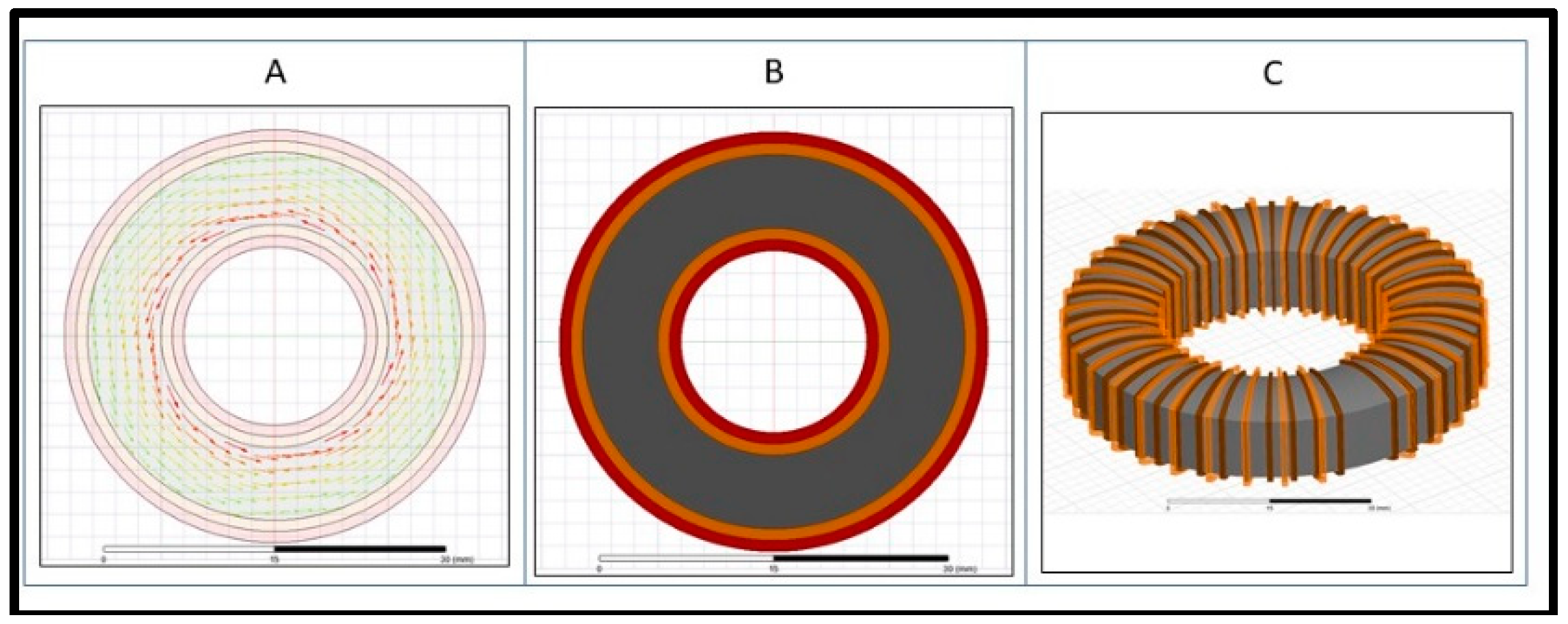
3.3. Case 3: A Conventional 360° Wound Toroid Core Transformer
3.4. Case 4: A Modified 360° Wound Toroid Core Transformer
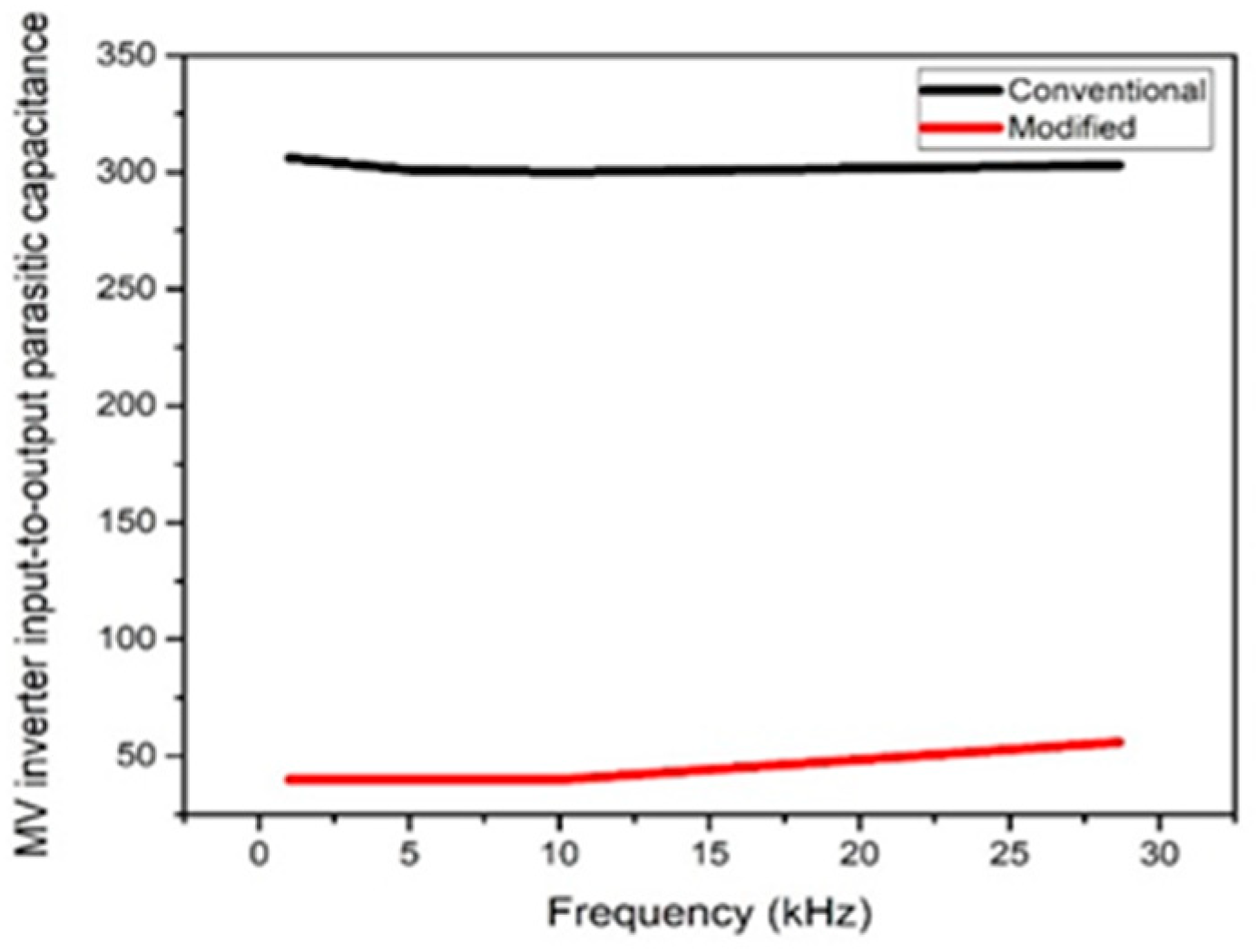
4. Calculation of the Transformer Inter-Winding Capacitance
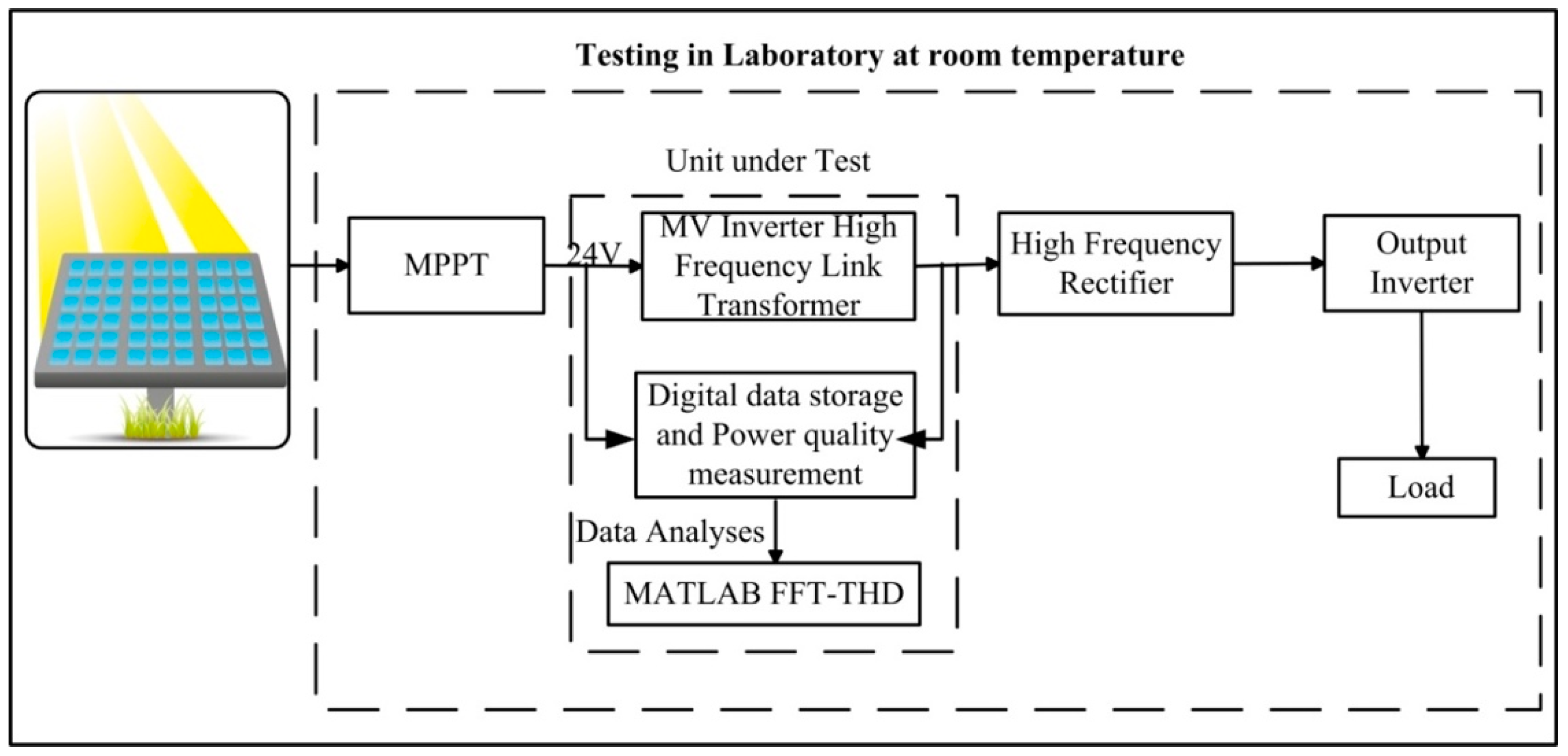
5. Experimental Setup
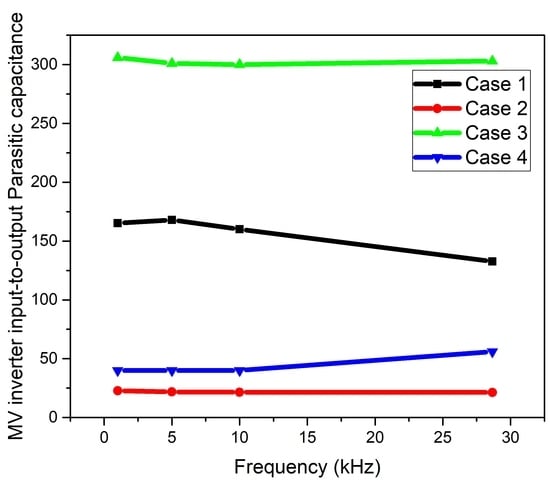
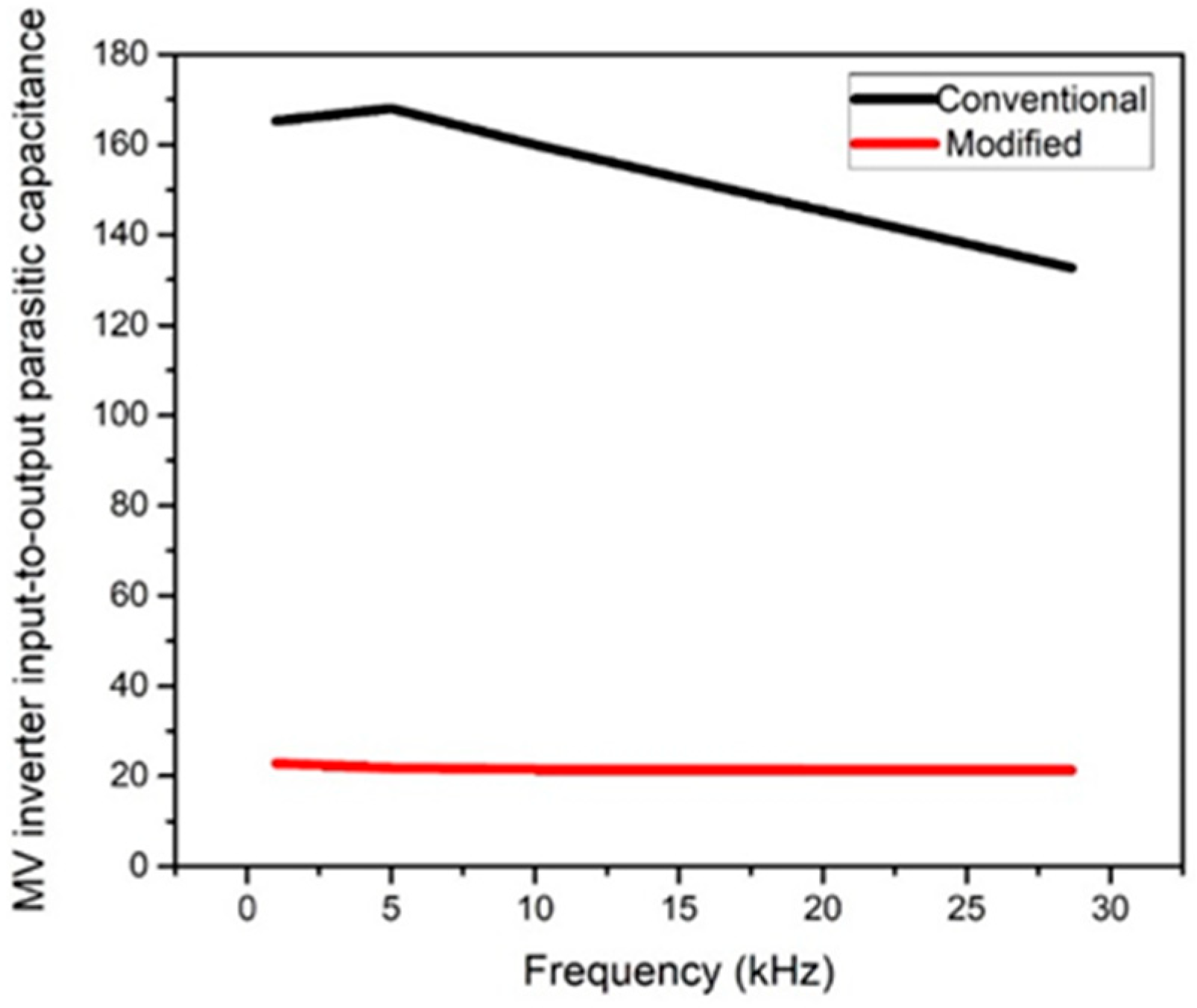
6. Results and Discussion
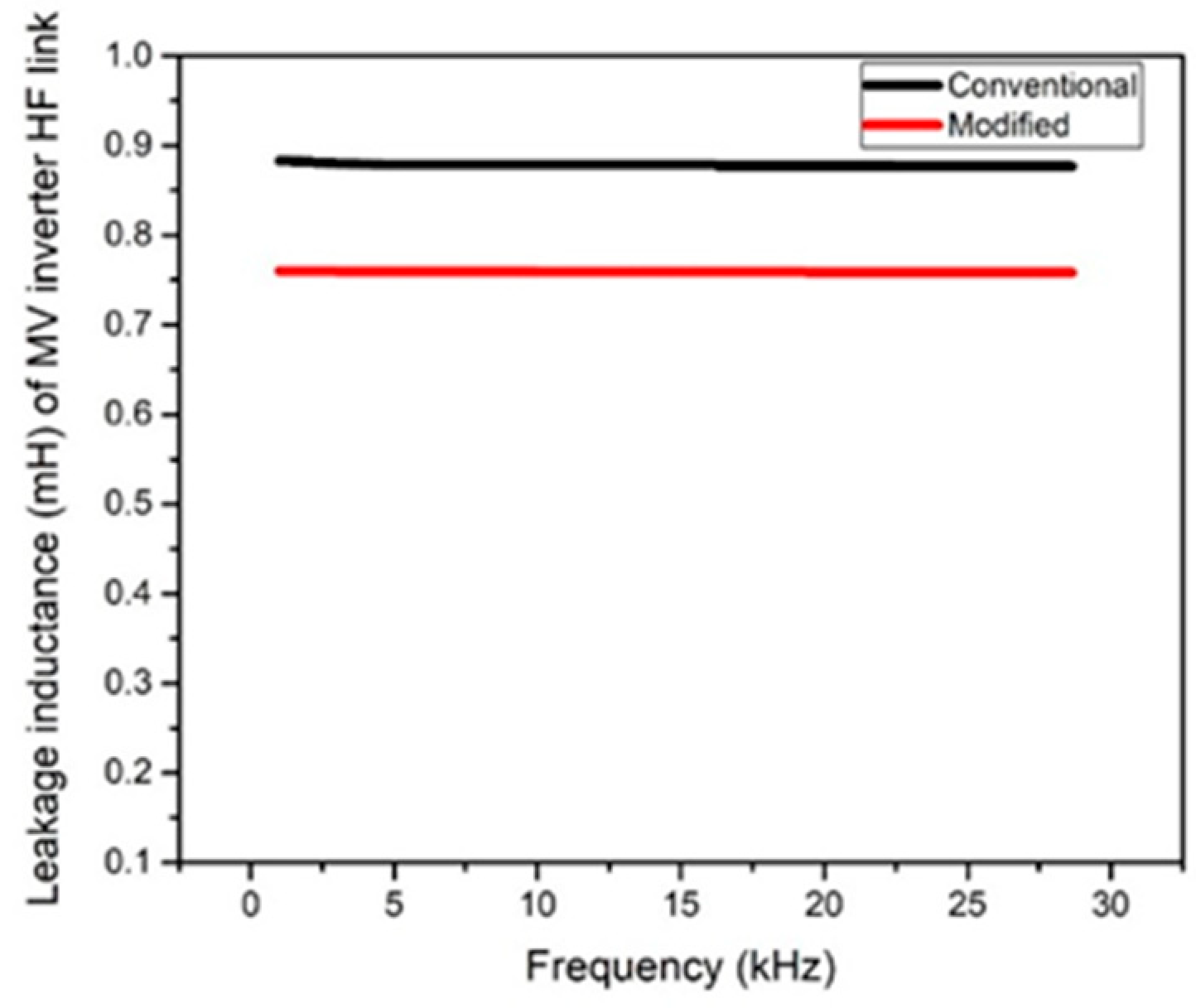
6.1. Toroidal Transformer with 180° Sectored Winding
6.2. Toroidal Transformer with 360° Sectored Winding
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gu, W.J.; Liu, R. A study of volume and weight vs. frequency for high-frequency transformers. In Proceedings of the IEEE Power Electronics Specialist Conference (PESC 1993), Seattle, WA, USA, 20–24 June 1993; pp. 1123–1129. [Google Scholar]
- Leibl, M.; Ortiz, G.; Kolar, J.W. Design and experimental analysis of a medium-frequency transformer for solid-state transformer applications. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 110–123. [Google Scholar] [CrossRef]
- Kulkarni, A.; John, V. New start-up scheme for HF transformer link photovoltaic inverter. IEEE Trans. Ind. Appl. 2017, 53, 232–241. [Google Scholar] [CrossRef]
- Basu, K.; Mohan, N. A high-frequency link single-stage PWM inverter with common-mode voltage suppression and source-based commutation of leakage energy. IEEE Trans. Power Electron. 2014, 29, 3907–3918. [Google Scholar] [CrossRef]
- De, D.; Ramanarayanan, V. A proportional $bm +$ multiresonant controller for three-phase four-wire high-frequency link inverter. IEEE Trans. Power Electron. 2010, 25, 899–906. [Google Scholar] [CrossRef]
- Hayashi, Y.; Matsugaki, Y.; Ninomiya, T. Design Consideration for High Step-up Nonisolated Multicellular dc-dc Converter for PV Micro Converters. Available online: https://www.hindawi.com/journals/je/2018/5098083/ (accessed on 11 June 2018).
- Kouro, S.; Leon, J.I.; Vinnikov, D.; Franquelo, L.G. Grid-connected photovoltaic systems: an overview of recent research and emerging PV converter technology. IEEE Ind. Electron. Mag. 2015, 9, 47–61. [Google Scholar] [CrossRef]
- Sathishkumar, P.; Krishna, T.N.V.; Himanshu; Khan, M.A.; Zeb, K.; Kim, H.-J. Digital soft start implementation for minimizing start up transients in high power DAB-IBDC converter. Energies 2018, 11, 956. [Google Scholar] [CrossRef]
- Alexander, S. Development of solar photovoltaic inverter with reduced harmonic distortions suitable for Indian sub-continent. Renew. Sustain. Energy Rev. 2016, 56, 694–704. [Google Scholar] [CrossRef]
- Sathishkumar, P.; Himanshu; Piao, S.; Khan, M.A.; Kim, D.-H.; Kim, M.-S.; Jeong, D.-K.; Lee, C.; Kim, H.-J. A blended SPS-ESPS control DAB-IBDC converter for a standalone solar power system. Energies 2017, 10, 1431. [Google Scholar] [CrossRef]
- Singh, R.; Taghizadeh, S.; Tan, N.M.L.; Pasupuleti, J. Battery energy storage system for PV output power leveling. J. Eng. 2018, 2018, 5098083. Available online: https://www.hindawi.com/journals/ape/2014/796708/ (accessed on 11 June 2018). [CrossRef]
- Bolduc, P.; Lehmicke, D.; Smith, J. Performance of a grid-connected PV system with energy storage. In Proceedings of the 23th IEEE Photovoltaic Specialists Conference (Cat. No.93CH3283-9), Louisville, KY, USA, 10–14 May 1993; pp. 1159–1162. [Google Scholar]
- Tan, N.M.L.; Abe, T.; Akagi, H. Design and performance of a bidirectional isolated DC–DC converter for a battery energy storage system. IEEE Trans. Power Electron. 2012, 27, 1237–1248. [Google Scholar] [CrossRef]
- McBee, K.D. Transformer aging due to high penetrations of PV, EV charging, and energy storage applications. In Proceedings of the 2017 Ninth Annual IEEE Green Technologies Conference (GreenTech), Denver, CO, USA, 29–31 March 2017; pp. 163–170. [Google Scholar]
- Bojoi, R.I.; Limongi, L.R.; Roiu, D.; Tenconi, A. Enhanced power quality control strategy for single-phase inverters in distributed generation systems. IEEE Trans. Power Electron. 2011, 26, 798–806. [Google Scholar] [CrossRef]
- Eltawil, M.A.; Zhao, Z. Grid-connected photovoltaic power systems: Technical and potential problems—A review. Renew. Sustain. Energy Rev. 2010, 14, 112–129. [Google Scholar] [CrossRef]
- Popavath, L.N.; Kaliannan, P. Photovoltaic-STATCOM with Low Voltage Ride through Strategy and Power Quality Enhancement in a Grid Integrated Wind-PV System. Electronics 2018, 7, 51. [Google Scholar] [CrossRef]
- Real-Calvo, R.; Moreno-Munoz, A.; Gonzalez-De-La-Rosa, J.J.; Pallares-Lopez, V.; Gonzalez-Redondo, M.J.; Moreno-Garcia, I.M. An embedded system in smart inverters for power quality and safety functionality. Energies 2016, 9, 219. [Google Scholar] [CrossRef]
- Li, Y.; Oruganti, R. A flyback-CCM inverter scheme for photovoltaic AC module application. Aust. J. Electr. Electron. Eng. 2009, 6, 301–309. [Google Scholar] [CrossRef]
- Pairodamonchai, P.; Suwankawin, S.; Sangwongwanich, S. Design and implementation of a hybrid output EMI filter for high-frequency common-mode voltage compensation in PWM inverters. IEEE Trans. Ind. Appl. 2009, 45, 1647–1659. [Google Scholar] [CrossRef]
- Wang, F.; Duarte, J.L.; Hendrix, M.A.M.; Ribeiro, P.F. Modeling and analysis of grid harmonic distortion impact of aggregated DG inverters. IEEE Trans. Power Electron. 2011, 26, 786–797. [Google Scholar] [CrossRef]
- Grady, W.M.; Santoso, S. Understanding power system hannonics. IEEE Power Eng. Rev. 2001, 21, 8–11. [Google Scholar] [CrossRef]
- Abdi, B.; Ranjbar, A.H.; Farabi, V.; Yazdanparast, M.S. Effect of transformer’s parameters on harmonic generation. Energy Procedia 2011, 12, 679–685. [Google Scholar] [CrossRef]
- Murthy-Bellur, D.; Kazimierczuk, M.K. Winding losses caused by harmonics in high-frequency flyback transformers for pulse-width modulated dc-dc converters in discontinuous conduction mode. IET Power Electron. 2010, 3, 804–817. [Google Scholar] [CrossRef]
- Zolfaghari, A.; Chan, A.; Razavi, B. Stacked inductors and transformers in CMOS technology. IEEE J. Solid-State Circuits 2001, 36, 620–628. [Google Scholar] [CrossRef]
- Portolan, A.; Hofsajer, I.W. The analysis and design of an inter-winding shielding structure of a high frequency transformer. In Proceedings of the 2007 IEEE Power Engineering Society Conference and Exposition in Africa-PowerAfrica, Johannesburg, South Africa, 16–20 July 2007; pp. 1–6. [Google Scholar]
- Nguyen-Duy, K.; Ouyang, Z.; Knott, A.; Andersen, M.A.E. Minimization of the transformer inter-winding parasitic capacitance for modular stacking power supply applications. In Proceedings of the 2014 16th IEEE European Conference on Power Electronics and Applications, Lappeenranta, Finland, 26–28 August 2014; pp. 1–10. [Google Scholar]
- Ali, M.U.; Nengroo, S.H.; Khan, M.A.; Zeb, K.; Kamran, M.A.; Kim, H.J. A real-time simulink interfaced fast-charging methodology of lithium-ion batteries under temperature feedback with fuzzy logic control. Energies 2018, 11, 1122. [Google Scholar]
- Ajami, A.; Farakhor, A.; Ardi, H. Minimisations of total harmonic distortion in cascaded transformers multilevel inverter by modifying turn ratios of the transformers and input voltage regulation. IET Power Electron. 2014, 7, 2687–2694. [Google Scholar] [CrossRef]
- Kashyap, M.; Kansal, S. Temperature control in transformer using intelligent system. In Proceedings of the 2015 2nd IEEE International Conference on Recent Advances in Engineering Computational Sciences (RAECS), Chandigarh, India, 21–22 December 2015; pp. 1–6. [Google Scholar]
- Hurezeanu, I.; Nicola, C.I.; Sacerdoţianu, D.; Nicola, M.; Aciu, A.M.; Niţu, M.C. Temperature control and monitoring system for power transformer windings using fiber optic sensors. In Proceedings of the 2016 IEEE International Symposium on Fundamentals of Electrical Engineering (ISFEE), Bucharest, Romania, 30 June–2 July 2016; pp. 1–4. [Google Scholar]
- Blache, F.; Keradec, J.P.; Cogitore, B. Stray capacitances of two winding transformers: equivalent circuit, measurements, calculation and lowering. In Proceedings of the 1994 IEEE Industry Applications Society Annual Meeting, Denver, CO, USA, 2–6 October 1994; pp. 1211–1217. [Google Scholar]
- Conway, D.W. Shielded Electrical Wire Construction, and Transformer Utilizing the same for Reduction of Capacitive Coupling. U.S. Patent 5,012,125, 30 April 1991. [Google Scholar]
- De León, F.; Purushothaman, S.; Qaseer, L. Leakage inductance design of toroidal transformers by sector winding. IEEE Trans. Power Electron. 2014, 29, 473–480. [Google Scholar] [CrossRef]
- Mathew, A.P.; Oksman, K.; Sain, M. Mechanical properties of biodegradable composites from poly lactic acid (PLA) and microcrystalline cellulose (MCC). J. Appl. Polym. Sci. 2005, 97, 2014–2025. [Google Scholar] [CrossRef]
- Silverajah, V.S.G.; Ibrahim, N.A.; Zainuddin, N.; Yunus, W.M.Z.W.; Hassan, H.A. Mechanical, thermal and morphological properties of poly (lactic acid)/epoxidized palm olein blend. Molecules 2012, 17, 11729–11747. [Google Scholar] [CrossRef] [PubMed]
- Mclyman, C.W. Transformer and Inductor Design Handbook; CRC Press: Boca Raton, FL, USA, 2004; Available online: https://www.taylorfrancis.com/books/9780203913598 (accessed on 31 March 2004).
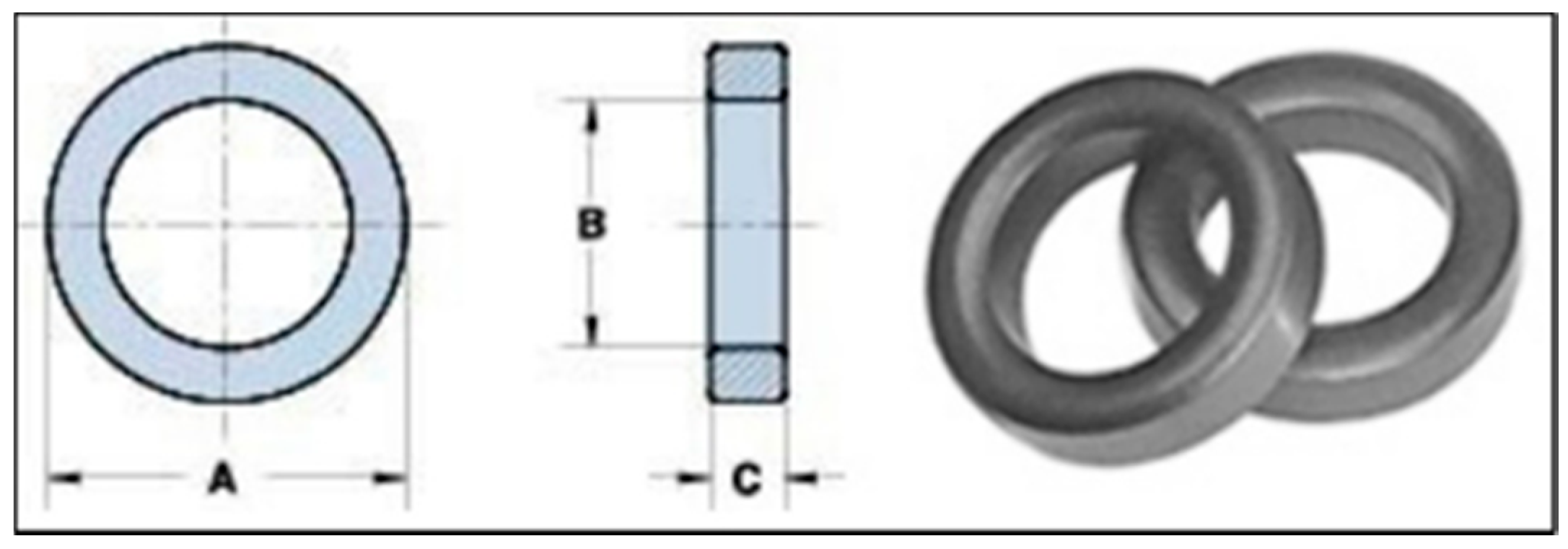


| Dim | mm | Mm tol | Nominal |
|---|---|---|---|
| A | 61.00 | ±1.30 | 2.400 |
| B | 35.55 | ±0.85 | 1.400 |
| C | 12.70 | ±0.50 | 0.500 |
| Electrical Properties | |
|---|---|
| AL (nH) | 2950 ± 25% |
| AE (cm2) | 1.58000 |
| ∑I/A (cm−1) | 9.20 |
| Ie (cm) | 14.50 |
| Ve (cm3) | 22.80000 |
| THDV | THDI | Risk |
|---|---|---|
| <8% | <5% | normal situation considerable |
| 8–15% | 5–50% | Minor harmonic pollution with malfunctions possibility |
| >15% | >50% | major harmonic pollution with malfunctions probability |
| Prototypes Physical Properties | Case 1 | Case 2 | Case 3 | Case 4 |
|---|---|---|---|---|
| Copper Wire standard | 24 AWG | 24 AWG | 24 AWG | 24 AWG |
| Primary Turns | 116 | 116 | 220 | 220 |
| Secondary Turns | 116 | 116 | 220 | 220 |
| Core Material (Table 1) | Ferrite 77 | Ferrite 77 | Ferrite77 | Ferrite 77 |
| Core shape | Ring | Ring | Ring | Ring |
| Permittivity (F/m) | 8.85 × 10−12 (Air) | 8.4190×10−12 (Air + PLA) | 8.85×10−12 (Air) | 8.419 × 10−12 (Air + PLA) |
| Inner Radius (mm) | 17.775 | 15.275 | 17.775 | 15.275 |
| Outer Radius (mm) | 30.5 | 32.5 | 30.5 | 32.5 |
| Primary Voltage (V) | 24 | 24 | 24 | 24 |
| Secondary Voltage (V) | ~24 | ~24 | ~24 | ~24 |
| Frequency (kHz) | 1–30 | 1–30 | 1–30 | 1–30 |
| 17.265 | 14.765 | 16.755 | 14.765 | |
| 30.5 | 32.5 | 31.01 | 32.5 | |
| 17.265 | 17.265 | 17.265 | 17.265 | |
| 30.5 | 30.5 | 30.5 | 30.5 |
| Case 1 | ||||||
| E1 | E2 | E3 | E4 | Etotal | Capacitanceeq (F) | |
| Energy (J) | 5.63 × 10−10 | 3.87 × 10−10 | 3.54 × 10−10 | 2.87 × 10−10 | 1.59 × 10−10 | 2.76 × 10−12 |
| Percentage % | 35.4 | 24.3 | 22.3 | 18 | 100 | |
| Case 2 | ||||||
| E1 | E2 | E3 | E4 | Etotal | Capacitanceeq (F) | |
| Energy (J) | 5.31 × 10−10 | 3.74 × 10−10 | 3.66 × 10−10 | 2.94 × 10−10 | 1.57 × 10−9 | 2.72 × 10−12 |
| Percentage % | 33.9 | 23.9 | 23.4 | 18.8 | 100 | |
| Case 3 | ||||||
| E1 | E2 | E3 | E4 | Etotal | Capacitanceeq (F) | |
| Energy (J) | 5.69 × 10−10 | 3.87 × 10−10 | 3.56 × 10−10 | 2.90 × 10−10 | 1.60 × 10−9 | 2.78 × 10−12 |
| Percentage % | 35.5 | 24.2 | 22.2 | 18.1 | 100 | |
| Case 4 | ||||||
| E1 | E2 | E3 | E4 | Etotal | Capacitanceeq (F) | |
| Energy (J) | 5.29 × 10−10 | 3.73 × 10−10 | 3.73 × 10−10 | 3.00 × 10−10 | 1.57 × 10−9 | 2.73 × 10−12 |
| Percentage % | 33.6 | 23.7 | 23.7 | 19 | 100 | |
| Source Input Voltage (V) | Case | THDV % | THDI % | ||
|---|---|---|---|---|---|
| Primary | Secondary | Primary | Secondary | ||
| 24 | 1 | 45.53 | 22.34 | 5.6 | 7.20 |
| 24 | 2 | 34.70 | 22.15 | 12.22 | 11.85 |
| 24 | 3 | 11.92 | 16.33 | 48.19 | 49.56 |
| 24 | 4 | 9.81 | 14.94 | 43.06 | 44.32 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Himanshu; Singh, H.; Kumar, P.S.; Ali, M.U.; Lee, H.Y.; Khan, M.A.; Park, G.S.; Kim, H.-J. High Frequency Transformer’s Parasitic Capacitance Minimization for Photovoltaic (PV) High-Frequency Link-Based Medium Voltage (MV) Inverter. Electronics 2018, 7, 142. https://doi.org/10.3390/electronics7080142
Himanshu, Singh H, Kumar PS, Ali MU, Lee HY, Khan MA, Park GS, Kim H-J. High Frequency Transformer’s Parasitic Capacitance Minimization for Photovoltaic (PV) High-Frequency Link-Based Medium Voltage (MV) Inverter. Electronics. 2018; 7(8):142. https://doi.org/10.3390/electronics7080142
Chicago/Turabian StyleHimanshu, Harsimran Singh, Pandiyan Sathish Kumar, Muhammad Umair Ali, Ho Yeong Lee, Muhammad Adil Khan, Gwan Soo Park, and Hee-Je Kim. 2018. "High Frequency Transformer’s Parasitic Capacitance Minimization for Photovoltaic (PV) High-Frequency Link-Based Medium Voltage (MV) Inverter" Electronics 7, no. 8: 142. https://doi.org/10.3390/electronics7080142
APA StyleHimanshu, Singh, H., Kumar, P. S., Ali, M. U., Lee, H. Y., Khan, M. A., Park, G. S., & Kim, H.-J. (2018). High Frequency Transformer’s Parasitic Capacitance Minimization for Photovoltaic (PV) High-Frequency Link-Based Medium Voltage (MV) Inverter. Electronics, 7(8), 142. https://doi.org/10.3390/electronics7080142