Distributed Sensory System of Surface Cracks Monitoring Based on Electrical Impedance Tomography
Abstract
1. Introduction
2. Modified Method of Surface Cracks Registration and Monitoring
- Formation of the initial conductivity matrix named MCI by measuring the conductivity between all pairs of contacts along the perimeter of a defect-free sensor film. The dimension of the MCI matrix is NC − 1 × NC − 1, where NC is a total number of boundary contacts. The element of the m-th row and the n-th column of the MCI matrix is equal to the conductivity measured between the m-th and n-th contacts. The MCI matrix is formed once at the calibration stage of the monitoring system, and stored in the system memory;
- Formation of the normalized matrix of film conductivity named MCN during registration and monitoring of cracks. The dimension of the MCN matrix is equal to the dimension of MCI. The element of the m-th row and the n-th column of the MCN matrix is defined as the result from dividing the conductivity of the sensor film measured between the m-th and n-th contacts in the monitoring process by the value of the element of the m-th row and the n-th column of the MCI matrix. The MCN matrix is redefined with the frequency specified by the requirements for the parameters of the monitoring system;
- Reconstruction of the image of cracks using the normalized MCN matrix of conductivity of film on a two-dimensional rectangular grid:where i, j are the grid nodes indexes; xi, yj are the grid nodes coordinates; I is the number of grid nodes along the x coordinate; J is the number of grid nodes along the y coordinate;R = {(xi, yj) | i = 1, 2, …, I; j = 1, 2, …, J},
- Digital filtering of cracks images in order to adjust the sensitivity threshold of the monitoring system and optimize the contrast of the recorded image.
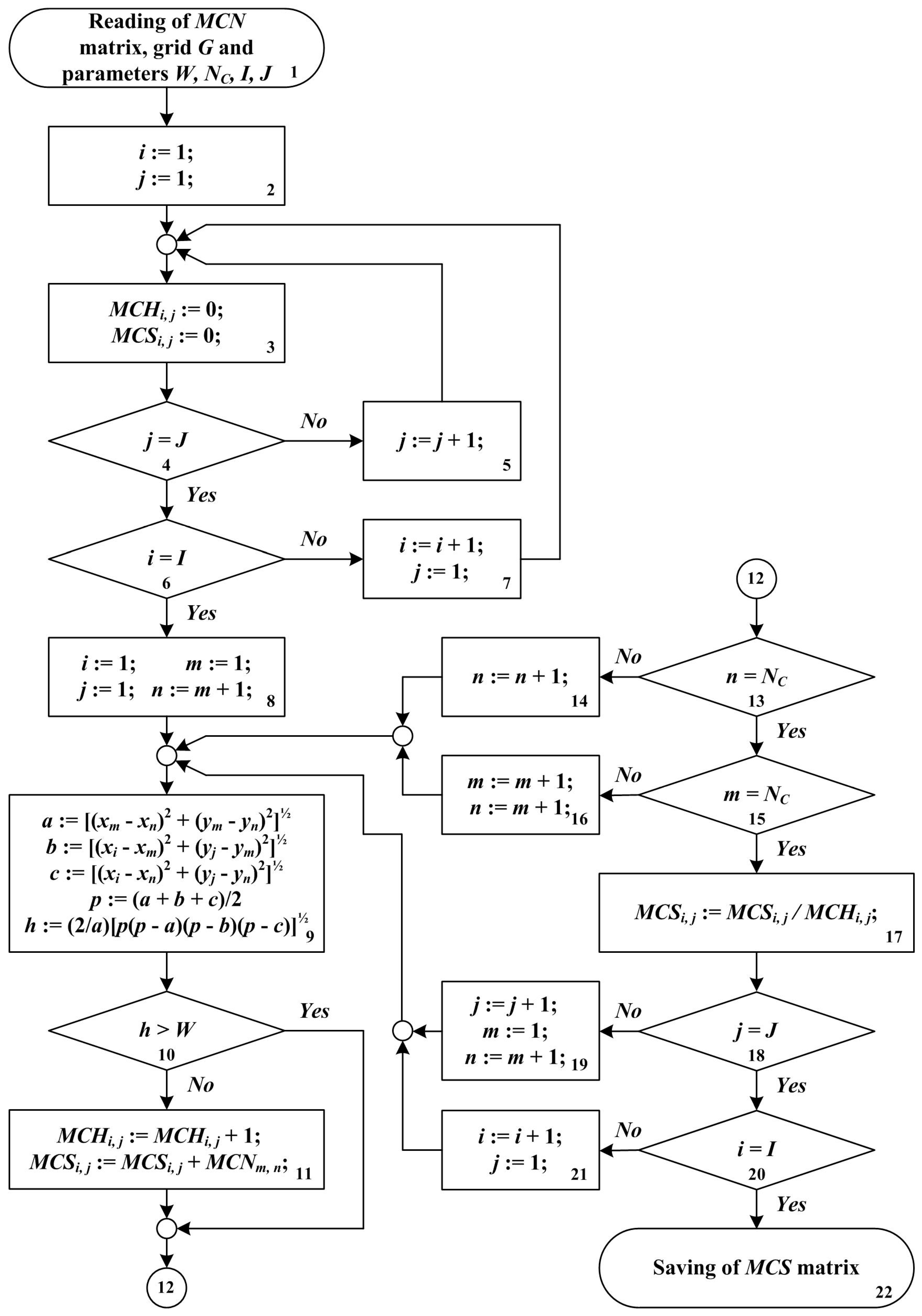
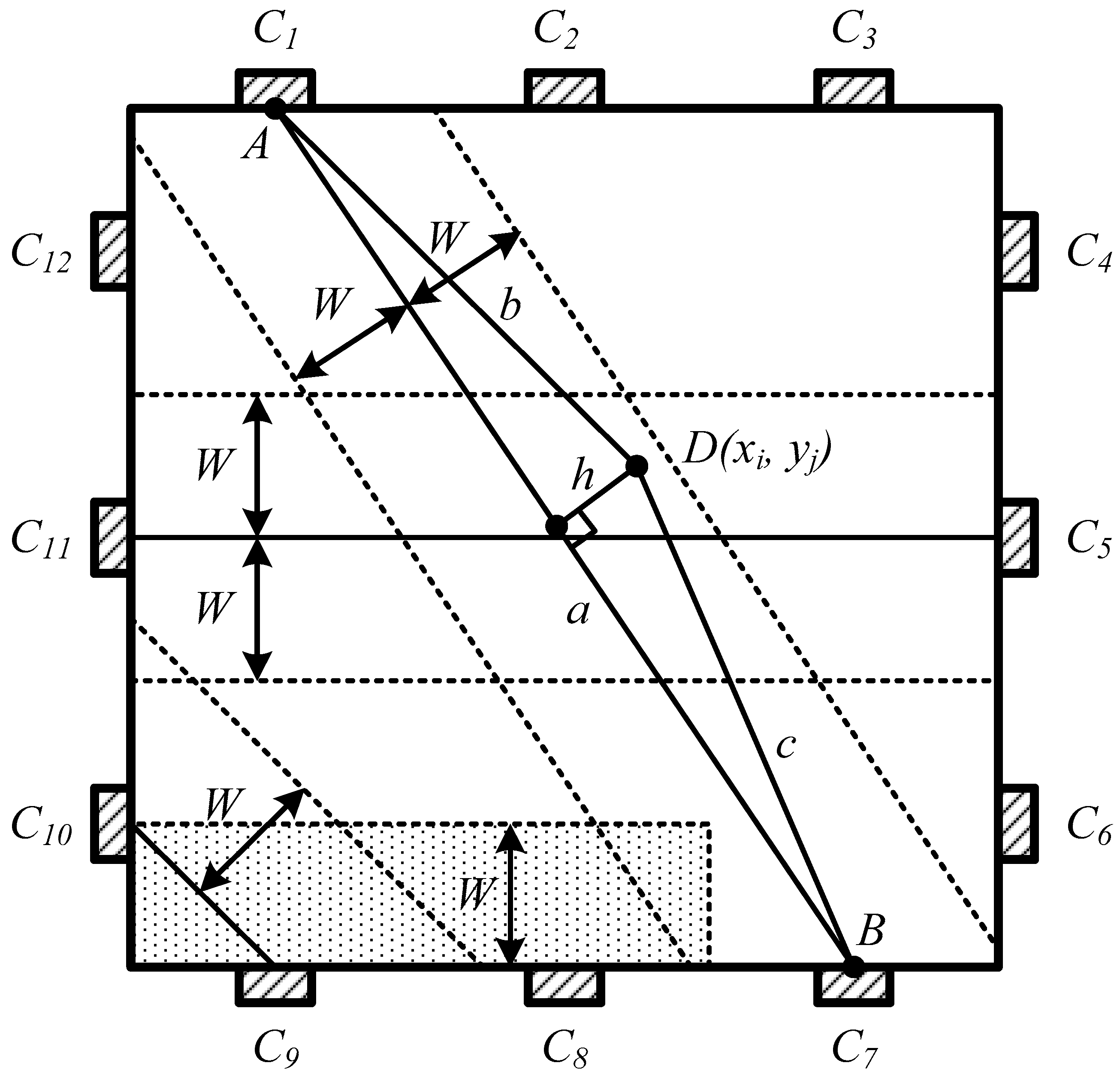
- Loading of the normalized matrix of conductivity MCN, grid R and parameter values W, NC, I, J (block 1 in Figure 1), where W is the half-width of the “conditional conduction channel” (Figure 2). Between adjacent contacts, the width of the CCC is assumed to be W; for example, between the contacts C8 and C9 in Figure 2. The parameter W is a tuning parameter. In the proposed method, the parameter W is a constant for all pairs of boundary contacts, including adjacent contacts. The minimum value of W is determined by the requirement that there are no nodes of the coordinate grid (xi, yj) that are not included in any CCC. Consequently in this case, W is defined by the sensor film size and the number of boundary contacts. However, the other versions of the proposed method with dependence on the W parameter on the distances between boundary contacts will be considered in following works;
- Formation of a matrix of conditional conduction channels named MCH and a matrix of averaged normalized values of the conductivity named MCS of dimension I × J corresponding to the dimension of the coordinate grid R, with zero elements (blocks 2–7 in Figure 1);
- Sequential execution for all nodes of the grid (xi, yj) in the following procedures:
- Determination of the total number of ССCs, which include the node (xi, yj), and assigning this value to the element of the i-th row and the j-th column of the MCH matrix (blocks 8–16 in Figure 1). The implementation of this procedure is shown in Figure 2 by the example of determining the belonging of the point D(xi, yj) to the conditional conduction channel between the contacts C1 and C7. For this purpose, a triangle ABD with vertices A and B at the central points of contacts C1 and C7 is constructed. The height h, dropped to the side AB from the vertex D is determined in accordance with the expressions presented in block 9 in Figure 1, where a, b, and c are the length of the sides of triangle ABD, and p is half of the triangle ABD perimeter.If h ≤ W then node (xi, yj) is included in the corresponding CCC and the value of element MCHi,j is incremented by 1 (blocks 10 and 11 in Figure 1);
- Determination of the element value of the i-th row and the j-th column of the matrix of averaged normalized values of the conductivity MCS (blocks 8–20 in Figure 1) by summing the elements of the normalized matrix of conductivity of the film MCN with the indexes m, n corresponding to the pairs of contacts whose CCCs include the (xi, yj) node (block 11 in Figure 1), and then dividing the sum by the element value of the i-th row and the j-th column of the MCH matrix (block 17 in Figure 1);
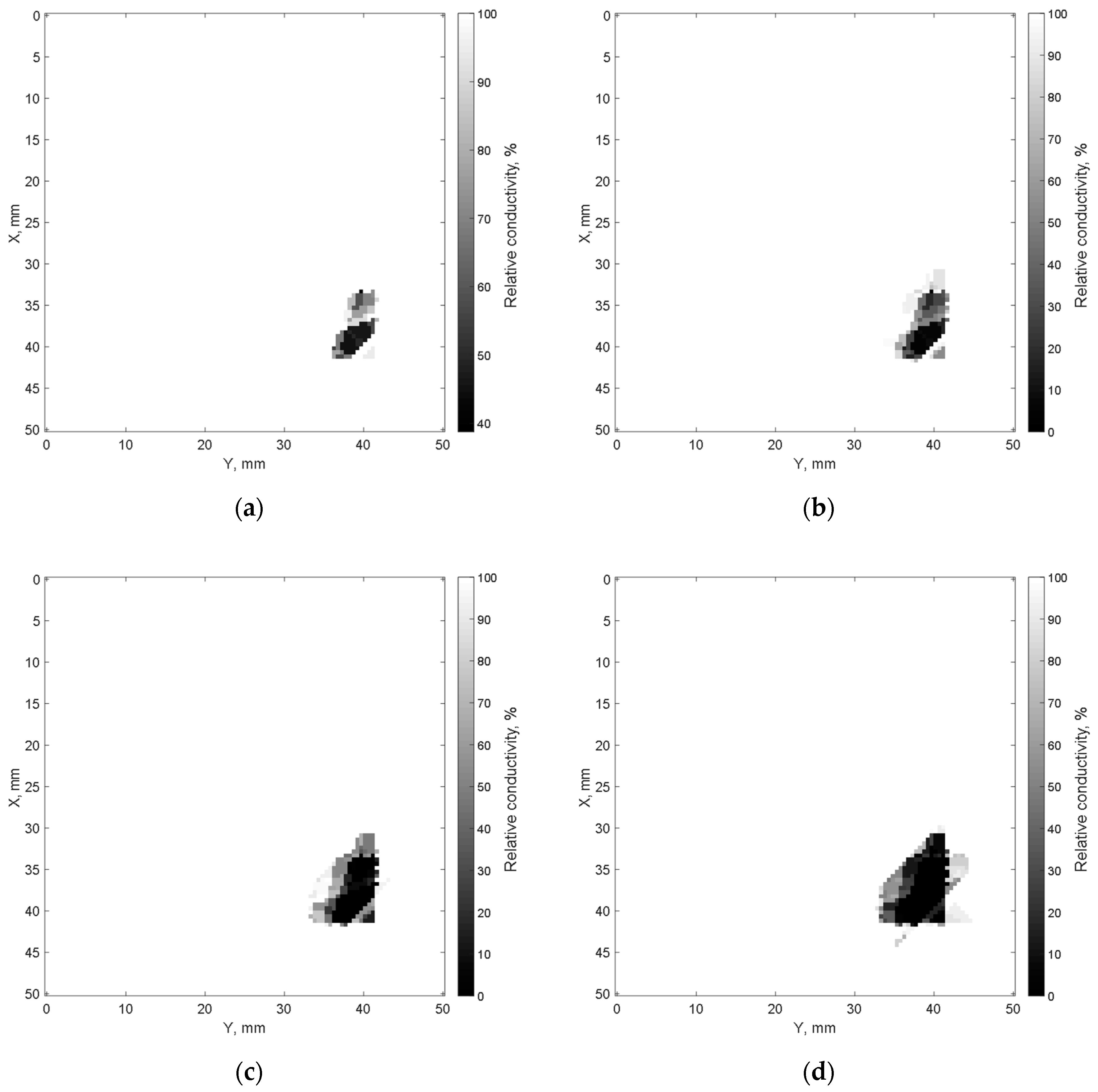
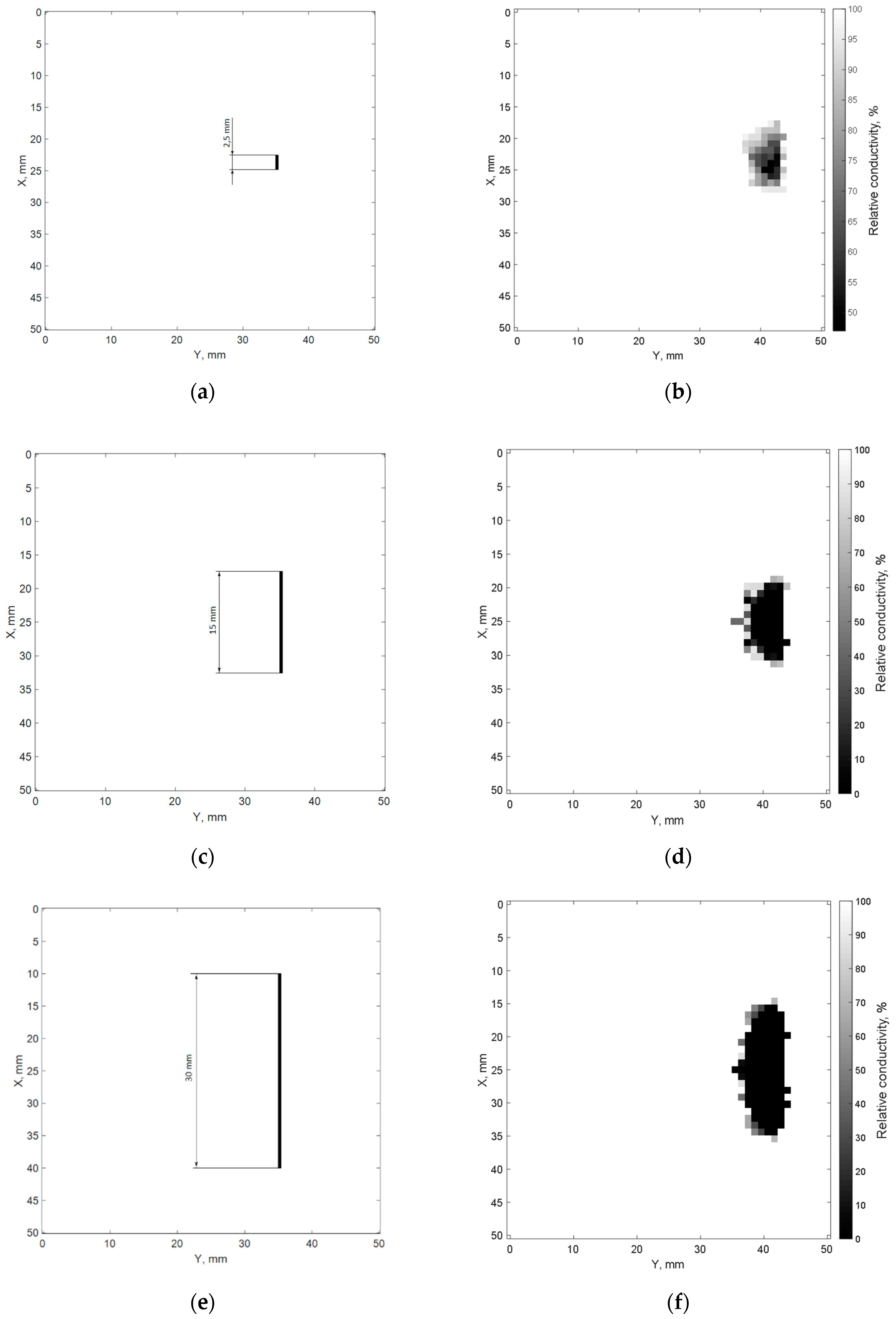
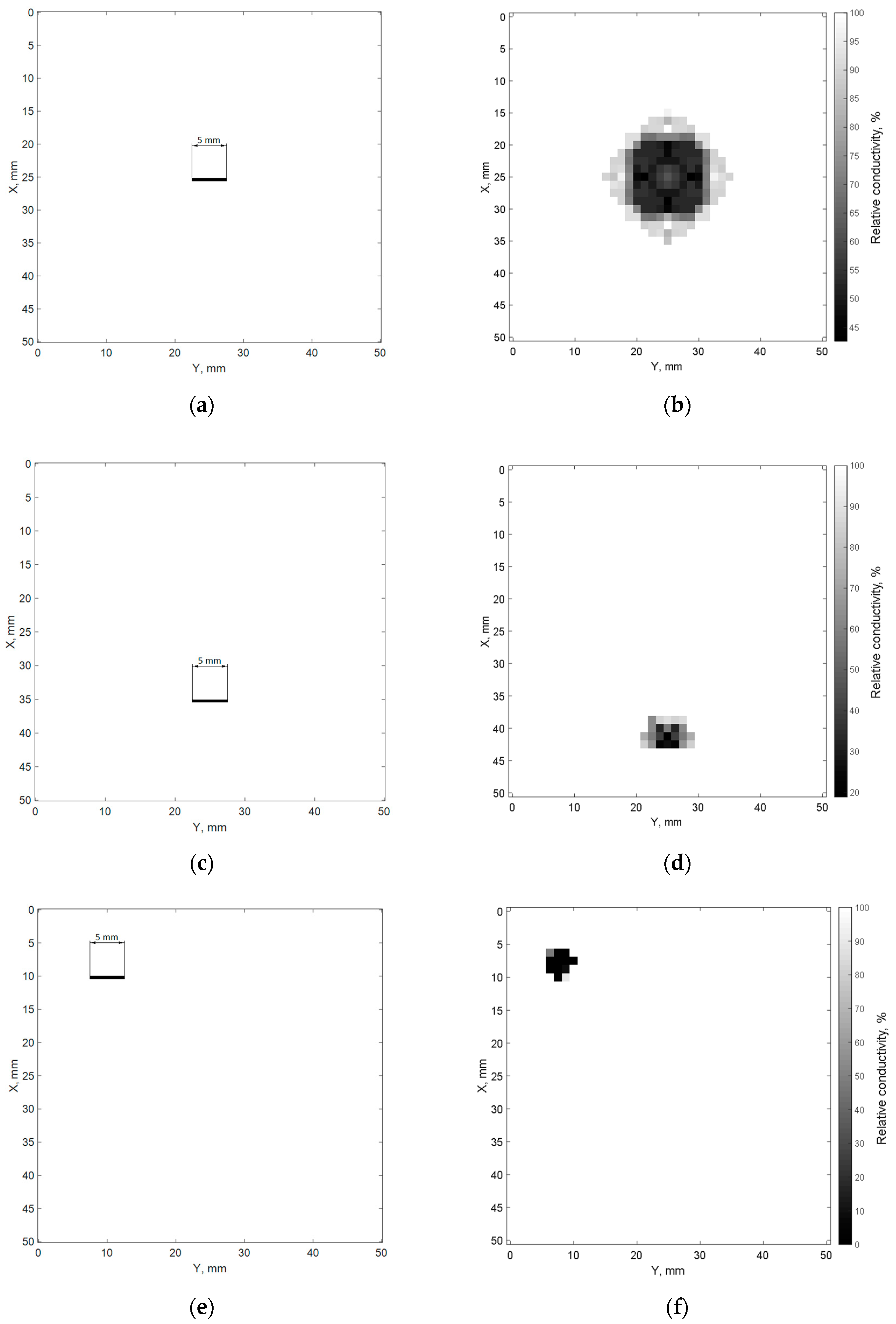
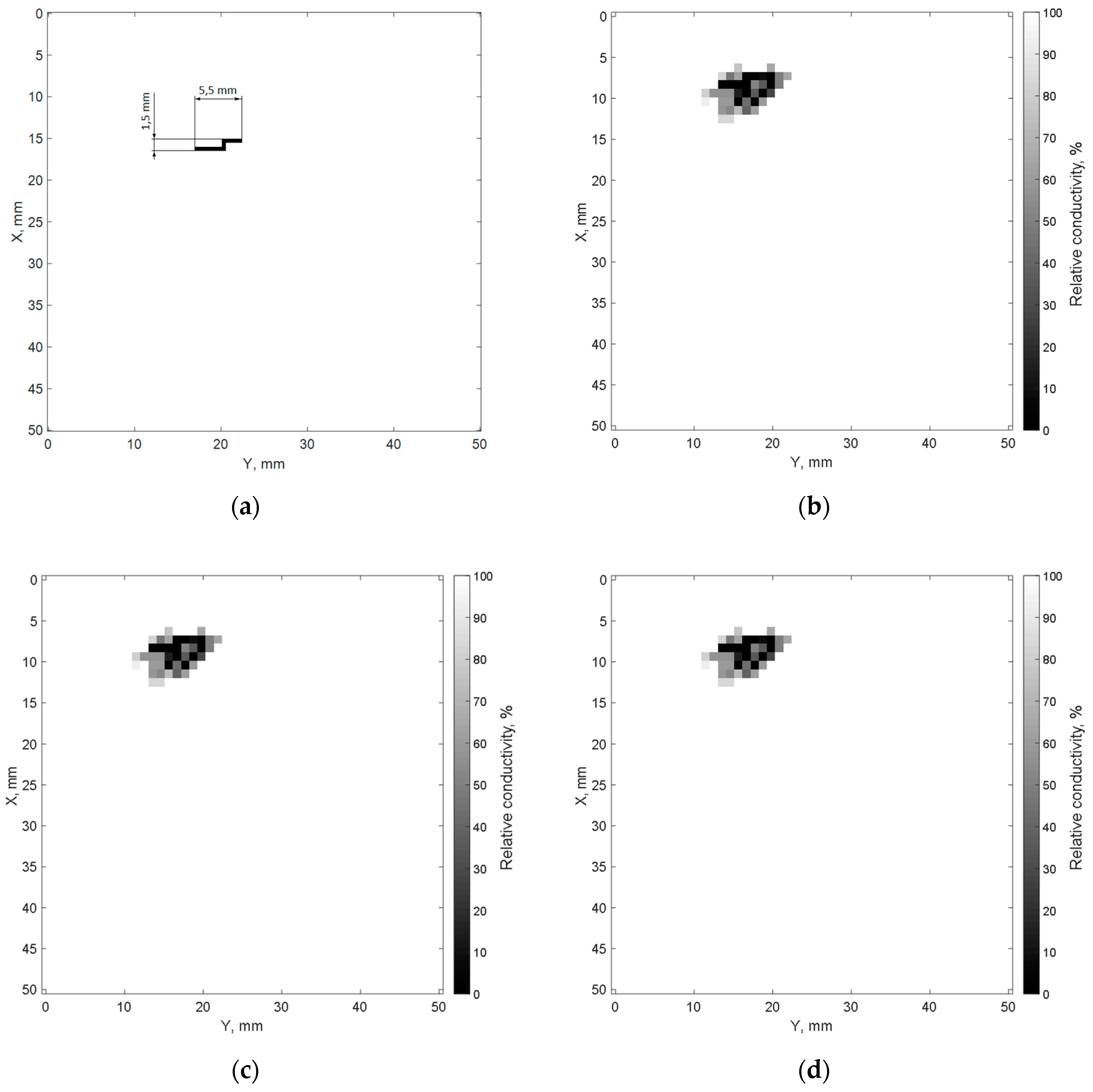
- Storing and transferring the matrix of averaged normalized values of specific conductivity MCS to a block of cracks images with digital filtering in order to optimize the contrast of the registered image (block 22 in Figure 1). Digital filtration of cracks images was performed in accordance with expressions (12) and (13):MCFi,j = MCSi,j + γ⋅(MCSi,j − CNTH);where MCSi,j is the element of the i-th row and j-th column of the matrix of average normalized values of specific conductivity; CNTH is a threshold normalized value of specific conductivity; γ, and KF are the digital filter coefficients; MCFi,j is an element of the i-th row and the j-th column of the matrix named MCF from the results of digital filtering.CNTH = min(MCS) + KF⋅[1 − min(MCS)],
3. Imitative Modeling Software Package
- Recording of the nodal values of the defect-free sensor film specific conductivity σi,j in the matrix MCI. Initial spatial distribution of the specific conductivity may be defined as uniform to imitate an ideal sensor film or as random given fluctuations of the conductivity to imitate a real film;
- Imitation of cracks by setting low values of specific conductivity σi,j in certain grid nodes (xi, yj) according to the necessary form and size of the crack;
- Numerical solution of the finite-difference representation (18) of the Laplace Equation (1) on the two-dimensional rectangular grid (11) for the sensor film without defects, as well as for the sensor film with cracks:where i, j are the node indexes excluding boundary nodes; σi,j, σi+1,j, σi–1,j, σi,j+1, σi,j–1 are the nodal values of the sensor film specific conductivity; φi,j, φi+1,j, φi–1,j, φi,j+1, φi,j–1 are the nodal values of the electrostatic potential; hx is a grid step along the direction x; hy is a grid step along the direction y.[(σi+1,j + σi,j)⋅(φi+1,j − φi,j) − (σi,j + σi–1,j)⋅(φi,j − φi–1,j)]/(2⋅hx2) +
+ [(σi,j+1 + σi,j)⋅(φi,j+1 − φi,j) − (σi,j + σi,j–1)⋅(φi,j − φi,j–1)]/(2⋅hy2) = 0,
i = 2, 3, …, I – 1; j = 2, 3, …, J − 1,For the contacts Cm and Cn, between which the conductivity is measured, the Dirichlet boundary conditions (19) are used:where Um,n is the voltage between contacts Cm and Cn.φi,j = Um,n,For the remaining boundaries of the sensor film the finite-difference representation (20) of the Neumann boundary conditions (3) are used:(φ2,j − φ1,j)/hx = 0;
(φI,j − φI–1,j)/hx = 0;
(φi,2 − φi,1)/hy = 0;
(φi,J − φi,J–1)/hy = 0; - Calculation of the spatial distributions of the normal component of current density jC on the boundaries of contacts Cm and Cn for the sensor film without defects, as well as for the sensor film with cracks using expressions (21) for the different locations of the contacts:jC1,j = σ1,j⋅(φ2,j − φ1,j)/hx;
jCI,j = σI,j⋅(φI,j − φI–1,j)/hx;
jCi,1 = σi,1 ⋅(φi,2 − φi,1)/hy;
jCi,J = σi,J⋅(φi,J − φi,J–1)/hy; - Calculation of the currents ICm and ICn, flowing through the contacts Cm and Cn, between which the conductivity of the sensor film without cracks is measured by numerical integration of the normal component of the current density over the area of the contacts. Verification of the condition (22):ICm + ICn = 0;
- Calculation of the currents JCm and JCn, flowing through the contacts Cm and Cn, between which the conductivity of the sensor film with cracks is measured, by numerical integration of the normal component of current density over the area of the contacts. Verification of the condition (23):JCm + JCn = 0;
- Assignment to the element of the m-th row and the n-th column of the matrix MCI of the conductivity value Gm,n between the contacts Cm and Cn for the film without cracks, determined by the expression (24):MCIm,n = Gm,n = |ICm|/Um,n;
- Assignment to the element of the m-th row and the n-th column of the matrix MCN of the conductivity value between the contacts Cm and Cn for the film with cracks normalized by the MCIm,n, determined by the expression (25):MCNm,n = (|JCm|/Um,n)/MCIm,n.
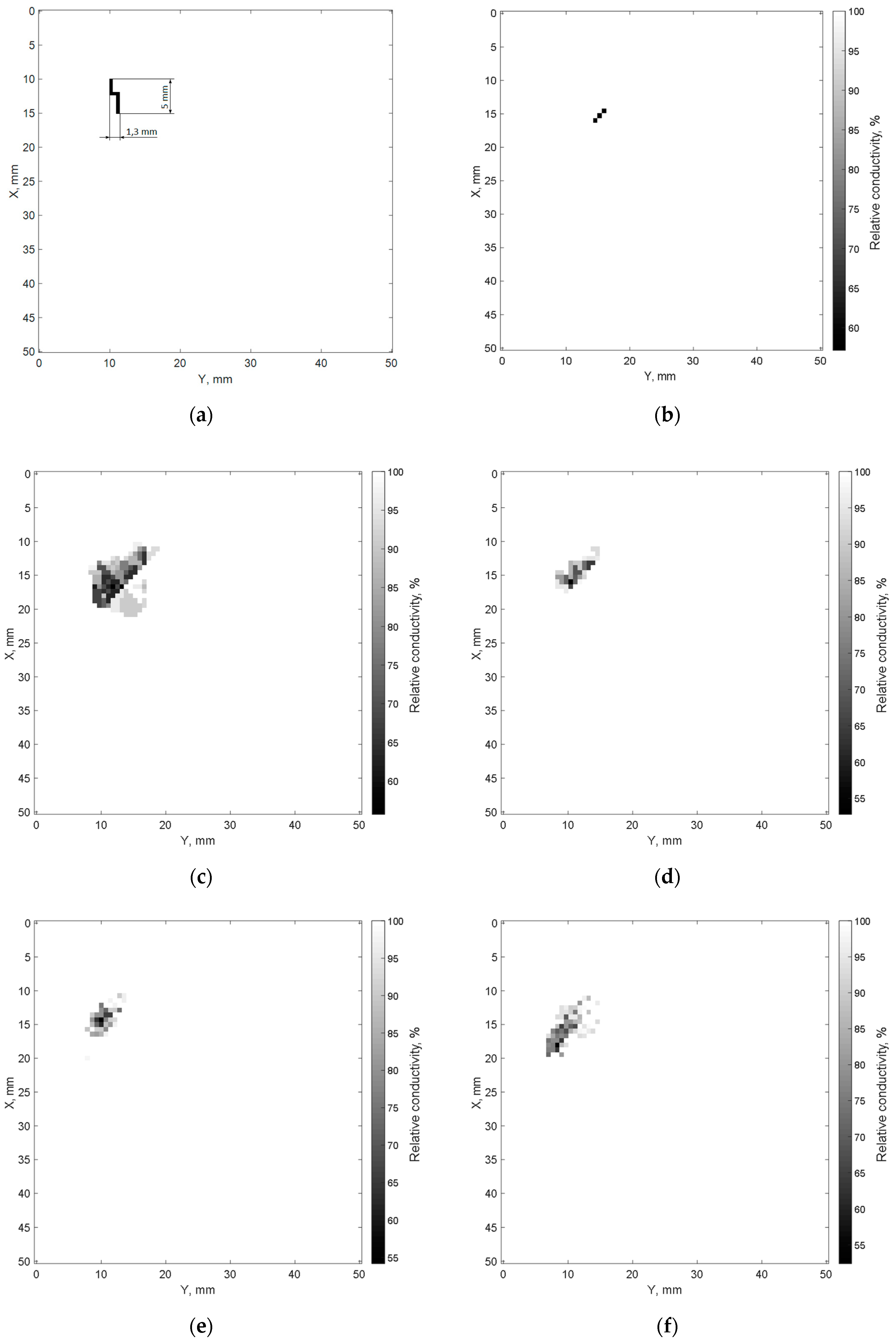
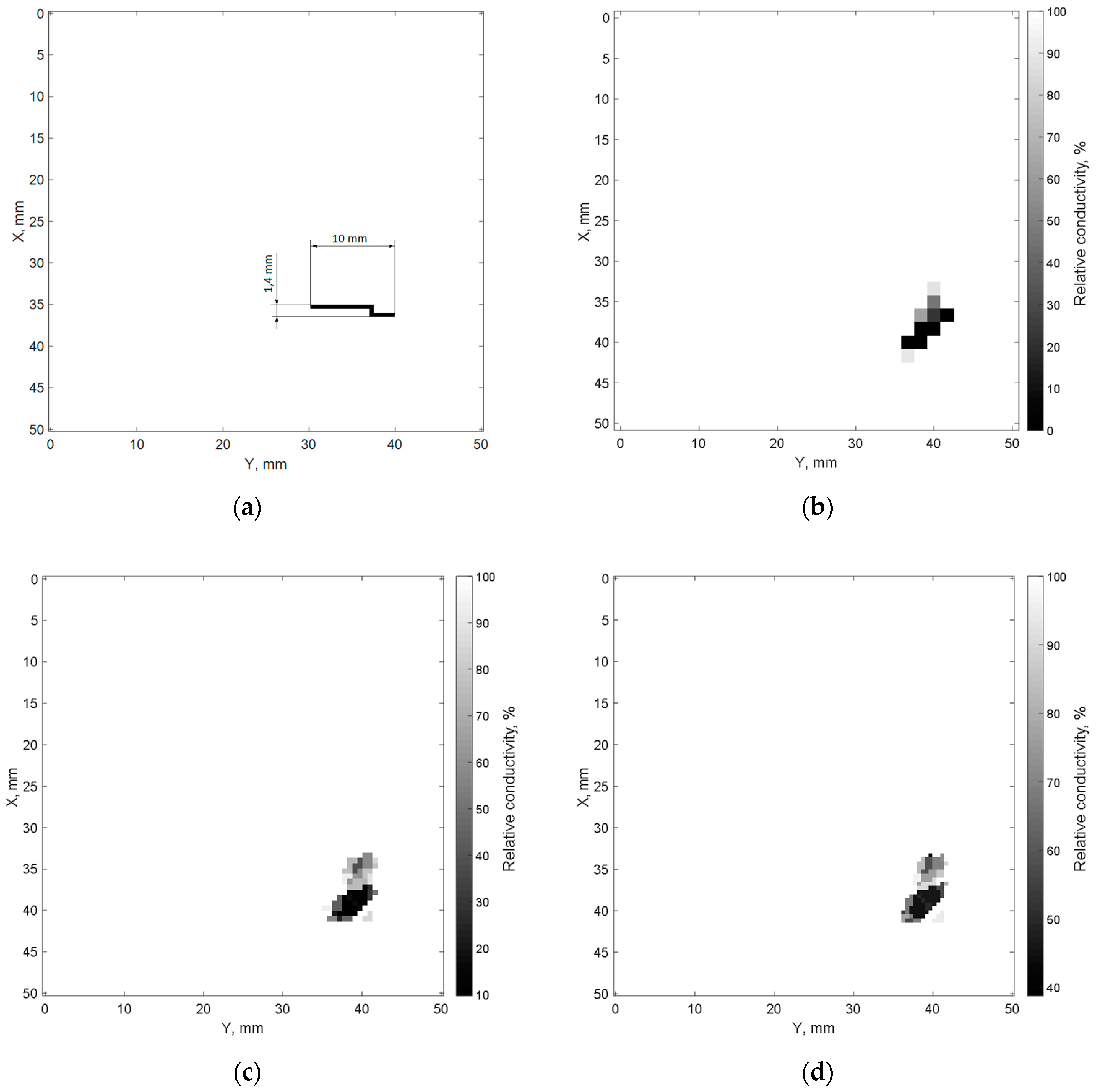
4. Results of Imitative Modeling and Discussion
- Number of contacts to the sensor film;
- Number of grid nodes;
- Digital filter parameters;
- Size of cracks;
- Location of cracks;
- Specific conductivity of the initial (defect-free) sensor film.
- supplement the system of registering and monitoring cracks by the temperature sensor of the sensor film;
- when forming the initial MCI conductivity matrix, carry out conductivity measurements between all pairs of contacts along the perimeter of a defect-free sensor film in the entire required temperature range with a certain increment in temperature set in accordance with the required accuracy of determining the size and location of the cracks. The MCI matrixes obtained for all temperature values must be stored in the system memory;
- when forming the normalized MCN matrix of film conductivity during the registration and monitoring of cracks, perform the normalization in accordance with expression (25) using elements of the MCI matrix corresponding to the current temperature sub-band recorded by the temperature sensor.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References and Note
- Rathod, V.R.; Anand, R.S.; Ashok, A. Comparative analysis of NDE techniques with image processing. Nondestruct. Test. Eval. 2012, 27, 305–326. [Google Scholar] [CrossRef]
- Turnbull, A. Characterising the early stages of crack development in environment-assisted cracking. Corros. Eng. Sci. Technol. 2017, 52, 533–540. [Google Scholar] [CrossRef]
- Robinson, M.J.; Strutt, J.E. On-line monitoring of crack propagation. Metals Technol. 1982, 9, 251–256. [Google Scholar] [CrossRef]
- Bernasconi, A.; Carboni, M.; Comolli, L.; Galeazzi, R.; Gianneo, A.; Kharshiduzzaman, M. Fatigue crack growth monitoring in composite bonded lap joints by a distributed fiber optic sensing system and comparison with ultrasonic testing. J. Adhes. 2016, 92, 739–757. [Google Scholar] [CrossRef]
- Muneesh, M.; Annamdas, V.M.G.; Pang, J.L.H.; Asundi, A.; Tjin, S.C. Crack monitoring using multiple smart materials; fiber-optic sensors & piezo sensors. Int. J. Smart Nano Mater. 2017, 8, 41–55. [Google Scholar] [CrossRef]
- Noethen, M.; Jia, Y.; Meyendorf, N. Simulation of the surface crack detection using inductive heated thermography. Nondestruct. Test. Eval. 2012, 27, 139–149. [Google Scholar] [CrossRef]
- Isaeva, A.S.; Konoplev, B.G.; Ryndin, E.A. Analysis of a two-dimensional symmetric problem on extension of a Al-polyimide-Cu layered structure with a model crack. Tech. Phys. Lett. 2015, 41, 599–601. [Google Scholar] [CrossRef]
- Konoplev, B.G.; Ryndin, E.A.; Isaeva, A.S.; Denisenko, M.A. System of Surface Defect Monitoring Based on a Distributed Crack Sensor. Electronics 2017, 81, 1–7. [Google Scholar] [CrossRef]
- Tallman, T.N.; Gungor, S.; Wang, K.W.; Bakis, C.E. Tactile imaging and distributed strain sensing in highly flexible carbon nanofiber/polyurethane nanocomposites. Carbon 2015, 95, 485–493. [Google Scholar] [CrossRef]
- Hallaji, M.; Pour-Ghaz, M. A new sensing skin for qualitative damage detection in concrete elements: Rapid difference imaging with electrical resistance tomography. NDT E Int. 2014, 68, 13–21. [Google Scholar] [CrossRef]
- Hallaji, M.; Seppänen, A.; Pour-Ghaz, M. Electrical impedance tomography-based sensing skin for quantitative imaging of damage in concrete. Smart Mater Struct. 2014, 23, 085001. [Google Scholar] [CrossRef]
- Tallman, T.N.; Gungor, S.; Wang, K.W.; Bakis, C.E. Damage detection and conductivity evolution in carbon nanofiber epoxy via electrical impedance tomography. Smart Mater Struct. 2014, 23, 045034. [Google Scholar] [CrossRef]
- Tallman, T.N.; Semperlotti, F.; Wang, K.W. Enhanced delamination detection in multifunctional composites through nanofiller tailoring. J. Intell. Mater. Syst. Struct. 2015, 26, 2565–2576. [Google Scholar] [CrossRef]
- Tallman, T.N.; Gungor, S.; Wang, K.W.; Bakis, C.E. Damage detection via electrical impedance tomography in glass fiber/epoxy laminates with carbon black filler. Struct Health Monit. 2015, 14, 100–109. [Google Scholar] [CrossRef]
- Tallman, T.N.; Wang, K.W. Damage and strain identification in multifunctional materials via electrical impedance tomography with constrained sine wave solutions. Struct Health Monit. 2016, 15, 235–244. [Google Scholar] [CrossRef]
- Saulnier, G.J.; Blue, R.S.; Newell, J.C.; Isaacson, D.; Edic, P.M. Electrical impedance tomography. IEEE Signal Process Mag. 2001, 18, 31–43. [Google Scholar] [CrossRef]
- Cherepenin, V.A.; Karpov, A.Y.; Korjenevsky, A.V.; Kornienko, V.N.; Kultiasov, Y.S.; Ochapkin, M.B.; Trochanova, O.V.; Meister, J.D. Three-dimensional EIT imaging of breast tissues: system design and clinical testing. IEEE Trans. Med. Imaging 2002, 21, 662–667. [Google Scholar] [CrossRef] [PubMed]
- Dharap, P.; Li, Z.; Nagarajaiah, S.; Barrera, E.V. Nanotube Film Based on Single-Wall Carbon Nanotubes for Strain Sensing. Nanotechnology 2004, 15, 379–382. [Google Scholar] [CrossRef]
- Hou, T.; Loh, K.J.; Lynch, J.P. Spatial conductivity mapping of carbon nanotube composite thin films by electrical impedance tomography for sensing applications. Nanotechnology 2007, 18, 1–9. [Google Scholar] [CrossRef]
- Loh, K.J.; Kim, J.; Lynch, J.P.; Kam, N.W.S.; Kotov, N.A. Multifunctional layer-by-layer carbon nanotube-polyelectrolyte thin films for strain and corrosion sensing. Smart Mater. Struct. 2007, 16, 429–438. [Google Scholar] [CrossRef]
- Ryndin, E.A. Program of defect modeling in a thin conducting film from the results of measuring the conductivity between peripheral contacts. Certificate of the Russian Federation on the state registration of a computer program No. 2017619586, 28 August 2017.
- Kuznetsov, E.V. Electrical and magnetic circuits. In Electrical Technics and Electronics; Lunin, V.P., Ed.; Yurayt Publishing House: Moscow, Russia, 2017; Volume 1, pp. 19–25. ISBN 978-5-534-00356-7. [Google Scholar]
- Bajda, L.I.; Dobrotvorsky, N.S.; Dushin, E.M.; Ismailov, Sh.Yu.; Mokienko, D.N.; Preobrazhensky, A.A.; Staroseltseva, E.A.; Fremke, L.V.; Tsvetkov, E.I. Electrical Measurements; Energiya: Leningrad, Russia, 1980; pp. 144–147. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ryndin, E.A.; Konoplev, B.G.; Kulikova, I.V. Distributed Sensory System of Surface Cracks Monitoring Based on Electrical Impedance Tomography. Electronics 2018, 7, 131. https://doi.org/10.3390/electronics7080131
Ryndin EA, Konoplev BG, Kulikova IV. Distributed Sensory System of Surface Cracks Monitoring Based on Electrical Impedance Tomography. Electronics. 2018; 7(8):131. https://doi.org/10.3390/electronics7080131
Chicago/Turabian StyleRyndin, Eugeny A., Boris G. Konoplev, and Irina V. Kulikova. 2018. "Distributed Sensory System of Surface Cracks Monitoring Based on Electrical Impedance Tomography" Electronics 7, no. 8: 131. https://doi.org/10.3390/electronics7080131
APA StyleRyndin, E. A., Konoplev, B. G., & Kulikova, I. V. (2018). Distributed Sensory System of Surface Cracks Monitoring Based on Electrical Impedance Tomography. Electronics, 7(8), 131. https://doi.org/10.3390/electronics7080131





