Distributed-Memory-Based FFT Architecture and FPGA Implementations

Abstract

A new class of fast Fourier transform (FFT) architecture, based on the use of distributed memories, is proposed for field-programmable gate arrays (FPGAs). Prominent features are high clock speeds, programmability, reduced look-up-table (LUT) and register usage, simplicity of design, and a capability to do both power-of-two and non-power-of-two FFTs. Higher clock speeds are a consequence of new algorithms and a more fine-grained structure compared to traditional pipelined FFTs, so clock speeds are typically >500 MHz in 65 nm FPGA technology. The programmability derives from the memory-based architecture, which is also scalable. Reduced LUT and register usage arises from a unique methodology to control word growth during computation that achieves high dynamic range, along with inherent systolic circuit characteristics: simple, regular, uniform arrays of processing elements, connected in nearest-neighbor fashion to minimize wiring lengths. The circuit goal was to maximize throughput and minimize the use of the FPGA LUT and register logic fabric. Comparison results from seven different designs, covering a spectrum of functionality (fixed-size, variable, floating-point and variable non-power-of-two FFTs), different FPGA vendors (Intel and Xilinx) and different FPGA types, showed increases in throughput per logic cell up to 181% with an average improvement of 94%.

1. Introduction

The discrete Fourier transform (DFT) is one of the most prominent signal processing algorithms and is used in a variety of applications within engineering, computer science, physics, and mathematics [1,2]. Since many of these applications are real-time or involve computations on large data sets, special purpose parallel circuitry coupled with fast Fourier transform (FFT) algorithms for reducing DFT computation times, is essential. For example, real-time demands are illustrated by the variety of today’s wireless transmission protocols:

• Run-time choice of DFT sizes: scalable orthogonal frequency division multiplexing (OFDM) in Long Term Evolution (LTE) [3] and 802.11ax [4].
• Large transform sizes: LTE, 802.11ax with 2048-points; Digital Video Broadcasting-Second Generation Terrestrial (DVD-T2) [5], 32,768-points.
• High throughputs from multiple-input–multiple-output (MIMO) data streams and carrier aggregation: 8 × 8 MIMO in both uplink and downlink plus 160 MHz bandwidths in 802.11ax [4].
• Non-power-of-two DFTs: LTE single carrier frequency division multiplexing (SC-FDMA) with 35 transform sizes [3]; Digital Television Terrestrial Multimedia Broadcasting [6], 3780 points.

Additionally, many applications such as imaging radar [7], medical imaging [8], molecular dynamics [9], and scientific computing [10] inherently require a high dynamic range, so floating-point support may also be a necessity.

In support of this range of applications, we introduce an FFT architecture that can be easily programmed to meet different requirements. For example, it can naturally perform any transform size, including non-power-of-two, that can be expressed as powers of different radices. As a demonstration of this capability, we have implemented four very different types of FFT circuits (fixed-size, variable, floating-point with and without embedded hardware support, and variable non-power-of-two) all using the same architecture.

Additionally, given the growing usage of field programmable gate array (FPGA) technology [11,12,13], our algorithm/architecture has been designed to make very efficient usage of FPGA features and offers very high-performance options. In seven different FFT implementations, involving different FPGA types and vendors, we show here an average increase in our design metric, throughput per FPGA logic cell, of 94% compared to commercial designs and other reported implementations.

Therefore, the unique feature of our architecture is that it offers a very wide range of functionality and at the same time can provide the best throughput per FPGA logic cell. Other architectures support either functionality or performance, but not both. Our circuits are also compact, simple, regular, scalable, uniform, and are based on nearest neighbor communications which minimizes wiring lengths, so circuits can run near the intrinsic FPGA clocking speed limits, features not found in other architectures.

In Section 2.1, the rationale for focusing on FPGA technology is discussed, followed by a review of related work in Section 2.2. Included here as well is a summary explaining how this work builds on our earlier FFT realizations. Section 3, Section 4 and Section 5 describe the architecture at three different levels of abstraction. Section 3.1 discusses how a re-indexing of the standard mathematical expression for a DFT becomes the algorithmic basis for our circuit. An example of data movement within the array structure follows in Section 3.2. Section 4 presents an overall circuit architecture and reviews the reachable transform sizes that are possible. Section 5 analyzes the circuit implementation and examines how programmability is achieved and dynamic range enhanced. Section 6 offers seven FFT circuit examples: fixed-size power-of-two circuits in Section 6.2 (256- and 1024-point), a variable power-of-two circuit in Section 6.3 (128/256/512/1024/2048-points), floating-point circuits in Section 6.4 (256- and 1024-point) with and without FPGA IEEE 754 embedded hardware support, and in Section 6.5 a variable non-power-of-two circuit that can compute 35 different DFT sizes. Most design examples were chosen with wireless applications in mind, in particular LTE and 802.11ax. Section 7 provides a high-level summary of our comparative architectural advantages, that codifies our success in meeting the implementation goal of higher throughputs per logic cell.

2. Background

2.1. FPGA Implementations

The implementation focus here is on the use of FPGAs as the primary hardware platform. These devices have evolved rapidly since they first appeared in 1985 for use as “glue” logic within complex heterogeneous circuit boards. Now, they are being used across a wide spectrum of applications such as cloud processors, robotics, automotive systems, unmanned vehicles, hardware simulation, search engines, mobile devices, industrial controls, and high-performance computing [11]. Possibilities for in situ reconfigurability should expand this list [12].

Unique FPGA characteristics can have a significant impact on circuit design strategies. For example, modern FPGAs as an implementation platform offer large numbers of embedded elements, such as multipliers and memories, leading to very different design tradeoffs compared to ASIC implementations [13]. The number of such embedded elements continues to grow (up to ~4000 multipliers and ~12,000 20 K-bit memories on Intel 14 nm FPGAs are now available [14]), further increasing the possibilities for FPGAs to displace their ASIC equivalents. The same FPGA type can also have many different mixes of embedded elements and logic cells that support the requirements of different applications. There is more concern over whether a design fits into an FPGA rather than leaving unused embedded elements [13].

The relevance to FFT architectures is that, while most of the past design focus has been on reducing memory and the required number of multipliers in support of ASIC designs, this is no longer always a vital issue in the context of FPGA target hardware. A corollary is that our architecture would not be efficacious in an ASIC hardware context because multiplier usage was not minimized. Thus, our design strategy is to produce circuits that minimize the FPGA look-up-table (LUT) and register fabric usage rather than embedded element usage, since this is the essential programmable or more computationally expensive part of the FPGA. Given that all FPGAs have a fixed number of embedded elements available, it makes sense to utilize them to the greatest extent possible by exploring new circuit optimization strategies, rather than allowing them to be potentially wasted. An additional motivation is that the fabric is the source of most of the FPGA dynamic power consumption, as opposed to the embedded elements, which is an important consideration since FPGAs are increasingly being used in mobile devices.

2.2. Related Work

Most high performance FFT designs have appeared in the form of direct or modified decimation-in-time or frequency flow graphs, implemented as either delay feedback or delay commutator circuits (good reviews are available in [15,16]). These “pipelined” FFTs are computationally efficient and make effective use of hardware. However, the circuit architectures are typically coarser grained, irregular in structure, difficult to scale, best suited for power-of-two transforms, and lack programmability.

There are also “memory-based” FFT designs (for reviews see [17,18]) which are usually more flexible and use fewer hardware resources than their pipelined counterpart, although high throughput is difficult to achieve and they are not inherently scalable.

A substantial number of systolic array (SA) designs have been proposed for DFT computations and are attractive because of their simplicity, regularity, uniformity, scalability, locality of interconnections, and suitability for non-power-of-two transforms [19,20,21,22,23]. However, they require substantial hardware, typically N/2 to 4N real multipliers (where N is the transform size), yet do not provide a corresponding performance improvement. The FFT circuit architecture described here relies additionally on a systolic flow, but is far smaller in array size than other systolic designs.

Our architectural model is also memory-based, but is very different compared to traditional memory-based approaches, as can be seen in Figure 1. Here, a traditional memory-based design (Figure 1a) contains a plurality of large arithmetic units for butterfly computations, connected to a similar plurality of memories. The difficulty in such designs is to sequence data to and from the memories using the data control unit shown in Figure 1a such that available bandwidth is maximized, butterfly units are fully utilized, and in-place computations are carried out. Alternatively, our architecture does the same thing, but at a finer level of granularity. From Figure 1b, the array can be seen to consist of many very small processing elements (PEs), each containing a few registers and a multiplier or adder, or both. Each PE reads and writes to a typically small memory (M in Figure 1b) and aggregate bandwidth is limited only by the number of PEs, hence its description as a distributed-memory-based architecture (DMBA). The well-known scalability of systolic algorithms [19] means that high bandwidths, and thus performance, are achieved by simply increasing the array size. It is much more difficult to increase the number of butterfly and memory units for traditional memory-based designs.

As shown in Figure 1b, each PE is locally connected to its neighbors, which keeps interconnections short—an important feature because programmable interconnects can account for 50–90% of the total FPGA area, 70–80% of the total delay, and 60–85% of the total power consumption [24]. The systolic DMBA proposed here was designed using a true space–time mapping tool that generates latency optimal solutions [25], so that implementations are fundamentally localized. Therefore, because of the fine PE granularity and localized wiring, with good place-and-route compilers, higher clock speeds are obtainable compared to traditional pipelined designs. For example, the power-of-two circuits presented here all run with worst-case clock speeds of over 500 MHz using 65 nm FPGA technology, speeds which are higher than any other similar FPGA FFT circuits of which we are aware and approach the clock speed limits of the FPGA fabric (Section 6). Additionally, lower power is possible due to reduced interconnection usage.

The implementation goal for our FPGA designs is to improve circuit efficiencies, defined by throughput per logic cell. Throughput improvement results from the higher clock speeds mentioned above, as well as the reduced number of clock cycles needed per DFT, as outlined in Section 6.3. Reduction in use of LUTs and registers derives from the simplicity and regularity of the DMBA, as well as the algorithmic mappings used. The combined benefit for a large variety of circuit types is summarized in the conclusion (Section 7).

Although this paper is based to some extent on [26], new implementations of floating-point FFTs are described as well as new results for LTE wireless SC-FDMA DFTs. Additionally, the variable FFT results have been updated to reflect newer FPGA hardware and design software. There are also some earlier concept demonstrations of fixed-size FFT circuits in older FPGA technology [25,27,28], although the circuit architecture described here is much improved. In particular, these earlier designs (1) did not employ the simple PE-memory processing flow shown in Figure 1b; (2) required an entirely separate processing step and support hardware to perform the twiddle operations, which has been eliminated here; (3) used inefficient PE memory management schemes, replaced here by “in-place” RAM read/write operations and agglomeration of output buffers, reducing the number of embedded PE RAMs by more than a factor of 2; (4) utilized some fixed scaling, whereas here there is no fixed scaling; and (5) were constrained to the fixed, non-programmable base-b processing described in [25]. Here, additional architectural support for programmability has been added so that any transform length is reachable (Section 4.4). As an example, for a 1024-point FFT [27], these improvements reduced the number of embedded memories by roughly a factor of two and reduced the number of LUTs and registers by ~58%.

3. Algorithm

If a DFT can be factored into a product of small numbers, the basic idea is for the DMBA to sequentially perform an appropriate series of transforms on these to produce the DFT output. To do this, the DMBA performs a series of butterfly computations that are distributed across the entire array. The DMBA has a uniform hardware pipeline in that all PEs are identical and they all perform the same computations. In contrast, a traditional pipelined architecture, which is also deeply pipelined, typically uses different, coarser-grained hardware at each stage.

In the remainder of this section, the algorithmic foundation for the DMBA is briefly described and an example design is provided. The fact that the DMBA is a uniform array of PEs allows it to be programmed to exhibit different functionalities. For example, in Section 3.3 it is shown that the DMBA can do other important kernel operations such as matrix–matrix and matrix–vector multiplication.

3.1. Base-b Algorithm

The DFT is defined as:

$$Z(k)={\displaystyle \sum _{n=0}^{M-1}{W}_M^{nk}}X(n)$$

(1)

where M is the transform length, X(n) are the time domain input values, Z(k) are the frequency domain outputs and $W_M=\hspace{0.17em}{e}^{-j(2\pi /M)}$. In matrix terms, (1) may be represented as

$$Z=CX$$

(2)

where C is a coefficient matrix containing elements $W_M^{nk}$. If M can be factored as $M=N_1{N}_2$, then applying the reindexings $n=n_1+N_1{n}_2$ and $k=k_1+N_1{k}_2$ with $n_1=0,1,\dots ,N_1-1$, $k_1=0,1,\dots ,N_1-1$, $n_2=0,1,\dots ,N_2-1$, $k_2=0,1,\dots ,N_2-1$, it can be shown that if $N_1/N_2$ is an integer value and N₂ = b, where b is the “base”, (1) becomes

$$\begin{array}{l}{Y}_b=W_b•C_{M1}{X}_b\\ Z_b=C_{M2}{Y}_b^t\end{array}$$

(3)

where W_b is an $N_1\times N_1$ matrix with elements $W_b\left[k_1,n_1\right]=W_M^{n_1{k}_1}$, C_M1 is a N₁ × b coefficient matrix with elements $C_{M1}\left[k_1,n_2\right]=W_{N_2}^{n_2{k}_1}$, X_b is a b × N₁ matrix with elements $X_b\left[n_2,n_1\right]=X\left(n_1+N_1{n}_2\right)$, Y_b is a $N_{1}x{N}_1$ matrix with elements Y_b[k₁,n₁] = Y(k₁,n₁) from [25], C_M2 is an b × N₁ coefficient matrix with elements $C_{M2}\left[k_2,n_1\right]=W_{N_2}^{n_1{k}_2}$, Z_b is an b × N₁ matrix containing the transform outputs $Z_b\left[k_2,k_1\right]=Z\left(k_1+k_2{N}_1\right)$, “$•$” indicates element-by-element multiplication and t denotes matrix transposition [25]. (Note that in this section, N₂ is used for the value b when there might be confusion about the use of “b” as a number or as a symbol to imply base-b processing). C_M1 and C_M2 contain M/b² sub-matrices ${\mathrm{C}}_b=\left[c_1^{}\left|c_2^{}\right|\dots |c_{{}_{N2}}^{}\right]$ with the form ${\mathrm{C}}_{M1}=\left[C_b^t\left|C_b^t\right|\dots \right]$ and ${\mathrm{C}}_{M2}=\left[C_b\left|C_b\right|\dots \right]$ due to the periodicity of $W_{N_2}$, and c_i are constant vectors.

The computation (3) can be carried out virtually as shown in Figure 2. Here, there are two N₁ × b arrays of PEs that do the matrix–matrix computations C_M1X_b and C_M2$Y_b^t$ using systolic algorithms [19] with the multiplication by W_b occurring in between the two arrays.

Two processing flows that achieve the same result are indicated in Figure 2: either X_b, containing the input data, is stored in an input buffer and C_M1 values are stored in PE registers in the left-hand side (LHS) PE array, or vice-versa. The systolic multiplication symmetry allows this option [19]. Then on the right-hand side (RHS), there is another input buffer for C_M2 containing all the radix-b butterfly coefficients that will be used (all preloaded before processing begins). During processing, data flows in groups of b and their movement is pipelined through the arrays of PEs. At the end of processing, the result Z_b is stored in registers associated with each of the RHS N₁ × b PEs.

3.2. Base b = 4 Systolic Array

The choice for power-or-two circuits, N₂ = b = 4 (“base-4”), represents a good tradeoff between circuit performance and circuit complexity. This selection results in

$$c_1=\left[\begin{array}{c}1\\ 1\\ 1\\ 1\end{array}\right], c_2=\left[\begin{array}{c}1\\ -j\\ -1\\ j\end{array}\right], c_3=\left[\begin{array}{c}1\\ -1\\ 1\\ -1\end{array}\right],c4=\left[\begin{array}{c}1\\ j\\ -1\\ -j\end{array}\right] \mathrm{and} C_b=\left[\begin{array}{cccc}1& 1& 1& 1\\ 1& -j& -1& j\\ 1& -1& 1& -1\\ 1& j& -1& -j\end{array}\right]$$

where C_b above is the coefficient matrix for a four-point DFT, describing a radix-4 decimation in time butterfly and j is an imaginary number. Consequently, in (3) the matrix multiplications by C_M1 and C_M2 represent repeated use of a radix-4 butterfly.

The computational flow is illustrated for N₁ = 4 with the architecture shown in Figure 3, corresponding to a transform size M = 16. The matrix multiplication C_M1X_b is performed on the LHS. It is obtained from the 4 × 4 input stream X_b that is clocked into the PE array at time steps as shown and multiplied by the values of C_M1 stored internally in the LHS array PEs. The multiplier PEs contain coefficients W_ri for row i of W_b and produce Y_b^t = W_b • C_M1X_b. Finally, the RHS array of PEs accumulates in place (one matrix element per PE) the result Z_b, from Y_b^t and the streaming input C_M2.

Note that the matrix products C_M1X_b and C_M2Y_b^t involve only exchanges of real and imaginary parts plus additions, because the elements of C_M1 and C_M2 contain only ±1 or $\pm j$, whereas the product in (2) requires complex multiplications. The distribution of the elements in C_M2 does not impose significant bandwidth requirements because full complex numbers are not used.

The computational advantages of the matrix algorithm form (3) is evident when compared to the traditional direct form (2), in that the size of the coefficient matrix W_b in (3) is M/4 × M/4 vs. the M × M size of C in (2). Consequently, the matrix–vector multiply (2) requires M² multiplications, whereas the element-by-element multiply of (3) requires only M²/16.

3.3. Matrix–Matrix Systolic Array

While the array shown in Figure 3 performs a 16-point transform (M = N₁N₂, N₁ = 4, N₂ = 4), the basic structure can be used to perform other transform sizes in conceptually the same way. For example, a 15-point transform could be performed as a five-point transform followed by a three-point transform using the structure shown in Figure 4. Here, the LHS SA reads a 3 × 5 array of input data, X_b, and performs three five-point transforms. Next, the multiplier PEs perform the twiddle multiplications with $W_{15}^{nm}$, n = 0, 1, 2, 3, 4, m = 0, 1, 2, stored in a small ROM, and finally the RHS performs five three-point transforms.

In Section 6.5, it is shown how an array with b = 6 can be used to do a set of 35 different non-power-of-two computations for the LTE wireless protocol.

4. Architecture

4.1. Introduction

While the DMBA described in Section 3 is efficient for small transforms, large transforms would require an excessive number of PEs. For example, to do a 1024-point DFT, choosing a base-4 approach would require N₁ = 1024/4 = 256, meaning the DMBA would require 256 PE rows (a “PE row” contains all LHS, multiplier, and RHS PEs along a single horizontal data flow path in Figure 4). This inefficiency can be seen in the first equation of (3), which is rewritten as

$$Y_b{=W}_b•\left[\begin{array}{c}\begin{array}{c}{C}_b\\ C_b\\ ⋮\end{array}\\ C_b\end{array}\right]{\mathrm{X}}_b$$

(4)

(Notation in this section follows that in [25] to maintain consistency.) Equation (4) shows that C_b is applied multiple times to X_b, computing the same result each time. Clearly, it would be best to keep the size of X_b small to avoid the repeated computations. A natural way to do this is to factor the transform size as N = N₃N₄. Here, the N₃ × N₄ DFT matrix X contains input samples x_i that are arranged x₁, x₂, ..., x_N4 on row 1, x_N4+1, x_N4+2, ..., x_2*N4, on row 2, etc. Using the “row/column” factorization, which is the traditional method to simplify and reduce DFT computations, this requires computation of two sets of smaller DFTs using (3), N₄ transforms of length N₃ (referred to as column DFTs) and N₃ transforms of length N₄ (referred to as row DFTs). In between column and row transforms, it is necessary to multiply each of the N points by the twiddle factor,

$$W_N^{i,k}=e^{-j\left(\frac{2\pi ik}{N}\right)}, i = 0, 1, \dots , N_3 - 1, k = 0, 1, \dots , N_4 - 1.$$

(5)

To summarize, the DFT is computed using two levels of factorization. The first is the row/column factorization described above, N = N₃N₄, followed by a second factorization, M = N₁N₂, where M applies to either the row or column DFTs. The second factorization leads to the base-b FFT processing flow described in the remainder of this section and in more detail in Section 5.

4.2. Row/Column Factorization

4.2.1. Architecture

An illustration of the row/column data flow is shown in Figure 5 and is essentially the same as in Figure 2, with different labeling. It shows two (N₃/b) × b PE arrays connected by a (N₃/b) × 1 array of complex multipliers. Each PE on the LHS and RHS contains the PE logic shown in Figure 6 with the addition of a small dual-port RAM to store results. RHS PEs write to the RAM and LHS PEs read from it (Figure 7). The column and row DFTs based on (3) are described below and again M refers to the transform size of either the column or row DFTs.

In the RHS PE, M is a RAM memory, connected as shown in Figure 7 and Figure 8. The LUTs are responsible for multiplying incoming data x by real and imaginary unity values stored in register c and arriving from the bottom in the RHS PEs (the output buffer RAM is not shown).

4.2.2. Column DFTs

An input buffer feeds the LHS with column data X_bci, i = 1, ..., N₄, from the N₃ × N₄ DFT matrix, with each array of column elements organized as an M = N₃ = N_1ci × b matrix where c refers to column data. Also, each PE in the (N₃/b) × b LHS contains an element of the N_1ci × b matrix C_M1. The systolic matrix–matrix multiplication result C_M1 X_bci then flows out of the LHS through the multiplier array shown in Figure 5, where the coefficient multiplication by W_b = W_M = W_N3—stored in ROM—produces $Y_{bci}^t$. A second systolic matrix–matrix multiplication is then performed by the RHS with inputs $Y_{bci}^t$ from the left and C_M2 from the bottom, producing the results Z_bci, which are stored in a distributed fashion in RHS PE RAMs and become the X_bri for row DFTs after the twiddle multiplication by $W_N$.

4.2.3. Row DFTs

The processing in this step, based on (3) with M = N₄ = N_1ri × b, is identical to that for the column DFTs with two exceptions. First, there is a juxtaposition of the C_M1 values with the X_bri row inputs. In this case, the row X_bri values are retrieved from the PE internal RAMs, while the C_M1 values now flow into the LHS SA from the bottom. Second, the Z_bri FFT outputs are stored in a separate RAM output buffer, one per PE row, if normal order data output is desired.

One very important difference in the row DFT processing arises from situations where N₃ ≠ N₄. In this case, the structure of the base-b DMBA will be different for the column processing vs. row processing stages, e.g., one stage could have more PE rows than the other, so that a direct topological PE array match between the Z_b outputs of the column DFT stage and row DFT X_b inputs would not follow. For example, if N₃ = 32 and N₄ = 16, a base b = 4 DMBA during the column DFTs would require a RHS array of 8 × 4 PEs, since M = 32, and each PE RAM would store one element of each of the 8 × 4 Z_b column DFT outputs. However, row DFT processing would require a 4 × 4 input from PE RAMs to a 4 × 4 LHS array, since for this stage M = 16. This is not possible given the 8 × 4 Z_b PE array size.

A simple solution to this issue is to do the column processing but, using the example above (N₃ = 32, N₄ = 16), after the 16 32-point column DFTs, have data for each row DFT written to a single physical PE row. That means that with an 8 × 4 RHS physical array, at the end of column DFT processing the four RAMs in each physical PE row would contain data associated with four of the 32 DFT matrix rows. Note that after column processing, there are always b DFTs contained in the RAMs of a physical PE row because the array length is N3/b and the number of DFT rows is always N₃.

Finally, for the row DFT processing, each physical PE row emulates a virtual SA with 4 × 4 LHS and RHS PE arrays corresponding to M = 16. The flow of coefficients and data is essentially unchanged from that in Figure 5, except that all inputs X_b for a row DFT transform come from a single physical PE row and the Z_b outputs are saved within the same single physical PE row in a single output buffer RAM. More details on the rationale for this approach and the virtual processing associated with it are provided in [25].

4.3. Control, PE Structure and Memory

Systolic data flow is naturally best served by a similar flow of control. Therefore, for each clock cycle a control word is supplied by an external array controller to each column of PEs in Figure 6 and this flows upward in systolic registers, providing values for addresses, read/write enables, etc.

A PE structure is provided as shown in Figure 6 for a base-4 DMBA with M = 16. Note that multiplications in the LHS and RHS PEs are additions, as discussed in Section 3.2. For non-base-4 SAs, all LHS and RHS PEs would additionally contain a complex multiplier.

Total DMBA PE RAM “internal” memory needs to be N words. If input data to the DMBA is only available in natural order, a reordering RAM buffer of size ~N words is required. Similarly, an output RAM buffer of size ~N words is necessary if a natural output order is desired. All these RAM memories are simple dual port memories (one read and one write port).

4.4. Reachable Transform Sizes

As noted in Section 3.1, the derivation leading to (3) restricted N₁/b to integer values, so N₁ = bn, where n is an integer. Therefore, in the column/row factorization using (3) it follows that both N₃ and N₄ must be multiples of b² because M = N₁N₂ = (bn)b = nb². Then, since N = N₃N₄, transform lengths are restricted to integer multiples of b⁴ when using (3). In [25], the value b = 4 was used, so the circuits reported there were limited to transform sizes that were a multiple of 256. However, other values of b lead to different transform length constraints. For example, if the base b is chosen to be two, then the same analysis would show that a base-2 circuit design could perform any transform that is an integer multiple of 16. Additionally, it is possible that column processing might use one value of b and row processing another.

Finally, while the data flow described in Section 4.2 assumes that (3) is applied to both rows and columns, this is not a necessary requirement. As shown in Section 3.3, the DMBA can be used to do any transform size that can be performed as a matrix–vector or matrix–matrix operation. With this option, any transform size can be performed that can be expressed as multiples of powers of small numbers. Prime numbers are not excluded. For example, Section 6.5 describes a circuit that reaches any transform size N where N = 2^a3^b5^c6^d and a, b, c, d are integers.

4.5. Physical Array

The architecture shown in Figure 5 is a virtual representation of the array structure; however, the physical implementation is different. Since the LHS PEs and RHS PEs share a RAM, it is natural to move them to the same physical location to keep the interconnections short. This can be done by simply folding the RHS array on top of the LHS array as shown in Figure 7. The correspondence with the structure of the memory-based model described by Figure 1b is then clear.

5. Implementation

5.1. Introduction

The implementation goal was to minimize use of the LUT/register fabric and maximize clock speeds along with the circuit signal-to-quantization-noise-ratio (SQNR). Whereas our early DMBA designs were pure systolic, in that only nearest neighbor connections between PEs were allowed [25], there was some relaxation of this requirement here so that some connections were allowed over distances of a few PEs. FPGA programmable hardware fabrics include a rich interconnection mesh supporting a variety of wiring speeds. Consequently, this allowed several circuit changes to simplify the implementation at no cost in speed. Additionally, much effort was employed in optimizing the PE circuitry, as small improvements here are multiplied by the number of PEs.

No efforts were made to take advantage of unique FPGA architectural features to improve circuit efficiency, as done in [16], except for the Intel Arria 10 devices, where use was made of hardwired floating-point circuitry in the DSP blocks. In this way, the circuits have a generic applicability to any FPGA with DSP blocks and embedded memory.

In Section 5.2, the circuit details associated with the basic row and column DFT flows are described, followed by a short discussion on how the circuit is programmed. Finally, an analysis of the circuit’s SQNR attributes is covered in Section 5.3.

5.2. Row/Column Processing Details

The basic hardware used can be seen from Figure 8, which shows the flow of X_b and C_M1 in the first PE row, i.e., that connected directly to the input RAM and ROM buffers. Since the operations in all PE rows are identical, it is only necessary to describe data flow in one of the N₃/b PE rows.

The input buffer in Figure 8a contains addressing logic (not shown) that takes a continuous (normal order) serial stream of FFT input data, converts each FFT block into N₄ column sets X_bci, and then distributes these column sets to the b RAMs labeled “B”, so that each contains N₄N₃/b = N₄N_1ci values prior to the start of FFT processing. More input buffer detail is provided in [25].

With reference to Figure 3 and Figure 8, the column and row DFTs are described again in more detail below.

5.2.1. Column DFTs

For this stage, the multiplexors—mux in Figure 8a—supplying data to LHS PEs, is set to select its input from registers labeled “R”, which are present to permit systolic flow of X_bci from input buffer RAMs up through the LHS array. The LHS PEs in row 1 use preloaded c_M1 values, also selected by multiplexors, to perform vector–matrix products as a linear systolic array, producing the first row of C_M1X_bci. Successively produced elements are multiplied by appropriate elements of $W_b{ = W}_M{ = W}_{N_3}$ (stored in a ROM) and become the first row of $Y_{bci}^t$, i = 1, 2, …, N₄. As the RHS PE row 1 receives elements of $Y_{bci}^t$, it performs similar matrix–vector multiplications, producing the first column of Z_bci, i = 1, 2, …, N₄. Here, the elements C_M2 (not shown in Figure 8a or 8b) flow up through registers in the RHS SA from a small ROM (not shown) at the array bottom edge into RHS PEs.

After each column element of Z_bci is computed in the RHS PEs, a multiplexor selects it and sends it sequentially to a normalizer. Here, the growth in the word length at that point from the original n-bit input length is determined and a shift occurs so that the word is restored to n-bits with the shift amount saved as an exponent.

The final operation in the column DFT systolic flow is the twiddle multiplication by values of $W_N$ (5) stored in a ROM. The output of the multiplier feeds a bus that connects that PE row’s b PE internal simple dual-port RAM memories “M”. Each memory receives enable signals so that the elements of Z_bci flow to the correct memory.

5.2.2. Row DFTs

Conceptually, the processing during this step (Figure 8b) with M = N₄ based on (1) closely follows that for the column DFTs, with two minor differences. First, the LHS PE input multiplexors are set to take the X_bri inputs from the internal PE memories “M” and C_M1 values from the bottom ROM in Figure 8b, so C_M1 X_bri is computed using a systolic flow of C_M1 values into the LHS SA. Second, the Z_bri outputs (normalized n-bit values plus exponents) are stored in the simple dual-port output buffer “B” instead of the internal memories (equivalent to twiddle multiplication by 1).

5.2.3. Programmability

The notion of DMBA programmability means providing a capability for cycling various small groups of data appropriately from input buffers or internal RAMs through the array and back, so that the desired butterfly operations can be performed efficiently and quickly. Thus, the goal has been to provide an array architecture and implementation sufficiently general that this abstract programming model can aptly be applied to any type of DFT computation.

Additionally, it should be noted that other non-FFT, application-specific operations can be realized as well, such as cyclic prefix insertion in LTE and other OFDM protocols. A cyclic prefix is a copy of the end of the IFFT output, which is prepended to the transmitted signal and acts as a guard against multi-path signals [3].

As a programming example, a 100-point transform could be factored as (5 × 5) × 4. In this case, it would be necessary to perform four 25-point column transforms followed by 25 four-point row transforms with a twiddle multiplication in between. Each 25-point transform would most naturally be done using (3) and LHS/RHS b × b arrays with b = 5. The four-point row transforms are done in the four PEs of each LHS PE row as values are read in from memory; the RHS then only stores these results in the output buffer.

The control structure used to implement the desired level of programmability can vary. For simple transforms, such as the power-of-two examples (Section 6.2 and Section 6.3), finite state machines can be used. For more complex examples, such as the LTE example (Section 6.5), more general loop-based Verilog code could be used with loop parameter values specified in a small ROM memory. In either case, different transform sizes are performed on the same array by simply adjusting the various loop parameters used to control flow of data in and out of the DMBA.

A major benefit of a programmable circuit is that the computational hardware can be highly optimized, since it can be reused for different applications. In the case of the DMBA, even small optimizations are useful because they are replicated in all the PEs.

5.3. Dynamic Range

SQNR is another important circuit attribute which should be maximized, while at the same time minimizing fixed-point word lengths, because longer words necessitate bigger memories/multipliers and increase critical path lengths. The SQNR is obtained from the expression

$$\mathrm{SQNR}={10 \log }_{10}\frac{{{\displaystyle \sum }}_{i=0}^{N-1}{\left(\mathrm{abs}\left(z_i\right)\right)}^2}{{{\displaystyle \sum }}_{i=0}^{N-1}{\left(\mathrm{abs}(z_i-z_i^{\mathrm{ref}}\right)}^2}$$

(6)

where the summation is over complex outputs z_i and the superscript “ref” refers to the value of z_i obtained using Matlab’s double precision floating-point FFT routine. Here, SQNR is always computed using complex inputs comprised of random real and imaginary numbers.

A variety of scaling methodologies have been proposed to deal with word length growth during an FFT computation. One common scheme is to scale arithmetic results so that a fixed word length is used throughout the computation. This leads to simplified hardware, but lower SQNR because the scaling occurs even if there is no overflow. A second popular scheme is to use block floating point (BFP) arithmetic, an adaptive approach that scales all data at a particular processing stage if there is register overflow. In this case, an exponent register associated with the entire transform block is incremented each time this occurs to keep track of total scaling. Use of BFP arithmetic provides better SQNR than fixed scaling because scaling only occurs upon overflow; however, extra circuit overhead is necessary and its use can limit implementation options. Both these methods are well-suited to memory-based architectures, where there is not always an implementation option to increase register size as the computation proceeds. SQNR example results using these two approaches are provided in

Table 1. SQNR values for different FFT scaling methodologies (16-bit input data and 1024-point transform).

	Method	SQNR (db)
[29]	Scaling	49
[30]		53
[31]	BFP	56
Intel [32]		57
DMBA	BFP/Floating Point	83

. The Intel results were obtained from Matlab simulations based on the provided bit-accurate FFT model for streaming (continuous I/O) fixed size FFTs.

For the DMBA, control of word-length growth is performed in the normalizer circuit in Figure 8, which scales fixed-point data back to the n-bit length of the input data. The scaling is done separately on each row of the N₃ × N₄ DFT matrix and the maximum scaling amount for that row of the DFT matrix results in an exponent value. Therefore, at the end of the column processing, there are N₃ different exponents stored. Normally, for an N-point FFT using BFP scaling, a single exponent applies to all N data values; however, since there are N₃ different exponent values here, the SQNR values can be higher than for BFP scaling.

To support this method of scaling, a BFP control block has been added, as shown in the expanded level of detail in Figure 9. This control unit contains 2 × N₃ registers to keep track of maximum exponents. The factor of 2 required is because row/column processing stages overlap, and it can be necessary to simultaneously keep track of the scaling exponent values from each stage. A comparator is included in the BFP control block to test for the maximum exponent in each of the N₃ DFT matrix rows.

During the row DFT processing, when X_bri mantissa and exponent values are read from the RAMs (“M” in Figure 9), the exponent values are subtracted from the corresponding maximum exponent value for that DFT matrix row and the difference is supplied to a shifter. The shifter then normalizes the mantissa value so that all X_bri input values have the same exponent. When an FFT block is being computed, the N₃ maximum exponent values stored in the BFP control block are added to the corresponding output exponents as data is streamed out of the output buffer “B” in Figure 9. Each output value then has a real and imaginary mantissa and a single exponent. A simple output converter has been tested that will convert each to a standard BFP format (single exponent per FFT block); however, it reduces dynamic range.

To summarize, DMBA word growth control is based on an enhanced BFP and floating-point methodology that achieves SQNR values typically 20 to 30 db higher than other circuits with the same fixed-point input word length, as shown in Table 1. This is important because FPGA architectures from Intel and Xilinx have a word length “boundary” of 18-bits due to their 18-bit multiplier and memory designs. Consequently, circuits that allow word growth would encounter significantly increased resource usage when word lengths are increased beyond 18-bits to achieve SQNR >80 db. Finally, it should be noted that minimizing word lengths for a given SQNR also reduces LUT and register fabric usage in FPGAs. The hardware cost of using this scheme represents approximately a 15% hardware overhead penalty.

6. Results

6.1. Introduction

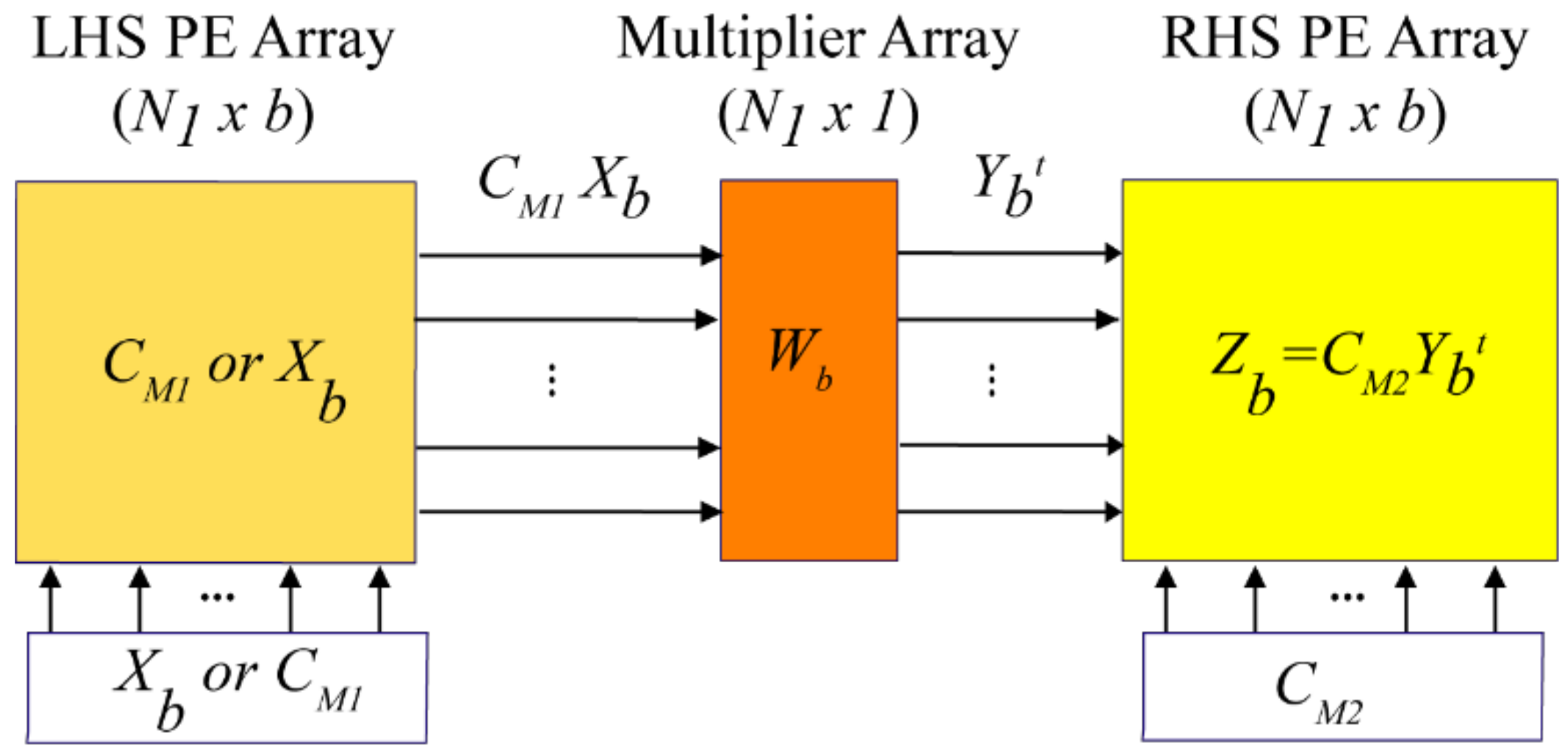
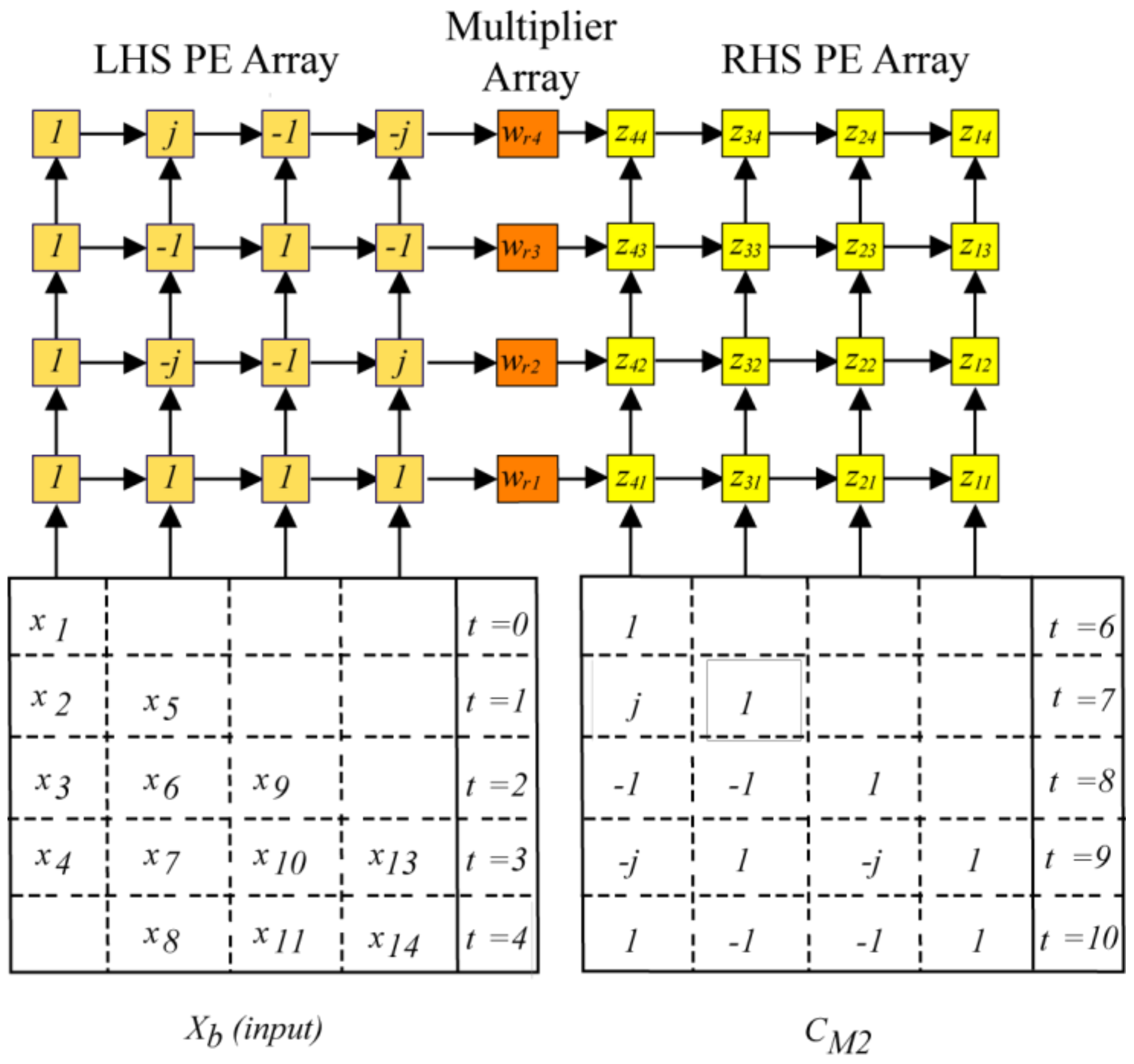
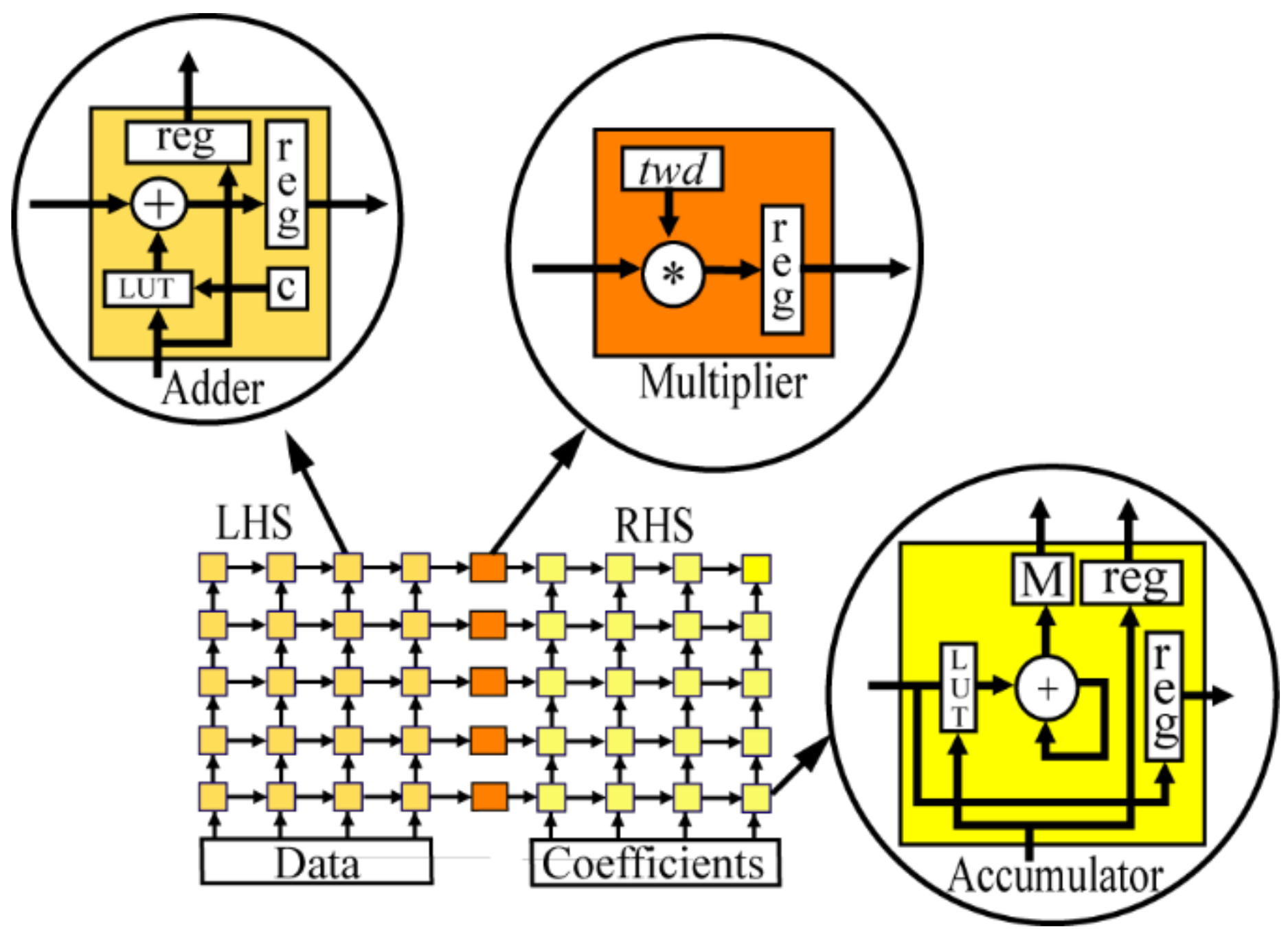
In this section, seven different FPGA FFT implementations are described, with the purpose of demonstrating how the same architecture can be used for a range of applications. The first two designs (Section 6.2) are fixed-size power-of-two FFTs (256-points and 1024-points) that take computational advantage of the radix-4 butterfly matrix in which case the LHS/RHS PE multipliers are replaced by adders because C_M1/2 contains only {±1, ±j} (see Figure 3). The third design (Section 6.3) is like the first, but adds a requirement for run-time choice of FFT size. The last three power-of-two FFT circuits (Section 6.4) use single-precision floating-point formats (IEEE 754), one of which targets the latest in FPGA embedded floating-point hardware support. Finally, in Section 6.5, a complex, non-power-of-two design is presented that uses mixed-radices and offers run-time FFT choice, yet has the a very simple programming model for performing any size of FFT.

Additionally, comparisons to other FPGA implementations are included. This is often difficult because circuit properties can vary considerably, due to the different CMOS technologies/speed-grades, embedded circuit types, LUT/register fabric architecture, FFT functionality, word growth control, circuit architectures, and the FPGA tools and tool settings used. Consequently, the goal was to provide more accurate comparisons by using close to identical circuit functionality, SQNR, target FPGA hardware, tools, and settings as possible. A range of different FPGA types and technologies were chosen to add variety to the comparisons.

Although it is common to compare FFT architectures based on a table with entries representing resources used and transform times as a function of transform size N, this only works well when there is a direct correspondence between N and hardware, as in the case of pipelined FFTs. Memory-based architectures do not share this one-to-one correspondence, so a useful table would be difficult to construct. Additionally, there are many design issues impacting resource usage and speed that cannot be addressed in such tables. Therefore, the focus in this section is on circuitry that has been successfully compiled with the same tool settings, and then simulated and tested using complex random input data followed by comparisons of output data to Matlab generated values. In some cases where noted testing has also been done using FPGA development hardware boards. In this way the comparisons are comprehensive and thus more useful.

In the comparisons with Intel FPGAs, Intel’s Quartus synthesizer, and place-and-route design tools were used, and the Timequest static timing analyzer determined worst-case maximum clock frequencies (Fmax) at 85 C. For Xilinx FPGAs, ISE 14.7 tools for synthesis and place-and-route were used. All Fmax or clock rate values are the same as the complex data sample rate, except where noted, and were obtained by choosing the highest values from at least three different compiler seeds. All SQNR values were calculated using at least 500 blocks of random FFT complex input data. For 16-bit word length input circuits, all twiddle factors were 18-bits, except where noted. Real multipliers were 18-bits, except for the floating-point circuits. All designs support forward and inverse transforms except where noted.

All results include a measure of circuit efficiency, our primary metric of design success, defined by the throughput obtained per logic cell, given terms of registers and LUTs, as follows:

$$\mathit{Efficiency} = \mathrm{100,000} \text{×} \mathit{throughput}/\frac{\mathit{LUTs} + \mathit{registers}}{2}$$

(7)

where throughput is expressed in transforms/µs. Another logic cell choice would have been to use slices for Xilinx devices and adaptive logic modules (ALMs) for Altera devices, but this information was not available in many of the circuits used in the comparisons.

6.2. 256-Point and 1024-Point Streaming (Normal Order In and Out) Fixed-Size FFTs

For these two transform sizes, the FFT circuits targeted the same hardware, Stratix III EP3SE50F484C2 FPGAs (65 nm technology) and comparisons are made to Intel [32], Gird [33] and Spiral [34] circuits.

The Intel circuit is based on a mixed radix-4/2 20-bit pipelined FFT that uses BFP (single exponent per FFT block) to achieve a similar SQNR as the DMBA FFT circuits [32]. The SQNR results for the Intel circuits were obtained from a bit-accurate Matlab model created along with the circuit by the Intel FFT generators (IPv13.1). Here, the ALM is the basic unit of a Stratix III FPGA (two variable size LUTs, two registers, plus other logic). An M9K is a 9216-bit memory with a word length up to 36-bits.

Compared to the Intel circuits,

Table 2. Comparisons of commercial (Intel, DMBA, Gird) and Spiral fixed-size FFT circuits.

Circuit	Intel	DMBA	Spiral	Intel	DMBA	Spiral	Gird
	20-Bits	16-Bits	20-Bits	20-Bits	16-Bits	20-Bits	16-Bits
Transform Size	256			1024
ALMs	4261	3982	3632	4394	4357	5237	n.a.
LUTs	4416	6046	3934	4632	6426	3517	5649
Registers	7841	6437	7413	8206	6718	9411	6190
Memory (M9Ks)	38	31	44	38	31	79	52
Memory(K-bits)	49	41	85	195	145	362	n.a.
Real Multipliers	24	33	112	24	33	144	96
Fmax (MHz)	387	566	292	382	533	293	263
SQNR	88	87	86	81	83	80	n.a.
µj/FFT	1.3	1.1	n.a.	6.4	4.3	n.a.	n.a.
(µsec) per FFT	0.66	0.45	0.44	2.7	1.9	1.7	3.9
Thrpt/logic cell	25	35	40	5.8	7.9	8.9	4.3

shows that the DMBA FFTs use fewer registers, ALMs, and M9Ks, with throughput rates that are 46%/40% higher for 256/1024-points, leading to better values of throughput per logic cell (7) by 44%/36%. Note that there are significant improvements in power dissipation as well (results obtained from Quartus Power Play Power Analyzer tool). For 256-points, it is possible to use LUTs for the DMBA circuit’s internal memory, so that only 15 M9Ks are necessary. In this case, the number of ALMs would be approximately the same as for the Intel version.

As part of a larger project to automate the development of signal processing algorithms, the Spiral designs come from a parameterized tool that generates Verilog code for fixed-point and floating-point fixed-size power-of-two FFTs. Here, forward, streaming designs with scaling to prevent errors were chosen. Bi-directional transforms were not an option. Like the Intel circuit a higher word length was required for comparable SQNR, obtained from Verilog simulations. Unlike the other designs considered here, the Spiral circuits process two complex words per cycle, so transforms complete in N/2 cycles. The Spiral circuits use fewer LUTs, but more registers, M9Ks and multipliers. So while these circuits achieve marginally better throughputs per logic cell, memory (M9K) and multiplier usage are significantly higher by 42%/245% and ×3.4/×4.4 for the 256/1024-point designs.

In Table 2, the commercial Gird Systems IP core is a 16-bit, streaming, decimation-in-frequency, radix-4 core and results are shown for an Intel Stratix IV FPGA (EP4SE230C4). The Stratix III and IV FPGAs use different fabrication technologies (65 nm and 40 nm), but their architectures are the same, so the comparisons, except for speed (C4 is a lower speed grade), are somewhat useful. It is important to note that the circuit uses scaling of results in intermediate stages to control word growth, so that likely the SQNR for this circuit is much less than all the other designs in the table. Like the Intel and Spiral designs, if a 20-bit circuit were used, all the Gird resource numbers would increase significantly.

6.3. Variable FFT Streaming (Normal Order In and Out)

In this section, a variable streaming FFT circuit is described that provides a run-time choice of 128/256/512/1024/2048 transform sizes as required for 802.11ax [4] and LTE protocols [3]. For this circuit with b = 4, it was natural to choose a factorization with N₃ = 16 for all transform sizes. This choice leads to simple 4 × 4 SAs, as in Figure 3 and Figure 6, for the 16-point column transforms with processing based on (3). All the desired twiddle factors W_N can be conveniently found among the elements of W₂₀₄₈.

After the column DFTs, it would be possible to perform each of the N₄-point row transforms using (3) exclusively; however, better efficiency is achieved by factoring some of the row DFTs again (N₄ = N₅N₆) and differently for each transform size, so row DFTs are broken into two steps. The rows in

Table 3. Values of N₄, N₅ and N₆ used for five transform sizes, N, and factorizations, F.

N	N4	F	N5	F	N6	F
128	8	(4 × 2)	-	-	-	-
256	16	(4 × 4)	-	-	-	-
512	32	-	8	(4 × 2)	4	(4 × 1)
1024	64	-	4	(4 × 1)	16	(4 × 4)
2048	128	-	8	(4 × 2)	16	(4 × 4)

show how each DFT transform of the 16 DFT matrix rows of length N₄ is performed in the SAs. For 128/512/2048-points, the factorization “4 × 2” means that an 8-point transform is done as a four-point transform in the LHS SA followed by a 2-point transform in the RHS SA. For 1024 and 512-points, “4 × 1” means the LHS SA only does the four-point transforms. In Table 3, all 16-point transforms are factored as “4 × 4” and follow the base-4 processing defined by (3) and shown in Figure 3. For example, to do a 2048-point transform, each row of length N₄ = 128 is factored with N₅ = 8 and N₆ = 16. Therefore, for these row transforms, 16 8-point transforms are computed using both LHS and RHS SAs (“4 × 2”), followed by eight 16-point DFTs (“4 × 4”) using (3). The linear multiplier array in Figure 3 is used to perform all associated twiddle multiplications.

The motivation for factoring the row transforms or column transforms is that, like other FFT circuits, it reduces the overall cycle counts. In our case, it is necessary to ensure that a transform can be completed in <N cycles, so that with pipelining overhead, the high-speed clock (Fmax in all the tables) can run at the highest speed permitted by the FPGA technology, architecture and compilation technology. In all cases in Table 3, these factorizations allowed the computation to complete in less than N clock cycles. Of course, total computation cycles or latency for a transform is longer than this due to the deep pipelining used to maintain the clock speed.

The variable FFT circuit uses the same PE array circuit as that for the fixed-point designs in Section 6.2, with the addition of more RAM memory and different finite-state machine control. The 2048-word twiddle memory is encoded so that it does not use more M9Ks than the fixed size 1024-point circuit in Section 6.2 [35].

In

Table 4. Comparisons of commercial (Intel, DMGA) and other streaming variable FFT circuits (16-bit, run-time choice of sizes).

Circuit	Intel	DMBA	[36]	[4]
ALMs	6089	4785	n.a.	n.a.
LUTs	5453	7020	1143	80,088
Registers	9752	7044	1754	47,129
Memory (K-bits)	203	290	n.a.	117
Memory (M9Ks)	28	42	n.a.	n.a.
Real Multipliers	68	33	4	n.a.
Fmax (MHz)	283	490	200	111
SQNR (average)	90	84	n.a.	n.a.
FFT 2048pts (us)	7.2	4.2	57	2.3
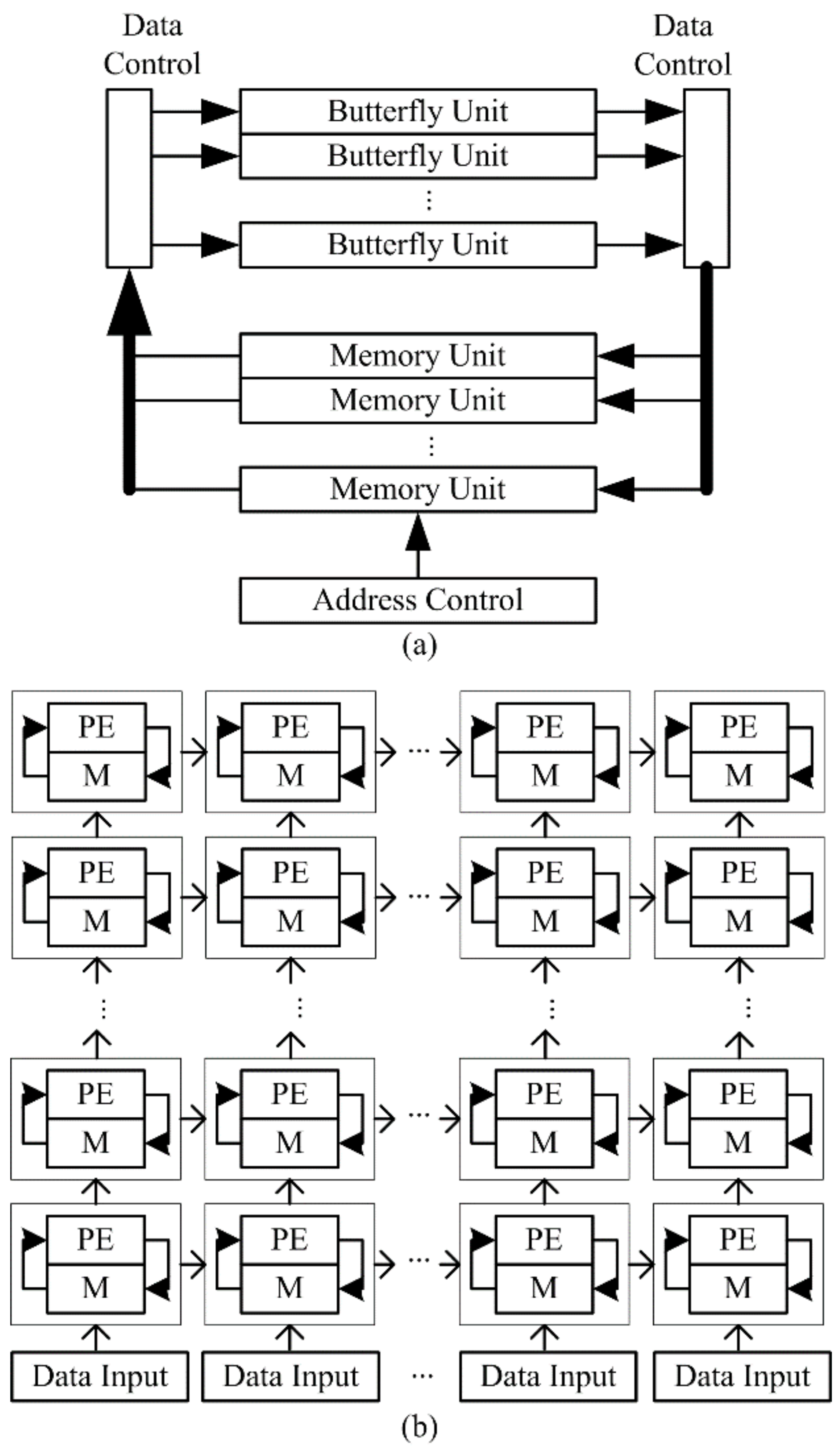
Thrpt/logic cell	1.8	3.4	1.2	0.68

, the DMBA is compared with three other FFT circuits, spanning a range of architectural possibilities. At one end of the spectrum is a memory-based FFT [36] (Figure 1a), where small circuit size is typically a priority, and as a result the number of clock cycles required to complete an FFT is much greater than N. Next is a traditional pipelined FFT based on a single-path radix-2² delay-feedback (SDF) architecture from Intel [37]. Like most pipelined FFTs, N clock cycles are required to perform an N-point transform. Finally, at the other end of the spectrum, by adding parallelism based on multi-path delay commutator (MDC) and SDF stages, a circuit architecture that computes the FFT in much less than N [4] clock cycles is included. All the circuits allow run-time choice of 128/256/512/1024/2048-point transform sizes, except for [36] which also offers 16/32/64-points and [4] which does all but 128-points, but does offer a multi-mode capability for processing some transform sizes in parallel.

In Table 4, three of the designs (DMBA, Intel, [4]) used the same Stratix IV EP4SGX530KH40C3 FPGA (−3 speed grade). The other design used a 5SGSMD5K2F40C2 Stratix V FPGA (28 nm technology). Since the Stratix V FPGA uses a more advanced architecture, is based on better CMOS technology, and is the fastest −2 speed-grade, the results for [36] in Table 4 could potentially yield better results.

It is important to note in Table 4 that the DMBA Fmax of 490 MHz is limited not by the FPGA fabric, but is a result of the maximum operating speed of the simple dual port embedded RAMs used. The TimeQuest generated DMBA Fmax associated with the LUT/register fabric is >500 MHz. Note that the DMBA FFT circuit operation at 500 MHz was verified using a development board based on an Intel Stratix III EP3SL150F1152C2 FPGA.

The memory-based design [36] is a 16-bit radix-2 FFT with two butterfly units and uses a 16-bit twiddle factor. The tradeoffs show that although this memory-based design uses 6.1/4.0 times fewer LUTs/registers than the DMBA, it runs 13.6 times slower, even using a faster FPGA speed grade and technology.

For the Intel 16-bit pipelined FFT (IPv17.1), the values in Table 4 show that the Intel circuit uses 27%/38% more ALMs/registers, but the DMBA uses 29% more LUTs; however, the higher DMBA throughput leads to a better throughput per logic cell by 87% (2048-points), even with the RAM speed restriction. This Intel FFT is slower than Intel’s fixed-point FFT (Section 6.2) because the 16-bit input word length grows to 28-bits at the output, which was done to keep SQNR high. Processing these longer word lengths and likely larger multipliers slows down the Intel SDF speed. It should be noted as well that for the Intel circuit any post-processing, such as that needed for common operations such as convolutions, would require 28-bit circuitry rather than the 16-bit DMBA word-length, thus nearly doubling the resource usage. Finally, the DMBA FFT has been successfully programmed and tested to support cyclic prefix generation and insertion needed for the targeted LTE protocols, whereas the Intel circuit would require a separate 28-bit circuit to perform this function.

The last circuit in Table 4 [4] is a parallel pipelined FFT circuit based on radix-2 MDC and radix-2⁴ SDF stages, all of which have 8 I/O ports. Data output is not in natural order, so a reordering circuit would be necessary to make this design closely comparable. The parallel operation provides processing of eight complex samples per clock and reduces overall latency, but the added circuit complexity results in 11.4/6.7 times more LUTs/registers, yet achieves an FFT throughput time that is only 83% faster than the DMBA. Although the latency (first point in to first point out) in clock cycles (299 for 2048-points) is 11.7 times less than that of the DMBA (3507 clock cycles for 2048-points), the latency in time is 2.69 µs vs. 7.16 µs for the DMBA, an improvement of only 2.7-fold. With a reordering output buffer, the improvement would be reduced by approximately two-fold [4].

6.4. Floating Point FFT

6.4.1. Introduction

Ideally, floating-point FFT implementations in custom embedded applications should be used because they offer a much higher dynamic range and, as a byproduct, bypass the design hassle of analyzing fixed-point word lengths, including how to properly scale operations to minimize word growth and avoid overflow. In Section 6.4.2, two such floating-point designs that generate IEEE 754 single-precision outputs are presented. These target FPGAs with traditional fixed-point embedded multipliers, where a substantial amount of LUT/register overhead is required to facilitate the floating-point operations. A third implementation is presented in Section 6.4.3 based on a new class of FPGAs that provide embedded hardware support for IEEE 754 single-precision. With all the difficult arithmetic moved into embedded hardware, these FPGAs achieve a long-sought goal of simultaneously offering high dynamic range with substantially reduced need for LUTs and registers.

6.4.2. Floating-Point without FPGA Embedded Hardware Support

Here, 256-point and 1024-point streaming floating-point FFT circuits (normal order in and out), which provide an IEEE 754 32-bit single-precision formatted complex outputs, are presented and compared. The Intel versions (IPv16.1) [37] are based on a mixed radix-4/2 pipeline and only available as variable streaming FFTs. The DMBA circuits are fixed-size but contain control support for other sizes. The DMBA takes 24-bit fixed-point input data, whereas the Intel equivalent accepts 32-bit single-precision inputs. The Intel circuit provides streaming operation, but only does forward transforms, whereas the DBMA is bi-directional. An input converter added to the DMBA to provide an IEEE 754 input format would add little overhead. The Spiral circuits use same parameters as the fixed-size designs of Section 6.2, except that floating-point precision is selected.

As noted in Section 5.3 for the DMBA, during the row DFTs, all DMBA computations use a floating-point scaling scheme, so to achieve an IEEE 754 single-precision format only a small output conversion circuit is necessary. To achieve the desired precision, the fixed-point circuits on which it is based (Section 6.2) have a substantially larger 28-bit internal word length.

Example performance and resource usage data are provided in

Table 5. Comparisons of commercial (Intel, DMBA) and Spiral single-precision floating-point FFT circuits, when the FPGA has no embedded floating-point support.

Circuit	Intel	DMBA v1	DMBA v2	Spiral	Intel	DMBA	Spiral
Transform	256-Points				1024-Points
ALMs	10,834	7137	7834	22,039	13,559	7186	27,014
LUTs	16,519	11,050	12,006	16,818	21,801	11,193	21,252
Registers	15,545	10,431	12,535	32,946	18,169	10,495	42,054
Memory (M9Ks)	54	62	30	36	87	62	90
Real Multipliers	48	129	129	96	64	129	128
Fmax (MHz)	299	456	426	260	285	386	260
Thrpt/logic cell	7.3	16.6	13.6	8.2	1.4	3.5	1.6

for a Stratix IV EP4SE360H29C2 FPGA target (−2 speed grade). For the 256-point DMBA circuit in Table 5, there are two different design versions: v1 uses M9K RAMs for all internal memory and v2 uses the Stratix IV memory logic array block (MLAB) that allows LUTs to function as internal memories. As can be seen in Table 5, using MLABs reduces the number of M9K memory blocks to 30 from 62.

For the important LUT/register fabric, the Intel designs use far more resources, e.g., almost 100% more LUTs for the 1024-point transform. This also implies more power dissipation, as our experience shows that the FPGA LUT, register and wiring fabric is the primary source of power dissipation. Intel memory usage in terms of M9Ks is also greater—80%/40% for 256(v2)/1024-point designs. Similarly, the Spiral designs use far more LUTs and especially registers, up to ×3.2/×4.0 more for the 256/1024-point designs. For the two transform sizes the DMBA shows ×2.3/×2.5 and ×2.0/×2.2 higher throughputs per logic cell than the Intel and Spiral circuits, largely due to the reduced usage of LUTs and registers. The reduction in DMBA hardware used is important as it can move the tradeoffs between fixed and floating-point attractively in the direction of the floating-point option. The larger word lengths in the DMBA lead to critical paths in the much larger multipliers, which limits Fmax compared to the smaller fixed-point versions in Section 6.2.

Since the DMBA designs are based on fixed-point implementations with shifters for normalization of internal values, measurements of the circuit precision are provided in

Table 6. Error comparisons for single-precision floating-point FFT circuits in Table 5.

Circuit	Intel	DMBA	Spiral	Intel	DMBA	Spiral
Transform	256-Point			1024-Point
Mean	2.4 × 10−7	3.1 × 10−8	3.5 × 10−7	2.9 × 10−7	4.2 × 10−8	4.4 × 10−7
Std Deviation	2.5 × 10−7	3.1 × 10−8	4.2 × 10−7	3.4 × 10−7	7.7 × 10−8	5.6 × 10−7
Maximum	2.4 × 10−5	4.3 × 10−6	3.4 × 10−5	9.1 × 10−5	2.7 × 10−5	8.2 × 10−5

for both the 256 and 1024-pt circuits. Input data was Matlab generated random real/imaginary 24-bit fixed-point numbers for the DMBA and the same converted to single-precision floating point for the Intel circuits (FFT IP v17.1 Modelsim and Matlab models) and Spiral circuits. The comparison reference is double precision Matlab.

The mean absolute error numbers were obtained by subtracting the reference output value from each circuit output, taking the magnitude of this and then dividing by the magnitude of the reference value for that output point. The maximum absolute error is the largest of these errors computed over all 500 blocks of input data.

In terms of mean absolute error, the Intel and Spiral designs here are ~7 times less accurate for both transform sizes. The standard deviation for both 256-point and 1024-point Intel designs are also much larger values, consistent with the bigger maximum errors in the Intel designs. Similar improvements can be seen for other data input types such as single sinusoids.

6.4.3. Floating Point with Embedded Hardware Support

FPGA signal processing options have improved significantly with the introduction of hardwired floating-point embedded hardware. For example, Arria 10 FPGAs are the industry’s first FPGAs that natively support a single-precision floating-point DSP mode as well as standard and high-precision fixed-point multiplications in embedded circuitry. The single-precision floating-point DSP block mode is IEEE 754 compliant and includes an IEEE 754 single-precision floating-point adder and IEEE 754 single-precision floating-point multiplier.

To illustrate the benefits of this new FPGA technology, 1024-point streaming FFT transforms (normal order in and out) were implemented.

Table 7. Commercial single-precision 1024-point floating-point FFT circuit comparisons, when the FPGA has embedded floating-point support.

Circuit	Intel	DMBA v1	DMBA v2
ALMs	4852	2251	4106
LUTs	6058	3531	6795
Registers	10,844	4969	6121
Memory (M20Ks)	20	62	30
MLAB Memory Bits	4136	4776	70,312
DSP Blocks	64	96	96
Fmax (MHz)	432	585	572
Thrpt/logic cell	5.0	13.4	8.7

presents results compiled for an Arria10 10AS066H1F34E1SG FPGA (20 nm technology) device. In choosing resources, two versions of the DMBA circuit are shown: “v1” used M20K memories (20 K bits) for the internal FFT PE memories and “v2” used MLABs for this. The Intel FFT (IPv16.1) uses a mixed radix-4/2 delay feedback pipeline. In the Arria FPGA, an ALM contains two 4-input adaptive LUTs, four registers, plus other logic.

Several important conclusions can be drawn from the resource and performance numbers in Table 7:

• Use of the embedded DSP floating-point hardware drastically reduces the need for LUTs and registers. For example, the DMBA design (v1) in Table 7, compared to the Intel Stratix IV fixed-point multiplier implementation (Table 5), used 6.2 times fewer LUTs and 3.7 times fewer registers.
• The Intel design in Table 7, compared to the DMBA (v1), used 2.2 times more ALMs, 1.7 times more LUTs, and 2.2 times more registers, leading to throughput per logic cell numbers that were 169% better. The DMBA “v2” trades off embedded memory (M20Ks) for LUTs, but still used 15% fewer ALMs.
• For the same Arria 10 FPGAs, the DMBA provided 35% higher throughputs.
• The DMBA design clock rates are at Fmax values very near the Arria 10 “restricted” speed limit of 608 MHz. This example shows that DMBA circuits are better able to take advantage of all the built-in speed provided by FPGAs.

The key to reducing the LUT/register fabric usage when designing FFTs for Intel 10 FPGAs is to move as much of the processing into the embedded DSP blocks as possible. These DSP blocks provide several basic floating-point primitives: multiplication, accumulation and addition. The DMBA architecture focuses on using just these primitives, as shown in Figure 6. Here, the PEs on the LHS perform floating-point addition, the multiplier array PEs perform floating-point multiplication, and the RHS PEs perform floating-point accumulation with sums passed to memory M in Figure 1 and Figure 8.

Most of the registers used in the DMBA structure (Table 7) supported the fast systolic passing of coefficients and intermediate data between PEs, but about 17% are used to register inputs of the floating-point multipliers and might in the future be absorbed into the DSP block.

About 25% of the 2251 ALMs in Table 7 provide the control needed to do many transform sizes. This number can be significantly reduced for single transform sizes.

As FPGAs such as Intel Arria 10 and Stratix 10 inevitably become cheaper, the choice of floating-point hardware will naturally become more prevalent due to the relatively small LUT and register usage required by the DMBA.

6.5. Non-Power-of-Two Circuit (LTE)

6.5.1. Introduction

SC-FDMA is a part of the LTE protocol [3] used for up-link data transmission. It involves a DFT pre-coding of the transmitted signal, where the DFT can be any one of 35 transform sizes from 12-points to 1296-points, with N = 2^a3^b5^c and a, b, c positive integers. The rationale for targeting FPGAs is due to the rapidly growing FPGA use in communications applications, e.g., base stations and remote radio heads at the top of cell phone towers. Here, we provide results of mapping the DMBA to Xilinx Virtex-6 devices.

6.5.2. Related Work

To compute high performance run-time transforms for N ≠ 2ⁿ, a variety of mixed radix approaches have been proposed [38,39,40,41]. The performance of the different designs is primarily related to the complexity of the butterfly unit design.

Both Xilinx [41] and Intel [38] use a memory-based architecture as in Figure 1a, consisting of a single multi-port memory that sends/receives data to/from a single arithmetic unit that performs the required butterfly computations. For these designs, the number of clock cycles per DFT is greater than the transform size N, so it is not possible to continuously stream data into and out of the circuit. In the Xilinx design, the arithmetic unit can do radix 2, 3, and five-point butterflies using parallel and pipelined hardware. It can perform two radix-2 operations per clock cycle, one radix-3 or radix-4 operation per cycle and one radix-5 operation in two clock cycles. The Intel design uses a simpler butterfly unit which results in lower performance, but also reduced LUT/register usage.

The other designs are different from those discussed above in that they either use a higher radix memory-based design [39] or a pipelined architecture [40] to reduce the overall number of cycles needed to compute a DFT to less than the actual transform size N.

6.5.3. DMBA Design Approach

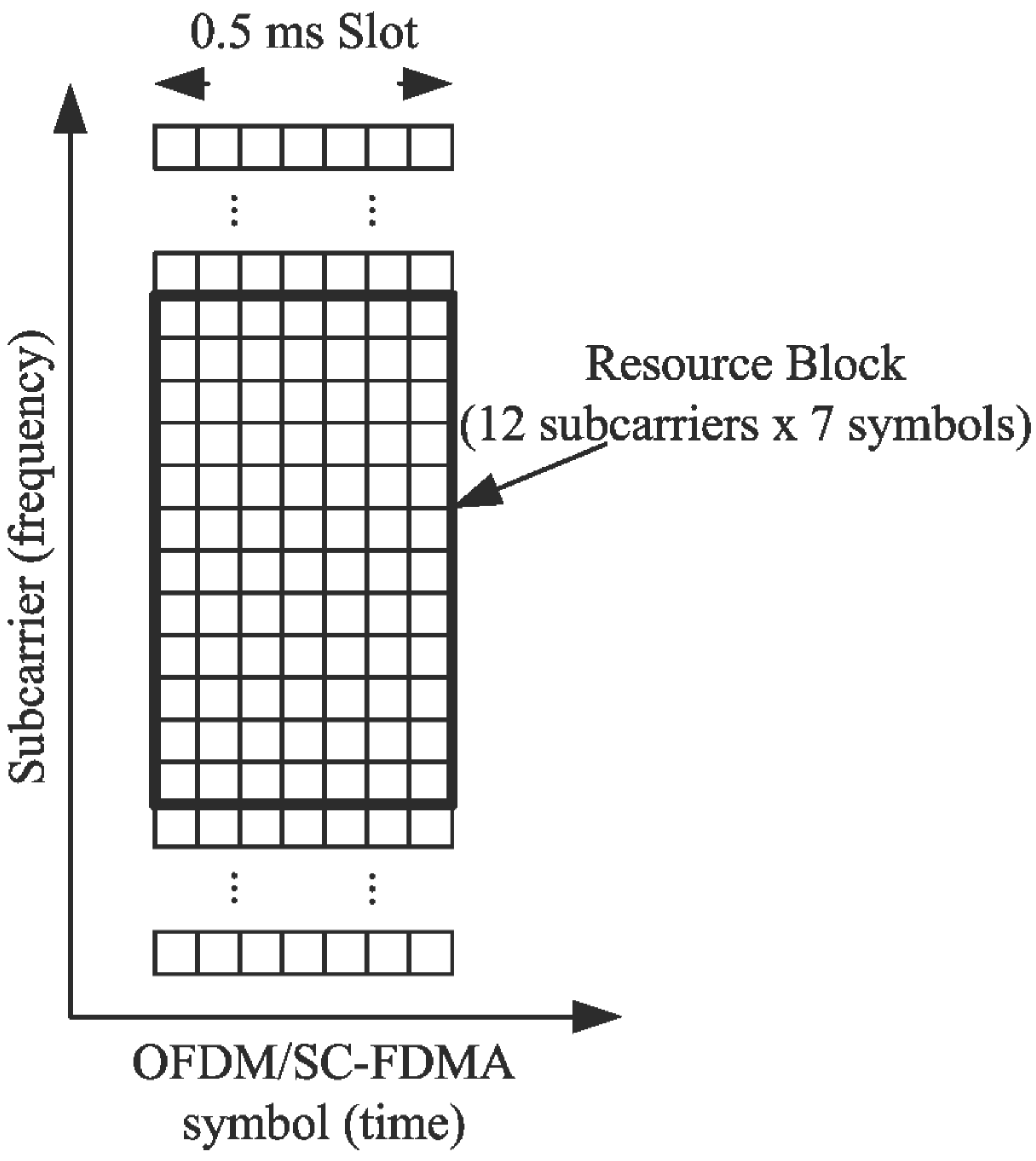
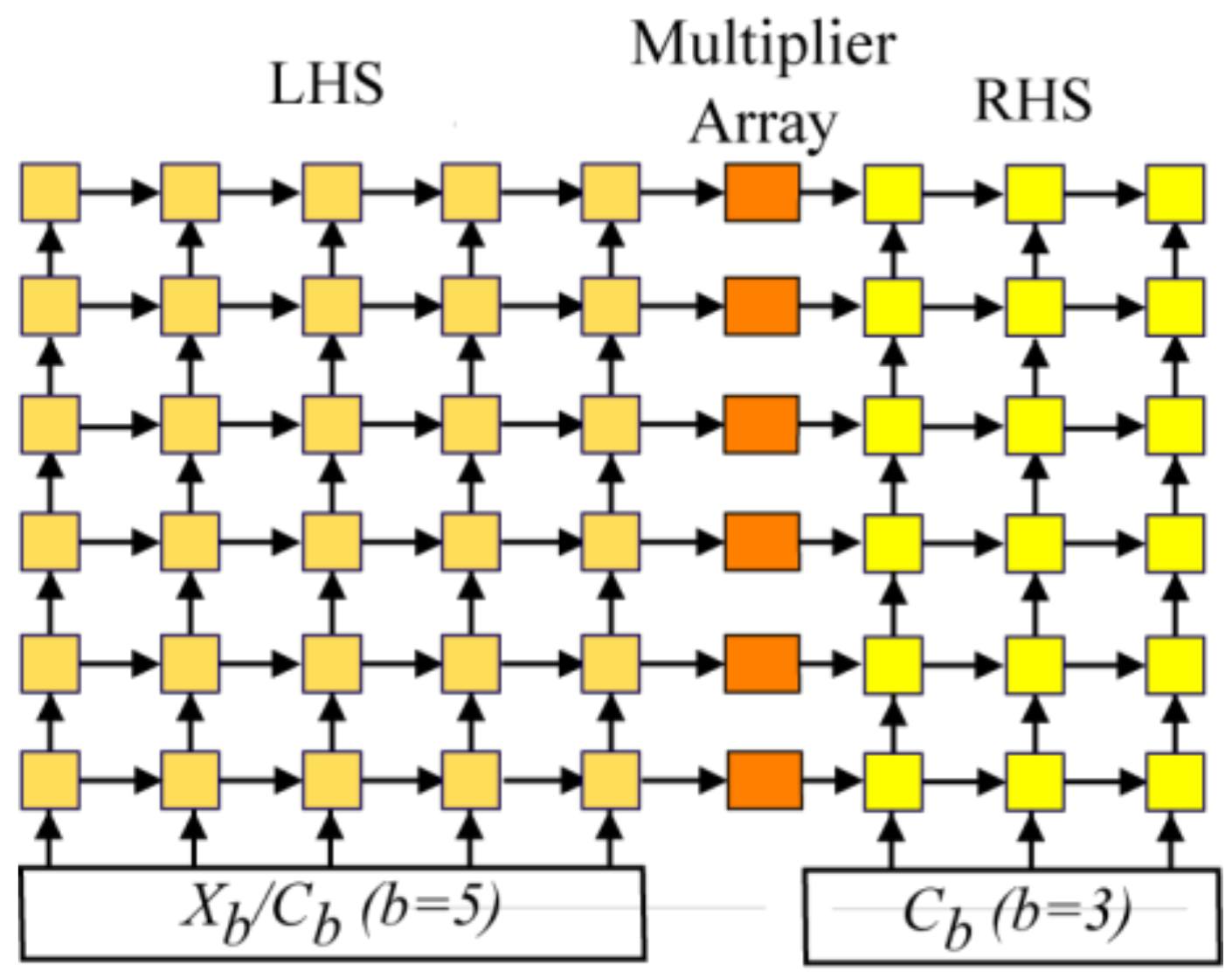
Although the value of N can be obtained with just radices 2, 3 and 5, the architecture chosen here is based on a value of b = 6, so that radix-6 is an option. This value was selected because all SC-FDMA DFT sizes include a factor of 6, since a LTE resource block (RB) or the smallest group of subcarriers used by the SC-FDMA protocol (Figure 10) has at least 12 subcarriers. Therefore, using a radix-6 option translates to more efficient processing for all 35 sizes. The actual structure of the architecture is then that of Figure 5 with b = 6. This choice means that the array also contains sub-set b × b arrays with b = 2, 3, 4 and 5, so base-2, 3, 4, and 5 processing can also be performed.

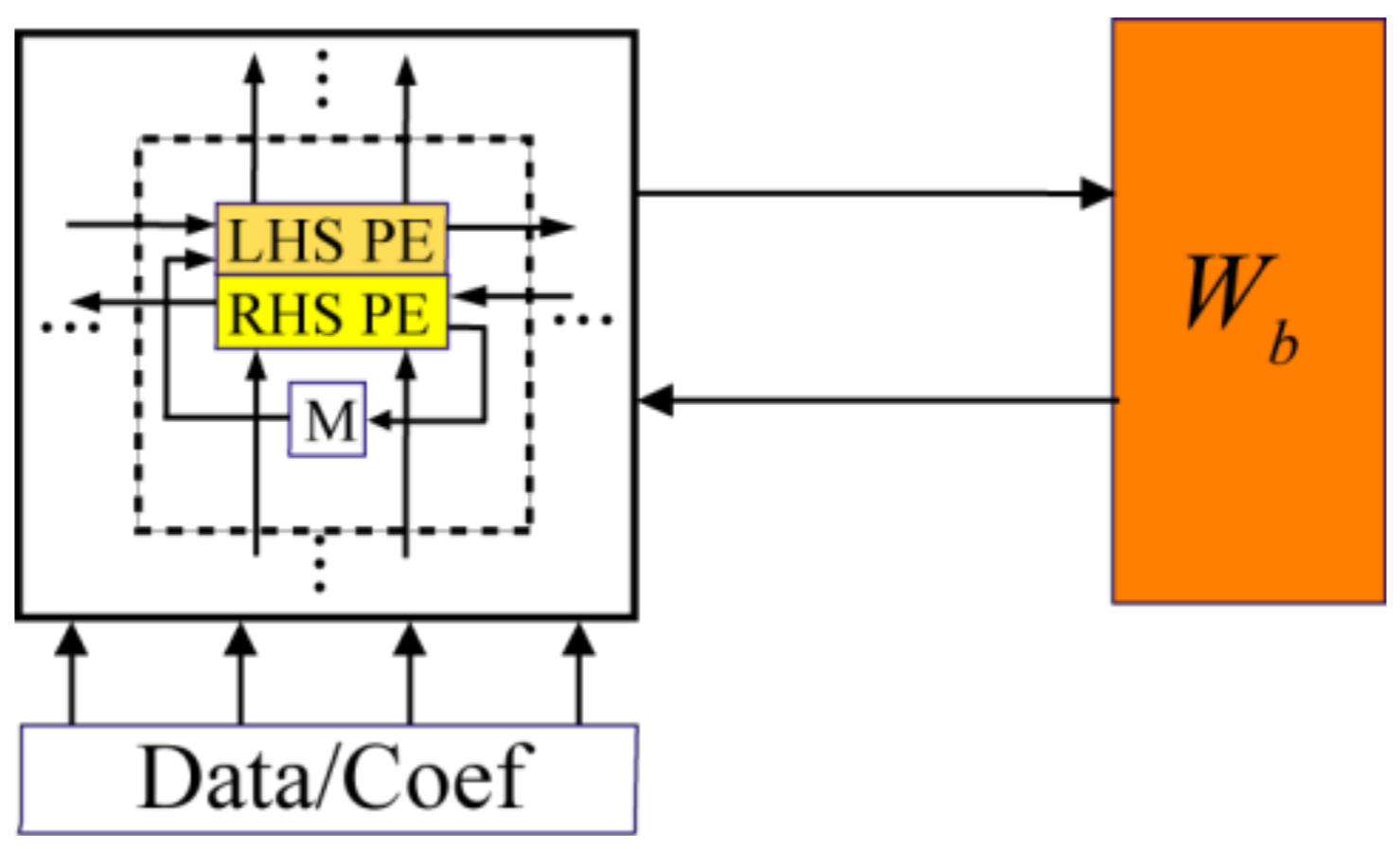
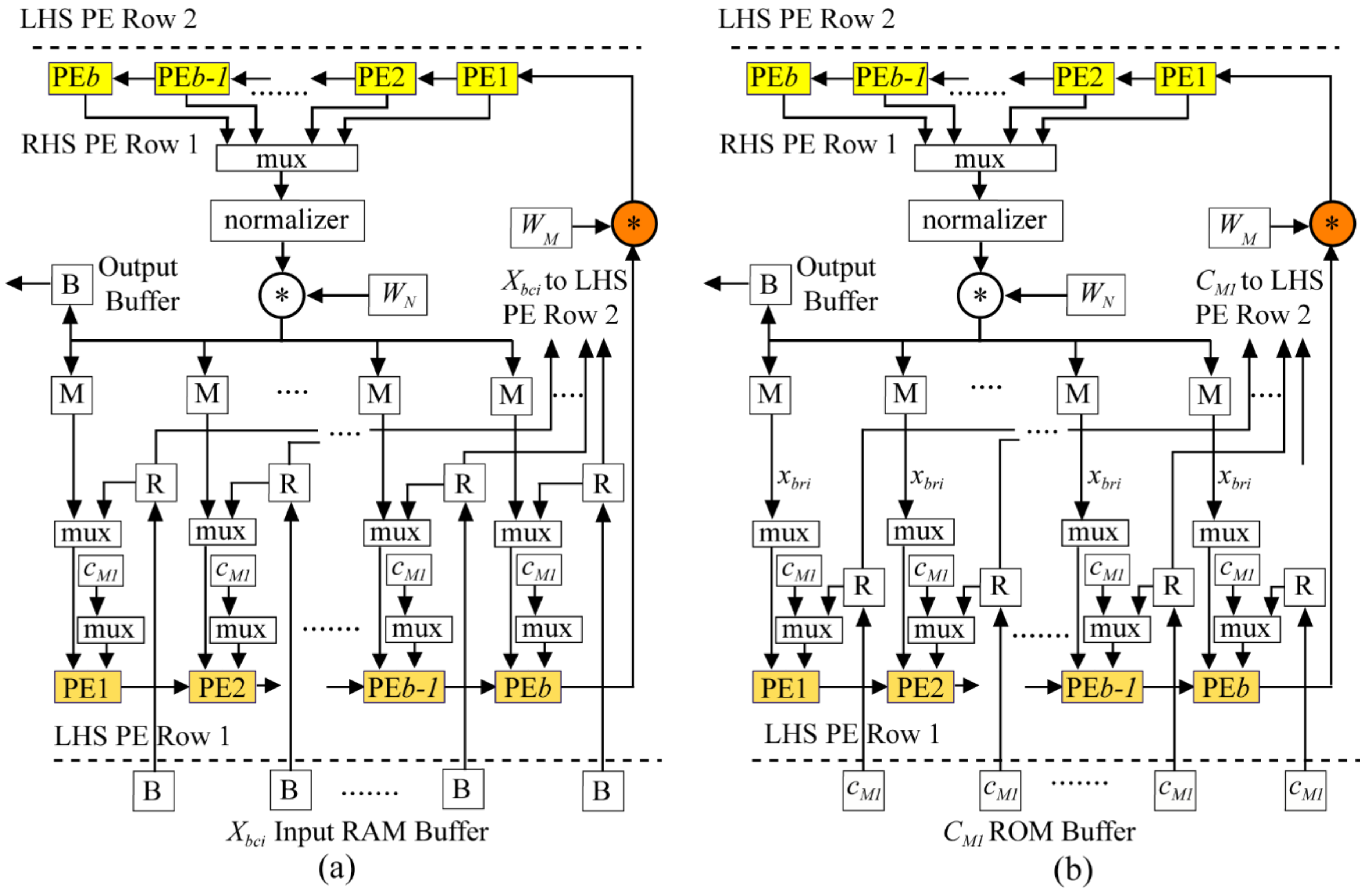
A physical array structure with b = 6 would result in higher throughputs than needed for SC-FDMA applications. Consequently, the physical array consists of only one of the PE rows in Figure 8. In other words, each virtual LHS, RHS, and multiplier PE column in the array is projected (collapsed vertically) onto a single PE row. Thus, there are six RAM memories associated with the six LHS/RHS combination PEs. This linear array emulates the operations of the 2-D b × b virtual array of Figure 5, but completes a DFT computation a factor of six times slower.

6.5.4. On-the-Fly-Twiddle Coefficient Calculation

Since the goal of this design was to provide a run-time option to compute any number of transform sizes, the number of twiddle coefficients that would need to be stored could be unbounded. The total number of twiddle values needed for LTE SC-FDMA itself is about 6500 words. There are schemes for reducing twiddle factor storage to as little as N/8 based on sin/cos symmetries [35], but these are only useful for power-of-two based FFTs.

For this reason, an approach based on a programmable on-the-fly-generation of the twiddle values for a DFT size has been adopted. This twiddle coefficient engine uses a single complex multiplier, a table of twiddle seed values, and a set of size parameters as a basis for doing this. The iterative equation $W_{\mathit{twd}}^{\mathit{next}}{ = W}_{\mathit{twd}}^{\mathit{last}}{W}^n$, where ${W = e}^{-2\pi j/N}$ and $W^n$ is a seed value, is used to generate values for a particular DFT size given the starting seed.

It would be possible to generate the N twiddle values for a transform size with a single seed value, however there is more circuit complexity involved in doing this because the twiddle factors must be generated in a special order due to the algorithms used. Additionally, there are numerical considerations that come into play as well. A better tradeoff was to use a separate seed for each column of a twiddle matrix. For example, if a 960-point DFT is factored as 30 × 32, 32 seed values would be needed to generate all twiddles.

In the implementation of the LTE SC-FDMA, the twiddle generation circuit required only 937 words of memory to hold all twiddle seeds needed for 35 DFT sizes. The logic needed to implement the entire programmable twiddle circuit was only about 10% of the circuit hardware.

6.5.5. Programmability

The base-6 circuit described here was programmed at a more abstract level than the base-4 circuits in Section 6.2, Section 6.3 and Section 6.4. It used a single RAM memory to hold parameters that determine the specific factorizations and execution orderings used for loop index ranges in the Verilog coded control modules.

To illustrate the programmed data flow, consider the example N = 540 = N₃ × N₄. Since our implementation consists of 6 × 6 SAs, it would be most efficient to choose the factorization N₃N₄ = 36 × 15 = 6² × (3 × 5) because this makes best use of all the hardware. In this case, the processing consists of 15 36-point column DFTs followed by 36 15-point row DFTs. The input X_b is stored in the input buffers in such a way that it is accessible as a sequence of blocks X_bci, i = 1, …, 15 of 6 × 6 column data. Then, the 36-point column DFTs are done using (3) with M = N₃ = 36 = N_1ciN₂ = 6 × 6, $C_{M1}{ = C}_{M2 }{ = C}_b$ (b = 6) and $C_b^{i,k}{ = e}^{-j\left(\frac{2\pi \mathrm{ik}}{b}\right)}$, i = 0, 1, …, b − 1; k = 0, 1, …, b − 1. Each X_bci enters the array at the bottom of the LHS SA (Figure 5 and Figure 8) and flows upward with systolic matrix–matrix multiplications performed as before. As each of these 36-point column DFTs are computed, they are multiplied by elements in the 36 × 15 twiddle matrix W₅₂₀ which are generated on-the-fly. During this processing, all PEs are used with 100% efficiency.

After twiddle multiplication by W₅₄₀, the multiplexor in Figure 8a is used to store data for the 15-point row DFTs in a way that they can be accessed as 3 × 5 data input blocks, X_bri, i = 1, …, 36, from the internal PE RAMs. Each of the six PE virtual rows is responsible for storing six DFT matrix rows as six 3 × 5 blocks in associated internal RAMs.

For the row DFTs, not all the LHS/RHS PEs are used. Rather, as shown in Figure 4, the LHS side SA reads from RAMs in five of the six PE columns to do the five-point transforms by multiplication of these data blocks by C₅ values fed from the bottom of the LHS array. The multiplier array then multiplies these transform values arriving from the LHS array by appropriate elements of a 3 × 5 twiddle matrix stored in a small ROM. Finally, only three PE columns are used on the RHS array to perform all the three-point transforms. Results are stored in an output buffer and are output in normal order.

The control hardware is aware of the number of rows/columns used in the LHS and RHS arrays during the computations, the different coefficient and twiddle matrices required, the read/write memory addresses, the sequencing in/out of data storage and retrieval patterns, etc. All this parameter information is saved essentially as a table in the ROM memory. The programmability arises because when a DFT size is requested, the corresponding table is read from ROM and used to set loop values in the Verilog control code. The number of different DFT sizes that can be supported is then only limited by the size of this parameter memory.

It is important to note that the same architecture can be programmed to perform power-of-two FFTs as well. This is important, as almost all wireless protocols—including LTE—require power-of-two computations and having both options available in the same circuit could be useful for future wireless applications.

6.5.6. DMBA LTE SC-FDMA Transform Throughput and Latency

Table 8. Throughput (T), latency (L) as a function of transform size (N) for 35 SC-FDMA DFT sizes.

N	T	L	N	T	L	N	T	L
1296	2592	5006	576	1154	2211	180	365	609
1200	3601	5798	540	1081	2096	144	289	569
1152	3458	5516	480	962	1878	120	244	424
1080	2160	4178	432	864	1694	108	221	390
972	3891	5550	384	770	1510	96	200	347
960	2881	4599	360	721	1412	72	149	283
900	1801	3464	324	651	1244	60	124	243
864	1728	3350	300	601	1168	48	102	206
768	2304	3686	288	578	1143	36	36	133
720	1440	2798	240	481	951	24	24	95
648	1296	2522	216	437	717	12	12	66
600	1201	2338	192	384	759

shows, for each SC-FDMA transform size N, the corresponding throughputs (T) and latencies (L) in clock cycles for the design. In this context, latency is defined as the number of clock cycles it takes to finish the first transform in a series of transforms. The DMBA FFT cycle counts are based on Modelsim Verilog simulations. Note that for the smaller transform sizes, 12-, 24-, and 36-points, the circuit supports constant streaming of the data into and out of the circuit.

6.5.7. Comparison with Commercial Circuits

In this section, the proposed LTE SC-FDMA DMBA is compared to Xilinx and Intel versions of the same circuit. To provide a more relevant metric than throughput and latency numbers, we calculated the length of time necessary to compute an LTE RB, as shown diagrammatically in Figure 10. For example, 1296 subcarriers would imply processing a maximum of 108 resource blocks. This is a good performance comparison metric in that it requires both low latency and high throughput.

(a) Xilinx [41]

A Vertix-6 (XC6VLX75T-3ff7484) FPGA was used as the target hardware for both the Xilinx and the DMBA. The Xilinx LogiCORE IP version 3.1 was used to generate a 16-bit version of their DFT because the SQNR of 60.0 db (mean over all 35 transform sizes) was comparable to the DMBA 12-bit circuit with mean SQNR = 63.3. Xilinx LogiCORE includes a bit accurate C model, callable as a Matlab mex function, that was used to obtain Xilinx SQNR values.

The resource comparisons in

Table 9. LTE commercial circuit technology comparisons.

Circuit	FPGA	LUT	Reg	Blk RAM	Mult 18-Bit	Fmax (MHz)	RB Avg	Thrpt Norm
DMBA	Virtex-6	2915	2581	19	72	401	16.6N	1.00
Xilinx	Virtex-6	3851	4326	10	16	407	23.4N	0.72
DMBA	Stratix III	3816	3188	29	60	417	16.6N	1.00
Intel	Stratix III	2600	n.a.	17	32	260	32.9N	0.31

use a block RAM normalized to 18-kbits, so that a Xilinx 36-kbit block RAM is considered equal to two 18-kbit RAMs. Also, the “RB Avg” column provides the average number of cycles (over all 35 DFT sizes) it takes to compute the DFT for the seven symbols defined by a RB as a function of the transform size N. Finally, the Fmax value (here Fmax is not the sample rate) and the number of RB cycles are combined, providing a measure of the throughput, which was normalized to 1 in our design (higher is better). Table 9 shows that Xilinx LUT usage is higher by 32%, register usage by 68%, average computational cycles by 41% while normalized throughput is 39% higher for the DMBA. Consequently, the overall combined gain is significant.

In terms of throughput in clock cycles, the Xilinx average over 35 DFT sizes was 3.3N, whereas that for the DMBA was only 2.1N. If these numbers are used as a measurement basis to calculate throughput per logic cell (7), then the DMBA efficiency is 130% higher.

The 401 MHz Fmax clock speed is lower than the other DMBA Fmax values in earlier examples because the critical path here is in the control hardware rather than the array structure itself. Additional control-level pipelining would be necessary to move the critical path out of the control hardware.

(b) Intel [38]

Unlike Xilinx, Intel does not offer a DFT LTE core; however, they have published results of an example design running on a Stratix III FPGA that provides a useful basis for comparison. This design example is different compared to the DMBA here in that it does not offer a 1296-point transform option and the outputs are not in normal order. Adding buffer circuitry to sort the output data would require additional logic and add ~N additional words of memory (~5 Stratix III M9K RAM blocks) to the numbers shown in Table 9.

For comparison, the DMBA was also targeted to a Stratix III FPGA (EP3SE110F780C2). The Intel implementation uses less logic but is far slower, both in terms of the lower values of Fmax and the increased number of cycles to complete the RB computation. Consequently, the DMBA design had about three times higher throughput while LUT usage was only ~47% higher (some of this could be due to a lower speed grade used in the Intel design—this was not specified). It should be noted that the Intel latencies would be relatively understated given that data output is not in normal order.

The DMBA FFT circuit operation at 450 MHz was demonstrated on an Intel Stratix III EP3SL150F1152C2 FPGA using a development board.

6.5.8. Other FPGA LTE Implementations

The other two designs are different from those in Table 9 in that they use a higher radix [39] or a pipelined FFT [40] (single-path delay feedback) architecture to reduce the overall number of cycles needed to compute a DFT in less than the actual transform size N. This means it is possible to have a streaming architecture, e.g., one where data flows continuously into and out of the circuit (Fmax is the same as the sample rate).

No SQNR data was supplied to indicate the circuit precision, although the internal precision in [39] was 18-bits and [40] used a mixed floating point (the same exponent for real and imaginary words) and block floating point. Details regarding latency are not discussed in these papers; however, comparison is still instructive and performance can be estimated based on throughput alone, which is more important than latency for computing resource blocks.

The comparison results for Virtex FPGAs are shown in

Table 10. LTE non-commercial circuit technology comparisons with DBMA.

Circuit	FPGA	LUT	Reg	Blk RAM	Mult (18-Bit)	Fmax (MHz)	Thrpt (Cycles)	Thrpt Norm
[39]	Virtex-5	7791	n.a.	7	44	123	N	0.64
[40]	Virtex-6	10,768	786	45	41	61	N	0.32
DMBA	Virtex-6	2915	2581	19	72	401	2.1N	1.00

. For the DMBA, the average throughput as a function of N for all 35 transform sizes is 2.1N, which is a factor of two higher than the other implementations. However, these more complex architectures require far more LUT hardware, 2.7 times and 3.7 times for [39] and [40], respectively. Although [40] uses fewer registers, this is less meaningful because the 10:1 ratio of LUTs:registers in FPGA hardware leads to imbalances that can cause many registers to be inaccessible. Additionally, using a normalized throughput like that in Table 9, the DMBA could be correspondingly faster by perhaps 56% for [39] and 3-fold for [40]. FPGA details would be needed for an accurate clock speed comparison.

7. Conclusions

We have demonstrated a new class of FFT architecture that combines the flexibility and programmability of memory-based designs with the high throughputs available from array-based hardware. The architecture is particularly well suited to FPGA implementations and offers circuits that are simple, regular, and uniform with the interconnection locality and speed of SAs, and with the computational efficiency of pipelined FFTs.

As mentioned in the introduction, the primary goal was to improve circuit efficiency as measured by the throughput obtained per logic cell (7) repeated below.

$$\mathit{Efficiency} = \mathrm{100,000} \text{×} \mathit{throughput}/\frac{\mathrm{LUTs} + \mathit{registers}}{2}$$

In

Table 11. Improvement in efficiency per the above formula, all circuits.

Function	Circuit	Size (Points)	FPGA	Efficiency Increase (%)
Fixed	Intel	256	Stratix III	44
Fixed	Spiral	256	Stratix III	−12
Fixed	Intel	1024	Stratix III	36
Fixed	Spiral	1024	Stratix III	−11
Variable	Intel	128:2048	Stratix IV	87
Variable	[36]	16:2048	Stratix V	181
Flt.Pt.	Intel	256	Stratix IV	128
Flt.Pt.	Spiral	256	Stratix IV	103
Flt.Pt.	Intel	1024	Stratix IV	150
Flt.Pt.	Spiral	1024	Stratix IV	117
Flt.Pt.	Intel	1024	Arria 10	169
SC-FDMA	Xilinx	12:1296	Virtex 6	130

, the last column provides the percentage efficiency increase for the DMBA, obtained by taking the ratio of efficiencies of other circuits in the various comparison tables in Section 6. As can be seen, this varies from a low of −12% to as high as 181%, with an average 94%. The efficiency increase obtained for the Spiral fixed-point circuits are likely not statistically significant in the context of such complex circuits, yet they require substantially increased usage of memories (M9K) and multipliers by 42%/245% and ×3.4/×4.4 for the 256/1024-point designs.

Even though the architecture was optimized primarily to reduce register and LUT usage, memory usage was improved in more than half the circuits. In general, more multipliers are used but, as noted in Section 2.1, large numbers of these are available.

A more detailed list of the comparative benefits is as follows:

• Architecture suitability for a wide range of both power-of-two and non-power-of-two transform sizes, so that all Section 6 example circuits could be based on the same architecture, whereas the Intel designs rely on several architectures to do the equivalent.
• Improved throughput rates resulting from high clock speeds and new algorithms (>500 MHz for 65 nm FPGA technologies).
• Reduced use of FPGA LUT and register fabric. For example, Intel’s latest IEEE 754 floating-point FFTs using an Arria 10 FPGA target device required 2.2/1.7/2.2 times more ALMs/LUTs/registers for a 1024-point FFT than our DMBA equivalent, which also has a 39% higher throughput (Table 7).
• A 20 to 30 db increase in SQNR derived from the combined block floating point and floating-point scaling scheme (Table 1).
• Programmability (Table 3 and Table 8) supporting mixed radices, plus non-FFT functions such as cyclic prefix insertion.
• Throughput scalability by increasing the PE array length, N₃/b, using more than one array to do the column processing or increasing the size of b.
• Ability to do 2-D and 3-D transforms by not performing the row/column twiddle multiplications.

Finally, circuit performance and verification were confirmed in FPGA hardware as well as behavioral Matlab and Verilog RTL simulations for both power-of-two and non-power-of-two classes of circuits. By providing high performance, hardware efficiency, and programmability, our DMBA can be used to meet the expanding spectrum of future applications for FFTs.