Implementation of a Single-Phase SST for the Interface between a 13.2 kV MVAC Network and a 750 V Bipolar DC Distribution
Abstract
:1. Introduction
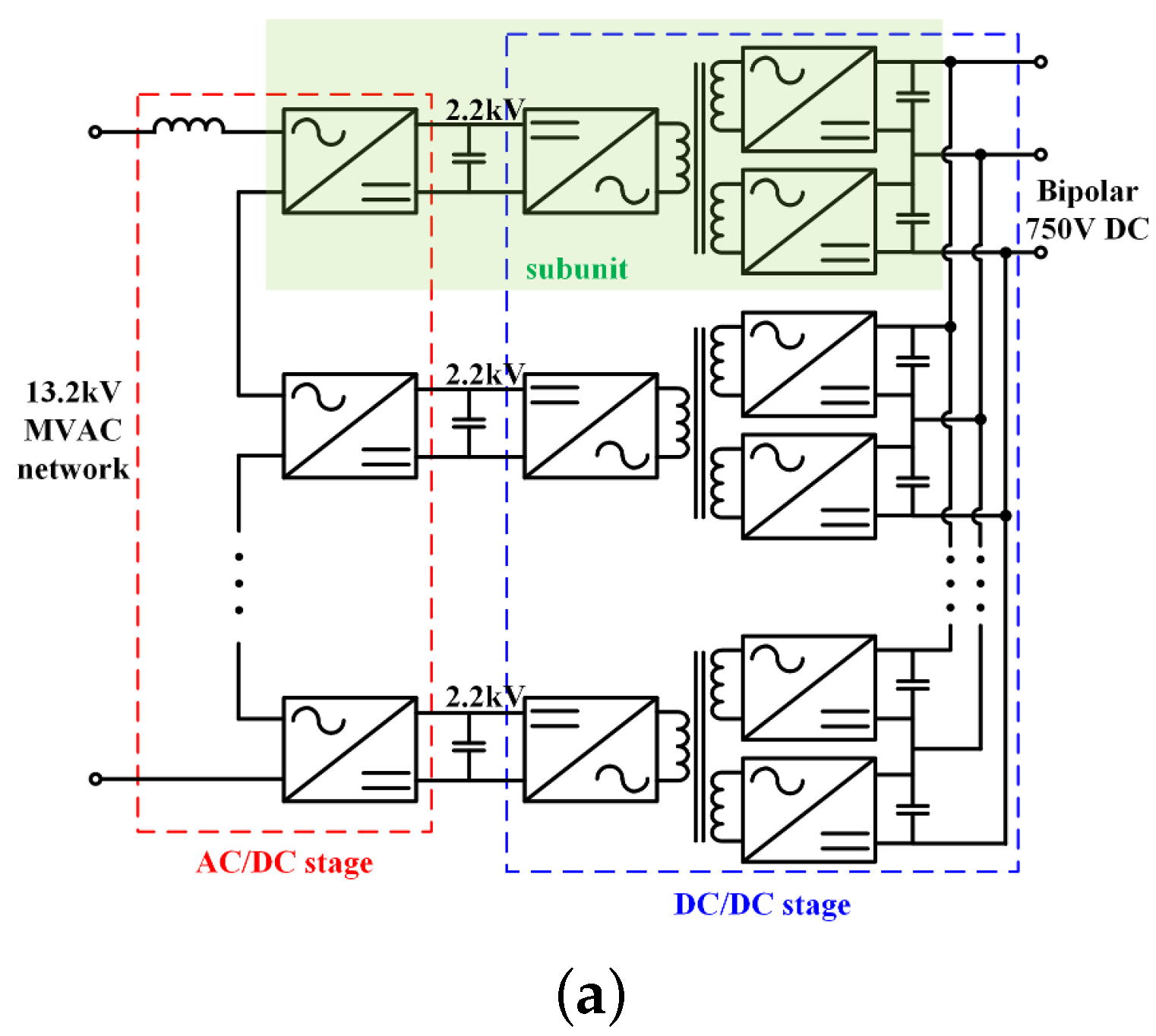
2. Structure of the SST Prototype
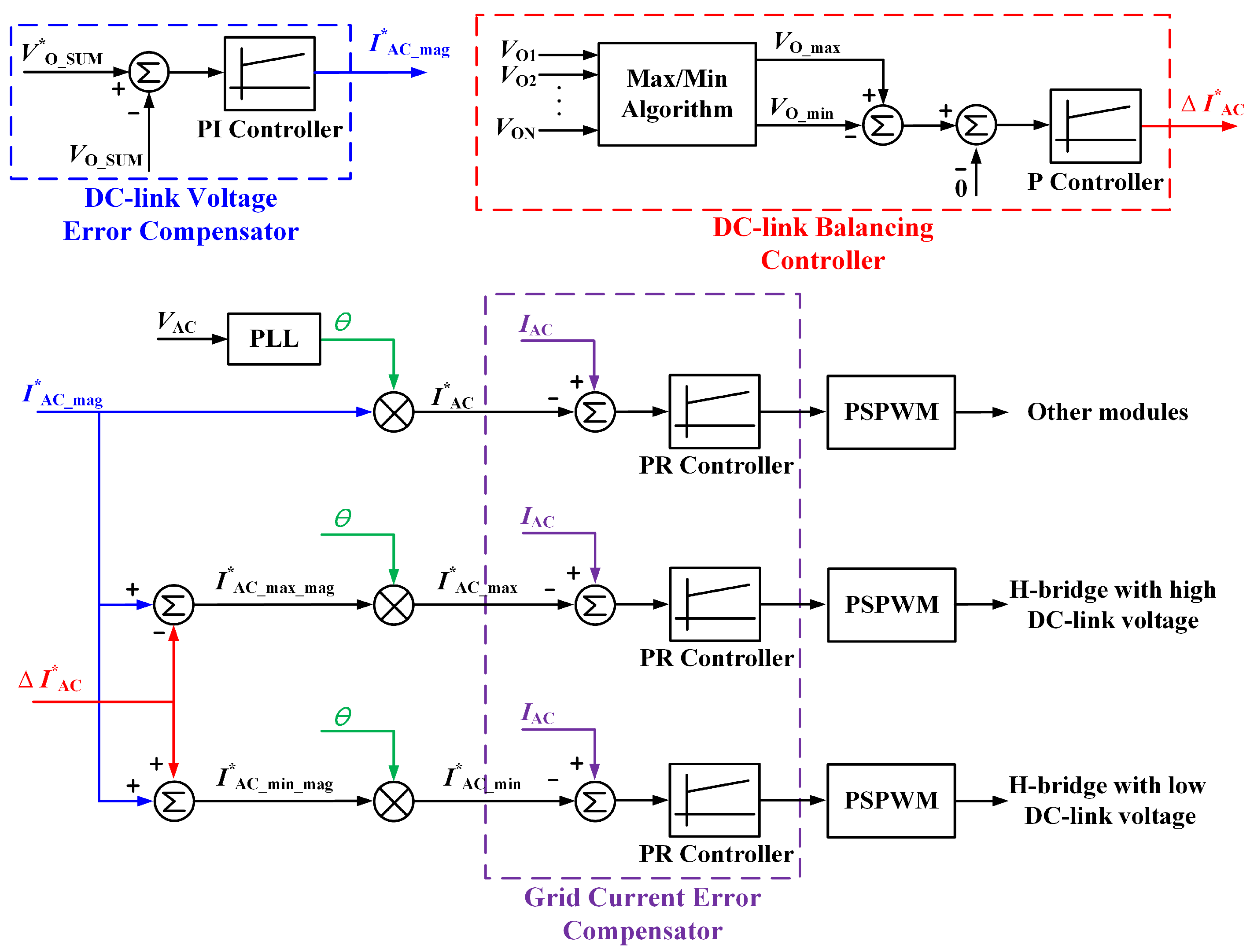
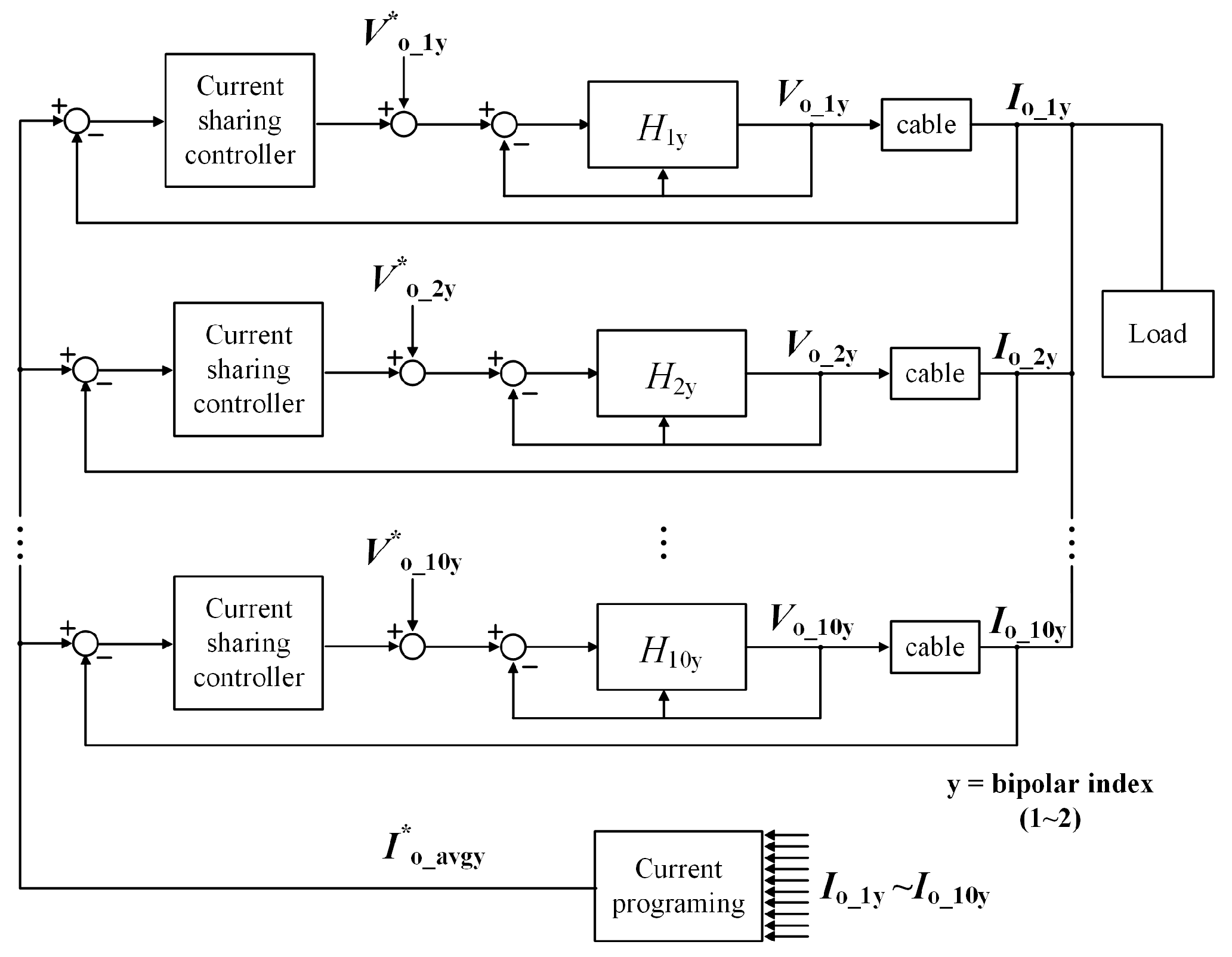
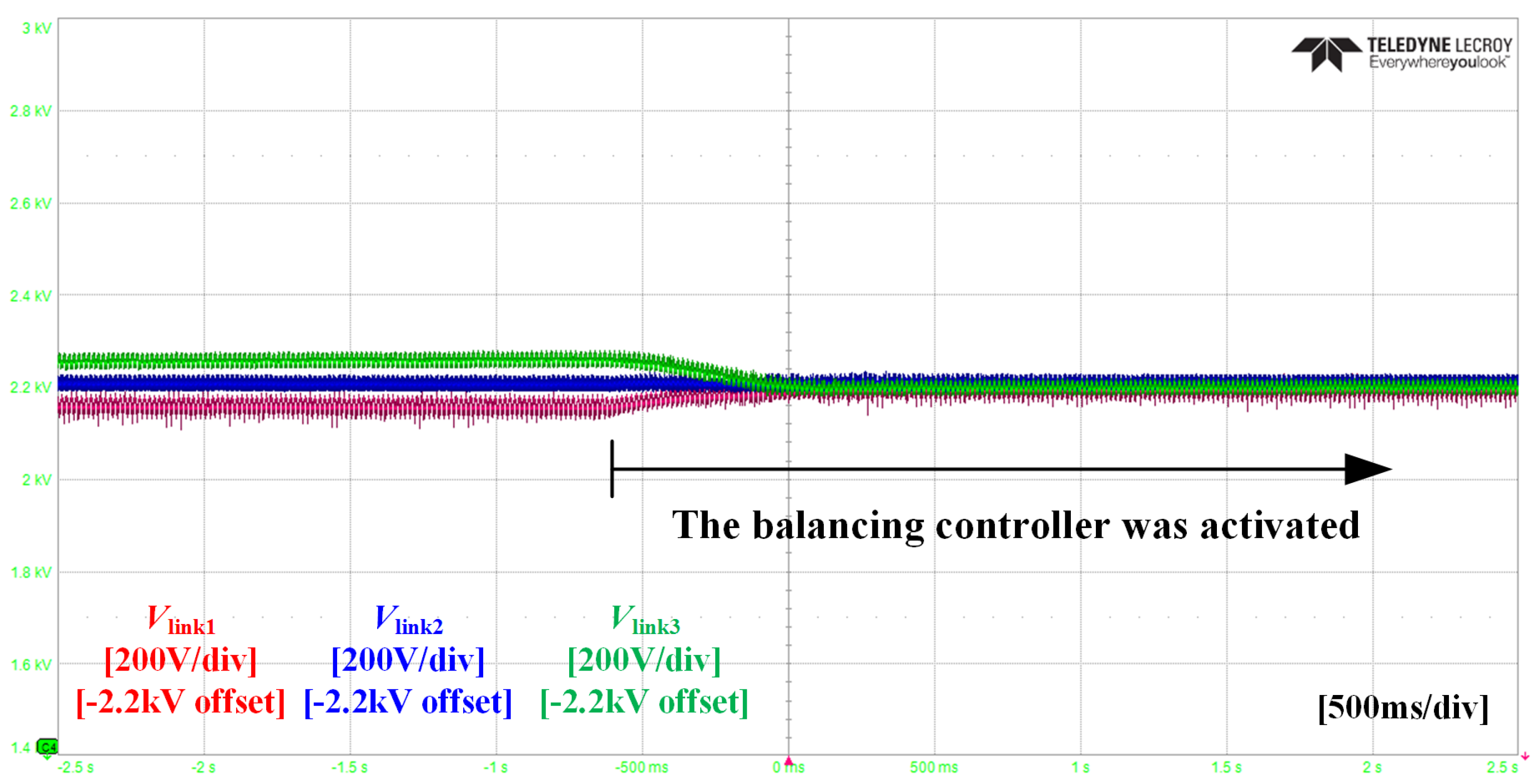
3. A Simple and Practical Voltage Balancing Controller for CHB
4. Analysis of the TAB Converter
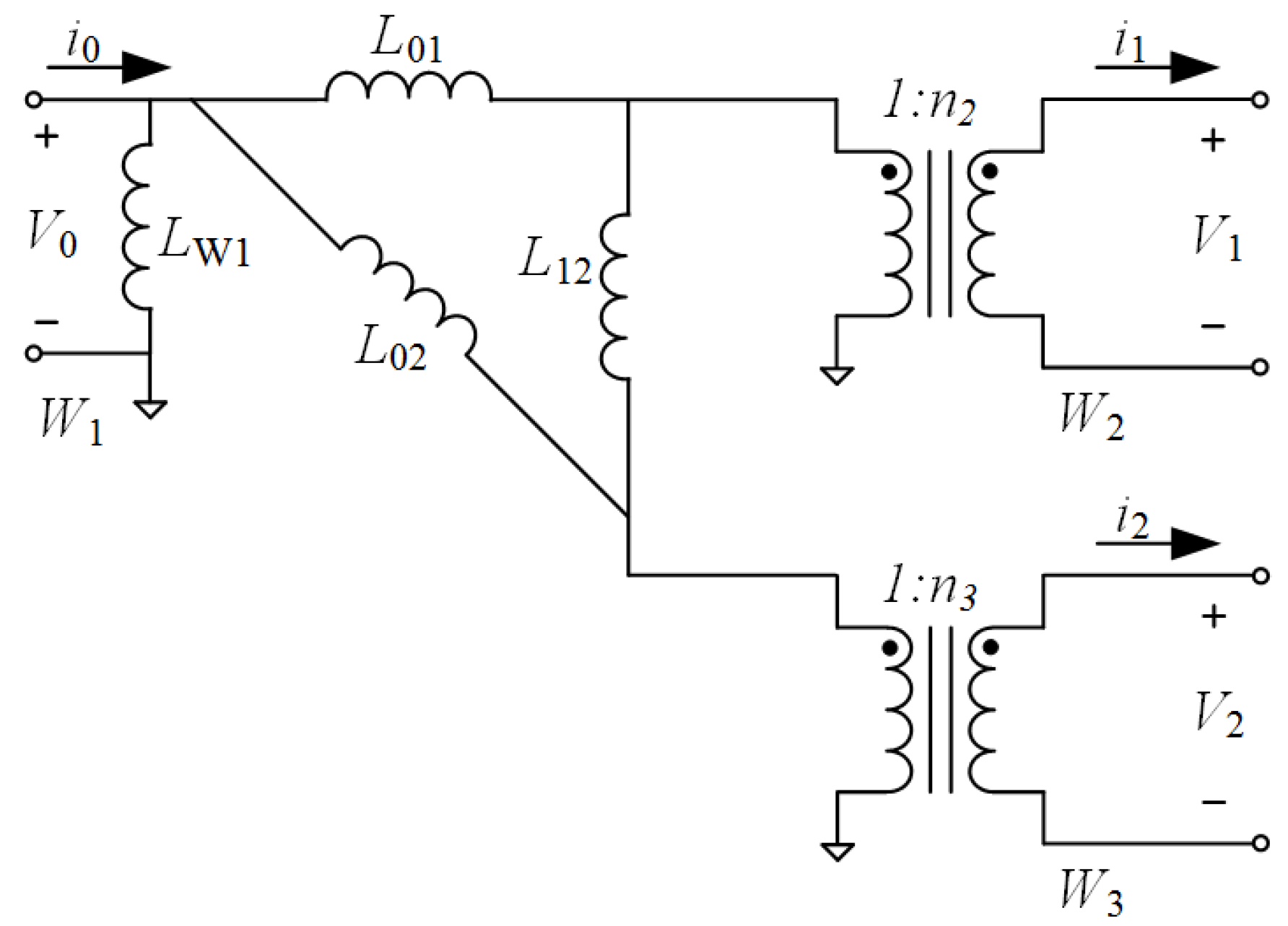
4.1. Modeling of the Three Windings Coupled Transformer
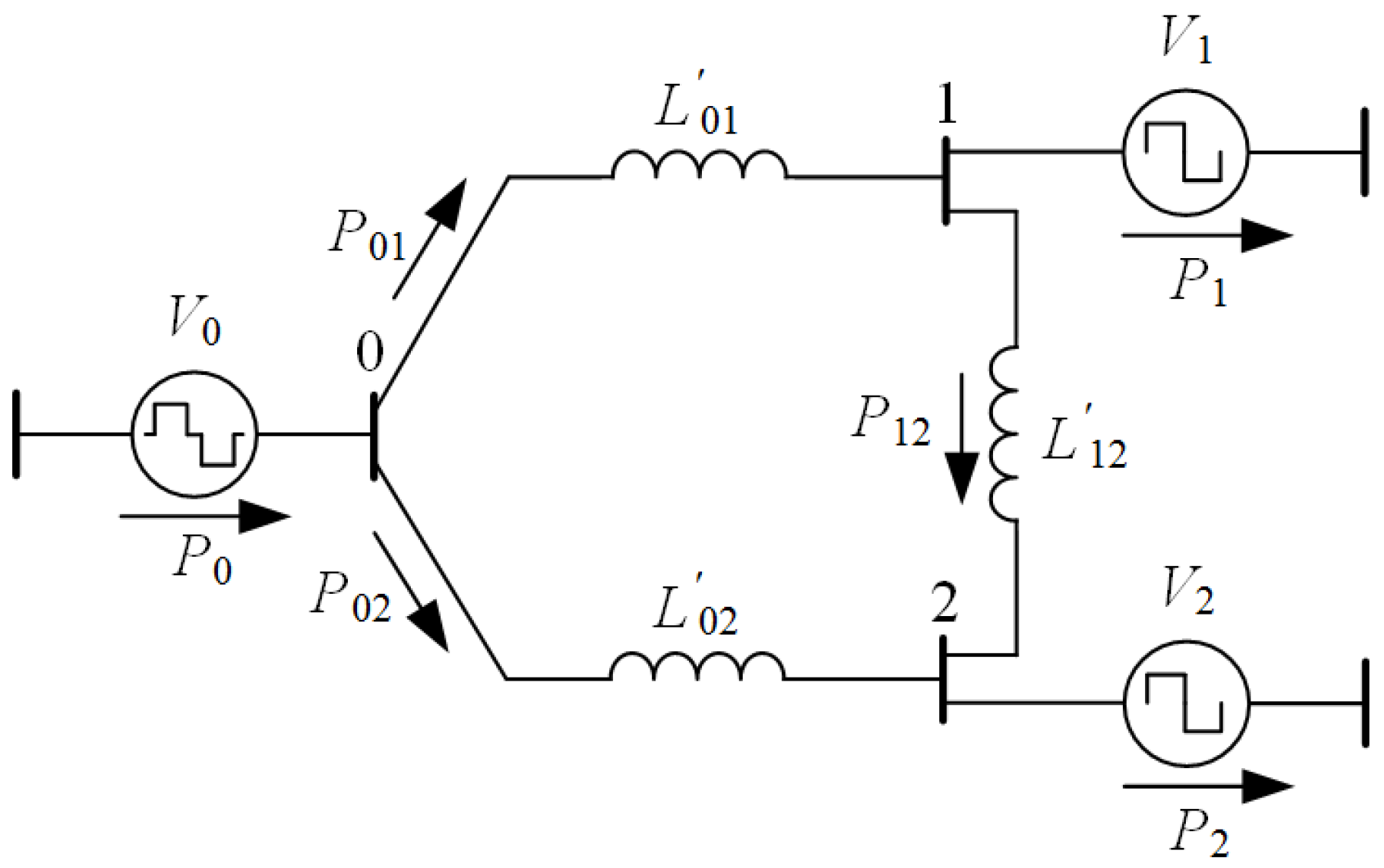
4.2. Power Transfer Modeling of the TAB Converter
4.3. Controller Design
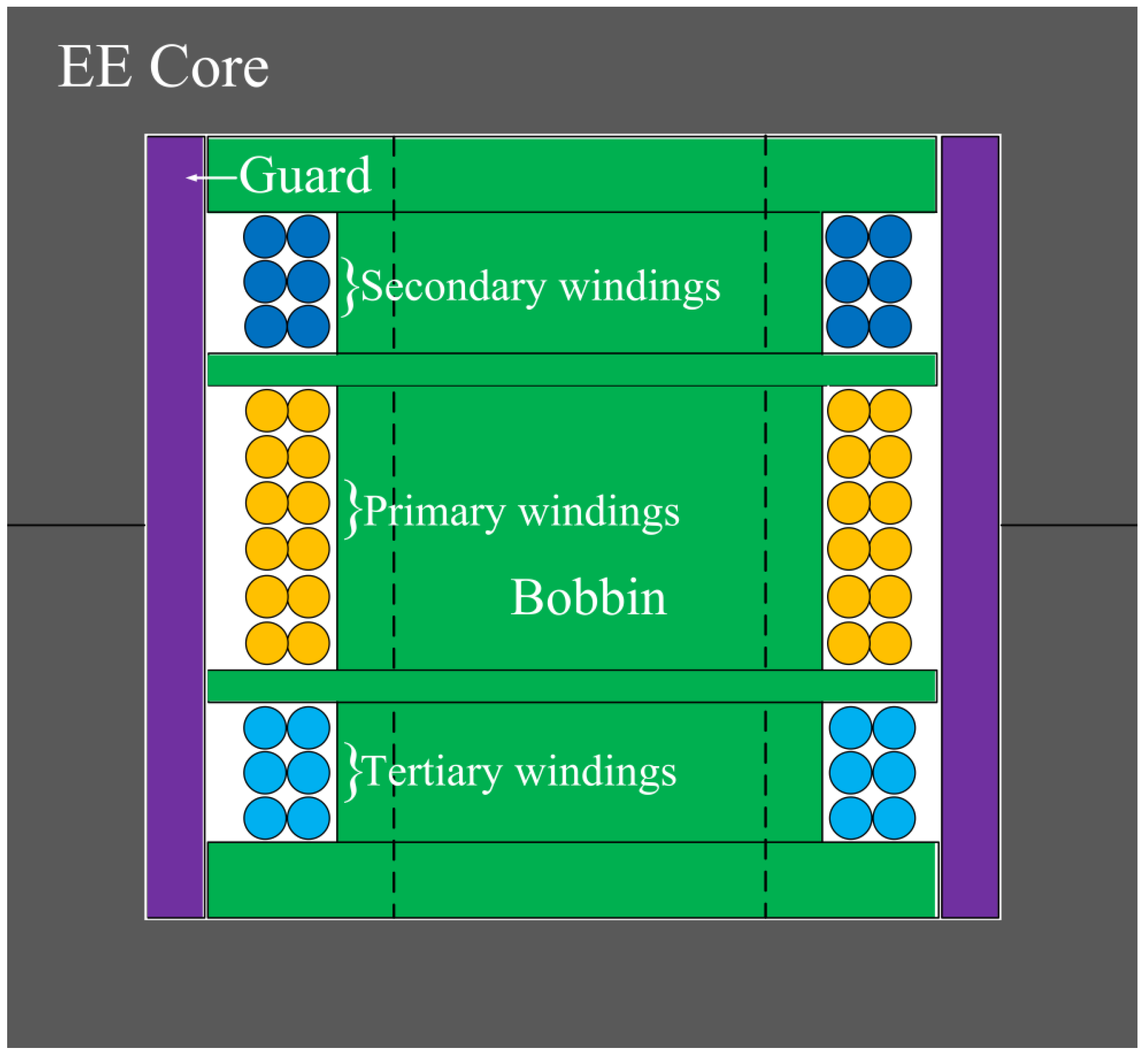
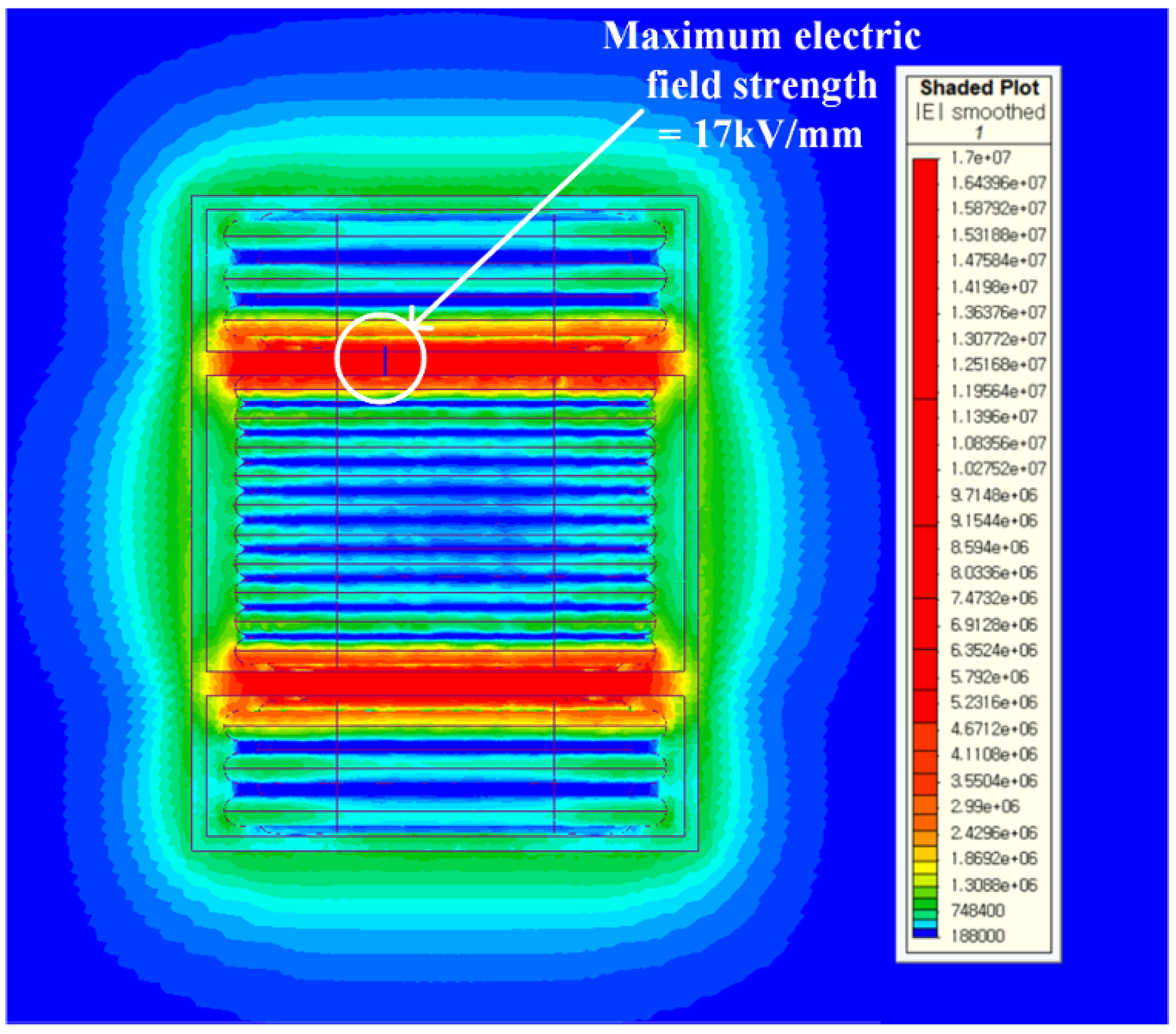
5. Transformer
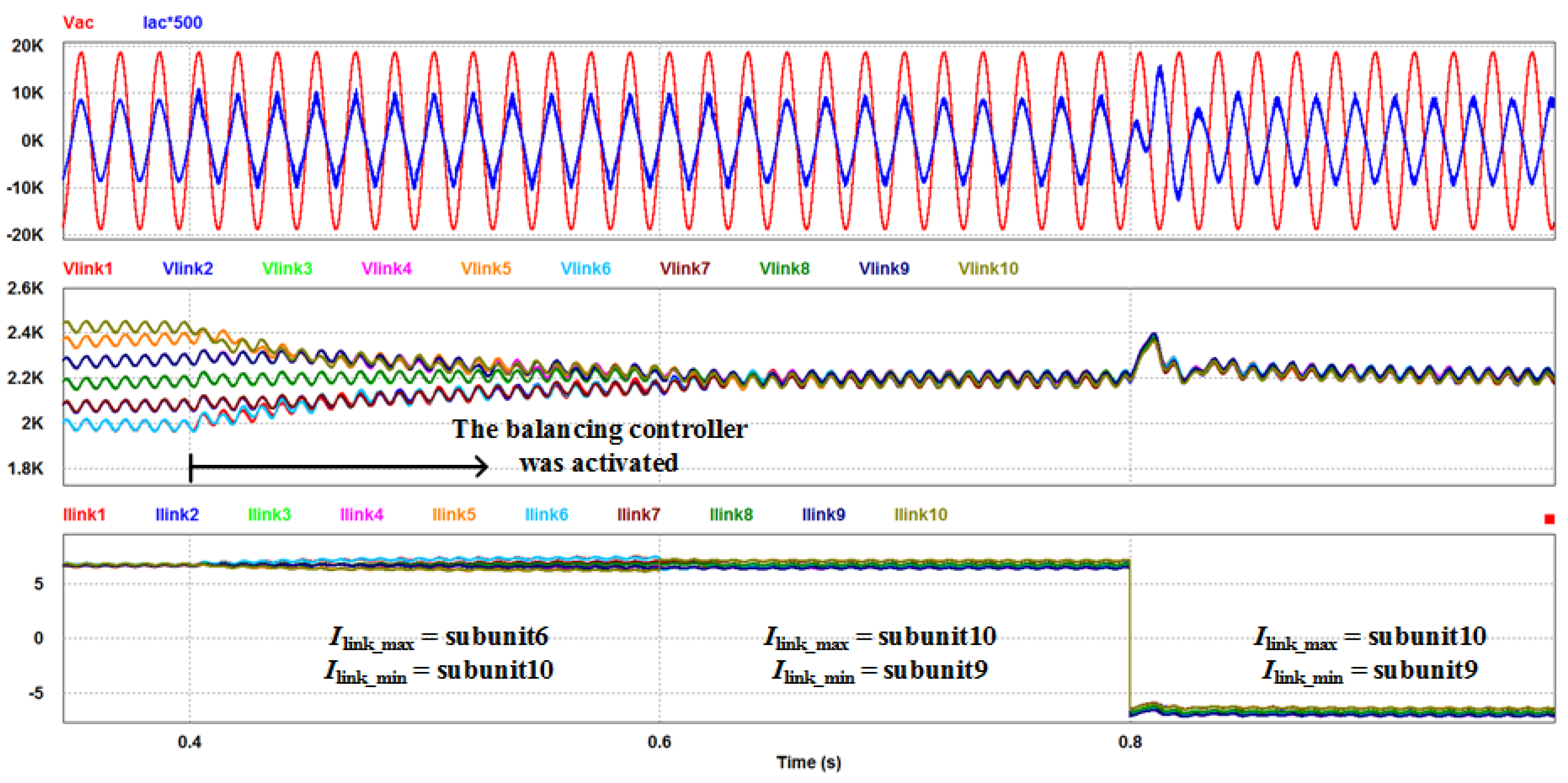
6. Simulation
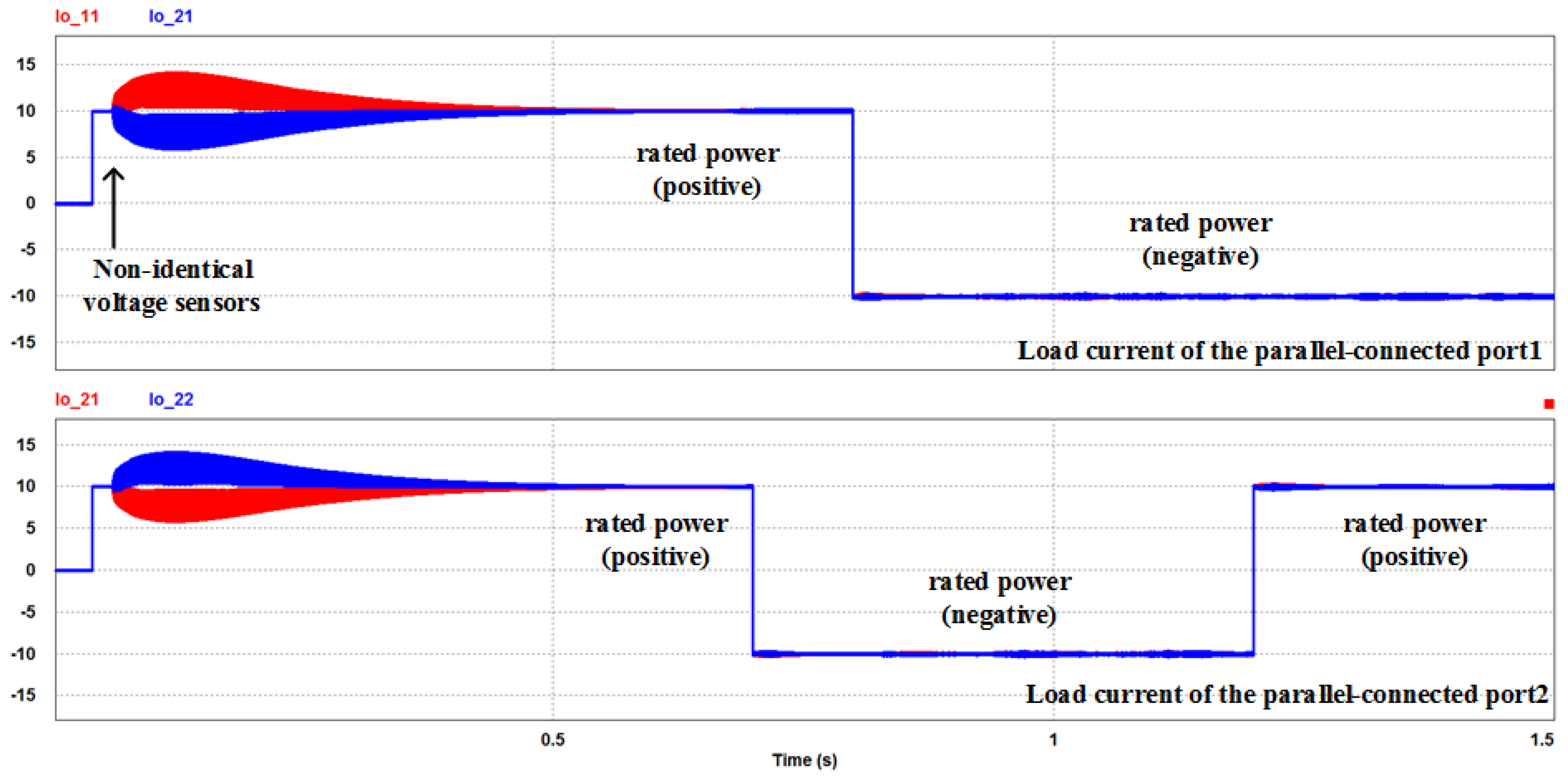
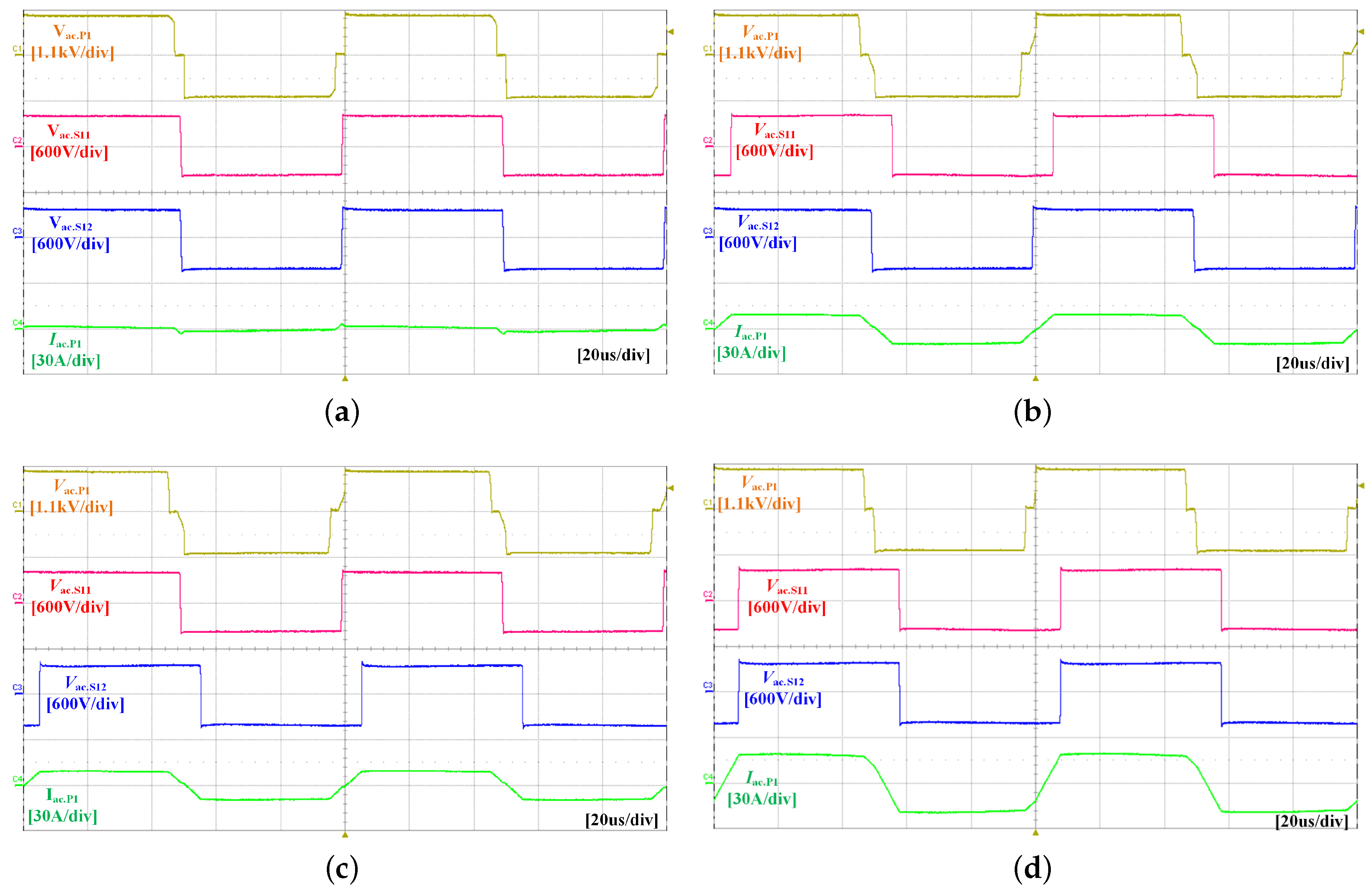
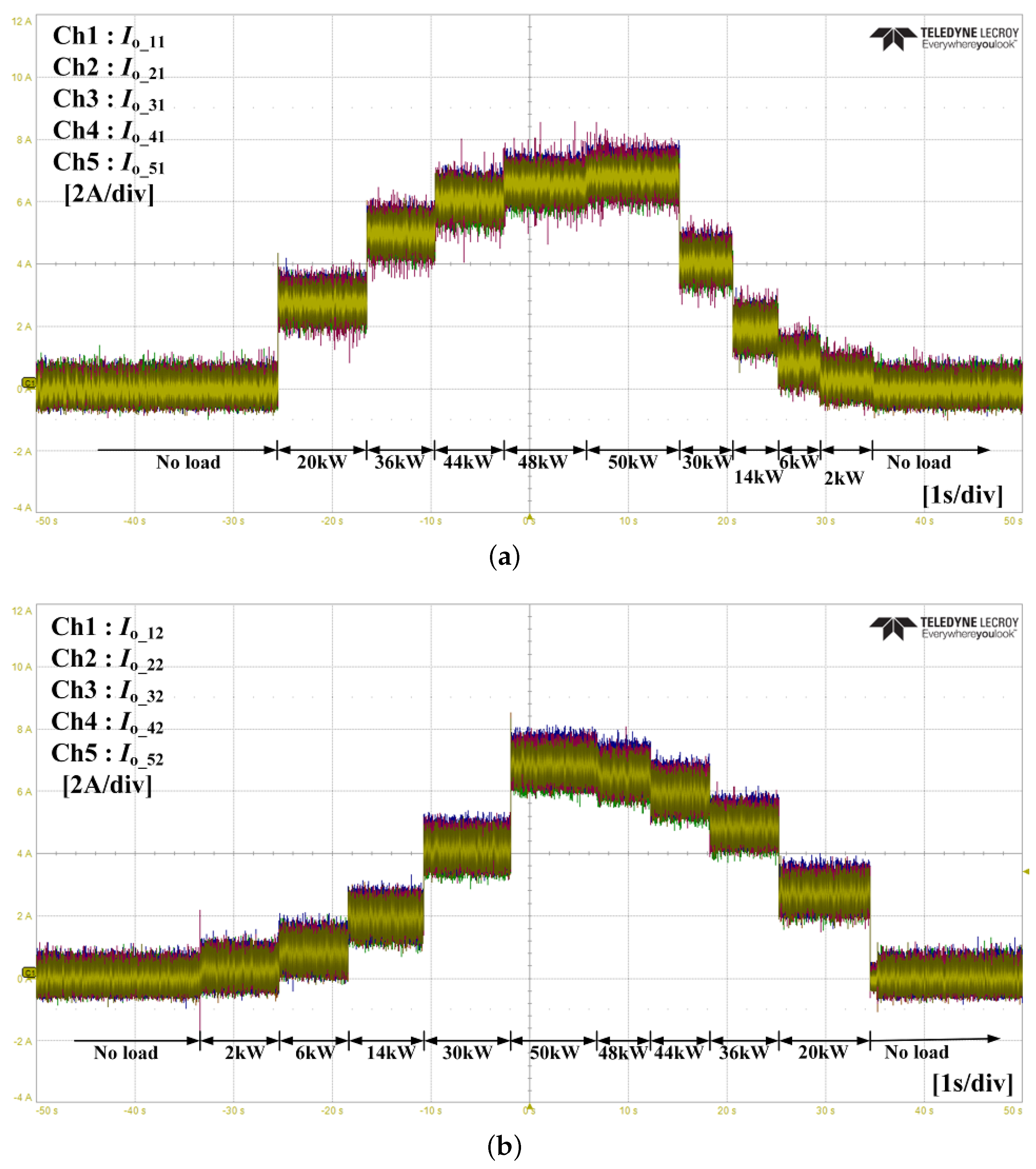
7. Experiment
8. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Agelidis, V.G.; Demetriades, G.D.; Flourentzou, N. Recent Advances in High-Voltage Direct-Current Power Transmission Systems. In Proceedings of the 2006 IEEE International Conference on Industrial Technology, Mumbai, India, 15–17 December 2006; pp. 206–213. [Google Scholar]
- Blaabjerg, F.; Ma, K. Future on Power Electronics for Wind Turbine Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2013, 1, 139–152. [Google Scholar] [CrossRef]
- Kouro, S.; Malinowski, M.; Gopakumar, K.; Pou, J.; Franquelo, L.G.; Wu, B.; Rodriguez, J.; Perez, M.A.; Leon, J.I. Recent Advances and Industrial Applications of Multilevel Converters. IEEE Trans. Ind. Electron. 2010, 57, 2553–2580. [Google Scholar] [CrossRef]
- Flourentzou, N.; Agelidis, V.G.; Demetriades, G.D. VSC-Based HVDC Power Transmission Systems: An Overview. IEEE Trans. Power Electron. 2009, 24, 592–602. [Google Scholar] [CrossRef]
- Hammons, T.J.; Woodford, D.; Loughtan, J.; Chamia, M.; Donahoe, J.; Povh, D.; Bisewski, B.; Long, W. Role of HVDC transmission in future energy development. IEEE Power Eng. Rev. 2000, 20, 10–25. [Google Scholar] [CrossRef]
- Rodriguez-Diaz, E.; Savaghebi, M.; Vasquez, J.C.; Guerrero, J.M. An overview of low voltage DC distribution systems for residential applications. In Proceedings of the 2015 IEEE 5th International Conference on Consumer Electronics—Berlin (ICCE-Berlin), Berlin, Germany, 6–9 September 2015; pp. 318–322. [Google Scholar]
- She, X.; Burgos, R.; Wang, G.; Wang, F.; Huang, A.Q. Review of solid state transformer in the distribution system: From components to field application. In Proceedings of the 2012 IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 15–20 September 2012; pp. 4077–4084. [Google Scholar]
- She, X.; Huang, A. Solid state transformer in the future smart electrical system. In Proceedings of the 2013 IEEE Power Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013; pp. 1–5. [Google Scholar]
- Bignucolo, F.; Bertoluzzo, M.; Fontana, C. Applications of the solid state transformer concept in the electrical power system. In Proceedings of the 2015 AEIT International Annual Conference (AEIT), Naples, Italy, 14–16 October 2015; pp. 1–6. [Google Scholar]
- Shah, D.G.; Crow, M.L. Stability Design Criteria for Distribution Systems With Solid-State Transformers. IEEE Trans. Power Deliv. 2014, 29, 2588–2595. [Google Scholar] [CrossRef]
- Wang, G.; Baek, S.; Elliott, J.; Kadavelugu, A.; Wang, F.; She, X.; Dutta, S.; Liu, Y.; Zhao, T.; Yao, W.; et al. Design and hardware implementation of Gen-1 silicon based solid state transformer. In Proceedings of the 2011 Twenty-Sixth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Fort Worth, TX, USA, 6–11 March 2011; pp. 1344–1349. [Google Scholar]
- Bifaretti, S.; Zanchetta, P.; Watson, A.; Tarisciotti, L.; Clare, J.C. Advanced Power Electronic Conversion and Control System for Universal and Flexible Power Management. IEEE Trans. Smart Grid 2011, 2, 231–243. [Google Scholar] [CrossRef]
- Zhao, C.; Dujic, D.; Mester, A.; Steinke, J.K.; Weiss, M.; Lewdeni-Schmid, S.; Chaudhuri, T.; Stefanutti, P. Power Electronic Traction Transformer-Medium Voltage Prototype. IEEE Trans. Ind. Electron. 2014, 61, 3257–3268. [Google Scholar] [CrossRef]
- Dujic, D.; Zhao, C.; Mester, A.; Steinke, J.K.; Weiss, M.; Lewdeni-Schmid, S.; Chaudhuri, T.; Stefanutti, P. Power Electronic Traction Transformer-Low Voltage Prototype. IEEE Trans. Power Electron. 2013, 28, 5522–5534. [Google Scholar] [CrossRef]
- Zhao, C.; Weiss, M.; Mester, A.; Lewdeni-Schmid, S.; Dujic, D.; Steinke, J.K.; Chaudhuri, T. Power electronic transformer (PET) converter: Design of a 1.2 MW demonstrator for traction applications. In Proceedings of the International Symposium on Power Electronics Power Electronics, Electrical Drives, Automation and Motion, Sorrento, Italy, 20–22 June 2012; pp. 855–860. [Google Scholar]
- Cecati, C.; Dell’Aquila, A.; Liserre, M.; Monopoli, V.G. A passivity-based multilevel active rectifier with adaptive compensation for traction applications. IEEE Trans. Ind. Appl. 2013, 39, 1404–1413. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, A.Q.; Song, W.; Bhattacharya, S.; Tan, G. Small-Signal Model-Based Control Strategy for Balancing Individual DC Capacitor Voltages in Cascade Multilevel Inverter-Based STATCOM. IEEE Trans. Ind. Electron. 2009, 56, 2259–2269. [Google Scholar] [CrossRef]
- Dell’Aquila, A.; Liserre, M.; Monopoli, V.G.; Rotondo, P. An energy-based control for an n-H-bridges multilevel active rectifier. IEEE Trans. Ind. Electron. 2005, 52, 670–678. [Google Scholar] [CrossRef]
- Zhao, T.; Wang, G.; Zeng, J.; Dutta, S.; Bhattacharya, S.; Huang, A.Q. Voltage and power balance control for a cascaded multilevel solid state transformer. In Proceedings of the 2010 Twenty-Fifth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Palm Springs, CA, USA, 21–25 February 2010; pp. 761–767. [Google Scholar]
- Zhao, T.; Wang, G.; Bhattacharya, S.; Huang, A.Q. Voltage and Power Balance Control for a Cascaded H-Bridge Converter-Based Solid-State Transformer. IEEE Trans. Power Electron. 2013, 28, 1523–1532. [Google Scholar] [CrossRef]
- Barrena, J.A.; Marroyo, L.; Vidal, M.Á.R.; Apraiz, J.R.T. Individual Voltage Balancing Strategy for PWM Cascaded H-Bridge Converter-Based STATCOM. IEEE Trans. Ind. Electron. 2008, 55, 21–29. [Google Scholar] [CrossRef]
- She, X.; Huang, A.Q.; Zhao, T.; Wang, G. Coupling Effect Reduction of a Voltage-Balancing Controller in Single-Phase Cascaded Multilevel Converters. IEEE Trans. Power Electron. 2012, 27, 3530–3543. [Google Scholar] [CrossRef]
- Wang, H.; Cheng, Q.; Li, M.; Chen, G.; Deng, L. The study of single-phase PWM rectifier based on PR control strategy. In Proceedings of the 26th Chinese Control and Decision Conference (2014 CCDC), Changsha, China, 31 May–2 June 2014; pp. 3818–3823. [Google Scholar]
- Park, Y.M.; Yoo, J.Y.; Lee, S.B. Practical Implementation of PWM Synchronization and Phase-Shift Method for Cascaded H-Bridge Multilevel Inverters Based on a Standard Serial Communication Protocol. IEEE Trans. Ind. Appl. 2008, 44, 634–643. [Google Scholar] [CrossRef]
- Kheraluwala, M.N.; Gascoigne, R.W.; Divan, D.M.; Baumann, E.D. Performance characterization of a high-power dual active bridge DC-to-DC converter. IEEE Trans. Ind. Appl. 1992, 28, 1294–1301. [Google Scholar] [CrossRef]
- Zhao, B.; Song, Q.; Liu, W.; Sun, Y. Overview of Dual-Active-Bridge Isolated Bidirectional DC-DC Converter for High-Frequency-Link Power-Conversion System. IEEE Trans. Power Electron. 2014, 29, 4091–4106. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Zhao, T.; Wang, G.; Dutta, S.; Baek, S.; Du, Y.; Parkhideh, B.; Zhou, X.; Huang, A.Q. Design and development of Generation-I silicon based Solid State Transformer. In Proceedings of the 2010 Twenty-Fifth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Palm Springs, CA, USA, 21–25 February 2010; pp. 1666–1673. [Google Scholar]
- Engel, S.P.; Stieneker, M.; Soltau, N.; Rabiee, S.; Stagge, H.; de Doncker, R.W. Comparison of the Modular Multilevel DC Converter and the Dual-Active Bridge Converter for Power Conversion in HVDC and MVDC Grids. IEEE Trans. Power Electron. 2015, 30, 124–137. [Google Scholar] [CrossRef]
- Da Silva, M.M.; Pinheiro, H. Voltage balancing in flying capacitor converter multilevel using space vector modulation. In Proceedings of the 2017 IEEE 8th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Florianopolis, Brazil, 17–20 April 2017; pp. 1–5. [Google Scholar]
- Zhao, C.; Round, S.D.; Kolar, J.W. An Isolated Three-Port Bidirectional DC-DC Converter With Decoupled Power Flow Management. IEEE Trans. Power Electron. 2008, 23, 2443–2453. [Google Scholar] [CrossRef]
- Baek, S.; Roy, S.; Bhattacharya, S.; Kim, S. Power flow analysis for 3-port 3-phase dual active bridge dc/dc converter and design validation using high frequency planar transformer. In Proceedings of the 2013 IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 15–19 September 2013; pp. 388–395. [Google Scholar]
- De Doncker, R.W.A.A.; Divan, D.M.; Kheraluwala, M.H. A three-phase soft-switched high-power-density DC/DC converter for high-power applications. IEEE Trans. Ind. Appl. 1991, 27, 63–73. [Google Scholar] [CrossRef]
- Zhang, Z.; Andersen, M.A.E. High frequency AC inductor analysis and design for dual active bridge (DAB) converters. In Proceedings of the 2016 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 20–24 March 2016; pp. 1090–1095. [Google Scholar]
- Shah, M.; Ngo, K.D.T. Parameter extraction for the extended cantilever model of magnetic component windings. IEEE Trans. Aerosp. Electron. Syst. 2000, 36, 260–266. [Google Scholar] [CrossRef]
- Moonem, M.; Pechacek, C.; Hemandez, R.; Krishnaswami, H. Analysis of a Multilevel Dual Active Bridge (ML-DAB) DC-DC Converter Using Symmetric Modulation. Electronics 2015, 4, 239–260. [Google Scholar] [CrossRef]
- Moonem, M.A.; Krishnaswami, H. Analysis and control of multi-level dual active bridge DC-DC converter. In Proceedings of the 2012 IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 15–20 September 2012; pp. 1556–1561. [Google Scholar]
- Wu, Z.; Xue, Y.; Pan, L.; Li, D.; He, T.; Sun, L.; Yang, Y. Active disturbance rejection control based simplified decoupling for two-input-two-output processes. In Proceedings of the 2017 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017; pp. 399–404. [Google Scholar]
- Vasanthakumar, D.; Srikanth, V. DC-DC converter control using IP controller. In Proceedings of the 2014 International Conference on Computation of Power, Energy, Information and Communication (ICCPEIC), Chennai, India, 16–17 April 2014; pp. 245–249. [Google Scholar]
- Segaran, D.; Holmes, D.G.; McGrath, B.P. Enhanced Load Step Response for a Bidirectional DC-DC Converter. IEEE Trans. Power Electron. 2013, 28, 371–379. [Google Scholar] [CrossRef]
- Huang, Y.; Tse, C.K. Circuit Theoretic Classification of Parallel Connected DC-DC Converters. IEEE Trans. Circuits Syst. I Regul. Pap. 2007, 54, 1099–1108. [Google Scholar] [CrossRef]
- Luo, S.; Ye, Z.; Lin, Ra.; Lee, F.C. A classification and evaluation of paralleling methods for power supply modules. In Proceedings of the 30th Annual IEEE Power Electronics Specialists Conference, Charleston, SC, USA, 1 July 1999; pp. 901–908. [Google Scholar]
- Du, S.B.Y.; Wang, G.; Bhattacharya, S. Design considerations of high voltage and high frequency transformer for solid state transformer application. In Proceedings of the IECON 2010–36th Annual Conference on IEEE Industrial Electronics Society, Glendale, AZ, USA, 7–10 November 2010; pp. 421–426. [Google Scholar]
- IEEE Standard for General Requirements for Dry-Type Distribution and Power Transformers; IEEE Std C57.12.01-2015 (Revision of IEEE Std C57.12.01-2005); IEEE: Piscataway, NJ, USA, 2015; pp. 1–52.
- Schwodiauer, R.; Neugschwandtner, G.; Bauer-Gogonea, S.; Bauer, S.; Heitz, J.; Bauerle, D. Dielectric and electret properties of novel Teflon PTFE and PTFE-like polymers. In Proceedings of the10th International Symposium on Electrets (ISE 10), Athens, Greece, 22–24 September 1999; pp. 313–316. [Google Scholar]
- Dowcorning. Sylgard 170 Silicone Elastomer. In Sylgard Datasheet; Dowcorning: Midland, MI, USA, 2015. [Google Scholar]







| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Number of subunits | 10 | ||
| Line inductance | 40 | mH | |
| DC capacitance in DC-link | 370 | uF | |
| Rated DC voltage of DC-link | 2.2 | kV | |
| Switching frequency of the AC/DC stage | 1.8 | kHz | |
| DC capacitance in LVDC | 1 | mF | |
| Rated DC voltage of LVDC | ±750 | V | |
| Switching frequency of the DC/DC stage | 10 | kHz | |
| HFIT turn ratio | n | 0.34 | |
| Interfacing inductance between MVDC and LVDC | 140 | uH |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yun, H.-J.; Jeong, D.-K.; Kim, H.-S.; Kim, M.; Baek, J.-W.; Kim, J.-Y.; Kim, H.-J. Implementation of a Single-Phase SST for the Interface between a 13.2 kV MVAC Network and a 750 V Bipolar DC Distribution. Electronics 2018, 7, 62. https://doi.org/10.3390/electronics7050062
Yun H-J, Jeong D-K, Kim H-S, Kim M, Baek J-W, Kim J-Y, Kim H-J. Implementation of a Single-Phase SST for the Interface between a 13.2 kV MVAC Network and a 750 V Bipolar DC Distribution. Electronics. 2018; 7(5):62. https://doi.org/10.3390/electronics7050062
Chicago/Turabian StyleYun, Hyeok-Jin, Dong-Keun Jeong, Ho-Sung Kim, Myoungho Kim, Ju-Won Baek, Ju-Yong Kim, and Hee-Je Kim. 2018. "Implementation of a Single-Phase SST for the Interface between a 13.2 kV MVAC Network and a 750 V Bipolar DC Distribution" Electronics 7, no. 5: 62. https://doi.org/10.3390/electronics7050062
APA StyleYun, H.-J., Jeong, D.-K., Kim, H.-S., Kim, M., Baek, J.-W., Kim, J.-Y., & Kim, H.-J. (2018). Implementation of a Single-Phase SST for the Interface between a 13.2 kV MVAC Network and a 750 V Bipolar DC Distribution. Electronics, 7(5), 62. https://doi.org/10.3390/electronics7050062





