Stand-Alone Microgrid Inverter Controller Design for Nonlinear, Unbalanced Load with Output Transformer
Abstract
1. Introduction
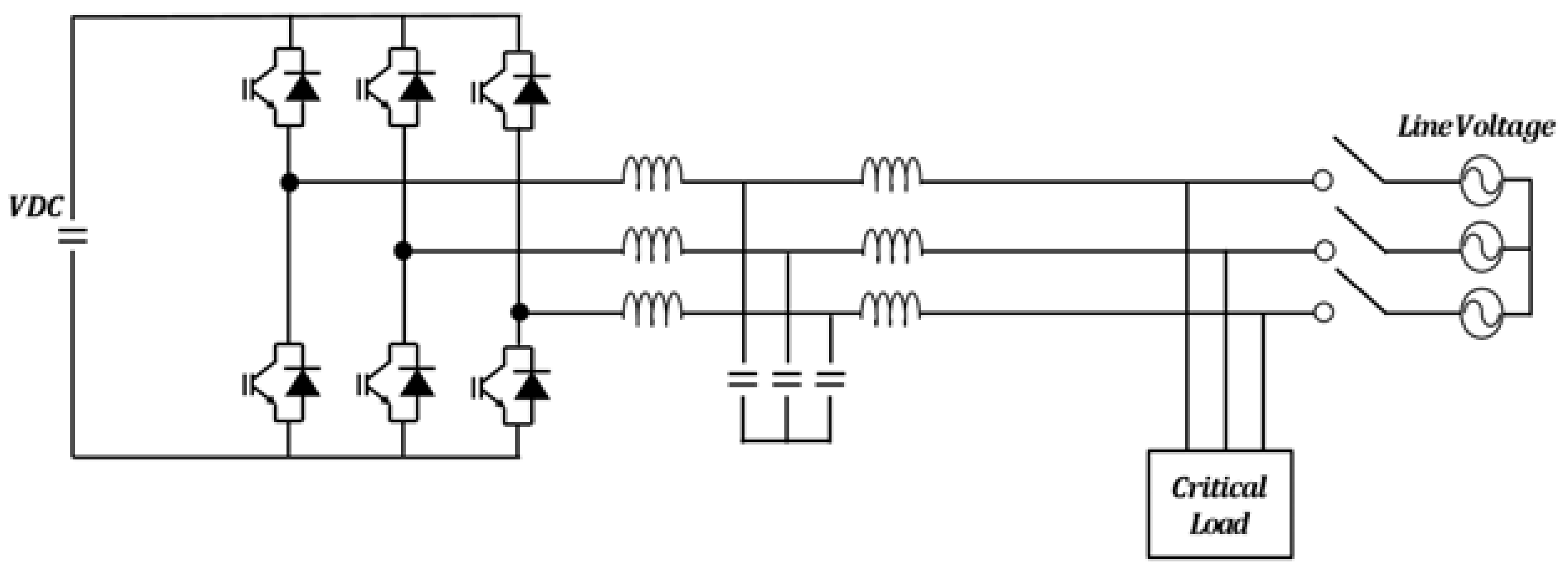
2. Stand-Alone Inverter Design Considering Output Transformer
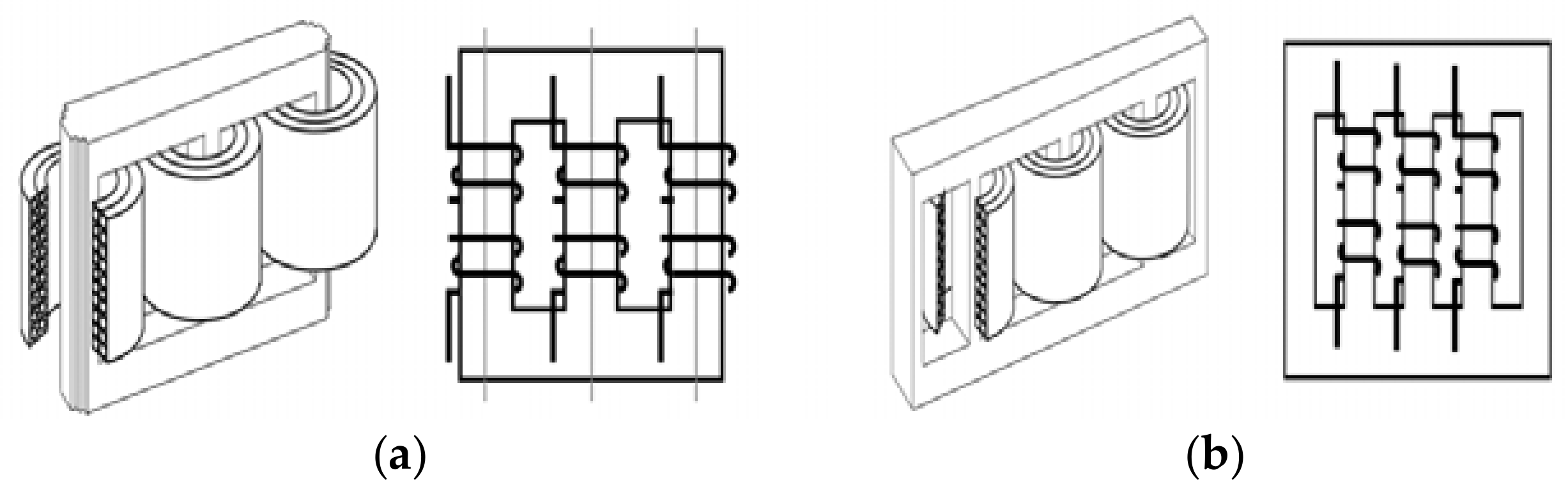
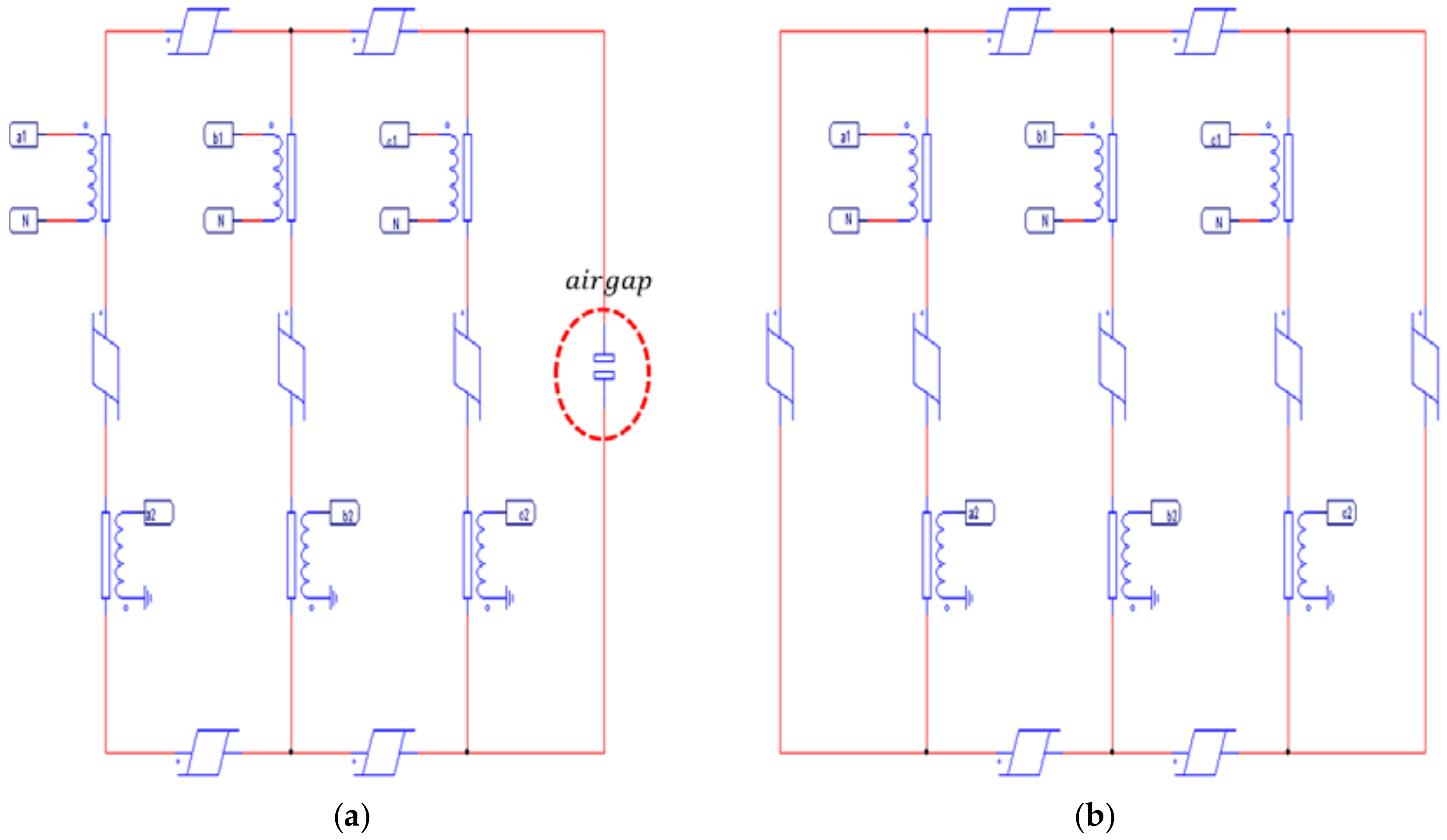
2.1. Changes in Zero Sequence Component According to Transformer Structure
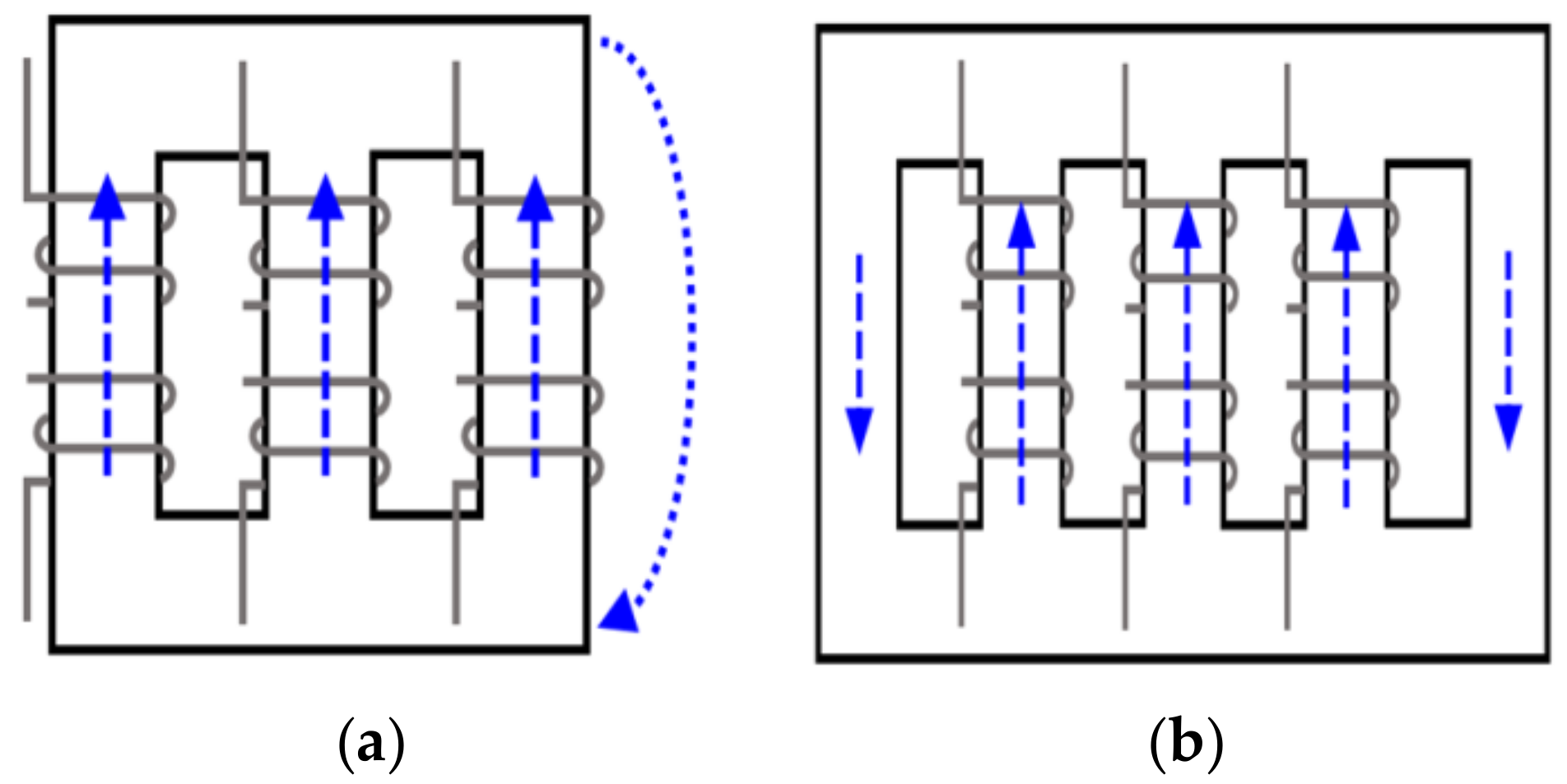
2.2. Zero-Sequence-Component Control Technique in a Five-Limb Core-Type Transformer
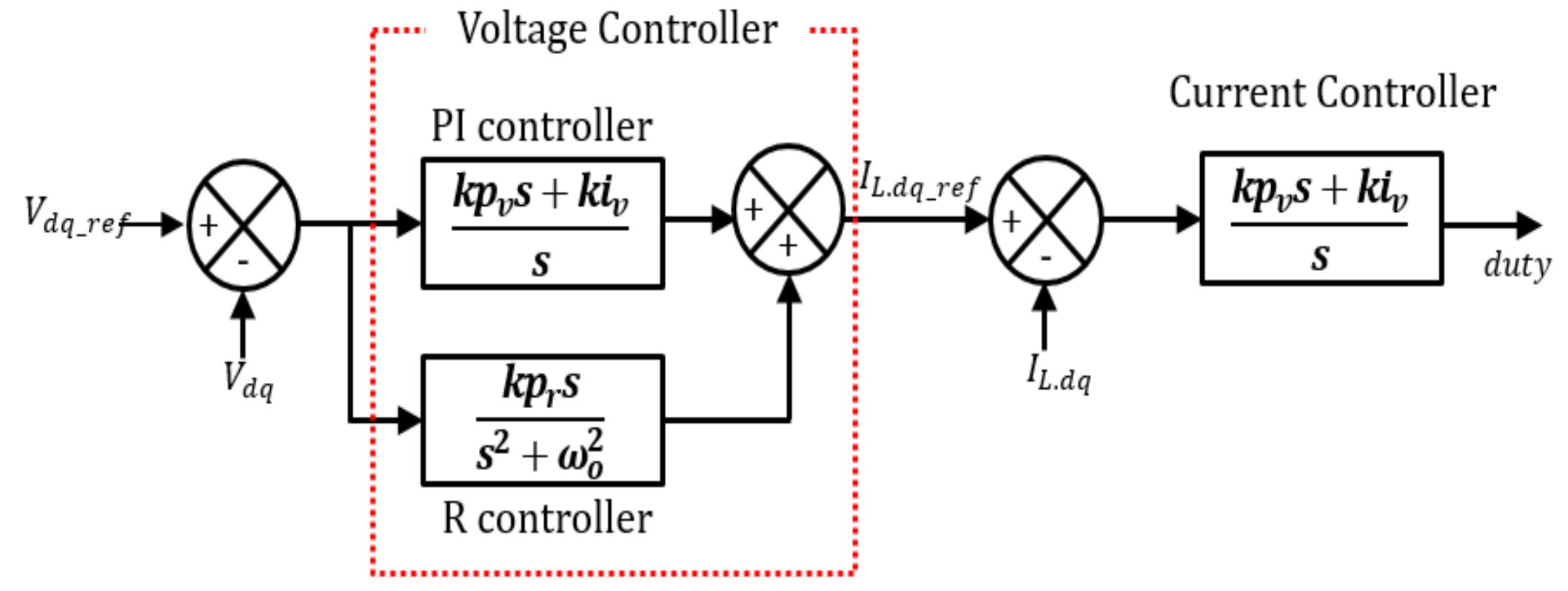
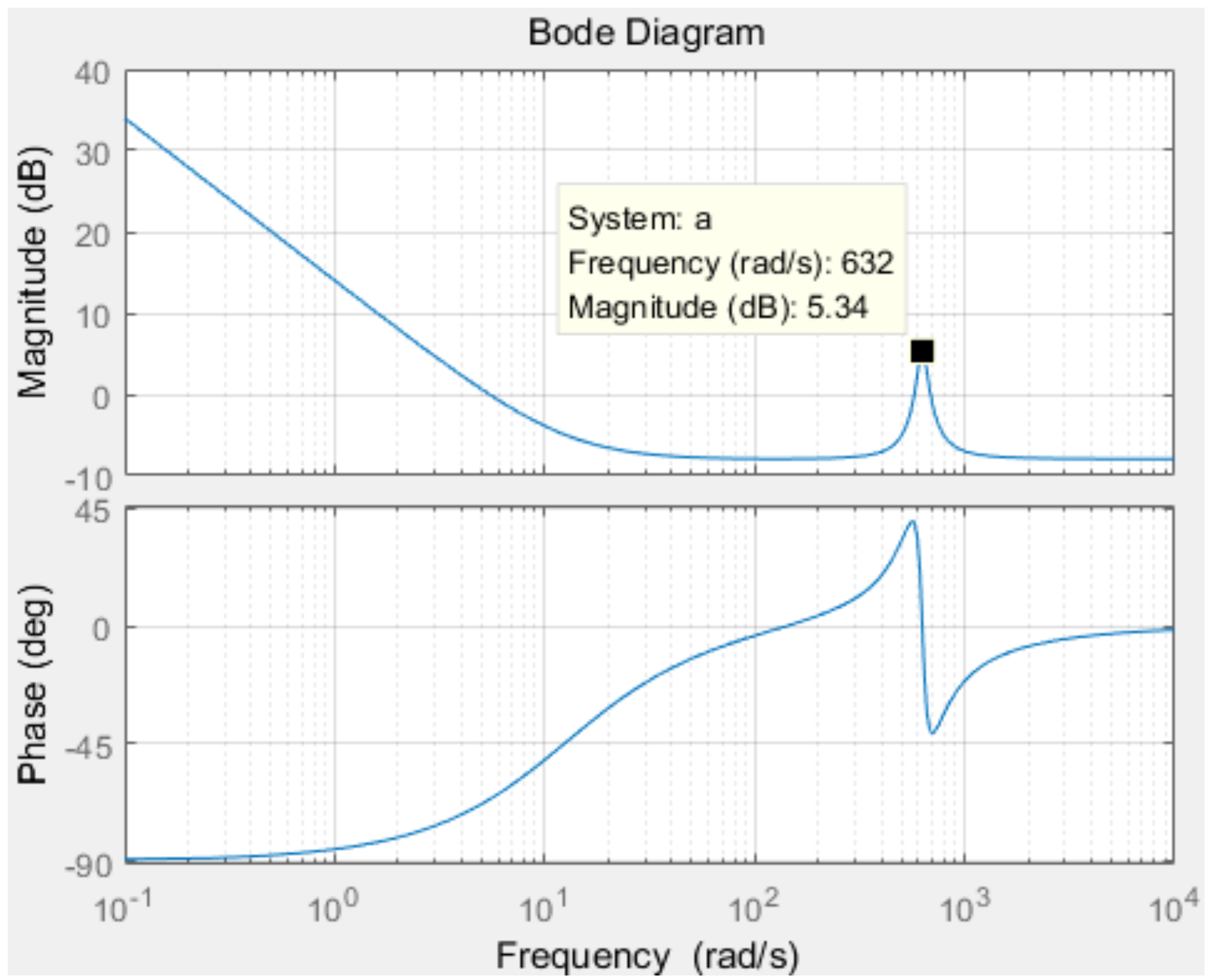
2.3. Negative-Sequence-Component Control Technique
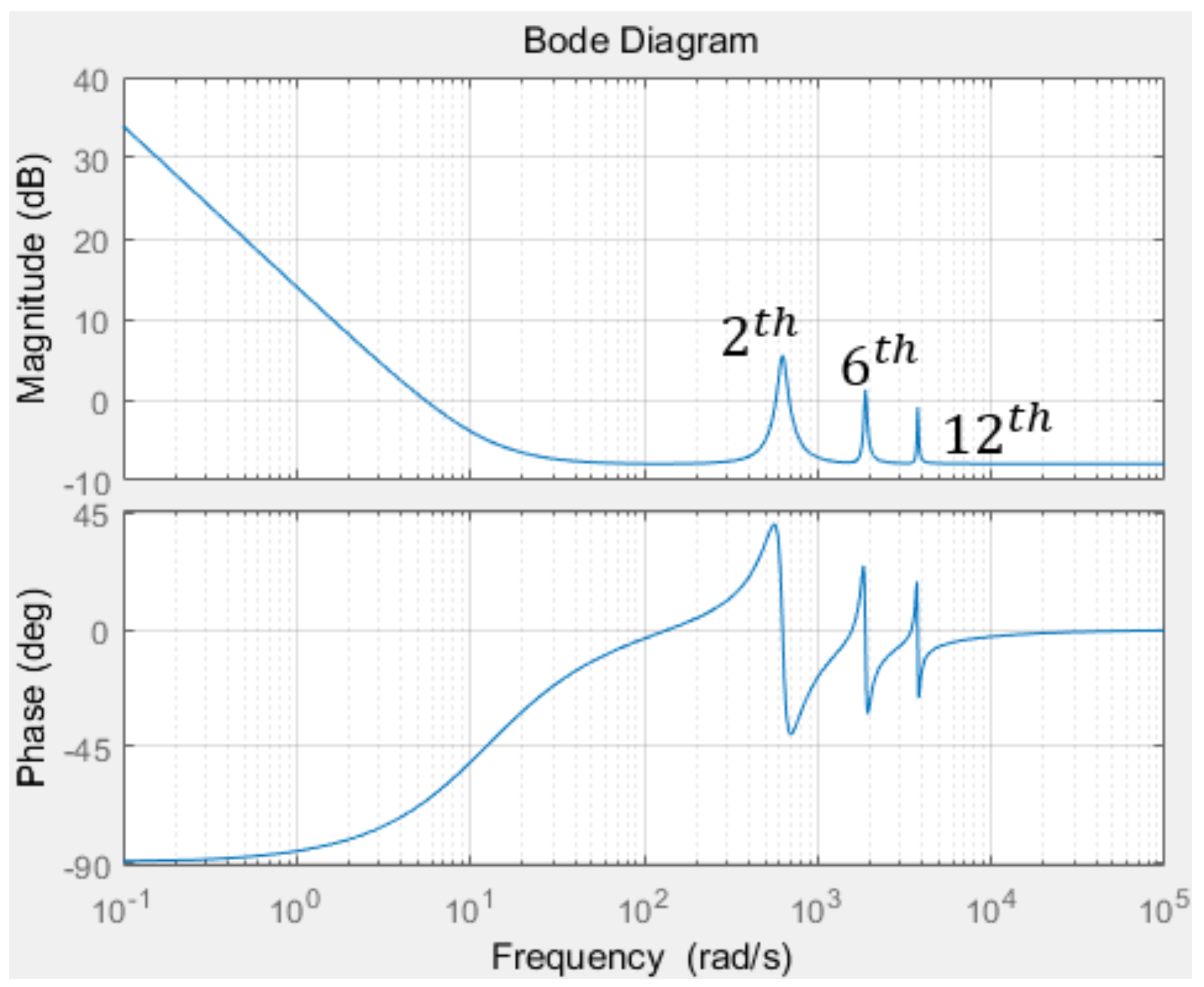
2.4. Nonlinear Compensation Using PI + MR Controller
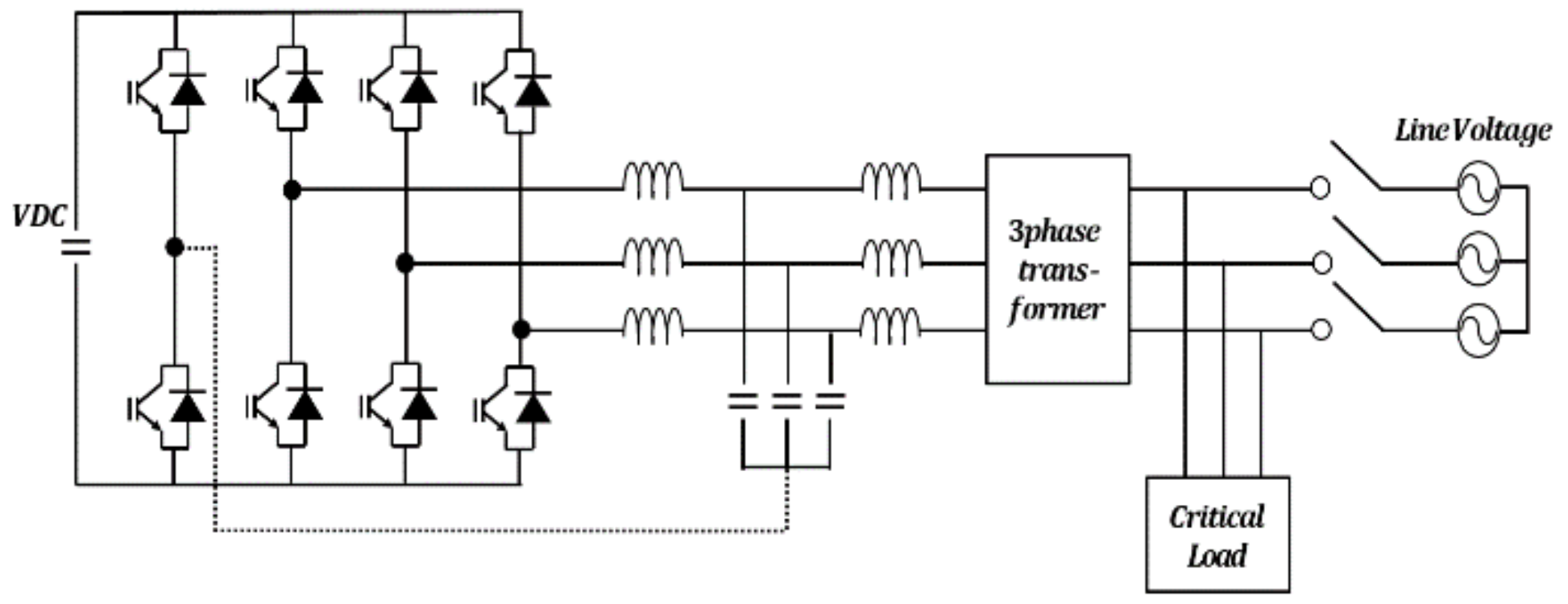
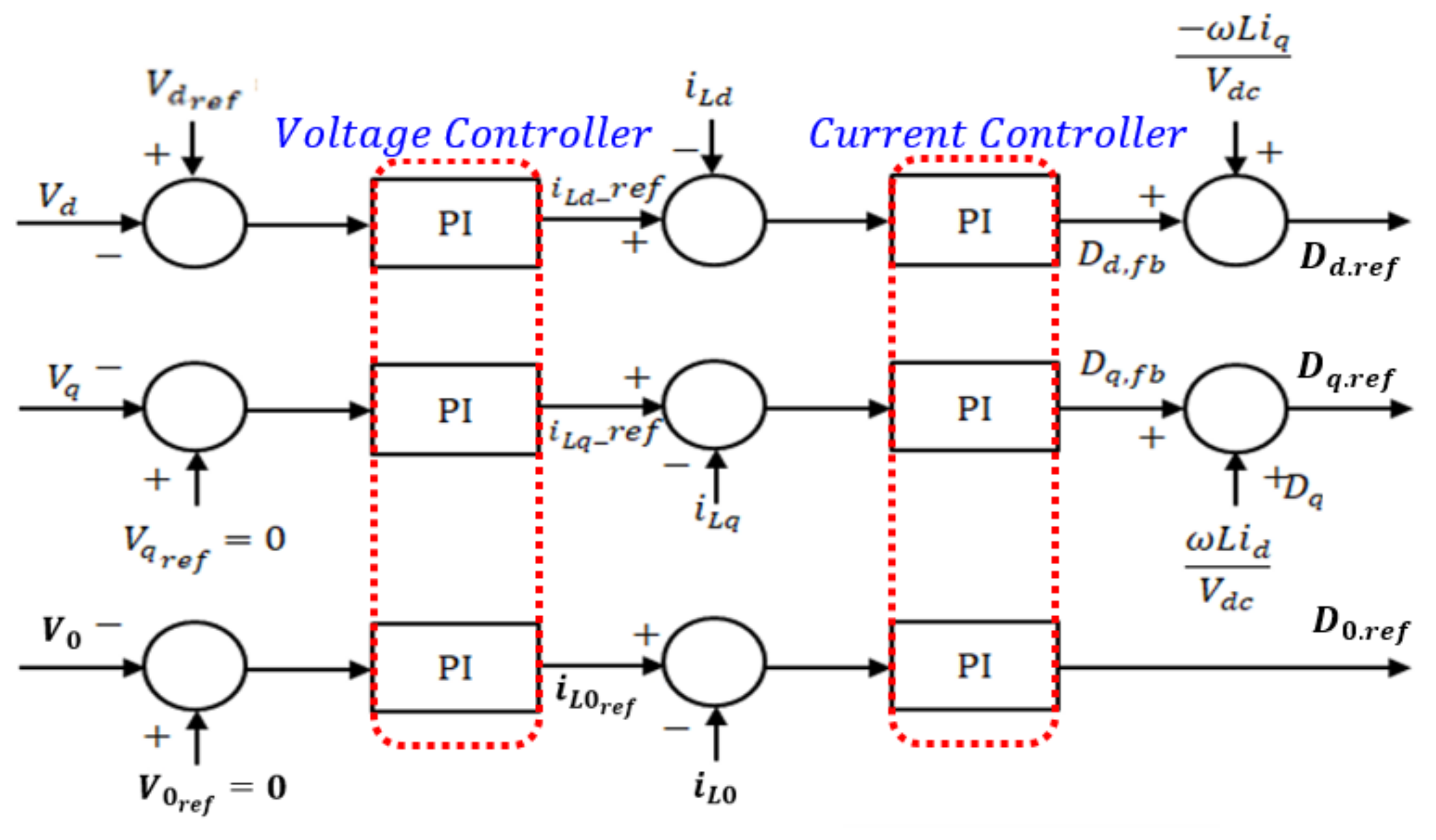
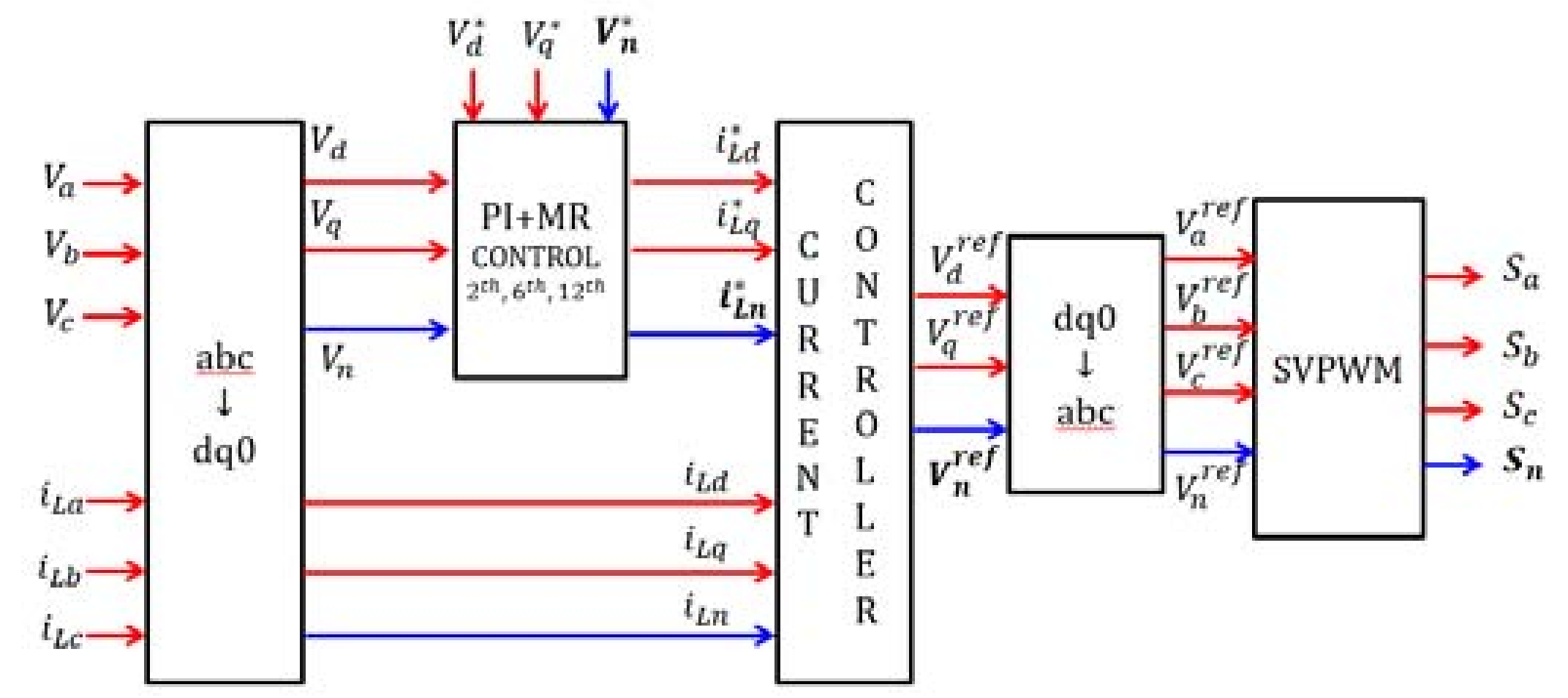
2.5. Microgrid Inverter Controller Design
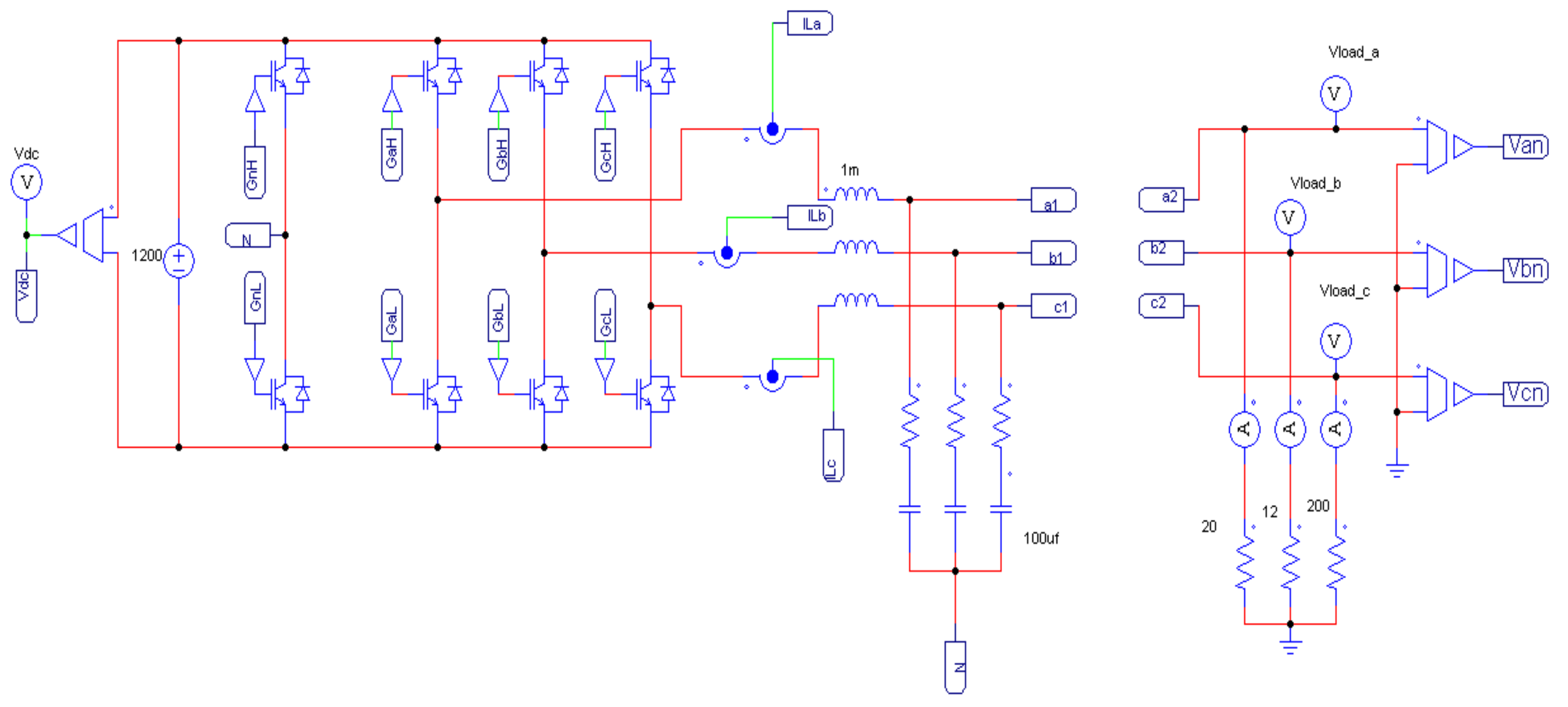
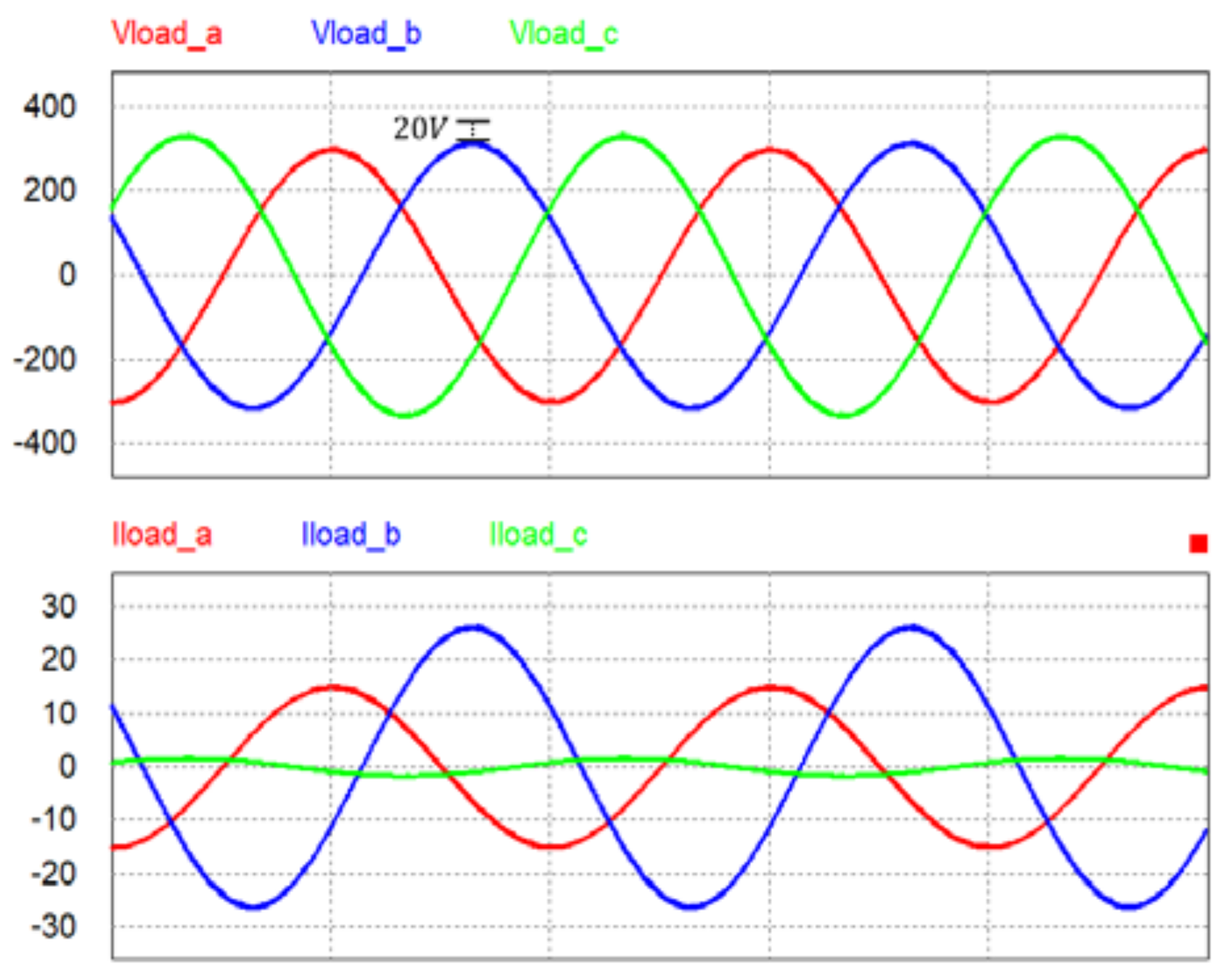
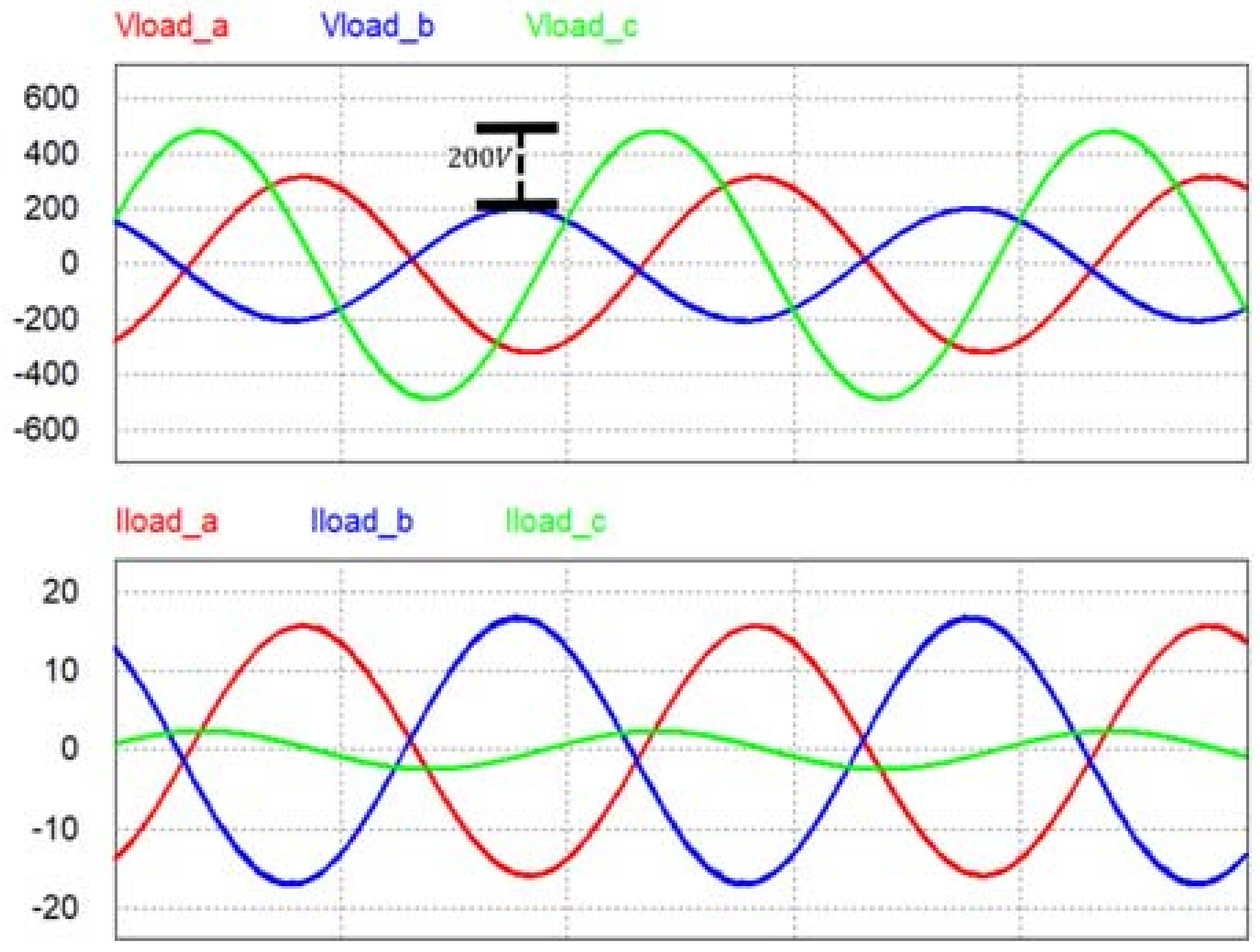
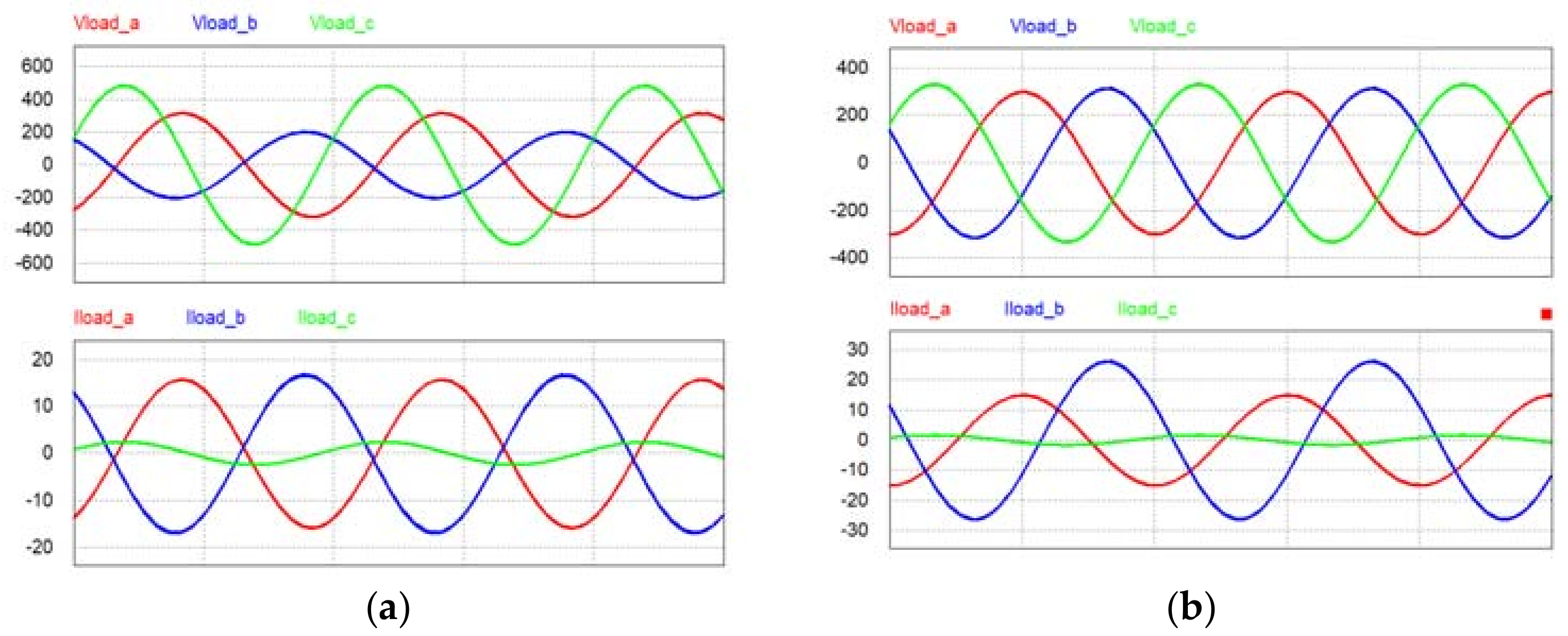
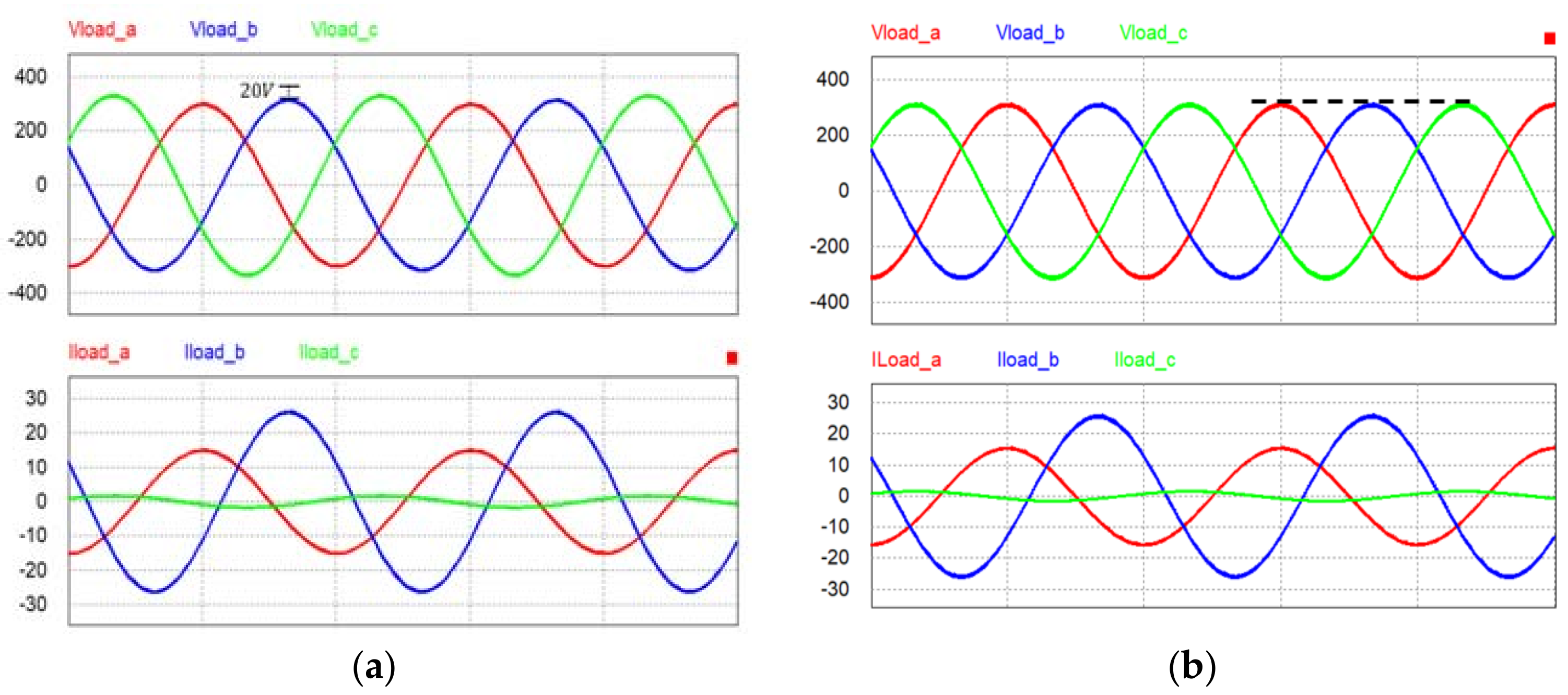
3. Simulation
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Lasseter, R.H. Certs microgrid. In Proceedings of the IEEE International Conference on System of Systems Engineering, San Antonio, TX, USA, 16–18 April 2007; pp. 1–5. [Google Scholar]
- Ackermann, T.; Andersson, G.; Soder, L. Electricity market regulations and their impact on distributed generation. In Proceedings of the Electric Utility Deregulation and Restructuring and Power Technologies, London, UK, 4–7 April 2000; pp. 608–613. [Google Scholar]
- Parlak, K.S.; Ozdemir, M.; Aydemir, M.T. Active and reactive power sharing and frequency restoration in a distributed power systme consisting of two UPS units. Electr. Power Energy Syst. 2009, 31, 220–226. [Google Scholar] [CrossRef]
- Hatziargyriou, N.; Asano, H.; Iravani, R.; Marnay, C. Microgrids. IEEE Power Energy Mag. 2007, 5, 78–94. [Google Scholar] [CrossRef]
- Walling, R.A.; Saint, R.; Dugan, R.C.; Burke, J.; Kojovic, L.A. Summary of distributed resources impact on power delivery systems. IEEE Trans. Power Deliv. 2008, 23, 1636–1644. [Google Scholar] [CrossRef]
- Moreira, C.L.; Resende, F.O.; Lopes, J.A.P. Using low voltage microgrids for service restoration. IEEE Trans. Power Syst. 2007, 22, 395–403. [Google Scholar] [CrossRef]
- Fortescue, C.L. Method of symmetrical coordinates applied to the solution of polyphase networks. AIEE Trans. 1918, 37, 1027–1140. [Google Scholar]
- Hague, B. The method of symmetrical coordinates in the theory of polyphaser circuits. Sel. Eng. Pap. 1926, 1. [Google Scholar] [CrossRef]
- El-Barbari, S.; Hofmann, W. Digital control of a four leg inverter for standalone photovoltaic systems with unbalance load. In Proceedings of the Twenty-sixth Annual conference of IEEE Industrial Electronics Society (IECON 2000), Nagoya, Japan, 22–28 October 2000; pp. 729–734. [Google Scholar]
- Vechiu, I.; Curea, O.; Camblong, H. Transient operation of a four-leg inverter for autonomous applications with unbalance load. IEEE Trans. Power Electron. 2010, 25, 399–407. [Google Scholar] [CrossRef]
- Doan, V.T.; Kim, K.Y.; Choi, W.; Kim, D.W. Design of a hybrid controller for the three-phase four-leg voltage-source inverter with unbalance load. J. Power Electron. 2017, 17, 181–189. [Google Scholar] [CrossRef]
- Priya, N.A.; Mabel, M.C. Control methods for four-leg voltage source inverter. In Proceedings of the International Conference on Devices, Circuits and Systems (ICDCS), Coimbatore, India, 15–16 March 2012; pp. 44–48. [Google Scholar]
- Senjyu, T.; Nakaji, T.; Uezato, K.; Funabashi, T. A hybrid power system using alternative energy facilities in isolated island. IEEE Trans. Energy Convers. 2005, 20, 406–414. [Google Scholar] [CrossRef]
- Jo, H.; Cho, S.; Shin, C.; Cha, H. Zero sequence impedance of Yg-Yg three phase core type transformer. Trans. Korean Inst. Electr. Eng. 2016, 65, 940–945. [Google Scholar] [CrossRef]
- Shin, D.Y.; Park, Y.W.; Cha, H.J. A case study on malfunction of OCGR and inaccuracy of watt-hour meter in distributed generation system. Trans. Korean Inst. Electr. Eng. 2008, 57, 1349–1355. [Google Scholar]
- Shin, D.Y.; Yun, D.H.; Cha, H.J. Problem analysis by iron core structure of the transformer on asymmetric three phase lines and prevention measures. Trans. Korean Inst. Electr. Eng. 2012, 61, 1536–1541. [Google Scholar] [CrossRef]
- Sin, C.; Lim, K.; Petrus, S.D.; Choi, J. Controller design of stand-alone or grid-connected inverter to compensate harmonics caused by nonlinear load. Trans. Korean Inst. Power Electron. 2017, 22, 440–448. [Google Scholar]
- Rodriuez, P.; Luna, A.; Candlea, I.; Mujal, R.; Teodorescu, R.; Blaabjerg, F. Multiresonant frequency-locked loop for grid synchronization of power converters under distorted grid conditions. IEEE Trans. Ind. Electron. 2011, 58, 127–138. [Google Scholar] [CrossRef]
- He, J.; Li, Y.W.; Blaabjerg, F.; Wang, X. Active harmonic filtering using current-controlled, grid-connected DG units with closed-loop power control. IEEE Trans. Power Electron. 2014, 29, 642–653. [Google Scholar]
- He, J.; Li, Y.W. Hybrid voltage and current control approach for DG Grid interfacing converters with LCL filters. IEEE Trans. Ind. Electron. 2013, 60, 1797–1809. [Google Scholar] [CrossRef]
- Lim, K.; Choi, J. PR control based cascaded current and voltage control for seamless transfer of microgrid. In Proceedings of the International Future Energy Electronics Conference (IFEEC’2015), Taipei, Taiwan, 1–4 November 2015; pp. 1–6. [Google Scholar]
- Bhattacharya, S.; Divan, D.M. Synchronous frame based controller implementation for a hybrid series active filter system. In Proceedings of the Thirtieth IAS Annual Meeting Industry Applications Conference, Orlando, FL, USA, 8–12 October 1995; pp. 2531–2540. [Google Scholar]
- Bhattacharya, S.; Divan, D.M.; Banerjee, B. Synchronous reference frame based harmonic isolator using series active filter. In Proceedings of the EPE (European Power Electronics and drives), Florence, Italy, 1991; Volume 3, pp. 30–35. [Google Scholar]
- Choi, H.S.; Choi, S.J. An effective gyrator-based transformer modeling using PSIM. Trans. Korean Inst. Power Electron. 2016, 21, 207–214. [Google Scholar] [CrossRef]
- Chiniforoosh, S.; Atighechi, H.; Davoudi, A.; Jatskevich, J.; Yazdani, A.; Filizadeh, S.; Saeedifard, M.; Martinez, J.A.; Sood, V.; Strunz, K.; et al. Dynamic average modeling of front-end diode rectifier loads considering discontinuous conduction mode and unbalanced operation. IEEE Trans. Power Deliv. 2012, 27, 421–429. [Google Scholar] [CrossRef]
- Takahashu, I. Power factor improvement of a diode rectifier circuit by dither signal. In Proceedings of the IEEE Industry Applications Society Annual Meeting, Seattle, WA, USA, 7–12 October 1990; pp. 1289–1294. [Google Scholar]
- Villablanca, M.E.; Nadal, J.I. Current distortion reduction in six-phase parallel-connected AC/DC rectifiers. IEEE Trans. Power Deliv. 2008, 23, 953–959. [Google Scholar] [CrossRef]
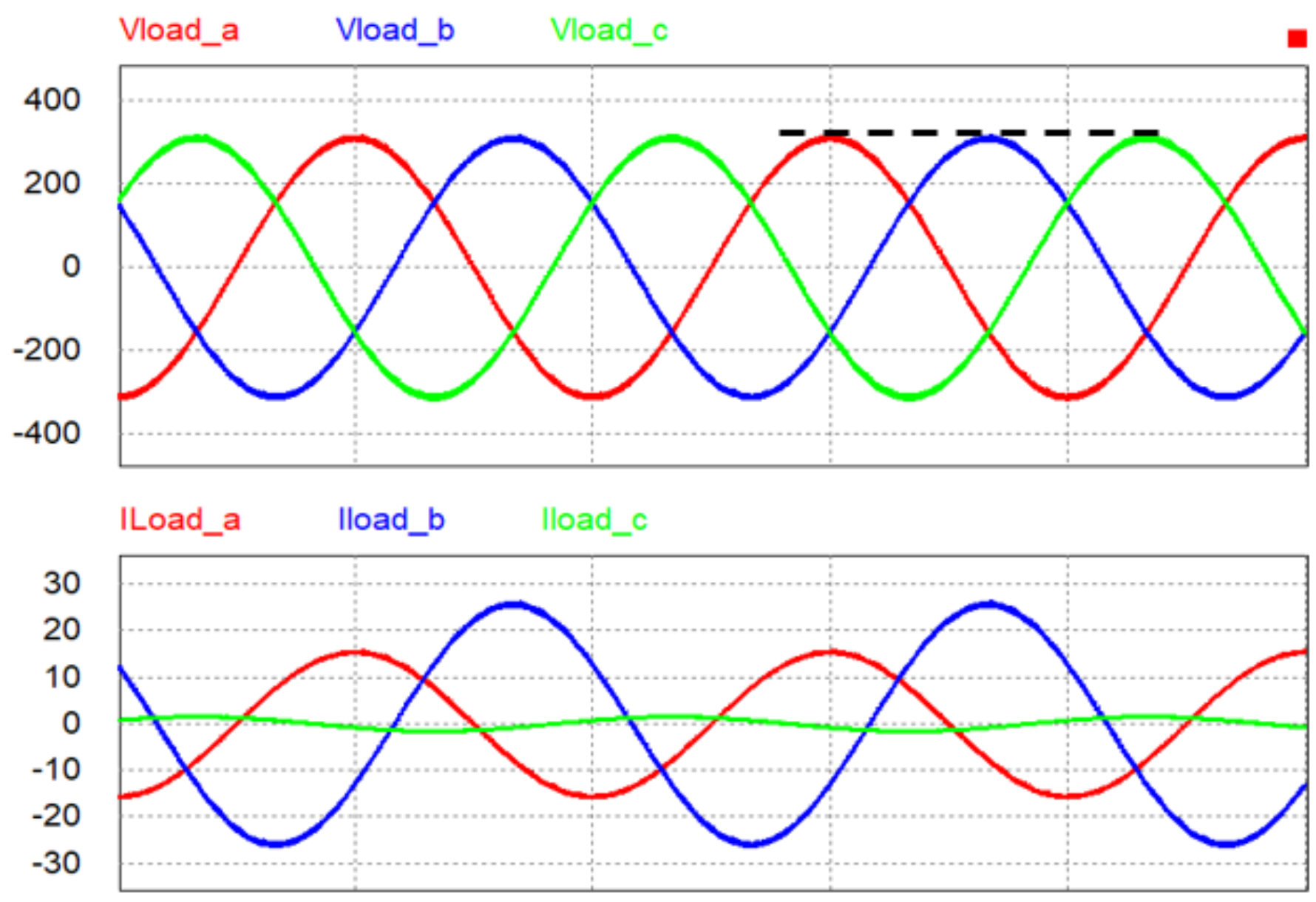
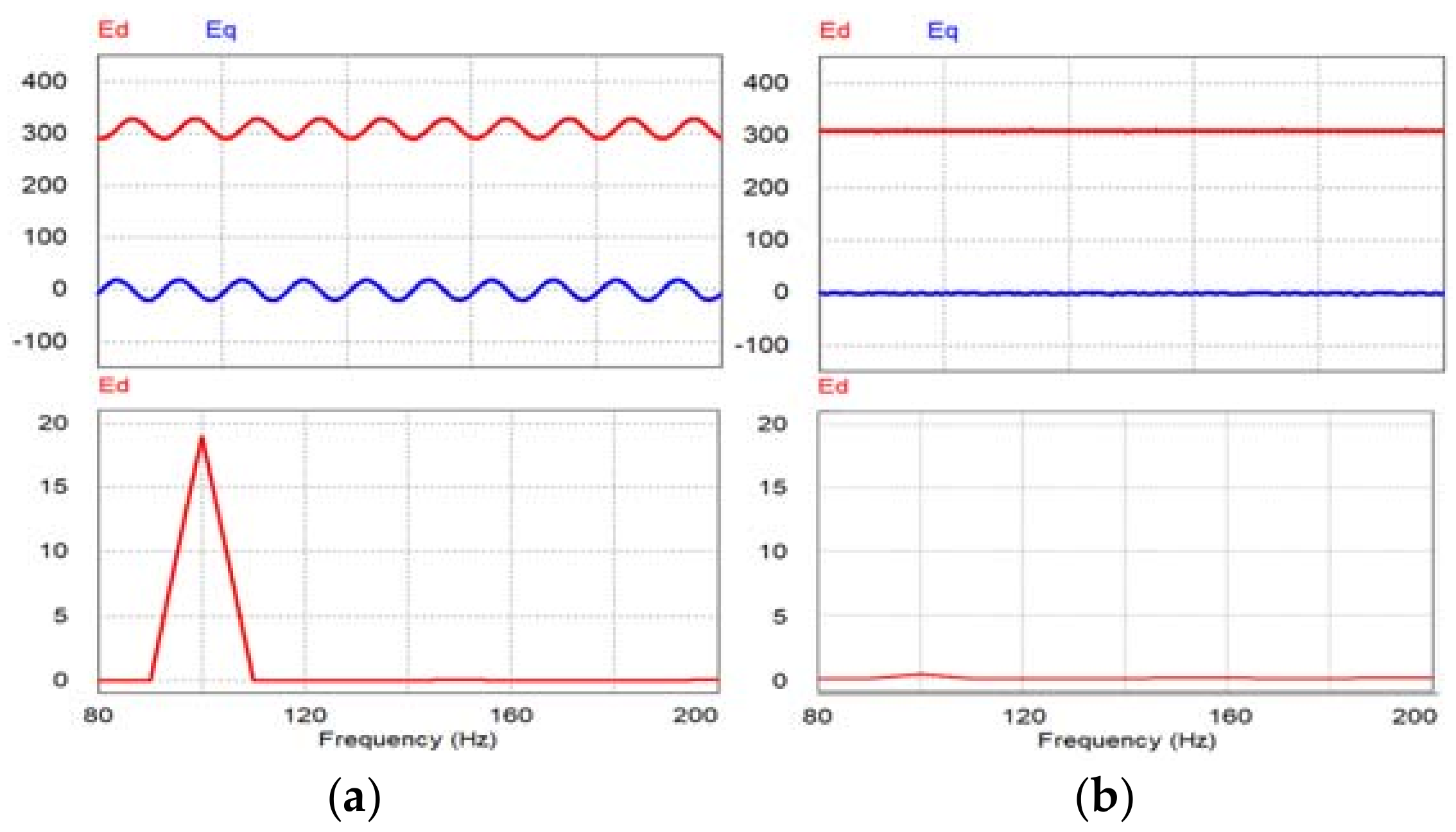
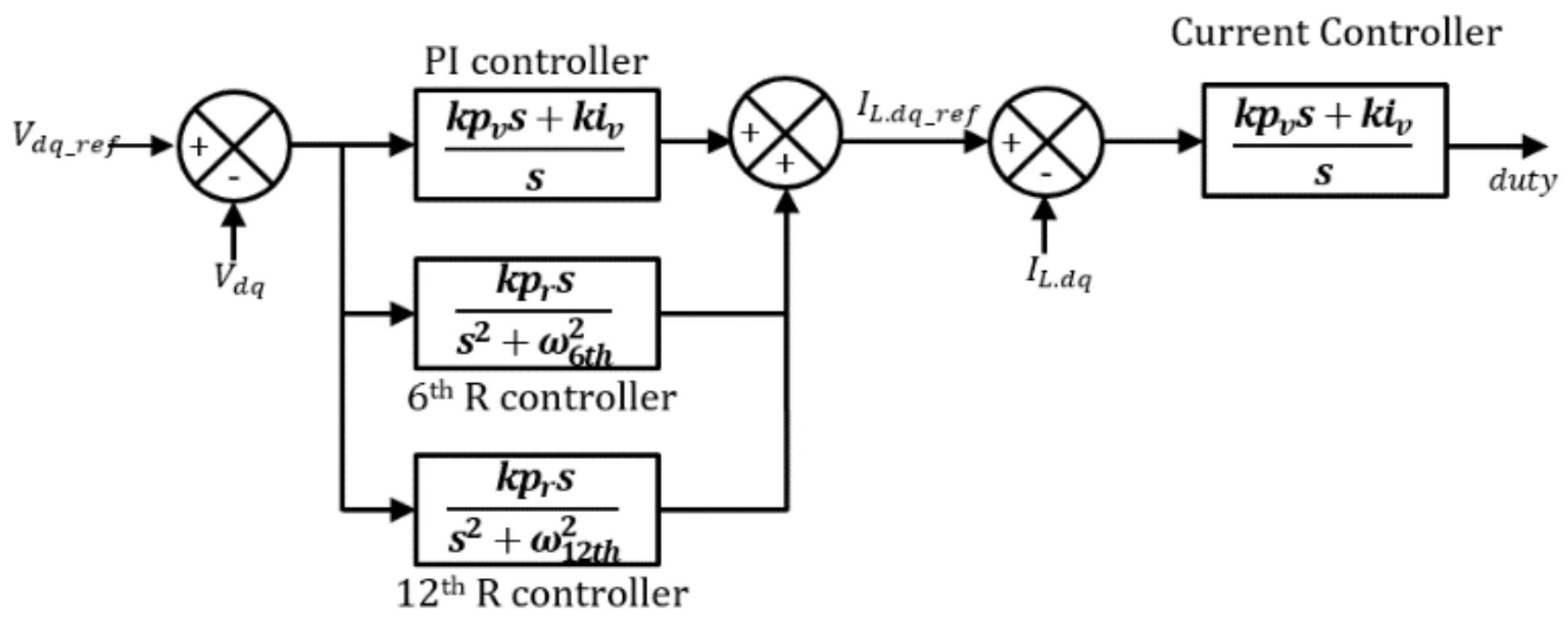
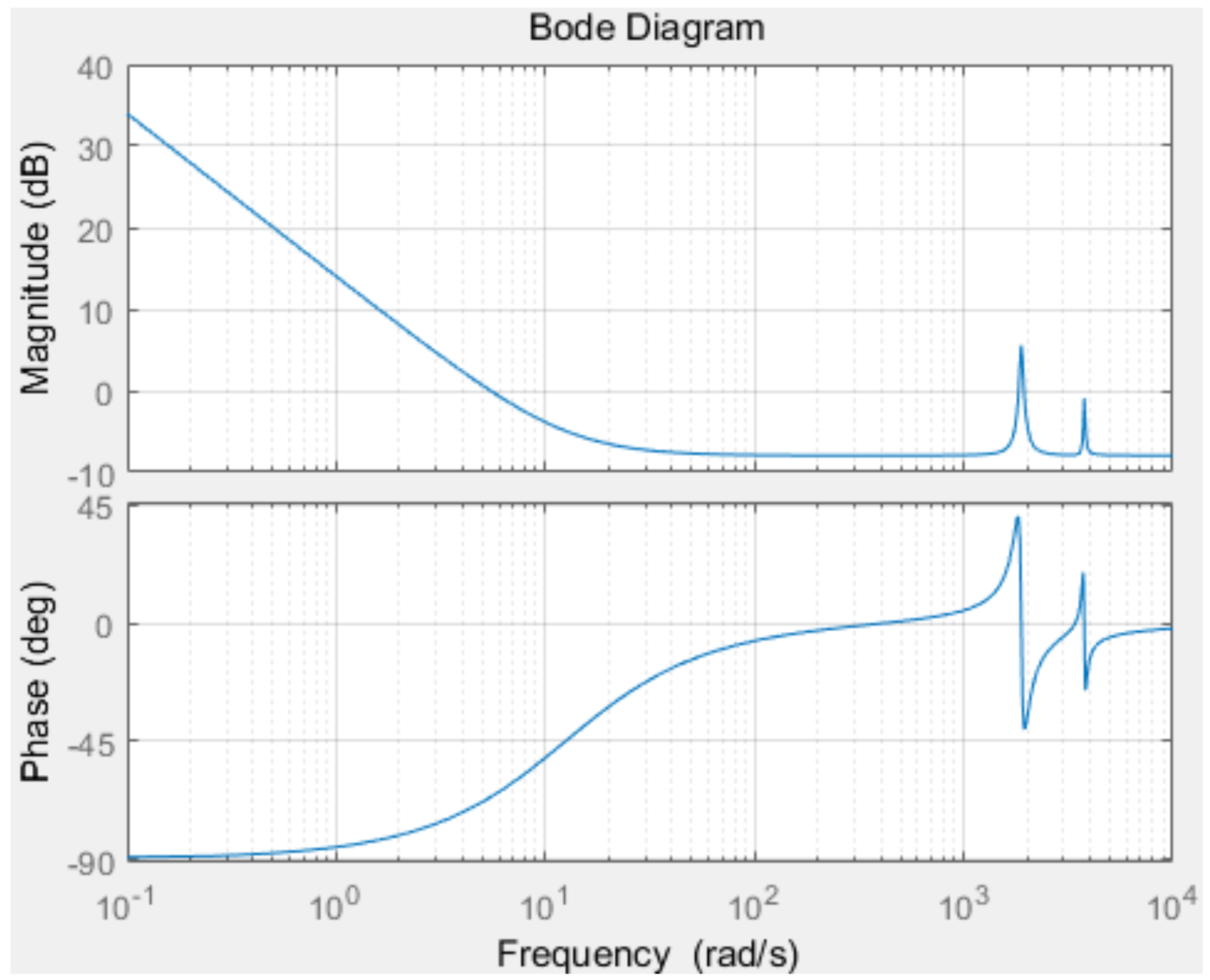
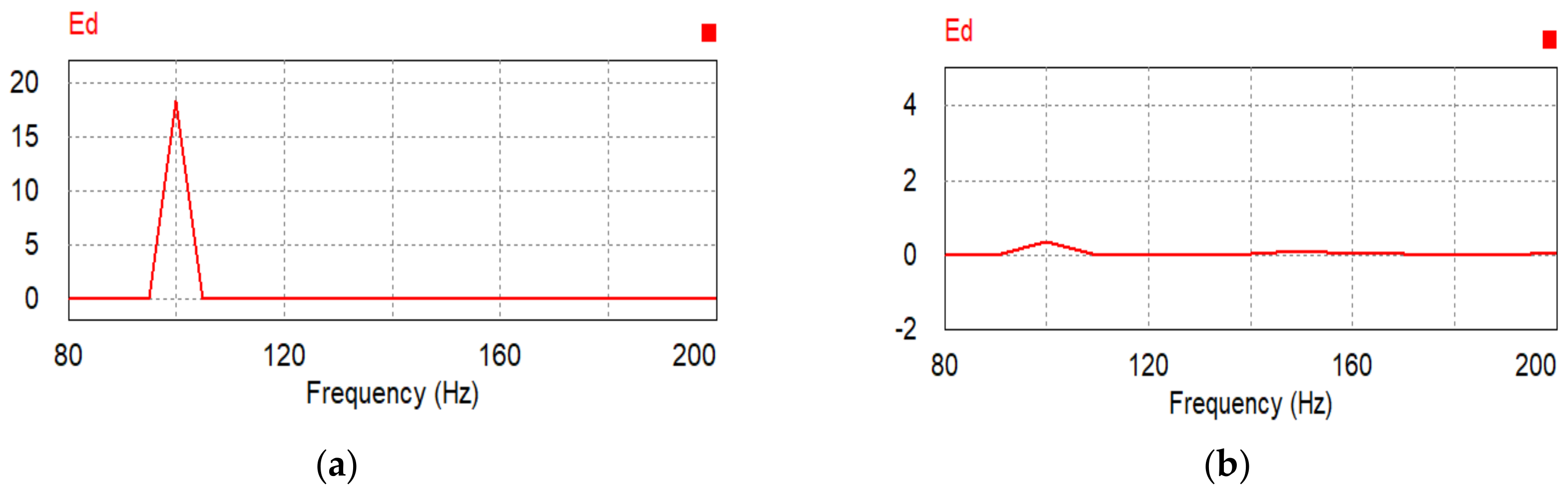
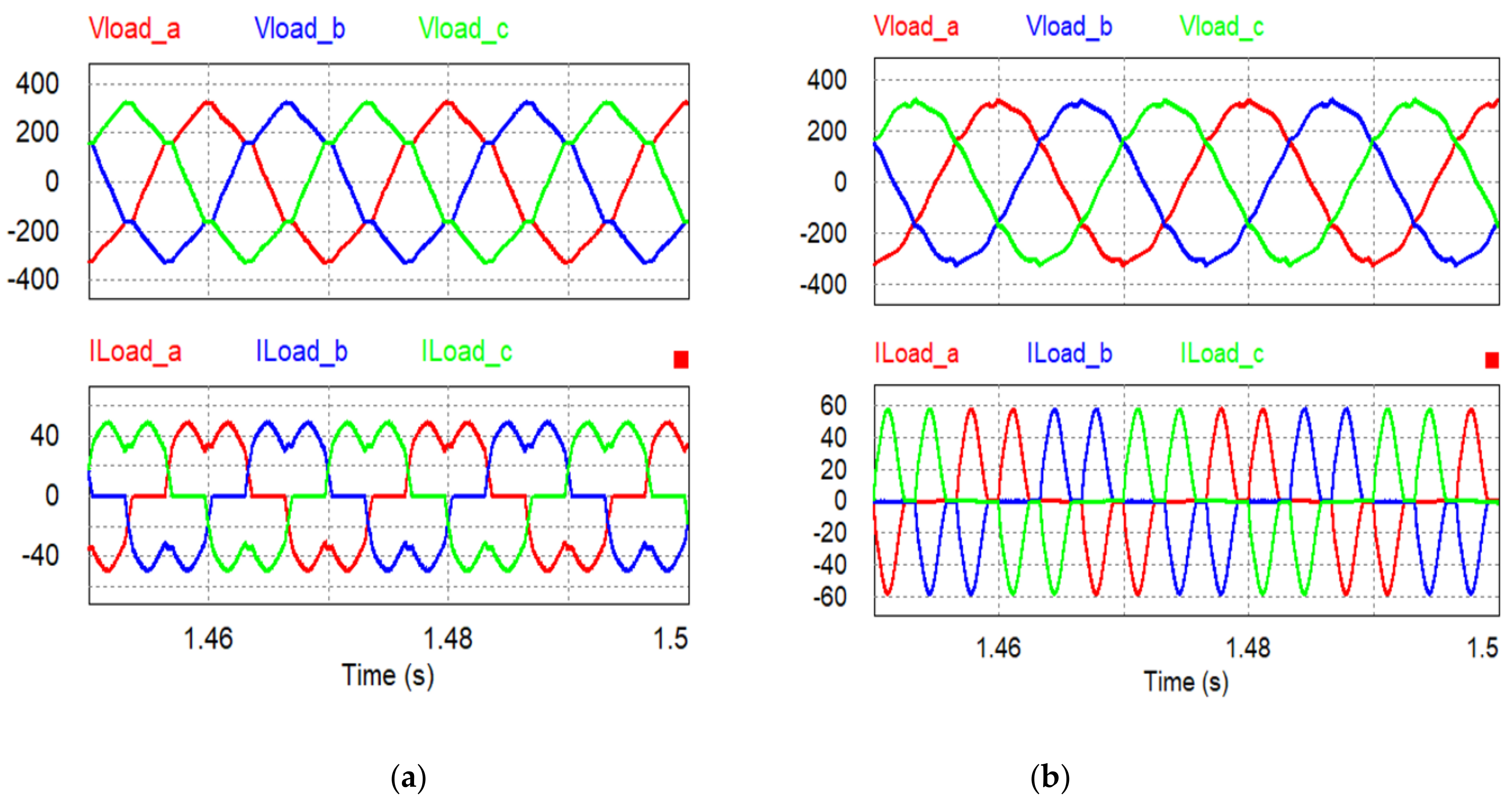
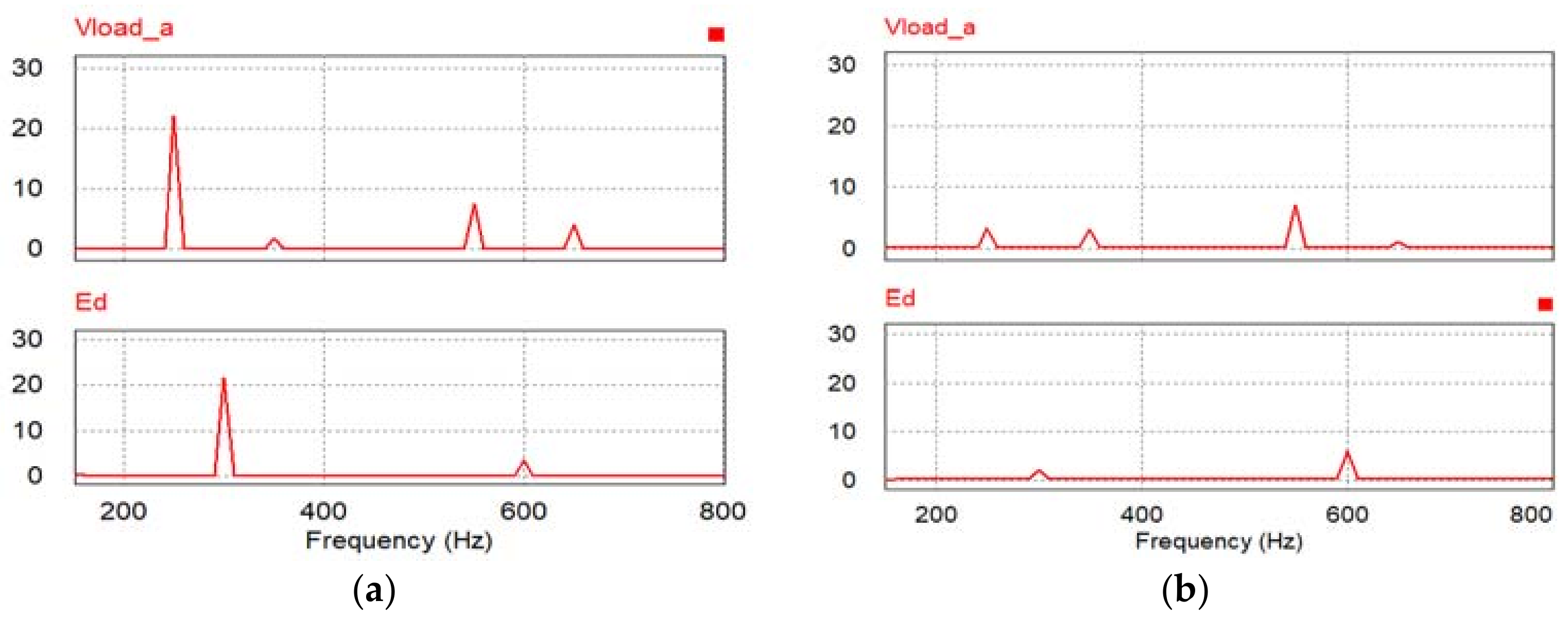
| Parameter | Value |
|---|---|
| Rated power | 200 kW |
| Output voltage | 380 V |
| Line frequency | 50 Hz |
| Inverter | Three-phase, four-wire |
| Transformer core type | Five-lime core transformer |
| Balance load | 20 Ω |
| Unbalanced load | 20 Ω, 12 Ω, 200 Ω |
| Nonlinear load | Three-phase diode rectifier |
| Filter inductor | 2 mH |
| Output capacitor | 100 μF |
| Voltage controller bandwidth | 15 Hz |
| Current controller bandwidth | 1 kHz |
| Resonant controller gain (2th, 6th, 12th) | 10, 6, 4 |
| THD | Conventional Controller | Resonant Controller |
|---|---|---|
| Voltage | 0.08 | 0.05 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lim, J.-U.; Kim, H.-W.; Cho, K.-Y.; Bae, J.-H. Stand-Alone Microgrid Inverter Controller Design for Nonlinear, Unbalanced Load with Output Transformer. Electronics 2018, 7, 55. https://doi.org/10.3390/electronics7040055
Lim J-U, Kim H-W, Cho K-Y, Bae J-H. Stand-Alone Microgrid Inverter Controller Design for Nonlinear, Unbalanced Load with Output Transformer. Electronics. 2018; 7(4):55. https://doi.org/10.3390/electronics7040055
Chicago/Turabian StyleLim, Jae-Uk, Hag-Won Kim, Kwan-Yuhl Cho, and Joung-Hwan Bae. 2018. "Stand-Alone Microgrid Inverter Controller Design for Nonlinear, Unbalanced Load with Output Transformer" Electronics 7, no. 4: 55. https://doi.org/10.3390/electronics7040055
APA StyleLim, J.-U., Kim, H.-W., Cho, K.-Y., & Bae, J.-H. (2018). Stand-Alone Microgrid Inverter Controller Design for Nonlinear, Unbalanced Load with Output Transformer. Electronics, 7(4), 55. https://doi.org/10.3390/electronics7040055




