1. Introduction
Quantum Key Distribution (QKD) is an application of quantum cryptography—the process of exploiting quantum effects to establish secure communications between two authorized users, Alice and Bob, in the presence of an unwanted third party, Eve. QKD protocols promise unconditionally secure communications through exchange of encoded photons, which, due to their quantum nature, are altered in a detectable way if they are observed by an unauthorized eavesdropper [
1].
In conventional QKD protocols such as BB84 [
2], the original QKD protocol, a photon is randomly encoded in one of a pre-determined set of quantum states by Alice. Alice transmits the photon to Bob who obtains partial information on Alice’s encoding by performing a randomly selected projective measurement on the photon. Subsequently Alice reveals partial information on her encoding over an open classical channel. Along with the measurement results, this additional information allows Bob to identify the original encoding state of a subset of the transmitted photons with certainty. The encoding of this subset constitutes the raw shared secret key that Alice and Bob use for encrypted communications [
3]. As Eve does not have access to the results of Bob’s measurements, she lacks the necessary information to infer the secret bits.
Since 1984, other protocols have been proposed to address security vulnerabilities in implementations of BB84 [
4,
5,
6,
7,
8]. One such protocol is Measurement-Device-Independent QKD (MDI-QKD), depicted in
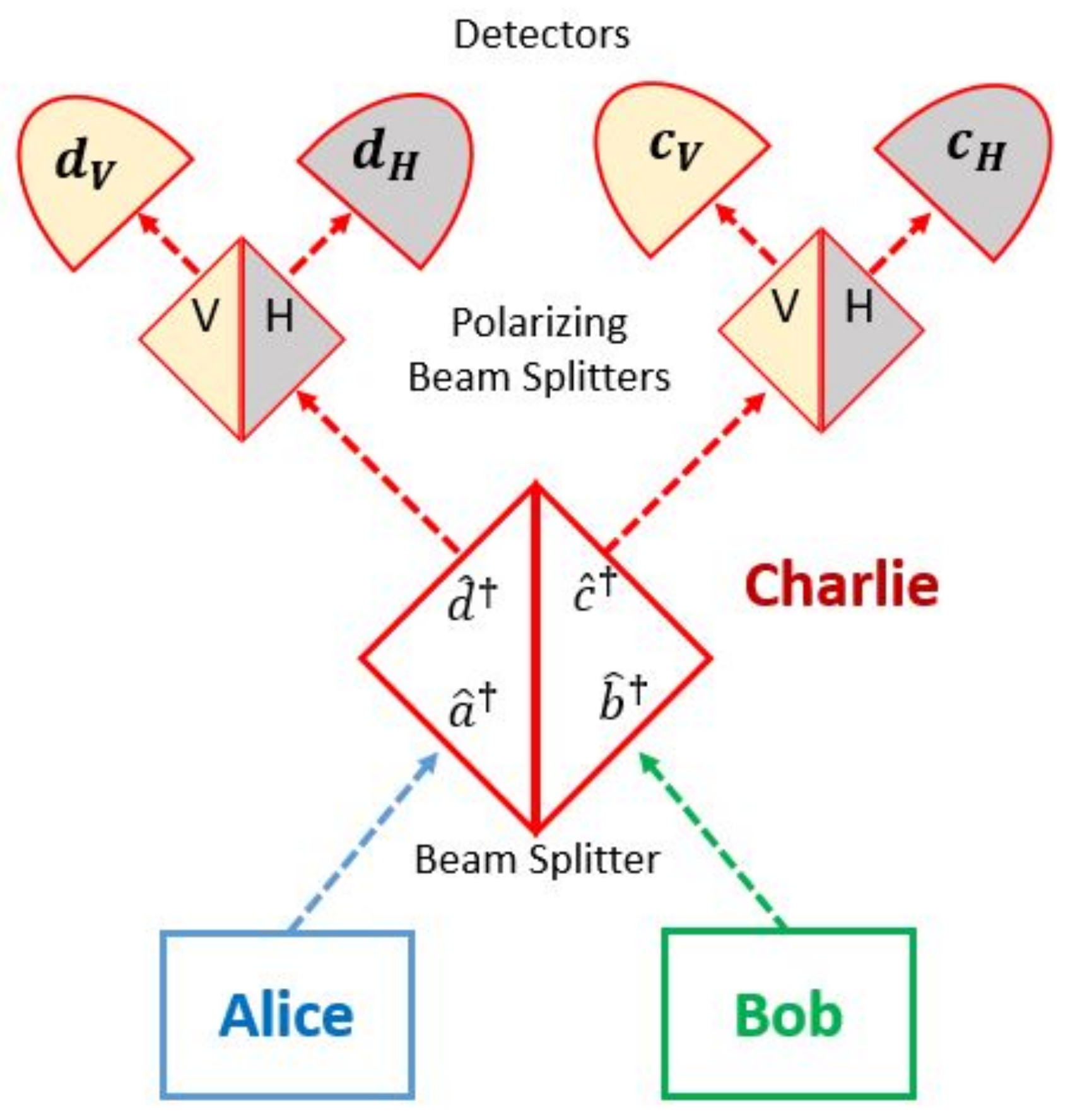
Figure 1, which addresses the vulnerability of Bob’s measurement to malicious signals introduced on the quantum channel by Eve. MDI-QKD moves the act of photon measurement from Bob to an untrusted third party, Charlie (shown in red). Alice and Bob each send one polarization-encoded photon to Charlie, who subjects them to two-photon interference in a symmetric 50:50 beam splitter, followed by polarization-sensitive detection via a pair of polarizing beam splitters and four single-photon detectors, each corresponding to a polarization and beam splitter output port (
,
,
,
). Charlie publicly announces which detectors registered photons. Subsequently, Alice and Bob publicly announced which polarization basis (horizontal-vertical or antidiagonal-diagonal) they used for encoding. From this information and their private knowledge of their own photon encodings, Alice and Bob can infer one bit of shared secret key in 25% of the exchanges under ideal circumstances.
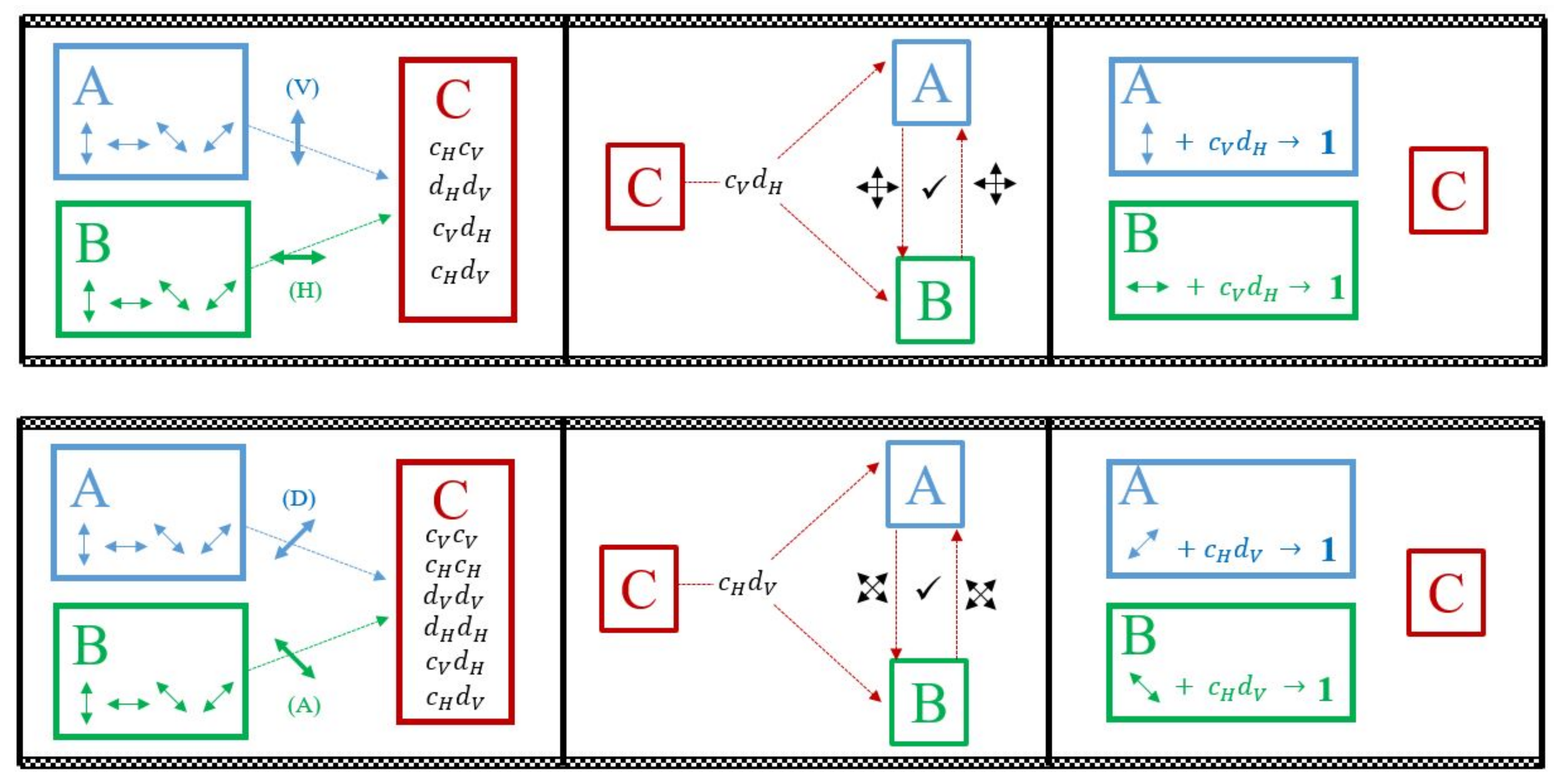
Figure 2 demonstrates these steps explicitly for two key attempts—one in the horizontal-vertical basis and one in the antidiagonal-diagonal basis. The blue and green arrows denote communication on a sensitive quantum channel, while red arrows denote communication on an open classical channel visible to Charlie. Similarly,
Table 1 displays all possible same-basis input states, Charlie’s potential detection states for each input, and the shared bit value associated with a given input state. When Alice and Bob choose opposite encoding bases for a trial, that trial is discarded and no key is generated. The same-basis inputs
and
cannot be used to generate a key bit because Charlie can infer the bit from his measurement and knowledge of the encoding basis. There are also some detected states for antidiagonal-diagonal basis encodings that can occur for multiple input states, making them unusable for key generation.
Despite its immunity from eavesdropping attacks on the detector, MDI-QKD is susceptible to physical non-idealities that can limit the key generation rate by introducing quantum bit errors, which are physically indistinguishable from perturbations caused by Eve’s measurements [
9]. In addition to detector inefficiencies, dark count rates [
10] and polarization errors, MDI-QKD is also susceptible to bit errors caused by timing differences [
7] and photon distinguishability in pulse envelope, bandwidth and wavelength [
11]. Prior research has addressed polarization and timing errors [
10], as well as the feasibility of implementing the protocol utilizing weak coherent pulses from independent laser sources [
11], but significant assumptions about photon source characteristics remain unexplored.
In this paper, we analyze the impact of error tolerances in photon polarization encoding, timing, wavelength and bandwidth on the quantum bit error rate (QBER) of an otherwise ideal MDI-QKD implementation using single photon sources with Gaussian pulse envelopes. In
Section 2 we specify the photon temporal wave functions and apply the formalism of quantum optics to calculate probabilities for Charlie’s measurement outcomes as a function of Alice’s and Bob’s encoding choices and the tolerances of their photon sources. In
Section 3 we describe our Monte Carlo simulation of the MDI-QKD protocol based on these probabilities to determine the associated Quantum Bit Error Rate (QBER). In
Section 4 we present the results of our simulations and discuss the sensitivity of MDI-QKD to various contributions to photon distinguishability. We conclude the paper in
Section 5 with a discussion of the implications of our results for studying practical implementations of MDI-QKD and identify possible extensions to our work.
2. Two-Photon Interference in the Polarizing Beam Splitter
The MDI-QKD protocol relies on quantum interference of two indistinguishable photons incident on a 50:50 beam splitter [
10,
12]. This interference, known as the Hong-Ou-Mandel (HOM) effect, suppresses the probability that two identical photons simultaneously entering the beam splitter through different ports will be detected exiting the beam splitter through different ports; they must always exit the beam splitter together [
13]. Distinguishable photons under the same circumstances show no such correlations. Ideally, photons employed in MDI-QKD are identical in every physical characteristic except (potentially) their polarization angles. Under these conditions, two identically polarized photons will always exhibit HOM interference; however, non-idealities in the photon sources or beam splitter characteristics give rise to partial distinguishability and a non-zero probability of unexpected coincidence events—observation of ostensibly indistinguishable photons exiting different beam splitter ports [
11,
14,
15].
We apply the formalism of quantum optics following the development of Loudon [
16] to relate the probabilities of coincidence events, and ultimately the performance limits of MDI-QKD systems, to photon source tolerances. Alice and Bob independently prepare single photon pulses characterized by temporal wave functions
and polarization angles
. The input state at the beam splitter is then the product state
where
and
are the creation operator densities for horizontally and vertically polarized photons at the
a and
b beam splitter inputs, and
is the 4-mode vacuum. Normalization is achieved by requiring
The beam splitter output state
can be constructed from the input state using the beam splitter transformation,
where
T and
R are the transmission and reflection amplitudes of the symmetric beam splitter, subject to the unitarity conditions
and
and
are the creation operator densities for horizontally and vertically polarized photons at the
c and
d beam splitter outputs. Applying (
3) to (
1) we find
The right hand side of (
5) can be written as a summation of terms each contributing amplitudes to one of the 10 mutually exclusive experimental outcomes:
where, for example,
corresponds to the outcome in which one photon is counted in detector
and one photon is counted in detector
. The probability of the outcome
is then
The dependence of the outcome probabilities on the photon wave functions can be expressed in terms of the overlap integral [
16]
With
as defined in (
9), the probabilities for each of the detection events are
In order to make specific predictions, we model the photon wave functions
as Gaussian wave packets with center angular frequency
, bandwidth
, and beam splitter arrival time
. Using the normalized wave functions
the overlap integral evaluates to
Combining (
10) and (
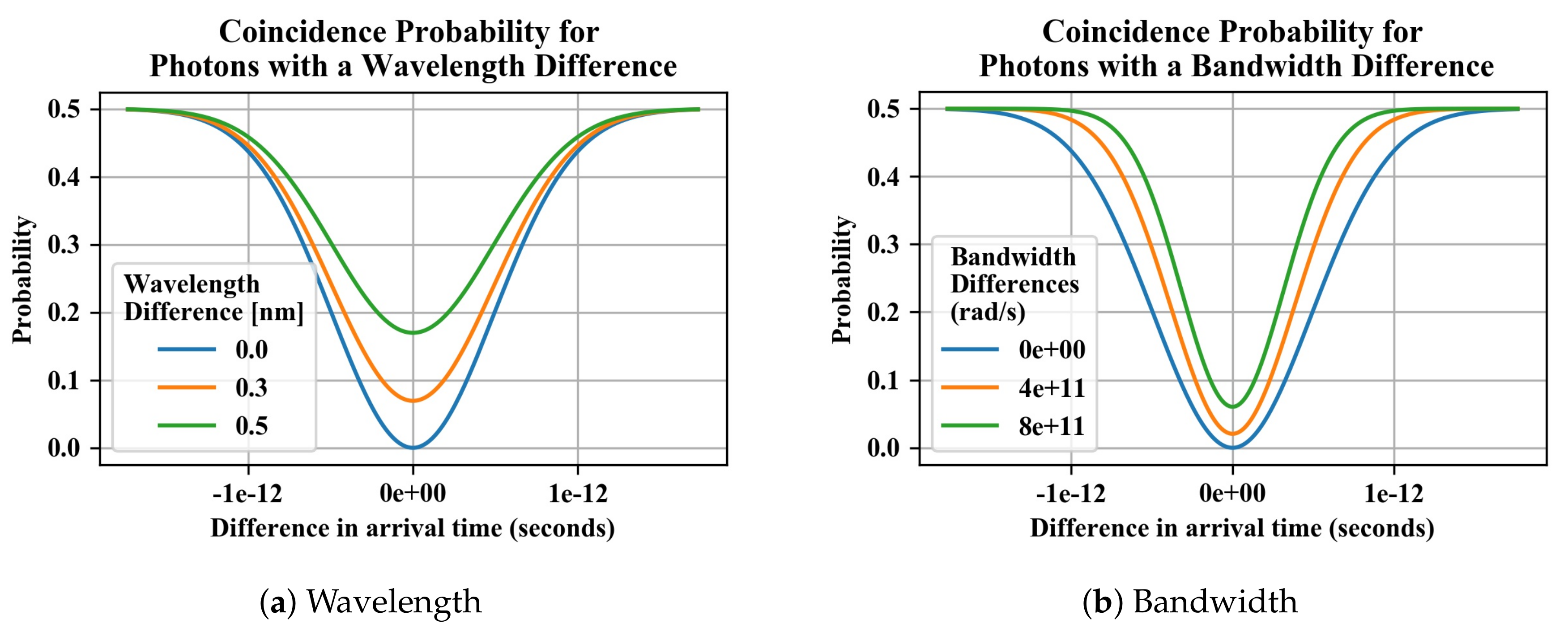
12) we model the HOM effect, as in
Figure 3, where the incomplete suppression of coincidence events as a result of photon wavelength and pulse bandwidth differences is apparent. We also use these results in Monte Carlo simulations of the MDI-QKD protocol, as discussed in
Section 3, to determine the associated QBER.
3. Monte Carlo Simulation Methodology
To determine the MDI-QKD QBER for achievable single photon source tolerances, we perform Monte Carlo simulations utilizing the probabilities of (
10) and the overlap integral of (
12). The single photon source parameters (wavelength
nm, wavelength tolerance
nm, pulse bandwidth
rad/s, pulse bandwidth tolerance
rad/s, synchronization tolerance
ps, and polarization angle tolerance
) are selected consistently with those described by Kaltenbaek et al. [
17], who report a
HOM-interference visibility using independent single photon sources in an entanglement swapping experiment that is functionally identical to a MDI-QKD implementation. They report the standard deviation of their pulse synchronization and the full-width-at-half-maximum of the filters used to limit fluctuations in the photon wavelengths. We estimate the bandwidth of their pulses on the basis of the width of their HOM-dips and assume a 1% relative fluctuation. The assumed polarization standard deviation is typical of laboratory optics [
18]. The results of [
17] are particularly relevant because the two photon sources used are completely independent, communicating only via an electronic synchronization signal, just as required for MDI-QKD. The simulation procedure is outlined below.
- (1)
Construct -element arrays of Alice’s and Bob’s randomly selected basis choices.
- (2)
Construct -element arrays of Alice’s and Bob’s randomly selected raw keys bits.
- (3)
Compare Alice’s and Bob’s random basis selections and discard trials corresponding to opposite-basis selection from further consideration, retaining trials.
- (4)
Compute the photon polarization angles for each photon in each trial from the choices of basis, raw key bits, and polarization error tolerances.
- (5)
Compute the photon wavelength errors for each photon in each trial from the photon wavelength tolerances.
- (6)
Compute the bandwidth of each photon pulse in each trial from the mean bandwidth and the bandwidth tolerances.
- (7)
Compute the photon arrival time synchronization error for each trial from the synchronization time tolerance.
- (8)
Use the results of steps (4) through (7) to calculate the probability of each possible measurement outcome for each trial.
- (9)
For each trial select a particular measurement outcome in accordance with the probabilities calculated in step (8).
- (10)
Discard unusable trials and flip Bob’s key bit in accordance with the results of step (9), retaining bits.
- (11)
Compare Alice’s and Bob’s sifted keys to determine the
[
19].
This procedure is implemented in Python 3 [
20] and executed with version 4.4.0-Windows-x86_64 of Anaconda3 [
21]. Random measurement outcomes are selected by calls to the numpy.random.choice() routine of the numpy package [
22]. The code is fully documented and provided in the online supplement.
Given the source parameters and tolerances, the QBER is a well-defined quantity for an infinitely long sifted key, and can be estimated to the desired precision by averaging the QBERs obtained from repeated simulations of finite key length. Random bit errors will obey Poisson statistics, so we expect the sample standard deviation of their rate to scale as .
4. Simulation Results and Discussion
Employing the procedure described in
Section 3, averages over 1000 simulations using raw keys with lengths
to 1,024,000 bits give QBERs of
. The observed sample standard deviation of the QBER follows the expected dependence on the length of the sifted key. These results are consistent with the HOM-interference visibility reported in [
17]. The fraction of bits discarded due to opposite basis selection or unusable measurement results are also in line with expectations—approximately 25% of the raw key bits are retained in the sifted key.
Additionally, we explore the consequences of systematically relaxing photon source tolerances to determine the sensitivity of the QBER to fluctuations in wavelength, pulse bandwidth, polarization angle, and source synchronization. The results of these simulations are shown in
Figure 4. Each point in the figure represents the average QBER from 100 iterations with
for a fixed set of photon source parameters. The standard deviations of (a) photon wavelength; (b) pulse bandwidth; (c) polarization angle; and (d) photon synchronization are varied relative to their nominal values, indicated by orange diamonds, while other photon source parameters are held fixed. As expected, the QBER increases with increasing probability of photon distinguishability due to source fluctuations.
In our simulation of the MDI-QKD protocol, we obtain Alice’s and Bob’s sifted keys, from which we can identify specific bit errors and calculate the QBER explicitly. In a fielded QKD system, a sifted key that contains errors is not useful for encrypted communication and neither party alone possesses sufficient information to identify and correct these errors. Further, the finite QBER sets a information-theoretic non-zero upper bound on how much information Eve might have obtained about the sifted key by eavesdropping on the quantum channel. All bit errors in our simulated sifted key are attributable to finite source tolerances rather than an eavesdropper. However, in practice, bit errors due to the actions of Eve on the quantum channel are physically indistinguishable from bit errors arising from finite source tolerances (or other system imperfections), and thus, in a rigorous security analysis, bit errors arising from all sources must be attributed to information gained by Eve [
1].
The process of removing bit errors and Eve’s information from the sifted keys to obtain a shorter secure shared key is called key distillation. The first step of the process is the estimation of the QBER. This can be achieved by publicly comparing a random sample of bits from the sifted key. As the selected bits are revealed on an open channel, they must be discarded, reducing the length of the sifted key. For given key distillation and QKD protocols, the QBER determines the fraction of the remaining key bits that must be consumed to achieve the desired error free and secure key. If the QBER exceeds a protocol-dependent threshold, this fraction is greater than one and the key distillation fails [
23]. Even if the QBER does not exceed the threshold, the length of the distilled key can be a tiny fraction of the length of the original sifted key, making the absolute rate of secure shared key generation prohibitively low. For these reasons, minimizing all sources of bit errors, including those due to finite photon source tolerances, is critical for MDI-QKD system performance.
Assuming the QBER does not exceed the failure threshold, classical error correction and privacy amplification protocols are applied to the remaining sifted key to complete the key distillation. The extensive literature addressing the application of error correction and privacy amplification to QKD protocols is summarized by Nielsen and Chuang . In particular, it is known that effective error correction and privacy amplification protocols exist for the BB84 protocol when the QBER is below 11%, and this threshold is believed to be acceptable for all similar QKD protocols [
24,
25]. MDI-QKD, as we have formulated it, is not identical to BB84. However, it is similar in that, from the point of view of Alice, MDI-QKD is functionally equivalent to BB84 if she conceptualizes Charlie as an agent of Bob. Accordingly, we expect the threshold QBER for MDI-QKD to be no less than 11%, which is significantly above the QBER we obtained in our simulation of realistic source non-idealities.
The practical implementation of MDI-QKD depends on limiting bit errors due to incomplete HOM interference. By simulating the MDI-QKD protocol using photon source tolerances from a well-characterized two-photon interference study, we demonstrate both good agreement with experiment and the ability to relate the achievable visibility to fluctuations in specific photon properties. From the plots in
Figure 4, it is clear that the QBER is sensitive to both photon wavelength and pulse timing. Modest increases in the trial-to-trial fluctuations of photon wavelengths and arrival times lead to significant increases in the QBER, while suppressing either of these fluctuations results in a factor of two improvement. In contrast, the QBER is relatively insensitive to changes in the bandwidth standard deviation and polarization angle standard deviation, even if these fluctuations are suppressed entirely.
The sensitivity of the QBER to wavelength and timing fluctuations points to the need for design tradeoffs to optimize system performance. In the experiment of [
17], wavelength fluctuations are limited by narrow filters that block out-of-tolerance photons from reaching the detectors. While this enhances the HOM visibility, it also reduces the detection rate. As QKD performance is measured on the basis of the rate at which secret key can be generated, there is a point of diminishing returns when the QBER is improved at the expense of transmission rate. Similar reasoning applies to photon synchronization if improvements in the timing of pulse generation come at the expense of a reduced probability of generating a photon. A reduction in the detection rate could also occur with tighter polarization angle and pulse bandwidth control without improvement in the QBER, thus reducing overall QKD system performance.
Even though the QBER is not particularly sensitive to bandwidth fluctuations in the region of parameter space under consideration, the sensitivity to pulse synchronization is closely related to the nominal bandwidth. As the bandwidth is inversely proportional to the temporal width of the pulse, larger bandwidth pulses are shorter in duration, thus requiring tighter synchronization tolerances to ensure large wave function overlap, reliable HOM interference, and a low QBER. We also note that the use of very narrow wavelength filters has the potential to complicate the analysis by altering the shape of the photon wave function.