Multi-Agent Cooperative Control Consensus: A Comparative Review
Abstract
:1. Introduction
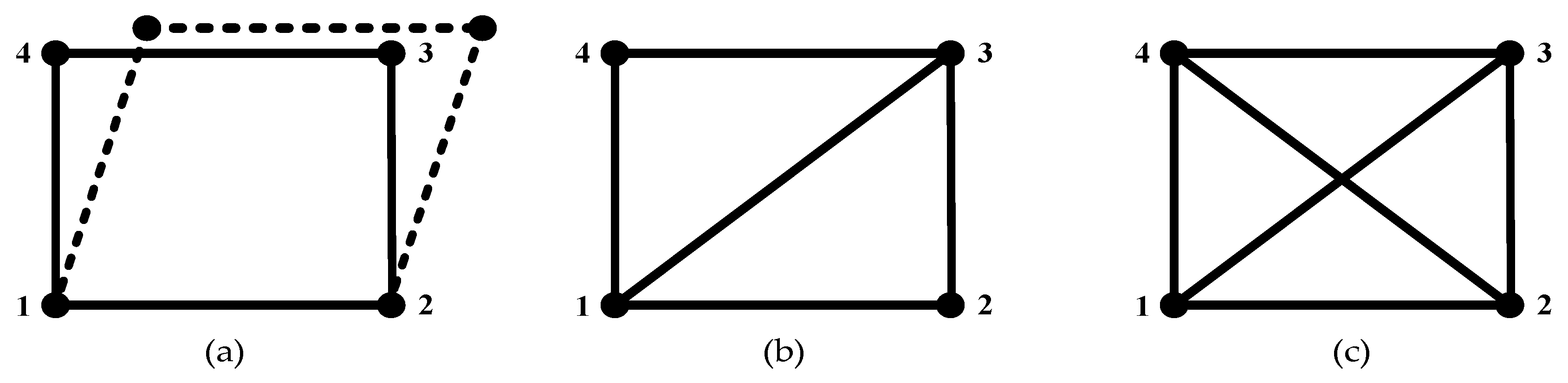
2. Preliminaries
3. Theoretical Progress in Consensus
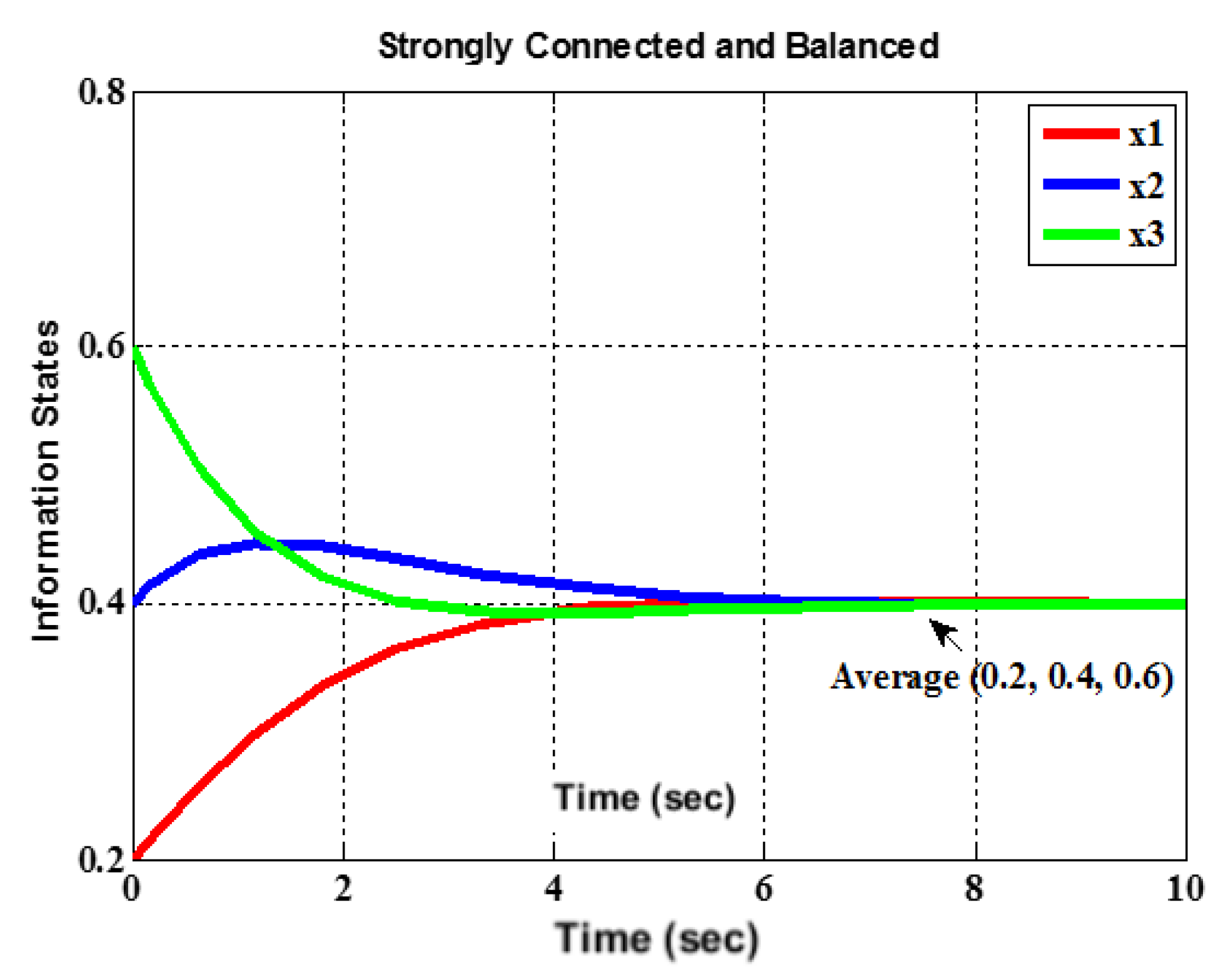
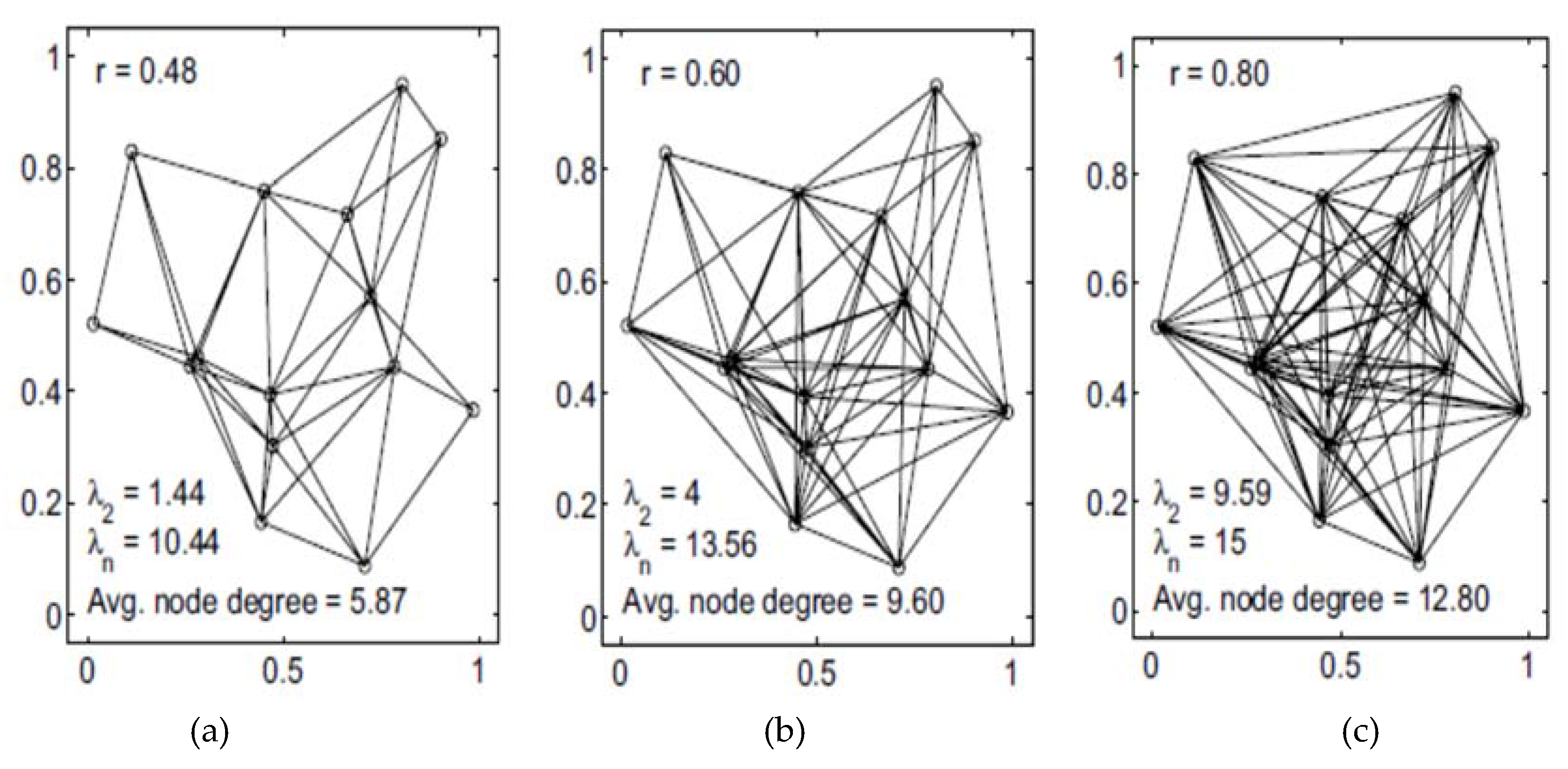
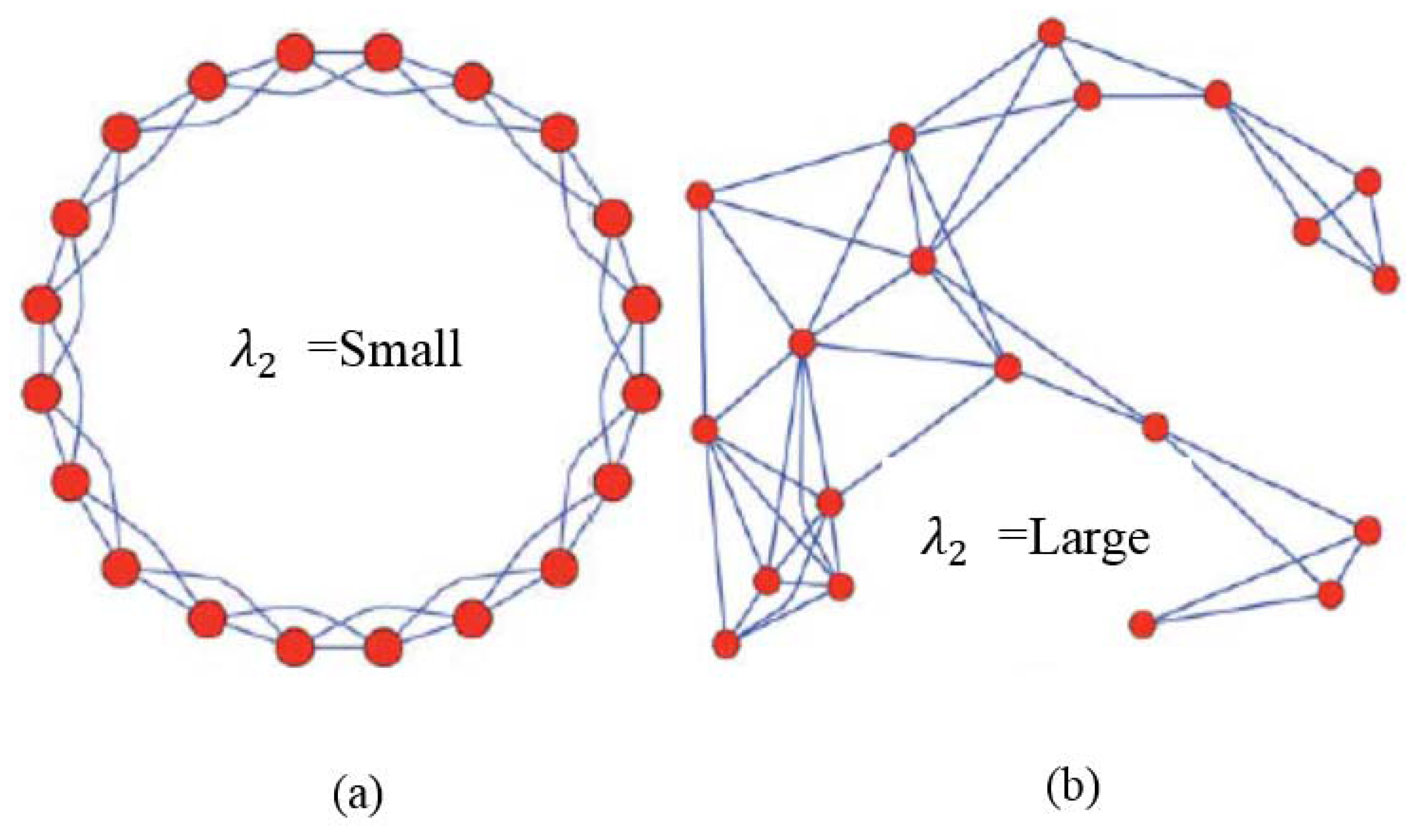
3.1. Convergence Analysis for Time-Invariant Topology
3.2. Convergence Analysis for Complex Dynamic Systems
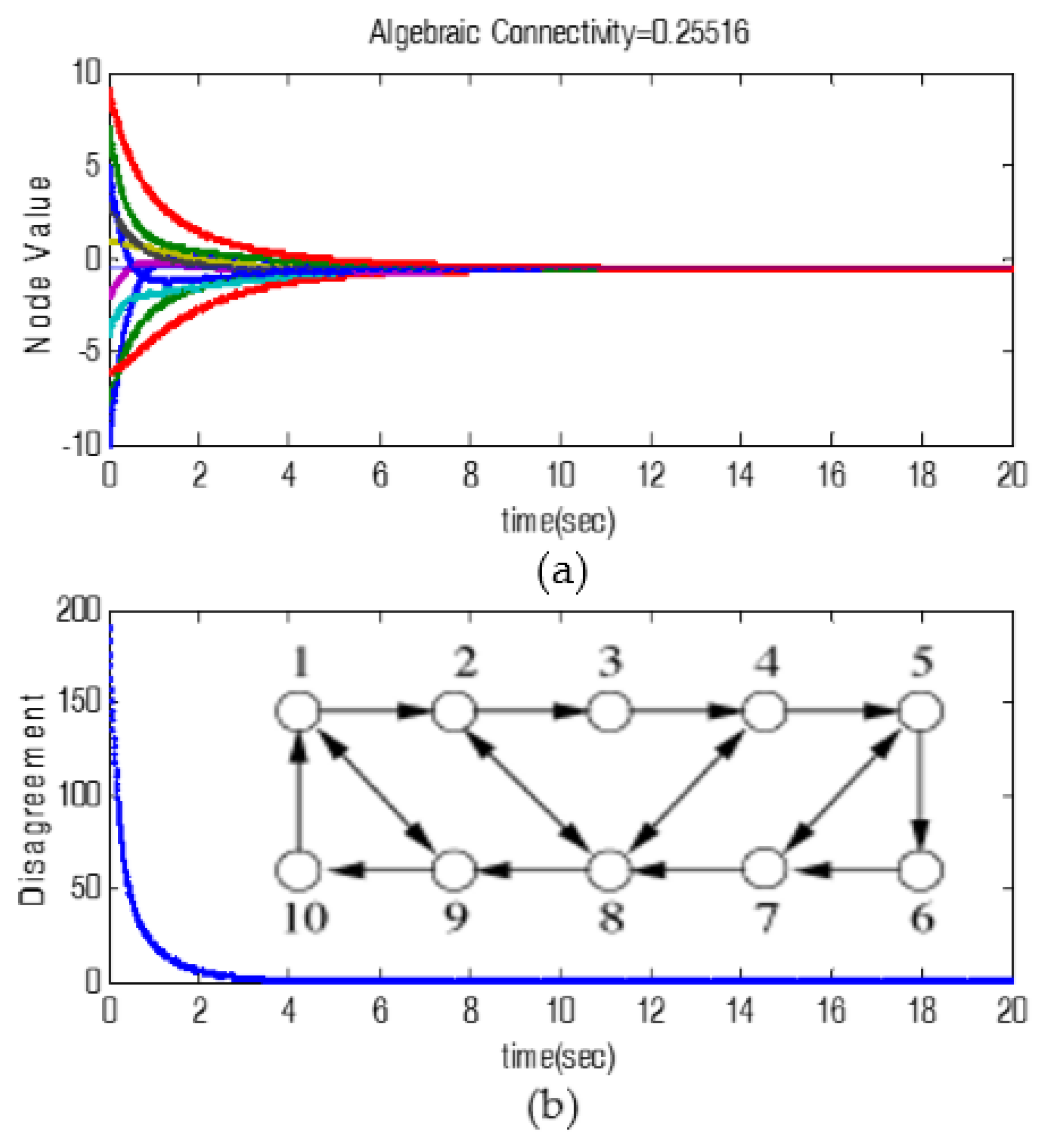
3.2.1. Switching Network
3.2.2. Synchronization Network
3.3. Convergence Speed in Finite Time
3.4. Heterogeneous Agents
4. Convergence Constraints due to Practical Limitations
4.1. Computation, Execution, Control and Communication Delays
4.2. Quantization & Sample-Data Consensus
5. Application of Consensus in Multi-Agent Network
- Multi-agent flocking means to achieve some common group objectives by interacting with each other.
- Swarm is an approach of multi-agent system that takes inspiration from social animals that exhibit a self-organized behavior. Through local interactions and simple rules, swarm agents focus flexible, scalable and robust collective behaviors for the coordination of multi-agent system.
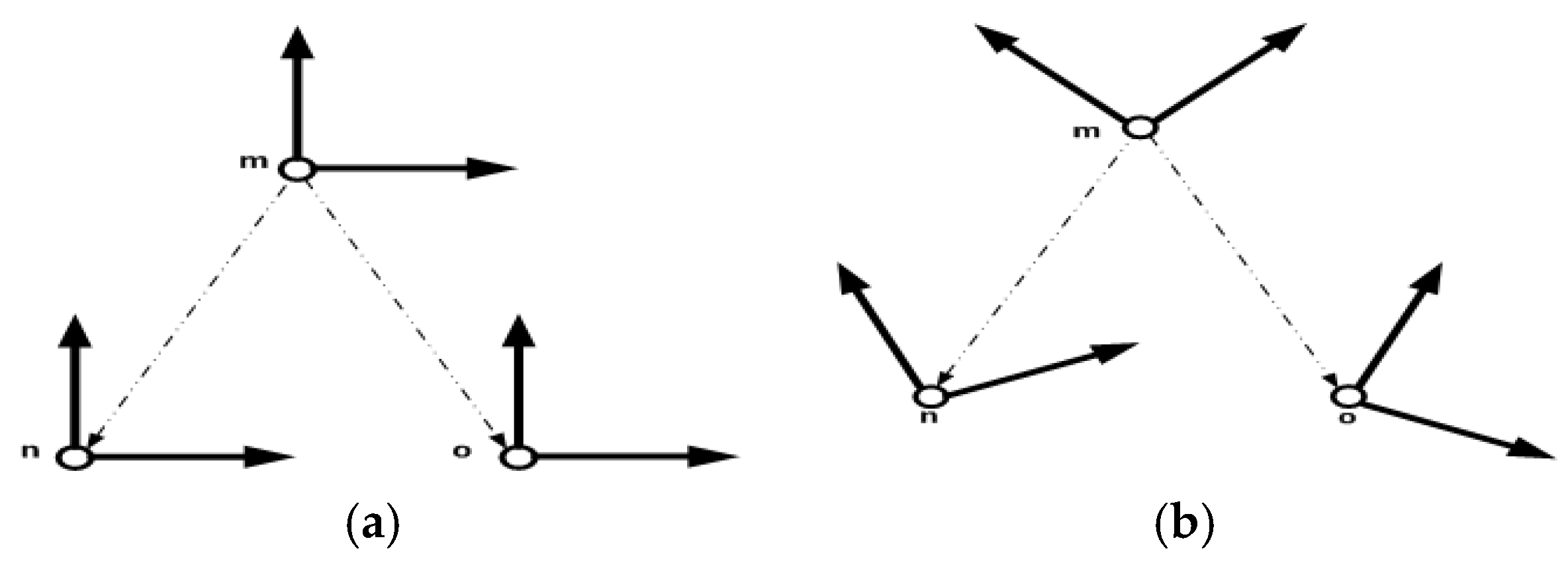
5.1. Rendezvous
5.2. Formation Control
- In position-based control, agents sense their own position with respect to the global coordinate system.
- In displacement-based control, agents sense the relative position of its neighbor with respect to the global coordinate system.
- In distance-based control, agents sense the relative position of its neighbor with respect to own local coordinate system.
6. Discussion
6.1. Consensus
- Existing control strategies for multi-agent consensus and formation focus on simple system dynamics using basic connectivity assumption and Laplacian matrix, so higher order dynamics or nonlinear dynamics is still needed to be investigated.
- Using heterogeneous agents, more work is required in the field of consensus for more complicated nonlinear dynamic so that each agent can choose the best responses based on its own objectives.
6.2. Formation
- Global stability properties for general rigid and persistent formation are yet to be investigated (Only triangle formation is done so far).
- For formation producing the network topology is assumed to be undirected which is not applicable to many practical applications.
- More research efforts on distance-based formation with moving leader is needed.
6.3. Obstacle Avoidance
- Multi-agent consensus for complex obstacles is still to be investigated, where the task connectivity preservation and collision avoidance issues are important.
7. Conclusions
Conflicts of Interest
References
- Ren, W.; Beard, R.W.; Atkins, E.M. Information Consensus in Multivehicle Cooperative Control. IEEE Control Syst. Mag. 2007, 27, 71–82. [Google Scholar] [CrossRef]
- Zang, X.; Iqbal, S.; Zhu, Y.; Liu, X.; Zhao, J. Applications of Chaotic Dynamics in Robotics. Rev. Int. J. Adv. Robot. Syst. 2015, 13. [Google Scholar] [CrossRef]
- Zang, X.Z.; Yu, W.T.; Zhang, L.; Iqbal, S. Path Planning Based on Bi-RRT Algorithm for Redundant Manipulator. In Proceedings of the International Conference on Electrical, Automation and Mechanical Engineering (EAME 2015), Phuket, Thailand, 26–27 July 2015; pp. 189–191. [Google Scholar]
- Reynolds, C.W. Flocks, herds and schools: A distributed behavioral model. ACM SIGGRAPH Comput. Graph. 1987, 21, 25–34. [Google Scholar] [CrossRef]
- Vicsek, T.; Czirók, A.; Ben-Jacob, E.; Cohen, I.; Shochet, O. Novel Type of Phase Transition in a System of Self-Driven Particles. Phys. Rev. Lett. 1995, 75, 729–732. [Google Scholar] [CrossRef] [PubMed]
- Dessmark, A.; Fraigniaud, P.; Kowalski, D.R.; Pelc, A. Deterministic rendezvous in graphs. Algorithmica 2006, 46, 69–96. [Google Scholar] [CrossRef]
- Zheng, R.; Sun, D. Rendezvous of unicycles: A bearings-only and perimeter shortening approach. Syst. Control Lett. 2013, 62, 401–407. [Google Scholar] [CrossRef]
- Mao, Y.; Dou, L.; Fang, H.; Chen, J. Flocking of multi-robot systems with connectivity maintenance on directed graphs. J. Syst. Eng. Electron. 2014, 25, 470–482. [Google Scholar] [CrossRef]
- Chen, C.; Chen, G.; Guo, L. Consensus of flocks under M-nearest-neighbor rules. J. Syst. Sci. Complex. 2015, 28, 1–15. [Google Scholar] [CrossRef]
- Morin, A.; Caussin, J.; Eloy, C.; Bartolo, D. Collective motion with anticipation: Flocking, spinning and swarming. Phys. Rev. E 2015, 91, 012134. [Google Scholar] [CrossRef] [PubMed]
- Brambilla, M.; Ferrante, E.; Birattari, M.; Dorigo, M. Swarm robotics: A review from the swarm engineering perspective. Swarm Intell. 2013, 7, 1–41. [Google Scholar] [CrossRef]
- Guo, Y.; Balakrishnan, M. Complete coverage control for nonholonomic mobile robots in dynamic environments. In Proceedings of the IEEE International Conference on Robotics and Automation, Orlando, FL, USA, 15–19 May 2006; pp. 1704–1709. [Google Scholar]
- Ji, M.; Egerstedt, M. Distributed coordination control of multiagent systems while preserving connectedness. IEEE Trans. Robot. 2007, 23, 693–703. [Google Scholar] [CrossRef]
- Liu, S.; Sun, D.; Zhu, C. Coordinated motion planning for multiple mobile robots along designed paths with formation requirement. IEEE/ASME Trans. Mechatron. 2011, 16, 1021–1031. [Google Scholar] [CrossRef]
- Li, X.; Sun, D.; Yang, J. A bounded controller for multirobot navigation while maintaining network connectivity in the presence of obstacles. Automatica 2013, 49, 285–292. [Google Scholar] [CrossRef]
- Stump, E.; Jadbabaie, A.; Kumar, V. Connectivity management in mobile robot teams. In Proceedings of the 2008 IEEE International Conference on Robotics and Automation (ICRA), Pasadena, CA, USA, 19–23 May 2008; pp. 1525–1530. [Google Scholar]
- Savla, K.; Notarstefano, G.; Bullo, F. Maintaining Limited-Range Connectivity among Second-Order Agents. SIAM J. Control Optim. 2006, 48, 187–205. [Google Scholar] [CrossRef]
- Tardioli, D.; Mosteo, A.R.; Riazuelo, L.; Villarroel, J.L.; Montano, L. Enforcing Network Connectivity in Robot Team Missions. Int. J. Robot. Res. 2010, 29, 460–480. [Google Scholar] [CrossRef]
- Mesbahi, M.; Egerstedt, M. Graph Theoretic Methods in Multiagent Network, 1st ed.; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Olfati-Saber, R.; Murray, R.M. Consensus problems in networks of agents with switching topology and time-delays. IEEE Trans. Autom. Control 2004, 49, 1520–1533. [Google Scholar] [CrossRef]
- Fiedler, M. Algebraic Conectivity of Graphs. Czechoslov. Math. J. 1973, 23, 298–305. [Google Scholar]
- Kim, Y.; Mesbahi, M. On maximizing the second smallest eigenvalue of a state-dependent graph Laplacian. IEEE Trans. Autom. Control 2006, 51, 116–120. [Google Scholar] [CrossRef]
- Ren, W.; Beard, R.W.; McLain, T.W. Coordination Variables and Consensus Building in Multiple Vehicle Systems. In Cooperative Control; Lecture Notes in Control and Information Science; Springer: Berlin/Heidelberg, Germany, 2005; Volume 309, pp. 439–442. [Google Scholar]
- Wang, X.F.; Chen, G. Synchronization in scale-free dynamical networks: Robustness and fragility. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2002, 49, 54–62. [Google Scholar] [CrossRef]
- Wang, X.F.; Chen, G. Synchronization in Small-World Dynamical Networks. Int. J. Bifurc. Chaos 2002, 12, 187–192. [Google Scholar] [CrossRef]
- Ren, W.; Beard, R.W. Consensus seeking in multiagent systems under dynamically changing interaction topologies. IEEE Trans. Autom. Control 2005, 50, 655–661. [Google Scholar] [CrossRef]
- Moreau, L. Stability of multiagent systems with time-dependent communication links. IEEE Trans. Autom. Control 2005, 50, 169–182. [Google Scholar] [CrossRef]
- Yu, W.; Chen, G.; Lü, J. On pinning synchronization of complex dynamical networks. Automatica 2009, 45, 429–435. [Google Scholar] [CrossRef]
- Wu, X.; Xu, C. Global synchronization of hybrid coupled neural networks with time-varying delay. In Proceedings of the Seventh International Conference on Computational Intelligence and Security (CIS), Hainan, China, 3–4 December 2011; Volume 1. [Google Scholar]
- Olshevsky, A.; Tsitsiklis, J.N. Convergence Speed in Distributed Consensus and averaging. SIAM J. Control Optim. 2009, 48, 33–55. [Google Scholar] [CrossRef] [Green Version]
- Kim, Y. Bisection Algorithm of Increasing Algebraic Connectivity by Adding an Edge. IEEE Trans. Autom. Control 2010, 55, 170–174. [Google Scholar]
- Zhou, J.; Wang, Q. Convergence speed in distributed consensus over dynamically switching random networks. Automatica 2009, 45, 1455–1461. [Google Scholar] [CrossRef]
- Hui, Q. Finite-Time Rendezvous Algorithms for Mobile Autonomous Agents. IEEE Trans. Autom. Control 2011, 56, 207–211. [Google Scholar] [CrossRef]
- Wang, X.; Hong, Y. Finite-time consensus for multi-agent networks with second-order agent dynamics. IFAC Proc. Vol. 2008, 17, 15185–15190. [Google Scholar] [CrossRef]
- Cao, Y.; Ren, W.; Meng, Z. Decentralized finite-time sliding mode estimators and their applications in decentralized finite-time formation tracking. Syst. Control Lett. 2010, 59, 522–529. [Google Scholar] [CrossRef]
- Yuan, Y.; Stan, G.B.; Barahona, M.; Shi, L.; Goncalves, J. Decentralised minimal-time consensus. In Proceedings of the 50th IEEE Conference on Decision and Control and European Control Conference (CDC-ECC), Orlando, FL, USA, 12–15 December 2011; pp. 4282–4289. [Google Scholar]
- Li, S.; Wang, J.; Luo, X.; Guan, X. A new framework of consensus protocol design for complex multi-agent systems. Syst. Control Lett. 2011, 60, 19–26. [Google Scholar] [CrossRef]
- Lee, T.H.; Park, J.H.; Ji, D.H.; Jung, H.Y. Leader-following consensus problem of heterogeneous multi-agent systems with nonlinear dynamics using fuzzy disturbance observer. Complexity 2014, 19, 20–31. [Google Scholar] [CrossRef]
- Cao, M.; Morse, A.S.; Anderson, B.D.O. Agreeing asynchronously. IEEE Trans. Autom. Control 2008, 53, 1826–1838. [Google Scholar]
- Fang, L.; Antsaklis, P.J. Asynchronous consensus protocols using nonlinear paracontractions theory. IEEE Trans. Autom. Control 2008, 53, 2351–2355. [Google Scholar] [CrossRef]
- Huang, C.; Ye, X. Cooperative Output Regulation of Heterogeneous Multi-Agent Systems: An H-infinity Criterion. IEEE Trans. Autom. Control 2014, 59, 267–273. [Google Scholar] [CrossRef]
- Hong, Y.; Wang, X.; Jiang, Z.P. Distributed output regulation of leader–follower multi-agent systems. Int. J. Robust Nonlinear Control 2013, 23, 48–66. [Google Scholar] [CrossRef]
- Su, Y.; Huang, J.; Graph, A. Cooperative Output Regulation With Application to Multi-Agent Consensus Under Switching Network. IEEE Trans. Syst. 2012, 42, 864–875. [Google Scholar]
- Tian, Y.P.; Liu, C.L. Consensus of multi-agent systems with diverse input and communication delays. IEEE Trans. Autom. Control 2008, 53, 2122–2128. [Google Scholar] [CrossRef]
- Moreau, L. Stability of continuous-time distributed consensus algorithms. In Proceedings of the 43rd IEEE Conference on Decision and Control, Nassau, Bahamas, 14–17 December 2004; Volume 4, pp. 3998–4003. [Google Scholar]
- Olfati-Saber, R. Ultrafast consensus in small-world networks. In Proceedings of the American Control Conference, Portland, OR, USA, 8–10 June 2005; pp. 2371–2378. [Google Scholar]
- Olfati-Saber, B.R.; Fax, J.A.; Murray, R. Consensus and Cooperation in Networked Multi-Agent Systems. Proc. IEEE 2007, 95, 215–233. [Google Scholar] [CrossRef]
- Zhang, Y.; Tian, Y.P. Consensus of data-sampled multi-agent systems with random communication delay and packet loss. IEEE Trans. Autom. Control 2010, 55, 939–943. [Google Scholar] [CrossRef]
- Bokharaie, V.S.; Mason, O.; Verwoerd, M. D-stability and delay-independent stability of homogeneous cooperative systems. IEEE Trans. Autom. Control 2010, 55, 2882–2885. [Google Scholar] [CrossRef]
- Nuño, E.; Ortega, R.; Basañez, L.; Hill, D. Synchronization of networks of nonidentical euler-lagrange systems with uncertain parameters and communication delays. IEEE Trans. Autom. Control 2011, 56, 935–941. [Google Scholar] [CrossRef]
- Xiao, F.; Wang, L. Asynchronous consensus in continuous-time multi-agent systems with switching topology and time-varying delays. IEEE Trans. Autom. Control 2008, 53, 1804–1816. [Google Scholar] [CrossRef]
- Liang, J.; Wang, Z.; Liu, Y.; Liu, X. Global synchronization control of general delayed discrete-time networks with stochastic coupling and disturbances. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2008, 38, 1073–1083. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Slotine, J.J.E. Contraction analysis of time-delayed communications and group cooperation. IEEE Trans. Autom. Control 2006, 51, 712–717. [Google Scholar] [CrossRef]
- Kashyap, A.; Başar, T.; Srikant, R. Quantized consensus. In Proceedings of the 2006 IEEE International Symposium on Information Theory, Seattle, WA, USA, 9–14 July 2006; pp. 635–639. [Google Scholar]
- Carli, R.; Bullo, F. Quantized Coordination Algorithms for Rendezvous and Deployment. SIAM J. Control Optim. 2009, 48, 1251–1274. [Google Scholar] [CrossRef]
- Li, T.; Fu, M.; Xie, L.; Zhang, J. Distributed Consensus With Limited Communication Data Rate. IEEE Trans. Autom. Control 2011, 56, 279–292. [Google Scholar] [CrossRef]
- Tatikonda, S.; Mitter, S. Control under communication constraints. IEEE Trans. Autom. Control 2004, 49, 1056–1068. [Google Scholar] [CrossRef]
- Nair, G.N.; Evans, R.J. Exponential stabilisability of finite-dimensional linear systems with limited data rates. Automatica 2003, 39, 585–593. [Google Scholar] [CrossRef]
- Elia, N.; Mitter, S.K. Stabilization of linear systems with limited information. IEEE Trans. Autom. Control 2001, 46, 1384–1400. [Google Scholar] [CrossRef]
- Fu, M.; Xie, L. The Sector Bound Approach to Quantized Quantized Feedback Control. IEEE Trans. Autom. Control 2005, 50, 1698–1711. [Google Scholar]
- Nair, G.N.; Evans, R.J. Stabilizability of Stochastic Linear Systems with Finite Feedback Data Rates. Soc. Ind. Appl. Math. J. Control Optim. 2004, 43, 413–436. [Google Scholar] [CrossRef]
- Liberzon, D. On Stabilization of Linear Systems with Limited Information. IEEE Trans. Autom. Control 2003, 48, 304–307. [Google Scholar] [CrossRef]
- Brockett, R.W.; Liberzon, D. Quantized Feedback Stabilization of Linear Systems. IEEE Trans. Autom. Control 2000, 45, 1279–1289. [Google Scholar] [CrossRef]
- Andreasson, M.; Dimarogonas, D.V.; Sandberg, H.; Johansson, K.H. Distributed control of networked dynamical systems: Static feedback, integral action and consensus. IEEE Trans. Autom. Control 2014, 59, 1750–1764. [Google Scholar] [CrossRef]
- Frasca, P.; Carli, R.; Fagnani, F.; Zampieri, S. Average consensus by gossip algorithms with quantized communication. In Proceedings of the 47th IEEE Conference on Decision and Control, Cancun, Mexico, 9–11 December 2008; pp. 1–6. [Google Scholar]
- Xie, G.; Liu, H.; Wang, L.; Jia, Y. Consensus in networked multi-agent systems via sampled control: Fixed topology case. In Proceedings of the American Control Conference, St. Louis, MO, USA, 10–12 June 2009; pp. 4525–4530. [Google Scholar]
- Gao, Y.; Wang, L. Sampled-data based consensus of continuous-time multi-agent systems with time-varying topology. IEEE Trans. Autom. Control 2011, 56, 1226–1231. [Google Scholar] [CrossRef]
- Hayakawa, T.; Matsuzawa, T.; Hara, S. Formation Control of Multi-Agent Systems with Sampled Information. In Proceedings of the 45th IEEE Conference on Decision and Control, San Diego, CA, USA, 13–15 December 2006; pp. 4333–4338. [Google Scholar]
- Gao, Y.; Wang, L. Consensus of multiple double-integrator agents with intermittent measurement. Int. J. Robust Nonlinear Control 2010, 20, 1140–1155. [Google Scholar] [CrossRef]
- Jadbabaie, A.; Lin, J.; Morse, A.S. Coordination of groups of mobile autonomous agents using nearest neighbor rules. IEEE Trans. Autom. Control 2003, 48, 968–969. [Google Scholar]
- Lin, Z.; Broucke, M.; Francis, B. Local control strategies for groups of mobile autonomous agents. IEEE Trans. Autom. Control 2004, 49, 622–629. [Google Scholar] [CrossRef]
- Olfati-Saber, R. Flocking for multi-agent dynamic systems: Algorithms and theory. IEEE Trans. Autom. Control 2006, 51, 401–420. [Google Scholar] [CrossRef]
- Sun, Y. Stability analysis of flocking for multi-agent dynamic systems. Nonlinear Anal. Real World Appl. 2013, 14, 1075–1081. [Google Scholar] [CrossRef]
- Soysal, O.; Sahin, E. Probabilistic Aggregation Strategies in Swarm Robotics Systems. In Proceedings of the 2005 IEEE Swarm Intelligence Symposium, Pasadena, CA, USA, 8–10 June 2005. [Google Scholar]
- Liu, W.; Winfield, A.F.; Sa, J.; Chen, J.; Dou, L. Towards energy optimisation: Emergent task allocation in a swarm of foraging robots. Adapt. Behav. 2007, 15, 289–305. [Google Scholar] [CrossRef]
- Brambilla, M.; Pinciroli, C.; Birattari, M.; Dorigo, M. Property-driven design for swarm robotics. In Proceedings of the 11th International Conference on Autonomous Agents and Multiagent Systems, Valencia, Spain, 4–8 June 2012. [Google Scholar]
- Ducatelle, F.; Di Caro, G.A.; Pinciroli, C.; Gambardella, L.M. Self-organized cooperation between robotic swarms. Swarm Intell. 2011, 5, 73–96. [Google Scholar] [CrossRef]
- Smith, S.L.; Broucke, M.E.; Francis, B.A. Curve Shortening and Rendezvous Problem for Mobile Autonomous Robots. IEEE Trans. Autom. Control 2007, 52, 1154–1159. [Google Scholar] [CrossRef]
- Lin, J.; Morse, A.S.; Anderson, B.D.O. The Multi-Agent Rendezvous Problem. Part 1: The Synchronous Case. SIAM J. Control Optim. 2007, 46, 2096–2119. [Google Scholar] [CrossRef]
- Lin, J.; Morse, A.S.; Anderson, B.D.O. The Multi-Agent Rendezvous Problem. Part 2: The Asynchronous Case. SIAM J. Control Optim. 2004, 46, 2120–2147. [Google Scholar] [CrossRef]
- Lin, J.; Morse, A.S.; Anderson, B.D.O. The multi-agent rendezvous problem—The asynchronous case. In Proceedings of the 43rd IEEE Conference on Decision and Control, Nassau, Bahamas, 14–17 December 2004; Volume 2, pp. 1926–1931. [Google Scholar]
- Ren, W.; Cao, Y. Distributed Coordination of Multi-Agent Networks: Emergent Problems, Models and Issues; Springer: New York, NY, USA, 2010. [Google Scholar]
- Laman, G. On Graphs and Rigidity of Plane Skeletal Structures. J. Eng. Math. 1970, 4, 331–340. [Google Scholar] [CrossRef]
- Hendrickx, J.M.; Anderson, B.D.O.; Delvenne, J.C.; Blondel, V.D. Directed graphs for the analysis of rigidity and persistence in autonomous agent systems. Int. J. Robust Nonlinear Control 2007, 17, 960–981. [Google Scholar] [CrossRef]
- Oh, K.K.; Park, M.C.; Ahn, H.S. A survey of multi-agent formation control. Automatica 2014, 53, 424–440. [Google Scholar] [CrossRef]
- Ren, W. Multi-vehicle consensus with a time-varying reference state. Syst. Control Lett. 2007, 56, 474–483. [Google Scholar] [CrossRef]
- Dong, W.; Farrell, J.A. Consensus of multiple nonholonomic systems. In Proceedings of the 47th IEEE Conference on Decision and Control, Cancun, Mexico, 9–11 December 2008; No. 2. pp. 2270–2275. [Google Scholar]
- Coogan, S.; Arcak, M. Scaling the size of a formation using relative position feedback. Automatica 2012, 48, 2677–2685. [Google Scholar] [CrossRef]
- Wen, G.; Duan, Z.; Chen, G.; Theory, A.G. Distributed Consensus of Multi-Agent Systems with General Linear Node Dynamics through Intermittent Communications. In Proceedings of the 24th Chinese Control and Decision Conference (CCDC), Taiyuan, China, 23–25 May 2012; pp. 1–5. [Google Scholar]
- Coogan, S.; Arcak, M.; Egerstedt, M. Scaling the size of a multiagent formation via distributed feedback. In Proceedings of the 50th IEEE Conference on Decision and Control and European Control Conference (CDC-ECC), Orlando, FL, USA, 12–15 December 2011; pp. 994–999. [Google Scholar]
- Fax, J.A.; Murray, R.M. Information Flow and Cooperative Control of Vehicle Formations. IEEE Trans. Autom. Control 2004, 49, 1465–1476. [Google Scholar] [CrossRef]
- Martini, S.; Fagiolini, A.; Zichittella, G.; Egerstedt, M.; Bicchi, A. Decentralized classification in societies of autonomous and heterogenous robots. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011; pp. 32–39. [Google Scholar]
- Kang, S.; Park, M.; Lee, B.; Ahn, H.; Graph, A. Distance-based Formation Control with a Single Moving Leader. In Proceedings of the American Control Conference (ACC), Portland, OR, USA, 4–6 June 2014. [Google Scholar]
- Abbas, W.; Egerstedt, M. Robust Graph Topologies for Networked Systems. IFAC Proc. Vol. 2012, 45, 85–90. [Google Scholar] [CrossRef]
- Pavone, M.; Frazzoli, E. Decentralized policies for geometric pattern formation. In Proceedings of the American Control Conference (ACC), New York, NY, USA, 9–13 July 2007; pp. 3949–3954. [Google Scholar]
- Meng, Y.; Guo, H.; Jin, Y. A morphogenetic approach to flexible and robust shape formation for swarm robotic systems. Robot. Auton. Syst. 2013, 61, 25–38. [Google Scholar] [CrossRef] [Green Version]
- Cao, M.; Yu, C.; Anderson, B.D.O. Formation control using range-only measurements. Automatica 2011, 47, 776–781. [Google Scholar] [CrossRef]
- Cucker, F.; Dong, J.G. A general collision-avoiding flocking framework. IEEE Trans. Autom. Control 2011, 56, 1124–1129. [Google Scholar] [CrossRef]
- Hernandez, S.; Paley, D.A. Three-dimensional motion coordination in a spatiotemporal flowfield. IEEE Trans. Autom. Control 2010, 55, 2805–2810. [Google Scholar] [CrossRef]
- Hu, J.; Feng, G. Distributed tracking control of leader-follower multi-agent systems under noisy measurement. Automatica 2010, 46, 1382–1387. [Google Scholar] [CrossRef]
- Ren, W. Distributed cooperative attitude synchronization and tracking for multiple rigid bodies. IEEE Trans. Control Syst. Technol. 2010, 18, 383–392. [Google Scholar] [CrossRef]
- Wang, X.; Hong, Y.; Huang, J.; Jiang, Z. A Distributed Control Approach to Robust Output Regulation of Networked Linear Systems. IEEE Trans. Autom. Control 2010, 55, 1853–1857. [Google Scholar] [CrossRef]
- Cao, Y.; Ren, W. Distributed coordinated tracking with reduced interaction via a variable structure approach. IEEE Trans. Autom. Control 2012, 57, 33–48. [Google Scholar]

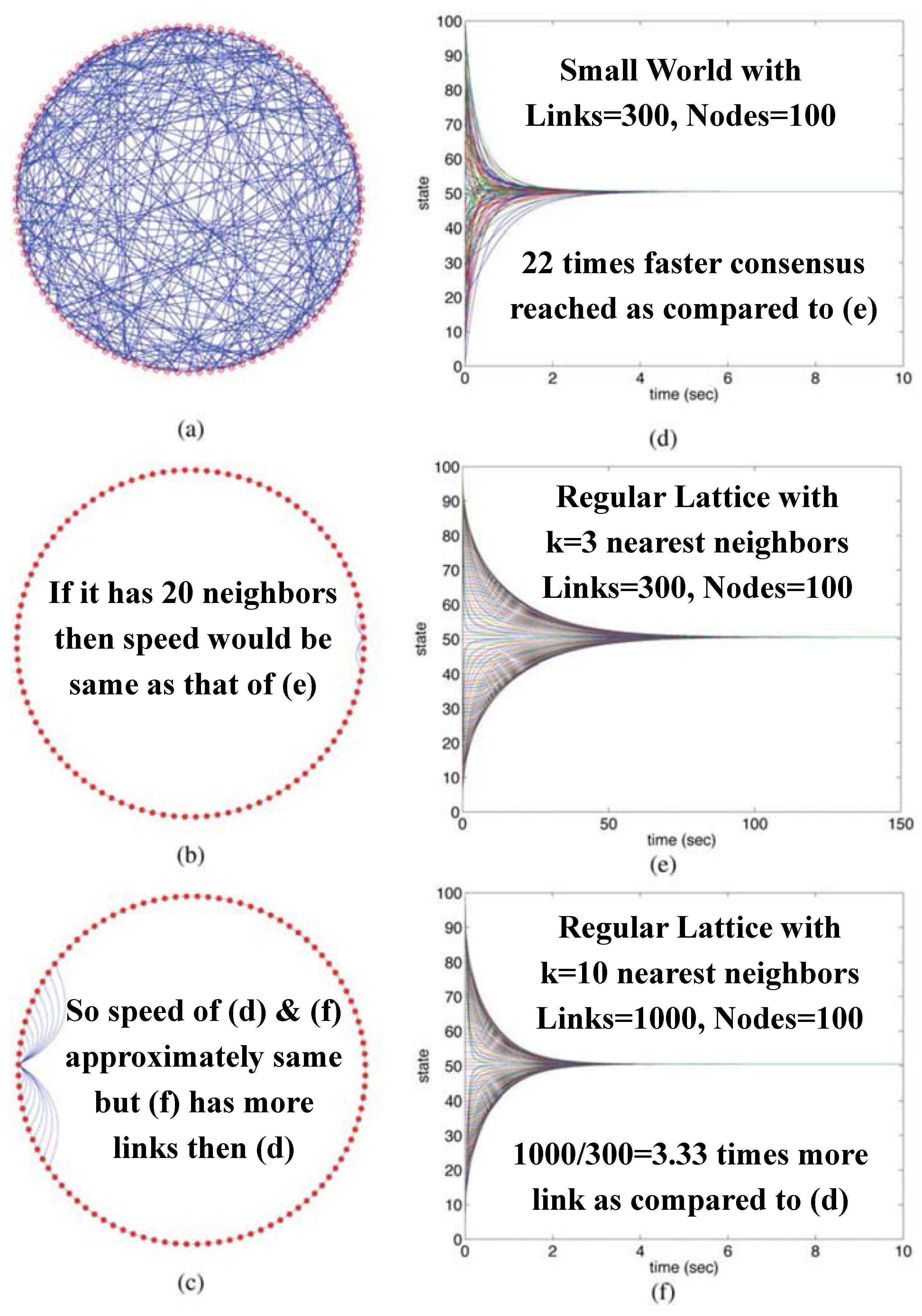
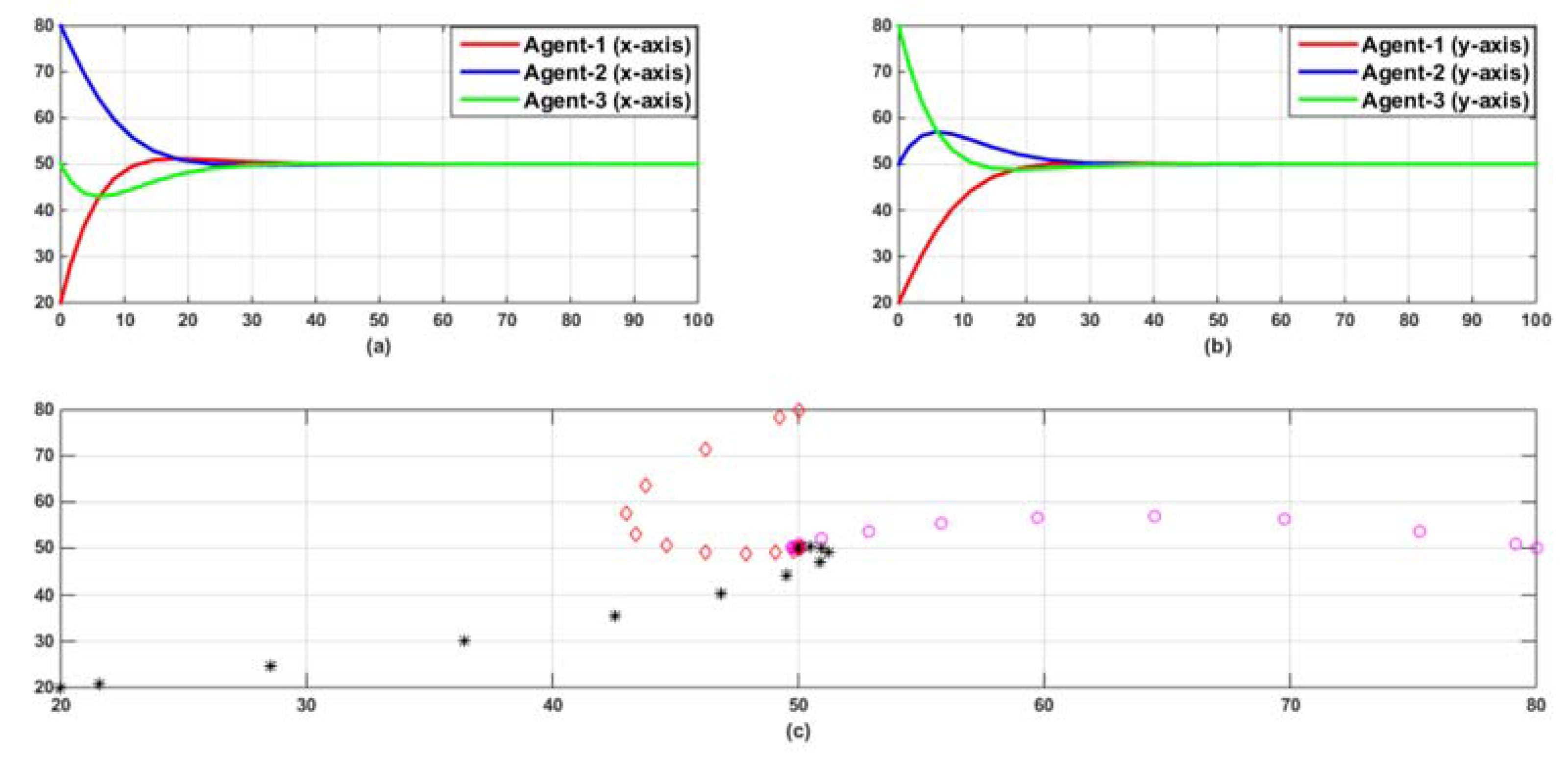
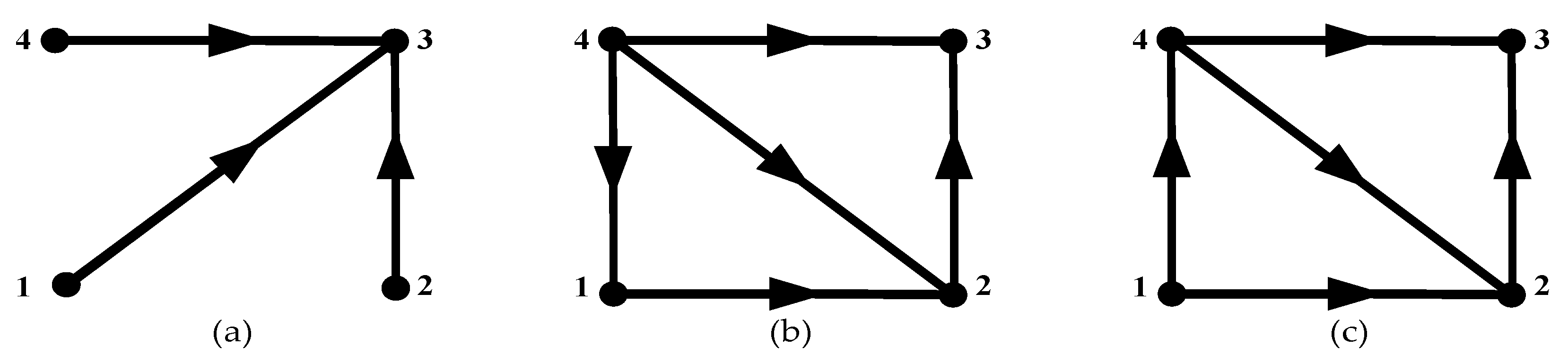
| Continuous | Discrete | |
|---|---|---|
| Dynamics | ||
| Key Matrix | ||
| Eigen Value |
| Protocol | Source | |
|---|---|---|
| Consensus | [20,26,70,71] | |
| Flocking | [5,8,9,72,73] | |
| Swarming | [74,75,76,77] |
| Position-Based | Displacement-Based | Distance-Based | |
|---|---|---|---|
| Sensed Variables | Positions of agents | Relative positions of neighbors | Relative positions of neighbors |
| Controller Variables | Positions of agents | Relative positions of neighbors | Inter-agent distance |
| Coordinate System | A global coordinate system | Orientation aligned local coordinate systems | Local Coordinate systems |
| Interaction Topology | Usually not required | Connectedness or existence of spanning tree | Rigidity or persistence |
| Sensing Capabilities Formation Control | Strengths | Bottlenecks | References |
|---|---|---|---|
| Position-based | • Easy to implement • Simple mechanism | Costly because GPS system is required | [86,87,88] |
| Displacement-based | • Spanning tree required for directed network • Connectedness required for undirected network | Orientation aligned local coordinate system | [20,89,90,92] |
| Distance-based | • Less sensing capabilities required • Less global information required | Complicated because system is non-linear | [93,94] |
| Time-Varying Formation Control | Control Objective | Methodologies | References |
|---|---|---|---|
| Formation Producing | Pre-specified pattern without a group reference | Matrix theory, Lyapunov, Graph rigidity, Receding horizon approach, Leaderless flocking, Inverse agreement problem, Circulation formation | [96,97,98,99] |
| Formation Tracking | Pre-specified pattern with a particular group reference | Matrix theory, Lyapunov, Gradient-based function, Variable structural based law | [100,101,102,103] |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gulzar, M.M.; Rizvi, S.T.H.; Javed, M.Y.; Munir, U.; Asif, H. Multi-Agent Cooperative Control Consensus: A Comparative Review. Electronics 2018, 7, 22. https://doi.org/10.3390/electronics7020022
Gulzar MM, Rizvi STH, Javed MY, Munir U, Asif H. Multi-Agent Cooperative Control Consensus: A Comparative Review. Electronics. 2018; 7(2):22. https://doi.org/10.3390/electronics7020022
Chicago/Turabian StyleGulzar, Muhammad Majid, Syed Tahir Hussain Rizvi, Muhammad Yaqoob Javed, Umer Munir, and Haleema Asif. 2018. "Multi-Agent Cooperative Control Consensus: A Comparative Review" Electronics 7, no. 2: 22. https://doi.org/10.3390/electronics7020022
APA StyleGulzar, M. M., Rizvi, S. T. H., Javed, M. Y., Munir, U., & Asif, H. (2018). Multi-Agent Cooperative Control Consensus: A Comparative Review. Electronics, 7(2), 22. https://doi.org/10.3390/electronics7020022







