Adaptive Block-Based Approach to Image Noise Level Estimation in the SVD Domain
Abstract
1. Introduction
2. Noise Level Estimation in the SVD Domain
3. Proposed Adaptive Block-Based Noise Level Estimation Algorithm in the SVD Domain
3.1. Overview of the Proposed Noise Level Estimation Algorithm in the SVD Domain
- (1)
- Tessellate an input image into r × r blocks.
- (2)
- Randomly select 40% of blocks and perform the singular value decomposition on each block to obtain a sequence of singular values , where i = 1, 2, … r, and j denotes the block index, where j = 1, … D. Here, D represents a total number of selected blocks.
- (3)
- Each image block is processed via a sequence of steps presented in Figure 2. For each jth block of image A, the average value of the singular value tail is evaluated using (2) to obtain (M). The singular value tail length is set to M = 0.75r. An AWGN with deviation is added to the selected image patches to obtain a new set of image patches that are now associated with the image B. For each jth block of image B, the average value of the singular value tail is evaluated using (3) to obtain (M). From each jth block, a noise level estimate is obtained using (4). The initial noise level estimate for the entire image is obtained as the average value of D independent noise level estimates. Each of these D noise level estimates is associated with one image block. These estimates are obtained using the initialized singular value length M and parameter values. This denotes the end of the first stage of the proposed noise level estimation algorithm.
- (4)
- If the coarse noise level estimate, obtained in the first stage of the proposed noise level estimation algorithm, is below a specified threshold for a give block size, the algorithm enters the second stage. Otherwise, the algorithm is terminated, and the final noise level estimate is equated to the initial noise level estimate.
- (5)
- The second stage of the proposed algorithm adopts the following results from the first stage: (i), (i) and .
- (6)
- The length of the singular value tail is adjusted according to the initial noise level estimate. A simple function is proposed to define the relationship between the adjusted M′ value and the initial noise levels estimate Here, the apostrophe is placed next to the variable to denote that the variable has been adjusted in the second stage of the algorithm.
- (7)
- Parameter is adjusted based on the modified singular value tail length M′.
- (8)
- (M′) and (M′) are evaluated using the adjusted singular value tail length M′ and Equations (2) and (3), respectively. Furthermore, the singular value sequences (i), (i) are adopted from the first stage and thus, the singular value decomposition is avoided in the second stage of the algorithm.
- (9)
- From each jth block, a noise level estimate is obtain using (4) and the adjusted parameter . The final noise level estimate for the entire image is obtained as the average of D independent noise level estimates, where each estimate is associated with one image block. The individual estimates are based on the adjusted singular value tail length M′ and the adjusted parameter . This denotes the end of the second stage of the algorithm.
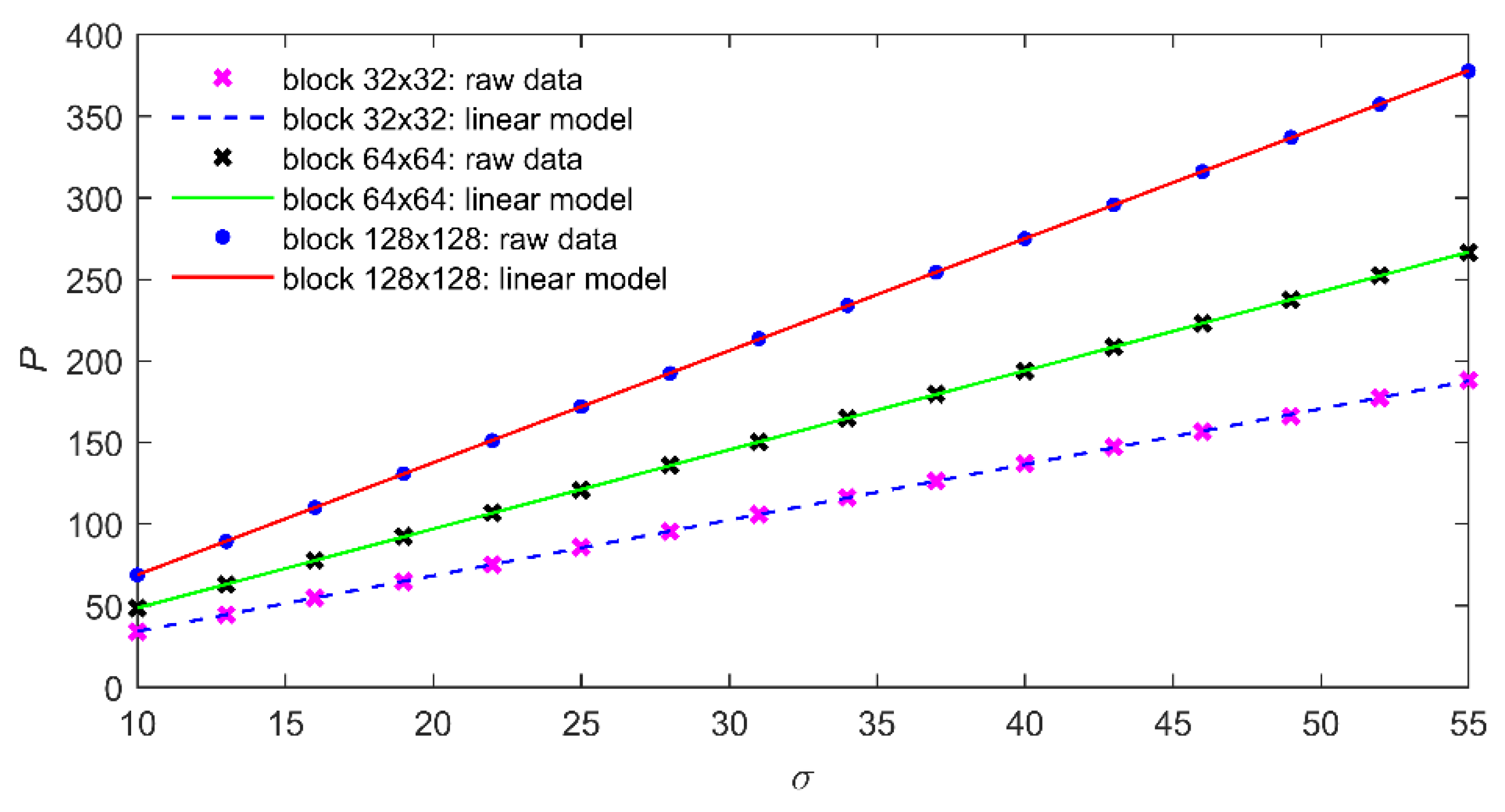
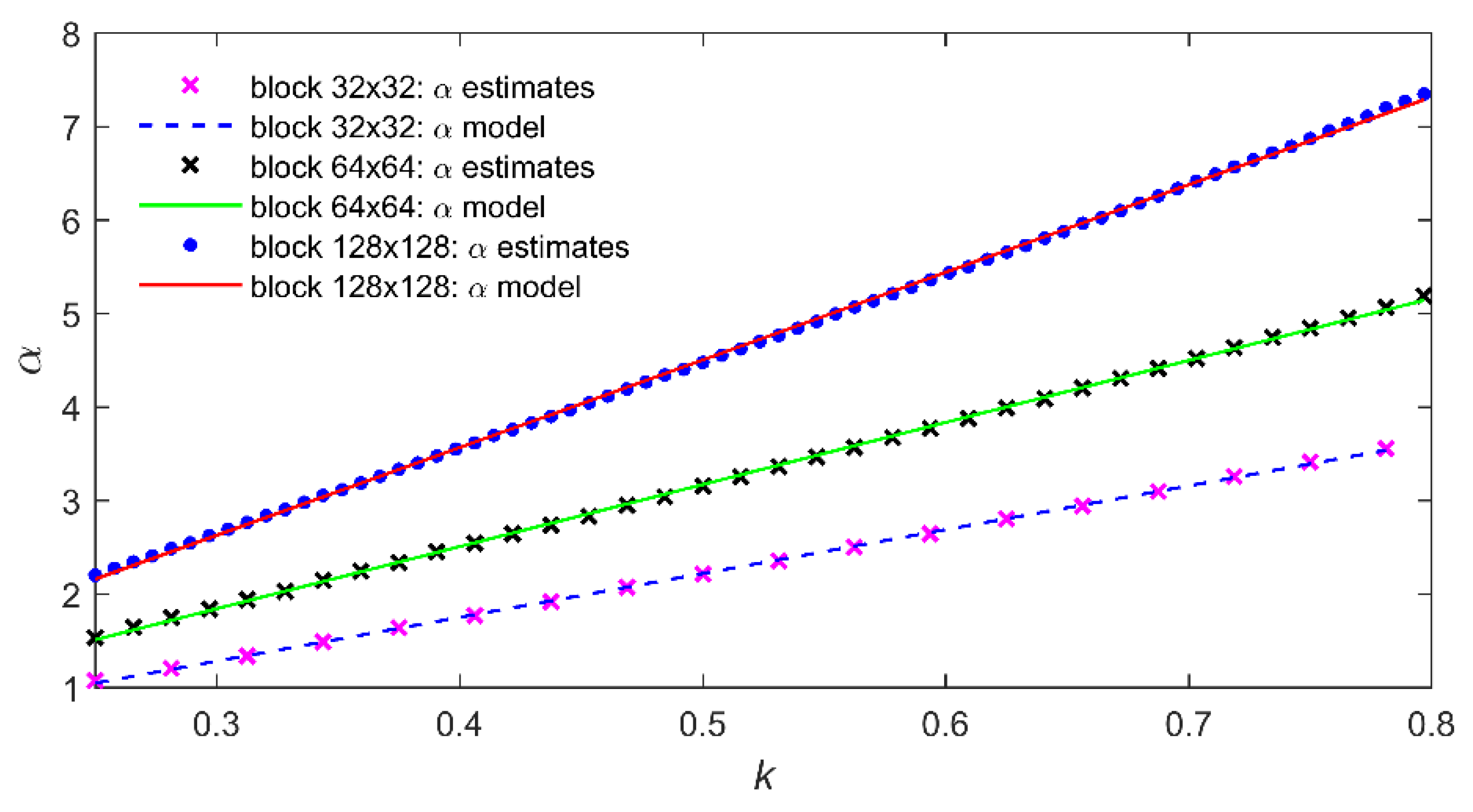
3.2. Determining the Value of the Slope Paramter α
3.3. Adjusting the Singular Value Tail Length Based on the Initial Noise Level Estimates
4. Results and Discussion
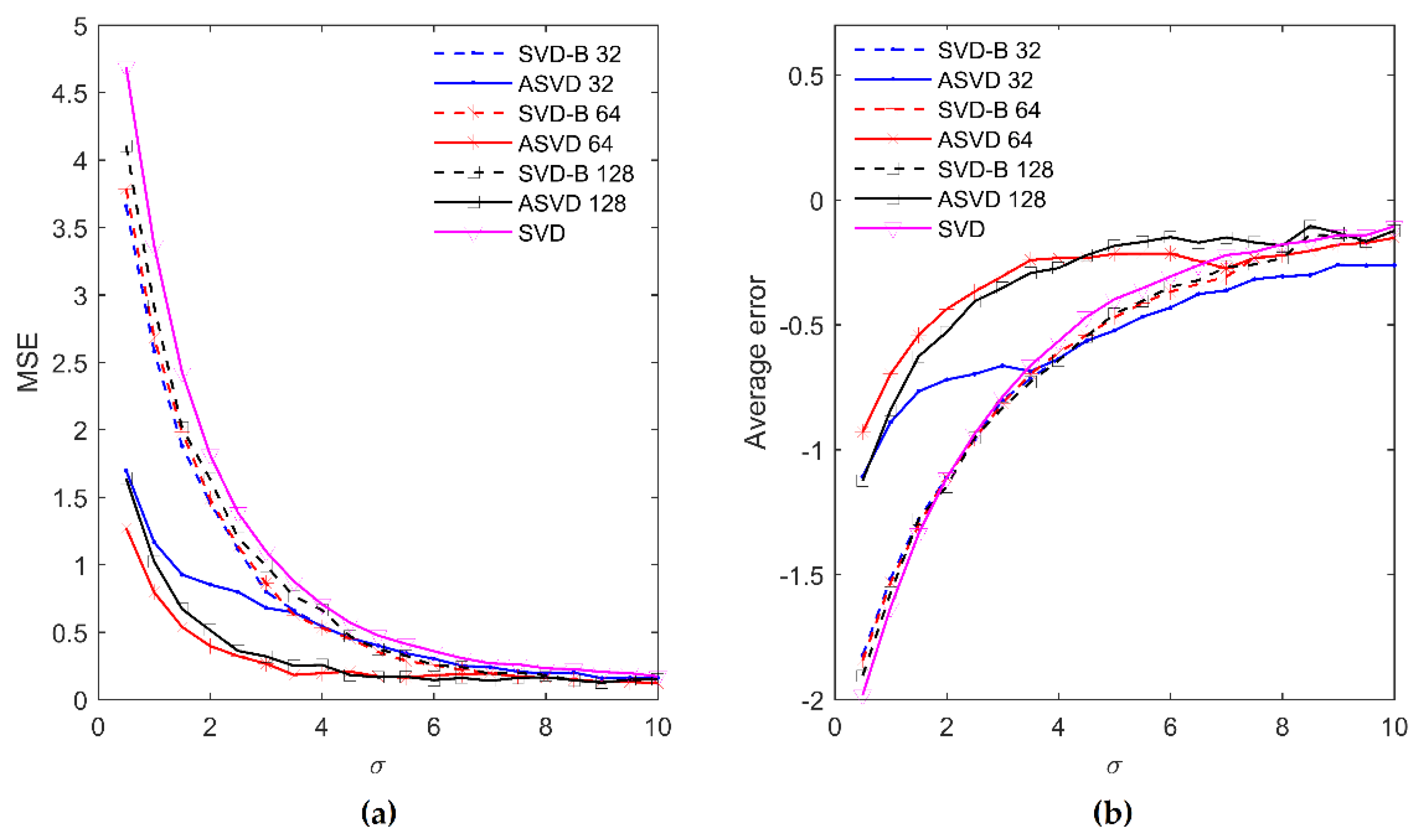
4.1. MSE and Average Noise Level Estimation Error
4.2. Computational Time
5. Conclusions
Supplementary Materials
Funding
Conflicts of Interest
Appendix A
| Noise Level, | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 | 4.5 | 5.0 | 5.5 | 6.0 | 6.5 | 7.0 | 7.5 | 8.0 | 8.5 | 9.0 | 9.5 | 10.0 | |
| 0.250 | 1.050 | 1.155 | 0.875 | 0.932 | 1.002 | 1.101 | 0.675 | 0.653 | 0.748 | 0.677 | 0.606 | 0.569 | 0.657 | 1.024 | 0.769 | 0.589 | 0.707 | 0.756 | 0.470 | 0.513 |
| 0.266 | 1.291 | 0.985 | 0.865 | 0.862 | 0.715 | 0.719 | 0.849 | 0.656 | 0.660 | 0.579 | 0.832 | 0.837 | 0.533 | 0.592 | 0.794 | 0.614 | 0.501 | 0.425 | 0.552 | 0.492 |
| 0.281 | 1.177 | 1.201 | 0.895 | 0.868 | 0.804 | 0.737 | 0.679 | 0.442 | 0.759 | 0.795 | 0.520 | 0.641 | 0.587 | 0.512 | 0.728 | 0.508 | 0.617 | 0.528 | 0.596 | 0.481 |
| 0.297 | 1.200 | 1.037 | 0.864 | 0.672 | 0.678 | 0.798 | 0.653 | 0.584 | 0.762 | 0.556 | 0.680 | 0.464 | 0.662 | 0.437 | 0.462 | 0.516 | 0.532 | 0.593 | 0.460 | 0.591 |
| 0.313 | 1.271 | 1.000 | 0.662 | 0.797 | 0.703 | 0.614 | 0.841 | 0.457 | 0.625 | 0.613 | 0.682 | 0.644 | 0.498 | 0.457 | 0.539 | 0.518 | 0.549 | 0.456 | 0.557 | 0.548 |
| 0.328 | 1.093 | 0.900 | 0.799 | 0.854 | 0.912 | 0.672 | 0.756 | 0.656 | 0.640 | 0.567 | 0.536 | 0.759 | 0.549 | 0.523 | 0.722 | 0.668 | 0.729 | 0.642 | 0.505 | 0.400 |
| 0.344 | 0.963 | 1.162 | 0.743 | 0.789 | 0.565 | 0.616 | 0.561 | 0.367 | 0.649 | 0.474 | 0.456 | 0.466 | 0.396 | 0.540 | 0.427 | 0.381 | 0.484 | 0.536 | 0.487 | 0.431 |
| 0.359 | 1.151 | 0.990 | 0.778 | 0.934 | 0.607 | 0.685 | 0.643 | 0.648 | 0.613 | 0.767 | 0.692 | 0.561 | 0.604 | 0.394 | 0.535 | 0.563 | 0.446 | 0.624 | 0.517 | 0.383 |
| 0.375 | 1.173 | 0.942 | 0.673 | 0.720 | 0.593 | 0.573 | 0.718 | 0.630 | 0.462 | 0.525 | 0.578 | 0.576 | 0.525 | 0.412 | 0.487 | 0.458 | 0.472 | 0.420 | 0.327 | 0.396 |
| 0.391 | 1.110 | 0.939 | 0.844 | 0.741 | 0.635 | 0.702 | 0.540 | 0.514 | 0.488 | 0.569 | 0.498 | 0.474 | 0.426 | 0.460 | 0.431 | 0.413 | 0.559 | 0.542 | 0.439 | 0.370 |
| 0.406 | 1.140 | 1.051 | 0.696 | 0.784 | 0.669 | 0.563 | 0.575 | 0.596 | 0.577 | 0.445 | 0.589 | 0.512 | 0.553 | 0.502 | 0.515 | 0.401 | 0.464 | 0.385 | 0.447 | 0.427 |
| 0.422 | 1.198 | 0.976 | 0.662 | 0.658 | 0.773 | 0.763 | 0.533 | 0.488 | 0.554 | 0.540 | 0.601 | 0.392 | 0.501 | 0.468 | 0.430 | 0.530 | 0.334 | 0.497 | 0.373 | 0.480 |
| 0.438 | 1.108 | 0.856 | 0.714 | 0.822 | 0.701 | 0.686 | 0.623 | 0.553 | 0.792 | 0.484 | 0.486 | 0.461 | 0.373 | 0.442 | 0.651 | 0.438 | 0.439 | 0.418 | 0.428 | 0.426 |
| 0.453 | 1.080 | 0.983 | 0.697 | 0.750 | 0.626 | 0.683 | 0.527 | 0.583 | 0.486 | 0.566 | 0.374 | 0.460 | 0.458 | 0.346 | 0.452 | 0.329 | 0.427 | 0.412 | 0.354 | 0.362 |
| 0.469 | 1.121 | 0.826 | 0.779 | 0.652 | 0.679 | 0.552 | 0.632 | 0.586 | 0.625 | 0.470 | 0.477 | 0.447 | 0.476 | 0.374 | 0.387 | 0.397 | 0.366 | 0.419 | 0.406 | 0.261 |
| 0.484 | 1.390 | 0.927 | 0.766 | 0.610 | 0.525 | 0.571 | 0.361 | 0.430 | 0.471 | 0.486 | 0.446 | 0.528 | 0.357 | 0.445 | 0.362 | 0.333 | 0.390 | 0.368 | 0.234 | 0.325 |
| 0.500 | 1.198 | 0.922 | 0.731 | 0.637 | 0.681 | 0.570 | 0.608 | 0.617 | 0.529 | 0.458 | 0.453 | 0.488 | 0.454 | 0.549 | 0.357 | 0.429 | 0.416 | 0.311 | 0.463 | 0.329 |
| 0.516 | 1.179 | 0.903 | 0.732 | 0.655 | 0.597 | 0.585 | 0.578 | 0.391 | 0.496 | 0.583 | 0.458 | 0.381 | 0.456 | 0.486 | 0.402 | 0.357 | 0.404 | 0.379 | 0.385 | 0.342 |
| 0.531 | 1.306 | 0.818 | 0.753 | 0.553 | 0.618 | 0.608 | 0.486 | 0.468 | 0.475 | 0.599 | 0.426 | 0.463 | 0.475 | 0.482 | 0.463 | 0.453 | 0.420 | 0.464 | 0.337 | 0.384 |
| 0.547 | 1.254 | 0.849 | 0.728 | 0.596 | 0.619 | 0.606 | 0.581 | 0.595 | 0.597 | 0.505 | 0.452 | 0.467 | 0.456 | 0.437 | 0.379 | 0.402 | 0.441 | 0.348 | 0.349 | 0.342 |
| 0.563 | 1.364 | 0.958 | 0.725 | 0.713 | 0.524 | 0.524 | 0.495 | 0.390 | 0.466 | 0.422 | 0.481 | 0.442 | 0.327 | 0.297 | 0.468 | 0.299 | 0.335 | 0.318 | 0.235 | 0.305 |
| 0.578 | 1.423 | 1.047 | 0.769 | 0.675 | 0.535 | 0.591 | 0.481 | 0.433 | 0.495 | 0.455 | 0.488 | 0.422 | 0.322 | 0.420 | 0.442 | 0.448 | 0.321 | 0.422 | 0.340 | 0.347 |
| 0.594 | 1.460 | 1.075 | 0.825 | 0.613 | 0.490 | 0.501 | 0.475 | 0.542 | 0.505 | 0.395 | 0.497 | 0.362 | 0.367 | 0.368 | 0.350 | 0.326 | 0.377 | 0.310 | 0.210 | 0.319 |
| 0.609 | 1.558 | 1.021 | 0.872 | 0.572 | 0.587 | 0.429 | 0.481 | 0.430 | 0.441 | 0.505 | 0.472 | 0.355 | 0.469 | 0.349 | 0.404 | 0.305 | 0.330 | 0.324 | 0.279 | 0.310 |
| 0.625 | 1.680 | 1.235 | 0.904 | 0.688 | 0.622 | 0.457 | 0.448 | 0.475 | 0.501 | 0.409 | 0.460 | 0.352 | 0.358 | 0.368 | 0.312 | 0.296 | 0.304 | 0.305 | 0.284 | 0.261 |
| 0.641 | 1.725 | 1.202 | 0.875 | 0.754 | 0.584 | 0.513 | 0.481 | 0.440 | 0.460 | 0.414 | 0.370 | 0.418 | 0.369 | 0.349 | 0.308 | 0.316 | 0.300 | 0.269 | 0.335 | 0.264 |
| 0.656 | 2.288 | 1.360 | 1.073 | 0.881 | 0.675 | 0.542 | 0.518 | 0.496 | 0.407 | 0.421 | 0.408 | 0.459 | 0.313 | 0.284 | 0.260 | 0.303 | 0.283 | 0.265 | 0.209 | 0.226 |
| 0.672 | 1.881 | 1.552 | 1.025 | 0.743 | 0.584 | 0.572 | 0.417 | 0.471 | 0.366 | 0.390 | 0.326 | 0.390 | 0.294 | 0.358 | 0.312 | 0.324 | 0.301 | 0.244 | 0.243 | 0.273 |
| 0.688 | 2.345 | 1.645 | 1.212 | 0.843 | 0.735 | 0.572 | 0.498 | 0.416 | 0.432 | 0.425 | 0.383 | 0.336 | 0.327 | 0.316 | 0.304 | 0.272 | 0.273 | 0.289 | 0.249 | 0.270 |
| 0.703 | 2.855 | 1.853 | 1.505 | 1.094 | 0.871 | 0.627 | 0.537 | 0.528 | 0.432 | 0.387 | 0.451 | 0.327 | 0.385 | 0.328 | 0.262 | 0.280 | 0.253 | 0.256 | 0.289 | 0.221 |
| 0.719 | 3.111 | 2.289 | 1.603 | 1.135 | 0.874 | 0.747 | 0.556 | 0.584 | 0.455 | 0.464 | 0.398 | 0.292 | 0.362 | 0.320 | 0.281 | 0.270 | 0.337 | 0.236 | 0.250 | 0.286 |
| 0.734 | 3.256 | 2.427 | 1.723 | 1.406 | 1.034 | 0.835 | 0.737 | 0.604 | 0.497 | 0.463 | 0.384 | 0.314 | 0.356 | 0.304 | 0.262 | 0.328 | 0.248 | 0.316 | 0.235 | 0.243 |
| 0.750 | 3.769 | 2.573 | 1.757 | 1.389 | 1.156 | 0.851 | 0.748 | 0.666 | 0.530 | 0.469 | 0.481 | 0.381 | 0.394 | 0.310 | 0.383 | 0.292 | 0.252 | 0.266 | 0.253 | 0.259 |
| 0.766 | 3.822 | 3.091 | 2.190 | 1.892 | 1.409 | 1.140 | 0.831 | 0.613 | 0.633 | 0.557 | 0.503 | 0.485 | 0.391 | 0.396 | 0.359 | 0.366 | 0.341 | 0.339 | 0.320 | 0.266 |
| 0.781 | 5.042 | 3.726 | 3.223 | 2.417 | 1.604 | 1.348 | 1.207 | 0.892 | 0.937 | 0.673 | 0.610 | 0.536 | 0.522 | 0.456 | 0.438 | 0.472 | 0.396 | 0.357 | 0.354 | 0.411 |
| 0.797 | 5.725 | 4.606 | 3.424 | 2.460 | 2.190 | 1.863 | 1.382 | 1.224 | 1.050 | 0.920 | 0.755 | 0.691 | 0.511 | 0.508 | 0.410 | 0.507 | 0.421 | 0.363 | 0.386 | 0.287 |
| Noise Level, | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 | 4.5 | 5.0 | 5.5 | 6.0 | 6.5 | 7.0 | 7.5 | 8.0 | 8.5 | 9.0 | 9.5 | 10.0 | |
| 0.250 | 1.110 | 1.208 | 1.045 | 0.901 | 0.899 | 0.912 | 1.177 | 0.968 | 0.777 | 0.971 | 0.877 | 0.979 | 0.685 | 0.681 | 0.892 | 1.019 | 0.958 | 0.963 | 1.047 | 1.118 |
| 0.266 | 1.062 | 0.977 | 0.765 | 0.813 | 0.712 | 0.622 | 0.831 | 0.525 | 0.586 | 0.660 | 0.568 | 0.704 | 0.502 | 0.601 | 0.784 | 0.524 | 0.440 | 0.590 | 0.485 | 0.493 |
| 0.281 | 1.326 | 1.211 | 0.877 | 0.782 | 0.560 | 0.599 | 0.677 | 0.647 | 0.418 | 0.502 | 0.460 | 0.504 | 0.525 | 0.532 | 0.364 | 0.371 | 0.422 | 0.362 | 0.425 | 0.429 |
| 0.297 | 1.010 | 0.935 | 0.564 | 0.551 | 0.678 | 0.645 | 0.693 | 0.621 | 0.479 | 0.544 | 0.513 | 0.536 | 0.561 | 0.465 | 0.660 | 0.490 | 0.551 | 0.612 | 0.470 | 0.482 |
| 0.313 | 1.034 | 0.847 | 0.738 | 0.758 | 0.589 | 0.661 | 0.590 | 0.590 | 0.710 | 0.500 | 0.588 | 0.437 | 0.446 | 0.636 | 0.413 | 0.548 | 0.653 | 0.435 | 0.435 | 0.368 |
| 0.328 | 1.018 | 0.900 | 0.795 | 0.620 | 0.880 | 0.920 | 0.750 | 0.646 | 0.768 | 0.922 | 0.759 | 0.680 | 0.598 | 0.816 | 0.628 | 0.703 | 0.740 | 0.639 | 0.636 | 0.736 |
| 0.344 | 1.014 | 0.889 | 0.748 | 0.762 | 0.622 | 0.522 | 0.623 | 0.531 | 0.503 | 0.485 | 0.399 | 0.418 | 0.481 | 0.500 | 0.392 | 0.547 | 0.376 | 0.467 | 0.424 | 0.410 |
| 0.359 | 1.089 | 0.842 | 0.655 | 0.597 | 0.582 | 0.531 | 0.452 | 0.468 | 0.662 | 0.464 | 0.470 | 0.523 | 0.397 | 0.586 | 0.402 | 0.362 | 0.591 | 0.422 | 0.346 | 0.328 |
| 0.375 | 1.087 | 0.875 | 0.585 | 0.655 | 0.601 | 0.735 | 0.647 | 0.582 | 0.518 | 0.601 | 0.607 | 0.558 | 0.565 | 0.491 | 0.555 | 0.532 | 0.566 | 0.418 | 0.592 | 0.448 |
| 0.391 | 1.235 | 0.882 | 0.762 | 0.635 | 0.615 | 0.614 | 0.502 | 0.399 | 0.339 | 0.450 | 0.348 | 0.452 | 0.318 | 0.355 | 0.345 | 0.323 | 0.330 | 0.364 | 0.303 | 0.385 |
| 0.406 | 0.998 | 0.606 | 0.729 | 0.682 | 0.514 | 0.535 | 0.615 | 0.679 | 0.502 | 0.597 | 0.510 | 0.348 | 0.600 | 0.462 | 0.495 | 0.436 | 0.448 | 0.363 | 0.500 | 0.420 |
| 0.422 | 0.978 | 0.690 | 0.607 | 0.566 | 0.615 | 0.514 | 0.530 | 0.644 | 0.436 | 0.513 | 0.530 | 0.565 | 0.458 | 0.466 | 0.384 | 0.386 | 0.320 | 0.506 | 0.407 | 0.405 |
| 0.438 | 0.981 | 0.701 | 0.691 | 0.676 | 0.645 | 0.623 | 0.677 | 0.662 | 0.615 | 0.641 | 0.683 | 0.651 | 0.587 | 0.478 | 0.538 | 0.512 | 0.532 | 0.598 | 0.438 | 0.401 |
| 0.453 | 0.913 | 0.734 | 0.804 | 0.832 | 0.695 | 0.870 | 0.817 | 0.755 | 0.648 | 0.636 | 0.660 | 0.842 | 0.754 | 0.653 | 0.626 | 0.781 | 0.684 | 0.666 | 0.664 | 0.453 |
| 0.469 | 1.122 | 0.775 | 0.671 | 0.542 | 0.564 | 0.557 | 0.503 | 0.421 | 0.563 | 0.425 | 0.344 | 0.388 | 0.467 | 0.354 | 0.304 | 0.294 | 0.362 | 0.339 | 0.363 | 0.395 |
| 0.484 | 1.022 | 0.764 | 0.678 | 0.617 | 0.615 | 0.714 | 0.641 | 0.655 | 0.613 | 0.559 | 0.611 | 0.634 | 0.553 | 0.497 | 0.642 | 0.599 | 0.561 | 0.524 | 0.452 | 0.462 |
| 0.500 | 1.082 | 0.857 | 0.641 | 0.594 | 0.522 | 0.445 | 0.519 | 0.472 | 0.442 | 0.405 | 0.397 | 0.386 | 0.373 | 0.418 | 0.340 | 0.413 | 0.304 | 0.359 | 0.412 | 0.344 |
| 0.516 | 0.993 | 0.764 | 0.718 | 0.577 | 0.591 | 0.520 | 0.586 | 0.525 | 0.474 | 0.472 | 0.487 | 0.596 | 0.567 | 0.446 | 0.469 | 0.386 | 0.462 | 0.479 | 0.403 | 0.455 |
| 0.531 | 1.385 | 0.973 | 0.591 | 0.611 | 0.523 | 0.579 | 0.572 | 0.461 | 0.468 | 0.467 | 0.369 | 0.418 | 0.350 | 0.284 | 0.320 | 0.329 | 0.338 | 0.327 | 0.387 | 0.249 |
| 0.547 | 1.199 | 0.881 | 0.644 | 0.575 | 0.545 | 0.428 | 0.469 | 0.359 | 0.331 | 0.376 | 0.375 | 0.358 | 0.350 | 0.352 | 0.373 | 0.405 | 0.430 | 0.341 | 0.348 | 0.289 |
| 0.563 | 1.242 | 0.981 | 0.691 | 0.551 | 0.471 | 0.472 | 0.471 | 0.434 | 0.471 | 0.437 | 0.442 | 0.382 | 0.355 | 0.345 | 0.370 | 0.358 | 0.381 | 0.330 | 0.337 | 0.286 |
| 0.578 | 1.310 | 0.980 | 0.716 | 0.552 | 0.500 | 0.551 | 0.403 | 0.435 | 0.347 | 0.421 | 0.353 | 0.366 | 0.403 | 0.295 | 0.339 | 0.323 | 0.374 | 0.342 | 0.261 | 0.242 |
| 0.594 | 1.407 | 0.940 | 0.674 | 0.556 | 0.617 | 0.501 | 0.452 | 0.424 | 0.506 | 0.413 | 0.467 | 0.399 | 0.401 | 0.381 | 0.439 | 0.296 | 0.343 | 0.294 | 0.314 | 0.355 |
| 0.609 | 1.448 | 1.009 | 0.732 | 0.551 | 0.477 | 0.438 | 0.404 | 0.406 | 0.410 | 0.380 | 0.380 | 0.399 | 0.372 | 0.410 | 0.356 | 0.341 | 0.324 | 0.342 | 0.351 | 0.368 |
| 0.625 | 1.641 | 1.100 | 0.774 | 0.627 | 0.556 | 0.469 | 0.417 | 0.399 | 0.328 | 0.401 | 0.350 | 0.352 | 0.380 | 0.350 | 0.317 | 0.301 | 0.320 | 0.260 | 0.313 | 0.296 |
| 0.641 | 1.690 | 1.142 | 0.754 | 0.568 | 0.517 | 0.459 | 0.422 | 0.430 | 0.369 | 0.347 | 0.324 | 0.377 | 0.380 | 0.322 | 0.416 | 0.310 | 0.266 | 0.274 | 0.333 | 0.251 |
| 0.656 | 1.848 | 1.290 | 0.953 | 0.674 | 0.559 | 0.440 | 0.489 | 0.405 | 0.364 | 0.303 | 0.298 | 0.330 | 0.281 | 0.299 | 0.292 | 0.293 | 0.271 | 0.222 | 0.254 | 0.263 |
| 0.672 | 1.865 | 1.162 | 0.847 | 0.615 | 0.568 | 0.456 | 0.425 | 0.421 | 0.351 | 0.351 | 0.364 | 0.304 | 0.313 | 0.313 | 0.334 | 0.269 | 0.320 | 0.248 | 0.320 | 0.274 |
| 0.688 | 1.932 | 1.285 | 0.961 | 0.727 | 0.556 | 0.459 | 0.432 | 0.379 | 0.330 | 0.327 | 0.295 | 0.329 | 0.296 | 0.308 | 0.232 | 0.273 | 0.244 | 0.272 | 0.243 | 0.240 |
| 0.703 | 2.211 | 1.462 | 0.983 | 0.797 | 0.634 | 0.471 | 0.421 | 0.400 | 0.401 | 0.338 | 0.316 | 0.367 | 0.279 | 0.288 | 0.264 | 0.248 | 0.358 | 0.274 | 0.291 | 0.232 |
| 0.719 | 2.603 | 1.725 | 1.193 | 0.954 | 0.725 | 0.515 | 0.441 | 0.388 | 0.314 | 0.304 | 0.297 | 0.257 | 0.299 | 0.262 | 0.253 | 0.250 | 0.217 | 0.240 | 0.272 | 0.312 |
| 0.734 | 2.821 | 2.059 | 1.589 | 1.180 | 0.859 | 0.647 | 0.490 | 0.507 | 0.330 | 0.367 | 0.330 | 0.286 | 0.312 | 0.295 | 0.229 | 0.226 | 0.216 | 0.231 | 0.198 | 0.233 |
| 0.750 | 3.096 | 1.935 | 1.379 | 0.961 | 0.804 | 0.676 | 0.565 | 0.412 | 0.380 | 0.335 | 0.318 | 0.292 | 0.281 | 0.272 | 0.257 | 0.240 | 0.283 | 0.238 | 0.207 | 0.211 |
| 0.766 | 3.337 | 2.191 | 1.639 | 1.193 | 0.999 | 0.715 | 0.581 | 0.477 | 0.348 | 0.360 | 0.320 | 0.278 | 0.298 | 0.280 | 0.237 | 0.231 | 0.250 | 0.226 | 0.203 | 0.252 |
| 0.781 | 3.842 | 2.709 | 2.048 | 1.414 | 1.256 | 0.897 | 0.724 | 0.533 | 0.544 | 0.442 | 0.385 | 0.291 | 0.304 | 0.270 | 0.229 | 0.210 | 0.261 | 0.191 | 0.220 | 0.202 |
| 0.797 | 4.696 | 3.692 | 2.540 | 1.904 | 1.434 | 1.203 | 1.003 | 0.859 | 0.639 | 0.578 | 0.491 | 0.439 | 0.353 | 0.336 | 0.276 | 0.259 | 0.268 | 0.264 | 0.248 | 0.227 |
| Noise Level, | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 | 4.5 | 5.0 | 5.5 | 6.0 | 6.5 | 7.0 | 7.5 | 8.0 | 8.5 | 9.0 | 9.5 | 10.0 | |
| 0.250 | 1.417 | 1.072 | 1.032 | 0.882 | 0.768 | 0.835 | 0.726 | 0.770 | 0.645 | 0.540 | 0.616 | 0.655 | 0.544 | 0.591 | 0.811 | 0.690 | 0.648 | 0.635 | 0.724 | 0.755 |
| 0.281 | 1.175 | 1.072 | 0.989 | 0.826 | 0.944 | 0.949 | 0.901 | 0.917 | 0.894 | 0.728 | 0.739 | 0.704 | 0.753 | 0.714 | 0.673 | 0.678 | 0.724 | 0.721 | 0.775 | 0.667 |
| 0.313 | 1.215 | 1.165 | 1.244 | 1.041 | 1.193 | 1.136 | 1.056 | 1.051 | 1.018 | 1.065 | 0.880 | 1.038 | 0.965 | 0.841 | 0.963 | 0.887 | 0.856 | 0.988 | 0.891 | 0.772 |
| 0.344 | 1.063 | 0.946 | 0.809 | 0.744 | 0.804 | 0.874 | 0.766 | 0.699 | 0.607 | 0.824 | 0.807 | 0.700 | 0.713 | 0.748 | 0.646 | 0.619 | 0.617 | 0.602 | 0.584 | 0.686 |
| 0.375 | 1.234 | 0.867 | 0.784 | 0.679 | 0.678 | 0.604 | 0.640 | 0.523 | 0.534 | 0.506 | 0.423 | 0.442 | 0.442 | 0.401 | 0.421 | 0.457 | 0.421 | 0.429 | 0.392 | 0.332 |
| 0.406 | 1.046 | 0.989 | 0.947 | 0.814 | 0.846 | 0.878 | 0.809 | 0.772 | 0.884 | 0.779 | 0.799 | 0.822 | 0.786 | 0.772 | 0.726 | 0.696 | 0.767 | 0.701 | 0.658 | 0.610 |
| 0.438 | 1.137 | 0.863 | 0.772 | 0.733 | 0.612 | 0.586 | 0.555 | 0.618 | 0.542 | 0.597 | 0.517 | 0.543 | 0.508 | 0.514 | 0.503 | 0.434 | 0.484 | 0.508 | 0.510 | 0.477 |
| 0.469 | 1.255 | 0.901 | 0.722 | 0.696 | 0.598 | 0.602 | 0.490 | 0.547 | 0.479 | 0.514 | 0.463 | 0.555 | 0.492 | 0.479 | 0.478 | 0.432 | 0.343 | 0.371 | 0.364 | 0.378 |
| 0.500 | 1.191 | 0.882 | 0.739 | 0.676 | 0.592 | 0.581 | 0.542 | 0.522 | 0.502 | 0.499 | 0.480 | 0.470 | 0.487 | 0.507 | 0.416 | 0.393 | 0.423 | 0.399 | 0.404 | 0.375 |
| 0.531 | 1.300 | 0.926 | 0.740 | 0.664 | 0.648 | 0.640 | 0.527 | 0.510 | 0.624 | 0.524 | 0.533 | 0.529 | 0.475 | 0.483 | 0.454 | 0.456 | 0.431 | 0.400 | 0.466 | 0.416 |
| 0.563 | 1.254 | 0.932 | 0.780 | 0.661 | 0.593 | 0.575 | 0.564 | 0.550 | 0.523 | 0.540 | 0.521 | 0.525 | 0.495 | 0.523 | 0.442 | 0.473 | 0.433 | 0.467 | 0.452 | 0.424 |
| 0.594 | 1.194 | 0.894 | 0.733 | 0.664 | 0.633 | 0.610 | 0.622 | 0.653 | 0.585 | 0.631 | 0.613 | 0.621 | 0.569 | 0.557 | 0.604 | 0.614 | 0.609 | 0.541 | 0.563 | 0.544 |
| 0.625 | 1.593 | 1.111 | 0.787 | 0.634 | 0.596 | 0.508 | 0.478 | 0.458 | 0.462 | 0.425 | 0.411 | 0.419 | 0.478 | 0.390 | 0.370 | 0.365 | 0.383 | 0.384 | 0.388 | 0.355 |
| 0.656 | 1.489 | 0.993 | 0.744 | 0.626 | 0.578 | 0.540 | 0.540 | 0.515 | 0.534 | 0.555 | 0.532 | 0.541 | 0.557 | 0.543 | 0.549 | 0.543 | 0.529 | 0.550 | 0.564 | 0.487 |
| 0.688 | 1.746 | 1.125 | 0.810 | 0.659 | 0.574 | 0.520 | 0.448 | 0.461 | 0.425 | 0.458 | 0.485 | 0.424 | 0.471 | 0.498 | 0.445 | 0.465 | 0.439 | 0.479 | 0.434 | 0.460 |
| 0.719 | 2.308 | 1.622 | 1.117 | 0.856 | 0.647 | 0.530 | 0.476 | 0.412 | 0.404 | 0.373 | 0.359 | 0.333 | 0.332 | 0.344 | 0.326 | 0.295 | 0.293 | 0.301 | 0.311 | 0.333 |
| 0.750 | 2.731 | 1.943 | 1.387 | 0.990 | 0.728 | 0.591 | 0.498 | 0.396 | 0.373 | 0.339 | 0.312 | 0.299 | 0.282 | 0.277 | 0.299 | 0.287 | 0.309 | 0.268 | 0.289 | 0.335 |
| 0.781 | 2.846 | 1.988 | 1.476 | 1.028 | 0.780 | 0.609 | 0.482 | 0.405 | 0.347 | 0.301 | 0.289 | 0.298 | 0.283 | 0.280 | 0.297 | 0.281 | 0.302 | 0.320 | 0.307 | 0.325 |
References
- Chervyakov, N.; Lyakhov, P.; Kaplun, D.; Butusov, D.; Nagornov, N. Analysis of the quantization noise in discrete wavelet transform filters for image processing. Electronics 2018, 7, 135. [Google Scholar] [CrossRef]
- Turajlic, E.; Karahodzic, V. An Adaptive Scheme for X-ray Medical Image Denoising using Artificial Neural Networks and Additive White Gaussian Noise Level Estimation in SVD Domain. In Proceedings of the International Conference on Medical and Biological Engineering (CMBEBIH 2017), Sarajevo, Bosnia and Herzegovina, 16–18 March 2017; pp. 36–40. [Google Scholar]
- Uwe, S.; Kevin, S. Bayesian deblurring with integrated noise estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2011), Colorado Springs, CO, USA, 20–25 June 2011; pp. 2625–2632. [Google Scholar]
- Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K. Image denoising by sparse 3-d transform-domain collaborative filtering. IEEE Trans. Image Process. 2007, 16, 2080–2095. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Tanaka, M.; Okutomi, M. Single-image noise level Estimation for blind denoising. IEEE Trans. Image Process. 2013, 22, 5226–5237. [Google Scholar] [CrossRef] [PubMed]
- Elder, J.H.; Zucker, S.W. Local scale control for edge detection and blur estimation. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 699–716. [Google Scholar] [CrossRef]
- Arbelaez, P.; Maire, M.; Fowlkes, C.; Malik, J. Contour detection and hierarchical image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 898–916. [Google Scholar] [CrossRef] [PubMed]
- Fu, P.; Sun, X.; Sun, Q. Hyperspectral image segmentation via frequency-based similarity for mixed noise estimation. Remote Sens. 2017, 9, 1237. [Google Scholar] [CrossRef]
- Jan, L.; Fridrich, J.; Goljan, M. Digital camera identification from sensor pattern noise. IEEE Trans. Inf. Forens. Sec. 2006, 1, 205–214. [Google Scholar]
- Greenberg, S.; Aladjem, M.; Kogan, D. Fingerprint image enhancement using filtering techniques. Real-Time Imaging 2002, 8, 227–236. [Google Scholar] [CrossRef]
- Lee, J.S.; Hoppel, K. Noise modeling and estimation of remotely sensed images. In Proceedings of the 12th Canadian Symposium on Remote Sensing Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 10–14 July 1989; pp. 1005–1008. [Google Scholar]
- Wang, S.; Liu, H.; Xie, K.; Chen, Z.; Zhang, J. Noise level estimation using gradients of image blocks. In Proceedings of the 5th International Conference on Computer Science and Network Technology (ICCSNT 2016), Changchun, China, 10–11 December 2016; pp. 758–761. [Google Scholar]
- Huang, X.; Chen, L.; Tian, J.; Zhang, X.; Fu, X. Blind noisy image quality assessment using block homogeneity. Comput. Electr. Eng. 2014, 40, 796–807. [Google Scholar] [CrossRef]
- Huang, X.; Chen, L.; Tian, J.; Zhang, X. Blind image noise level estimation using texture-based eigenvalue analysis. Multimed. Tools Appl. 2016, 75, 2713–2724. [Google Scholar] [CrossRef]
- Abramova, V. A Blind Method for Additive Noise Variance Evaluation Based on Homogeneous Region Detection Using the Fourth Central Moment Analysis. Telecommun. Radio Eng. 2015, 74, 1651–1669. [Google Scholar] [CrossRef]
- Olsen, S.I. Estimation of noise in images: An evaluation. Graph. Models Image Proc. 1993, 55, 319–323. [Google Scholar] [CrossRef]
- Bilcu, R.C.; Vehvilainen, M.A. New Method for Noise Estimation in Images. In Proceedings of the IEEE-EURASIP International Workshop on Nonlinear Signal and Image Processing, Sapporo, Japan, 18–20 May 2005. [Google Scholar]
- Tai, S.C.; Yang, S.M. A fast method for image noise estimation using Laplacian operator and adaptive edge detection. In Proceedings of the 3rd International Symposium on Communications, Control, and Signal Processing, St. Julians, Malta, 12–14 March 2008; pp. 1077–1081. [Google Scholar]
- Shin, D.; Park, R.; Yang, S.; Jung, J. Block-based noise estimation using adaptive Gaussian filtering. IEEE Trans. Consum. Electron. 2005, 51, 218–226. [Google Scholar] [CrossRef]
- Yang, S.M.; Tai, S.C. Fast and reliable image-noise estimation using a hybrid approach. J. Electron. Imaging 2010, 19, 033007:1–033007:15. [Google Scholar] [CrossRef]
- Turajlic, E. A fast noise level estimation algorithm based on adaptive image segmentation and Laplacian convolution. In Proceedings of the 40th International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO 2017), Opatija, Croatia, 22–26 May 2017; pp. 486–491. [Google Scholar]
- Tang, C.; Yang, X.; Zhai, G. Dual-transform based noise estimation. In Proceedings of the IEEE International Conference on Multimedia and Expo (ICME 2012), Melbourne, Australia, 9–13 July 2012; pp. 991–996. [Google Scholar]
- Manjón, J.V.; Coupé, P.; Buades, A. MRI noise estimation and denoising using non-local PCA. Med. Image Anal. 2015, 22, 35–47. [Google Scholar] [CrossRef] [PubMed]
- Ponomarenko, M.; Gapon, N.; Voronin, V.; Egiazarian, K. Blind estimation of white Gaussian noise variance in highly textured images. J. Electron. Imaging 2018, 13, 382:1–382:5. [Google Scholar] [CrossRef]
- Ghazi, M.M.; Erdogan, H. Image noise level estimation based on higher-order statistics. Multimed. Tools Appl. 2017, 76, 2379–2397. [Google Scholar] [CrossRef]
- Chen, G.; Zhu, F.; Heng, A.P. An efficient statistical method for image noise level estimation. In Proceedings of the IEEE International Conference on Computer Vision (ICCV 2015), Santiago, Chile, 7–13 December 2015; pp. 477–485. [Google Scholar]
- Khmag, A.; Ramli, A.R.; Al-Haddad, S.A.R.; Kamarudin, N. Natural image noise level estimation based on local Blind image noise level estimation ics for blind noise reduction. Vis. Comput. 2018, 34, 575–587. [Google Scholar] [CrossRef]
- Liu, W.; Lin, W. Additive white Gaussian noise level estimation in SVD domain for images. IEEE Trans. Image Process. 2013, 22, 872–883. [Google Scholar] [CrossRef] [PubMed]
- Liu, W. Additive white Gaussian noise level estimation based on block SVD. In Proceedings of the IEEE Workshop on Electronics, Computer and Applications, Ottawa, ON, Canada, 8–9 May 2014; pp. 960–963. [Google Scholar]
- Du, K.L.; Swamy, M.N.S. Search and Optimization by Metaheuristics; Birkhäuser: Basel, Switzerland, 2016; pp. 153–173. ISBN 978-33-1941-191-0. [Google Scholar]




| Block Size | Noise Level, | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 | 13 | 16 | 19 | 22 | 25 | 28 | 31 | 34 | 37 | 40 | 43 | 46 | 49 | 52 | 55 | |
| 32 × 32 | 34.03 | 44.38 | 54.64 | 64.66 | 75.13 | 85.68 | 95.47 | 105.73 | 116.09 | 126.44 | 136.95 | 147.06 | 156.63 | 166.05 | 177.33 | 188.04 |
| 64 × 64 | 48.41 | 62.75 | 77.71 | 92.29 | 106.69 | 120.87 | 135.98 | 150.27 | 164.64 | 179.61 | 193.63 | 208.48 | 222.75 | 237.31 | 252.43 | 266.41 |
| 128 × 128 | 68.76 | 89.26 | 110.05 | 130.81 | 151.01 | 171.88 | 192.20 | 213.55 | 233.85 | 254.18 | 274.84 | 295.64 | 315.90 | 336.92 | 357.17 | 377.57 |
| Block Size | a1 | a0 | MSE |
|---|---|---|---|
| 32 × 32 | 4.6891 | −0.1262 | |
| 64 × 64 | 6.6399 | −0.1501 | |
| 128 × 128 | 9.3753 | −0.1852 |
| Block Size | b1 | b0 | Min EMSE |
|---|---|---|---|
| 32 × 32 | 0.097059 | 0.347166 | 0.446314 |
| 64 × 64 | 0.040105 | 0.438450 | 0.399865 |
| 128 × 128 | 0.022484 | 0.543005 | 0.461783 |
| Test Image | Method | Noise Level, | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 | 4.5 | 5.0 | 5.5 | 6.0 | 6.5 | 7.0 | 7.5 | 8.0 | 8.5 | 9.0 | 9.5 | 10 | ||
| Barbara | SVD-B 128 | 4.90 | 3.44 | 2.27 | 1.77 | 1.16 | 1.24 | 0.89 | 0.39 | 0.424 | 0.328 | 0.346 | 0.278 | 0.227 | 0.116 | 0.144 | 0.118 | 0.022 | 0.063 | 0.026 | 0.095 |
| ASVD 128 | 0.74 | 0.28 | 0.11 | 0.11 | 0.02 | 0.05 | 0.04 | 0.02 | 0.031 | 0.017 | 0.030 | 0.025 | 0.043 | 0.056 | 0.036 | 0.080 | 0.028 | 0.066 | 0.026 | 0.095 | |
| SVD-B 64 | 3.89 | 2.75 | 1.68 | 1.15 | 0.76 | 0.68 | 0.70 | 0.38 | 0.259 | 0.210 | 0.140 | 0.081 | 0.076 | 0.097 | 0.035 | 0.042 | 0.053 | 0.029 | 0.048 | 0.036 | |
| ASVD 64 | 0.28 | 0.09 | 0.02 | 0.01 | 0.03 | 0.05 | 0.02 | 0.03 | 0.041 | 0.029 | 0.044 | 0.058 | 0.020 | 0.065 | 0.037 | 0.042 | 0.053 | 0.029 | 0.048 | 0.036 | |
| SVD-B 32 | 3.64 | 2.41 | 1.59 | 1.17 | 0.86 | 0.59 | 0.42 | 0.33 | 0.249 | 0.210 | 0.137 | 0.119 | 0.057 | 0.073 | 0.071 | 0.051 | 0.029 | 0.027 | 0.047 | 0.039 | |
| ASVD 32 | 0.68 | 0.30 | 0.19 | 0.20 | 0.20 | 0.32 | 0.40 | 0.33 | 0.249 | 0.210 | 0.137 | 0.119 | 0.057 | 0.073 | 0.071 | 0.051 | 0.029 | 0.027 | 0.047 | 0.039 | |
| Boat | SVD-B 128 | 2.96 | 2.06 | 1.04 | 0.95 | 0.53 | 0.30 | 0.25 | 0.18 | 0.155 | 0.115 | 0.066 | 0.060 | 0.036 | 0.010 | 0.013 | 0.013 | 0.036 | 0.014 | 0.011 | 0.009 |
| ASVD 128 | 0.50 | 0.23 | 0.08 | 0.03 | 0.02 | 0.01 | 0.01 | 0.02 | 0.030 | 0.008 | 0.017 | 0.027 | 0.017 | 0.029 | 0.040 | 0.018 | 0.060 | 0.017 | 0.011 | 0.009 | |
| SVD-B 64 | 2.94 | 1.69 | 1.10 | 0.73 | 0.67 | 0.36 | 0.24 | 0.21 | 0.107 | 0.098 | 0.070 | 0.035 | 0.033 | 0.020 | 0.020 | 0.025 | 0.029 | 0.015 | 0.017 | 0.020 | |
| ASVD 64 | 0.33 | 0.16 | 0.04 | 0.02 | 0.02 | 0.02 | 0.01 | 0.02 | 0.016 | 0.006 | 0.008 | 0.012 | 0.028 | 0.017 | 0.021 | 0.025 | 0.029 | 0.015 | 0.017 | 0.020 | |
| SVD-B 32 | 2.61 | 1.74 | 1.16 | 0.81 | 0.57 | 0.38 | 0.29 | 0.19 | 0.137 | 0.157 | 0.074 | 0.085 | 0.039 | 0.042 | 0.030 | 0.038 | 0.029 | 0.049 | 0.012 | 0.027 | |
| ASVD 32 | 0.52 | 0.27 | 0.13 | 0.11 | 0.08 | 0.08 | 0.26 | 0.19 | 0.137 | 0.157 | 0.074 | 0.085 | 0.039 | 0.042 | 0.030 | 0.038 | 0.029 | 0.049 | 0.012 | 0.027 | |
| Crowd | SVD-B 128 | 2.31 | 1.89 | 1.08 | 0.85 | 0.50 | 0.40 | 0.30 | 0.18 | 0.132 | 0.055 | 0.028 | 0.016 | 0.021 | 0.012 | 0.024 | 0.012 | 0.039 | 0.049 | 0.044 | 0.059 |
| ASVD 128 | 0.13 | 0.05 | 0.02 | 0.02 | 0.05 | 0.06 | 0.07 | 0.06 | 0.064 | 0.078 | 0.116 | 0.122 | 0.072 | 0.060 | 0.046 | 0.048 | 0.076 | 0.067 | 0.044 | 0.059 | |
| SVD-B 64 | 2.05 | 1.39 | 1.07 | 0.75 | 0.47 | 0.27 | 0.15 | 0.10 | 0.042 | 0.041 | 0.041 | 0.026 | 0.013 | 0.029 | 0.014 | 0.024 | 0.053 | 0.046 | 0.023 | 0.018 | |
| ASVD 64 | 0.02 | 0.05 | 0.04 | 0.07 | 0.09 | 0.09 | 0.15 | 0.11 | 0.110 | 0.076 | 0.044 | 0.043 | 0.036 | 0.051 | 0.024 | 0.024 | 0.053 | 0.046 | 0.023 | 0.018 | |
| SVD-B 32 | 1.90 | 1.14 | 0.75 | 0.45 | 0.34 | 0.19 | 0.12 | 0.08 | 0.046 | 0.054 | 0.012 | 0.025 | 0.017 | 0.016 | 0.013 | 0.014 | 0.024 | 0.030 | 0.028 | 0.038 | |
| ASVD 32 | 0.01 | 0.03 | 0.02 | 0.03 | 0.02 | 0.02 | 0.02 | 0.08 | 0.046 | 0.054 | 0.012 | 0.025 | 0.017 | 0.016 | 0.013 | 0.014 | 0.024 | 0.030 | 0.028 | 0.038 | |
| Town | SVD-B 128 | 6.63 | 4.90 | 3.57 | 2.76 | 1.97 | 1.60 | 1.17 | 0.96 | 0.892 | 0.621 | 0.607 | 0.443 | 0.356 | 0.346 | 0.277 | 0.277 | 0.235 | 0.220 | 0.221 | 0.238 |
| ASVD 128 | 2.92 | 1.88 | 1.31 | 0.88 | 0.58 | 0.48 | 0.34 | 0.35 | 0.332 | 0.230 | 0.266 | 0.217 | 0.188 | 0.220 | 0.209 | 0.231 | 0.212 | 0.220 | 0.221 | 0.238 | |
| SVD-B 64 | 5.85 | 4.19 | 3.02 | 2.55 | 1.80 | 1.38 | 1.00 | 0.83 | 0.718 | 0.495 | 0.429 | 0.382 | 0.349 | 0.267 | 0.146 | 0.226 | 0.218 | 0.218 | 0.148 | 0.123 | |
| ASVD 64 | 2.01 | 1.19 | 0.76 | 0.59 | 0.40 | 0.33 | 0.24 | 0.22 | 0.252 | 0.189 | 0.210 | 0.201 | 0.280 | 0.254 | 0.146 | 0.226 | 0.218 | 0.218 | 0.148 | 0.123 | |
| SVD-B 32 | 5.34 | 3.72 | 2.63 | 1.90 | 1.55 | 1.01 | 0.90 | 0.72 | 0.578 | 0.434 | 0.370 | 0.379 | 0.286 | 0.280 | 0.206 | 0.287 | 0.201 | 0.182 | 0.175 | 0.199 | |
| ASVD 32 | 2.57 | 1.60 | 1.14 | 0.90 | 1.12 | 0.93 | 0.90 | 0.72 | 0.578 | 0.434 | 0.370 | 0.379 | 0.286 | 0.280 | 0.206 | 0.287 | 0.201 | 0.182 | 0.175 | 0.199 | |
| Girlface | SVD-B 128 | 2.07 | 0.96 | 0.78 | 0.54 | 0.26 | 0.14 | 0.13 | 0.09 | 0.066 | 0.023 | 0.029 | 0.018 | 0.014 | 0.020 | 0.015 | 0.016 | 0.011 | 0.018 | 0.021 | 0.010 |
| ASVD 128 | 0.77 | 0.28 | 0.16 | 0.10 | 0.04 | 0.01 | 0.02 | 0.01 | 0.004 | 0.007 | 0.014 | 0.017 | 0.011 | 0.015 | 0.021 | 0.022 | 0.012 | 0.022 | 0.021 | 0.010 | |
| SVD-B 64 | 2.58 | 1.30 | 0.86 | 0.60 | 0.52 | 0.29 | 0.25 | 0.18 | 0.119 | 0.106 | 0.051 | 0.076 | 0.050 | 0.061 | 0.024 | 0.020 | 0.035 | 0.012 | 0.022 | 0.024 | |
| ASVD 64 | 0.96 | 0.45 | 0.23 | 0.15 | 0.15 | 0.07 | 0.06 | 0.06 | 0.035 | 0.036 | 0.017 | 0.045 | 0.032 | 0.055 | 0.024 | 0.020 | 0.035 | 0.012 | 0.022 | 0.024 | |
| SVD-B 32 | 2.52 | 1.61 | 1.15 | 0.88 | 0.53 | 0.42 | 0.32 | 0.26 | 0.130 | 0.184 | 0.126 | 0.099 | 0.084 | 0.050 | 0.051 | 0.041 | 0.056 | 0.091 | 0.089 | 0.030 | |
| ASVD 32 | 1.18 | 0.63 | 0.43 | 0.41 | 0.23 | 0.28 | 0.31 | 0.26 | 0.130 | 0.184 | 0.126 | 0.099 | 0.084 | 0.050 | 0.051 | 0.041 | 0.056 | 0.091 | 0.089 | 0.030 | |
| Car | SVD-B 128 | 2.91 | 1.48 | 1.11 | 1.35 | 1.32 | 0.85 | 0.80 | 0.50 | 0.435 | 0.365 | 0.131 | 0.219 | 0.114 | 0.249 | 0.297 | 0.174 | 0.036 | 0.100 | 2.906 | 1.484 |
| ASVD 128 | 0.61 | 0.20 | 0.16 | 0.13 | 0.22 | 0.17 | 0.15 | 0.05 | 0.065 | 0.091 | 0.024 | 0.065 | 0.066 | 0.122 | 0.211 | 0.141 | 0.030 | 0.102 | 0.611 | 0.198 | |
| SVD-B 64 | 2.98 | 2.59 | 2.04 | 1.19 | 1.12 | 0.66 | 0.67 | 0.38 | 0.586 | 0.312 | 0.345 | 0.202 | 0.291 | 0.202 | 0.058 | 0.111 | 0.175 | 0.076 | 2.980 | 2.586 | |
| ASVD 64 | 0.33 | 0.20 | 0.19 | 0.07 | 0.07 | 0.03 | 0.06 | 0.02 | 0.137 | 0.049 | 0.109 | 0.092 | 0.220 | 0.183 | 0.058 | 0.111 | 0.175 | 0.076 | 0.329 | 0.204 | |
| SVD-B 32 | 3.26 | 2.45 | 1.68 | 1.43 | 1.12 | 0.79 | 0.67 | 0.62 | 0.463 | 0.427 | 0.327 | 0.268 | 0.251 | 0.280 | 0.209 | 0.251 | 0.228 | 0.117 | 3.256 | 2.454 | |
| ASVD 32 | 0.61 | 0.50 | 0.35 | 0.38 | 0.47 | 0.58 | 0.67 | 0.62 | 0.463 | 0.427 | 0.327 | 0.268 | 0.251 | 0.280 | 0.209 | 0.251 | 0.228 | 0.117 | 0.608 | 0.499 | |
| Method | SVD | SVD-B 32 | ASVD 32 | SVD-B 64 | ASVD 64 | SVD-B 128 | ASVD 128 |
| Time (s) | 0.0811 | 0.0590 | 0.0596 | 0.0396 | 0.0401 | 0.0403 | 0.0408 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Turajlic, E. Adaptive Block-Based Approach to Image Noise Level Estimation in the SVD Domain. Electronics 2018, 7, 397. https://doi.org/10.3390/electronics7120397
Turajlic E. Adaptive Block-Based Approach to Image Noise Level Estimation in the SVD Domain. Electronics. 2018; 7(12):397. https://doi.org/10.3390/electronics7120397
Chicago/Turabian StyleTurajlic, Emir. 2018. "Adaptive Block-Based Approach to Image Noise Level Estimation in the SVD Domain" Electronics 7, no. 12: 397. https://doi.org/10.3390/electronics7120397
APA StyleTurajlic, E. (2018). Adaptive Block-Based Approach to Image Noise Level Estimation in the SVD Domain. Electronics, 7(12), 397. https://doi.org/10.3390/electronics7120397





