Virtual Machine Placement via Bin Packing in Cloud Data Centers

Abstract

With the increasing size of cloud data centers, the number of users and virtual machines (VMs) increases rapidly. The requests of users are entertained by VMs residing on physical servers. The dramatic growth of internet services results in unbalanced network resources. Resource management is an important factor for the performance of a cloud. Various techniques are used to manage the resources of a cloud efficiently. VM-consolidation is an intelligent and efficient strategy to balance the load of cloud data centers. VM-placement is an important subproblem of the VM-consolidation problem that needs to be resolved. The basic objective of VM-placement is to minimize the utilization rate of physical machines (PMs). VM-placement is used to save energy and cost. An enhanced levy-based particle swarm optimization algorithm with variable sized bin packing (PSOLBP) is proposed for solving the VM-placement problem. Moreover, the best-fit strategy is also used with the variable sized bin packing problem (VSBPP). Simulations are done to authenticate the adaptivity of the proposed algorithm. Three algorithms are implemented in Matlab. The given algorithm is compared with simple particle swarm optimization (PSO) and a hybrid of levy flight and particle swarm optimization (LFPSO). The proposed algorithm efficiently minimized the number of running PMs. VM-consolidation is an NP-hard problem, however, the proposed algorithm outperformed the other two algorithms.

1. Introduction

In the cloud environment, many tasks may require resources from multiple resource providers [1]. There is a vast number of physical machines (PMs) in a cloud data center [2]. Virtualization technology provides a facility of virtual machines (VMs). The users can run their applications on VMs. The facilities’ virtualization technology provides sharing of memory, CPU and storage resources [2]. Multiple applications on VMs perform a task submitted by a user [3]. A bi-directional communication between a user and application needs to use the network resources. In task processing, the capacity of network resources plays an important role.

There are two main parts of cloud computing: front end and back end. A user can only see the front end which consists of a browser, connections etc. A back-end comprises servers, components, data storage, hosts etc. [4]. Cloud computing provides three services: software as a service (SaaS), platform as a service (PaaS), and infrastructure as a service (IaaS). SaaS provides a facility to use the software online instead of installing or purchasing it; It provides access through a web browser. PaaS is a middle-ware between SaaS and IaaS. It represents a whole environment for testing, deploying, updating and managing applications. IaaS provides hardware components including servers, network, and storage etc. Examples of SaaS, PaaS, and IaaS are shown in Figure 1.

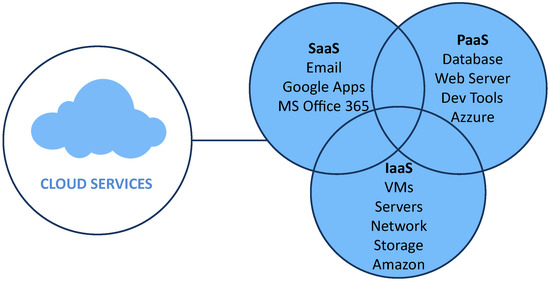
Figure 1. Cloud Services.

Mathematically, the process of managing and designing cloud computing is stated as an optimization problem [4]. Load balancing is the main objective of a cloud data center. Two main approaches are used for load balancing of a cloud. These are VM-integration and intelligent task assignment. VM-integration includes efficient placement of VMs and migration of VMs. The basic idea of VM-placement is to place the VMs according to each host capacity. VM-migration includes the process of moving tasks from over-loaded or underloaded server to normal server. VM-migration is triggered when a critical value is reached. Intelligent task assignment is another approach to balance the load of a network efficiently. It is the process of selecting the appropriate VM according to the size and capacity of a VM. However, migration of a task increases the total cost. Intelligent task assignment also increases cost. VM-placement is an efficient way to balance the load of a cloud data center. Most of the cloud computing problems including scheduling and load balancing can be done through bin packing problem (BPP) variants.

This paper is an extension of [5]. The extended paper presents an enhanced levy-based particle swarm optimization (PSO) with variable sized bin packing (PSOLBP) algorithm based on best-fit strategy. Variable sized bin packing is used to balance the load of a cloud data center. The initial steps are similar to simple PSO. The processes of making swarm in search space, finding local best and global best are all the same as PSO. If the probability is greater than 0.5, the position and the velocity of each particle are updated using a simple PSO method, otherwise levy flight is used to update velocity and position of the particle.

The remaining part of the paper is organized as follows: related work is covered in Section 2, PSO and levy flight algorithms are presented in Section 3 and Section 4. The proposed algorithm is described in Section 5 while problem formulation is done in Section 6 and the bin packing problem is presented in Section 7. Simulation results are discussed in Section 8. Conclusion and future work are included in Section 9.

1.1. Limitations of Research and Contributions

Cloud computing is a kind of distributed computing [1]. A cloud data center normally contains a large number of PMs [2]. Cloud service providers offer consumers the facility of VMs to run their applications [2]. The main objective of VMs is to minimize the usage of PMs [2]. The size of cloud data centers is increasing dramatically so the number of VMs and applications are also rising rapidly. The expeditious growth of Internet services causes an unbalanced load of data center resources. To balance the resources of cloud data centers, two main approaches are used: VM-integration and intelligent task assignment. VM-integration includes migration of VMs and optimal placement of VMs in a cloud data center. The basic idea of VM-placement is to place the VMs reasonably according to the processing capacity of each host. VM-migration is triggered when the utilization rate of VM reaches a critical value. In an intelligent task assignment, a suitable host is selected according to the size of a task and resource consumption of a task. However, it increases the overall operational cost [3]. VM-placement through variable-sized bin packing is an efficient strategy [4].

An efficient VM-placement algorithm is needed to reduce the usage of PMs. In this paper, an efficient strategy is proposed to solve the VM placement problem in cloud data centers. The proposed technique is a hybrid of PSO and levy flight. Furthermore, bin packing is used to minimize the utilization rate of PMs. The best-fit strategy is used to reduce the resource wastage of cloud resources. The best fit algorithm packs the maximum number of VMs into a small number of PMs. The sole purpose of bin packing and best-fit strategy is efficient utilization of cloud resources. Bin packing saves energies and reduces cost. The proposed algorithm is examined on ten well-known unimodal and multimodal benchmark functions. The main contributions of the work are listed below:

• An improved levy-based PSO algorithm is proposed to solve the VM-placement problem
• Variable-sized bin packing is used to minimize the utilization rate of the running PMs
• The best-fit strategy is used to achieve an optimal solution without wasting any space of a running PM
• Efficient use of cloud data center resources, i.e., packing a PM to its capacity without wasting any resource

1.2. Implementation Practice Guidelines

The proposed technique is the hybrid of levy flight and PSO. The initial steps are similar to those of a simple PSO including:

• Random distribution of population
• Evaluation of all particle fitness value
• Finding the personal best and global best values

If the probability is greater than or equal to 0.5, the velocity and position of each particle are updated through PSO. Otherwise, use levy flight to update the velocity of the particle. The particle’s velocity value becomes the value of its position. Bin packing is then used to pack the maximum number of VMs into a small number of PMs. The main purpose of bin packing is to avoid wastage of resources, save energies and reduce cost.

2. Related Work

In [1], the authors proposed a decentralized-belief-propagation-based method (PD-LBP) to enhance the performance of task allocation in the cloud environment. In PD-LBP, the set of tasks and agents both change constantly. In this paper, two steps (pruning and decomposition) are considered. The achievements of the proposed method involve the best allocation of big scale tasks and efficient performance in the dynamic cloud environment. However, PD-LBP is not feasible, i.e., an agent can execute only one sub-task.

Yang et al. solved the VM auto-scaling and VM-to-PM packing problem via shadow routing based approach in [2]. The main purpose of the proposed work is to minimize the usage of PMs by intelligently packing a number of VMs in it. It is done to save energies and minimize operational cost. The proposed algorithm does not need to resolve the problem “from scratch”. It adapts automatically according to the demand of requests. However, when there are a large number of VMs in a single PM, there must be a chance of congestion in it.

The authors in [3] proposed a layered VM-migration algorithm to balance the load of network resources. Two types of the algorithms are presented in this paper. The proposed work achieved a powerful balancing of network resources. However, migration of one task at a time increases delay.

Abdel-Basset in [4] proposed an improved levy-based whale optimization algorithm. The main purpose of the proposed scheme is to efficiently place the VMs with respect to the available bandwidth in cloud computing. This work optimally balanced the load of a network. However, the tasks and cloud size are increasing rapidly, due to which initial placement of VMs is not an efficient way to balance the load.

In [6], R. Jensi et al. enhanced PSO by introducing a levy flight to update the velocity of a particle. The given algorithm has been tested on 21 well-known test functions. Proposed approach enhanced the capability of global search and increased convergence efficiency. However, this algorithm is used to solve linear problems.

The authors proposed a multi-objective grey-wolf optimization algorithm in [7]. It mimics the hunting behavior of grey wolves. A fixed size archive is also integrated to save and retrieve Pareto optimal solutions. However, the proposed algorithm cannot handle uncertainties.

In [8], authors formulated cost as a function of consumed and overhead energy by the server. This paper provides an efficient VM-placement approach. However, there is no guarantee of renewable energy availability.

Djabir et al. proposed a priority assignment algorithm in [9]. Four priority levels are defined for charging and discharging vehicles to stable grid load especially during on-peak hours. Electric vehicles communicate with a power supply station. Station take electricity from the grid. Cloud is used to store the data of grid for permanent storage. However, the disposal of batteries results in global warming.

The authors proposed a pricing scheme in [10]. Two types of instances are considered. One is on-demand instance and the other is reserved instance. The tariff policy for on-demand instance is like pay as you go. Reserved instance is for the users having long-term demands. However, the user has to give upfront payment for reserved instance.

Hui et al. considered energy-aware VM-consolidation and VM-migration for green cloud computing in [11]. The authors proposed a space-aware best-fit decreasing algorithm (SABFD). The VM-migration is also done on the basis of high CPU utilization rate. The paper saves energy and assures service level agreement (SLA). However, the migration cost is greater when VMs migrate too many times.

A hybrid genetic wind-driven (GWD) algorithm is proposed by Javaid et al. in [12]. In a smart grid, an energy management controller is designed for the residential area based on the heuristic algorithm to flatten the load in grid area network. The proposed work scheduled the load of a single and multiple homes. However, there is a chance of delay whenever the request rate is high.

In [13], authors proposed a network-topology-aware redundant VM-placement optimization algorithm to minimize the consumption of network resources. The main objective of the proposed technique is to increase the reliability of cloud resources. However, this approach does not work for a complex cloud.

The authors in [14] proposed a novel orchestration method, i.e., a placement algorithm to deploy the VMs automatically. It also manages the high availability zone. The main objective of the paper is the global load balancing of multi-zone clouds. The proposed work efficiently schedule the tasks of a cloud. However, the cost is increased.

Vakilinia et al. proposed integer quadratic program (IQP) with linear and quadratic constraints in [15]. The main objective of the proposed work is an optimization of power in data center. The proposed work optimized the power consumption of servers, migration cost and network communication via VM-placement. However, the given approach does not work for large-scale system.

The authors in [16] proposed a hybrid artificial bee ant colony optimization (HABACO) for resource management in smart grid. The proposed work enhanced the performance of cloud computing. The main focus of the presented work is the efficient utilization of smart devices. However, the proposed algorithm does not work well for multiple load balancing applications.

Muqadda et al. proposed a hybrid gray wolf differential evolution (HGWDE) to balance the load between generation and demand for electric power in [17]. The proposed work optimized electricity cost and peak load demand. However, the cost is increased, and there is a trade-off between user comfort and cost.

In [18], the authors proposed a hybrid elephant adaptive cuckoo search (HEAC) algorithm to reduce the electricity bill and peak to average ratio. It also maximizes user comfort. The proposed work give incentives to consumers. The main focus of the proposed work is to efficiently utilize the available energy. However, the consumption cost is increased.

The authors in [19] presented a multi-level join VM-placement and migration algorithm (MJPM) to reduce the operational cost. It also increases the quality of services through VM-placement. The proposed work improved energy consumption. However, the migration cost is increased due to the migration of one task at a time.

Adia et al. proposed a home energy management system to balance the load through coordination in [20]. The main objective of the proposed work is to optimize the energy consumption. It minimized the electricity cost and peak to average ratio. However, user comfort is ignored and it is the important factor to be considered.

In [21], the authors proposed an evolutionary accretive comfort algorithm for optimal energy consumption patterns. It maximizes user comfort and reduces cost, and energy consumption. However, there is no solution for renewable energy shortage.

Irfan et al. proposed a secure distributed adaptive bin packing algorithm in [22]. The proposed work efficiently allocated bins in cloud data centers. The main objective of the paper is efficient usage of cloud resources. It minimized the number of active servers and improved energy efficiency. However, cloud data centers are very complex, only relying on initial placement cannot balance the load of a network.

Deep Q-learning based code offloading method is proposed in [23]. The main objective of the proposed work is to reduce network delay or latency. It support heterogeneous and mobile and geographically distributed mobile devices. The proposed work achieved energy efficiency in terms of computation offloading solutions. However, the cost is increased by deploying number of fogs and applying machine learning.

Habibi et al. proposed a request distribution method in a federated cloud environment in [24]. The main objective of the proposed work is to efficiently distribute the requests of users or VMs according to their resources. The behavior of each request at a time is considered. However, considering one request at a time is not realistic, because most of the time, number of users send multiple requests at a time.

In [25], authors proposed an IOFollow scheme. This work improved the VM efficiency and migration performance. The main objective of this work is to increase the performance of computer server resources. Energy efficiency is also considered. It scheduled the migration sequence according to the sequence of requests coming from users. It also improved the efficiency of cache management. However, the migration of one task at a time may increase delay and cost.

The authors in [26] proposed a simplex linear programming (SLP) method. In distributed cloud data centers, the hierarchical structure is also presented to show connections between them. The technique presented in this paper is HM-SM-GrEA. This work is done allocate the resources optimally. The user requirements and services provided by resources are also considered in SLA and QoS. The main achievement of the proposed work is reliability and availability of resources. The cost and response time should be minimized and reliability and availability should be maximized. So there is a trade-off between above objectives. However, there is a chance of more power consumption to fulfil the requirements of a user.

Liu et al. proposed a VM-placement algorithm using evolutionary computing in [27]. It is done through ant colony system (ACS). This work is done to minimize the number of active physical servers i.e., utilization of underloaded servers to save energy. The main achievements of the paper are global optimization, energy saving, and efficient use of different resources. However, VM-placement is not an efficient way because the cloud data centers are very complex.

The authors in [28] proposed a framework to solve the VM-placement problem based on multi objective genetic algorithm (GA) and Bernoulli simulation. The main objective of this work is to minimize the number of running physical servers and reduce the resource wastage in each physical server. This work is implemented in the real cloud platform and helped the company to optimize the VM-placement problem efficiently. The operational cost is also reduced. However, the given work is not efficient enough to handle big data. The data is increasing rapidly and this problem should be tackled.

The authors in [29] proposed a hierarchical state space model. The authors have also modified the transactive control systems in the smart grid. This work is done to manage the fluctuation of wind. The authors have also described the advantages and challenges of the cloud platform. Furthermore, resilient frequency regulation is proposed to mitigate the challenges of intermittent wind. The given work provides robustness, optimality and flexibility of system resilience. However, the cost of energy is increased by deploying more wind turbines.

A novel architecture is proposed for cloud computing in [30]. The resources of cloud computing are leveraged to enable the consumption prediction. A time series forecasting is also done to uniformly distribute the load of a cloud. A concept of controllability is also given to detect the connectivity loss. However, detecting a connection loss is not a solution. A solution is still needed to ensure the continuity of the network.

Liu et al. proposed a cloud energy storage pool in [31]. This is basically a pool of energy resources to provide the services of storage to small customers. The main objective of the proposed work is to minimize the energy storage cost. Cloud energy storage provided the facility of energy storage to the consumers at a cheap cost. Two models are presented in this paper. In the first model it is assumed that the consumer and cloud energy storage operator both have accurate forecast of load. In the second model, it is assumed that cloud energy storage operators do not have perfect prediction of the load. However, the implementation leads to the extra power loss.

The authors in [32] proposed an energy efficient approach for cloud data centers. The main focus of the proposed work is to reduce the energy consumption of servers and cloud data centers. The VM-placement problem through GA is also considered. This work is done to avoid the network congestion, save network energy and to increase the transmission capacity of a network. The proposed work minimized the transmission load and energy consumption. However, VM-placement is an NP-hard problem. This problem still needs to be optimized.

Munshi et al. proposed smart grid eco system for big data in [33]. It is based on the Lambda architecture. It can perform real time operations on distributed data. It is also stores the data of smart grid devices such as smart meters, graphical and video data. The authors presented the implementation of smart grid big data on cloud computing platform. Furthermore, data mining applications are also performed on real data of smart grids. Data mining applications make groups of smart meter readings on the basis of load consumption. However, there is a chance of congestion when considering big data.

The authors proposed an efficient identity-based encryption with equality test scheme along with bilinear pairing in [34]. It is done to reduce the time consumption. The main focus of the proposed work is to improve the performance of a cloud. Storage overhead, security energy consumption and computational cost are considered to make the system efficient. The proposed scheme reduced the computational cost effectively. The authors claim that their technique can deploy a cloud more efficiently. However, the energy consumption is increased.

The authors considered bi-objective problems in [35]. They investigated how to minimize the migration cost to save as much energy as possible. The authors designed a consolidation score function to give the optimum solutions of the aforementioned objectives. An improved grouping genetic algorithm is proposed on the basis of swap operation and greedy heuristics. The major concerns of the proposed work is an optimal VM-consolidation and reduction of energy consumption of cloud data centers. However, the VM-consolidation is an NP-hard problem. This problem still needs to be optimized.

The author proposed AVVMC to solve VM placement problem in [36]. They used ACO for this purpose. The basic purpose of work done is to minimize the power consumption and wastage of cloud resource. The proposed work efficiently balanced the network resources. However, VM placement is an NP-hard problem.

A detailed survey of different VM placement techniques is presented by Challita et al. in [37]. The techniques are discussed to minimize power consumption, maximize utilization of resources, prevent network congestion and reduce power cost. Detailed comprehension of VM placement algorithms is discussed. However, critical analysis is not done.

The authors proposed reputation-based model in [38]. The sole purpose of the proposed work is to provide quality of services. The cost is also considered in a multi-cloud environment. Furthermore, response time is optimized. However, there is a chance of congestion. So, a mechanism is required to avoid delay.

The related work is given in Table 1.

Table 1. Related Work.

Techniques	Objectives	Achievements	Limitations
Decentralized belief propagation based method (PD-LBP) [1]	Performance of task allocation	Best allocation of big tasks and efficient performance in dynamic cloud	An agent can execute only one subtask
Shadow routing based approach [2]	VM auto-scaling and VM-to-PM packing	Save energies and minimize operational cost	Chance of congestion in cloud data center
Layered VM-migration algorithm [3]	Migration of VMs	Efficiently balanced the network resources	Migration of one task at a time may increase delay
Improved levy-based whale optimization algorithm [4]	VM-placement	Efficiently balanced the load of a network	Initial placement of VMs is not an efficient way to balance the load of a whole network
Particle swarm optimization with levy flight (PSOLF) [6]	Increase convergence efficiency	Enhanced global search	Only proposed for linear problems
Multi-objective grey wolf optimization algorithm [7]	Multi-objective problem solving	Fixed size archive is integrated along with leader selection method	The proposed algorithm cannot handle uncertainties
VM-placement approach [8]	Cost minimization	Reduced energy consumption	There is no guarantee of renewable energy availability
Priority assignment algorithm [9]	Charging and discharging of electric vehicle	Stabled grid during on-peak hours	Disposal of batteries results in global warming
Cost-oriented model [10]	On-peak hours grid stability	Efficient tariff policies for users	User has to give upfront payment for reserved instance
Energy aware VM-consolidation and space aware best decreasing algorithm [11]	Save energy	Saved energy and assured SLA	Migration cost is great when VMs migrate too many times
Hybrid genetic wind-driven (GWD) algorithm [12]	Load flattening in grid area network	Scheduled the load of a single home as well as multiple homes	Chance of delay whenever the request rate is high
Network-topology-aware redundant VM-placement optimization algorithm [13]	Minimize the network resources consumption	Optimal VM-placement	Does not work for complex cloud
VM-placement algorithm [14]	Global load balancing of a cloud	Efficient cloud scheduling	Cost is increased
Secure distributed adaptive bin packing algorithm [22]	Efficient usage of resources and minimize number of active servers	Improved energy efficiency and minimized number of running servers	Initial placement cannot balance the load of a network
Deep Q-learning based code offloading method [23]	Reduce network delay	Efficient energy consumption	Cost is increased
Hierarchical state space model [29]	Manage fluctuation of wind	Provides robustness, optimality and flexibility	Energy cost is increased
Novel architecture for cloud computing platform [30]	Distribute the load of cloud using time series forecasting	Efficiently balanced the load of a cloud	A mechanism is needed to ensure the continuity of the network
Cloud energy storage pool [31]	Provide energy storage resources to consumers at cheap cost	Minimized the storage cost	Extra power loss to implement energy storage pool

3. Particle Swarm Optimization Algorithm

The PSO is a swarm-intelligence-based meta-heuristic technique for the solution of continual optimization problem [6]. It is a simple, intelligent and powerful algorithm. It mimics the social behavior of fishes and birds. In PSO, a particle is a candidate solution for an optimization problem. A number of particles integrate together to make a swarm and search for a good solution of a given optimization problem as shown in Figure 2. A search space is a set of all possible positions. Each particle has some position and it shows a possible solution of the fitness function in d-dimension search space. Each particle i maintains two vectors in search space [6]:

Figure 2. Swarm of Particles.

Position vector $X_i=[x_{i1},x_{i2}\dots x_{id}]$ and

Velocity vector describes the movement of a particle.

Velocity vector $V_i=[v_{i1},v_{i2}\dots v_{id}].$

Each particle has its own best experience known as personal best (pbest) and all particles have best experience called as global best (gbest). It helps the particles to move in the d-dimension search space.

pbest of particle i in d-dimension search space is represented as [6]:

$pbes{t}_i=[p_{i1},p_{i2},p_{i3},\dots ,p_{id},]$

gbest in d-dimension search space is represented as [6]:

$gbes{t}_i=[g_1,g_2,g_3,\dots ,g_d,]$

In initialization phase, a random initial position and velocity is given to each particle.

3.1. Update Position

The position of the particle consists of a value given by the objective function. Each particle memorizes the position of the best solution while moving in search space. Following equation is used to find the position of a particle [6]:

$$X_i^{(t+1)}=X_i^{(t)}+V_i^{(t+1)}$$

(1)

where $X_i^{(t+1)}$ represents the position of ith particle at iteration $t+1$, $V_i^{(t+1)}$ is the velocity of ith particle at iteration $t+1$ and $V_i$ is the velocity vector.

3.2. Update Velocity

A particle moves with a velocity at each iteration of the algorithm. A velocity is the sum of three components [6]:

• Previous velocity
• A velocity component that drives a particle towards the location in search space where it previously found the best solution
• A velocity through which the best solution found by neighbor particles in search space

Following equation is used to find the velocity of a particle [6]:

$$\begin{array}{c}\hfill V_i^{(t+1)}=\omega \times V_i^{(t)}+c1\times rand()\oplus (pbes{t}_i-X_i^t)\\ \hfill +c2\times rand()\oplus (gbest-X_i^t)\end{array}$$

(2)

where $\omega$ is inertia weight, c1 is cognitive weighting factor, c2 is a social weighting factor, rand () is a stochastic component of algorithm which is 0.5 and ⊕ shows the element by element multiplication. The graphical representation of Equations (1) and (2) is shown in Figure 3.

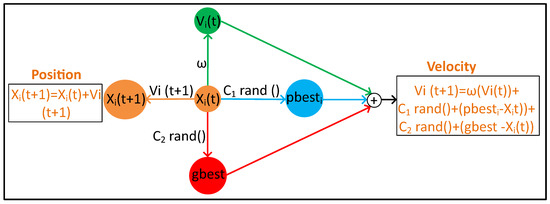
Figure 3. Graphical Representation of Personal Best and Global Best.

The values of c1 and c2 are used to check that the particles are effected more locally or globally. Inertia weight $(\omega )$ has controlling effect of previous velocity. It is used to balance exploitation and exploration rate. Following equation is used to calculate $\omega$ [6]:

$$\omega (t+1)={\omega }_{max}-\frac{{\omega }_{max}-{\omega }_{min}}{t_{max}}$$

(3)

where t is the current iteration, $t_{max}$ and $t_{min}$ shows the maximum and minimum inertia weights and $t_{max}$ is the maximum number of iteration. After updating position and velocity, minimum $(X_{min})$ and maximum $(X_{max})$ values for search range is assigned. Then, for each particle’s fitness value is calculated, pbest and gbest updates are performed. This procedure is continued until the stopping criteria is satisfied.

4. Levy Flight Algorithm

Levy flight is a class of random walk whose step length is drawn from levy distribution. Levy flight starts from one best-known location and generates a whole new generation at a distance which is randomly distributed according to levy distribution. The new generation will be evaluated to select the most encouraging one. Two steps are involved in levy flight:

• The selection of random direction
• The production of new steps

Levy distribution can be approximated as power-law when a step size is large. The formula of power-law is [6]:

$$L(s)\sim {\left|s\right|}^{-1-\beta }$$

(4)

where 0 $<\beta <$ 2 is an index.

4.1. Simple Levy Distribution

A levy distribution can be mathematically defined as [6]:

$$\begin{array}{c}\hfill D_{it}=\left\{\begin{array}{c}L(s,\gamma ,\mu )=\sqrt{\frac{\gamma }{2\pi }}exp\left[\begin{array}{c}\frac{\gamma }{2(s-\mu )}\end{array}\right]\frac{1}{{(s-\mu )}^{3{/}_2}},\hfill \\ \mathrm{if}0\le \mu \le s\le inf\hfill \\ 0,\mathrm{if}s\le 0\hfill \end{array}\right\}\end{array}$$

(5)

where $\mu$ is a shift parameter, $\gamma >0$ is a scale parameter used to control the scale of distribution.

4.2. Fourier Transform

Generally, levy distribution is defined in terms of Fourier transform [6].

$$F(k)=exp\left[\alpha \right|k{|}^{\beta }],0<\beta \le 2$$

(6)

where $\alpha$ is a scale factor which is 0.5. $\beta \in (0,2)$ is referred as levy index.

For random walk, the length of a step is calculated through mantegna’s algorithm as [6]:

$$S=\frac{u}{{\left|v\right|}^{1{/}_{\beta }}}$$

(7)

where u and v are drawn from normal distribution [6].

$$u\sim N(O,{\sigma }_u^2),v\sim N(O,{\sigma }_v^2)$$

(8)

where

$${\sigma }_u=\frac{\mathsf{\Gamma }(1+\beta )sin(\pi \beta {/}_2)}{\mathsf{\Gamma }(1+\beta {/}_2)\beta 2^{\beta -1}{/}_2}$$

(9)

Then the size of each step is calculated through

$$stepsize=0.01\times S$$

(10)

5. Proposed Levy Flight Particle Swarm Optimization with Variable Sized Bin Packing

In PSO, there is a problem of trapping and premature convergence in local optima. Many researchers used different techniques to improve PSO. This work focuses on updating the velocity using the levy flight method. The initial steps are similar to PSO, like random distribution of particles in search space, evaluation of all particles fitness value and the finding of pbest and gbest. When the probability is greater than or equal to 0.5, the velocity and position of each particle are updated using Equations (1) and (2). Otherwise, use Equation (12) and then a particle’s velocity becomes its position [6].

$$\omega =0.1+0.8\times \left(1-\frac{it}{Maxit}\right)$$

(11)

$$\begin{array}{c}\hfill V_i^{t+1}=\omega \times Lev{y}_{walk}(X_i^{(t)})+c1\times rand()\oplus (pbes{t}_i-X_i^t)\\ \hfill +c2\times rand()\oplus (gbest-X_i^t)\end{array}$$

(12)

The particle takes long jump toward its best positions. In distribution of levy flight, $\beta$ parameter performs a main role. The distribution can be changed differently by applying different values of $\beta$. In this paper, the value of $\beta$ is constant, i.e., 1.5.

The proposed phenomenon avoided loss of divergence while updating the velocity. This work improves a particle’s position after each iteration. The next position of a particle is calculated using Equation (13) [6].

$$X_i^{t+1}=V_i^{t+1}$$

(13)

and

$$Lev{y}_{walk}(X_i^{(t)})=(X_i^{(t)})+step\oplus random(size(X_i))$$

(14)

where

$$step=stepsize\oplus X_i^{(t)}$$

(15)

The fitness value of each particle is calculated after updating the velocity and position. If the particle has a better value then update its pbest. Otherwise, there is no need to update the pbest value. Then, find the gbest value of whole swarm. Repeat the procedure to achieve global optimum value. The pseudocode and flowchart of the PSOLF is given Algorithm 1 and Figure 4 [6].

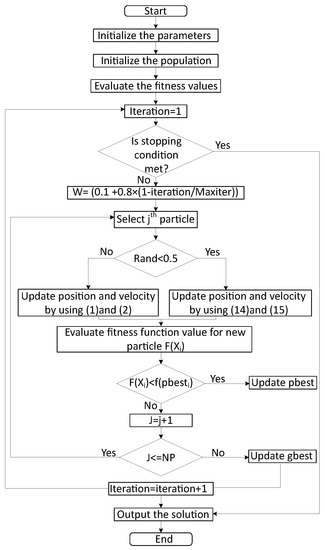
Figure 4. Flowchart of PSOLF.

Algorithm 1 Pseudocode of the PSOLF

6. Problem Formulation

In this paper, the problem of VM-placement is formulated as a “variable-sized bin packing problem (VSBPP)”with non-divisible items [4]. In VSBP, there are multiple bins of different capacities to pack a set of items. VSBPP can be defined as a set of indivisible items along with their weights and a set of variable-sized bins. The main objective of bin packing is to pack multiple items into a minimum number of bins in such a way that the wasted spaces of bins or the sum of costs are minimized. VSBPP can be described as follows [4]:

$$min\sum _{j=1}^n\sum _{k=1}^m{c}_k·y_{jk}$$

(16)

subject to

$$\sum _{j=1}^n{x}_{ij}=1$$

(17)

$$\sum _{k=1}^m{y}_{jk}\le 1$$

(18)

$$\sum _{i=1}^n{w}_i·x_{ij}\le \sum _{k=1}^m{W}_k·y_{jk}$$

(19)

$$c_k=\sum _{k=1}^m{W}_k·y_{jk}-\sum _{i=1}^n{w}_i·x_{ij}$$

(20)

$$x_{ij}\in \{0,1\}$$

$$y_{jk}\in \{0,1\}$$

$$\mathrm{for}i=1,\dots ,nj=1,\dots ,n\mathrm{and}k=1,\dots ,m$$

where n is number of items and available bins, m is the number of types used, $c_k$ is the cost or the wasted space of the bin of type k, $y_{jk}$ is a binary variable that shows if bin i of type k contains items, $x_{ij}$ is also a binary variable that indicates if item i is assigned to bin j, $w_j$ is weight of item and $W_k$ is bin capacity of type k. In the worst case, the number of bins is set to be equal to the number of items.

7. Bin Packing Problem

Bin packing is a process of fitting tasks neatly and efficiently inside the finite number of bin. The main objective of bin packing is to minimize the number of bins [4]. There are four main steps involved in the bin packing problem.

7.1. Lower Bound for the Problem

It is important to find the lower bound for the problem. Two steps are used to find the lower bound:

• Add all items
• Then divide them with total capacity of a bin

Graphical representation is given in Figure 5.

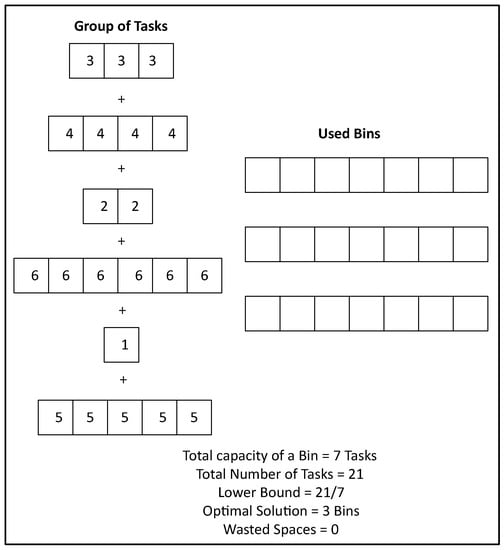
Figure 5. Lower Bound of a Problem.

7.2. First Fit Algorithm

Take a group of tasks as they come and try to fit them in a bin. A graphical example of first fit algorithm is given in Figure 6.

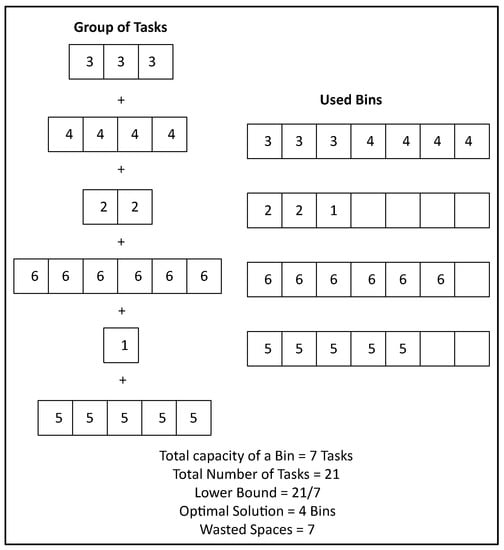
Figure 6. First Fit Algorithm.

7.3. Best Fit Algorithm

Arrange a group of tasks in descending order and then place them into a minimum number of bins as shown in Figure 7.

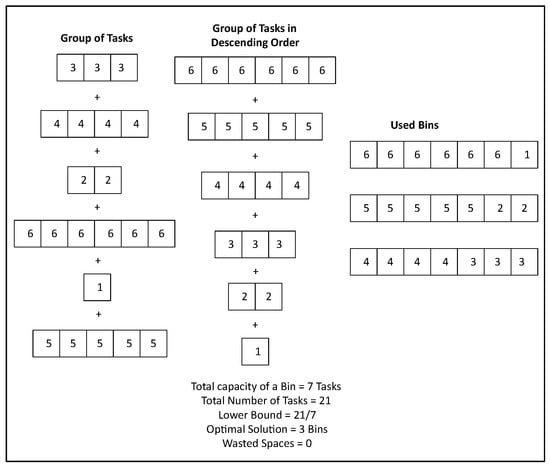
Figure 7. Best Fit Algorithm.

8. Simulation Results

The results are discussed in this section. For comparison purposes, the other two algorithms (PSO and LFPSO) are also implemented [6]. The simple PSO algorithm is trapped in local optima. LFPSO is a hybrid of PSO and levy flight. Levy flight is just used for random distribution of the particles. The proposed algorithm is also a hybrid of PSO algorithm and levy flight for VM-placement based on VSBPP. Levy flight is used to update the velocity of particles. The best-fit strategy is used along with VSBPP. Best fit strategy is used because it provides optimal results. Best fit strategy packs the maximum number of VMs in a single PM to avoid wastage of resources. The basic objective of this paper is to minimize the number of running PMs. The basic purpose of packing VMs into PMs is to save energy, minimize cost and reduce wastage of resources. The algorithm is proposed to provide optimal results for both single objective and multi objective problems. The proposed algorithm is tested on well-known unimodal and multimodal benchmark functions [6]. The population size is based on the dimension, i.e., 30. Unimodal functions tested here can be considered as multimodal functions in a search space of high dimension. All the algorithms are executed on Matlab with a Windows operating system using Intel Core i7, 2.60 GHz, 3.88 GB RAM.

8.1. Benchmark Functions

Ten well-known benchmark test functions are listed in Table 2 in [6]. These benchmark functions are used to evaluate the performance of the proposed algorithm. Two types of benchmark functions are used: unimodal and multimodal. Unimodal functions have only one optimal solution, includes four functions (SPHERE, SCHWEFEL 2.22, ROSENBROCK and NOISE). They can be taken as a multimodal function in search space of high dimension. Multimodal functions have two or more objective functions. Six complex multimodal functions are SCHWEFEL 2.22, RASTRIGIN, ACKLEY, GRIEWANK, PENALIZED1 and PENALIZED2. The control parameters for the above algorithms are given in Table 3 [6].

Table 2. Benchmark Functions.

S. No.	Function Name	Formula	Dimension	Search Range
1	$SPHER{E}^{\ast }$	$f_1(x)={\sum }_{i=1}^d{x}_i^2$	30	[$-100$,100]
2	$SCHWEFEL{2.22}^{\ast }$	$f_2(x)={\sum }_{i=1}^n|x_i|+{\prod }_{i=1}^n\left|x_i\right|$	30	[−100,100]
3	$ROSENBROC{K}^{\ast }$	$f_3(x)={\sum }_{i=1}^{d-1}[(1-x_i^2)+100{(x_{i+1}-x_i^2)}^2]$	30	[−100,100]
4	$NOIS{E}^{\ast }$	$f_4(x)={\sum }_{i=1}^{n}i{x}_i^4+random()(0,1)$	30	[−100,100]
5	$SCHWEFEL{2.26}^{+}$	$f_5(x)=418.9828\ast d-{\sum }_{i=1}^d[x_{i}sin(\sqrt{|x_i|})]$	30	[−100,100]
6	$RASTRIGI{N}^{+}$	$f_6(x)=10d+{\sum }_{i=1}^d[x_i^2-10cos(2\pi x_i)]$	30	[−100,100]
7	$ACKLE{Y}^{+}$	$f_7(x)=-20exp[-0.2\sqrt{1/d{\sum }_{i=1}^d{x}_i^2}]$	30	[−100,100]
8	$GRIEWAN{K}^{+}$	$f_8(x)=1/4000{\sum }_{i=1}^d{x}_i^2-{\prod }_{i=1}^{d}cos(x_i/\sqrt{i})+1$	30	[−100,100]
9	$PENALIZED{1}^{+}$	$f_9(x)=\pi /n(10{sin}^2(\pi y_1))+{\sum }_{i=1}^{n-1}{(y_i-1)}^2\left[(i+10{sin}^2(\pi y_{(i+1)}))\right]+{(y_n-1)}^2+{\sum }_{i=1}^{n}u(x_i,10,100,4)$	30	[−100,100]
		$y_i=1+1/4(x_i+1),u_{x_i},a,k,m=\left\{\begin{array}{cc}k{(x_i-a)}^m,\hfill & \hfill \mathrm{for}{x}_i\le a\\ 0,\hfill & \hfill \mathrm{for}-a\le x_i\le a\\ k{(x_i-1)}^m,\mathrm{for}{x}_i<-a\hfill \end{array}\right\}$
10	$PENALIZED{2}^{+}$	$f_{10}(x)=1/10({sin}^2(3\pi y_1)+{\sum }_{i=1}^{n-1}{(x_i-1)}^2\left[(1+{sin}^2(3\pi x_{(i+1)}))\right]+{(x_n-1)}^2[1+{sin}^2(2\pi x_n)]+{\sum }_{i=1}^{n}u(x_i,5,100,4)$	30	[−100,100]

Table 3. Input Parameters.

Parameters	PSO	LFPSO	PSOLBP
Population size (NP)	20	20	20
Maximum Fes	200,000	200,000	200,000
c1, c2	1.1931	1.1931	1.1931
Inertia weight $(\omega )$	0.7213	$\omega =(Maxiter-it/Maxit)$	$\omega =0.1+0.8\times (1-it/Maxit)$

8.2. Comparison of Algorithms

Three algorithms PSO [6], LFPSO [6], and PSOLBP are tested for each function independently for about ten times on search space of dimension 30. LFPSO achieved better results than simple PSO [6] however, the improved results are less when compared with the PSOLBP algorithm. PSOLBP outperforms other two algorithms for four benchmark functions (NOISE, RASTRIGIN, ACKLEY and GRIEWANK). LFPSO performs better for three functions, i.e., SCHWEFEL 2.26, PENALIZED1 and PENALIZED2. While simple PSO gets optimal results for the SPHERE, SCHWEFEL 2.22 and ROSENBROCK. Simple PSO works better for unimodal functions and being trapped for multimodal functions [6]. The LFPSO working is the same as that of PSO; the random distribution of the population is done through levy flight. Proposed algorithm is a hybrid of simple PSO and levy flight. Mostly, steps of PSO are followed; however, velocity is found using Mantegna’s algorithm. PSOLBP performs much better than the simple PSO and LFPSO algorithms.

8.2.1. Discussion of Convergence Progress

The convergence graphs of PSO, LFPSO and PSOLBP are graphically shown in Figure 8 and Figure 9 to solve the ten well known test functions for search space of dimension 30. The convergence progress of PSO, LFPSO and PSOLBP with unimodal benchmark functions (SPHERE, SCHWEFEL 2.22, ROSENBROCK and NOISE) is presented in Figure 8. While Figure 9 shows the convergence progress for multimodal benchmark functions (SCHWEFEL 2.26, RASTRIGIN, ACKLEY, GRIEWANK, PENALIZED1 and PENALIZED2).

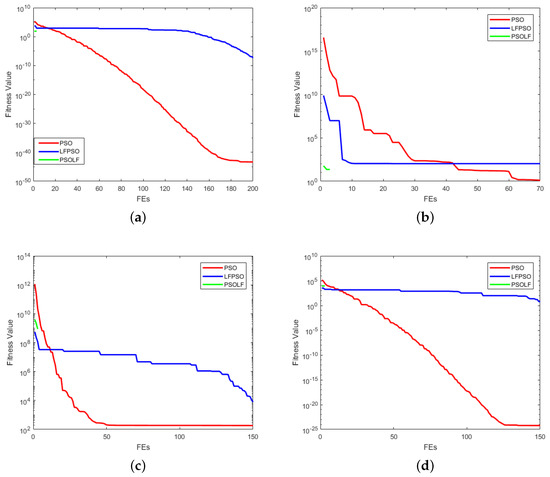
Figure 8. Unimodal Functions. (a) SPHERE; (b) SCHWEFEL 2.22; (c) ROSENBROCK; (d) NOISE.

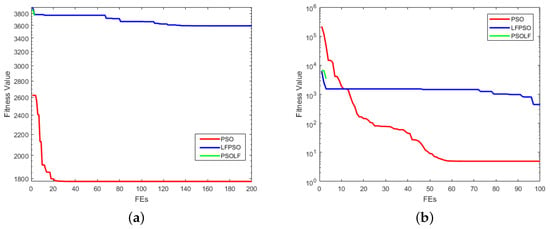
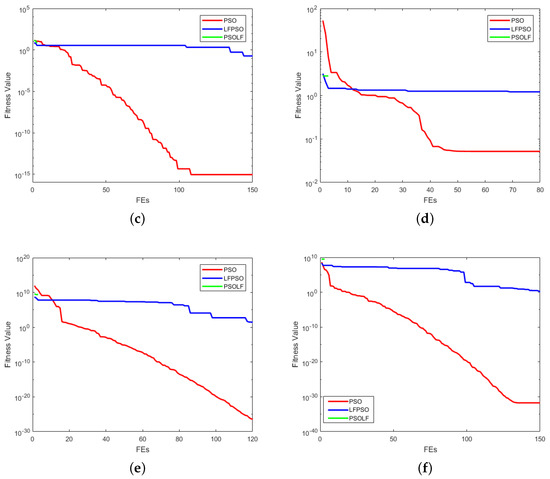
Figure 9. Multimodal Functions. (a) SCHWEFEL2.26; (b) RASTRIGIN; (c) ACKLEY; (d) GRIEWANK; (e) PENALIZED1; (f) PENALIZED2.

For SPHERE function, PSO, LFPSO and PSOLBP obtained best results. PSOLBP converges quickly and achieves the global optimal solution faster.

In SCHWEFEL 2.22 function, PSO performed better than LFPSO. LFPSO does not perform well. PSOLBP convergence behavior is very fast and achieved optimal value.

On ROSENBROCK function, PSO performed better than other two algorithms. LFPSO is trapped in local minima. However, PSOLBP gets stuck in local optimization.

Even PSO progress for NOISE is not good. PSO not performed well for a unimodal function i.e., NOISE. LFPSO and proposed PSOLBP performed well for NOISE.

For SCHWEFEL 2.26, LFPSO performed well. PSO converges but get trapped. However, PSOLBP is also gets stuck in local minima.

For RASTRIGIN, ACKLEY and GRIEWANK, PSOLBP seems to be better than PSO and LFPSO. However, LFPSO outperformed PSO and PSOLBP for PENALIZED1. For PENALIZED2, PSO and LFPSO performed better than PSOLBP.

The proposed PSOLBP performance and convergence behavior is better than other two algorithms. PSOLBP very fastly reaches optimal solution.

8.2.2. Unimodal Functions

Four unimodal test functions are used. They are used for single optimization problems. A simple PSO performs better for single optimization problems trapped in local optima. In a high dimensional search space, these functions can be considered as multimodal test functions. Simple PSO performed well for SPHERE, SCHWEFEL 2.22 and ROSENBROCK. While PSOLBP gave better results for NOISE.

In SPHERE, SCHWEFEL 2.22 and ROSENBROCK, the simple PSO algorithm is being trapped in local optima. PSO outperformed other two algorithms. The three algorithms are executed for 10 times to check the adaptivity of the proposed algorithm. However, the proposed algorithm performed well for NOISE. The PSO algorithm find global optimal or near global optimal value using SPHERE, SCHWEFEL 2.22 and ROSENBROCK. While LFPSO performed well for SPHERE in global optimization. For global optimization, PSOLBP gives better results with SPHERE, SCHWEFEL 2.22 and NOISE.

PSOLBP is insensitive to dimensionality. Extensive simulations are done after increasing and decreasing the dimension of the search space.

8.2.3. Multimodal Functions

Six multimodal functions are considered to provide solutions for two or more optimization problems. SCHWEFEL 2.26, RASTRIGIN, ACKLEY, GRIEWANK, PENALIZED1 and PENALIZED2 are tested with three algorithms. PSO does not perform well for more than one objective function problem. LFPSO performed well for SCHWEFEL 2.26, PENALIZED1 and PENALIZED2. While the proposed PSOLBP outperformed other algorithms for three functions i.e., RASTRIGIN, ACKLEY and GRIEWANK. The PSOLBP is proposed to give optimum results for more than one objective function. For global optimization, PSO does not performed efficiently. LFPSO performed well in global optimization problems with SCHWEFEL 2.26, PENALIZED1 and PENALIZED2. PSOLBP achieved better results with RASTRIGIN, ACKLEY and GRIEWANK for global optimization.

8.3. PSOLBP

PSOLBP outperforms the other two algorithms when tested on benchmark functions; it is used with VSBPP. In PSOLBP, the random distribution of the population is done through simple PSO. The positions of the particles are also found through PSO. The levy flight is used to update the velocity of the particles. A best-fit strategy is used to pack the maximum number of VMs into PMs. The main objective of the proposed work is to minimize the usage of running PMs. The utilization rate of PMs is minimized to save energies and cost. Bin packing problem is considered to avoid wastage of resources and increase the efficiency of a cloud. A new PM is allocated when an old one is fully packed. With the number of iterations, the utilization rate of running PMs become less. It can be noticed from Figure 10 that after some point the utilization rate of PMs is zero.

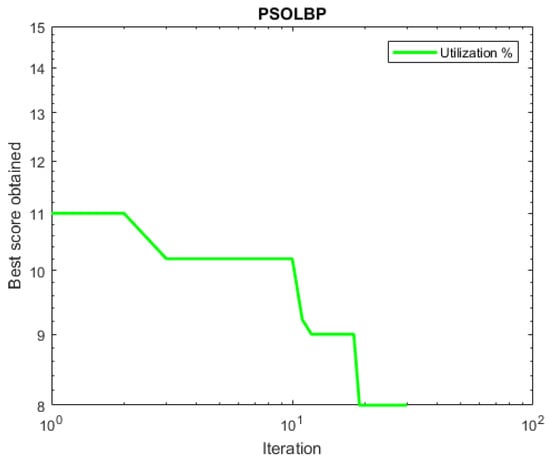
Figure 10. PSOLBP.

9. Conclusions

Cloud computing is turning into an emerging field. Cloud data centers are very complex. The technology evolves causing the influx of a large amount of information. Efficient management of cloud computing is needed. VM-integration and intelligent task assignment are used to optimally manage the load of a cloud data center. This paper proposed an efficient VM-placement algorithm. An enhanced PSOLBP is applied to the variable-sized bin packing problem. This is the hybrid of two algorithms: levy flight and PSO. The best-fit strategy is used in BPP. Extensive simulations are done to verify the efficiency and adaptivity of the proposed algorithm. Through this, the overall performance of a cloud data center is improved. To evaluate the performance of the given algorithm, ten benchmark functions are used. The proposed algorithm is easy to understand and simple to implement. It is also insensitive to dimensionality.

Future Studies

VM-placement is an NP-hard problem and most real-world engineering problems have more than one objective to be optimized. So, further optimization is required to solve multi-objective problems. In the future, the proposed algorithm will probably be used to solve multi-objective VM-placement, as well as dynamic migration and scheduling problems.