Computationally Efficient Channel Estimation in 5G Massive Multiple-Input Multiple-output Systems
Abstract
:1. Introduction
2. System Model
2.1. Minimum Mean Square Error Signal Detection
2.2. Log Likelihood Ratio Calculation
3. Low Complexity Signal Detection
3.1. Neumann Series Expansion
3.2. Gauss–Seidel Algorithm
4. Proposed Algorithm
4.1. Hybrid Iterative Algorithm Structure
- Step 1: For the diagonal approximation’s initial value setting, Equation (4) can be converted to ; is a symmetric positive definite matrix and a diagonally dominant matrix, so is also a diagonally dominant matrix.
- Step 2: Determine the initial solution using instead of :Since is a diagonal matrix, it is obvious that calculating requires only low complexity, and the initial value, , is set to the initial value of the SD algorithm according to Equation (15).
- Step 3: The iterative results of the first two GS algorithms are represented by the SD algorithm, and the second GS iteration result can be expressed as:
- Step 4: Combine single SD and GS iterations into one hybrid iteration by substituting Equation (17) andThis represents the first two GS iterations as Equation (18); update the mixed iteration value , and then perform the next GS iteration.
- Step 5: Using the GS iteration using Equation (14), ideal estimated value of the transmitted signal vector can be obtained by setting the appropriate number of iterations, i:Then, is related to the complex domain for the next soft decision, so the hybrid iterative algorithm can converge very quickly after a small number of iteration.
4.2. Approximate Log-Likelihood Ratio Calculation
4.3. Complexity Analysis
4.3.1. Initial Value and First Iteration Calculation
4.3.2. GS iteration
4.3.3. LLR calculation
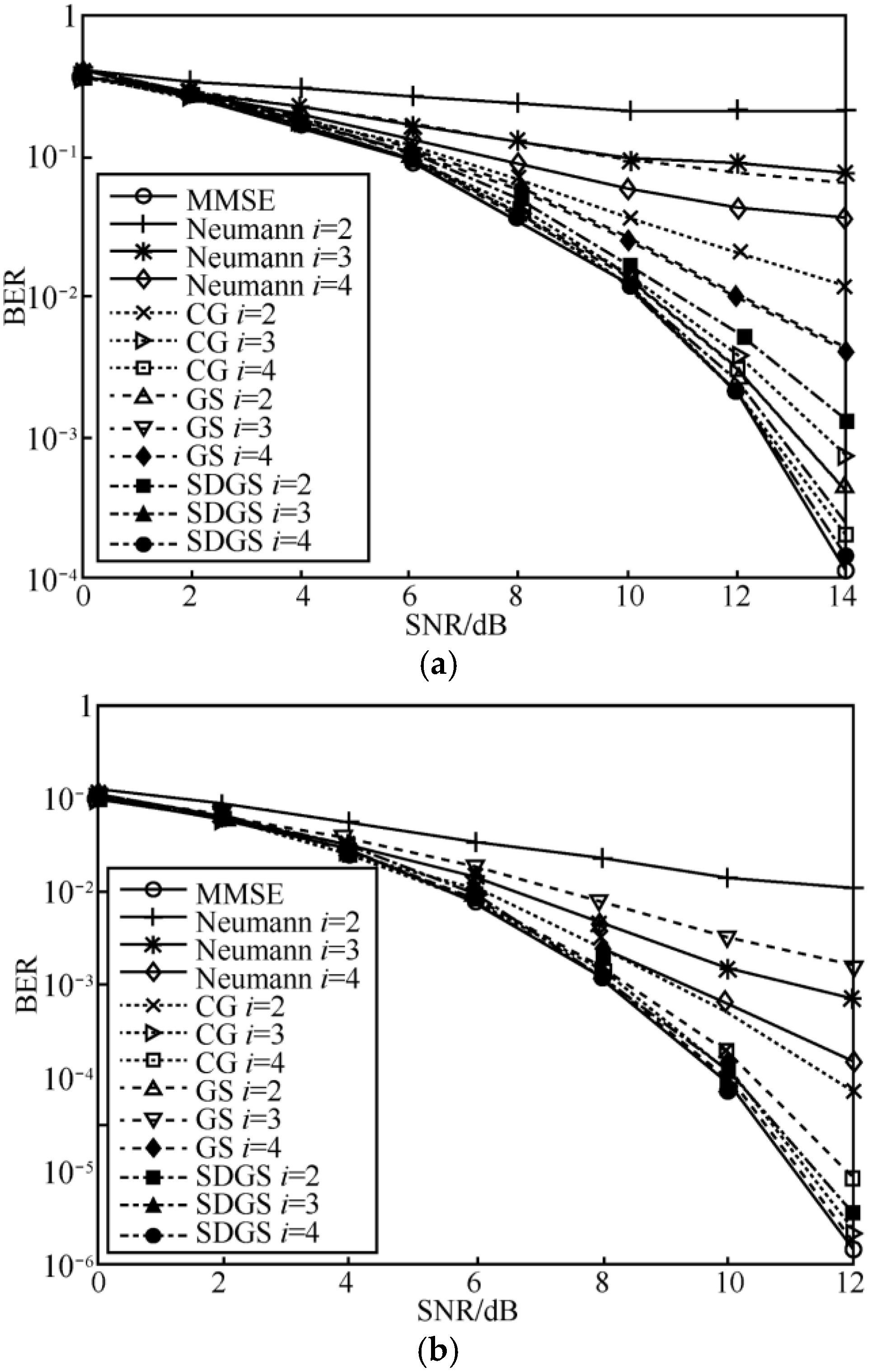
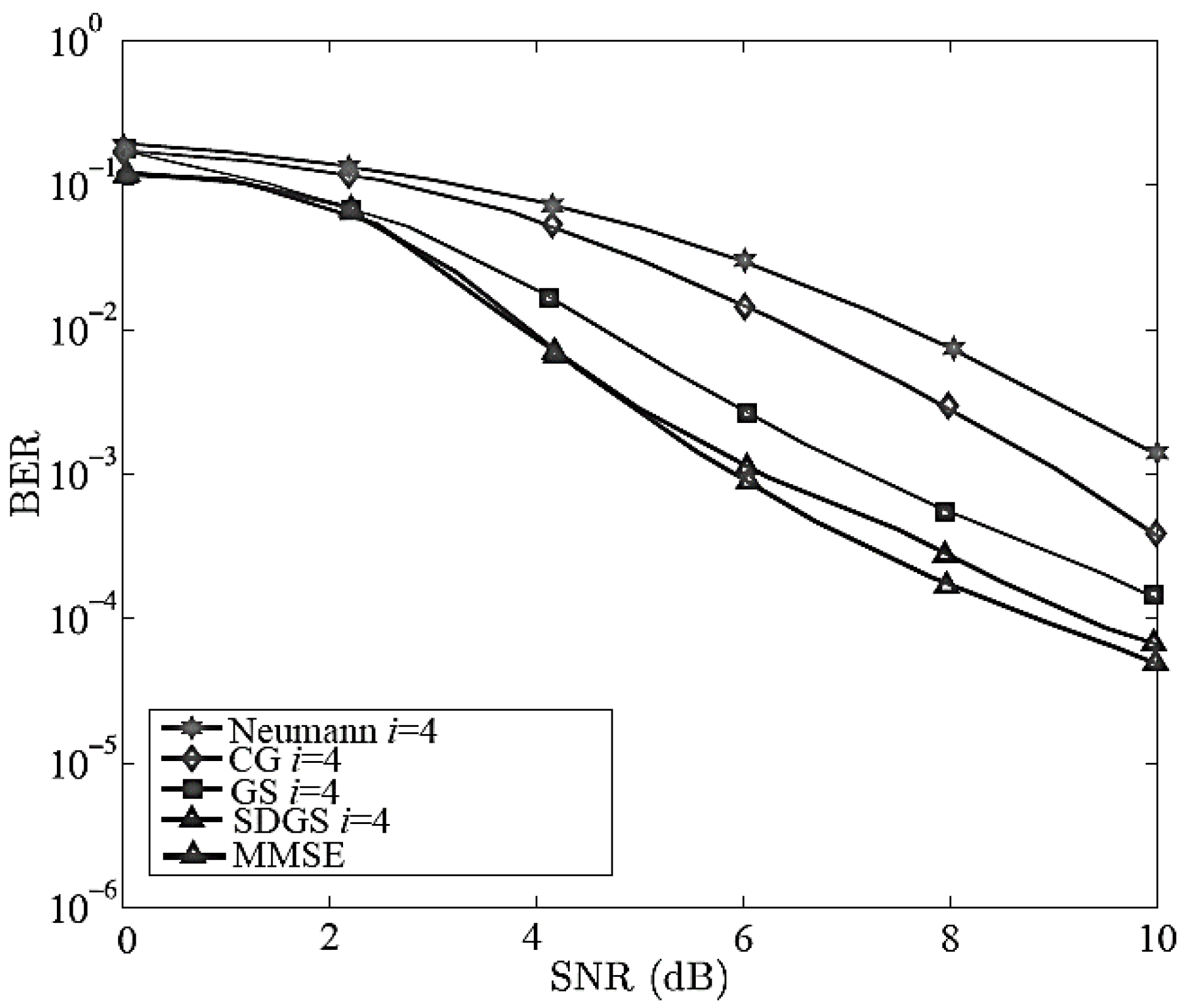
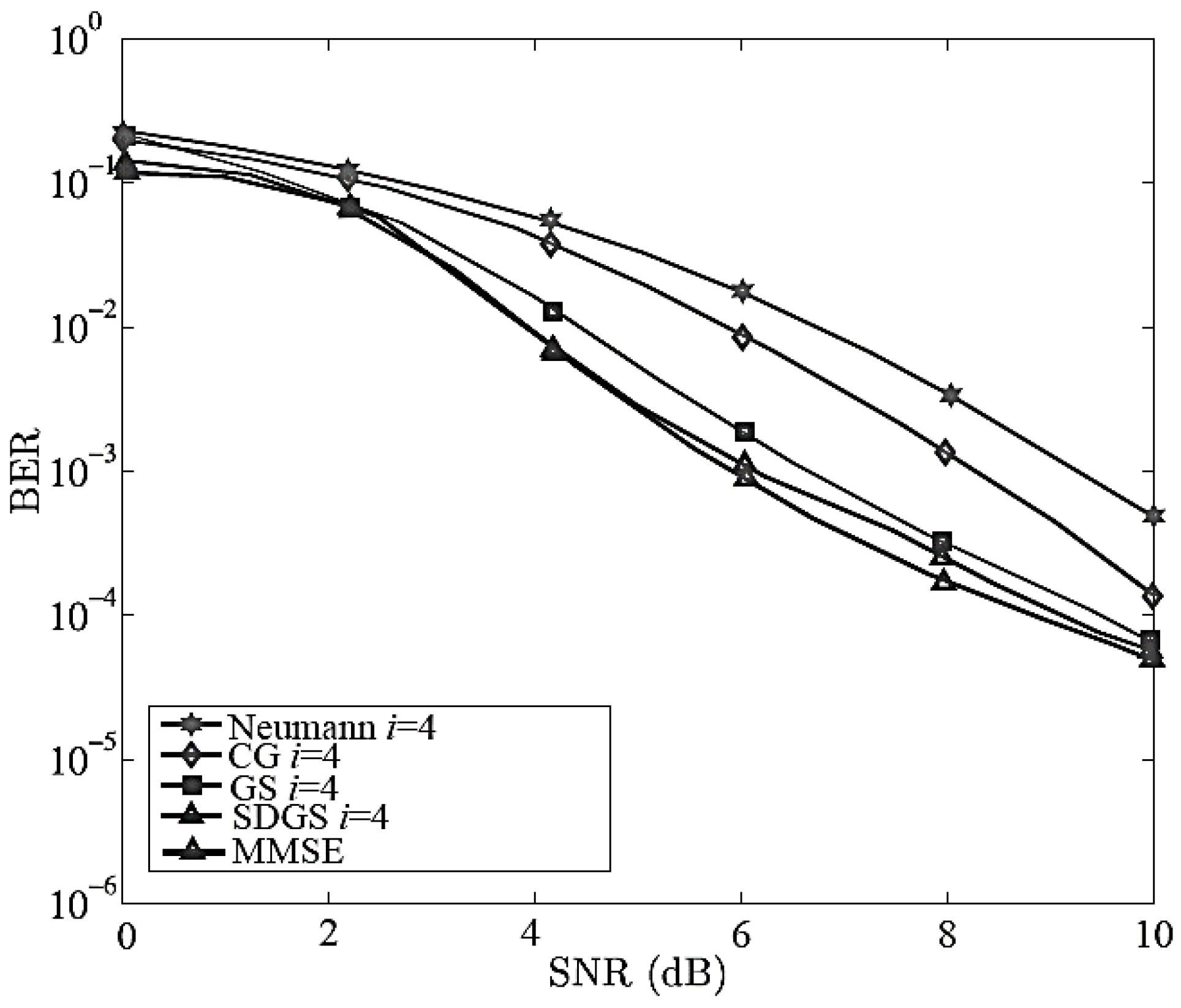
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chang, Y.K.; Ueng, F.B.; Jhang, Y.W. Turbo MIMO-OFDM Receiver in Time-Varying Channels. KSII Trans. Internet Inf. Syst. 2018, 12, 3704–3724. [Google Scholar]
- Tseng, S.M.; Chen, Y.F. Average PSNR Optimized Cross Layer User Grouping and Resource Allocation for Uplink MU-MIMO OFDMA Video Communications. IEEE Access 2018, 6, 50559–50571. [Google Scholar] [CrossRef]
- Ghosh, A.; Ratasuk, R.; Mondal, B.; Mangalvedhe, N.; Thomas, T. LTE-advanced: Next-generation wireless broadband technology. IEEE Wirel. Commun. 2010, 17, 10–22. [Google Scholar] [CrossRef]
- Khan, I.; Zafar, M.H.; Jan, M.T.; Lloret, J.; Basheri, M.; Singh, D. Spectral and Energy Efficient Low-Overhead Uplink and Downlink Channel Estimation for 5G Massive MIMO Systems. Entropy 2018, 20, 92. [Google Scholar] [CrossRef]
- Rusek, F.; Persson, D.; Lau, B.K.; Larsson, E.G.; Marzetta, T.L.; Edfors, O.; Tufvesson, F. Scaling up MIMO: Opportunities and challenges with very large arrays. IEEE Signal Process. Mag. 2012, 30, 40–60. [Google Scholar] [CrossRef]
- Larsson, E.G.; Edfors, O.; Tufvesson, F.; Marzetta, T.L. Massive MIMO for next-generation wireless systems. IEEE Commun. Mag. 2014, 52, 186–195. [Google Scholar] [CrossRef]
- Marzetta, T.L. Noncooperative cellular wireless with unlimited numbers of base station antennas. IEEE Trans. Wirel. Commun. 2010, 9, 3590–3600. [Google Scholar] [CrossRef]
- Khan, I.; Singh, D. Efficient compressive sensing based sparse channel estimation for 5G massive MIMO systems. AEU-Int. J. Electron. Commun. 2018, 89, 181–190. [Google Scholar] [CrossRef]
- Ngo, H.Q.; Larsson, E.G.; Marzetta, T.L. Energy and spectral efficiency of very large multiuser MIMO systems. IEEE Trans. Commun. 2011, 61, 1436–1449. [Google Scholar]
- Dai, L.; Wang, Z.; Yang, Z. Spectrally efficient time-frequency training OFDM for mobile large-scale MIMO systems. IEEE J. Sel. Areas Commun. 2013, 31, 251–263. [Google Scholar] [CrossRef]
- Benmimoune, M.; Driouch, E.; Ajib, W. Joint antenna selection in grouping in Massive MIMO Systems. In Proceedings of the 10th International Symposium on Communication Systems, Networks and Digital Signal Processing (CSNDSP), Prague, Czech Republic, 20–22 July 2016; pp. 1–6. [Google Scholar]
- Khan, I. A Robust Signal Detection Schemefor 5G Massive Multiuser MIMO Systems. IEEE TVT. 2018, 67, 9567–9604. [Google Scholar]
- Wu, M.; Yin, B.; Wang, G.; Dick, C.; Cavallaro, J.R.; Studer, C. Large-scale MIMO detection for 3GPP LTE: Algorithms and FPGA implementations. IEEE J. Sel. Top. Signal Process. 2014, 85, 916–929. [Google Scholar] [CrossRef]
- Tang, C.; Liu, C.; Yuan, L.; Xing, Z. High precision low complexity matrix inversion based on Newton iteration for data detection in the massive MIMO. IEEE Commun. Lett. 2016, 20, 490–493. [Google Scholar] [CrossRef]
- Gao, X.; Dai, L.; Yuen, C.; Zhang, Y. Low-complexity MMSE signal detection based on Richardson method for large-scale MIMO systems. In Proceedings of the Vehicular Technology Conference, Vancouver, BC, Canada, 14–17 September 2014; pp. 1–5. [Google Scholar]
- Gao, X.; Dai, L.; Hu, Y.; Wang, Z.; Wang, Z. Matrix inversion-less signal detection using SOR method for uplink large-scale MIMO systems. In Proceedings of the IEEE Global Communications Conference, Qingdao, China, 8–12 December 2014; pp. 3291–3295. [Google Scholar]
- Hu, Y.; Wang, Z.; Gaol, X.; Ning, J. Low-complexity signal detection using the CG method for uplink large-scale MIMO systems. In Proceedings of the IEEE International Conference on Communications, Macau, China, 19–21 November 2014; pp. 477–481. [Google Scholar]
- Hageman, L.A. The Iterative Solution for Large Linear Systems; Academic Press: Manhattan, NY, USA, 1971; pp. 9–22. [Google Scholar]
- Dai, L.; Gao, X.; Su, X.; Han, S.; Chih-Lin, I.; Wang, Z. Low-complexity soft-output signal detection based on a Gauss-Seidel method for uplink multiuser large-scale MIMO systems. IEEE Trans. Veh. Technol. 2014, 64, 4839–4845. [Google Scholar] [CrossRef]
- Wu, M.; Yin, B.; Vosoughi, A.; Studer, C.; Cavallaro, J.R.; Dick, C. Approximate matrix inversion for high-throughput data detection in the large-scale MIMO uplink. In Proceedings of the International Symposium on Circuits & Systems, Beijing, China, 19–23 May 2013; pp. 12155–12158. [Google Scholar]

| Algorithm | Real Multiplications | Performance |
|---|---|---|
| NS [11] | General | |
| CG [15] | Better | |
| GS [17] | Better | |
| SDGS | Optimal |
| Parameter | Value |
|---|---|
| Number of transmitter antennas | 64–128 |
| Number of receiver antennas | 16 |
| Baseband modulation mode | 16 QAM |
| Signal-to-noise ratio (SNR) | 10–12 dB |
| Code rate | ½ |
| Channel characteristics | Uncorrelated Rayleigh fading |
| Number of iterations | 1000 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, I.; Zafar, M.H.; Ashraf, M.; Kim, S. Computationally Efficient Channel Estimation in 5G Massive Multiple-Input Multiple-output Systems. Electronics 2018, 7, 382. https://doi.org/10.3390/electronics7120382
Khan I, Zafar MH, Ashraf M, Kim S. Computationally Efficient Channel Estimation in 5G Massive Multiple-Input Multiple-output Systems. Electronics. 2018; 7(12):382. https://doi.org/10.3390/electronics7120382
Chicago/Turabian StyleKhan, Imran, Mohammad Haseeb Zafar, Majid Ashraf, and Sunghwan Kim. 2018. "Computationally Efficient Channel Estimation in 5G Massive Multiple-Input Multiple-output Systems" Electronics 7, no. 12: 382. https://doi.org/10.3390/electronics7120382
APA StyleKhan, I., Zafar, M. H., Ashraf, M., & Kim, S. (2018). Computationally Efficient Channel Estimation in 5G Massive Multiple-Input Multiple-output Systems. Electronics, 7(12), 382. https://doi.org/10.3390/electronics7120382





