Equivalent Circuit Model for Cu(In,Ga)Se2 Solar Cells Operating at Different Temperatures and Irradiance
Abstract
1. Introduction
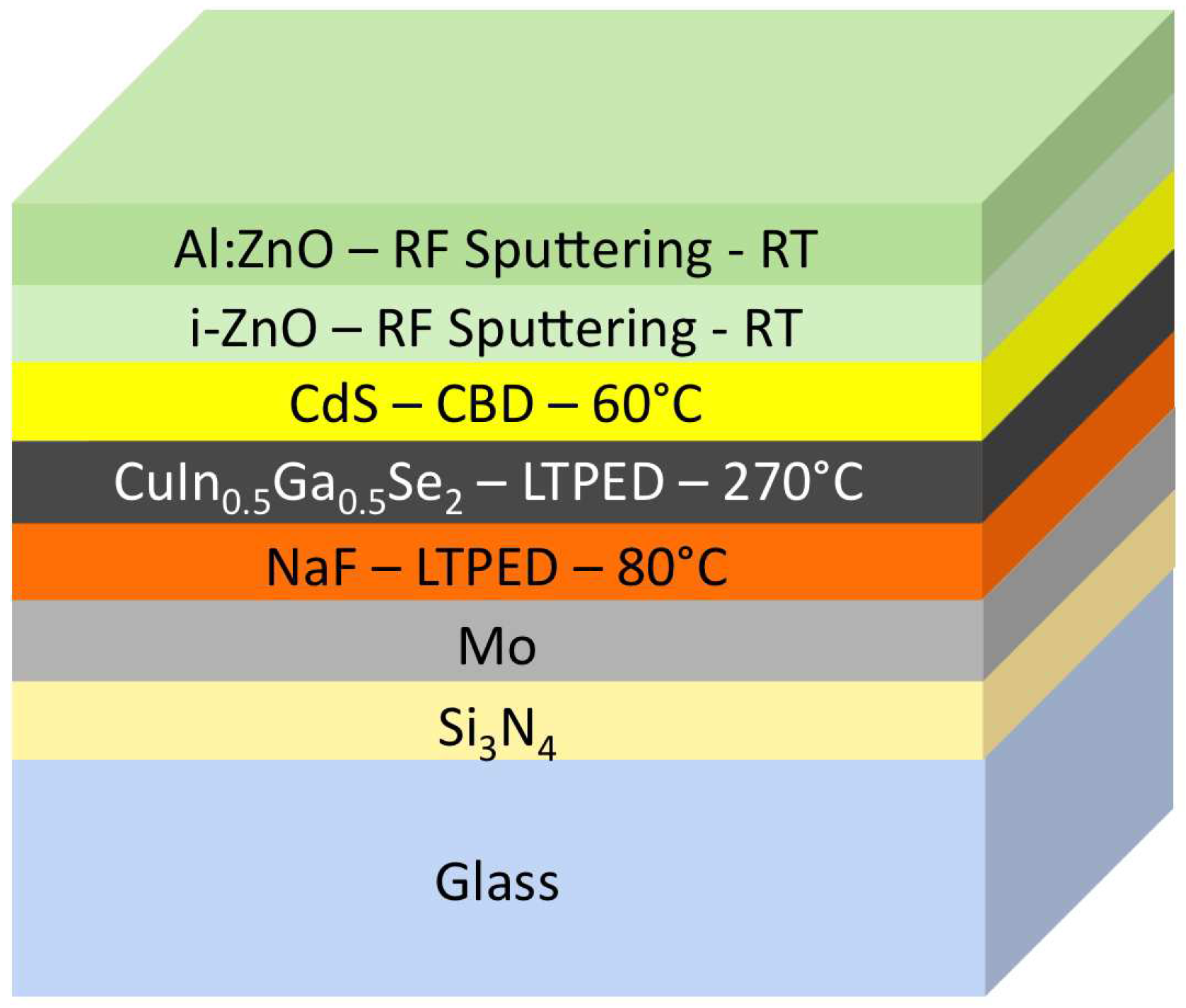
2. Experimental Setup and Measurements
- A class ABB solar simulator equipped with a xenon lamp was used to reproduce the solar spectrum;
- three air mass filters were used to shape the spectrum;
- a system to sense and tune the temperature of the cells made by a thermocouple, a Peltier cell and a temperature controller was used to set and check cell temperature;
- a curve-tracer was used to extract the current from the cells by setting a voltage in the range [−0.2, 1] V with a step of 0.01 V;
- a calibrated test cell measured the irradiance;
- all the acquisition and measurements were controlled by a LabVIEW interface.
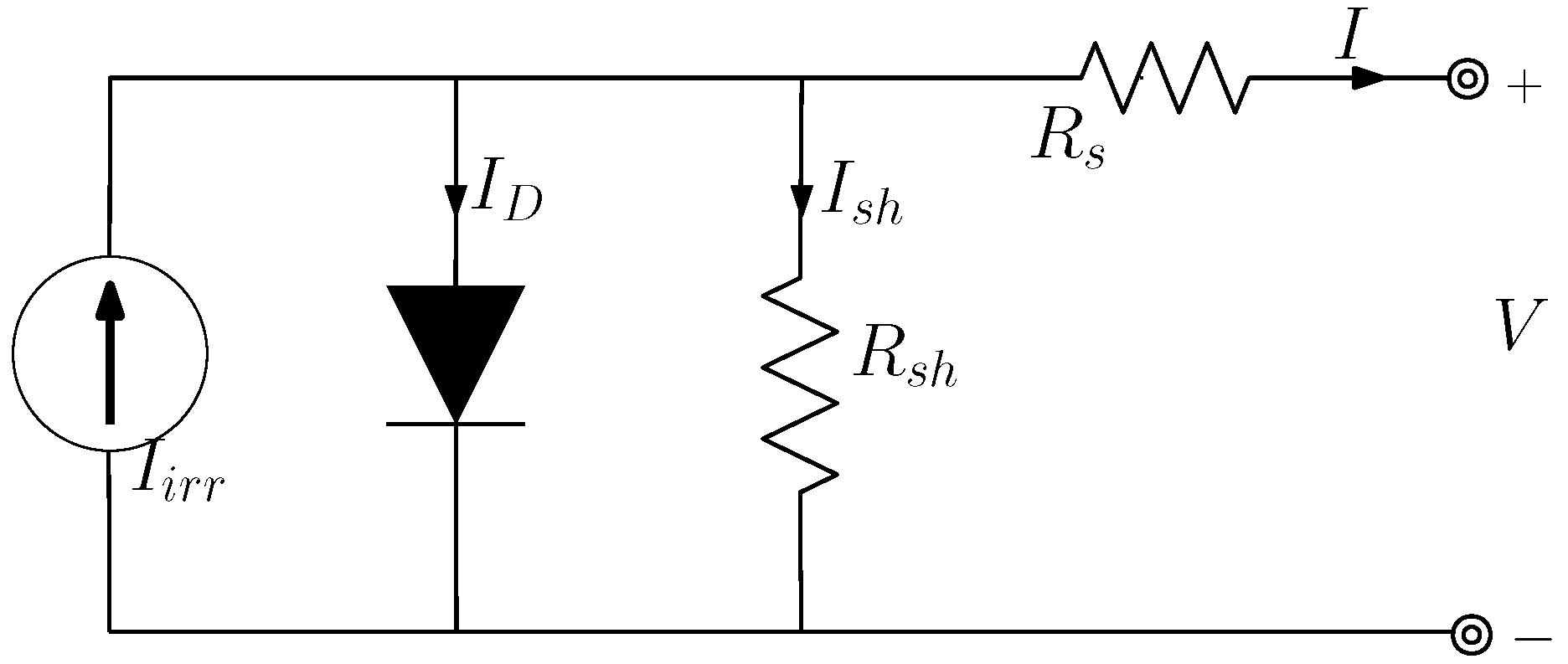
3. Identification of the One-Diode Model from Measurements
- Initial determination of the model parameters by solving the reduced-form problem (i.e., extraction of n and ). The problem is solved by means of the least squares method on I-V curves in the voltage range (0–). The algorithm iteratively adjusts [n, ] by minimizing the squared error between computed and measured current samples.
4. Model for Irradiance and Temperature Dependence
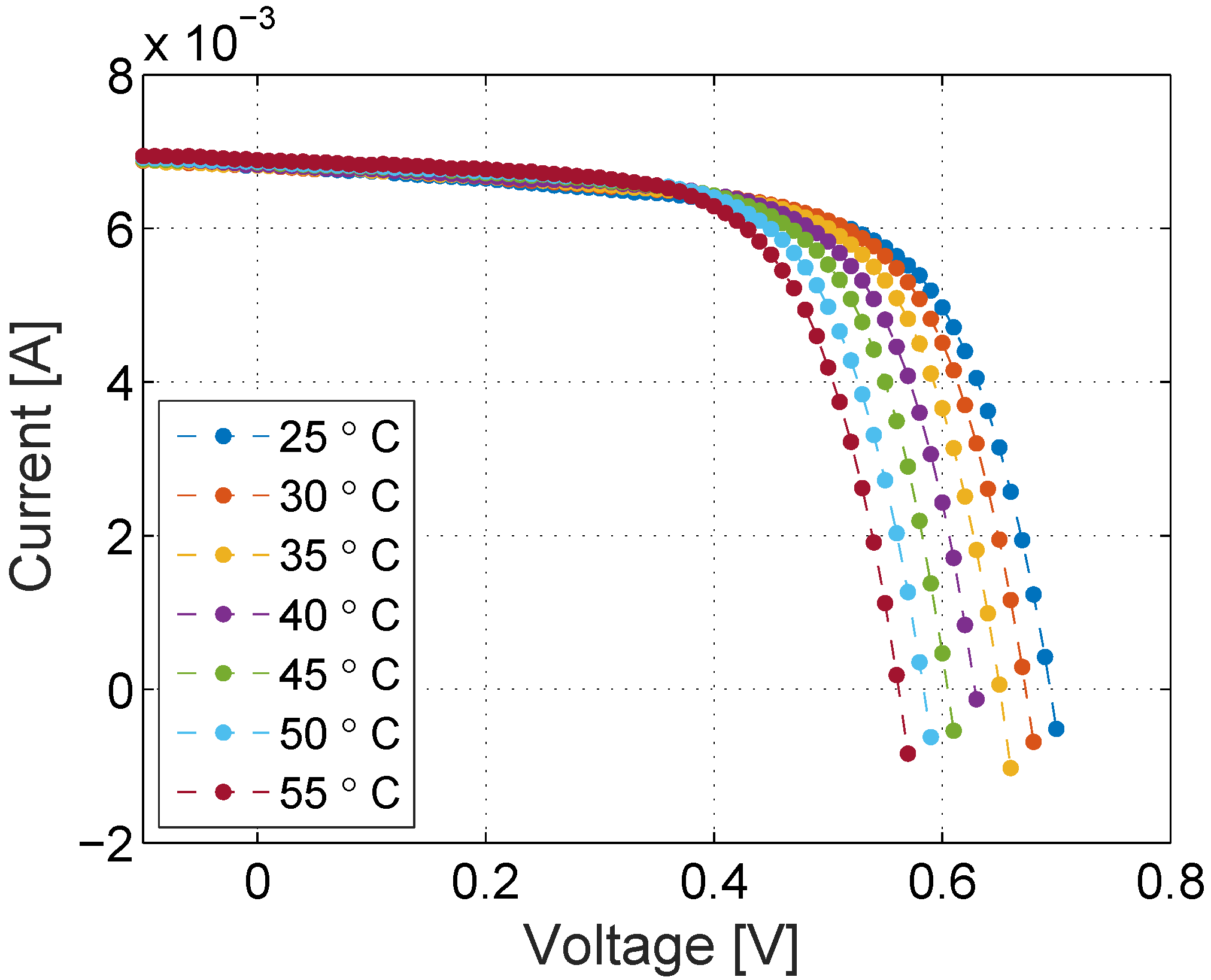
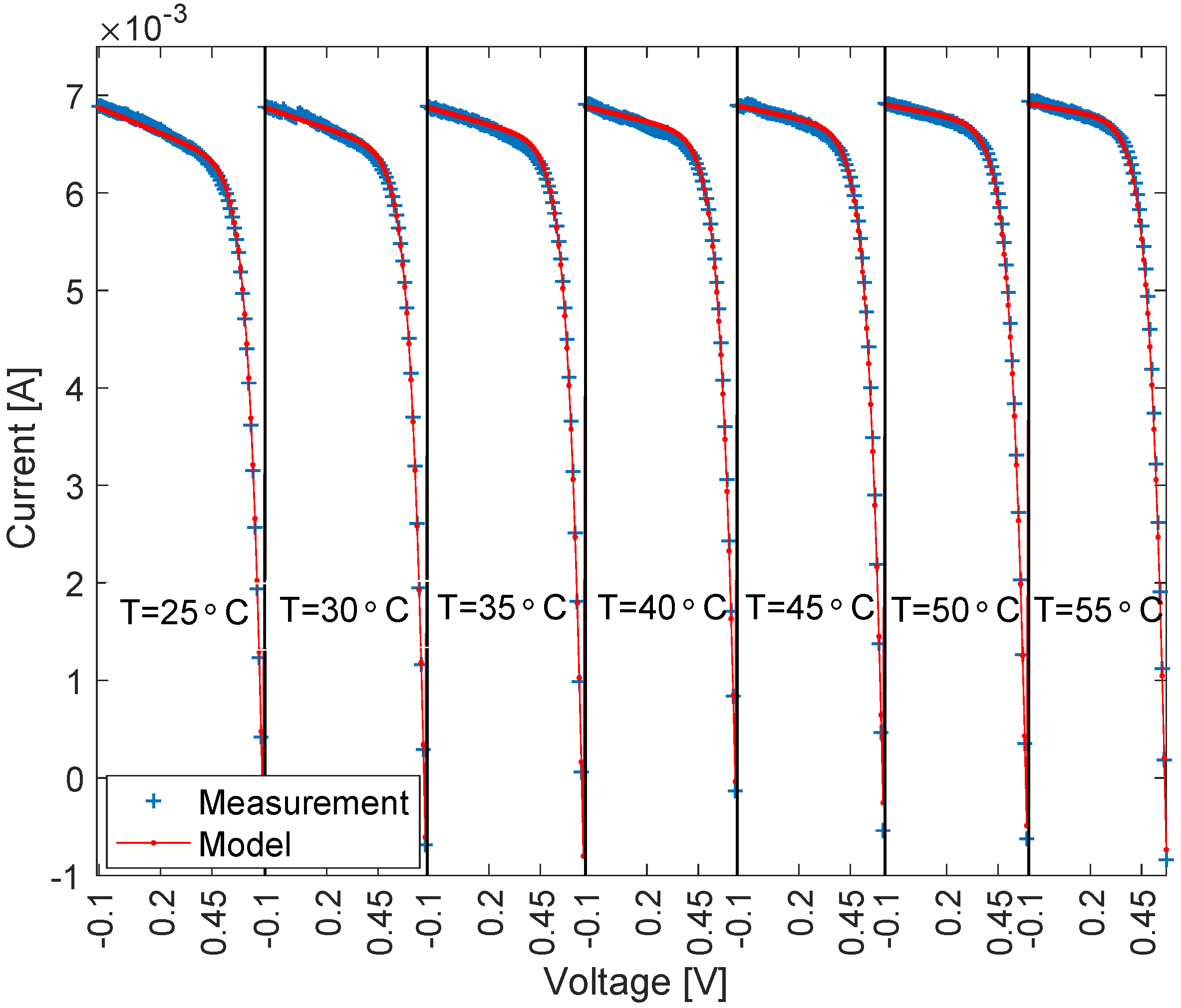
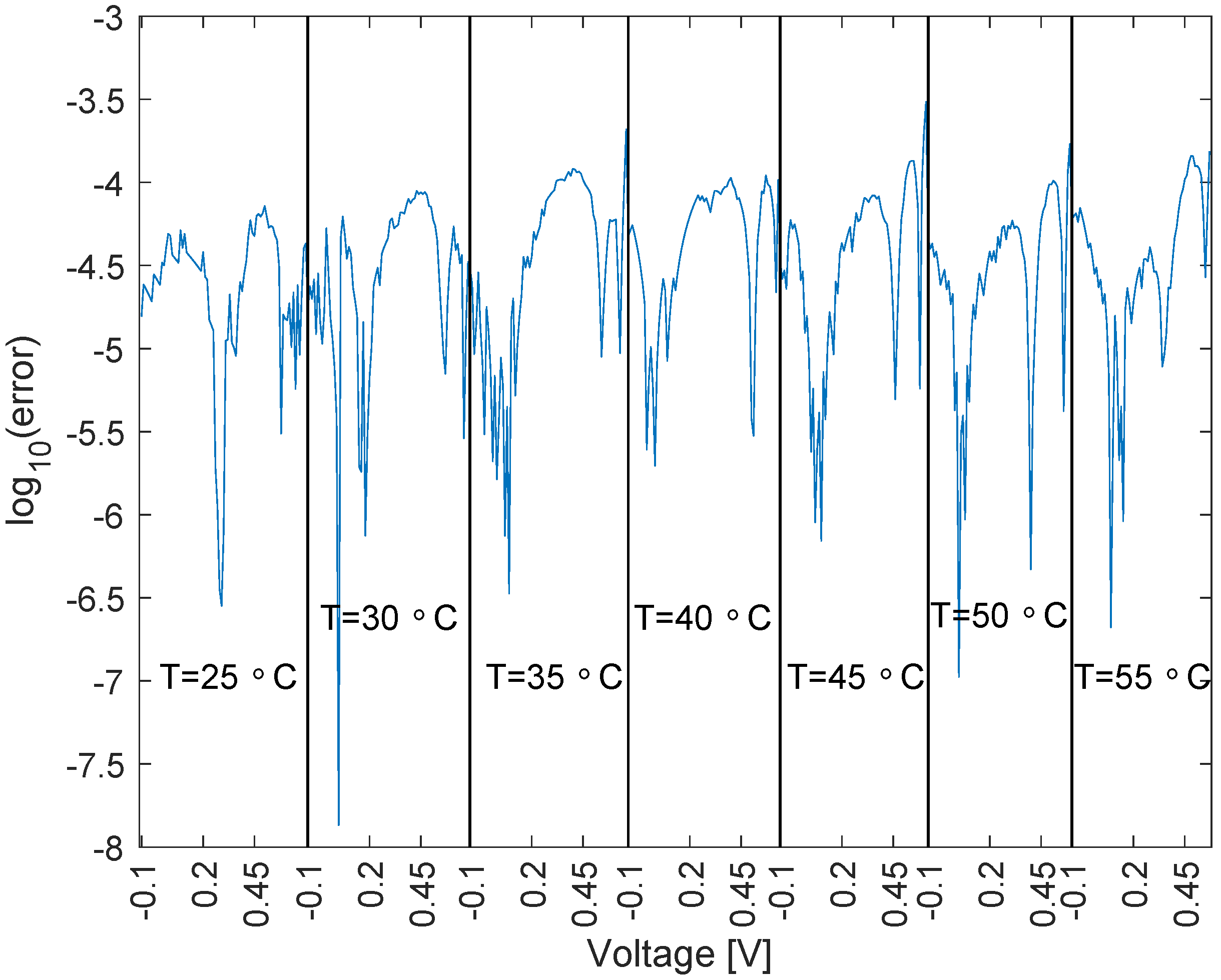
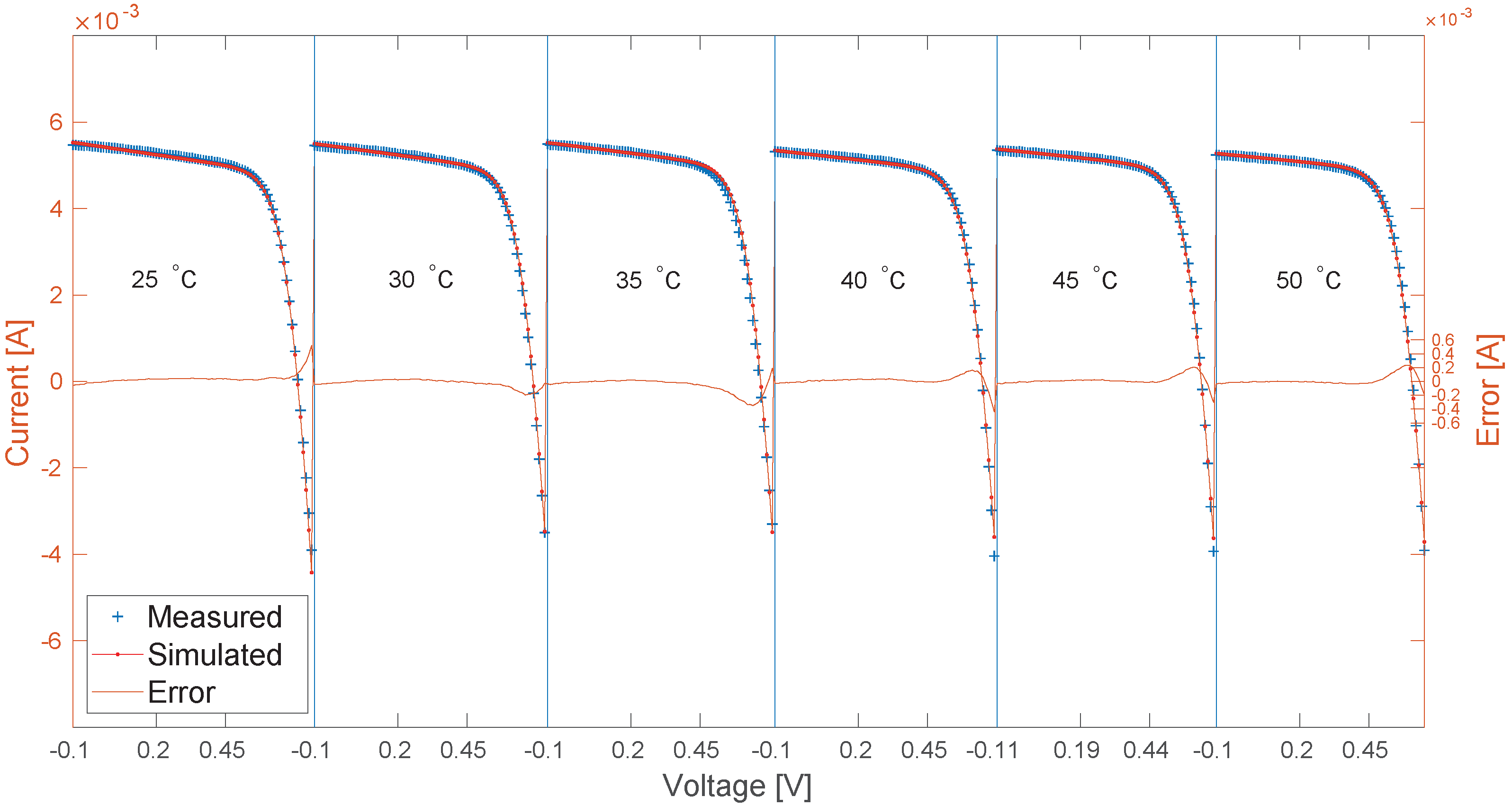
4.1. Temperature Set
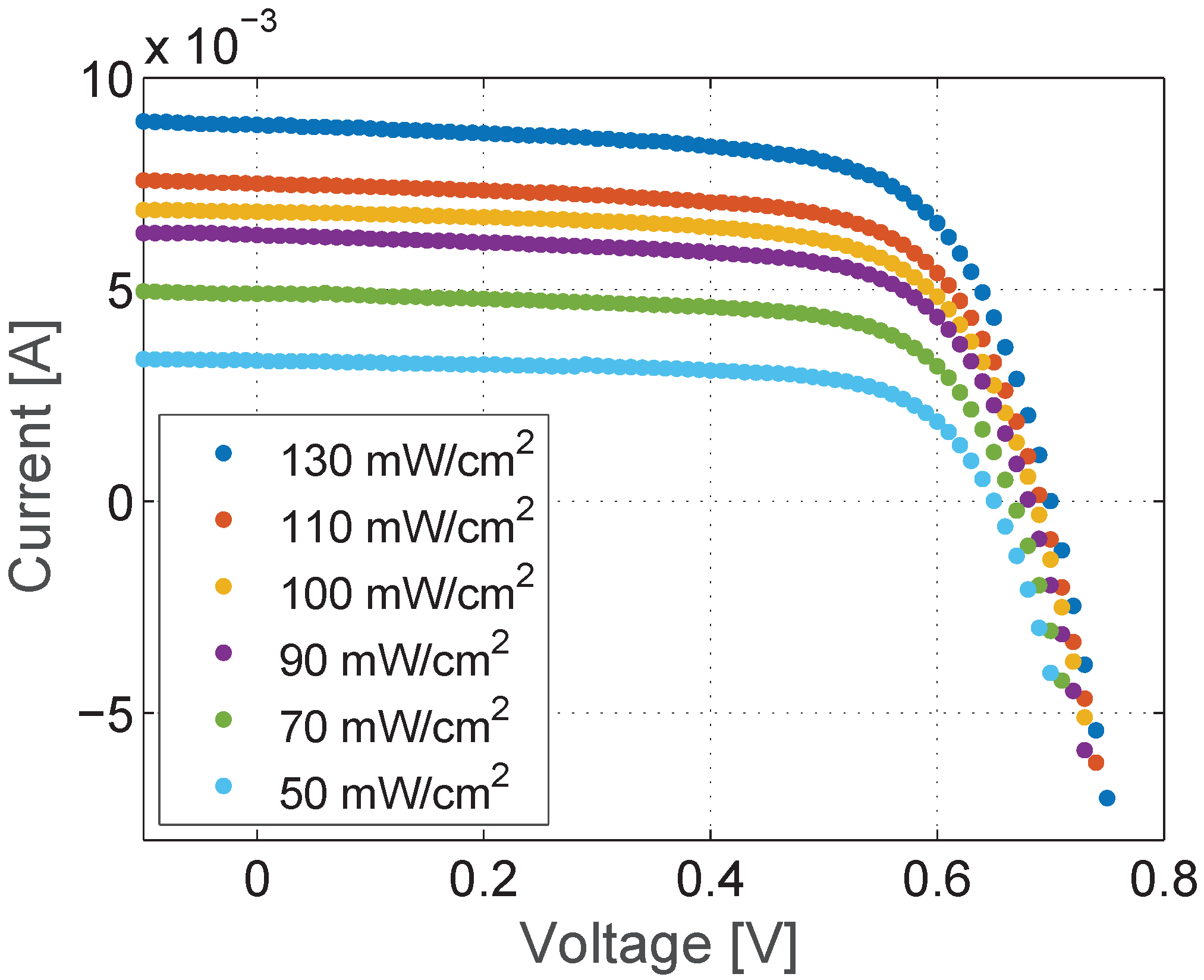
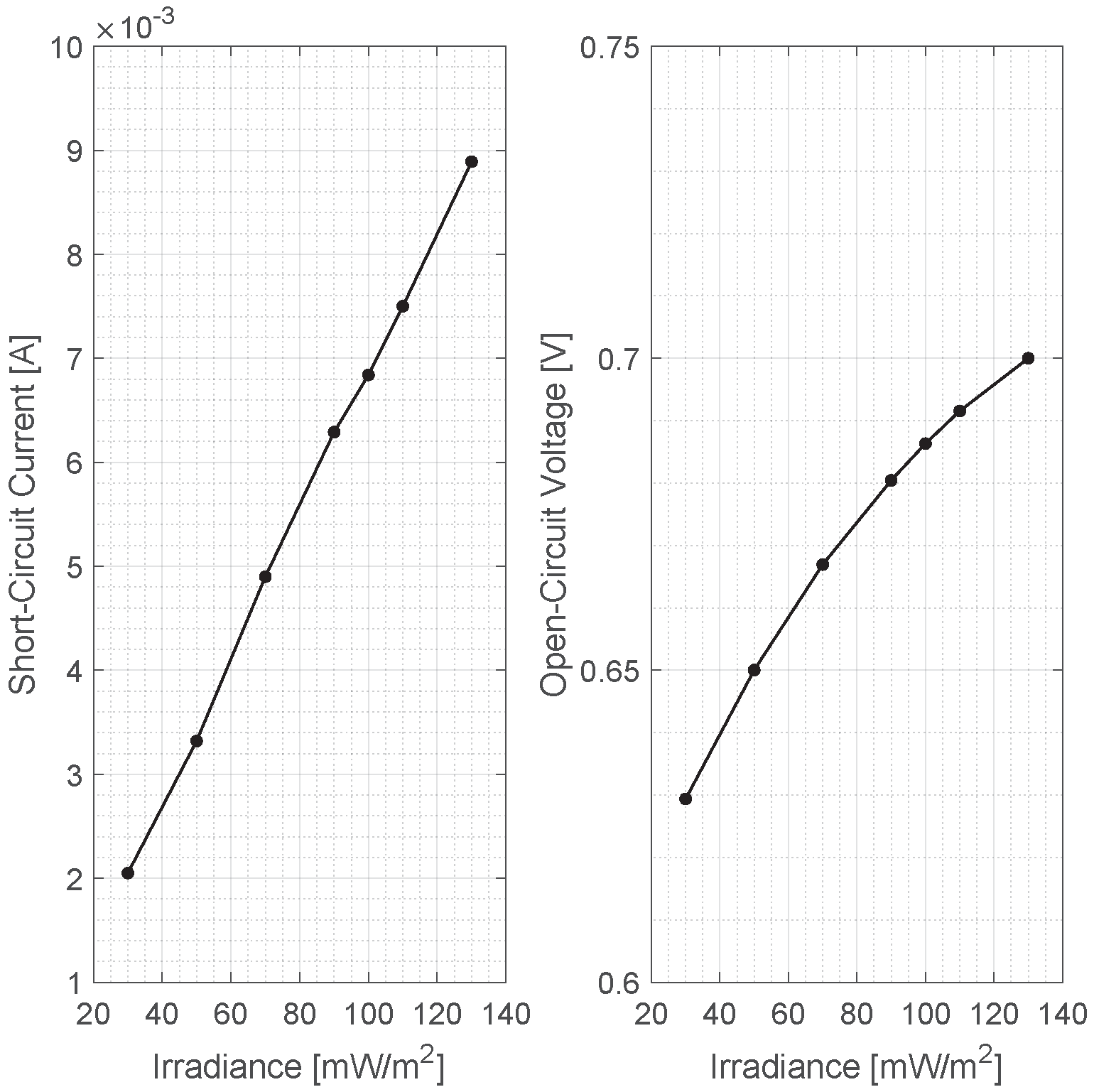
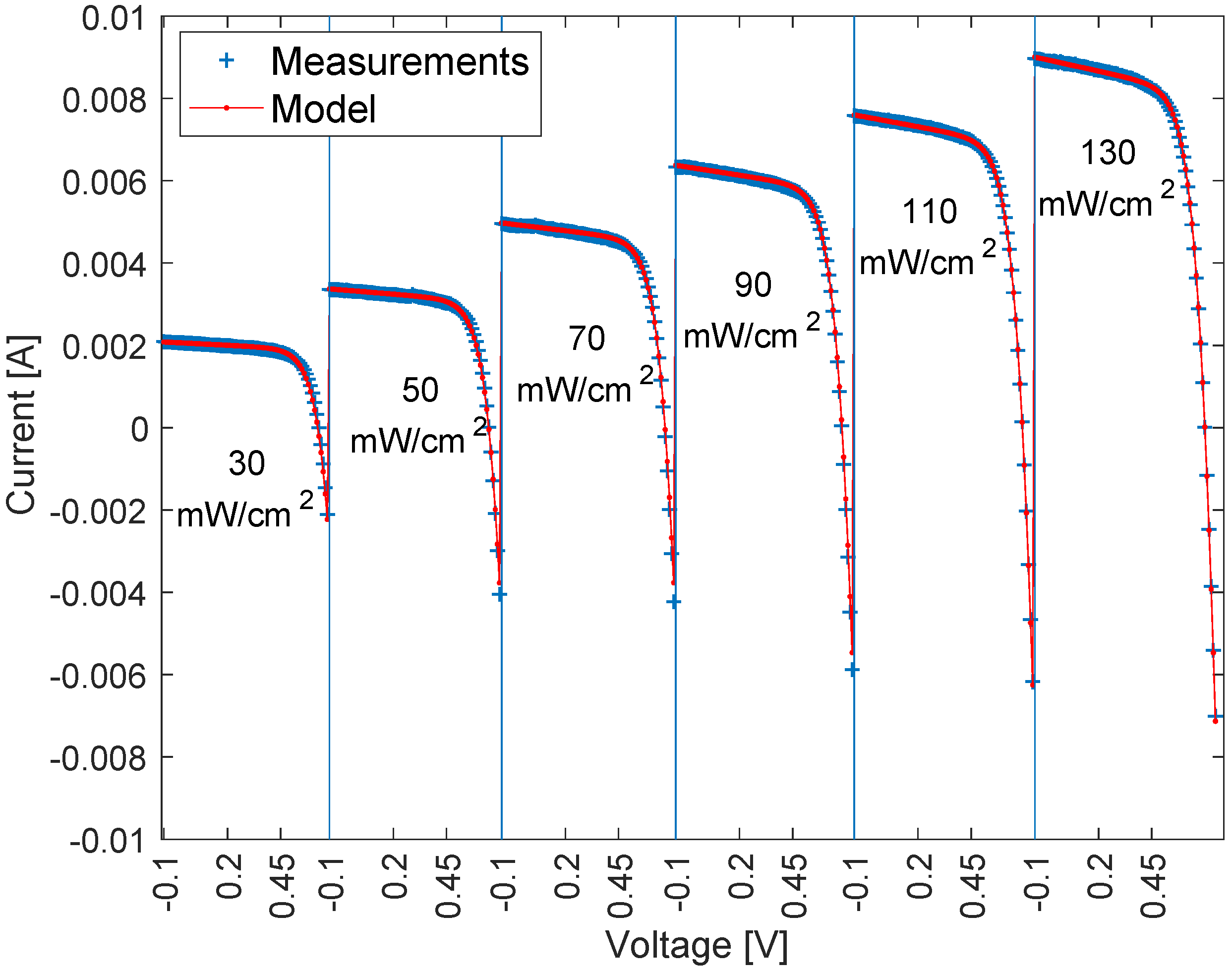
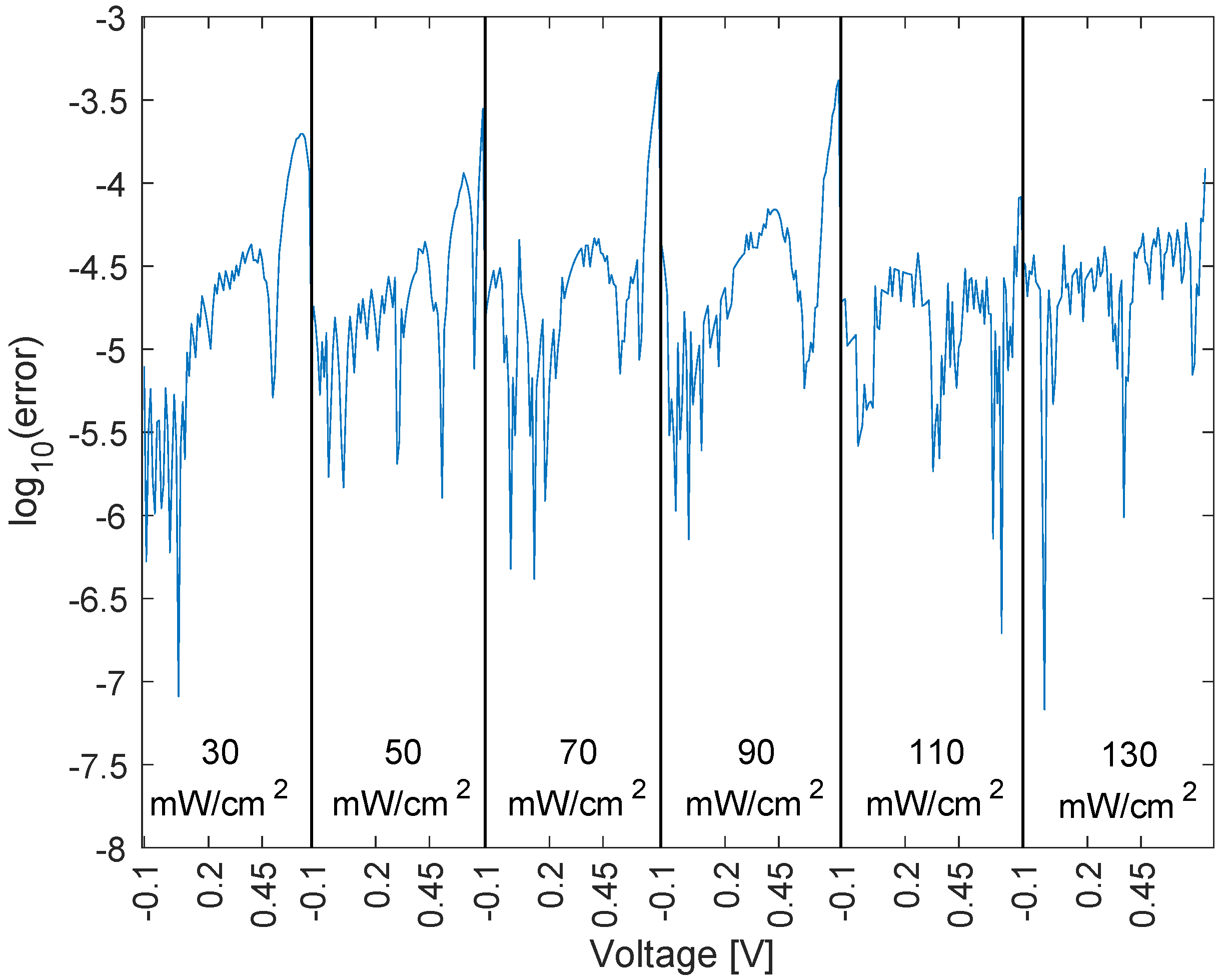
4.2. Irradiance Set
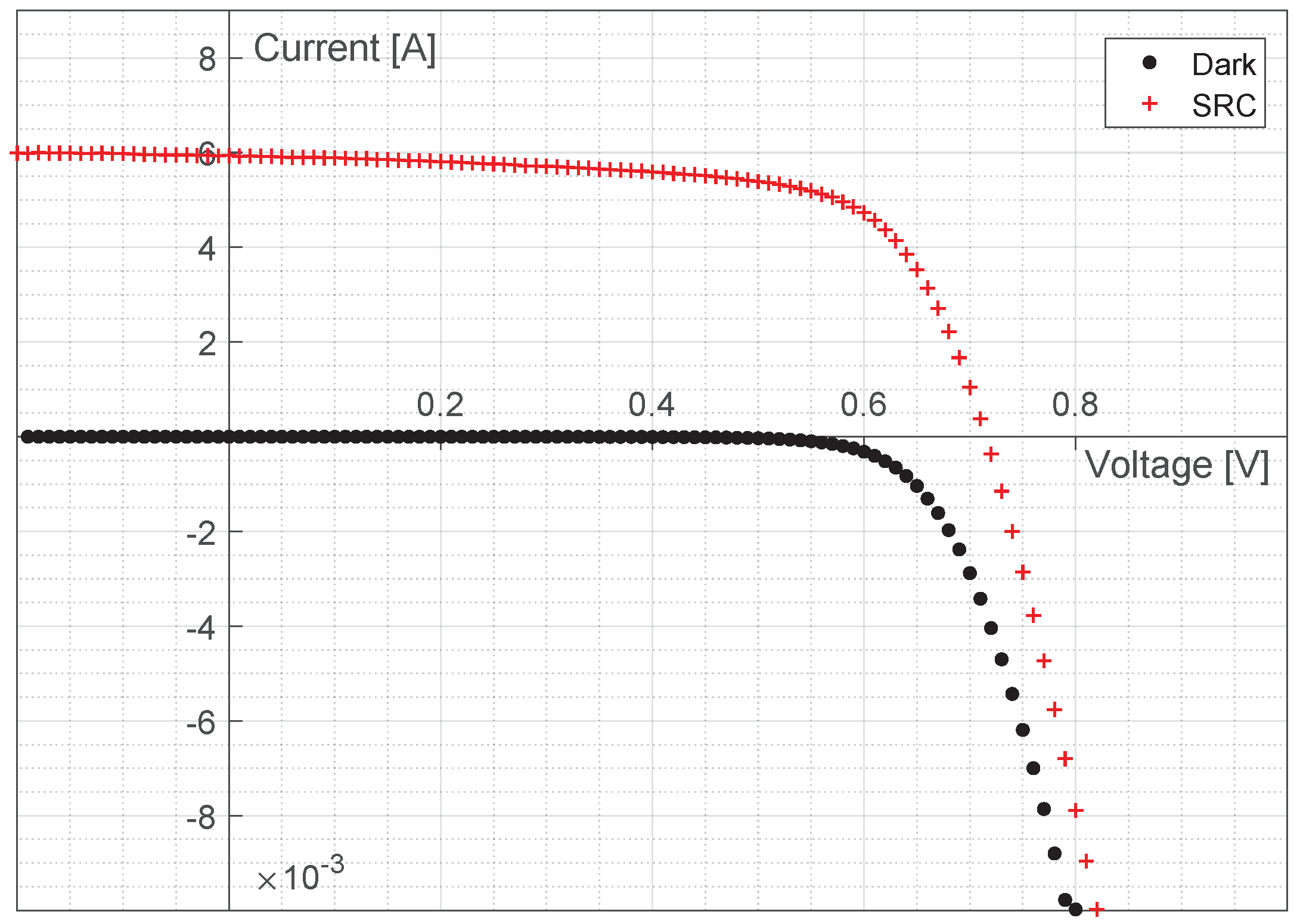
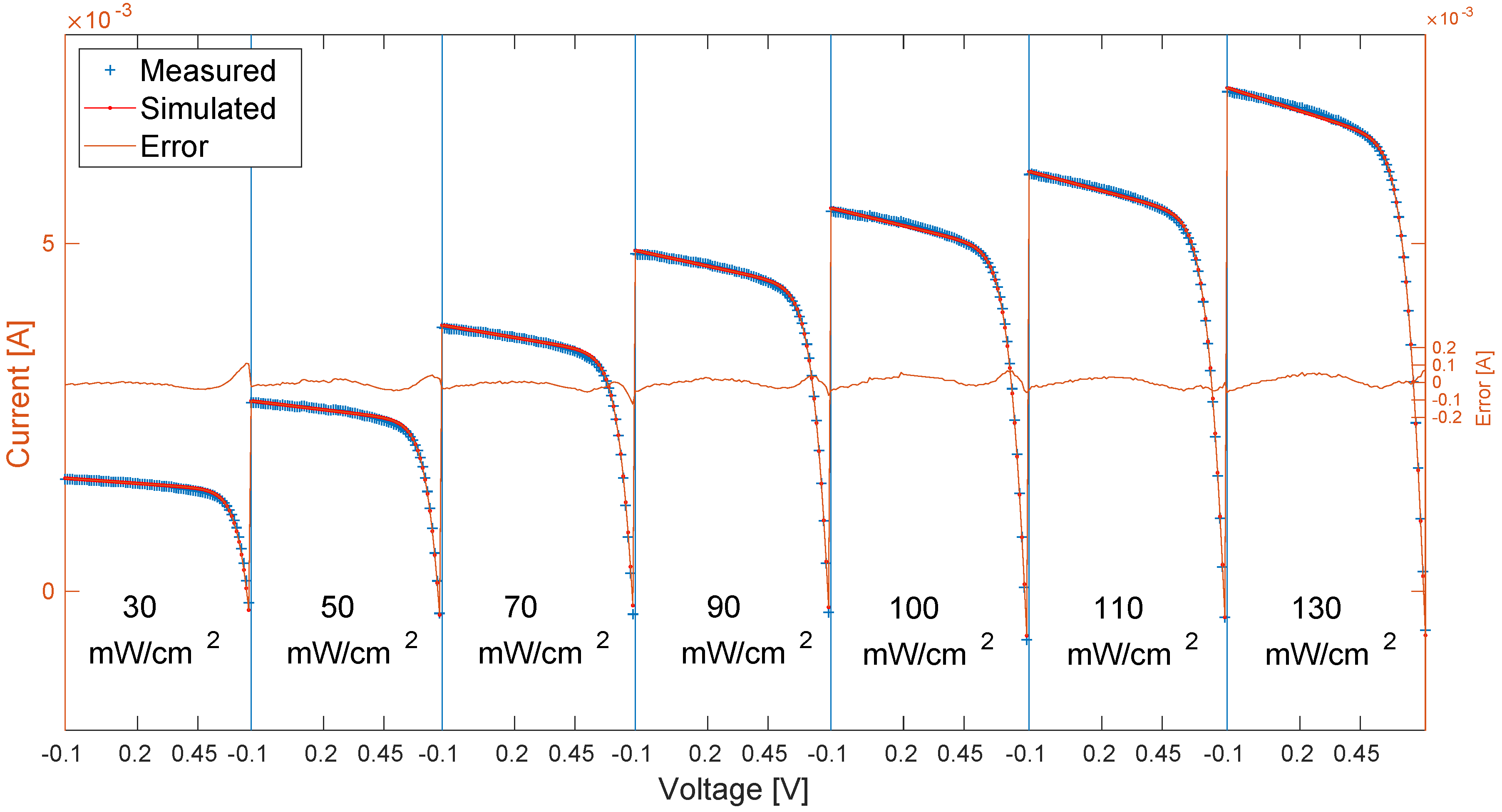
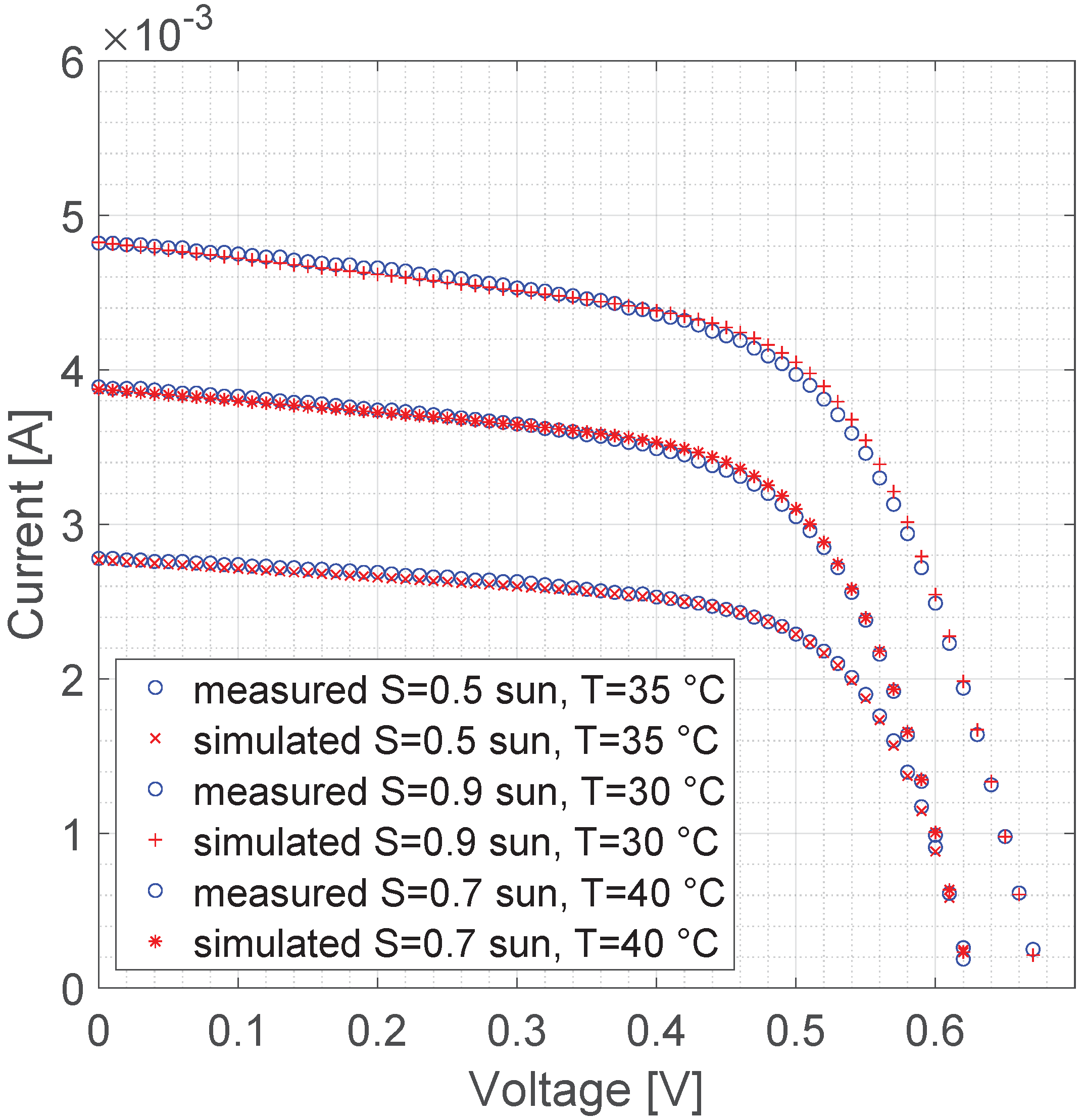
5. Validation of the Proposed Model on a Further Measurement Set
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shafarman, W.N.; Siebentritt, S.; Stolt, L. Cu(InGa)Se2 Solar Cells. In Handbook of Photovoltaic Science and Engineering; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2011; pp. 546–599. [Google Scholar] [CrossRef]
- Liu, J.; Zhuang, D.; Luan, H.; Cao, M.; Xie, M.; Li, X. Preparation of Cu(In,Ga)Se2 thin film by sputtering from Cu(In,Ga)Se2 quaternary target. Prog. Nat. Sci. Mater. Int. 2013, 23, 133–138. [Google Scholar] [CrossRef]
- Salomé, P.M.; Fjällström, V.; Szaniawski, P.; Leitao, J.P.; Hultqvist, A.; Fernandes, P.A.; Teixeira, J.P.; Falcao, B.P.; Zimmermann, U.; da Cunha, A.F.; et al. A comparison between thin film solar cells made from co-evaporated CuIn1−xGaxSe2 using a one-stage process versus a three-stage process. Prog. Photovolt. Res. Appl. 2015, 23, 470–478. [Google Scholar] [CrossRef]
- Paul, S.; Lopez, R.; Repins, I.L.; Li, J.V. Study of charge transport properties in a ZnO/CdS/Cu (In, Ga) Se2 solar cell via admittance spectroscopy. J. Vac. Sci. Technol. B Nanotechnol. Microelectron. Mater. Process. Meas. Phenom. 2018, 36, 022904. [Google Scholar] [CrossRef]
- Jackson, P.; Wuerz, R.; Hariskos, D.; Lotter, E.; Witte, W.; Powalla, M. Effects of heavy alkali elements in Cu(In,Ga)Se2 solar cells with efficiencies up to 22.6%. Phys. Status Solidi (RRL) Rapid Res. Lett. 2016, 10, 583–586. [Google Scholar] [CrossRef]
- Rampino, S.; Bissoli, F.; Gilioli, E.; Pattini, F. Growth of Cu(In,Ga)Se2 thin films by a novel single-stage route based on pulsed electron deposition. Prog. Photovolt. Res. Appl. 2013, 21, 588–594. [Google Scholar] [CrossRef]
- Mazzer, M.; Rampino, S.; Gombia, E.; Bronzoni, M.; Bissoli, F.; Pattini, F.; Calicchio, M.; Kingma, A.; Annoni, F.; Calestani, D.; et al. Progress on low-temperature pulsed electron deposition of CuInGaSe2 solar cells. Energies 2016, 9, 207. [Google Scholar] [CrossRef]
- Haque, M.M.; Rahman, M.M.; Chowdhury, M.I.B. Current-voltage characteristics of CdS/CIGS thin film solar cells: An analytical approach. In Proceedings of the 2014 1st International Conference on Non Conventional Energy (ICONCE 2014), Kalyani, India, 16–17 January 2014; pp. 24–27. [Google Scholar] [CrossRef]
- Rahim, A.B.; Hasan, A.S.; Biswas, P.; Ullah, A.; Chowdhury, M.I.B. Analytical modeling of J-V characteristics of CIGS based thin film solar cell considering voltage and space dependent electric field in the absorber layer. In Proceedings of the 2015 International Conference on Advances in Electrical Engineering (ICAEE), Dhaka, Bangladesh, 17–19 December 2015; pp. 368–371. [Google Scholar] [CrossRef]
- Lee, K.S.; Chung, Y.D.; Park, N.M.; Cho, D.H.; Kim, K.H.; Kim, J.H.; Kim, S.J.; Kim, Y.H.; Noh, S.K. Analysis of the Current-voltage Curves of a Cu(In,Ga)Se2 Thin-film Solar Cell Measured at Different Irradiation Conditions. J. Opt. Soc. Korea 2010, 14, 321–325. [Google Scholar] [CrossRef]
- Sun, X.; Silverman, T.; Garris, R.; Deline, C.; Alam, M.A. An Illumination- and Temperature-Dependent Analytical Model for Copper Indium Gallium Diselenide (CIGS) Solar Cells. IEEE J. Photovolt. 2016, 6, 1298–1307. [Google Scholar] [CrossRef]
- Attivissimo, F.; Adamo, F.; Carullo, A.; Lanzolla, A.M.L.; Spertino, F.; Vallan, A. On the performance of the double-diode model in estimating the maximum power point for different photovoltaic technologies. Measurement 2013, 46, 3549–3559. [Google Scholar] [CrossRef]
- Parisi, A.; Curcio, L.; Rocca, V.; Stivala, S.; Cino, A.C.; Busacca, A.C.; Cipriani, G.; La Cascia, D.; Di Dio, V.; Miceli, R.; et al. Thin film CIGS solar cells, photovoltaic modules, and the problems of modeling. Int. J. Photoenergy 2013, 2013, 817424. [Google Scholar] [CrossRef]
- Werner, B.; KoŁodenny, W.; Prorok, M.; Dziedzic, A.; Żdanowicz, T. Electrical modeling of CIGS thin-film solar cells working in natural conditions. Sol. Energy Mater. Sol. Cells 2011, 95, 2583–2587. [Google Scholar] [CrossRef]
- Hishikawa, Y.; Tobita, H.; Sasaki, A.; Yamagoe, K.; Onuma, T.; Tsuno, Y. Current-voltage characteristics of novel PV devices under various irradiance and temperature conditions. In Proceedings of the 2013 IEEE 39th Photovoltaic Specialists Conference (PVSC), Tampa, FL, USA, 16–21 June 2013; pp. 1417–1422. [Google Scholar] [CrossRef]
- Atse, L.; de Waal Arjen, A.C.; Schropp, R.E.; Faaij, A.P.; van Sark, W.G. Comprehensive characterisation and analysis of PV module performance under real operating conditions. Prog. Photovolt. Res. Appl. 2017, 25, 218–232. [Google Scholar] [CrossRef]
- Gray, J.L. The Physics of the Solar Cell. In Handbook of Photovoltaic Science and Engineering; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2005; pp. 61–112. [Google Scholar] [CrossRef]
- Soto, W.D.; Klein, S.; Beckman, W. Improvement and validation of a model for photovoltaic array performance. Sol. Energy 2006, 80, 78–88. [Google Scholar] [CrossRef]
- Laudani, A.; Fulginei, F.R.; Salvini, A. Identification of the one-diode model for photovoltaic modules from datasheet values. Sol. Energy 2014, 108, 432–446. [Google Scholar] [CrossRef]
- Laudani, A.; Riganti Fulginei, F.; Salvini, A.; Lozito, G.M.; Coco, S. Very fast and accurate procedure for the characterization of photovoltaic panels from datasheet information. Int. J. Photoenergy 2014, 2014, 946360. [Google Scholar] [CrossRef] [PubMed]
- Laudani, A.; Fulginei, F.R.; Salvini, A. High performing extraction procedure for the one-diode model of a photovoltaic panel from experimental I?V curves by using reduced forms. Sol. Energy 2014, 103, 316–326. [Google Scholar] [CrossRef]
- Laudani, A.; Fulginei, F.R.; Salvini, A.; Parisi, A.; Pernice, R.; Galluzzo, F.R.; Cino, A.C.; Busacca, A.C. One diode circuital model of light soaking phenomena in Dye-Sensitized Solar Cells. Opt. Int. J. Light Electron Opt. 2018, 156, 311–317. [Google Scholar] [CrossRef]
- Rampino, S.; Armani, N.; Bissoli, F.; Bronzoni, M.; Calestani, D.; Calicchio, M.; Delmonte, N.; Gilioli, E.; Gombia, E.; Mosca, R.; et al. 15% efficient Cu (In, Ga) Se2 solar cells obtained by low-temperature pulsed electron deposition. Appl. Phys. Lett. 2012, 101, 132107. [Google Scholar] [CrossRef]
- Paul, S.; Grover, S.; Repins, I.L.; Keyes, B.M.; Contreras, M.A.; Ramanathan, K.; Noufi, R.; Zhao, Z.; Liao, F.; Li, J.V. Analysis of Back-Contact Interface Recombination in Thin-Film Solar Cells. IEEE J. Photovolt. 2018, 8, 871–878. [Google Scholar] [CrossRef]
- Lindahl, J.; Keller, J.; Donzel-Gargand, O.; Szaniawski, P.; Edoff, M.; Törndahl, T. Deposition temperature induced conduction band changes in zinc tin oxide buffer layers for Cu (In, Ga) Se2 solar cells. Sol. Energy Mater. Sol. Cells 2016, 144, 684–690. [Google Scholar] [CrossRef]
- Carrasco, M.; Laudani, A.; Lozito, G.M.; Mancilla-David, F.; Riganti Fulginei, F.; Salvini, A. Low-Cost Solar Irradiance Sensing for PV Systems. Energies 2017, 10, 998. [Google Scholar] [CrossRef]
- Espinosa-Gavira, M.; Agüera-Pérez, A.; González de la Rosa, J.; Palomares-Salas, J.; Sierra-Fernández, J. An On-Line Low-Cost Irradiance Monitoring Network with Sub-Second Sampling Adapted to Small-Scale PV Systems. Sensors 2018, 18, 3405. [Google Scholar] [CrossRef] [PubMed]
- Faba, A.; Gaiotto, S.; Lozito, G.M. A novel technique for online monitoring of photovoltaic devices degradation. Sol. Energy 2017, 158, 520–527. [Google Scholar] [CrossRef]
- Öztürk, S.; Canver, M.; Çadırcı, I.; Ermiş, M. All SiC Grid-Connected PV Supply with HF Link MPPT Converter: System Design Methodology and Development of a 20 kHz, 25 kVA Prototype. Electronics 2018, 7, 85. [Google Scholar] [CrossRef]
- Laudani, A.; Lozito, G.M.; Lucaferri, V.; Radicioni, M.; Riganti Fulginei, F.; Salvini, A.; Coco, S. An analytical approach for maximum power point calculation for photovoltaic system. In Proceedings of the 2017 IEEE European Conference on Circuit Theory and Design (ECCTD), Catania, Italy, 4–6 September 2017; pp. 1–4. [Google Scholar]
- Liu, C.L.; Chen, J.H.; Liu, Y.H.; Yang, Z.Z. An asymmetrical fuzzy-logic-control-based MPPT algorithm for photovoltaic systems. Energies 2014, 7, 2177–2193. [Google Scholar] [CrossRef]
- Li, C.; Chen, Y.; Zhou, D.; Liu, J.; Zeng, J. A high-performance adaptive incremental conductance MPPT algorithm for photovoltaic systems. Energies 2016, 9, 288. [Google Scholar] [CrossRef]
- Yaden, M.F.; Melhaoui, M.; Gaamouche, R.; Hirech, K.; Baghaz, E.; Kassmi, K. Photovoltaic system equipped with digital command control and acquisition. Electronics 2013, 2, 192–211. [Google Scholar] [CrossRef]

| Parameter | Measured Value |
|---|---|
| 27.4 ± 1.3 mA/cm2 | |
| 0.686 ± 0.010 V | |
| FF | 0.67 ± 0.02 |
| 12.6 ± 0.82% | |
| 135 kΩcm2 (*) | |
| 12 Ωcm2 (*) |
| 50 mW/cm2 | 90 mW/cm2 | 110 mW/cm2 | |
|---|---|---|---|
| (A) | 0.003328 | 0.006292 | 0.007516 |
| (A) | 4.913 × 10−10 | 1.958 × 10−9 | 3.316 × 10−9 |
| (Ω) | 1.802 × 103 | 1.077 × 103 | 1.030 × 103 |
| (Ω) | 3.611 | 3.153 | 3.342 |
| n | 1.618 | 1.777 | 1.847 |
| 25 °C | 40 °C | 55 °C | |
|---|---|---|---|
| (A) | 0.006840 | 0.006848 | 0.006899 |
| (A) | 1.018 × 10−9 | 9.904 × 10−9 | 1.771 × 10−7 |
| (Ω) | 925 | 1243 | 1807 |
| (Ω) | 3.877 | 2.606 | 2.882 |
| n | 1.729 | 1.740 | 1.887 |
| Case | MSE |
|---|---|
| Case 1 (30 °C–45 °C) | 3.0651 × 10−9 |
| Case 2 (35 °C–55 °C) | 3.1132 × 10−9 |
| Case 3 (25 °C–40 °C–55 °C) | 2.8143 × 10−9 |
| Case 4 (complete dataset) | 2.7682 × 10−9 |
| Case | MSE |
|---|---|
| Case 1 (30 mW/cm2–110 mW/cm2) | 3.8654 × 10−9 |
| Case 2 (complete dataset) | 3.4023 × 10−9 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bronzoni, M.; Colace, L.; De Iacovo, A.; Laudani, A.; Lozito, G.M.; Lucaferri, V.; Radicioni, M.; Rampino, S. Equivalent Circuit Model for Cu(In,Ga)Se2 Solar Cells Operating at Different Temperatures and Irradiance. Electronics 2018, 7, 324. https://doi.org/10.3390/electronics7110324
Bronzoni M, Colace L, De Iacovo A, Laudani A, Lozito GM, Lucaferri V, Radicioni M, Rampino S. Equivalent Circuit Model for Cu(In,Ga)Se2 Solar Cells Operating at Different Temperatures and Irradiance. Electronics. 2018; 7(11):324. https://doi.org/10.3390/electronics7110324
Chicago/Turabian StyleBronzoni, Matteo, Lorenzo Colace, Andrea De Iacovo, Antonino Laudani, Gabriele Maria Lozito, Valentina Lucaferri, Martina Radicioni, and Stefano Rampino. 2018. "Equivalent Circuit Model for Cu(In,Ga)Se2 Solar Cells Operating at Different Temperatures and Irradiance" Electronics 7, no. 11: 324. https://doi.org/10.3390/electronics7110324
APA StyleBronzoni, M., Colace, L., De Iacovo, A., Laudani, A., Lozito, G. M., Lucaferri, V., Radicioni, M., & Rampino, S. (2018). Equivalent Circuit Model for Cu(In,Ga)Se2 Solar Cells Operating at Different Temperatures and Irradiance. Electronics, 7(11), 324. https://doi.org/10.3390/electronics7110324








