Competition in Service Provision between Slice Operators in 5G Networks
Abstract
1. Introduction
- A business model for VNOs is proposed, where the resources are outsourced to an InP and supplied to the VNOs through network slicing.
- A game theory-based analysis of the competition between the VNOs that implement such business model is performed.
- The Nash equilibrium of such competition game is calculated and it is shown that results in a resource allocation that matches the entitlement or contribution of each VNO.
Related Work
2. Model
2.1. System Model
2.2. Economic Model
3. Game Model and Analysis
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- NGMN Alliance. Description of Network Slicing Concept. In Next Generation Mobile Networks, White Paper; NGMN Alliance: Frankfurt am Main, Germany, 2016. [Google Scholar]
- Jiang, M.; Condoluci, M.; Mahmoodi, T. Network slicing management & prioritization in 5G mobile systems. In Proceedings of the European Wireless Conference, EW 2016, Oulu, Finland, 18–20 May 2016; pp. 197–202. [Google Scholar]
- Samdanis, K.; Costa-Perez, X.; Sciancalepore, V. From network sharing to multi-tenancy: The 5G network slice broker. IEEE Commun. Mag. 2016, 54, 32–39. [Google Scholar] [CrossRef]
- NGMN Alliance. 5G white paper. In Next Generation Mobile Networks, White Paper; NGMN Alliance: Frankfurt am Main, Germany, 2015. [Google Scholar]
- Vives, X. Oligopoly Pricing: Old Ideas and New Tools; MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Niyato, D.; Hossain, E. Competitive pricing for spectrum sharing in cognitive radio networks: Dynamic game, inefficiency of nash equilibrium, and collusion. IEEE J. Sel. Areas Commun. 2008, 26, 192–202. [Google Scholar] [CrossRef]
- Guijarro, L.; Pla, V.; Tuffin, B.; Maille, P.; Vidal, J.R. Competition and Bargaining in Wireless Networks with Spectrum Leasing. In Proceedings of the 2011 IEEE Global Telecommunications Conference (GLOBECOM 2011), Houston, TX, USA, 5–9 December 2011; pp. 1–6. [Google Scholar]
- Duan, L.; Huang, J.; Shou, B. Economics of femtocell service provision. IEEE Trans. Mob. Comput. 2013, 12, 2261–2273. [Google Scholar] [CrossRef]
- Guijarro, L.; Pla, V.; Vidal, J.R.; Martinez, J. Femtocell operator entry decision with spectrum bargaining and service competition. IEEE Commun. Lett. 2012, 16, 1976–1979. [Google Scholar] [CrossRef]
- Guijarro, L.; Pla, V.; Vidal, J.R.; Naldi, M. Maximum-profit two-sided pricing in service platforms based on wireless sensor networks. IEEE Wirel. Commun. Lett. 2016, 5, 8–11. [Google Scholar] [CrossRef]
- Guijarro, L.; Pla, V.; Vidal, J.R.; Naldi, M. Game theoretical analysis of service provision for the Internet of Things based on sensor virtualization. IEEE J. Sel. Areas Commun. 2017, 35, 691–706. [Google Scholar] [CrossRef]
- Liu, C.; Li, K.; Xu, C.; Li, K. Strategy configurations of multiple users competition for cloud service reservation. IEEE Trans. Parallel Distrib. Syst. 2016, 27, 508–520. [Google Scholar] [CrossRef]
- Liu, C.; Li, K.; Li, K.; Buyya, R. A new cloud service mechanism for profit optimizations of a cloud provider and its users. IEEE Trans. Cloud Comput. 2017. [Google Scholar] [CrossRef]
- Li, K.; Liu, C.; Li, K.; Zomaya, A.Y. A framework of price bidding configurations for resource usage in cloud computing. IEEE Trans. Parallel Distrib. Syst. 2016, 27, 2168–2181. [Google Scholar] [CrossRef]
- Han, B.; Tayade, S.; Schotten, H.D. Modeling profit of sliced 5G networks for advanced network resource management and slice implementation. In Proceedings of the 2017 IEEE Symposium on Computers and Communications (ISCC), Heraklion, Greece, 3–6 July 2017; pp. 576–581. [Google Scholar]
- Han, B.; Feng, D.; Ji, L.; Schotten, H.D. A Profit-Maximizing Strategy of Network Resource Management for 5G Tenant Slices. arXiv, 2017; arXiv:1709.09229. [Google Scholar]
- Han, B.; Lianghai, J.; Schotten, H.D. Slice as an Evolutionary Service: Genetic Optimization for Inter-Slice Resource Management in 5G Networks. IEEE Access 2018. [Google Scholar] [CrossRef]
- Caballero, P.; Banchs, A.; de Veciana, G.; Costa-Pérez, X. Network slicing games: Enabling customization in multi-tenant networks. In Proceedings of the INFOCOM 2017-IEEE Conference on Computer Communications, Atlanta, GA, USA, 1–4 May 2017; pp. 1–9. [Google Scholar]
- Oladejo, S.O.; Falowo, O.E. 5G network slicing: A multi-tenancy scenario. In Proceedings of the 2017 IEEE GlobalWireless Summit (GWS), Cape Town, South Africa, 15–18 October 2017; pp. 88–92. [Google Scholar]
- Ben-Akiva, M.E.; Lerman, S.R. Discrete Choice Analysis: Theory and Application to Travel Demand; MIT Press: Cambridge, MA, USA, 1985; Volume 9. [Google Scholar]
- Maillé, P.; Tuffin, B. Telecommunication Network Economics: From Theory to Applications; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Reichl, P.; Tuffin, B.; Schatz, R. Logarithmic laws in service quality perception: Where microeconomics meets psychophysics and quality of experience. Telecommun. Syst. 2011, 52, 587–600. [Google Scholar] [CrossRef]
- Train, K.E. Discrete Choice Methods with Simulation; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Courcoubetis, C.; Weber, R. Pricing Communication Networks: Economics, Technology and Modelling; John Wiley & Sons: Cambridge, MA, USA, 2003. [Google Scholar]
- Price, T.C. Using co-evolutionary programming to simulate strategic behaviour in markets. J. Evol. Econ. 1997, 7, 219–254. [Google Scholar] [CrossRef]
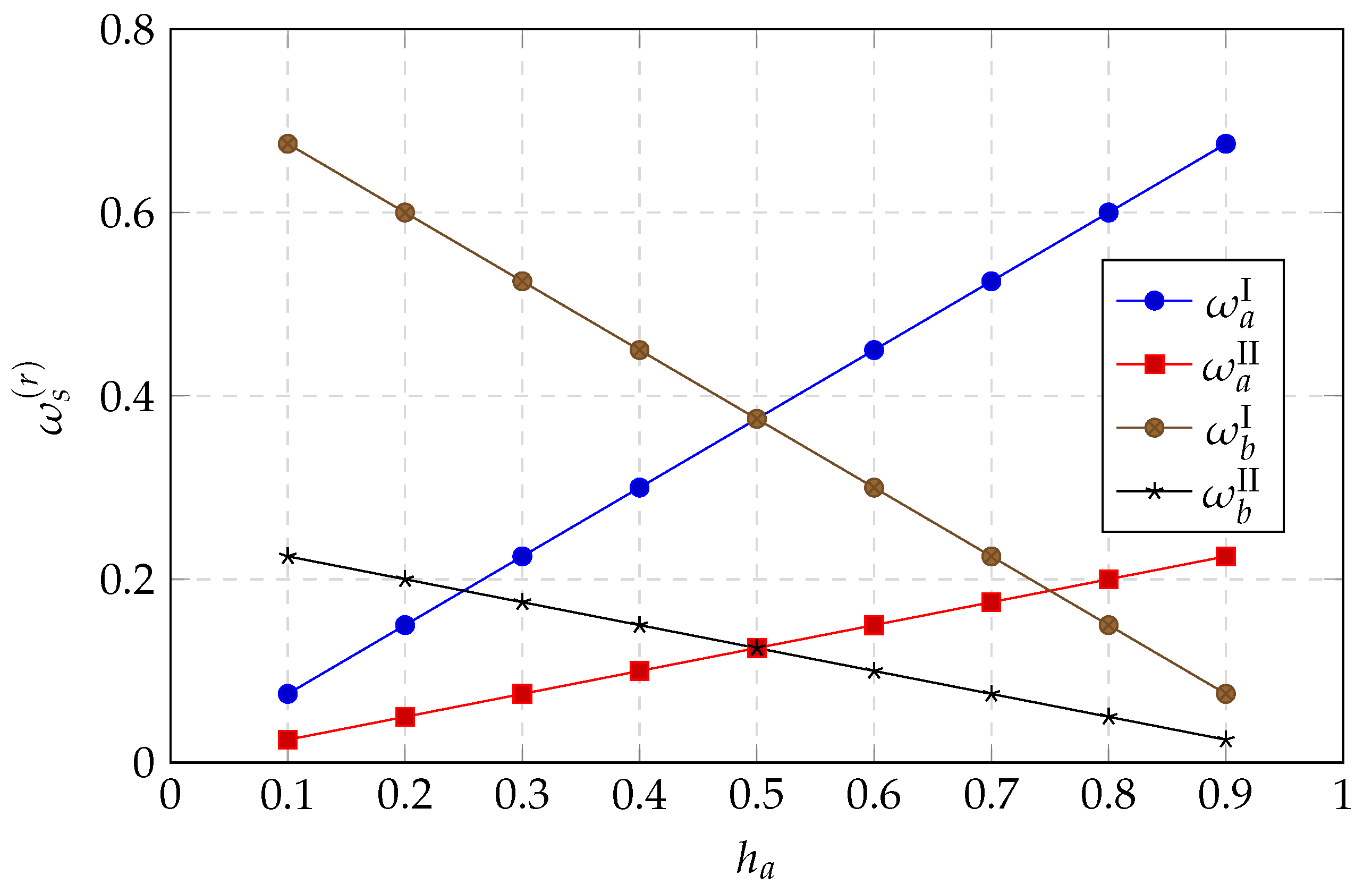
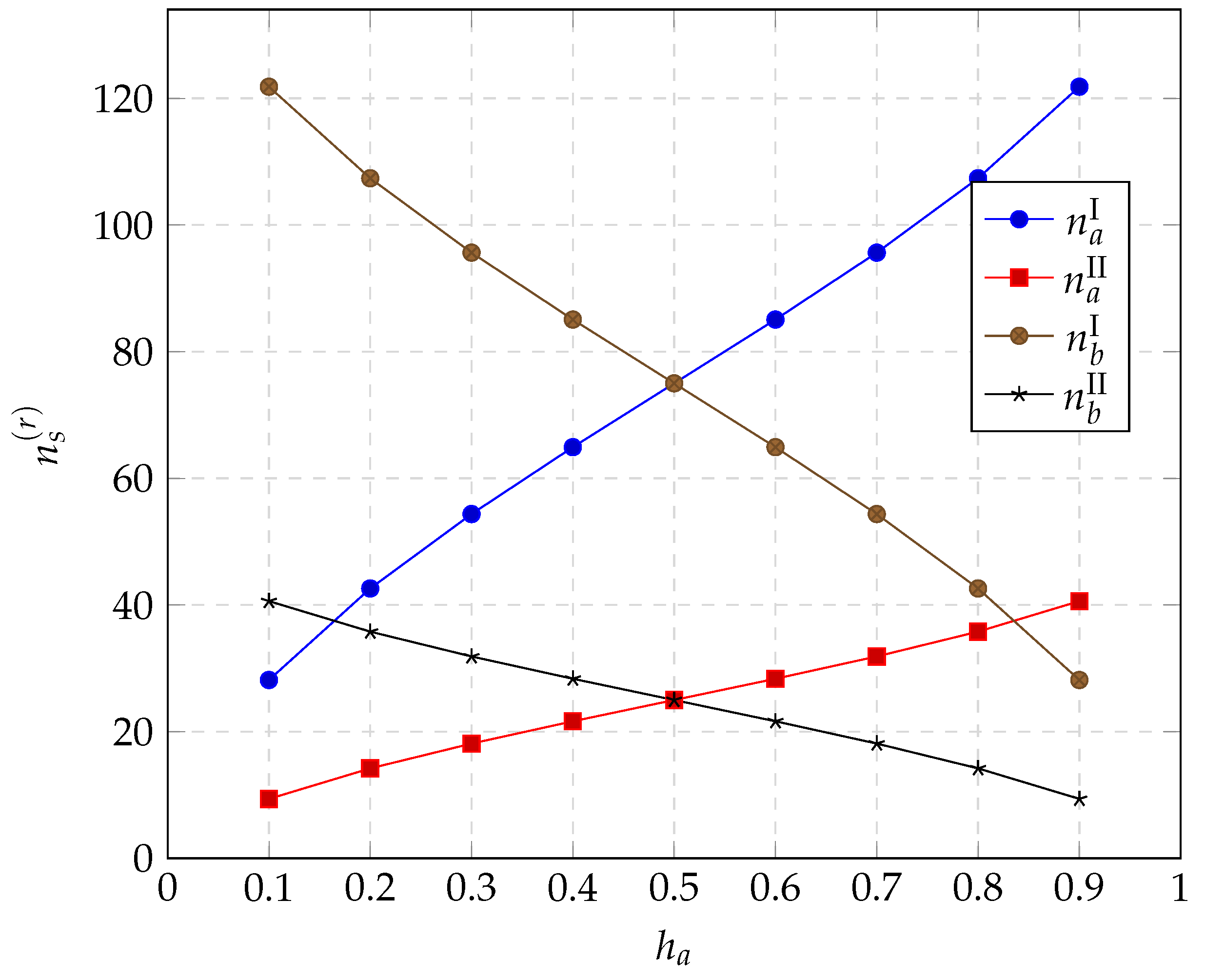
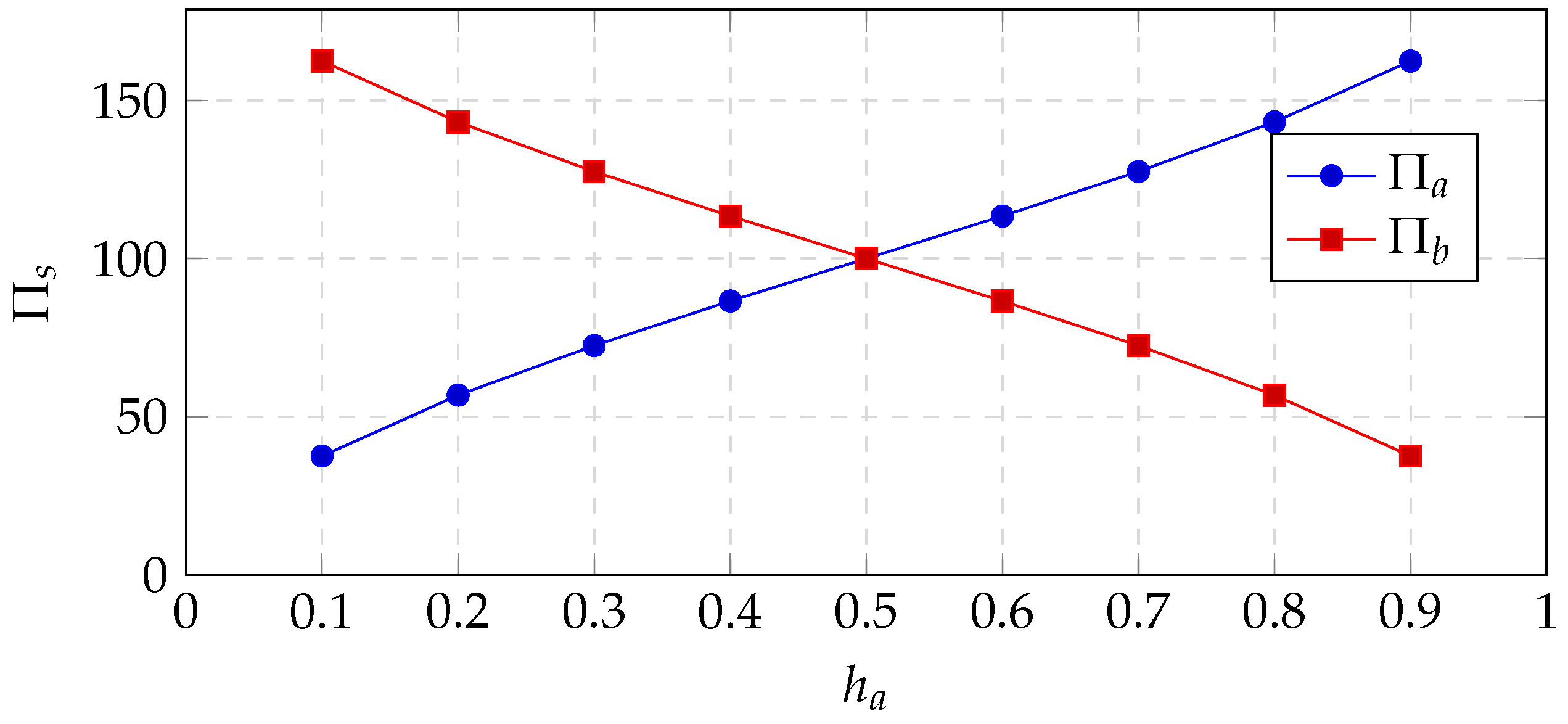
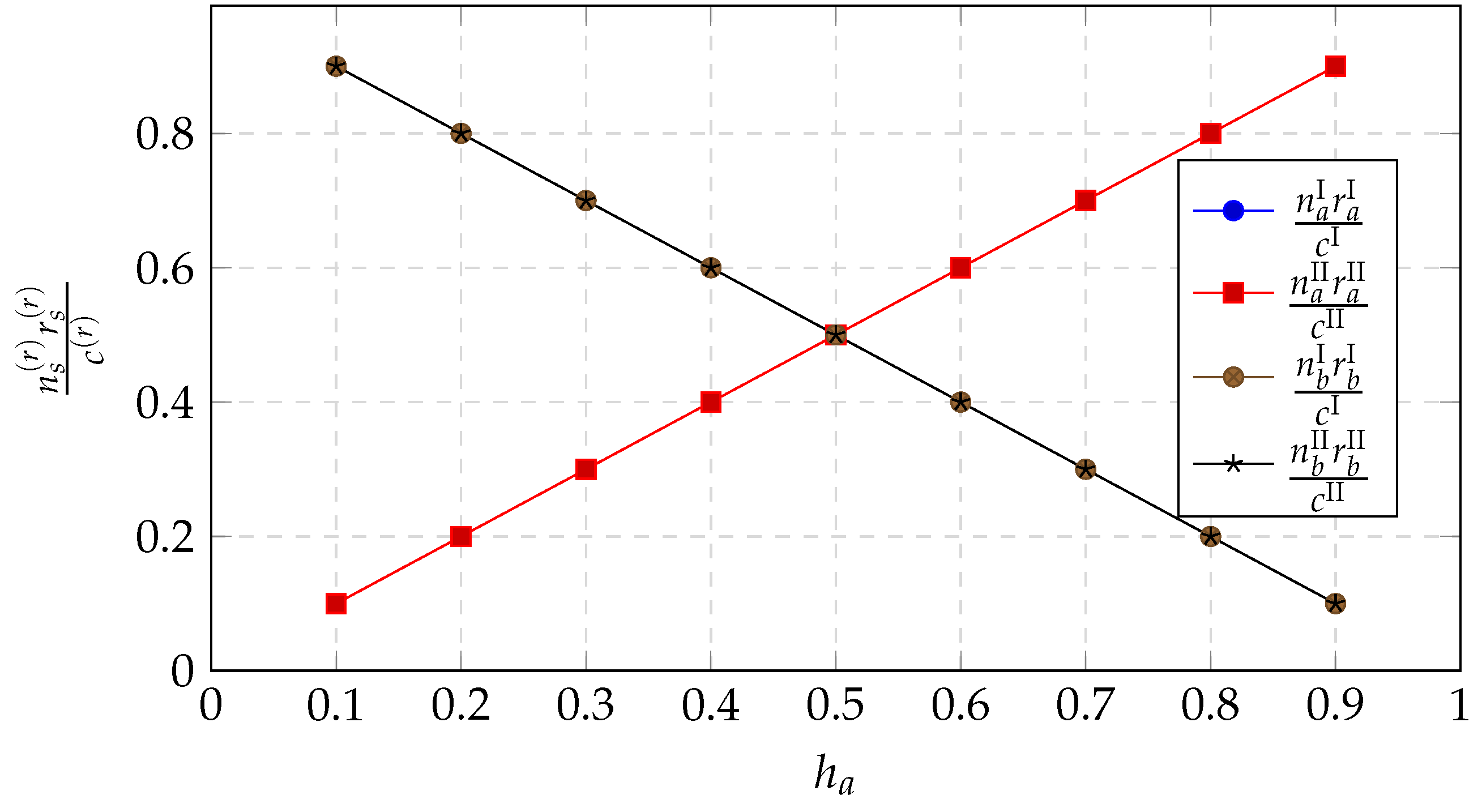
| Parameter | Value |
|---|---|
| 2.0 | |
| 0.5 | |
| 1.5 | |
| 150.0 | |
| 50.0 | |
| p | 1.0 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guijarro, L.; Vidal, J.R.; Pla, V. Competition in Service Provision between Slice Operators in 5G Networks. Electronics 2018, 7, 315. https://doi.org/10.3390/electronics7110315
Guijarro L, Vidal JR, Pla V. Competition in Service Provision between Slice Operators in 5G Networks. Electronics. 2018; 7(11):315. https://doi.org/10.3390/electronics7110315
Chicago/Turabian StyleGuijarro, Luis, Jose R. Vidal, and Vicent Pla. 2018. "Competition in Service Provision between Slice Operators in 5G Networks" Electronics 7, no. 11: 315. https://doi.org/10.3390/electronics7110315
APA StyleGuijarro, L., Vidal, J. R., & Pla, V. (2018). Competition in Service Provision between Slice Operators in 5G Networks. Electronics, 7(11), 315. https://doi.org/10.3390/electronics7110315







