Turbojet Engine Industrial Min–Max Controller Performance Improvement Using Fuzzy Norms
Abstract
1. Introduction
- Steady-state control loop to calculate the steady state fuel flow according to the engine operating condition,
- Transient control loop to control the engine acceleration and deceleration in response to the power lever angle (PLA),
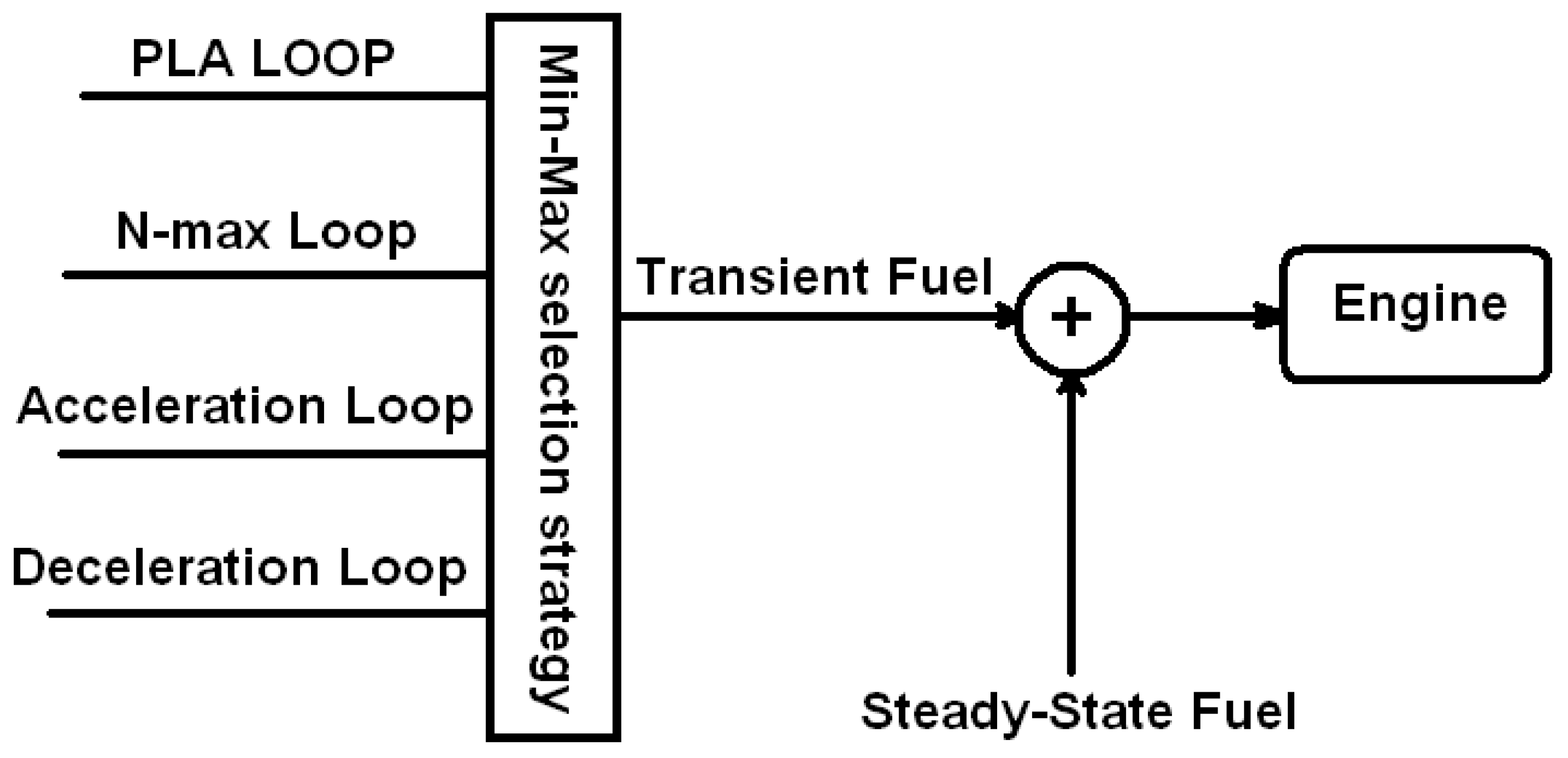
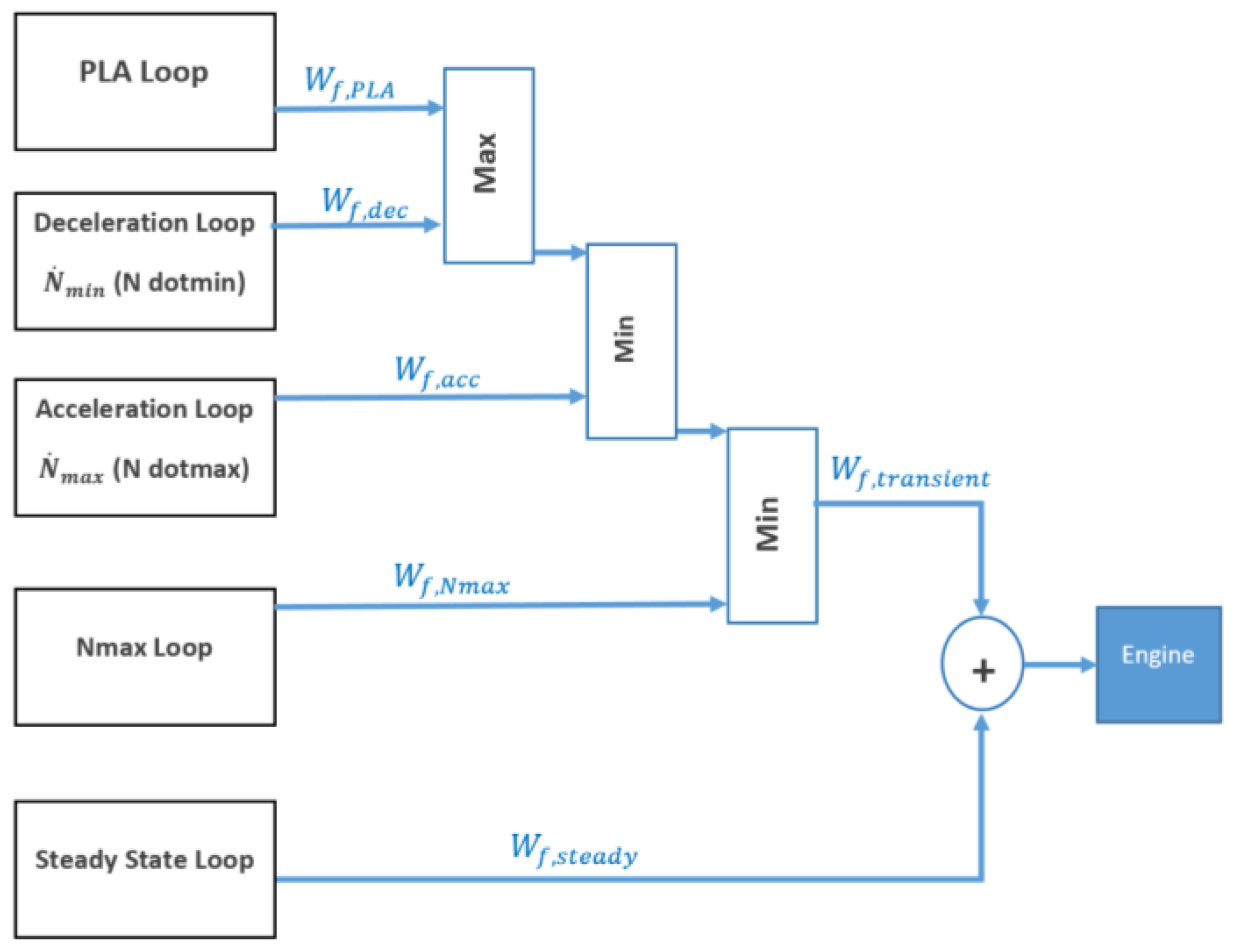
- Physical limitation control loops to satisfy the engine constraints including the engine stall, flameout, over speed, and over temperature limitations.
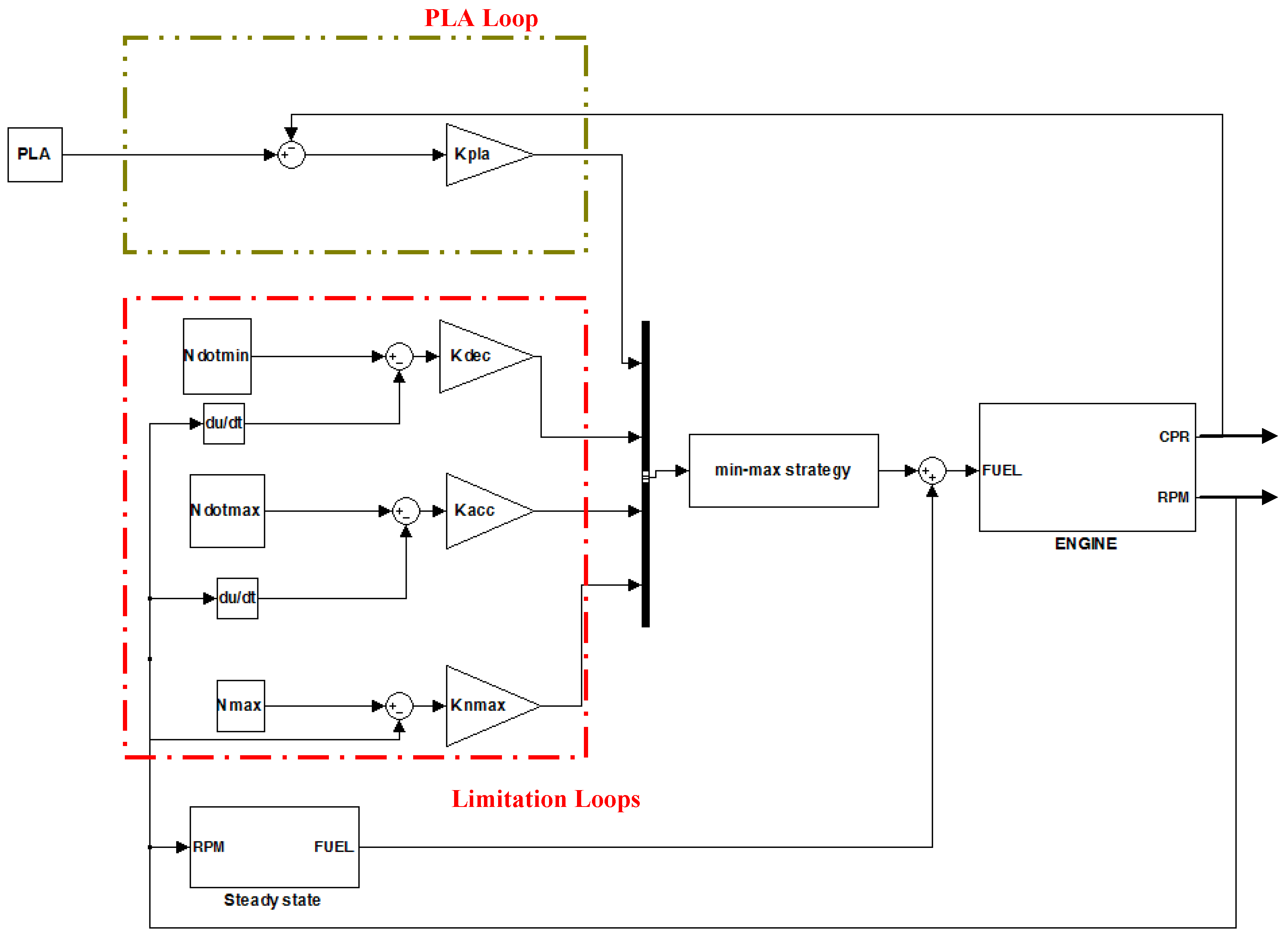
2. Problem Formulation
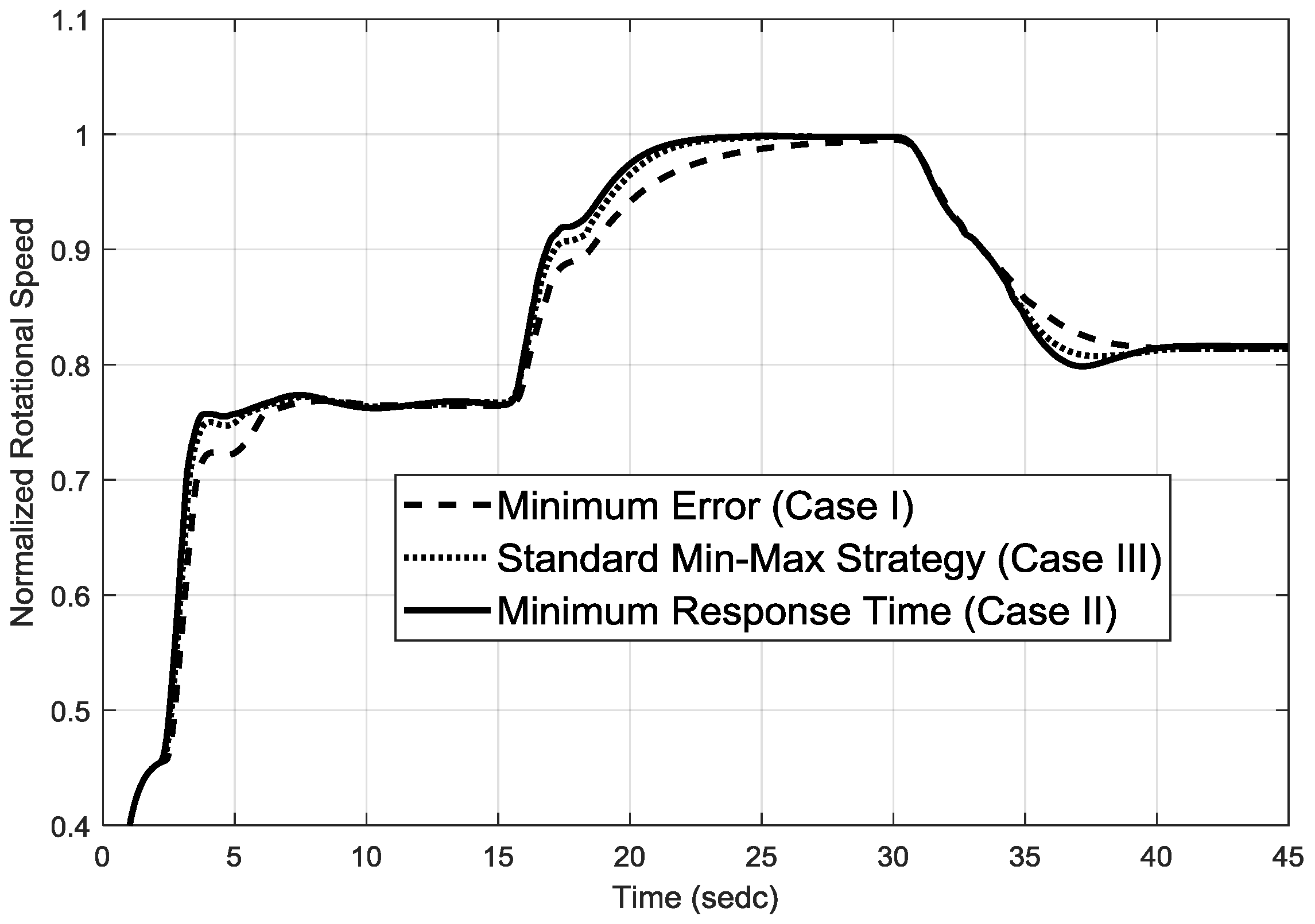
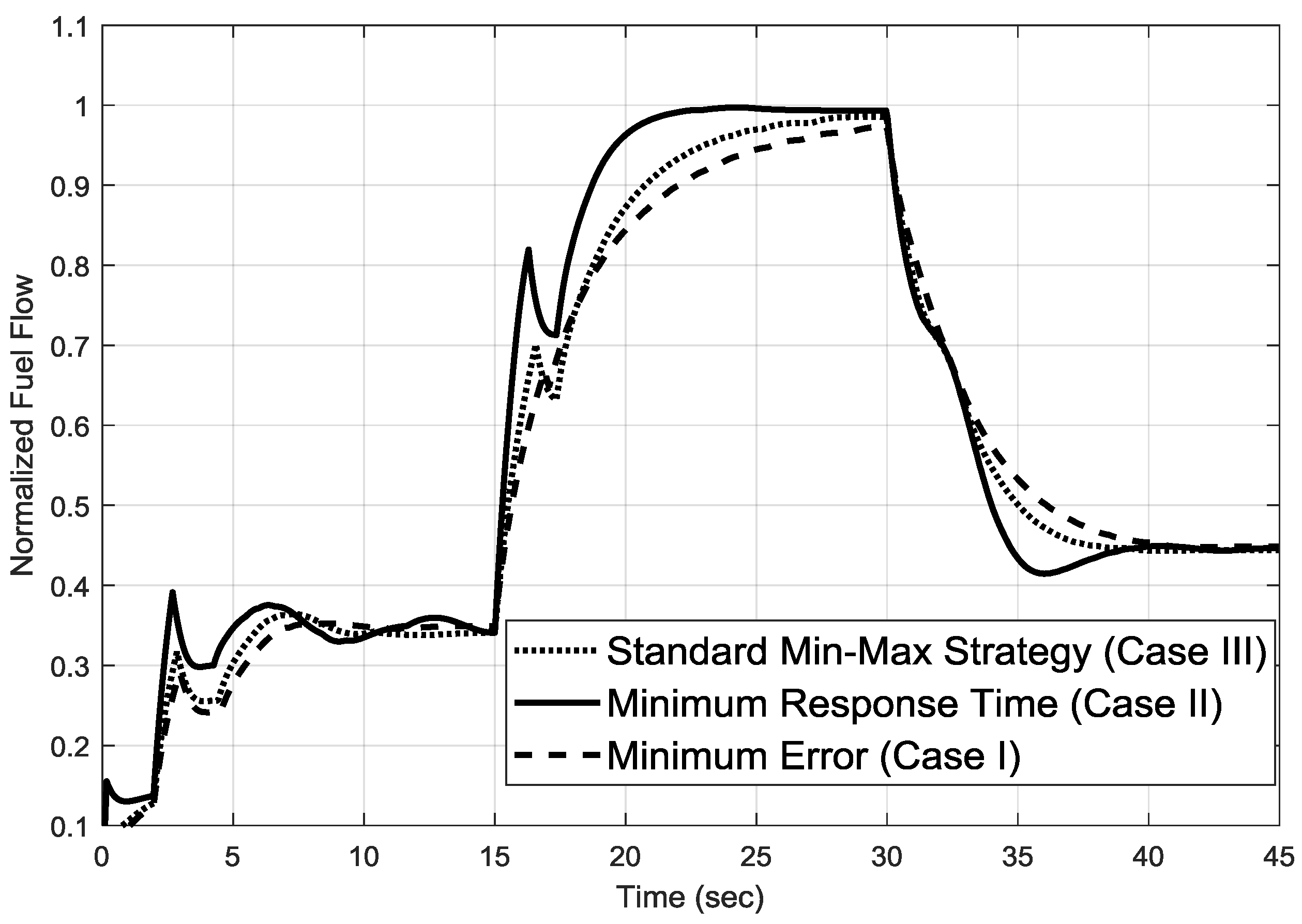
3. Simulation Results
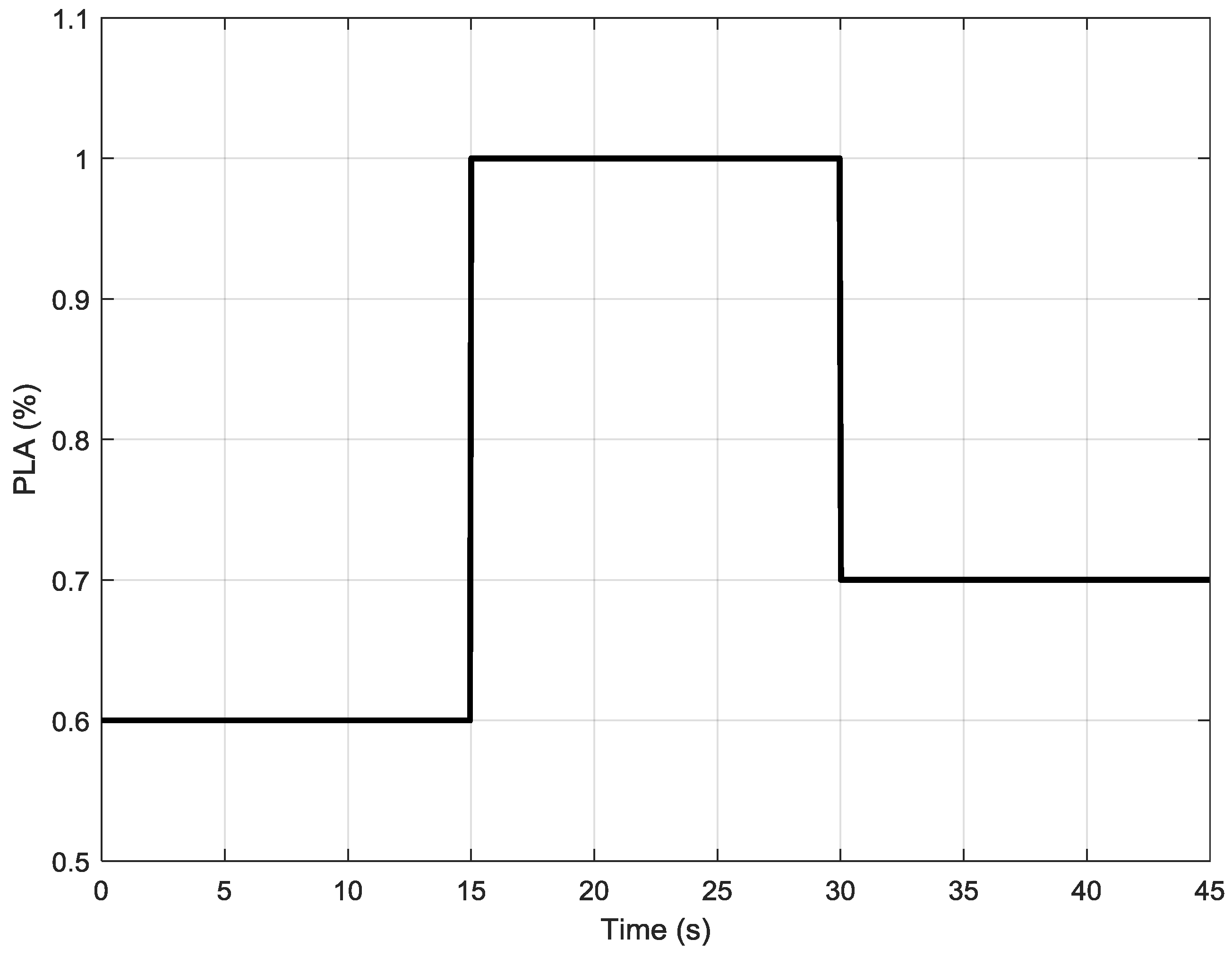
- Firstly, a predefined PLA profile is defined for the model. This command is a percentage of the available thrust that the pilot requires at any instantaneous time. Since the thrust is not measurable directly, other parameters (engine rotational speed or engine pressure ratio [38,39,40]) are used to translate the required thrust to a measurable parameter in Min–Max algorithm. In this study, the engine pressure ratio is used for this purpose.
- The Min–Max controller gets the PLA command as well as engine situation (acceleration, deceleration, rotational speed) and using the strategy described earlier calculates the appropriate fuel flow for the engine. The control law in each loop could be Proportional (P), Proportional-Integral (PI), or Proportional-Integral-Derivative (PID) algorithm [2].
4. Discussion
- The number of variables: the control modes for GTE can be summarized as a steady-state control mode (to satisfy the pilot demand), transient control mode (to satisfy an acceptable response time) and physical limitation control mode (to protect the engine against malfunctions). In an industrial control strategy for a turbojet engine, four different transient control loops are designed. One of them is in charge of the pilot demand (pilot lever angle (PLA) control loop) and three of them give guarantee about safe operation of the engine to protect the GTE against physical damages. However, the number of transient control loops would be increased in turbofan engines (two and three spool engines) and industrial gas turbine engines respect to many more constraints and parameters that should be considered for these types of GTEs. Therefore, the number of required runs would be increased noticeably, and it may not be affordable to solve the problem using direct search method.
- Control loop gains: another issue is that when the Min–Max selection strategy is changed, it could not be claimed that the tuned gains are optimal. In other words, after changing the selection strategy, control loop gains should be tuned again to get the maximum potential of the control structure. In this approach, we could get a Pareto Front from a set of possible cases rather than having just two or three cases. However, adding these parameters to the problem will increase the complexity of the problem noticeably and may not be affordable easily.
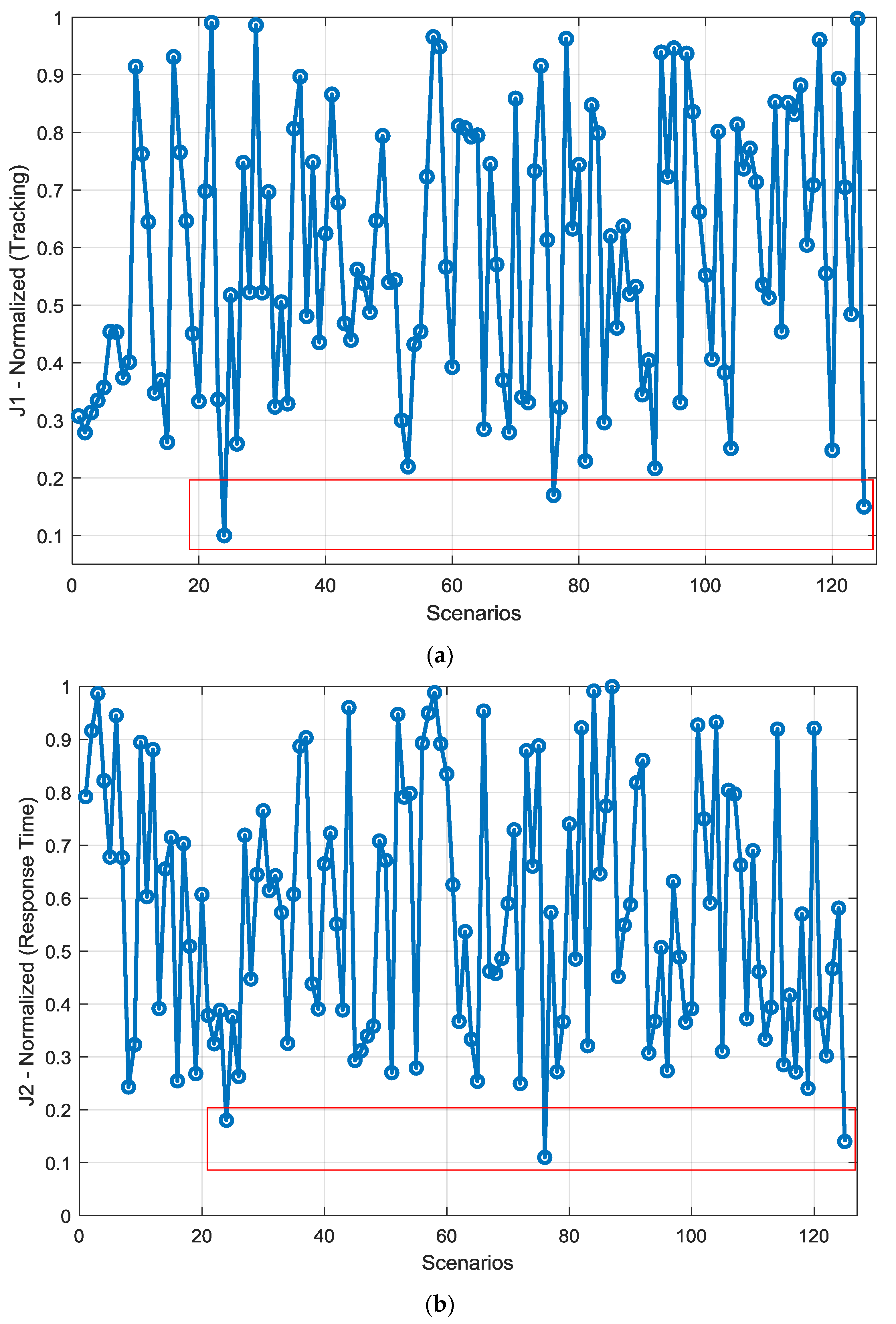
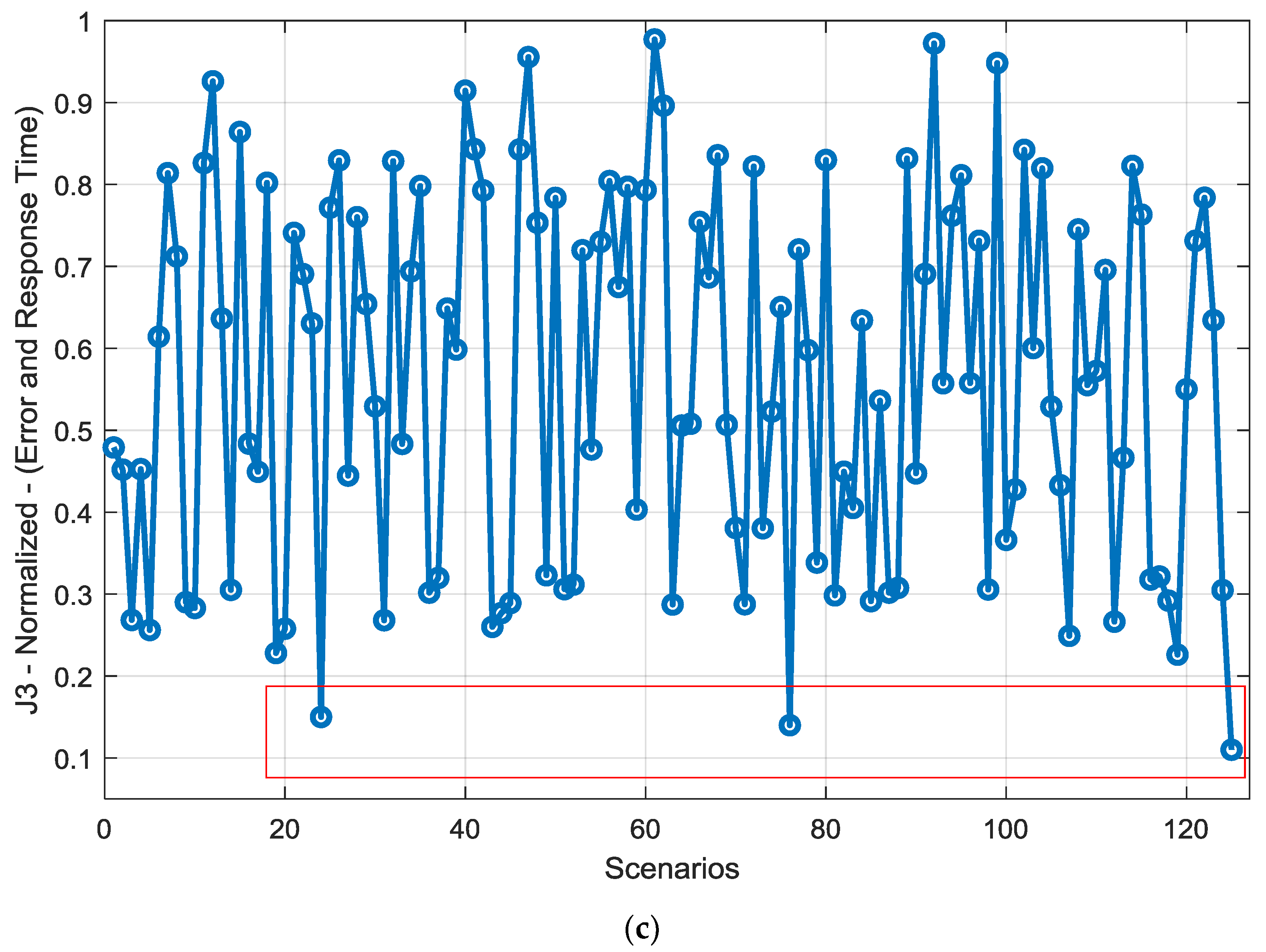
- Objective functions: the other issue is the performance indices defined for the problem. This paper considered the steady state error and the response time to the pilot command. However, there are many more objectives that could be considered for the controller enhancement like total fuel consumption in a mission, emission level, robustness and responses to the uncertainties etc. Addressing these objectives also needs a methodological approach and a problem formulation.
- Effects of uncertainty: the main structure of the proposed controllers are the same with the industrial Min–Max controllers which is robust and reliable. However, after replacing the simple mathematical functions with fuzzy norms, the controller should be tested again under uncertain conditions (e.g., different weather and flight conditions) to confirm the ability of the proposed approach in dealing with uncertainties.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jafari, S.; Montazeri-Gh, M. Evolutionary Optimization for Gain Tuning of Jet Engine Min-Max Fuel Controller. J. Propul. Power 2011, 27, 1015–1023. [Google Scholar] [CrossRef]
- Richter, H. Advanced Control of Turbofan Engines; Springer Science+Business Media: New York, NY, USA, 2012. [Google Scholar] [CrossRef]
- Spang III, H.A.; Brown, H. Control of jet engines. Control Eng. Pract. 1999, 7, 1043–1059. [Google Scholar] [CrossRef]
- Chirgwin, R. Airbus Confirms Software Brought down A400M Transport Plane. The Register, 31 May 2015; Sponsored: A Layman’s Guide on How to Operate Your SIEM Under the GDPR. [Google Scholar]
- Jaw, L.C.; Mattingly, J.D. Aircraft Engine Controls; American Institute of Aeronautics and Astronautics: New York, NY, USA, 2009; ISBN 978-1-60086-705-7. [Google Scholar]
- Moir, I.; Seabridge, A. Engine Control Systems; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2008. [Google Scholar] [CrossRef]
- Kreiner, A.; Lietzau, K. The Use of Onboard Real-Time Models for Jet Engine Control; MTU Aero Engines: Munich, Germany, 2002. [Google Scholar]
- Dambrosio, L.; Camporeale, S.M.; Fortunato, B. Performance of Gas Turbine Power Plants Controlled by One Step Ahead Adaptive Technique; ASME: München, Germay, 2000. [Google Scholar]
- Van Essen, H.; Lange, H. Nonlinear Model Predictive Control Experiments on a Laboratory Gas Turbine Installation; ASME: München, Germany, 2000. [Google Scholar]
- Orme, J.; Schkolnik, G. Flight Assessment of the Onboard Propulsion System Model for the Performance Seeking Control Algorithm on an F-15 Aircraft. In Proceedings of the 31st Joint Propulsion Conference and Exhibit, San Diego, CA, USA, 10 July–12 July 1995. [Google Scholar]
- Mohammadi, E.; Montazeri-Gh, M. Active Fault Tolerant Control with self-enrichment capability for gas turbine engines. Aerosp. Sci. Technol. 2016, 56, 70–89. [Google Scholar] [CrossRef]
- Montazeri-Gh, M.; Jafari, S.; Ilkhani, M.R. Application of particle swarm optimization in gas turbine engine fuel controller gain tuning. Eng. Optim. 2012, 4, 225–240. [Google Scholar] [CrossRef]
- Zeng, D.; Zhou, D.; Tan, C.; Jiang, B. Research on Model-Based Fault Diagnosi for a Gas Turbine Based on Transient Performance. Appl. Sci. 2018, 8, 148. [Google Scholar] [CrossRef]
- Chipperfield, A.; Fleming, P. Gas turbine engine controller design using multi-objective genetic algorithms. IEEE Trans. Ind. Electron. 1995, 43, 214–219. [Google Scholar] [CrossRef]
- Jafari, S.; Montazeri-Gh, M. Invasive Weed Optimization for Turbojet Engine Fuel Controller Gain Tuning. Int. J. Aerosp. Sci. 2013, 2, 138–147. [Google Scholar] [CrossRef]
- Salehi, A.; Montazeri-Gh, M. Hardware-in-the-loop simulation of fuel control actuator of a turboshaft gas turbine engine. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2018. [Google Scholar] [CrossRef]
- Aghasharifian Esfahani, H.; Montazeri-Gh, M. Designing and Optimizing Multi-Objective Turbofan Engine Control Algorithm Using Min-Max Method. Int. J. Comput. Sci. Inf. Secur. 2016, 14, 1040–1050. [Google Scholar]
- Salehi, A.; Montazeri-Gh, M. Black box modelling of a turboshaft gas turbine engine fuel control unit based on neural NARX. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2018. [Google Scholar] [CrossRef]
- Montazeri-Gh, M.; Fashandi, S.A.M.; Jafari, S. Theoretical and experimental study of a micro jet engine start-up behavior. Tehnicki Vjesnik 2018, 25, 839–845. [Google Scholar] [CrossRef]
- Rossi, L.; Sorce, A.; Traverso, A. Gas turbine combined cycle start-up and stress evaluation: A simplified dynamic approach. Appl. Energy 2017, 190, 880–890. [Google Scholar] [CrossRef]
- Jafari, S.; Khalaf, P.; Montazeri-Gh, M. Multi-Objective Meta Heuristic Optimization Algorithm with Multi Criteria Decision Making Strategy for Aero-Engine Controller Design. Int. J. Aerosp. Sci. 2014, 3, 6–17. [Google Scholar] [CrossRef]
- Montazeri-Gh, M.; Jafari, S.; Nasiri, M. Application of Particle Swarm Optimization in Gain Tuning of Integrated Flight and Propulsion Control. Int. J. Aerosp. Sci. 2013, 2, 55–70. [Google Scholar] [CrossRef]
- Zhang, J.; Kang, W.; Li, A.; Yang, L. Integrated flight/propulsion optimal control for DPC aircraft based on the GA-RPS algorithm. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2015, 230, 157–171. [Google Scholar] [CrossRef]
- Montazeri-Gh, M.; Nasiri, M.; Jafari, S. Real-time multi-rate HIL simulation platform for evaluation of a jet engine fuel controller. Simul. Modell. Pract. Theory 2011, 19, 996–1006. [Google Scholar] [CrossRef]
- Martucci, A.; Volponi, A.J. Fuzzy fuel flow selection logic for a real time embedded full authority digital engine control. J. Eng. Gas Turbines Power 2003, 125, 909–916. [Google Scholar] [CrossRef]
- Montazeri-Gh, M.; Yousefpour, H.; Jafari, S. Fuzzy logic computing for design of gas turbine engine fuel control system. In Proceedings of the 2nd IEEE International Conference on Computer and Automation Engineering (ICCAE), Singapore, 26–28 February 2010. [Google Scholar]
- Mohammadi, E.; Montazeri-Gh, M. A fuzzy-based gas turbine fault detection and identification system for full and part-load performance deterioration. Aerosp. Sci. Technol. 2015, 46, 82–93. [Google Scholar] [CrossRef]
- Bazazzadeh, M.; Badihi, H.; Shahriari, A. Gas Turbine Engine Control Design Using Fuzzy Logic and Neural Networks. Int. J. Aerosp. Eng. 2011, 2011, 1–12. [Google Scholar] [CrossRef]
- Mu, J.; Rees, D. Approximate Model Predictive Control for Gas Turbine Engines. In Proceedings of the 2004 American Control Conference, Boston, MA, USA, 30 June–2 July 2004. [Google Scholar]
- Pandey, A.; Oliveira, M. Model Predictive Control for Gas Turbine Engines. In Proceedings of the ASME Turbo Expo 2018: Turbomachinery Technical Conference and Exposition, Oslo, Norway, 11–15 June 2018. [Google Scholar]
- Bonfiglio, A.; Invernizzi, A.; Lanzarotto, D.; Palmieri, A.; Procopio, R. Definition of a sliding mode controller accounting for a reduced order model of gas turbine set. In Proceedings of the 52nd International Universities Power Engineering Conference (UPEC), Heraklion, Greece, 28–31 August 2017. [Google Scholar]
- Yang, S.; Wang, X.; Yang, B. Adaptive sliding mode control for limit protection of aircraft engines. Chin. J. Aeronaut. 2018, 31, 1480–1488. [Google Scholar] [CrossRef]
- Alkhazaleh, S.; Salleh, A.R. Fuzzy Soft Multiset Theory. Abstr. Appl. Anal. 2012, 2012, 350603. [Google Scholar] [CrossRef]
- Salleh, A.R.; Alkhazaleh, S. An application of soft multiset theory in decision making. In Proceedings of the 5th Saudi Science Conference, Makkah, Saudi Arabia, 16–18 April 2012. [Google Scholar]
- Lu, F.; Ye, Y.; Huang, J. Gas Turbine Engine Identification Based on a Bank of Self-Tuning Wiener Models Using Fast Kernel Extreme Learning Machine. Energies 2017, 10, 1363. [Google Scholar] [CrossRef]
- Rideau, J.F.; Guyader, G.; Cloarec, A. MICROTURBO Families of Turbojet Engine for Missiles and UAV’s From the TR60 to the new bypass turbojet engine generation. In Proceedings of the 44th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Hartford, CT, USA, 21–23 July 2008. [Google Scholar]
- Microturbo TRI 40/TRI 60 (2008); The Market for Missile/Drone/UAV Gas Turbine Engines; Forecast International: Newtown, CT, USA, 2009.
- Adibhatla, S. Propulsion control law design for the NASA STOVL controls technology program. In Proceedings of the AIAA International Powered Lift Conference, Santa Clara, CA, USA, 13–15 November 1993. [Google Scholar]
- Adibhatla, S.; Cooper, P.; Pajakiwski, A.; Romine, B.; Virnig, J.; Bodden, D. STOVL Controls Technology, Vol. I Integrated Flight/Propulsion Control Design. NASA Contractor Report 195361; NASA: New York, NY, USA, 1994. [Google Scholar]
- Dadd, G.J.; Sutton, A.E.; Greig, A.W.M. Multivariable control of military engines. In Proceedings of the Advanced Aero-Engine Concepts and Controls, Defense Research Agency, Farnborough, England, AGARD Presentation, Seattle, WA, USA, 1995. [Google Scholar]
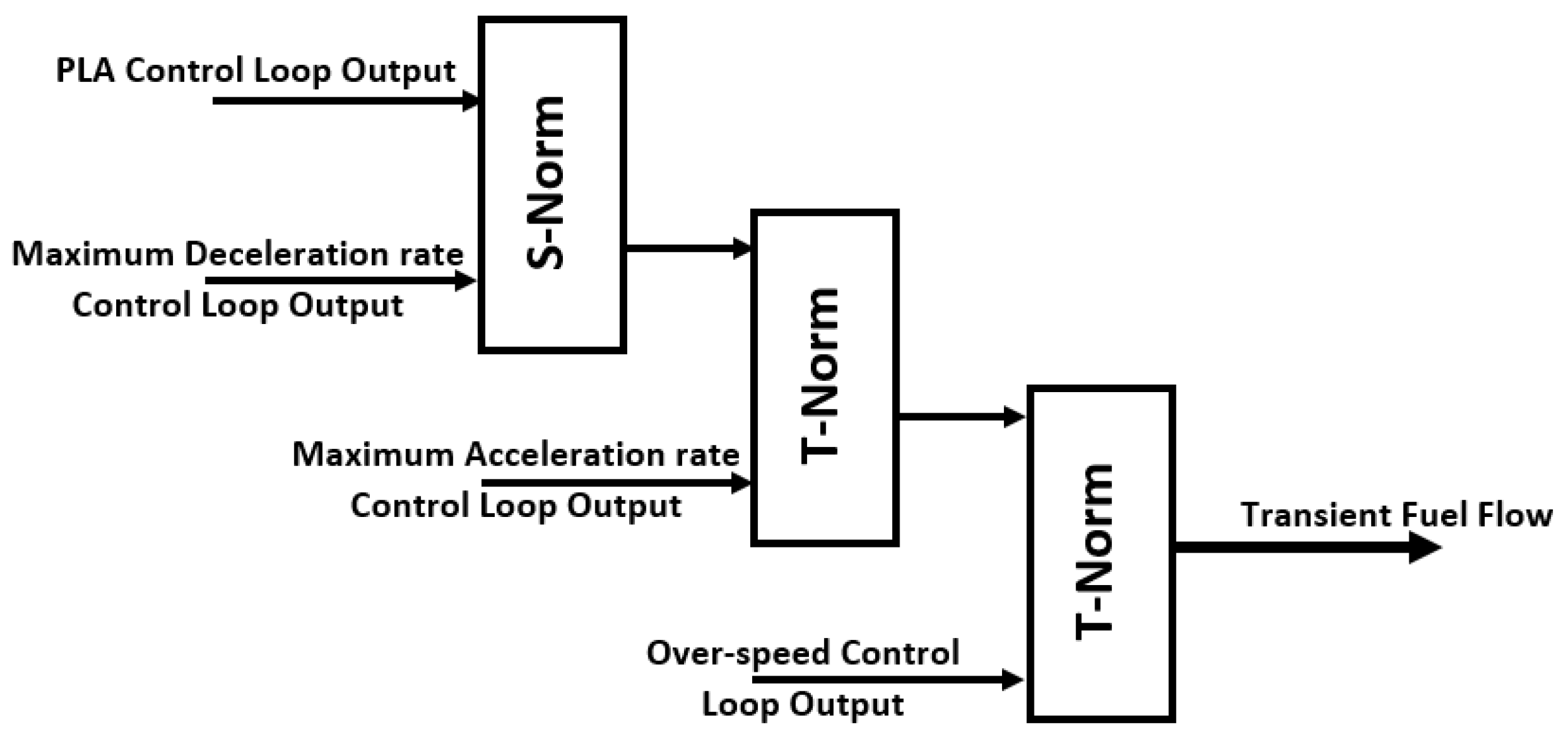

| Norms | Title | Formulation |
|---|---|---|
| t1 s1 | Bounded difference Bounded sum | t1(A,B) = max (0, A + B − 1) s1(A,B) = min (1, A + B) |
| t2 s2 | Einstein product Einstein sum | t2(A,B) = (AB/(2 − [ A + B − AB]) s2(A,B) = (A + B)/(1 + AB) |
| t3 s3 | Algebraic product Probabilistic sum | t3(A,B) = AB s3(A,B) = A + B − AB |
| t4 s4 | Hamacher product Hamacher sum | t4(A,B) = (AB)/(A + B − AB) s4(A,B) = (A + B − 2AB)/(1 − AB) |
| t5 s5 | Minimum Maximum | t5(A,B) = min (A,B) s5(A,B) = max (A,B) |
| Characteristics | Value |
|---|---|
| Type | Single Spool Turbojet |
| Length | 851 mm (33.5 in) |
| Diameter | 348 mm (13.7 in) |
| Dry weight | 61.2 kg (135 lb) |
| Compressor | 4 stage axial |
| Combustors | Annular |
| Turbine | Single Stage |
| Maximum thrust | 5.33 kN (1200 lbf) |
| Overall Pressure Ratio | 6.3:1 |
| Air mass flow | 8.14 kg/s (17.94 lb/s) |
| Specific fuel consumption: | 1.1 kg/(daN h) (1.03 lb/(lbf h)) |
| Maximum rotational Speed | 29,700 rpm |
| Thrust-to-weight ratio | 8.9:1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jafari, S.; Nikolaidis, T. Turbojet Engine Industrial Min–Max Controller Performance Improvement Using Fuzzy Norms. Electronics 2018, 7, 314. https://doi.org/10.3390/electronics7110314
Jafari S, Nikolaidis T. Turbojet Engine Industrial Min–Max Controller Performance Improvement Using Fuzzy Norms. Electronics. 2018; 7(11):314. https://doi.org/10.3390/electronics7110314
Chicago/Turabian StyleJafari, Soheil, and Theoklis Nikolaidis. 2018. "Turbojet Engine Industrial Min–Max Controller Performance Improvement Using Fuzzy Norms" Electronics 7, no. 11: 314. https://doi.org/10.3390/electronics7110314
APA StyleJafari, S., & Nikolaidis, T. (2018). Turbojet Engine Industrial Min–Max Controller Performance Improvement Using Fuzzy Norms. Electronics, 7(11), 314. https://doi.org/10.3390/electronics7110314






